- Faculty of Mathematics and Sciences, Institute of Earth Sciences, Hebrew University of Jerusalem, Jerusalem, Israel
Large landslides exhibit surprisingly long runout distances compared to a rigid body sliding from the same slope, and the mechanism of this phenomena has been studied for decades. This paper shows that the observed long runouts can be explained quite simply via a granular pile flowing downhill, while collapsing and spreading, without the need for frictional weakening that has traditionally been suggested to cause long runouts. Kinematics of the granular flow is divided into center of mass motion and spreading due to flattening of the flowing mass. We solve the center of mass motion analytically based on a frictional law valid for granular flow, and find that center of mass runout is similar to that of a rigid body. Based on the shape of deposits observed in experiments with collapsing granular columns and numerical simulations of landslides, we derive a spreading length . Spreading of a granular pile, leading to a deposit angle much lower than the angle of repose or the dynamic friction angle, is shown to be an important, often dominating, contribution to the total runout distance. The combination of the predicted center of mass runout and the spreading length gives the runout distance in a very good match to natural landslides.
1. Introduction
Landslides are natural hazards responsible for serious damage to life and property. Understanding their flow would allow us to predict their runout (horizontal travel distance), estimate their energy and reduce the associated risk. From the mechanical point of view, landslides are granular mass flowing down a hill slope and on a flat plane while spreading due to internal shear. However, the mechanical problem of evolution of a granular flow in the configuration depicted in Figure 1 have not been fully solved yet. In this paper, we give an analytical solution for the case when the slide can be modeled as a granular flow driven by gravity and mechanical interaction between grains. We predict the runout distance L and compare the prediction to natural landslides.
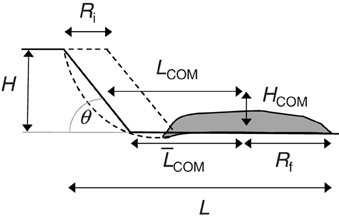
Figure 1. Geometry of the landslide model. The dashed line identifies the region of the original slope that was removed by the landslide. The shaded area is the final deposit of the landslide. Calculation of the total runout L is divided in two sub-problems: (a) the center-of-mass runout LCOM and (b) the initial and final spreads Ri and Rf. LCOM is derived from an analytical solution for granular flow of constant thickness on an inclined plane. Spreading of the landslide due to its flattening is included in the calculation of Rf.
Runout of landslides has attracted a lot of scientific interest. The most debated puzzle has been the “long runout landslides" problem: large landslides exhibit a surprisingly long runout that seems to violate common frictional behavior. For a rigid block of rock to travel the same distance as large landslides would require friction coefficient as low as 0.1, i.e., a small value compared to common friction coefficient of rocks ≃ 0.4–0.7 observed in laboratory scale experiments if no plastic processes operate.
The energy conservation for a rigid body sliding with constant friction coefficient μC yields [1] ρgHCOM = μCρgLCOM, or
where HCOM and LCOM are drop height and runout of the center of mass (COM), as shown in Figure 1. For the same reason, Heim's ratio H∕L (a.k.a apparent friction) is used as a proxy for friction coefficient of landslides. For ease of field measurements, H and L are the maximum drop height and runout (see Figure 1). Figure 2A shows Heim's ratio as a function of landslide volume, V, taken from Lucas et al. [2]. The data includes field data from literature and digital topography models using photogrammetry. Two surprising observations emerge: (a) Heim's ratio is not a constant like for the rigid block with constant friction coefficient, but decreases with landslide volume, and (b) the minimum value observed for largest landslides is as low as H∕L ≈ 0.1, i.e., considerably lower than friction coefficient of common rocks or soils. In other words, larger landslides achieve longer runouts on falling from a hill slope with given height. While field data is usually plotted in terms of Heim's ratio, the best collapse of data is achieved when plotting simply L as a function of V, as shown in Figure 2B. Legros [3] concludes that landslide spreading is essentially controlled by their volume, and not by H.
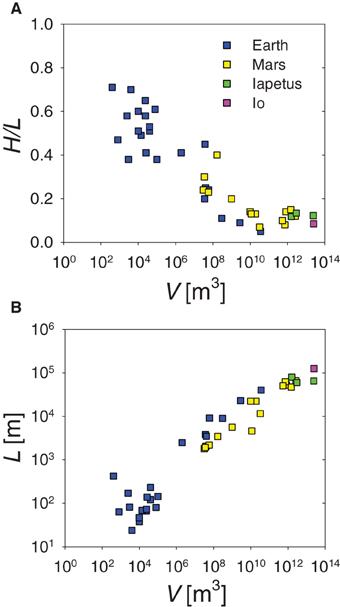
Figure 2. (A) Heim's ratio H∕L for a collection of landslides from the Earth (g = 9.81 ms−2), Mars (g = 3.73 ms−2), Iapetus (g = 0.223 ms−2), and Io (g = 1.796 ms−2), taken from Lucas et al. [2]. Note that Heim's ratio decreases with landslide volume to a value as low as ≈ 0.1, i.e., considerably lower than friction coefficient of common rocks or soils. (B) Runout as a function of landslide volume for the same collection of landslides.
Several processes have been suggested to solve the long runout puzzle, e.g. frictional heating of pore fluids [4, 5], fluidization [8–11], or plastic deformation due to melting of grains [6, 7] and flash weakening [2, 4]. Here, we study a purely mechanical problem of granular flow under a gravitational field. In that case, two processes might account for the long runout of landslides relative to rigid block sliding: (a) the friction decreases considerably with volume, e.g., due to changes in shear rate, and/or (b) spreading of grains relative to COM is larger for larger landslides.
Our knowledge about granular flows mostly comes from laboratory scale experiments and computer simulations. As a result, three flow regimes were classified [12]: “solid” in which grains interact via long-lasting frictional contacts and deform slowly, “gaseous” in which grains interact through short collisions compared to deformation time scale, and “liquid” which is a transition between the two previous. For flow down a slope, the three regimes can be attained by changing the slope angle θ [13, 14]. If θ is small, no flow is observed, only an elastic deformation. Once θ exceeds the angle of repose, the flow accelerates. Yet, the increasing rate of collisions eventually leads to a steady flow. If, however, the slope is steep enough the flow keeps accelerating because the energy that grains receive during free fall between collisions exceeds the dissipation. We can expect that most of landslides flow in the liquid regime, in which flow is possible yet not too vigorous, because they occur when a slope becomes unstable, i.e., close to the angle of repose.
Evolution of granular flows in the liquid regime has been solved only approximately using “shallow water models” or by means of computer simulations. Neither of the approaches has established scaling laws for runout distance with volume. “Shallow water models” arise from depth-averaged mass and momentum conservation equations, originally derived by Savage and Hutter [15]. The resulting equation for mean velocity neglects spatial variation of velocity inside the moving body. Hence, the shallow water model is less accurate if shear rate is large. Flow down a slope was studied by Savage and Hutter [15], Pouliquen and Forterre [16], Mangeney et al. [17], Faccanoni and Mangeney [18] and Capart and Hung [19], including analytical solutions for evolution of velocity, front position and thickness. Those studies do not address cessation of the flow, or prediction of runout or Heim's ratio. The later was done by Lucas et al. [2] within a semi-empirical model. They showed that Heim's ratio based on the analytical solution of Mangeney et al. [17] and Faccanoni and Mangeney [18] is compatible with field data if the value of basal friction coefficient is adjusted appropriately. However, the optimal value is significantly lower than that obtained from laboratory experiments.
An alternative to analytical models is granular dynamics simulations. Campbell et al. [20] carried out large scale discrete simulations, which showed Heim's ratio as a function of volume similar to field data. Staron and Lajeunesse [21] suggest that the volumetric effect is dominated by spreading of the granular mass relative to COM, while Heim's ratio for COM, HCOM∕LCOM is volume independent. Yet, no quantitative estimation of the two contributions (COM runout and spreading length) has been given.
Experiments and simulations regarding flow on an inclined plane revealed scaling of steady flow velocity with flow thickness h as ~h3∕2 [13, 14, 22, 23]. Later, this scaling was explained by dimensional analysis for friction coefficient [12, 23]. This opens a possibility that larger (thicker) slides achieve larger kinetic energy, which would result in longer runouts. However, unsteady flows, i.e., acceleration and deceleration and flow with varying thickness, have not been studied enough yet. In particular, the time scale over which landslide accelerate has not been derived. Consequently, it is not clear whether or how kinetic energy depends on landslide volume.
Another class of experiments is collapse of granular columns on a flat surface. A granular column that is initially supported by walls is suddenly released and spreads. Lajeunesse et al. [24] showed that the spread of the deposit is controlled by aspect ratio of the initial column, and that the slope angle at the foot of the deposit saturates at 5° (much lower than the angle of repose) for columns with large aspect ratios. Similar results were obtained in experiments by Lube et al. [25] and simulations by Utili et al. [26]. Granular column collapse experiments shed light on the role of spreading of landslide mass relative to COM. During their flow, landslides change their shape. They become thinner and spread along fronts and flanks as surface grains fall down or are squeezed out. As a consequence, total runout might be considerably larger than that due to COM.
In this work, we study kinematics of granular materials flowing down an inclined plane and decelerating on a flat plane thereafter. We solve the runout distance in two steps. First, we derive COM runout based on an analytical solution for velocity profile in granular flow of constant thickness. The prediction is compared to numerical simulations. Second, we account for the longitudinal spreading of the collapsing body. Finally, we compare the resulting runout to field data for natural landslides.
2. Methods
2.1. Simulations
The numerical simulations were used as a benchmark for analytical calculation of COM evolution. They employ the discrete element method (DEM) [27], in which the Newtonian equations of motion for a set of grains are solved in discrete steps.
Grains are modeled as disks with rotational and translational degrees of freedom. They interact via visco-elastic contact forces according to Hertz-Mindlin contact model [28, 29]
where and are normal and shear components of the contact force between grains i and j. Rij is the harmonic mean of the grains radii and ξij is the overlap between the two grains. Elastic moduli E = 1.31 × 1010 Pa and Poisson's ratio η = 0.235 were chosen to simulate quartz grains with density . Energy dissipation is governed by a normal damping (the second term in ) with damping coefficient γ = 0.8 and by the tangential friction . Restitution coefficient is not constant, but depends on velocities of colliding grains [28]. The tangential force is initially elastic, calculated from shear displacement Δs on contacts of the grains from the instant the contact was formed. Once the spring force exceeds the Coulomb friction criterion, the contact starts sliding with a constant shear force, , where the grain-grain friction coefficient is μgg = 0.5. Note that the grain-grain friction coefficient is not the same as the macroscopic dynamic friction coefficient, which is investigated below and found shear rate dependent.
Grain diameters were randomly drawn from a Gaussian distribution with both mean value and standard deviation equal to d. The distribution is however cut, so that all diameters fall within 0.8–1.2 d.
Periodic boundary conditions were applied in the direction of the flow, which is equivalent to constant thickness flow boundary condition used in the theory described below. The width of the simulation box along the flow direction was 96d (no size effects due to this scale were observed), while thickness of the flow varied among different simulations between h = 12−96d to test the volumetric scaling.
Equations of motion were integrated using the velocity Verlet algorithm [30] with a time step small enough to resolve elastic waves due to grain-grain collisions.
Granular systems are initiated as layers with random loose packing, standing on a flat horizontal surface made of grains with the same properties that are glued together and whose positions are fixed. Subject to vertical gravitational acceleration the grains sediment. Then we turn the slope at an inclination angle θ = 17−25°. The selected range can accommodate steady flows, see Silbert et al. [13] and Pouliquen [14] for a phase diagram of flow regimes. For lower inclination angles no flow is initiated, while larger inclination angles lead to unstable acceleration and breakdown of the “liquid” flow regime.
Velocity and density profiles were monitored during the run of simulations. The distance traveled by a landslide was calculated as a running integral of COM velocity. Once the traveled distance reached the length of the slope available for COM sliding, HCOM∕sin θ, for given HCOM and θ, the simulation was continued for θ = 0, i.e., on the flat plane, until the COM velocity decayed to zero.
2.2. Theory
In this section, we solve kinematics of granular flow in the geometry depicted in Figure 1 in order to obtain flow profiles and predict COM motion. For the derivation to be analytically tractable, we impose that thickness of the flow is constant and uniform. Driven by gravity, landslides preferentially spread along the slope direction rather than laterally. As a consequence, the flow is essentially two-dimensional with an elongated central homogeneous region. Assuming that this homogeneous region dominates the overall landslide momentum, its velocity average represents the COM velocity.
The longitudinal spreading reduces landslide's thickness, which is therefore not constant in time. It will be shown below that the COM runout does not vary significantly with thickness. Therefore, the prediction derived for the flow of constant thickness provides a good estimate for a general flow with an extensive homogeneous region.
The equation of motion for a two-dimensional flow of constant thickness is
where y is depth inside the flow measured from the top surface, t is time, v(y, t) is velocity along the flow direction, τ(y, t) is shear stress, g is gravitational acceleration and ρ is flow mass density (of a representative volume). The first term on the right hand side is the gravitational force, the second term is friction force that resists acceleration. ρ is considered uniform [13] and constant (a very week dependence on flow velocity has been found [12, 23, 31]).
To form a closed set of equations we need another relation between τ and v, i.e., a rheological law. Friction is known from physics and geophysics to depend on sliding velocity. The only local dimensionless quantity for dry granular flow that dissipates energy through visco-elastic collisions is the so-called inertial number I
where is shear rate (the negative sign is because y axis is pointing downwards), N(y, t) is normal stress, d is grain size and ρp is mass density of the grain material (2.5 × 103kgm−3 for sand). The friction coefficient μ (also dimensionless) can then be expressed as an expansion in I. The linearized version of the friction law is
where μ0 and β are material parameters (μ0 ≈ 0.55 and β ≈ 0.5 for sand [23]). This type of rheology, in which μ is a function of I, has been suggested and verified in laboratory experiments and simulations [12, 16, 23, 31] for variety of systems and boundary conditions. Since β has been found positive, friction increases with shear rate under constant normal stress, provided plastic processes are negligible.
The observed uniform and constant density ρ implies constant and linear normal stress N = ρg cos θy. This gives shear stress
where ν ≡ ρ∕ρp ≈ 0.55 is solid fraction [13]. The first term in Equation (6) is rate independent, and controls the flow under low shear rate. Neglecting the other term would, according to Equation (3), lead to uniform acceleration g(sin θ − μ0cos θ). The second term accounts for increase of friction with shear rate. As a result, flow becomes steady once the friction force balances the driving force.
We seek a solution of Equations (3) and (6) along with boundary conditions
where h is flow thickness. The boundary conditions say that: (a) the top surface of the slide is free of stresses, (b) the velocity at the bottom of the sliding mass is zero (the ground surface is rough), and (c) the initial velocity is v0.
The solution for velocity satisfying boundary conditions Equations (7a,b) is [Parez et al., under review]
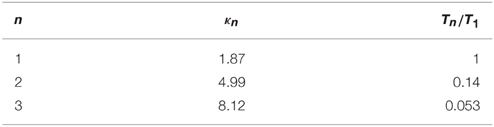
in which J2∕3(z) is a Bessel function of the first kind [32], constants κn are given in Table 1 for a few n and
The coefficients bn in the expansion are determined from the initial condition Equation (7c) using the orthogonality relation [32] .
Note that the solution Equation (8) is different depending whether θ is greater or lower than angle of repose θr (≈ 30° for sand). The first applies for acceleration down a slope while the latter for deceleration on the flat plane.
2.2.1. Acceleration Down a Slope
The down-slope flow starts when θ > θr. In that case, Equation (8) predicts acceleration toward a steady velocity given by the vp term, which is consistent with the Bagnold flow profile [13, 22]. The second term is the transient toward the steady velocity. Because T1 is sufficiently larger than the other Tn's (see Table 1), it dominates the time evolution after the very initial period. Keeping only the T1≡T term (we drop the subscript in the following) and imposing v0 = 0, velocity can be approximated as
Note that T has the meaning of the acceleration duration scale.
The COM velocity is calculated as the depth averaged velocity
The time ts the landslide's COM takes to reach the bottom of the slope is set by the length of the slope HCOM∕sin θ available to COM sliding
This time determines the velocity vs(y) = v(y, ts) and kinetic energy per unit mass reached at the bottom of the slope. We can calculate their values analytically for the following two limiting cases. If ts > > T, i.e., if the slide reaches a steady flow on the slope,
On the other hand, if ts < < T, i.e., the time to reach a steady flow is much larger than the time actually spent on the slope, then Equation (12) can be simplified as and we get
Note that kinetic energy per unit mass (and the same can be shown for COM velocity and other kinematic properties) reached at the bottom of the slope does not depend on thickness h (or volume) of the slide if ts < < T. This is in agreement with Campbell's et al. large scale simulations, see Figure 9 in Campbell et al. [20].
The origin of the independence of flow properties on slide thickness for ts < < T can be seen from the Taylor expansion of flow velocity Equation (11). Since both steady flow velocity and transient time T (see Equation 8) grow proportionally to ~h3∕2, the average flow acceleration vCOM(t → ∞)∕T is independent of thickness. Therefore, all slides satisfying ts < < T have the same evolution and reach the same depth-averaged properties (vCOM, ) at the slope end.
We have seen that acceleration of the landslide's COM is determined by relative magnitudes of ts and T. Since T is controlled by h, we can redefine this relation in terms of thickness. Using Equations (8) and (12) we can define a threshold thickness hthr for which ts = T
Hence, flow down a slope of length H∕sin θ is thickness-independent for slides with h > hthr, corresponding to the case ts < T.
2.2.2. Deceleration on a Flat Plane
Once a slide reaches the flat plane it decelerates, because no driving force acts in the direction of motion. The evolution of velocity during deceleration is predicted by Equation (8) with θ = 0 and , where . The initial velocity is chosen to match the final velocity on the slope, . Neglecting higher order terms than , velocity becomes
where the transient time is related to T derived for the acceleration on the slope inclined at θ as .
Once the velocity at given depth decays to zero, the layer becomes locked due to static friction and v = 0 thereafter. This happens at time tf(y), given by
The distance that COM of the slide travels on the flat plane is
While we can solve Equations (17) and (18) numerically, we can easily evaluate the maximum possible runout distance by assuming that friction has its minimum value μ0. In that case, velocity decreases with a constant and uniform rate, v(y, t) = vs(y) − μ0g(t − ts), resulting in the breaking distance
Hence, is proportional to kinetic energy per unit mass reached at the bottom of the slope, which ranges between the limiting values given by Equations (13) and (14).
2.2.3. COM Runout and Heim's Ratio
The COM runout is the total horizontal distance traveled by COM of a slide . Depending on relative magnitudes of h and hthr, the runout varies between the following two values
where we used Equations (19), (13), (14), and (15). Corresponding limiting values of Heim's ratio are
Note that tanθ > μ0 because the mass starts moving on a slope exceeding the effective friction angle arctan(μ0). Assuming θ = 30°−40°, Heim's ratio decreases from tanθ = 0.58−0.84 for small slides to μ0 = 0.55 for large slides. This range of values cannot explain the span observed for field data (see Figure 2), particularly the limiting value ≈ 0.1.
2.2.4. Spreading
Landslides change their shape during their flow. They become thinner while they spread along their perimeter, as grains on the surface fall down or are squeezed outwards. As a result, the horizontal extent of landslides, denoted as spread, changes. In this section, we estimate the spread of the final deposit based on the experiment by Lajeunesse et al. [24] and full landslide computer simulations by Campbell et al. [20].
Lajeunesse et al. performed experiments with granular columns that were suddenly released onto a flat plane and allowed to spread. The shape of the final deposit was conical with foot angle α depending on the aspect ratio a of the initial column. α decreased from angle of repose for a → 0 to a saturated value of for a > 3. The core of the conical deposit with base area identical to the original column was almost undisturbed. Grain size and ground surface had a little effect on the spread.
Similar results were found by Campbell et al. for slides flowing down a slope in the same geometry as here (see Figure 1). The shape of final deposits was conical with foot angle independent of slide volume for large slides. The order of strata inside the slide was preserved as in the initial state.
Note that in both experiments the angle of the deposited pile is much lower than the angle of repose (≈ 30°) if enough energy is provided for spreading.
Based on these results we might assume that natural landslides spread conically from their surface while the central region flows undisturbed, i.e., approximately described by Equation (11). We suggest that the foot angle is not a function of the initial aspect ratio, but more generally of energy per unit mass since it directly controls spreading even when the aspect ratio is low.
Assuming that deposits of large, long runout landslides studied here attain the threshold value αthr, volume V of their deposit is , where Rf is the spread of the deposit, i.e., radius of the cone base. Inversely, the spread depends on the landslide volume as
Deposits of natural landslides are not always conical. Sometimes, they are piled against the foot of the hill, or they are constrained by the landscape morphology. Yet, it is reasonable to expect that these constraints only change the pre-factor in Equation (22) while the V1∕3 scaling is still valid.
3. Results
3.1. COM Evolution
Figure 3 shows COM velocity evolution for landslides of different thickness. The quality of analytical prediction, Equation (11) (dashed lines), is tested against DEM simulations (solid lines) for θ = 17°, d = 0.1m and g = 9.81ms−2. The slight difference between the two sets of curves is due to non-zero slip velocity observed in simulations. Note that larger landslides reach larger final steady flow velocity, but in progressively longer time.
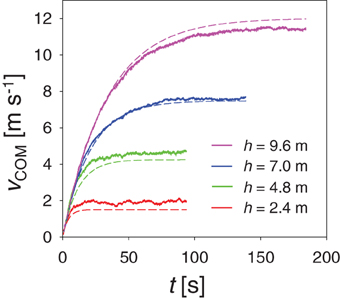
Figure 3. Center of mass velocity during acceleration down a slope for landslides of thickness h = 2.4 − 9.6 m. Simulation results (solid lines) are compared to analytical prediction (dashed lines) after Equation (11). Note that larger landslides reach larger steady flow velocity. However, it takes them correspondingly longer time.
On reaching the flat plane, landslides decelerate. In Figure 4, the decay of velocity profile is shown. The two sets of lines are simulation (solid lines) and analytical (Equation 16, dashed lines) results for h = 9.6m, θ = 17°, d = 0.1m, and g = 9.81ms−2. Since deep layers have lower velocity compared to the top of the landslide, they stop first. Consequently, the flow is confined to a gradually thinner layer near the top surface. The simulation profiles show a formation of a creeping layer at the depth where the flow stops. This is a non-local effect described in Kamrin et al. [33].
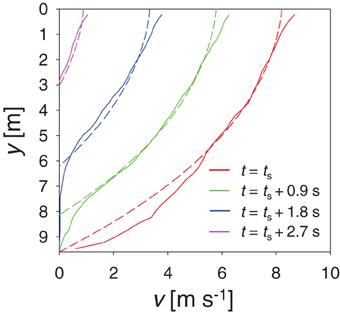
Figure 4. Velocity profiles at various time instants during deceleration of the h = 9.6 m thick slide on a flat plane. Simulation results (solid lines) are compared to the analytical prediction (dashed lines) after Equation (16). The flow depth is gradually reduced.
During the flow on the flat plane, landslides dissipate the kinetic energy achieved on the slope. Figure 5 shows how the kinetic energy is transformed into the distance reached on the flat plane, . Points denote simulation results, in which the kinetic energy was varied by changing HCOM, θ, h, d, or g. The line denotes the analytical prediction, Equation (19), derived for constant friction coefficient μ0. For low kinetic energies, the simulation data follow the analytic solution. With increasing kinetic energy, shear rate increases, and, according to Equation (5), friction also increases. As a consequence, the resulting runout is lower than predicted by Equation (19).
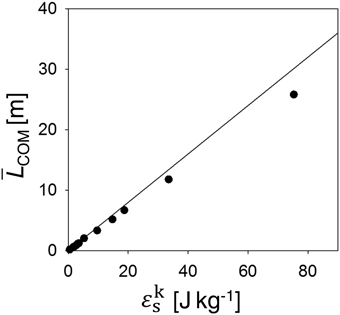
Figure 5. Center of mass runout on the flat plane as a function of the kinetic energy achieved on the slope. Simulation results (points) were obtained for various slope lengths H∕sin θ = 10−100 m and landslide thicknesses h = 1.2−9.6 m. The line denotes Equation (19), i.e., a deceleration distance derived for rate independent friction coefficient μ0.
3.2. Runout and Heim's Ratio
To calculate total runout we have to sum up the horizontal extent of the initial mass, COM runout and the spread of the final deposit (see Figure 1)
The initial extent can be estimated as Ri = (H−HCOM)∕tanθ. As shown in Equation (20), LCOM attains values between HCOM∕tanθ (thin slides relative to hthr) and HCOM∕μ0 (thick slides relative to hthr). Since for typical slopes (θ = 30°−40°) tanθ = 0.58−0.84 is comparable to μ0 = 0.55, we can approximate Ri + LCOM ≈ (H−HCOM)∕μ0 + HCOM∕μ0 = H∕μ0. Adding Rf from Equation (22) we arrive at
Note that the first term is identical to runout that would be achieved by COM of a rigid block sliding from height H with friction μ0. Runout of landslides is predicted to be longer by the spread length given by the second term.
In Figure 6, runout predicted from Equation (24) is compared to field observations. The field data (squares) is taken from Lucas et al. [2], and include values of H, L, and V for largest landslides observed in different planetary bodies. Circles denote the prediction of Equation (24) using the measured values of H and V for each landslide. The prediction matches the field observations over the whole range spanning 11 orders of magnitude.
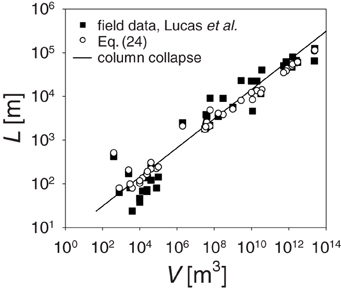
Figure 6. Runout as a function of landslide volume. Full squares are field observations taken from [2]. Open circles denote Equation (24), in which H and V are taken from the same field observations and . Solid line is 2Rf(V) (see Equation 22), i.e., a total spread of a deposit resulting from a granular column collapse.
The solid line in Figure 6 is 2Rf(V), i.e., as if L was equal to spread of a deposit resulting from a granular column collapse onto a horizontal surface. In the calculation of Rf from Equation (22), was used, based on the shape of deposits reported in Campbell et al. [20]. Since the 2Rf line fits the circles, calculated as H∕μ0 + Rf, the two terms in Equation (24) are comparable. Thus, spreading of grains makes the toe of a landslide separated from the COM by a same-order distance as COM is separated from the head of the scarp left from the landslide on the hill. In other words, the runout is a few times longer than that of a rigid block sliding from the same height, i.e., ≃ H∕μ0.
The fact that both terms of Equation (24) are of the same order of magnitude can be viewed as a relation between H and V1∕3. A closer examination of field data reveals that H = 1.5V1∕3 for landslides with V < 105 (for larger landslides the power is lower than 1∕3). In other words, landslide linear dimension V1∕3 is comparable to the fall height H. This allows the following interpretation: Long runout landslides are likely to remove mass along an entire slope from the top at elevation H down to the valley at elevation 0, as sketched in Figure 1, i.e., not only the top of the slope as often assumed in simulation works. Furthermore, the relation H~V1∕3 implies, using Equation (24), L~V1∕3, which was found empirically in previous works [2, 3, 21].
Finally, Figure 7 shows Heim's ratio H∕L. The field observations (squares) are compared to the prediction based on Equation (24) (circles) for the values of H and V observed for the same collection of landslides. Despite the general agreement, predicted values are systematically lower for landslide with V < 106m3. This might be because (a) relatively small landslides did not spread enough to achieve the minimum foot angle αthr of their deposits and thus their spread is overestimated, or (b) the approximations leading to the term H∕μ0, i.e., exchanging μ0 and tanθ, are too crude.
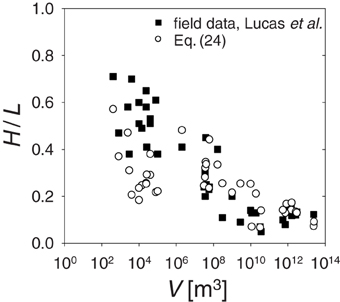
Figure 7. Heim's ratio as a function of landslide volume. Full squares are field observations taken from Lucas et al. [2]. Open circles are prediction based on Equation (24), in which H and V are taken from the same field observations and .
4. Discussion
Large landslides (V > 108) exhibit low Heim's ratio and corresponding long runout distance compared to sliding of a rigid body. This has traditionally been ascribed to processes that decrease friction coefficient (friction weakening), such as shear heating, flash weakening or fluidization [4–11]. These concepts require plastic processes or presence of pressurized pore fluids to reduce the frictional resistance, and achieve higher velocity and longer runout.
Natural landslides are likely subject to various processes that contribute to their runout distance. In this work, we study kinematics of granular flow, considering only granular mechanics. Yet, this simplest model, which does not require presence of fluids or rapid shearing, is consistent with field observations. In addition, many landslides are dry, and do not show evidence for rapid shearing or large scale melting of grains [34]. Deposits of many large landslides consist of sharp edged boulders of a similar size as in the original deposit, indicating granular flow rather than melting and plastic deformation.
Kinematics of landslides can be divided into COM motion and spreading relative to COM as the granular mass collapses. Analytical derivation, compared against DEM simulation, showed that the COM runout is nearly volume independent, and equal to H∕μ0 for large slides. Therefore, (a) increase of steady state velocity with landslide thickness, (see Equation 8), cannot explain increase of COM runout, and (b) a common friction coefficient μ0 ≈ 0.55 is too large to achieve Heim's ratio of 0.1. In previous works [2, 5–11, 20], long runout landslides have been explained by reduction in friction coefficient μ0, so that COM runout H∕μ0 is longer (and Heim's ratio is lower).
In contrast, the spreading length has not been quantified yet. Based on experiments with collapsing granular columns and computer simulations of landslides, we suggest that the spread of a landslide deposit is given by Equation (22), i.e., the radius of a shallow angle cone with volume identical to that of the landslide. Using the field observations of H and V for long runout landslides, the spreading length turns out to be the same order of magnitude as the COM runout, often being the dominant contribution. As a results, the calculated Heim's ratio drops to values as low as ≈ 0.1, in line with field observation, without the need for a reduced friction coefficient. In addition, the volumetric dependence of the spreading length accounts for the empirical scaling of landslide runout with volume L~V1∕3 [2, 3, 21].
While the long runout of large landslides can result from both friction weakening and spreading of granular mass, we can distinguish between the two mechanisms based on landslide velocity. The drop in friction coefficient leads to enhanced COM velocity, which is eventually transformed into long runout distance. On the other hand, spreading of grains takes place roughly evenly in all directions and does not affect the COM velocity. Therefore, we can compare maximum COM velocity of an actual landslide to the prediction assuming no friction reduction, i.e., Equation (11) at t = ts taken from Equation (12). Within the approximation ts < < T (large landslides typically do not reach steady flow) the predicted velocity is
If the observed maximum velocity of a landslide is larger than Equation (25), friction weakening operates. For example, for a slope with H = 100m and θ = 35° frictional weakening processes would lead to velocity exceeding 18ms−1.
The prediction of landslide spread is derived for conical deposits with a shallow, volume independent, foot angle αthr. Existence of such angle was observed in column collapse experiments, where deposits have self-similar shapes regardless of their volume for large enough aspect ratios of the original column. Why this angle saturates or what physical parameters control it if granular mass is collapsed on an inclined plane has not been investigated yet.
The present analytical solution might facilitate development of natural hazard assessment, and may be extended in the future to explore granular flows in different configurations and different rheologies. The model might be applied to study shaking of ground during earthquakes, liquefaction [29] or granular avalanches, e.g., those found to shape dunes on different planetary bodies [35].
5. Conclusions
Large landslides exhibit long runouts, exceeding several times the distance that would be achieved by a rigid block sliding from the same height. This has been traditionally explained by processes leading to frictional weakening, i.e., reduction of frictional resistance resulting in high velocity and long runout. We show that correct runout distance can be achieved by accounting for spreading of landslide mass without assuming any frictional weakening processes. Kinematics of a landslide can be divided into center of mass motion and spreading of the collapsing mass. We derive the center of mass motion analytically based on a frictional law valid for flow of dry granular materials, without frictional weakening. The resulting center of mass runout approaches H∕μ0, where H is the fall height and μ0 is friction coefficient, similarly to rigid block sliding. Maximum center of mass velocity is , where θ is the slope angle. If a landslide reach higher velocity, friction weakening processes are likely to operate. The distance between the toe of a landslide and its COM is due to spreading associated with flattening of the flowing mass. The spreading distance grows with landslide volume as , where αthr is the foot angle of the deposit. The spreading distance might exceed the center of mass runout several times, and thus allows for the long runouts observed for large natural landslides.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
We acknowledge fruitful discussions with R. Toussaint. The research leading to these results has received funding from the People Programme (Marie Curie Actions) of the European Union's Seventh Framework Programme FP7/2007-2013/ under REA grant agreement No. 316889.
Supplementary Material
The Supplementary Material for this article can be found online at: http://journal.frontiersin.org/article/10.3389/fphy.2015.00080
References
1. Dade, WB, and Huppert, HE. Long-runout rockfalls. Geology (1998) 26:803–6. doi: 10.1130/0091-7613(1998)026<0803:LRR>2.3.CO;2
2. Lucas, A, Mangeney, A, and Ampuero, JP. Frictional velocity-weakening in landslides on earth and on other planetary bodies. Nat Commun. (2014) 5:3417. doi: 10.1038/ncomms4417
3. Legros, F. The mobility of long-runout landslides. Eng Geol. (2002) 63:301–31. doi: 10.1016/S0013-7952(01)00090-4
4. Rice, JR. Heating and weakening of faults during earthquake slip. J Geophys Res. (2006) 111:B05311. doi: 10.1029/2005JB004006
5. Goren, L, and Aharonov, E. Long runout landslides: the role of frictional heating and hydraulic diffusivity. Geophys Res Lett. (2007) 34:L07301. doi: 10.1029/2006GL028895
7. Erismann, TH. Flowing, rolling, bouncing, sliding: synopsis of basic mechanisms. Acta Mech. (1986) 64:101–10. doi: 10.1007/BF01180101
8. Wang, FW, Sassa, K, and Wang, G. Mechanism of a long-runout landslide triggered by the august 1998 heavy rainfall in fukushima prefecture, japan. Eng Geol. (2002) 63:169–85. doi: 10.1016/S0013-7952(01)00080-1
9. Wang, G, and Sassa, K. Pore-pressure generation and movement of rainfall-induced landslides: effects of grain size and fine-particle content. Eng Geol. (2003) 69:109–25. doi: 10.1016/S0013-7952(02)00268-5
10. Okura, Y, Kitahara, H, Ochiai, H, Sammori, T, and Kawanami, A. Landslide fluidization process by flume experiments. Eng Geol. (2002) 65:65–78. doi: 10.1016/S0013-7952(02)00032-7
11. Melosh, HJ. The physics of very large landslides. Acta Mech. (1986) 64:89–99. doi: 10.1007/BF01180100
12. Forterre, Y, and Pouliquen, O. Flows of dense granular media. Annu Rev Fluid Mech. (2008) 40:1–24. doi: 10.1146/annurev.fluid.40.111406.102142
13. Silbert, LE, Ertas, D, Grest, GS, Halsey, TC, Levine, D, and Plimpton, SJ. Granular flow down an inclined plane: bagnold scaling and rheology. Phys Rev E (2001) 64:051302. doi: 10.1103/PhysRevE.64.051302
14. Pouliquen, O. Scaling laws in granular flows down rough inclined planes. Phys Fluids (1999) 11:542. doi: 10.1063/1.869928
15. Savage, SB, and Hutter, K. The motion of finite mass of granular material down a rough incline. J Fluid Mech. (1989) 199:177–215. doi: 10.1017/S0022112089000340
16. Pouliquen, O, and Forterre, Y. Friction law for dense granular flows: application to the motion of mass down a rough inclined plane. J Fluid Mech. (2002) 453:133–151. doi: 10.1017/S0022112001006796
17. Mangeney, A, Heinrich, P, and Roche, R. Analytical solution for testing debris avalanche numerical models. Pure Appl Geophys. (2000) 157:1081–96. doi: 10.1007/s000240050018
18. Faccanoni, G, and Mangeney, A. Exact solution for granular flows. Int J Num Anal Meth Goemech. (2013) 37:1408–33. doi: 10.1002/nag.2124
19. Capart, H, Hung, CY, and Stark, CP. Depth-integrated equations for entraining granular flows in narrow channels. J Fluid Mech. (2015) 765:R4. doi: 10.1017/jfm.2014.713
20. Campbell, CS, Cleary, PW, and Hopkins, M. Large-scale landslide simulations: global deformation, velocities and basal friction. J Geophys Res. (1995) 100:8267–83. doi: 10.1029/94JB00937
21. Staron, L, and Lajeunesse, E. Understanding how volume affects the mobility of dry debris flows. Geophys Res Lett. (2009) 36:L12402. doi: 10.1029/2009GL038229
22. Bagnold, RA. Experiments on a gravity-free dispersion of large solid spheres in a newtonian fluid under shear. Proc R Soc Lond Ser A (1954) 225:49. doi: 10.1098/rspa.1954.0186
24. Lajeunesse, E, Mangeney-Castelnau, A, and Vilotte, JP. Spreading of a granular mass on a horizontal plane. Phys Fluids (2004) 16:2371–81. doi: 10.1063/1.1736611
25. Lube, G, Huppert, H, Sparks, SJ, and Hallworth, MA. Axisymmetric collapse of granular columns. J Fluid Mech. (2004) 508:175–99. doi: 10.1017/S0022112004009036
26. Utili, S, Zhao, T, and Houlsby, GT. 3d dem investigation of granular column collapse: evaluation of debris motion and its destructive power. Eng. Geol. (2015) 186:3–16. doi: 10.1016/j.enggeo.2014.08.018
27. Cundall, PA, and Strack, OD. A discrete numerical model for granular assemblies. Geotechnique (1979) 29:47. doi: 10.1680/geot.1979.29.1.47
28. Schafer, J, Dippel, S, and Wolf, DE. Force schemes in simulations of granular materials. J Phys (1996) 6:5–20.
29. Goren, L, Aharonov, E, Sparks, D, and Toussaint, R. The mechanical coupling of fluid-filled granular material under shear. Pure Appl Geophys. (2011) 168:2289–323. doi: 10.1007/s00024-011-0320-4
30. Frenkel, D, and Smit, B. Understanding Molecular Simulations. San Diego, CA: AcademicPress (2002).
31. da, Cruz F, Emam, S, Prochnow, M, Roux, JN, and Chevoir, F. Rheophysics of dense granular materials: discrete simulation of plane shear flows. Phys Rev E (2005) 72:021309. doi: 10.1103/PhysRevE.72.021309
32. Abramowitz, M, and Stegun, IA. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. New York, NY: Dover Publications (1972).
33. Kamrin, K, and Koval, G. Nonlocal constitutive relation for steady granular flow. Phys. Rev. Lett. (2012) 108:178301. doi: 10.1103/PhysRevLett.108.178301
34. Shreve, RL. The blackhawk landslide. Spec Pap Geol Soc Am. (1968) 108:47. doi: 10.1130/spe108-p1
Keywords: long runout landslides, Heim's ratio, granular flows, granular materials, spreading, frictional weakening, apparent friction
Citation: Parez S and Aharonov E (2015) Long runout landslides: a solution from granular mechanics. Front. Phys. 3:80. doi: 10.3389/fphy.2015.00080
Received: 29 June 2015; Accepted: 09 September 2015;
Published: 06 October 2015.
Edited by:
Antonio F. Miguel, University of Evora, PortugalReviewed by:
Eric Josef Ribeiro Parteli, University of Cologne, GermanyBenjy Marks, University of Oslo, Norway
Copyright © 2015 Parez and Aharonov. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Stanislav Parez, Faculty of Mathematics and Sciences, Institute of Earth Sciences, Hebrew University of Jerusalem, Edmond J. Safra Campus, Givat Ram, Jerusalem 91904, Israel,c3RhbmlzbGF2LnBhcmV6QG1haWwuaHVqaS5hYy5pbA==
 Stanislav Parez
Stanislav Parez Einat Aharonov
Einat Aharonov