- 1Extraterrestrial Physics Group, Institute for Experimental and Applied Physics, University of Kiel, Kiel, Germany
- 2Space Research Institute, Austrian Academy of Sciences, Graz, Austria
Employing the fermion unification model based on the intrinsic SU(8) symmetry of a generalized Dirac equation, we discuss the fundamental interactions under the SU(8) = SU(2)⊗SU(4) symmetry group. The physics involved can describe all fermions, the leptons (electron and neutrino), and the colored up and down quarks of the first generation in the standard model (SM) by a complex SU(8) octet of Dirac spinor fields. The fermion interactions are found to be mediated by the unified SU(4) and SU(2) vector gauge boson fields, which include the photon, the gluons, and the bosons Z and W as well known from the SM, but also comprise new ones, namely three colored X bosons carrying a fractional hypercharge of ±4∕3 and transmuting leptons into quarks and vice versa. The full covariant derivative of the model is derived and discussed. The Higgs mechanism gives mass to the Z and W bosons, but also permits one to derive the mass of the colored X boson, for which depending on the choice of the values of the coupling constant, the estimates are 35 or 156 GeV, values that are well within reach of the LHC. The scalar Higgs field can also lend masses to the fermions and fix their physical values for given appropriate coupling constants to that field.
1. Introduction
The idea to unify the strong, weak and electromagnetic forces into a single force encompassing them all has been around for more than half a century, after what is now called the standard model (SM) of elementary particle physics (see e.g., the modern textbooks [1, 2]) was conceived in the the second half of the past century. Many attempts were since then made to extend the symmetry groups defining the SM, which is the amalgam of three gauge groups, SU(3)⊗SU(2)⊗U(1). Among the seminal works by Pati and Salam [3, 4] were the first to unify lepton-hadron symmetry and to consider the leptons as the fourth “color” within the SU(4) group. The influential theory by Georgi and Glashow [5] conjectured that strong, electromagnetic, and weak forces arise from a single fundamental interaction based on the symmetry gauge group SU(5). These early works and many others thereafter were reviewed by Salam in his Nobel lecture [6] addressing gauge unification of fundamental forces. It is not our intention here to review the ample subsequent work, but we refer to the recent paper (of which the present one is the continuation) by Marsch and Narita [7]. They developed a fermion unification model based on the intrinsic SU(8) = SU(2)⊗SU(4) symmetry of a generalized Dirac equation, which can accommodate and unify the eight basic stable fermions of the first family of the SM.
The SU(8) symmetry in that model comes from the intrinsic (combinatorial and representation-related) symmetry of the Dirac equation [8]. It is not a chiral theory but includes a single fermion mass, and thus breaks chiral symmetry by this mass term. Thus, it differs markedly from other unification scenarios based on the SU(8) group, such as the boson-fermion balanced SU(8) unification scheme incorporating graviton and gravitinos as suggested recently by Adler [9], or the earlier SU(8) unification model including flavors [10] and being designed for chiral families [11, 12], or the previous SU(8) unification theory including even supersymmetry by Leon et al. [13]. Yet it is worth noting that the generalized spinor in the Marsch-Narita model is constructed similarly than that proposed recently by Yablon [14], who discussed a grand unified SU(8) gauge theory based on baryons which are Yang-Mills magnetic monopoles. In the work of Marsch and Narita [7], the SU(4) subgroup of SU(8) plays a key role. Its associated hypercharge operator , which is defined by the generator λ15 of the SU(4) symmetry group, gives the fractional charge of the quarks in a natural way, and SU(4) is genuinely associated with a single lepton and three quarks.
Grand Unified Theory (GUT) [3, 5] invoked at the outset new vector bosons which mediate the interactions (among them hypercharge and color-charge transfers) between the quarks and leptons. Historically speaking, these bosons were estimated to be not in reach of the working particle accelerators. Yet after the detection of the W and Z bosons (for the recent results see [15]) of the weak interaction in the late eighties of the past century, the future looked much more promising, and even more so today after the revelation of the Higgs boson with an energy of about 125 GeV at the LHC in Geneva [16–19]. The search for new particles beyond the SM has already started [20]. From the theoretical point of view, for example in their technicolor model, Doff [21] and Doff and Natale [22] estimated the masses of vector gauge bosons in extensions of the SM. Many other extensions of the SM predict new scalar or vector bosons, called leptoquarks (LQs), which carry color-charge and fractional electric charges. Examples of such SM extensions include the above cited GUT models. Leptoquarks can decay, for instance into a pair of quark and lepton, and therefore experimental searches were already suggested to focus on such pair production caused by leptoquarks [23].
Employing the fermion unification model based on the intrinsic SU(8) symmetry of the generalized Dirac equation [7], we discuss here in detail the gauge fields under the SU(8) = SU(2)⊗SU(4) symmetry group. This unified gauge model can describe the electron, the neutrino, and the three colored up and down quarks of the first generation in the SM, as an SU(8) octet of Dirac spinor fields. Consequently, the fundamental fermion interactions are found to be mediated by the SU(4) and SU(2) vector gauge boson fields, which include the bosons Y and U like the bosons Z and W of the SM, but which also comprise three new colored X bosons, which carry a fractional hypercharge of ±4∕3 and can transmute leptons into quarks and vice versa. The Higgs mechanism then gives mass to these gauge bosons, and can also lend mass to the fermions. Given appropriate coupling constants to the Higgs field, the physical masses of all eight fermions can be fixed. The measured electron mass serves as a reference setting the spatial scale of the spinor fields by its Compton wavelength.
The main goal of this paper is to work out the above mentioned characteristics of the unified SU(2)⊗SU(4) gauge theory, and thereby to estimate the masses of the associated vector gauge bosons. After a short introduction to the generalized Dirac equation, we study the covariant derivative under SU(2)⊗SU(4) and discuss the Higgs mechanism.
2. The Generalized Dirac Equation
In this first introductory paragraph, we present the Dirac equation [7, 8] in an appropriate algebraic form, and provide some of the necessary mathematics required for the discussion in the subsequent sections. We use standard symbols, notations and conventional units as in Schwartz [1] and Kaku [2] for the Dirac equation [8], and set ℏ = c = 1. According to quantum mechanics the relativistic covariant four-momentum operator can be denoted as Pμ = (E, −p) = i∂μ = i(∂∕∂t, ∂∕∂x), which acts on the space-time variables of any spinor field ψ(x, t). The fermion mass is denoted by m and the same for any species identified later. We may also abbreviate the contravariant space-time location vector xμ = (t, x) as x. The Dirac equation [8] for a four-component standard Dirac spinor field ψ(x) reads as follows
We are free to choose the so-called Weyl [24] representation as our standard. Then the Dirac matrices can be written as
where the symbol 12 stands for the 2 × 2 unit matrix. We introduce the matrices α, β, and γ as
They obey α = βγ. In Equation (2) the Pauli matrices [25] have their standard form, which is given by the fundamental representation of the SU(2) group generators (see Appendix). The chiral (matrix) operator is defined as in any representation. Using the fact that σxσyσz = i12, it takes in the Weyl representation the form , and obeys , where 14 stands for the 4 × 4 unit matrix.
Following the recent work of Marsch and Narita [7] on the intrinsic SU(8) symmetry of a generalized Dirac equation, we can assemble, respectively, the neutrino and the red, green, blue up quarks into a large four-component spinor, a quadruplet of the SU(4) symmetry group, and similarly the red, green, blue down quarks and the electron into another large four-component spinor, which read
Here we use lower and upper case letters to indicate the Dirac spinor fields for the up and down hyperspin states. The Dirac equation [8] for both spinors reads as follows
These fermion quadruplets have the adequate form that is conveniently employed in the Yang-Mills theory [1, 2, 26, 27]. Given the number of four fermion degrees of freedom, we see that the SU(4) symmetry group unifies leptons with up and down quarks, and consequently SU(8) serves as a candidate for the grand symmetry group unifying the eight fermion species all together [7].
When considering each fermion on its own, for example the electron, we may choose its hypercharge to be either y = 1 or y = −1, but apparently SU(4) group theory prefers −1. The opposite charge is implied automatically for the antiparticle by the charge conjugation symmetry of Dirac's equation. Since there is an equality among the leptons and quarks, these four fermions are allowed to mix among themselves. The corresponding unifying symmetry group is SU(4) [2, 7, 28], which is unitary and four-dimensional in its fundamental representation. Thus, we can define a related hypercharge operator Y as a purely diagonal 4 × 4 matrix, which has the fermion hypercharges on its trace and can conveniently be written as . Consequently, the trace of Y must vanish as required by SU(4) group theory. The fractional charges of the quarks simply reflect the fact that there are three quark species, and thus the dimension of their subspace is 3, in association with the SU(3) group in its fundamental representation. SU(3) is a subgroup of SU(4), which has 15 generators [2, 28]. For the sake of completeness, and since we need them frequently, we quote the SU(4) generators in the Appendix.
We can now further combine the two large spinors of Equation (4) with an SU(2) doublet , and write the grand-multiplet Dirac equation in octet form in the Weyl representation after Equation (2) as
which includes an eight-component SU(8) vector built of Dirac spinors (Equation 6), and describes the kinetics of the eight free fermions of the first family or generation of the standard model (SM). The corresponding symmetry group is SU(8), which has the decomposition SU(2)⊗SU(4). The doublet , with the indices u (up) and d (down) referring to hyperspin, encompasses two four-component spinors as given in Equation (4) with the indices u = (r, g, b, l), and d = (R, G, B, L) given explicitly. Note that the lower-case indices refer to the electric charges (2/3, 2/3, 2/3, 0) for the three colored up quarks and the neutrino, and upper-case indices refer to the electric charges (−1∕3, −1∕3, −1∕3, −1) for the three colored down quarks and the electron [7].
3. Covariant Derivatives
Here we provide and discuss the mathematics associated with the covariant derivative for the SU(4) symmetry group. It has the generators in conventional normalization [1, 2], where the early-alphabet letters such as a and b are used to index the 15 generators of the SU(4) algebra as super- or subscript (see Appendix). According to the Yang-Mills theory [26] each generator is associated with a four-vector real gauge field which we name . Then the so-called connection field (summation convention over the index a is assumed) defines the covariant derivative
which replaces the normal derivative term in the Dirac Equation (5). Note that μ is a 4 × 4 four-vector matrix containing 15 independent gauge fields as elements. The coupling constant is conventionally named g′. Yet, note that the hypercharge group U(1) and SU(3) are now included in SU(4) as subgroups. Therefore, the SU(4) coupling constant should be that of SU(3) for the strong interaction. Thus, quantum hypercharge dynamics (QYD) and quantum chromodynamics (QCD) must have the same coupling constant at the outset.
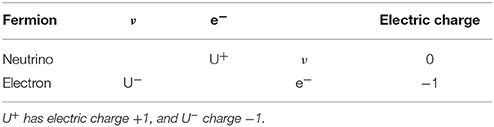
It turns out to be advantageous to combine the generators (or lambda matrices) pairwise to obtain the ladder operator concerning the color and electric charges. We combine the real non-diagonal lambda matrices to obtain six matrix pairs, such as . The six possible combinations are given appropriate names and are listed in the Appendix. Correspondingly, we may define the gauge fields, for example by introducing . To ease the notation, we omit the relativistic index μ at all gauge fields. Inspired by the work of Georgi and Glashow [5], the gluon gauge fields with index pairs (1, 2), (4, 5), (6, 7) are given the new names , and for the plus superscript, respectively, and their hermitian (complex) conjugates , , and , corresponding to the minus superscript. These gluons transfer or change color charge. The gauge fields with index pairs (9, 10), (11, 12), (13, 14) are given the new names for the plus superscript, which have the hermitian conjugates , , and for the minus superscript. Thus, we have the following definitions: , , , and , , . The X vector gauge bosons connect leptons with quarks, and transfer or change the electric as well as color charges. The possible transfer processes are illustrated in Table 1.

Table 1. SU(4) representation for exchange of lepton with quarks by help of the colored X gauge boson.
By making use of the above construction of the gauge bosons and associated lambda matrices, we can now rewrite the connection field (for the sake of simplicity we omit again the relativistic index μ at all vector gauge fields) in the following way:
Here we have renamed the gauge fields connected to the diagonal matrices as V3 = G3 and V8 = G8, indicating their nature as a gluon belonging to SU(3), and V15 = B. This hypercharge gauge field B is related to the diagonal hypercharge operator . Note that the connection is a hermitian operator, i.e., , owing to the properties of the lambda matrices and the complex gauge fields. Using the lambda matrices given in the appendix, we write μ as a 4 × 4 matrix, key elements of which are arranged in Table 1. Although the fractional hypercharge ±4∕3 of the X bosons appears somewhat unusual, yet it is natural when considering that this value corresponds to the hypercharge difference between quarks and lepton. The fractional hypercharge is an unavoidable consequence of the SU(4) symmetry.
The coupling of the hyperspin doublet to gauge fields is described and inspired by the theoretical scheme of the well-known theory of the weak interactions after Weinberg [29], Glashow [30], Salam [31], which is a key component of the SM. By noting that the hyperspin (indicated in (9) by an arrow) should not be confused with the normal fermion spin (intrinsic angular momentum) which is not relevant for the gauge interaction discussed here, we apply the scheme of Weinberg-Glashow rotation to relate the fundamental or free fermion octet state Ψfree with the interaction state Ψint as
The covariant derivative for the hyperspin gauge field is (by using U instead of W to avoid confusion in the nomenclature):
where the three generators of the SU(2) group symmetry are given by the three normal vector components, . We introduce the conventional ladder operators as , and the related complex gauge fields . Then the connection reads . Therefore, the covariant derivative including both the SU(4) and SU(2) gauge fields can be written concisely as
where the symbols 12, 14, 18 refer to the two-, four-, and eight-dimensional unit matrices, respectively. The quantities on the right hand are understood to be multiplied, element by element, with the matrices on their left side. For the sake of transparency, we express the matrices connected with SU(2) explicitly as
The complex operator Dμ in Equation (12) replaces ∂μ in the generalized Dirac equation (Equation 6), and acts on the octet spinor field Ψfree.
Following the procedures used in the SM for unifying the hypercharge and weak-charge interactions to form the electroweak interactions, we combine the terms involving the gauge field Bμ in SU(4), which is coupled to the hypercharge operator Y, with the gauge field Uzμ of SU(2) and mix them by the Weinberg-Glashow rotation as illustrated in Equation (9). The effects of these gauge fields on the charges of the fermions are further shown in the Tables 2, 3. We abbreviate the corresponding term in the matrix operator (Equation 12) as Mμ which is given by
Here we redefined the coupling constant for the SU(4) interaction into by including the factor in front of the original matrix λ15. We recall that is a non-trivial diagonal matrix. We now introduce two new fields Aμ and by the Weinberg-Glashow rotation [29, 30] as
Here θ is the associated rotation angle that is still to be determined. We abbreviate c = cosθ and s = sinθ. By replacing the old by the new fields in the operator Mμ, we obtain
or using 8 × 8 matrices Q and R
where the Q and R matrices are
and
Close inspection of Equations (17) and (18) shows that, if fcosθ = gsinθ = e (with e being the electric charge unit) for the particular angle θU, the matrices Q and R can become more transparent. The condition implies that , which defines the SU(2)⊗SU(4) equivalent to the Weinberg-Glashow [29, 30] angle tanθW of the SU(2)⊗U(1) electro-weak-interaction theory of the SM. The empirical values are sinθW = 0.4722 and cosθW = 0.8815 [1]. The coupling constant f is related to the hypercharge operator of the U(1) gauge field in the SM, whereas it is related to the hypercharge operator Y of the SU(4) gauge field in our model associated with the unified strong and hypercharge interactions. The SU(4) gauge field has the common coupling constant between strong and hypercharge interactions. In the SM we have gSM = e∕sinθW = 2.118e and , as obtained from measurements.
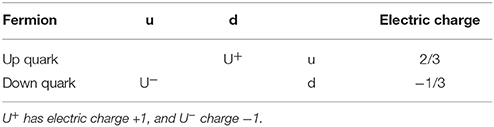
Table 3. SU(2) representation for exchange of up quark with down quark by help of the U gauge boson.
In our model there is no plausible reason to assume that the coupling constants g and g′ are different. We follow the ingenious intuition of Georgi and Glashow [5], “…that all elementary particle forces (strong, weak, and electromagnetic) are different manifestations of the same fundamental interaction involving a single coupling strength, the fine-structure constant.” In agreement with this statement we assume g = gSM and . Consequently, the values of our strong and weak coupling constants are then chosen as g′ = 0.923e and g = 2.118e. Therefore, we identify the U boson with the W bosons of the SM although we do not have a chiral theory. The finite fermion mass breaks chiral symmetry. In our unified field model we are always dealing with massive Dirac spinor fields and not two-component massless Weyl spinor fields. We will continue using the symbol U for the gauge bosons in order to indicate the difference from the W boson appearing in the chiral weak-interaction theory of the SM.
Once the rotation angle is fixed by the ratio of the coupling constants f and g, the entity Q turns out to be the SU(8) electromagnetic charge operator given by
with the electric charge obtained as . Of course the field Aμ then is the electromagnetic field. Similarly, we get for the effective weak charge operator in association with the neutral field the formula
For the fermion octet we thus obtain the diagonal-matrix electric charge operator
corresponding to three charged up quarks and the uncharged neutrino, and to the three charged down quarks and the electron. The electric charges of the three color variants of up and down quarks are the same, as was expected. Obviously, the trace of the charge operator Q sums up to zero, which expresses charge conservation among the eight fermions assembled in the SU(8) octet.
Another key trait of the present model is that the three up quarks and neutrino and the three down quarks and electron also carry what we call gray charge. We use this new term to indicate the charge that is associated with the operator (20) and originates from the SU(2) doublet (with hyperspin up and down corresponding to white and black). Upon insertion of the hypercharge operator Y into Equation (20), we obtain the diagonal-matrix gray-charge operator
The corresponding gray charges are defined as
With their gray charges all fermions couple to the gauge field Y (corresponding to the Z vector boson field of the SM) of the unified strong and weak interaction [7]. We like to stress that the traces of the Q and R matrices vanish, in compliance with the general property of the SU(8) symmetry-group generators, consisting of the 63 traceless 8 × 8 unitary matrices. Consequently, 3(q+ + q−) + l+ + l− = 0, which is obvious from (23). The gray charge brings about a new force (yielding what we may call Quantum Gray-Charge Dynamics, QGD) acting on the fermions, but differs essentially from the electromagnetic (QED) and strong (QCD) forces, which both are mediated by massless vector bosons (photons and gluons) related with the symmetry groups U(1) and SU(3) that is a subgroup of SU(4) considered here.
Returning to the initial expression (Equation 11) and using the full symbols for SU(4), we can write the covariant derivative as
We may rewrite the covariant derivative again explicitly in terms of the gluons G, the photon A, the Y boson, the U bosons, and the X bosons as follows:
The second bracket term corresponds to QCD, the third term to QED, the fourth and fifths terms to weak interactions, and finally the sixth to the strong interactions associated with the exchange of color-charge and hypercharge. The last six terms are of genuine SU(4) nature and do not exist in the SM! The covariant derivative in Equation (24) represents the unification of the strong interactions with the weak ones in our model. The link between the strong and the weak interactions leads to electromagnetism through SU(4) symmetry unifying QCD with QYD. SU(8) is the merger of the SU(4) interactions with the weak interactions associated with the hyperspin degree of freedom of the fermions. Apparently, the photon represented by Aμ and the associated electromagnetism emerge by the amalgamation of SU(4) with SU(2), which yields the unifying symmetry given by SU(8) = SU(2)⊗SU(4).
4. Higgs Mechanism and Masses of Bosons and Fermions
According to the paradigm described by the Higgs mechanism [1, 2, 32, 33] the vector gauge bosons of the SM acquire mass through the symmetry breaking introduced by the scalar Higgs field. Here we also rely on this mechanism for giving mass to six of the fifteen vector bosons stemming from (a = 9, ⋯ , 14) of the symmetry group SU(4). The eight gluons (a = 1, ⋯ , 8) associated with SU(3) will not be affected by this procedure and remain massless. So will the photon, described by the electromagnetic vector potential Aμ (related with ). We define, in connection with the Higgs field, in SU(4) the quadruplet ϕ and in SU(8) the octet as Φ of scalar boson fields. Unlike in the SM, the Higgs field carries color-charge and hypercharge and thus electric charge, but we aim at a chargeless boson breaking SU(8) symmetry. We define the quadruplet that is normalized to unity as well as the octet . They turn out to be of key importance for the subsequent calculations because of the construction QΦ0 = 0, i.e., Φ0 is the eigen-state (for charge zero) of the charge operator (Equation 21) coupling to the electromagnetic field. Close inspection of the lambda matrices as given in the appendix shows that
Moreover, the lambda matrices have the property that
where a and b may run from 9 to 13. The matrix products have a zero in the lowest right corner, and thus their expectation value vanishes. Furthermore, there are relations that help us to simplify the subsequent calculations involving the sigma matrices (see Appendix). For example, we find that
In the Lagrangian density [1] of the Higgs octet with the single boson field h(x), the kinetic term reads
where the covariant derivative (Equation 24) has to be inserted. As we are only interested here in the lowest order term, we assume the Higgs field to be represented by its vacuum expectation value that is traditionally named v = 〈h(x)〉 in the SM. Operation of the covariant derivative on h(x)Φ0 yields
Here use has been made of λaϕ0 = 0 (a = 1, ⋯ , 8) for the gluons, QΦ0 = 0, and that ∂μv = 0. As iDμh(x) is a hermitian operator, the lowest-order contribution to (Equation 30) is just given by the expectation value of the squared operator between the brackets in the above expression. When evaluating it all the linear mixing terms between the various boson fields vanish, and just their squares remain. The Lagrangian is then:
The coupling constant of the neutral colorless gauge field is given by the expectation value of the operator R(Y) as defined in (Equation 20). Note that Yϕ0 = −ϕ0, and then detailed calculation yields the simple result that . Thus, the squared coupling constant is given by (f2 + g2)∕4, like in the SM, yet note again that , and here g′ is the coupling constant of the strong interaction. From the above equation we can readily read off the masses of the vector gauge bosons:
Recalling the definition of the X, Y, and U bosons, we can finally write the boson mass terms generated by the symmetry-breaking Higgs mechanism in the Lagrangian as
Remember that there are three X bosons because there are three kinds of colored quarks, but only one U boson, since there is merely one sort of lepton. Concerning the SM, our Y conforms to Z and our U corresponds to W. The masses MZ and MW of the famous SM gauge bosons have been measured well [1, 2, 29].
Let us estimate the possible masses of the U bosons. Identifying W for the moment as U, and taking the known weak interaction coupling constant as g, we obtain mU = mW = 80.4 GeV, and further predict that the X boson mass should be larger than that of the U boson by the ratio of the coupling constants involved here, i.e., by the factor and . With the typical value αw = 0.032 for the weak and αs = 0.12 for the strong interaction (e.g., [1]), we obtain a ratio of 3.75 with the coupling constants taken at electro-weak scale of about 100 GeV. By the square root of 3.75, yielding 1.94, the X should be heavier than the U. As a result we derive an estimate of MX = 156 GeV, which is clearly within the reach of the LHC providing energies of several TeV. Similarly, we can estimate the mass of the Y boson from formula (33), yielding , and thus obtain MY = 207 GeV. This is more than twice as large as the Z boson mass of the SM, which is MZ = 91.2 GeV. The reason is that the strong interaction coupling constant g′ is here assumed to be about twice as large as the weak coupling constant g. However, the Z boson, although it has already been measured, would have no place in such a scenario, but it is replaced by the heavier Y boson.
On the other hand, its seems in the spirit of unification more adequate to assume the values g′ = 0.923e and g = 2.118e, as we calculated previously under the assumption that and g = gSM. This gives a ratio of g′∕g = 0.436, and leads to a less massive X boson with MX = 35 GeV. In that case the masses of the U and W, and of Y and Z are of course the same by the choice of the coupling constants. One wonders, however, that such a small boson has not yet been detected by the LHC or previous particle accelerators. Concerning the assumed approximate equality of the coupling constants we may cite Georgi and Glashow [5] again, saying that “…the essential thing about a theory of strong interactions based on an unbroken non-Abelian gauge symmetry is that the strength of strong interactions no longer depends on the existence of a large coupling constant. Even if the gauge coupling constant is small, say of order e, the infrared divergences of the theory can lead to phenomenological interactions strong enough to keep the quarks bound. What we want is not asymptotic freedom but infrared slavery.”
Let us finally address the problem of the fermion masses. In the Dirac equation (Equation 6) a single mass m is assumed for all fermions of the octet. Following the conventional procedure of the Yukawa coupling [1] as employed in the SM, we can give different physical masses to the fermions of the SU(8) octet by adding an apt term in the corresponding Lagrangian. The coupling constants of the up and down quarks are λu, d and the same for all colors, the one for the electron and neutrino are λe, ν. The related masses are determined by the Higgs field vacuum expectation value v, and thus we obtain the diagonal fermion mass matrix mv = diag(λu, λu, λu, λν, λd, λd, λd, λe)v. Unlike the original mass matrix m18 appearing in the Dirac equation (Equation 6), which involves the unit matrix, the Higgs-field-induced mass matrix mv is non-trivially diagonal, and therefore breaks the original SU(8) symmetry. After symmetry breaking the fermion mass term in the Lagrangian density reads
If we choose m to be the electron mass me and the electron coupling constant with the Higgs field to be zero (for the reason that the electron mass is the only directly measurable), λe = 0, we are then left with three free parameters, λν, λu, and λd, in the mass term in order to adjust all fermion masses of the first generation to their measured or inferred values.
5. Discussion and Conclusions
We presented a non-chiral fermion unification model based on the SU(8) = SU(2)⊗SU(4) symmetry group. The eight fermion species (i.e., the neutrino, the electron, and the colored up and down quarks) of the first generation of the SM are assembled into an SU(8) octet of massive Dirac spinor fields. The fermion interactions are mediated by the unified SU(4) and SU(2) vector gauge boson fields, which include not only the photon, the gluons and the massive bosons Y and U (which correspond to the Z and W of the SM) but also the three colored massive X bosons as new particles. The X bosons carry a fractional hypercharge of ±4∕3 or electric charge of ±2∕3, and can transmute leptons into quarks and vice versa. The full covariant derivative of this gauge model was derived and discussed. The Higgs mechanism can give mass to all charged vector bosons, to the uncolored Y and U as well as to the three colored X bosons.
The SU(4) subgroup treats the fermions on an equal footing. The related coupling constant (here named g′) could range between ge = e and gs ≈ 4ge (for αs = 0.118 and αe = 0.0073), which corresponds roughly to the two values of the boson mass MX as given above. Yet in the spirit of unification, it seems most reasonable to assume the values g′ = 0.923e and g = 2.118e, as we calculated them previously under the assumption that and g = gSM. This leads to a mass MX = 35 GeV of the X boson. In that case the masses of the U and W, and of Y and Z are of course the same by the choice of these coupling constants. In fact the vector field is akin to , and akin to of the SM. The related assignment of coupling constants is our preferred choice. Consequently, the SU(2) interaction sector of our non-chiral model is similar to the chiral weak interaction of the SM, with the corresponding gauge bosons having the same measured mass.
A common coupling constant seems quite plausible when one asks the question “Why should the physical mechanism of exchanging color-charge and hypercharge within the unified SU(2)⊗SU(4) symmetry have vastly different boson energies being associated with it?” Within the conventional GUT paradigm, the mass of the related hypothetical X boson turns out to be very large, about 1015 GeV when it is based on the logarithmic extrapolation by many orders of magnitude of the running coupling-constants involving the SM beta functions [1, 2]. However, our unification model suggests that the effects of color-charge transfer between quarks and leptons should already be relevant and acting below the 100 GeV scale. The covariant derivative (Equation 25) includes co-equal mathematical terms, involving photon (QED) and gluons (QCD) alike, of about the same order, and thus unifies these two gauge-field theories with massless vector bosons. Given that key trait of our model, electromagnetism (QED) is expected to play a more significant role in the formation of hadrons and mesons than the one usually ascribed to it by the SM.
The color-charge-exchange interactions will, like the weak interactions in the SM, be also very short-range while being mediated by the massive X gauge bosons. To provide a phenomenological analysis of the consequences of the presence of the X bosons requires detailed quantum-field-theoretical calculations on the basis of our new SU(2)⊗SU(4) model, a task that is left for future work. In addition to the X boson, we established here the Quantum Gray-charge Dynamics (QGD) as the consequence of SU(2) and SU(4) unification. QGD materializes due to the very short-range force associated with the massive vector gauge boson field , which is coupled to the gray charge represented by the operator R, and which mediates interactions between the eight fermions since they all carry that gray charge. Therefore, quarks and leptons can interact with each other not only through their electric but gray charge as well, and thus may likely form hitherto unknown bound states. In particular the electrically neutral and colorless neutrino can still interact with the electron and quarks via its gray charge. This offers new perspectives for the understanding and interpretation of fermion interactions. To evaluate the physics of QGD demands further detailed algebraic calculations which are beyond the limits of the present fundamental work.
Given an X-boson of mass 35 GeV, one may wonder why it, when having such a relatively small mass, has not yet been detected by the LHC or previous particle accelerators. According to Table 1; a colored X-boson transmutes a colored quark into a colorless lepton, or vice versa, and thus may decay into such a quark-lepton pair. As free quarks do not exist but immediately hadronize, the result of the X-boson decay will be hadron-lepton pairs which should be directly observable. The search for pair production of third-generation scalar leptoquarks in proton-proton collisions at LHC beyond 200 GeV up to 8 TeV has recently been reviewed [23]. There are probably many possible X-boson decay channels, given the multitude of hadrons and leptons of the three generations, and thus the decay signature expected near 35 GeV may in all not be clean and easily discernable. But the X-boson decay is expected to contribute to a wide event background way below 100 GeV. For example, in the search for signatures of the Higgs boson decay, the dilepton invariant mass data was recently found at LHC to peak broadly at the energy of 35-40 GeV (in [19] Figure 7) and at the energy of 30 GeV (in [17] Figure 1) in the background data accumulated from various decay modes. Similary, a broad peak in the background data of the dilepton invariant mass of the Z boson decay was, already long time ago, found by SPS at CERN around an energy of 30–40 GeV (as cited in [34] Figure 7.26, and [35] Figure 1). After the decay signatures of the X-boson have theoretically been clearly defined, a dedicated search for it, with careful background evaluation, should be carried out with the existing or future LHC data.
Finally, we like to mention that we did not treat here explicitly fermions of the second and the third generation, but just of the first generation as obtained from the generalized Dirac equation involving SU(2)⊗SU(4) symmetry and a single mass [7]. Our model should of course be expanded to describe additional fermions with higher masses, because particle colliders and other experiments showed and confirmed their existence. The simplest extension of our model would be to just add four more flavors (two generations) for the strange, charm, bottom and top quarks and the muon, tauon and their associated neutrinos, with the same basic mass m but complemented by corresponding Yukawa coupling terms with additional specific constants like in the SM. This model would be similar to yet more comprehensive than the SM, while being unified and encompassing the joint SU(2)⊗SU(4) symmetry groups, and therefore we plan to explore in the future its characteristic phenomenology in detail.
To add further new interactions to the model is another future aim. For example, the consideration (also going beyond the SM) of the prevailing topics of massive neutrino oscillations, or of the presumed and debated charged lepton flavor violation (CLFV, see e.g., [36]) of course requires to account for the two known heavier fermion families, but is beyond the scope of our paper. Like the SM, also the present model must be further developed to address such ongoing research topics. By doing this one may come up, for instant, with new constraints on the nature of cosmological dark matter, or on the genesis of baryons and leptons.
Author Contributions
EM algebraic derivations and drafting of the work. YN substantial contributions to the design of the work.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
EM gratefully acknowledges the institutional support by the Extraterrestrial Physics Group headed by Robert Wimmer-Schweingruber at the Institute for Experimental and Applied Physics of Kiel University in Germany. He also appreciates the support by the Space Research Institute in Graz, Austria, where during two stays some ideas of this paper were developed.
References
1. Schwartz MD. Quantum Field Theory and the Standard Model. Cambridge: Cambridge University Press (2014).
2. Kaku M. Quantum Field Theory, A Modern Introduction. New York, NY: Oxford University Press (1993).
3. Pati JC, Salam A. Unified lepton-hadron symmetry and a Gauge theory of the basic interactions. Phys Rev D (1973) 8:1240–61. doi: 10.1103/PhysRevD.8.1240
5. Georgi H, Glashow SL. Unity of all elementary-particle forces. Phys Rev Lett. (1974) 32:438–41. doi: 10.1103/PhysRevLett.32.438
6. Salam A. Gauge unification of fundamental forces. Rev Mod Phys. (1980) 52:525–38. doi: 10.1103/RevModPhys.52.525
7. Marsch E, Narita Y. Fermion unification model based on the intrinsic SU(8) symmetry of a generalized Dirac equation. Front Phys. (2015) 3:82. doi: 10.3389/fphy.2015.00082
8. Dirac PAM. The quantum theory of the electron. Proc R Soc Lond Math Phys Sci A (1928) A117:610–24. doi: 10.1098/rspa.1928.0023
9. Adler S. SU (8) family unification with boson fermion balance. Int J Mod Phys. (2014) 29:1450130. doi: 10.1142/S0217751X14501309
10. Kim CW, Roiesnel C. SU(8) grand unification. Phys Lett. (1980) 93B:343–6. doi: 10.1016/0370-2693(80)90528-6
12. Chkareuli JL. The SU(8) GUT for chiral families. Phys Lett B (1993) 300:361–6. doi: 10.1016/0370-2693(93)91346-O
13. León J, Quirós M, Ramón Medranom J. Towards a realistic supersymmetric SU8 model. Phys Lett B (1982) 118:365–8.
14. Yablon JR. Grand unified SU(8) gauge theory based on baryons which are Yang-Mills magnetic monopoles. J Mod Phys. (2013) 4:94–120. doi: 10.4236/jmp.2013.44A011
15. Chouridou S. On behalf of the ATLAS and CMS collaborations, Recent results on associated vector boson production with the ATLAS and CMS experiments. EPJ Web Conf. (2015) 90:04004. doi: 10.1051/epjconf/20159004004
16. ATLAS Collaboration. The ATLAS experiment at the CERN Large Hadron Collider. J Inst. (2008) 3:S08003.
17. ATLAS Collaboration. Observation of a new particle in the search for the Standard Model Higgs boson with the ATLAS detector at the LHC. Phys Lett B (2012) 716:1–29. doi: 10.1016/j.physletb.2012.08.020
19. CMS Collaboration. Observation of a new boson at a mass of 125 GeV with the CMS experiment at the LHC. Phys Lett B (2012) 716:30–61. doi: 10.1016/j.physletb.2012.08.021
20. Malek F. On behalf of the ATLAS and CMS Collaborations, 4th Symposium on Prospects in the Physics of Discrete Symmetries (DISCRETE2014). J Phys Conf Ser. (2015) 631:012045. doi: 10.1088/1742-6596/631/1/012045
21. Doff A. Gauge boson masses in a SU(2)TC⊗SU(3)L⊗U(1)X extension of the standard model. Phys Rev D (2010) 81:117702. doi: 10.1103/PhysRevD.81.117702
22. Doff A, Natale AA. 125 GeV scalar boson and SU(NTC)⊗SU(3)⊗U(1)X models. Phys Rev D (2013) 87:095004. doi: 10.1103/PhysRevD.87.095004
23. CMS Collaboration. Search for pair production of third-generation scalar leptoquarks and top squarks in protonproton collisions at s = 8TeV. Phys Lett B (2014) 739:229–49. doi: 10.1016/j.physletb.2014.10.063
25. Pauli W. Zur Quantenmechanik des magnetischen Elektrons. Z Physik (1927) 43:601–23. doi: 10.1007/BF01397326
26. Yang CN, Mills F. Conservation of isotopic spin and isotopic gauge invariance. Phys Rev. (1954) 96:191–5. doi: 10.1103/PhysRev.96.191
27. Cheng TP, Li LF. Gauge Theory of Elementary Particle Physics. Oxford: Oxford University Press (1983).
28. Sbaih MAA, Srour MKH, Hamada MS, Fayad HM. Lie algebra and representation of SU(4). Elect J Theor Phys. (2013) 10:9–26.
29. Weinberg S. A model of leptons. Phys Rev Lett. (1967) 19:1264–6. doi: 10.1103/PhysRevLett.19.1264
30. Glashow SL. Partial-symmetries of weak interactions. Nucl Phys. (1961) 22:579–88. doi: 10.1016/0029-5582(61)90469-2
31. Salam A. Weak and electromagnetic interactions. In: Svartholm N editor, Elementary Particle Theory: Relativistic Groups and Analyticity. Proceedings of the Eighth Nobel Symposium. Stockholm: Almquist and Wiksell (1968). pp. 367–77.
32. Higgs PW. Broken symmetries and the masses of gauge bosons. Phys Rev Lett. (1964) 13:508–9. doi: 10.1103/PhysRevLett.13.508
33. Englert F, Brout R. Broken symmetry and the mass of gauge vector bosons. Phys Rev Lett. (1964) 13:321–3. doi: 10.1103/PhysRevLett.13.321
34. Machner H. Einführung in die Kern- und Elementarteilchenphysik. Weinheim: Wiley-VCH Verlag (2005). doi: 10.1002/9783527662371
35. Arnison G, Astbury A, Aubert B, Bacci C, Bauer G, Bezaguet A, et al. UA1 Collaboration (CERN, Geneva, Switzerland), Further evidence for charged intermediate vector bosons at the SPS collider. Phys Lett B (1983) 129:273–82. doi: 10.1016/0370-2693(83)90860-2
36. Hambye T. CLFV and the origin of neutrino masses. Nucl Phys B Proc Suppl. (2014) 248–250:13–9. doi: 10.1016/j.nuclphysbps.2014.02.004
Appendix
SU(2) and SU(4) Matrices
The generators of the SU(2) group are determined by the Pauli matrices which read
The sigma ladder operators are defined as . They read explictly as follows:
The generators of the SU(4) group are given by the fifteen subsequent 4 × 4 matrices. Apparently, the group SU(3) is a subgroup of SU(4). Its eight generators can be read off from the lambdas and are contained in the upper left 3 × 3 submatrices of λ1 to λ8.
The λ matrices are hermitian, satisfy tr(λ2) = 2, and yield λ† = λ. It is appropriate to combine pairs of the non-diagonal matrices to form ladder operators (as it is usually done above for the Pauli matrices). These matrices are real, and so the hermitian conjugate is equal to the transposed matrix. Thus, we have . We can define similar combinations of the real nondiagonal lambda matrices to obtain the six matrix pairs , , , , , . By construction we have, e.g., , and similarly for all the others. Therefore, out of 12 we only quote here 6 of these matrices explicitly:
The diagonal matrices λ3, 8, 15 remain unchanged.
Keywords: SU(8) and SU(4) symmetry groups, fermion unification, generalized Dirac equation, colored massive gauge bosons, Higgs mechanism
Citation: Marsch E and Narita Y (2016) Fundamental Fermion Interactions via Vector Bosons of Unified SU(2)⊗SU(4) Gauge Fields. Front. Phys. 4:5. doi: 10.3389/fphy.2016.00005
Received: 16 November 2015; Accepted: 05 February 2016;
Published: 26 February 2016.
Edited by:
Stefano Morisi, University of Würzburg, GermanyCopyright © 2016 Marsch and Narita. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Yasuhito Narita, eWFzdWhpdG8ubmFyaXRhQG9lYXcuYWMuYXQ=
 Eckart Marsch1
Eckart Marsch1 Yasuhito Narita
Yasuhito Narita