- Center For Hydrogeology and Geothermics, University of Neuchâtel, Neuchâtel, Switzerland
Understanding the complex structure of karst networks is a challenge. In this work, we characterize the fractal properties of some of the largest coastal karst network systems in the world. They are located near the town of Tulum (Quintana Roo, Mexico). Their fractal dimension df, conductivity exponent and walk dimension dw are estimated using real space renormalization and numerical simulations. We obtain the following values for these exponents: df ≈ 1.5, dw ≈ 2.4, . We observe that the Einstein relation holds for these structures . These results indicate that coastal karst networks can be considered as critical systems and this provides some foundations to model them within this framework.
1. Introduction
Karst network structures are still poorly understood because of the lack of a general framework to study them [1], even if modeling and characterizing karst networks has been a long standing research topic [2–6].
It is estimated that karst features cover 20% of the globe's land surface [7]. Therefore, understanding karst structures is crucial for many practical purposes, from pollution issues to ground stability assessment. Karst networks result from the dissolution of rocks by water through chemical reactions [8]. Dissolution leads to the creation of complex connected structures (from small conduits to caverns) where water flows and encounters less resistance due to friction than in porous or fractured rocks.
In this paper, we focus on the analysis of karst networks located around the town of Tulum (Quintana Roo, Mexico). They are natural, underground, coastal, networks transporting water from inland to the sea. The area of Tulum hosts two of the largest water filled networks in the world: Ox Bel Ha and Sac Actun (above 200 km of connected conduits for each one [9]). Due to their large sizes and the relatively simple and homogeneous geology (horizontal carbonate platform) of the underground, we expect that these networks exhibit a well marked statistical signature characterizing the physical processes of their formation.
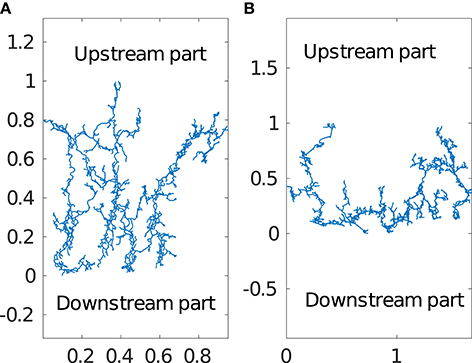
We analyze these networks (mapped by cave-divers) as spatially embedded graphs. The large horizontal extension (about 10 km) compared to their vertical extent (around 12m) allows us study these systems as embedded structure in plan view. Figure 1 shows Ox Bel Ha and Sac Actun (proportionally rescaled such that the maximal vertical extension is 1). Water flows from the upstream part (top of Figure 1) to the sea (bottom of the Figure).
In this paper, we propose a method to characterize karst systems using statistical mechanics tools and show that they exhibit fractal properties. We use the Song, Havlin, and Makse (SHM) renormalization scheme [10] to the study these networks. To our knowledge, this is the first application of the SHM renormalization scheme to compute the fractal dimension of spatially embedded networks. We then analyze the network transport properties in terms of diffusion (random walk simulation) and conductivity (solving Kirchhoff equations).
Fractal concepts are not new to karst systems, with previous studies characterizing karst structures as fractal objects. However, these studies were limited to estimating fractal dimensions of relatively small networks (1–10 km of connected conduits [11–14]). Reported fractal dimension range from 1.043 to 1.67. However, a clear, physically based overall picture is still missing, with no attention paid to the study of transport properties (conductivity and diffusion) that complete the characterization of karst networks as “standard” fractal structures.
We show through numerical experiments that the conductivity scales as a power law of the Euclidean distance between two points of the network for both Ox Bel Ha and Sac Actun. The two networks share a similar structure, in terms of fractal dimension df, random walk exponent dw and conductivity exponent . This is not surprising as they result from the same physical process in the same environment. The Einstein relation (we work in 2 dimensions, d = 2) holds in the 95% confidence intervals, and notice that is quite robust through renormalization. These results highlight the deep fractal nature of karst network around Tulum.
The structure of the paper is as follows. Section 2 presents the study of the fractal dimension of Tulum's karst networks and the network renormalization scheme. Section 3 describes the determination of the value of the conductivity exponent using Einstein relation and the numerically computed walk exponent for both networks. Section 4 investigates the validity of the scaling law hypothesis for conductivity and the Einstein relation. We finish with a discussion and perspectives for future work.
2. Fractal Dimension of Ox Bel Ha and Sac Actun
To apply standard box counting algorithms on a network, it is first necessary to convert it to a binary image. However, significant information about network's topology may be lost during this conversion, resulting in coarse-grained images of the network and lost connectivity information of the underlying structure. In this paper, we employ a different approach.
Ox Bel Ha and Sac Actun networks are planar spatial graphs. Distributions of link lengths1 and node degrees are narrow for both networks, see Figure 2. Thus, in terms of degree distribution and links sizes both networks are quite homogeneous. Some basic properties of these networks are listed on Table 1.
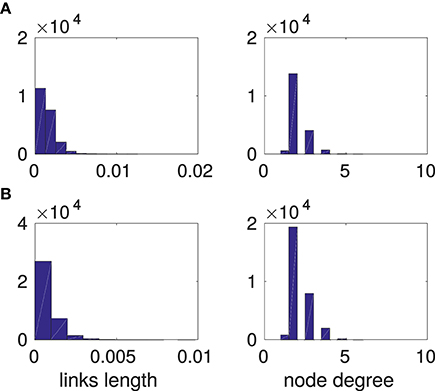
Figure 2. Links lengths size distribution and node degree distribution. Line (A) Ox Bel Ha, line (B) Sac Actun. Links length is computed on rescaled network hence it is a renormalized length.

Table 1. Basic networks properties for Ox Bel Ha and Sac Actun rescaled such that the maximal vertical extension is 1.
We apply the renormalization procedure proposed by Song et al. [10] to compute the fractal dimension of Ox Bel Ha and Sac Actun networks. Especially, we employ the Maximun-Excluded-Mass-Burning version of the scheme [15], which is adapted to the study of homogeneous networks. The procedure is illustrated in Figure 3. The network is tiled with boxes. A box is centered on a node of the network and contains all neighboring nodes separated, from the center, by a maximal chemical (topological) distance less than lB (the chemical distance between two nodes is the minimum number of links needed to go from one node to the other one). The parameter lB is named the box size. To build the renormalized network, each box is replaced by a single node. Two renormalized nodes (a and b) are linked if a link is connecting at least one node belonging to the box corresponding to a with one node of the box corresponding to b in the original network.
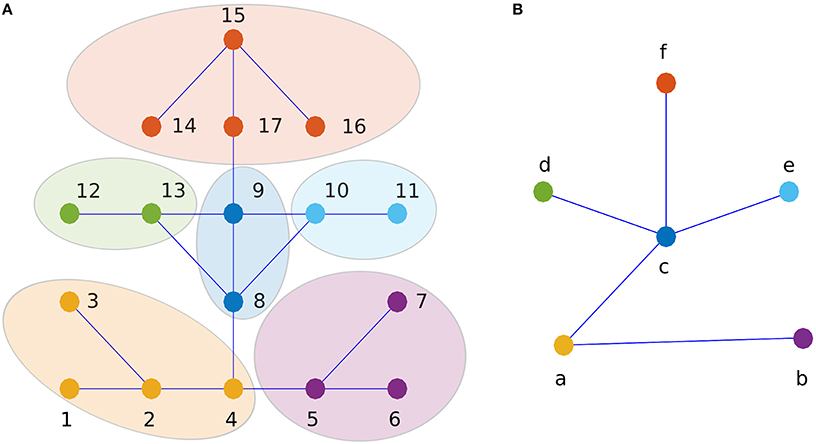
Figure 3. SHM renormalization scheme (the Maximun-Excluded-Mass-Burning version) illustrated on a generic network for a box of size lB = 2. (A) the initial network and (B) the first renormalization step. For example, on (A) renormalization of the yellow box (centered on the node 2) gives on (B) the yellow node labeled by a. The renormalized node, a, is located at the barycenter of the parents nodes 1, 2, 3, and 4. The procedure is repeated until the network collapse into an unique node. We can notice that the mean of links sizes grows from (A) to (B).
As we are dealing with spatial networks, a box (renormalized node) is located at the mean position of nodes that constitute it. At each renormalization step, we compute the mean of the distribution of link lengths and we take this as the characteristic length scale λ of the network. We notice that
where N is the number of nodes needed to tile the network Gλ and df is its fractal dimension. As lB has no physical significance in our study (due to cave divers mapping procedure), we take λ as the relevant length scale.
To illustrate the procedure, consider, as an example, the iterative building process of the 2 dimensional Sierpinski gasket as an inverse renormalization process (Figure 4). The number of nodes N(t) (i.e., the number of vertices) at the building step t is N(t) = 3(3t + 1) ∕ 2. Meanwhile, the links length λ(t) (the edge length) is reduced (compared to the t − 1 step) by a factor 2t. Therefore, assuming Equation (1) and t ≫ 1 we have,
which is the well-known Sierpinski gasket fractal dimension in 2 dimensions.
Figure 5 shows that the SHM renormalization scheme applied to spatially embedded planar networks succeeds (in the 95% confidence interval) to estimate the dimension of well-known fractal structures such as diffusion limited aggregate, percolation cluster and random space filling lattice. Computed fractal dimensions and reference values from Ben-Avraham and Havlin [16] are presented in Table 2. This gives us confidence on the relevance of the computed dimension for Ox Bel Ha and Sac Actun networks.
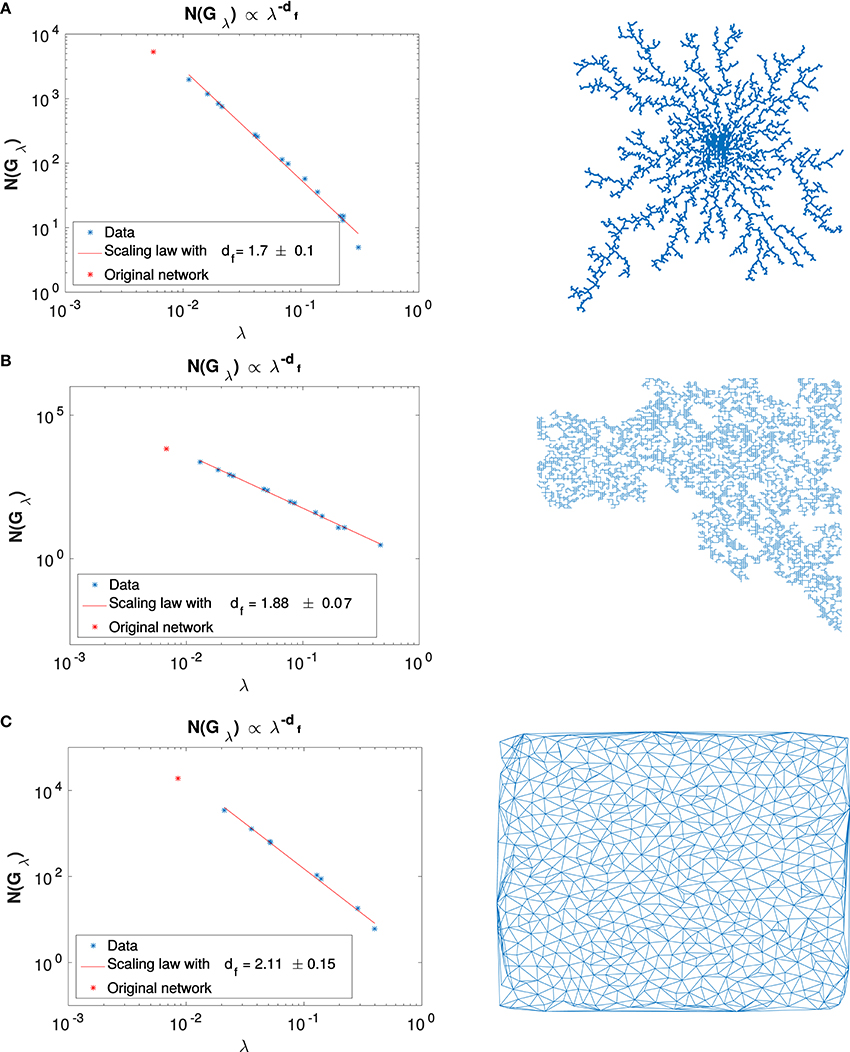
Figure 5. Fractal dimension computed through renormalization for (A) DLA, (B) percolated cluster, and (C) space filling networks.
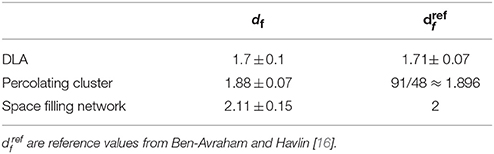
Table 2. df are fractal dimensions computed with the SHM's scheme (the estimated errors correspond the 95% confidence intervals).
Figure 6 illustrates four steps of the renormalization procedure applied to Ox Bel Ha. The renormalization scheme allows studying the large scale behavior of the network and how it evolves with scale. This procedure reveals the main structure of the network (analogous to its skeleton). One observes for example, in Figure 6 how large loops and main paths are highlighted.
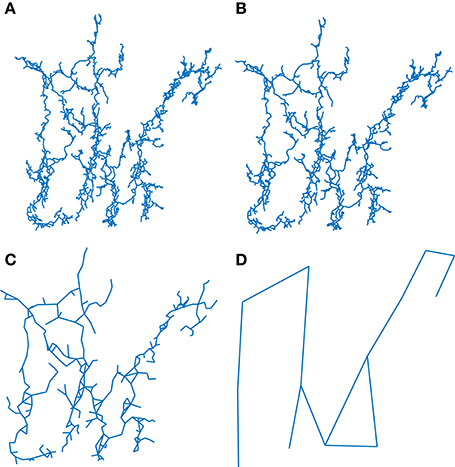
Figure 6. Renormalization scheme applied to Ox Bel Ha for lB = 2. (A) original network, (B–D) renormalized network after 2, 4, and 7 iterations.
Figures 7A,B show the results of the application of this procedure for the computation of the fractal dimensions for Ox Bel Ha and Sac Actun. Fractal dimensions of the two networks are quite close (considering the 95% confidence interval) and are around df ≈ 1.5. It is not surprising that these two networks are characterized by almost the same fractal dimension since they formed from the same physical processes, acting in the same environment at the same time.
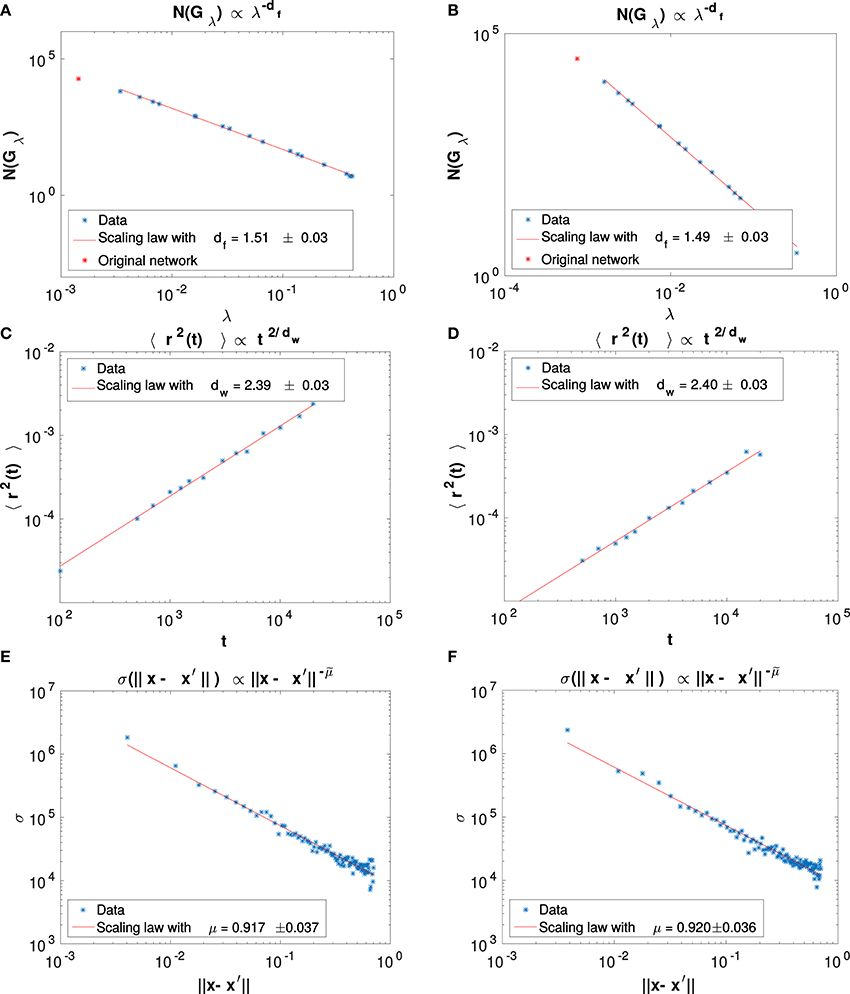
Figure 7. Numerical results for Ox Bel and Sac Actun respectively on the left column and on the right column. (A,B): fractal exponents. (C,D): walk exponents. (E,F): conductivity exponents. The estimated errors correspond the 95% confidence intervals for the fitted scaling laws.
3. Conductivity Exponent for Ox Bel Ha and Sac Actun
The results of the previous Section encourage further exploration of the fractal properties of Tulum's karst networks. It is well-known, see Ben-Avraham and Havlin [16], that the conductivity σ between two points of a fractal structure (e.g., a percolating cluster) follows a scaling law. The conductivity σ is a function of the Euclidean distance between these two points
with the conductivity exponent, L = ||x−x′||, x, x′ the location of two nodes of the network, and ||·|| the Euclidean distance. The conductivity exponent can be related to the structural properties of the fractal object (its fractal dimension and walk exponent) using the Einstein relation.
The Einstein relation links the conductivity to the diffusion coefficient D and the density n of the substrate (see again Ben-Avraham and Havlin [16])
Here, the substrate is the network which is embedded in the plane. Therefore, n depends on the spatial length scale L through the relation , with d = 2. The diffusion constant depends also on the length L of a walk of duration t and is . Diffusion is characterized by the walk exponent dw, and relates the mean square displacement 〈r2(t)〉 of a random walker with the displacement time t and position r(t):
with and r is the time averaged position of the walker.
Therefore, assuming Equation (4), we have the conductivity exponent
with
• d the dimension of the embedding space
• df the fractal dimension
• dw the random walk exponent
We compute dw on Ox Bel Ha and Sac Actun through random walk simulations. A random walk of t steps on a network is simply simulated taking a node randomly as the origin of the walk. From the origin the walker moves to one of its connected neighbors. The walk is stopped after t steps. Results are reported in Figure 7. Assuming Equation (6) we are able to compute the conductivity exponent for Ox Bel Ha and Sac Actun, results are reported on the last column of Table 3.
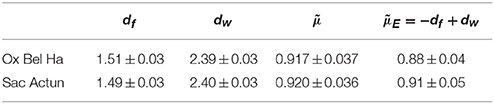
Table 3. Fractal dimension df, walk exponent dw, conductivity exponent , and the conductivity exponent given by Equation (6) for Ox Bel Ha and Sac Actun.
4. Flow Simulation and the Validity of the Einstein Relation
To examine the validity of Equation (6) for karst networks, we numerically investigate how the conductivity behaves between two randomly sampled nodes, A and B. Thus, we solve Kirchhoff equations [17] for Hagen-Poiseuille flow (or equivalently for a linear Ohm law) for the sub-network connecting A to B by imposing the inflow rate (we impose the same inflow rate for each sampled sub-network).
As we have no accurate information about the distribution of conduits radii (except a lower cut off, around 1 meter, due to the finite size of cave divers that mapped the network) we take it as unity. Hence the resistance of a link depends only of its length (which is peaked around λ).
Figure 7 shows plots of the conductivity with respect to the Euclidean distance and the value of the computed conductivity exponent are reported in Table 3. It is worth noticing that Einstein relation holds (in the 95% confidence interval) for karst networks around Tulum. It is not surprising as Ox Bel Ha and Sac Actun networks exhibit well marked fractal features. Moreover, the conductivity exponent seems to be invariant under renormalization for small characteristic length scales λ. At large scale, the value and the uncertainty on is larger. Figure 8 shows results of the computation of the conductivity exponent at different renormalization steps of Ox Bel Ha (a similar result holds for Sac Actun). This observation gives us confidence for modeling karst networks as a systems near criticality [18].
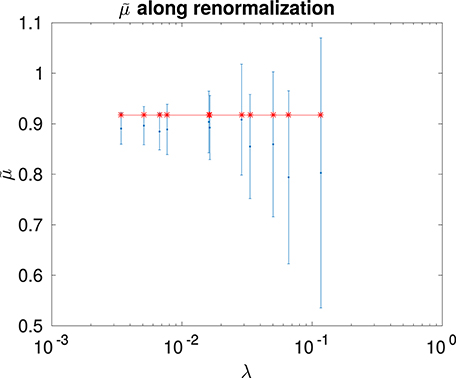
Figure 8. Conductivity exponent computed for Ox Bel Ha and its renormalizations at characteristic length scale λ. The line is the conductivity exponent of the original network.
5. Discussion
This study highlights the fractal properties of the karst networks around Tulum, Mexico. They behave as fractal structures. Networks are characterized by a scaling law for conductivity and anomalous diffusion. The Einstein relation holds for these structures.
We expect that these networks are not unique. Other coastal systems in the world, such as the ones encountered in Florida or in the Bahamas, are suspected to exhibit similar structures since they developed in geological and climatic environments (limestone platforms in a tropical and coastal area) similar to Tulum's karst networks.
Further analysis using data from such sites should be conducted to test our numerical results. Additional investigations (theoretical and numerical) should also conducted to determine the influence of turbulent flow on the conductivity exponent, and on the scaling hypothesis, because water flow in karst systems often occurs at high Reynolds number.
Our results indicate that the coastal karst networks of Tulum behave as self-similar structures, with well-behaved scaling properties. This suggests that karst systems can be studied and modeled in the framework of critical phenomena. Such models should be able to reproduce observed exponents and help explain the underlying process that results in the emergence of those values.
Author Contributions
MH conducted the analysis and wrote most of the paper. PR initiated the study, participated in the discussions and in the writing of the paper.
Funding
This work was funded by the Swiss National Science Foundation under the contract nb. 200021L_141298.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
The authors are grateful to James G. Coke IV, Bil Phillips, and Robbie Schmittner of Quintana Roo Speleological survey for having provided the data for the study, as well as two anonymous reviewers and Stephen A. Miller for having revised the final version of this manuscript.
Footnotes
1. ^A link does not represent a conduits but rather is the path between two sampled points in the network (a conduit can be mapped with N points and hence is represented by N − 1 links).
References
1. Hartmann A, Goldscheider N, Wagener T, Lange J, Weiler M. Karst water resources in a changing world: review of hydrological modeling approaches. Rev Geophys. (2014) 52:218–42. doi: 10.1002/2013RG000443
2. Kiraly L. Rapport sur l'état actuel des connaissances dans le domaine des caractères physiques des roches karstiques. In: Burger A, Dubertret L, editors. Hydrogeology of Karstic Terrains. paris: International Association of Hydrogeologists (1975). pp.53–67.
3. Cornaton F, Perrochet P. Analytical 1D dual-porosity equivalent solutions to 3D discrete single-continuum models. Application to karstic spring hydrograph modelling. J Hydrol. (2002) 262:165–76. doi: 10.1016/S0022-1694(02)00033-1
4. Hill ME, Stewart MT, Martin A. Evaluation of the MODFLOW-2005 Conduit Flow Process. Ground Water (2010) 48:549–59. doi: 10.1111/j.1745-6584.2009.00673.x
5. Jourde H, Cornaton F, Pistre S, Bidaux P. Flow behavior in a dual fracture network. J Hydrol. (2002) 266:99–119. doi: 10.1016/S0022-1694(02)00120-8
6. Borghi A, Renard P, Jenni S. A pseudo-genetic stochastic model to generate karstic networks. J Hydrol. (2012) 414:516–29. doi: 10.1016/j.jhydrol.2011.11.032
9. Kambesis PN, Coke JG IV. Overview of the controls on eogenetic cave and karst development in Quintana Roo, Mexico. In: Lace MJ, Mylroie JE, editors. Coastal Karst Landforms. Amsterdam: Springer (2013). pp. 347–73.
10. Song C, Havlin S, Makse HA. Self-similarity of complex networks. Nature (2005) 433:392–5. doi: 10.1038/nature03248
12. Kusumayudha SB, Zen M, Notosiswoyo S, Gautama RS. Fractal analysis of the Oyo River, cave systems, and topography of the Gunungsewu karst area, central Java, Indonesia. Hydrogeol J. (2000) 8:271–8. doi: 10.1007/s100400050014
13. Jeannin P, Groves C, Häuselmann P. Speleological investigations. In: Oldscheider N, Drew D, editors. Methods in Karst Hydrogeology. London: Taylor & Francis (2007). pp. 25–44.
14. Pardo-Iguzquiza E, Durán-Valsero JJ, Rodríguez-Galiano V. Morphometric analysis of three-dimensional networks of karst conduits. Geomorphology (2011) 132:17–28. doi: 10.1016/j.geomorph.2011.04.030
15. Song C, Gallos LK, Havlin S, Makse HA. How to calculate the fractal dimension of a complex network: the box covering algorithm. J Stat Mech. (2007) 2007:P03006. doi: 10.1088/1742-5468/2007/03/P03006
16. Ben-Avraham D, Havlin S. Diffusion and Reactions in Fractals and Disordered Systems. Cambridge: Cambridge University Press (2000).
Keywords: karst network, fractal, renormalization, Einstein relation, critical phenomena
Citation: Hendrick M and Renard P (2016) Fractal Dimension, Walk Dimension and Conductivity Exponent of Karst Networks around Tulum. Front. Phys. 4:27. doi: 10.3389/fphy.2016.00027
Received: 16 May 2016; Accepted: 20 June 2016;
Published: 30 June 2016.
Edited by:
Zbigniew R. Struzik, The University of Tokyo, JapanCopyright © 2016 Hendrick and Renard. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Martin Hendrick, bWFydGluLmhlbmRyaWNrQHVuaW5lLmNo
 Martin Hendrick
Martin Hendrick Philippe Renard
Philippe Renard