Quantization, Frobenius and Bi Algebras from the Categorical Framework of Quantum Mechanics to Natural Language Semantics

1. Introduction

Categorical compositional distributional semantics is a model of natural language that combines the statistical vector models of word meanings with the compositional models of grammar. The grammatical structures are modeled as morphisms of a compact closed category of grammatical types, the vector representations of word meanings are modeled as morphisms of the category of finite dimensional vector spaces, which is also a compact closed category. The passage from grammatical structure to vectorial meaning is by connecting the two categories with a structure preserving map, in categorial words, a functor.

$F:\text{Grammar}\Rightarrow \text{Meaning}$

This passage allows us to build vector representations for meanings of phrases and sentences, by using the vectors of the words and the grammatical structure of the phrase or sentence. Formally, this procedure is the application of the image of the functor on the grammatical structure to the meaning vectors of the words. Still more formally, given a string of words w₁w₂ ⋯ w_n, one first formalizes their grammatical structure as a morphism α in the compact closed category of grammar, introduced by Lambek and Lambek and Preller, as the categorical semantics of pregroup type-logical grammars, see Lambek [1, 2]. We denote these below by Preg. The vector meanings of words live the category of finite dimensional vector spaces, denoted below by FVect. The more concrete version of the above functor is thus as follows:

$F:Preg\Rightarrow FVect$

The functor F transforms α to a linear map in FVect. This linear map is applied to the vectors of the words within the phrase or sentence. The whole procedure is formalized below:

$(*)\overrightarrow{w_1{w}_2\cdots w_n}=F({\vec{w}}_1\otimes {\vec{w}}_2\otimes \cdots \otimes {\vec{w}}_n)$

Vectors of words, i.e., the ${\vec{w}}_i$'s are represented by morphims I → V of the category of finite dimensional vector spaces, for V the vector space in which the meaning of the word lives. The tensor product ⊗ between these morphisms is the categorical way of packing them together. This model, referred to by DisCoCat, for Categorical Compositional Distributional, was the first model that put together the vector meanings of words by taking into account their grammatical structure, in order to build a vector for the phrase or sentence containing the words.

DisCoCat relates to the categorical models of Quantum phenomena in two ways. One is through the function F; quoting from Coecke et al. [3]:

“A structure preserving passage to the category of vector spaces is not a one-off development especially tailored for our purposes. It is an example of a more general construction, namely, a passage long-known in Topological Quantum Field Theory (TQFT). This general passage was first developed by Atiyah [4] in the context of TQFT and was given the name “Quantization,” as it adjoins “quantum structure” (in terms of vectors) to a purely topological entity, namely the cobordisms representing the topology of manifolds. Later, this passage was generalized to abstract mathematical structures and recast in terms of functors whose co-domain was FVect by Baez and Dolan [5] and Kock [6]. This is exactly what is happening in our [DisCoCat] semantic framework: the sentence formation rules are formalized using type-logics and assigned quantitative values in terms of vector composition operations. This procedure makes our passage from grammatical structure to vector space meaning a “Quantization” functor. Hence, one can say that what we are developing here is a grammatical quantum field theory for Lambek pregroups. ”

The other connection is that the DisCoCat model, i.e., the tuple (Preg, FVect, F), was originally inspired by the categorial model of Quantum Mechanics, as developed by Abramsky and Coecke [7]. CQM, for Categorical Quantum Mechanics, models Quantum protocols using compact closed categories and their vector space instantiations (more specifically they use dagger compact closed categories and category of Hilbert spaces, which have also been used in DisoCat, e.g., see [8]). The aim of this review is to briefly describe the DisCoCat model and its recent extensions with Frobenius and Bi algebras. These extensions were inspired by extensions to categorical Quantum Mechanics: the work of Coecke et al. [9, 10] for the use of Frobenius Algebras and Coecke and Duncan [11] for Bialgebras. These extensions have enabled us to reason, in a structured way, about logical words of language such as relative pronouns “who, whom, what, that, which, etc.” and quantifiers “all, some, at least, at most, none, etc.”

In what follows, we will first review the advances made in the DisCoCat model in a chronological order; then go through the the core of theoretical underpinnings of the model and finally present some of the main experiments performed to validate the theoretical predictions.

2. A Chronological Overview of DisCoCat

The origins of the DisCoCat model goes back to the work of Clark and Pulman [12], presented in the AAAI Spring Symposium on Quantum Interaction (QI) in 2007. The paper discussed vector models of word meaning, otherwise known as distributional semantics, and outlined an open problem they faced. The open problem is how to extend distributional models so that they can assign vector meanings to phrases and sentences of language. In their proposed extended model, Clark and Pulman, inspired by the Harmonic Grammars of Smolensky [13], argue for the use of tensors. The vector meaning of a string of words w₁w₂ ⋯ w_n, as defined by them, is as follows:

$\overrightarrow{w_{!}{w}_1\cdots w_n}={\displaystyle \sum _i}{\vec{w}}_i\otimes {\vec{r}}_i$

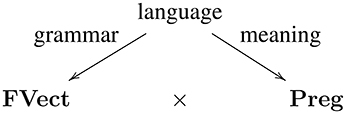
where ${\vec{r}}_i$ is a vector representing the grammatical role played by word w_i in the string. The problem with this model is that firstly, vector meanings of sentences grow as the sentence becomes larger and building tensor models for them becomes costly. Secondly, sentences that have different grammatical meanings live in different spaces and thus their meanings cannot be compared to each other. Further, Clark and Pulman do not provide any experimental support for their models. Subsequently, in a paper presented in QI in 2008, Stephen et al. [14], addressed the former two of these problems by presenting the first DisCoCat model. An extended version of this paper later appeared in Lambek's 90'th Festschrift [15] in 2010. The original DisCoCat model presented there worked along side the following triangle:

where the space between the FVect and Preg was interpreted as pairing. That is, instead of working with a functor between the two categories of grammar and meaning, there is only one category: the category whose objects are pairs (V, p) of V a vector space and p its grammatical type (i.e., the grammatical type of the words living in that category), and whose morphisms are also pairs (f : V → W, p ≤ q), for f : V → W a linear map and ≤ :p → q the partial ordering of the pregroup grammar. In this model, pregroups where treated as partial order categories. The functorial form of DisCoCat, described in the introduction, was fist introduced by Preller and Sadrzadeh [16] in 2010 and later connected to the Quantization of TQFT by Coecke et al. [3] in 2013. Similar connections, albeit not in a functorial form and not to TQFT but to CQM in general, were also drawn in a paper by Lambek [17]. It should be noted that the main contribution of Coecke et al. [3] was however, to extend the functorial passage and thus the DisCoCat from Lambek Pregroups to the original monoidal calculus of Lambek [18].

$F:\text{Monoidal Closed Cats}\Rightarrow \mathrm{FVect}$

Although grammar-aware vector space models of meaning existed for adjective noun phrases via the work of Baroni and Zamparelli [19], but the above DisCoCat model was the first one where this grammar-awareness was theoretically defined for all language constructs. Later, in 2013, in the paper by Grefenstette et al. [20], it was shown how the concrete constructions of Baroni and Zamparelli [19] can be used in the DisCoCat to build matrices and tensors for intransitive and transitive verbs. But extending these concrete models to words such as relative pronouns, quantifiers and prepositions proved to be problematic, due to data sparsity, as also shown in Baroni et al. [21].

The theoretical predictions of DisCoCat were first experimentally verified in a paper by Grefenstette and Sadrzadeh [22]. They presented an algorithm to build the matrices/tensors of the model and implemented it on intransitive and transitive verbs and further applied these to a disambiguation task. The intransitive version of the task was originally developed by Mitchell and Lapata [23], the extension to transitive was a novel contribution, leading to a dataset that was later used by the community in many occasions. In a short paper in the same year [24] presented a few extensions to the constructions of the latter model. The full set of results, together with extensions to adjective-noun phrases and sentences containing them, appeared in the journal article by Grefenstette and Sadrzadeh [25].

The model described above had one flaw, namely that sentences of different types acquired vectors that lived in different vectors spaces. This made it impossible to fully benefit from DisCoCat, one of whose original promises was an extension of the model of Clark and Pulman to one that one can actually compare sentences. This shortcoming was later overcome by Kartsaklis et al. [26], where it was shown that two possible applications of Frobenius algebras on the concrete model of Grefenstette and Sadrzadeh [22] solves the problem and leads us to a uniform sentence space.

After the above, DisCoCat has been extended to cover larger fragments of language and also it has been implemented on different vector models with different implementation parameters and experimented with in different settings. These latter contributions include the following:

• Prior disambiguation of tensors by sense-clustering and separating different meanings, based on the contexts in which the words appear. For the case of a verb, we first disambiguate its subject and objects by clustering, then build verb tensors using disambiguated versions of these vectors. The experimental support we provided for this work showed that the disambiguated models indeed perform better than their ambiguous versions, these results were presented in Kartsaklis et al. [27] and Kartsaklis and Sadrzadeh [28].

• Experiments in support of entangled tensors in the linguistics applications listed above. Our so called tensors are elements of tensor spaces, which are in turn built from spaces of the types of the corresponding words (e.g., a verb or an adjective). Some elements of such spaces are separable and some are not. In the separable case, for t ∈ A ⊗ B we have two other elements a ∈ A, b ∈ B such that t = a ⊗ b. In the non-separable case, this factorization will not be possible. In Quantum Mechanics, the non-separable elements correspond to entangled states of a physical system. A question arises that whether our linguistic tensors are separable or not. We answered this question by measuring the degree of entanglement of our tensors and showing that the ones with a higher degree led to better results, as presented in Kartsaklis and Sadrzadeh [29].

• Application of neural word embeddings in the tensor models. Recent work on deep neural nets has led to creation of large sets of vectors for words, referred to by word embeddings, as presented in Mikolov et al. [30, 31]. These vectors are now hosted by Google in their Tensor Flow platform¹. The popularity and good performance of the vectors in various tasks and models makes one ask whether or not they would work well in a tensor framework as well. The work in Milajevs et al. [32] showed that this is indeed the case.

• Developing a theory of entailment for the tensor models. Distributional semantics supports word-level entailment via a distributional inclusion hypothesis, where inclusion relations between features of words is put forward as a signal for the entailment relations between words. We showed how this model can be extended from word to sentence-level in a compositional fashion. We worked out different feature inclusion relations for features of sentences that were built using different compositional operations. We developed new datasets and measured performances of our feature inclusion relations, the results appeared in Kartsaklis and Sadrzadeh [33, 34].

We have also extended the model theoretically, where the major contributions are as follows:

• The use of Frobenius and Bi algebras to model linguistic phenomena that involve certain types of rearranging of information within phrases and sentences. An example of such a phenomena is relative and quantified clauses, such as “all men ate some cookies,” “the man who ate the cookies” and “the man whose dogs ate the cookies.” We extended the DisCoCat model from compact closed categories to ones with Frobenius and Bi algebras over them and showed how the copying and merging operations of these algebras allow us to model meanings of quantified and relative clauses and sentences. The work done here includes that of Clark et al. [35], Sadrzadeh et al. [36, 37], Hedges and Sadrzadeh [38] and Sadrzadeh [39].

• Density matrices are the core of vector space models of Quantum Mechanics and indeed it has been shown that the category of density matrices and completely positive maps is also a compact closed category. The question arises so as whether and how these matrices have applications in linguistics. The work of Piedeleu et al. [8], Balkir et al. [40, 41] and Bankova et al. [42] showed that density matrices can model different meanings of ambiguous words and that they can also model a hierarchy of these meanings and thus be applied to entailment.

3. Overview of Theory

This section reviews the theoretical framework of a DisCoCat. Its structure is as follows: in Section 3.1, we will review the distributional semantic models. We show how the motivating idea of these models are formalized in terms of vector representations and describe some theoretical and experimental parameters of the model and some of the major applications thereof. In Section 3.2. we review the grammatical model that was first used as a basis for compositional distributional models, namely the pregroup grammars of Lambek. We review the theory of pregroup algebras and exemplify its applications to reasoning about grammatical structures in natural language. In Section 3.3, we show how a functorial passage can be developed between a pregroup grammar, seen as a compact closed category, and the category of finite dimensional vector spaces and linear maps. We describe how this passage allows one to assign compositional vector semantics to words and sentences of language. This passage is similar to the one used in TQFT, where the grammatical part is replaced by the category of manifolds and cobordisms. Section 3.4, describes the theory of Frobenius and Bi algebras over compact closed categories. In Section 3.5, we show how these algebras can model meanings of relative and quantified clauses and sentences. In Section 3.6, we go through the graphical calculus of compact closed categories and Frobenius and Bi algebras over them. We exemplify how these are used in linguistics, where they depict flows of information between words of a sentence.

3.1. Vector Models of Natural Language

Given a corpus of text, a set of contexts and a set of target words, the vector models of words work with a so called co-occurrence matrix. This has at each of its entries “the degree of co-occurrence between the target word and the context,” developed amongst other by Salton et al. [43] and Rubenstein and Goodenough [44]. This degree is determined using the notion of a window: a span of words or grammatical relations that slides across the corpus and records the co-occurrences that happen within it. A context can be a word, a lemma, or a feature. A lemma is the canonical form of a word; it represents the set of different forms a word can take when used in a corpus. A feature represents a set of words that together express a pertinent linguistic property of a word. Given an m × n co-occurrence matrix, every target word t can be represented by a row vector of length n. For each feature c, the entries of this vector are a function of the raw co-occurrence counts, are computed as follows:

$ra{w}_f\left(t\right)=\frac{{\displaystyle {\sum }_{c}N\left(f,t\right)}}{k}$

for N(f, t) the number of times the t and f have co-occurred in the window. Based on L, the total number of times that t has occurred in the corpus, the raw count is turned into various normalized degrees. Some common examples are probability, conditional probability, likelihood ratio and its logarithm: The lengths of the corpus, window, and normalization scheme are parameters of the model, as are the sizes of the feature and target sets, there has been a plentiful of papers who study these parameters, for example see Lapesa and Evert [45], Bullinaria and Levy [46], and Turney [47].

The distance between the meaning vectors, for instance the cosine of their angle, provides an experimentally successful measure of similarity of their meanings. For example, in the vector space of Figure 1, cited from Coecke et al. [3], the angle between meaning vectors of “cat” and “dog” is small and so is the angle between meaning vectors of “kill” and “murder.” Such similarity measures have been implemented on large scale data (up to a billion words) to build high dimensional vector spaces (tens of thousands of basis vectors). These have been successfully applied to automatic generation of thesauri and other natural language tasks such as automatic indexing, meaning induction from text, and entailment, for example see Curran [48], Lin [49], Landauer and Dumais [50], Geffet and Dagan [51], and Weeds et al. [52].

FIGURE 1

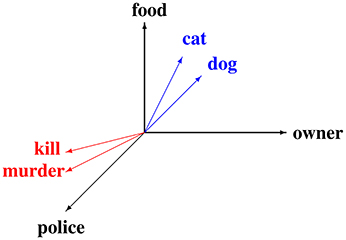
Figure 1. A subspace of a vector space model of meaning, built from real data, cited from Coecke et al. [3].

3.2. Pregroup Grammars

A pregroup algebra, as defined by Lambek [1], is a partially ordered monoid (P, ≤, ·, 1) where every element has a left and a right adjoint, which means that for every element p ∈ P we have a p^r ∈ P and a p^l ∈ P such that the following four inequalities hold:

$p·p^r\le 1\le p^r·p{p}^l·p\le 1\le p·p^l$

An example of a pregroup in arithmetics is the set of unbounded monotone functions on integers, where the monoid multiplication is function composition with the identity function its unit, and the left and right adjoints defined using min and max of integers. For reasons of space, we will not give these definitions here and refer the reader to Lambek [1, 2].

Pregroup algebras are applied to natural language via the notion of a pregroup grammar, defined to be a pair 〈D, S〉, where D is a pregroup lexicon and S ⊂ B is a set of designated types, containing types such as that of a declarative sentence s, and a question q. A pregroup lexicon is a binary relation D, defined as

$D\subseteq \Sigma \times T(B)$

where T(B) is the free pregroup generated over B (for the free construction see [1]).

Given a pregroup grammar, as specified in Lambek [1], one says that a string of words w₁w₂ ⋯ w_n of language is grammatical iff for 1 ≤ i ≤ n, there exists a (w_i, t_i) ∈ D, such that we have a type t ∈ T(B) ∩ D[Σ] such that the following partial order holds in T(B):

$t_1·t_2·\cdots ·t_n\le t$

An example of a pregroup lexicon is presented in Table 1:

TABLE 1

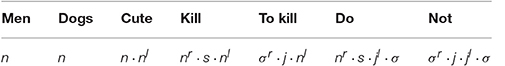
Table 1. Type assignments for a toy language in a Lambek pregroup; table from Coecke et al. [3].

The pregroup reductions corresponding sentences (1) “men kill dogs,” (2) “men kill cute dogs,” and (3) “men do not kill dogs” are as follows (all cited from [3]):

$\begin{array}{l}(1)n·n^r·s·n^l\le 1·s·1=s\hfill \\ (2)n·n^r·s·n^l·n·n^l·n\le 1·s·1·1=s\\ (3)n·n^r·s·j^l·\sigma ·{\sigma }^r·j·j^l·\sigma ·{\sigma }^r·j·n^l·n\\ \le 1·s·j^l·1·j·j^l·1·j·1=s·j^l·j·j^l·j\le s\end{array}$

3.3. Quantization

In order to formalize the structure preserving passage between syntax: pregroup grammars and semantics: vector models, we formalize both of these in the language of compact closed categories [53]. For this reason, we very briefly recall some definitions. A compact closed category has objects A, B; morphisms f : A → B; a monoidal tensor A ⊗ B that has a unit I; and for each object A two objects A^r and A^l together with the following morphisms:

$A\otimes A^r\stackrel{{ϵ}_A^r}{\to }I\stackrel{{\eta }_A^r}{\to }{A}^r\otimes A{A}^l\otimes A\stackrel{{ϵ}_A^l}{\to }I\stackrel{{\eta }_A^l}{\to }A\otimes A^l$

These morphisms have to satisfy certain other conditions, among which are the four yanking equations, which for reasons of space we will not give here. It is evident (and has also been proven, see for example [17, 54]), that pregroup algebras are compact closed categories. This is by taking the above ϵ and η maps to be the four adjoint inequalities of a pregroup algebra. Finite dimensional vector spaces with linear maps as morphisms are also compact closed categories, this has been shown by Kelly and Laplaza [53]. This category is symmetric, thus the left and right adjoints collapse to one, that is for V a finite dimensional vector space, we have V^l = V^r = V*, where V* is the dual space of V. In the presence of a fixed basis, however, one obtains the equivalence V ≡ V*. Assuming so, the ϵ and η maps are defined as follows, for ${\left\{{\vec{r}}_i\right\}}_i$ a fixed basis:

$\begin{array}{l}ϵ={ϵ}^l={ϵ}^r:V\otimes V\to ℝ \hfill \\ ::{\displaystyle \sum _{ij}{c}_{ij} {\overrightarrow{r}}_i\otimes {\overrightarrow{r}}_j}\mapsto {\displaystyle \sum _{ij}{c}_{ij}\langle {\overrightarrow{r}}_i\mid {\overrightarrow{r}}_j\rangle }\hfill \\ \eta ={\eta }^l={\eta }^r:ℝ\to V\otimes V^{*} ::1\mapsto {\displaystyle \sum _i{\overrightarrow{r}}_i\otimes {\overrightarrow{r}}_i}\hfill \end{array}$

Now we can define the structure preserving map via the following Quantization functor:

$F:\text{Preg}\Rightarrow \text{FVect}$

explicitly defined as follows:

• For n, s ∈ B and two atomic vector spaces W and S, we have F(n) = W and F(s) = S,

• For p, q ∈ T(B) \ (B ∪ {1}), we have F(p · q) = F(p) ⊗ F(q),

• For 1 ∈ T(B), we have F(1) = ℝ,

• For adjoints we have, F(p^r) = F(p^l) = F(p),

• For morphisms, we have F(p ≤ q) = F(p) → F(q).

We have now formally defined a DisCoCat: the tuple (Preg, FVect, F), as defined above. It is in this setting that one obtains vector representations for sentences by applying the definition (*) of introduction. For example, the vector representations of two of our example sentences above become as follows:

$\begin{array}{l}\overrightarrow{\mathrm{\text{men kill dogs}}}=({ϵ}_W\otimes 1_S\otimes {ϵ}_W)(\overrightarrow{\mathrm{\text{men}}}\otimes \overrightarrow{kill}\otimes \overrightarrow{dogs})\\ ={\displaystyle \sum _{ijk}}{c}_{ijk}\langle \overrightarrow{\mathrm{\text{men}}}\mid {\vec{w}}_i\rangle \langle {\vec{w}}_k\mid \overrightarrow{\mathrm{\text{dogs}}}\rangle {\vec{s}}_j\\ \overrightarrow{\mathrm{\text{men kill cute dogs}}}=\\ ({ϵ}_W\otimes 1_S\otimes {ϵ}_W\otimes {ϵ}_W)(\overrightarrow{\mathrm{\text{men}}}\otimes \overrightarrow{\mathrm{\text{kill}}}\otimes \overrightarrow{\mathrm{\text{cute}}}\otimes \overrightarrow{\mathrm{\text{dogs}}})\\ ={\displaystyle \sum _{ijk}}{\displaystyle \sum _{lm}}{c}_{ijk}{c}_{lm}\langle \overrightarrow{men}\mid {\vec{w}}_i\rangle \langle {\vec{w}}_k\mid {\vec{w}}_l\rangle \langle {\vec{w}}_m\mid \overrightarrow{dogs}\rangle {\vec{s}}_j\end{array}$

An important observation is that in this setting one obtains that, vector representations of words that have atomic types, e.g., men and dogs with type n are vectors $\overrightarrow{\text{men}},\overrightarrow{\text{dogs}}\in W$. The representations of other words, e.g., cute and kill with types n^rs and n^rsn^l are matrices ${\displaystyle \sum }_{ij}{c}_{ij}{\vec{w}}_i\otimes {\vec{w}}_j\in W\otimes W$ for ${\left\{\overrightarrow{w_i}\right\}}_i$ a basis for W and tensors ${\displaystyle {\sum }_{ijk}{c}_{ijk}{\overrightarrow{w}}_i\otimes {\overrightarrow{s}}_j\otimes {\overrightarrow{w}}_k\in W\otimes S\otimes W}$, for ${\left\{{\vec{s}}_j\right\}}_j$ a basis in S.

3.4. Frobenius and Bi Algebras

Both Frobenius and Bi algebras are defined over a symmetric monoidal category C. Frobenius Algebras were developed in their current from by Kock [6] and McCurdy [55], bialgebras by McCurdy [56] and Bonchi et al. [57]. Formally, they are both denoted by tuples (X, δ, ι, μ, ζ) where, for X an object of C, the triple (X, δ, ι) is an internal comonoid and the triple (X, μ, ζ) an internal monoid; i.e., the following are coassociative and counital, respectively associative and unital morphisms of C:

${\delta }_X:X\to X\otimes X{\iota }_X:X\to I{\mu }_X:X\otimes X\to X{\zeta }_X:I\to X$

One difference between these two is that the Frobenius algebra satisfies the following so-called Frobenius condition (due to [58] who originally introduced the algebraic form of these in the context of representation theorems for group theory):

$({\mu }_X\otimes 1_X)\circ (1_X\otimes {\delta }_X)={\delta }_X\circ {\mu }_X=(1_X\otimes {\mu }_X)\circ ({\delta }_X\otimes 1_X)$

The bialgebras satisfy a weaker version of this condition, referred to by Q3 in McCurdy [56]

${\delta }_X\circ {\mu }_X=({\mu }_X\otimes {\mu }_X)\circ (1_X\otimes {\sigma }_{X,X}\otimes 1_X)\circ ({\delta }_X\otimes {\delta }_X)$

for σ_X,X the symmetry morphism of the category C. Both these algebras do satisfy other conditions, which we will not give here.

In FVect, any vector space V with a fixed basis ${\left\{\overrightarrow{v_i}\right\}}_i$ has a Frobenius algebra over it, explicitly given by:

$\begin{array}{l}{\delta }_V::\overrightarrow{v_i}\mapsto \overrightarrow{v_i}\otimes \overrightarrow{v_i}{\iota }_V::\overrightarrow{v_i}\mapsto 1\\ {\mu }_V::\overrightarrow{v_i}\otimes \overrightarrow{v_j}\mapsto {\delta }_{ij}\overrightarrow{v_i}{\zeta }_V::1\mapsto {\displaystyle \sum _i}\overrightarrow{v_i}\end{array}$

where δ_ij is the Kronecker delta. These definitions were introduced in Coecke et al. [9, 10] to characterize vector space bases.

Bialgebras over vectors spaces were introduced in Coecke and Duncan [11] to characterize phases. For linguistic purposes, however, we use a different definition, first introduced in Hedges and Sadrzadeh [38]. Let V be a vector space with basis ${P}(U)$, where U is an arbitrary set. We give V a bialgebra structure as follows:

$\begin{array}{l}{\iota }_{{P}(U)}|A=1{\delta }_{{P}(U)}|A=|A\otimes |A\\ {\zeta }_{{P}(U)}=|U{\mu }_{{P}(U)}(|A\otimes |B)=|A\cap B\end{array}$

The Frobenius and the bialgebra δ act similarly here: they both copy their input, that is given a vector $\vec{\upsilon }$, the produce two copies of it $\vec{\upsilon }\otimes \vec{\upsilon }$. The slight difference in this special natural language instantiation is that the inputs to the bialgebra δ's are vectors whose basis are subsets of a universal set U, whereas the inputs to Frobenius algebra δ's can be any vector. The main difference between these two algebras are in their μ maps. The Frobenius μ, when inputted with two same vectors, returns one of them, the bialgebra μ acts on any two input vectors, but of course these both have to have as basis subsets of ${P}(U)$, and returns the “intersection” of these two vectors. By “intersection of vectors” we mean (as defined above), a vectors whose basis is the intersection of the basis of the input vectors.

The reason for working with the above bialgebras is that they are there to model generalized quantifiers of Barwise and Cooper [59]. These quantifiers are defined as maps with the type ${P}(U)\to {P}{P}(U)$. In order to see why, consider the following definition for the logical quantifiers “all” and “some”:

$\begin{array}{l}\left[\left[\mathrm{\text{some}}\right]\right](A)=\left\{X\subseteq U\mid X\cap A\ne \varnothing \right\}\\ \left[\left[\mathrm{\text{every}}\right]\right](A)=\left\{X\subseteq U\mid A\subseteq X\right\}\end{array}$

A similar method is used to define non-logical quantifiers, for example “most A” is defined to be the set of subsets of U that has “most” elements of A, “few A” is the set of subsets of U that contain “few” elements of A, and similarly for “several” and “many.” These functions can be formalized as relations over ${P}(U)$, where they will thus obtain the type ${P}(U)\to {P}(U)$. These relations can be formalized in the category of sets and relations, which is also compact closed. The above definitions are vector space generalizations of the bialgebras defined for relations. They enable us to work with intersection of these relations. This is an operation that allows Barwise and Cooper to formalize an important property of generalized quantifiers of natural language, i.e., that they are conservative. For details and the from-relation-to-vector embedding, see Hedges and Sadrzadeh [38].

3.5. Relative Pronouns and Quantifiers

In order to model relative pronouns and quantifiers, according to the developments of Clark et al. [35], Sadrzadeh et al. [36, 37], and Hedges and Sadrzadeh [38], one adds to the pregroup lexicon, the following assignments:

To subject relative pronouns “who, that, which,” we assign type n^rns^ln

To object relative pronouns “whom, that, which,” we assign type n^rnn^lls^l

To determiners of any role “a, the, all, every, some, none, at most, many, ⋯  ,” we assign type nn^l

The vectorial representations of the subject and object relative pronouns are as follows, respectively for each case:

$\begin{array}{l}\overrightarrow{\mathrm{\text{Sbj Rel}}}:=(1_W\otimes {\mu }_W\otimes {\zeta }_S\otimes 1_W)\circ ({\eta }_W\otimes {\eta }_W)\\ \overrightarrow{\mathrm{\text{Obj Rel}}}:=(1_W\otimes {\mu }_W\otimes 1_W\otimes {\zeta }_S)\circ ({\eta }_W\otimes {\eta }_W)\end{array}$

where the μ_W and ζ_S are maps of the Frobenius algebras defined over the W and S spaces. The vectorial representation of the determiners are as follows:

$\begin{array}{l}\overrightarrow{\mathrm{\text{determiner}}}:=(1_W\otimes {ϵ}_W)\circ (1_W\otimes {\mu }_W\otimes {ϵ}_W\otimes 1_W)\\ \circ (1_W\otimes \overline{\left[\left[d\right]\right]}\otimes {\delta }_W\otimes 1_{W\otimes W})\\ \circ (1_W\otimes {\eta }_W\otimes 1_{W\otimes W})\circ ({\eta }_W\otimes 1_W)\end{array}$

where the μ_W and δ_W maps are bialgebraic maps defined over the space $W=V_{{P}(U)}$, which is notation for a vector space spanned by the subsets of the set U. The $\overline{\left[\left[d\right]\right]}$ map has type W → W, it is a linear map that directly encodes the relational graph of the generalized quantifier d.

By applying definition (*) from the introduction, one obtains vectorial representations for relative clauses and quantified sentences. An example of the former is “men who eat cake,” which acquires the following vectorial representation:

$\begin{array}{l}\overrightarrow{\mathrm{\text{men who eat cake}}}:=(1_W\otimes {ϵ}_W)\circ ({ϵ}_W\otimes 1_{W\otimes S}\otimes {ϵ}_W\otimes 1_S\otimes {ϵ}_W)\\ (\overrightarrow{\mathrm{\text{men}}}\otimes \overrightarrow{\mathrm{\text{who}}}\otimes \overrightarrow{\mathrm{\text{eat}}}\otimes \overrightarrow{\mathrm{\text{cake}}})\end{array}$

This simplifies as follows, after opening up the meaning of “who” using the “Obj Rel” definition above:

$\begin{array}{l}({\mu }_W\otimes {ϵ}_W)(\overrightarrow{\mathrm{\text{men}}}\otimes \overrightarrow{\mathrm{\text{eat}}}\otimes \overrightarrow{\mathrm{\text{cake}}})\\ =({\mu }_W\otimes {ϵ}_W)\left({\displaystyle \sum _{k\in K}}{\vec{w}}_k\otimes ({\displaystyle \sum _{ij}}{\alpha }_{ij}{\vec{w}}_i\otimes {\vec{w}}_j)\otimes {\displaystyle \sum _{l\in L}}{\vec{w}}_l\right)\\ ={\displaystyle \sum _{ij,k\in K,l\in L}}{\alpha }_{ij}{\mu }_W({\vec{w}}_k\otimes {\vec{w}}_i)\otimes {ϵ}_W({\vec{w}}_j\otimes {\vec{w}}_l)\\ ={\displaystyle \sum _{ij,k\in K,l\in L}}{\alpha }_{ij}{\delta }_{ki}{\vec{w}}_i{\delta }_{jl}={\displaystyle \sum _{k\in K,l\in L}}{\alpha }_{kl}{\vec{w}}_k\end{array}$

An example of a quantified sentence is “most cats snore,” which acquires the following vectorial representation,

$({ϵ}_W\otimes 1_S)\circ (1_W\otimes {ϵ}_W\otimes 1_{W\otimes S})(\overrightarrow{\mathrm{\text{most}}}\otimes \overrightarrow{\mathrm{\text{cats}}}\otimes \overrightarrow{\mathrm{\text{snore}}})$

The above simplifies to the following

$({ϵ}_W)\circ (\overrightarrow{\left[\left[\mathrm{\text{most}}\right]\right]}\otimes {\mu }_W\otimes 1_S)\circ ({ϵ}_W\otimes 1_S)(\overrightarrow{\mathrm{\text{men}}}\otimes \overrightarrow{\mathrm{\text{snore}}})$

Different instantiations for U and S are provided in Hedges and Sadrzadeh [38], as an example consider U to be the set of words of language, in which case ${P}(U)$ represents the set of, what is called “lemmas” of language, i.e., the set of canonical forms of words. One takes $S=V_{{P}(S^{\prime })}$, for S′ an abstract sentence space, denoted by the symbol S in our previous examples. In this case, the above categorical definition takes a concrete instantiation as follows:

${\displaystyle \sum _{ijk}}{\displaystyle \sum _{B\in \left[\left[most\right]\right](\left[\left[cat\right]\right])}}{c}_i^{cat}{c}_{jk}^{snore}{c}_B^{most}\langle B\mid A_i\cap A_j\rangle |s_k$

where we have $\overrightarrow{\text{cats}}:={\displaystyle {\sum }_i{c}_i^{cat}|A_i}$ for A_i ⊆ U and $\overrightarrow{\text{snore}}:={\displaystyle {\sum }_{jk}{c}_{jk}^{snore}|A_j\otimes A_k}$, for A_j ⊆ U and |A_k a basis vector of S.

3.6. Diagrams

The compact closed categorical setting of Abramsky and Coecke comes equipped with a diagrammatic calculus, originally developed in Joyal and Street [60] and referred to by string diagrams. This calculus allows one to draw diagrams that depict the protocols of Quantum mechanics and simplify the computations thereof. For example see Figure 2 for the diagram for teleportation:

FIGURE 2

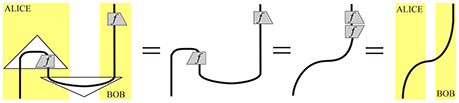
Figure 2. Diagram of information Flow in the teleportation protocol, cited from Abramsky et al. [7].

These diagrams depict the flow of information between the parties involved in the protocol and also simplify the tensor contraction computations. In the setting of language, every language construct can be seen as a protocol, with words as the involved parties. The same diagrammatic calculus has been widely used to show how information flows amongst the words of a phrase or sentence and to depict the meaning of the language unit resulting from it. In the interest of space, we will not introduce this diagrammatic calculus here, but provide examples, via the following Figures 3–5.

FIGURE 3

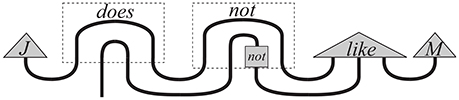
Figure 3. Diagram of information flow in the negative transitive sentence, cited from Preller and Sadrzadeh [16].

FIGURE 4

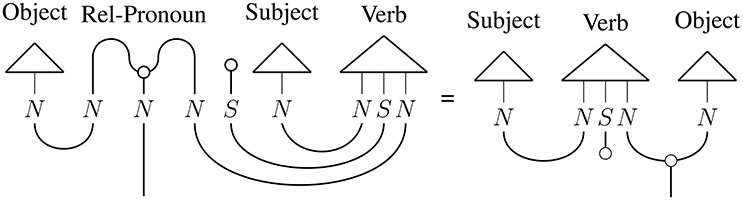
Figure 4. Diagram of information flow in a relative clause with an object relative pronoun, cited from Clark et al. [35].

FIGURE 5

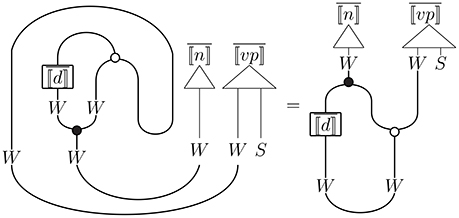
Figure 5. Diagram of Information Flow in a Sentence with a Quantified Subject, cited from Hedges and Sadrzadeh [38].

4. Overview of Experiments

Our first set of experiments was on two datasets, both consisting of pairs of transitive sentences with ambiguous verbs and their two eminent meanings. One of the datasets had adjectives modifying the subjects and objects, the other contained bare subjects and objects. The goal was to disambiguate verbs, based on the sentences in which they occurred. A non-compositional distributional approach to this task would be to build vector representations for verbs and their different meanings (in this case the two most eminent ones); then measure the cosine of the angle between the vector of the verb and those of the meanings and use this as a measure of disambiguation. In other words, if the vector of the verb was closer to one of the meaning vectors, that meaning would be chosen as the right meaning for the verb. This non-compositional method, however, does not take into account the specific sentence in which the verb has occurred. In our compositional version, we build a vector representation for each sentence of the dataset; specifically, we build a vector for the sentence with the verb in it, and two for the two sentences where the verb is replaced with one of its two eminent meanings. Then we compare the distances between these sentence vectors. The sentence vectors were built using different composition operators, and the non-compositional verb vector was taken as a comparison base line. The results show that one of the tensor composition methods, namely our Kronecker model, performed best. This was the first time 3 and 4 word sentences were used to disambiguate a single word. A precursor to this experiment, was that of Mitchell and Lapata [23], where ambiguous verbs were disambiguated using 2-word “Sbj Verb” or “Verb Obj” phrases.

A snapshot of two of these datasets are presented in Tables 2, 3. The first two entries are the two sentences in question and the last entry is a tag we gave to the sentences based on how similar the meanings of the sentences in the pair were. As you can see, the first dataset consists of “Sbj Verb Obj” sentences, the second dataset consists of sentences of the form “Adj Sbj Verb Adj Obj” where the subject and object are moreover modified by adjectives:

TABLE 2

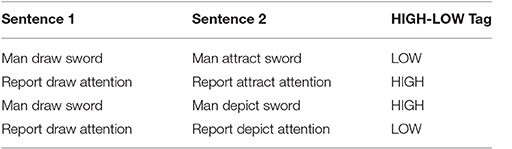
Table 2. Example entries from the transitive dataset, cited from Grefenstette and Sadrzadeh [25].

TABLE 3

Table 3. Example entries from the adjective-transitive dataset, cited from Grefenstette and Sadrzadeh [25].

We asked human annotators (on Amazon Turk) to assign a degree of similarity to each pair of the dataset, using a number from 1 to 7, ranking the degree of similarity of the sentences therein. If the sentence “Sbj Verb1 Obj” was ranked to have an average high similarity with the sentence “Sbj Verb2 Obj,” then we concluded that “Verb1” had the same meaning as “Verb2,” thus disambiguating it. We implemented different models to compute vectors for sentences and used the cosine of the angle between them as a measure of similarity. The results are presented in Table 4. In the “Sbj Verb Obj” dataset, the vectors built via the Kronecker model achieve the highest correlation with the annotators' judgments. This model is one of the DisCoCat models, a model that has consistently performed very well. In the “Adj Sbj Verb Adj Sbj” dataset, the model referred to by Categorical Adj has consistently performed the best. This model builds a matrix for the adjective and matrix multiplies it with the vector of the noun to obtain a vector for the adjective noun phrase. The exact results denote the degree of correlation (computed by using Spearman's ρ) between the human judgments and the judgments predicted by the models. These seem quite low, but so is the inter annotators agreement, presented in the last line of each table. This agreement is an upper bound for the experiment, denoting the degree to which the human annotators agreed amongst themselves about their similarity judgments. Having this upper bound in mind, we see that the “Adj Sbj Verb Adj Sbj” dataset performed better than the “Sbj Verb Obj” dataset (since it had larger compositional contexts), as it aligns to human judgment in about 60% of the time.

TABLE 4

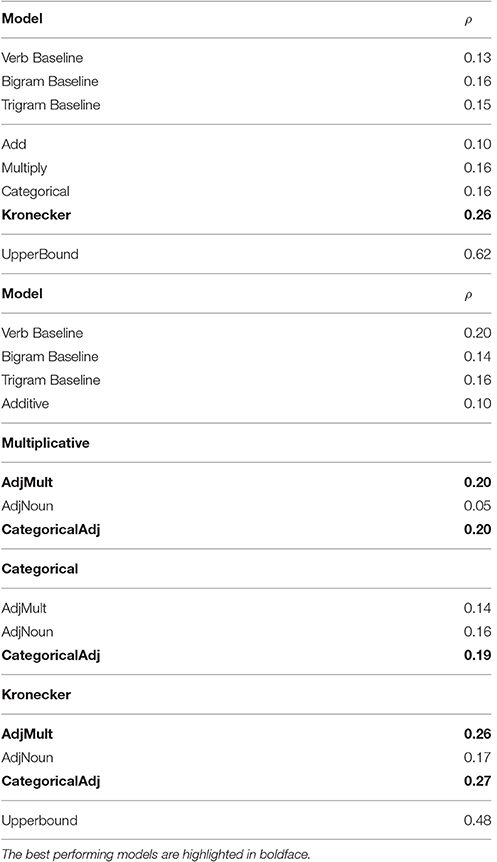
Table 4. Model correlation coefficients with human judgments, cited from Grefenstette and Sadrzadeh [25].

A criticism to this first set of experiments was that they relied on human judgments and that these were not done according to clear guidelines. One argument against lack of such a judgment was that human annotators were asked to judge the degree of similarity between sentences and that is a hard task. It was argued that similarity has different interpretations in different contexts and annotators might have had different interpretations (different to ours) in mind when judging the dataset. In a second task, we avoided this weakness by working on term-definition pairs mined from a junior dictionary. The terms were words and the definitions were short descriptions given by the dictionary as the meaning of the word. The goal was to distinguish which definition was describing which word. We built word vectors for the terms and phrase vectors for the definitions and used the cosine of the angle between these vector as a classifier. We collected five definitions whose vectors were closest to the vector of the verb and then verified whether the correct dictionary definition was amongst these five. The model that classified more terms to their correct definitions was considered to be the better model.

A snapshot of the dataset is presented in Table 5. The accuracy results are presented in Table 6, where the DisCoCat CopyObj model achieves the highest accuracy for the terms that are nouns, and the second best for terms that are verbs (28% vs. the accuracy of 30% reached by multiplying the word vectors).

TABLE 5

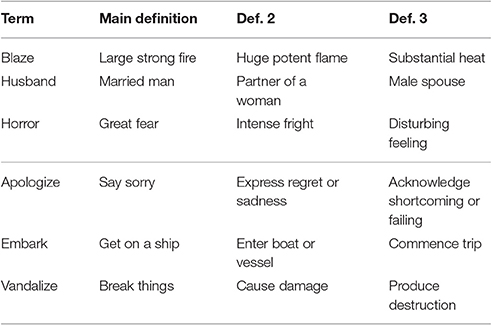
Table 5. Sample of the dataset for the term/definition comparison task, cited from Kartsaklis et al. [26].

TABLE 6

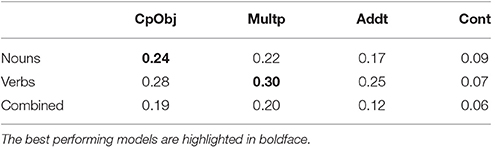
Table 6. Accuracy results for the term/definition comparison task, Kartsaklis et al. [26].

Based on this experiment, we formed a toy experiment and did a preliminary evaluation of the application of Frobenius algebras to modeling relative clauses. Similar to the above experiment, we mined term-description pairs from a dictionary, but this time the terms were chosen such that their descriptions had a relative pronoun in them. We then proceeded as before: built vectors for the term and for the description. A snapshot of the dataset is presented in Table 7.

TABLE 7

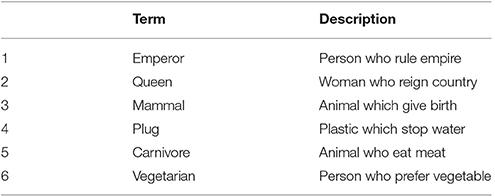
Table 7. Examples from a Term-Description dataset, cited from Sadrzadeh et al. [37].

The latter used three different composition operators: simple addition and point wise multiplication, i.e., we just added and point wise multiplied the word vectors within the descriptions to obtain a vector representation for the whole relative clause. We also built vector representations using the Frobenius model presented above and an extension of it to possessive relative pronoun “whose.” In the first two models, we had a choice of either building a vector for the relative pronoun or dropping it and thus treating it as noise. We presented results for both of these options. For the possessive Frobenius case, we had the choice of either building a vector for 's, or treating it as the unit vector. Again, we presented the results of both cases. We tested which model achieved a better accuracy (Acc) and a mean reciprocal rank (MRR). The results are presented in the Table 8, where both of the Frobenius models achieve the highest accuracy and MRR.

TABLE 8

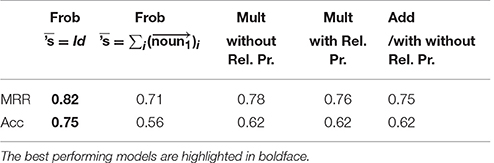
Table 8. Results for the Term-Description dataset, cited from Sadrzadeh et al. [37].

The differences between the two Frobenius models only applies to the possessive relative clauses, which were not reviewed in this article, in the benefit of space. In these models, one has to build a linear map for the “ 's ” phoneme. In one model we summed all the nouns that were modified by this morpheme, in the other, we simply took it to be the identity map, i.e., the unit map. In either case, the Frobenius model performed better than our other implemented models, e.g., the other two models in which we added the vectors of the words, taking into account the vector of the relative pronoun or ignoring it, and two other similar models where we multiplied them.

As another set of experiments, we used the neural word embeddings of Mikolov et al. [30]. The motivation behind this task was the popularity and success of the word embeddings. Often, when vector representations are built from scratch using count-based methods and on a given corpus, many parameters have to be taken into account (e.g., size of the window, the normalization scheme for the counts, the dimensions of the vector spaces and its size). The preprepared word embeddings provides a platform wherein new vectors need not be built for each task and parameters need not be individually tuned by each experimenter and for each experiment. The word embeddings provide a standard framework (to some extent) for all experimenters to do experiments and compare their results in a more unified manner. It also relieves us from the task of building the vectors ourselves.

We used the neural noun vectors of Mikolov et al. [30] and built adjective matrices and verb tensors and re-experimented with the disambiguation task presented above. The results are presented in Table 9. GS11 and KS14 denote the “Sbj Verb Obj” and “Adj Sbj Verb Adj Obj” datasets with count-based vectors, and NWE denotes both of these datasets together with the word embedding vectors.

TABLE 9

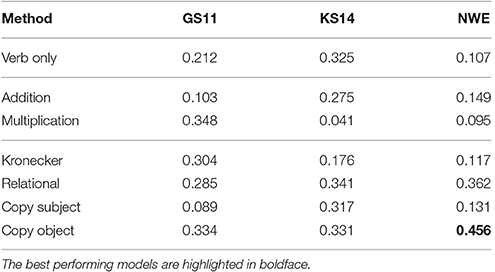
Table 9. Models correlation with human judgments for the disambiguation task with normal and neural (NWE) vectors, cited from Milajevs et al. [32].

Our hope was that one of the tensor-based models would do better here; this would indicate that the tensor models worked better regardless of their underlying vectors, count-baed or neural. This was shown to be indeed the case, as the DisCoCat CopyObj model achieves the highest correlation with human judgments.

5. Brief Summary and Future Work

In this paper, we reviewed the general field of categorical compositional distributional semantics, to which we referred as DisCoCat. This field introduces grammar awareness into vectors models of language, otherwise known as distributional semantics, thus enabling these models to build vectors for phrases and sentences, using the vectors of the words therein and their corresponding grammatical relations. The setting of a DisCoCat is that of a compact closed category, to which later Frobenius and Bi algebras were added to reason about relative pronouns and quantifiers. Compact closed categories, Frobenius and Bi algebras are also the building blocks of the categorical approach to Quantum Mechanics, known under the acronym CQM. Another connection to Quantum formalisms, is the structure preserving passage from grammatical structure to vectorial meaning, which is through a functor similar to the Quantization functor of Topological Quantum Field Theory. In this paper, we presented a chronology of the developments of the DisCoCat, briefly went through its theoretical underpinnings and its experimental validations.

What remains to be done is to relate the setting of DisCoCat to the Quantum logical approaches to language, such as the work done by Preller [61], by Widdows [62], and the original seminal work of Van Rijsbergen [63].

Author Contributions

The author confirms being the sole contributor of this work and approved it for publication.

Funding

Support by EPSRC for Career Acceleration Fellowship EP/J002607/1 and AFOSR International Scientific Collaboration grant FA9550-14-1-0079 is gratefully acknowledged by MS.

Conflict of Interest Statement

The author declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Footnotes

1. ^https://www.tensorflow.org/versions/r0.11/tutorials/word2vec/index.html

References

1. Lambek J. Type grammars revisited. In: Proceedings of LACL 97. vol. 1582 of Lecture Notes in Artificial Intelligence. Berlin, Heidelberg: Springer (1997).

2. Lambek J. From Word to Sentence: A Computational Algebraic Approach to Grammar. Monza: Polimetrica (2008).

Google Scholar

3. Coecke B, Grefenstette E, Sadrzadeh M. Lambek vs. Lambek: functorial vector space semantics and string diagrams for Lambek calculus. Ann Pure Appl Logic. (2013) 164:1079–100. doi: 10.1016/j.apal.2013.05.009

CrossRef Full Text | Google Scholar

4. Atiyah M. Topological quantum field theories. Publ Mathématique de l'Inst des Hautes Études Sci. (1989) 68:175–86. doi: 10.1007/BF02698547

CrossRef Full Text | Google Scholar

5. Baez J, Dolan J. Higher-dimensional algebra and topological quantum field theory. J Math Phys. (1995) 36:6073–105. doi: 10.1063/1.531236

CrossRef Full Text | Google Scholar

6. Kock J. Frobenius Algebras and 2D Topological Quantum Field Theories. Cambridge: Cambridge University Press (2003). doi: 10.1017/CBO9780511615443

CrossRef Full Text | Google Scholar

7. Abramsky S, Coecke B. A categorical semantics of quantum protocols. In: Proceedings of the 19th Annual IEEE Symposium on Logic in Computer Science. Washington, DC: IEEE Computer Science Press (2004). p. 415–25. doi: 10.1109/lics.2004.1319636

CrossRef Full Text | Google Scholar

8. Piedeleu R, Kartsaklis D, Coecke B, Sadrzadeh M. Open system categorical quantum semantics in natural language processing. In: Proceedings of the 6th Conference on Algebra and Coalgebra in Computer Science. Nijmegen (2015).

Google Scholar

9. Coecke B, Paquette ÉO, Pavlovic D. Classical and quantum structuralism. In: Gay S, Mackie I, editors. Semantical Techniques in Quantum Computation. Cambridge: Cambridge University Press (2009). p. 29–69. doi: 10.1017/CBO9781139193313.003

CrossRef Full Text | Google Scholar

10. Coecke B, Pavlovic D, Vicary J. A new description of orthogonal bases. Math Struct Comp Sci. (2013) 23:555–67. doi: 10.1017/S0960129512000047

CrossRef Full Text | Google Scholar

11. Coecke B, Duncan R. (2008). Interacting quantum observables. In: Proceedings of 35th International Colloquium on Automata, Languages, and Programming, Berlin: Springer (2008).

Google Scholar

12. Clark S, Pulman S. Combining symbolic and distributional models of meaning. In: Proceedings of the AAAI Spring Symposium on Quantum Interaction, Menlo Park: The AAAI Press (2007). p. 52–5.

Google Scholar

13. Smolensky P. Tensor product variable binding and the representation of symbolic structures in connectionist systems. Artif Intell. (1990) 46:159–216. doi: 10.1016/0004-3702(90)90007-M

CrossRef Full Text | Google Scholar

14. Stephen Clark BC, Sadrzadeh M. A compositional distributional model of meaning. In: Proceedings of the Second Symposium on Quantum Interaction (QI), London: College Publications (2008). p. 133–40.

Google Scholar

15. Coecke B, Sadrzadeh M, Clark S. Mathematical foundations for distributed compositional model of meaning. Lambek festschrift. Linguist Anal. (2010) 36:345–84.

16. Preller A, Sadrzadeh M. Bell states and negative sentences in the distributed model of meaning. In: Coecke B, Panangaden P, Selinger P. editors. Electronic Notes in Theoretical Computer Science, Proceedings of the 6th QPL Workshop on Quantum Physics and Logic, Amsterdam: Elsevier (2011).

Google Scholar

17. Lambek J. Compact monoidal categories from linguistics to physics. In: Coecke B, editor. New Structures for Physics. Lecture Notes in Physics. Berlin; Heidelberg: Springer (2010). p. 451–69. doi: 10.1007/978-3-642-12821-9_8

CrossRef Full Text | Google Scholar

18. Lambek J. The mathematics of sentence structure. Amer Math Monthly (1958) 65:154–70. doi: 10.2307/2310058

CrossRef Full Text | Google Scholar

19. Baroni M, Zamparelli R. Nouns are vectors, adjectives are matrices: representing adjective-noun constructions in semantic space. In: Conference on Empirical Methods in Natural Language Processing (EMNLP-10). Cambridge, MA (2010).

Google Scholar

20. Grefenstette E, Dinu G, Zhang Y, Sadrzadeh M, Baroni M. Multi-step regression learning for compositional distributional semantics. In: 10th International Conference on Computational Semantics (IWCS), Stroudsburg, PA: Association for Computational Linguistics (2013).

Google Scholar

21. Baroni M, Bernardi R, Do NQ, Shan CC. Entailment above the word level in distributional semantics. In: Proceedings of the 13th Conference of the European Chapter of the Association for Computational Linguistics. EACL '12, Stroudsburg, PA: Association for Computational Linguistics (2012). p. 23–32.

Google Scholar

22. Grefenstette E, Sadrzadeh M. Experimental support for a categorical compositional distributional model of meaning. In: Proceedings of Conference on Empirical Methods in Natural Language Processing (EMNLP), Stroudsburg, PA: Association for Computational Linguistics (2011). p. 1394–404.

Google Scholar

23. Mitchell J, Lapata M. Vector-based models of semantic composition. In: Proceedings of the 46th Annual Meeting of the Association for Computational Linguistics, Stroudsburg, PA: Association for Computational Linguistics (2008). p. 236–44.

Google Scholar

24. Grefenstette E, Sadrzadeh M. Experimenting with transitive verbs in a discocat. In: Proceedings of the GEMS 2011 Workshop on GEometrical Models of Natural Language Semantics. Stroudsburg, PA: Association for Computational Linguistics (2011). p. 62–6.

Google Scholar

25. Grefenstette E, Sadrzadeh M. Concrete models and empirical evaluations for the categorical compositional distributional model of meaning. Comput Linguist. (2015) 41:71–118. doi: 10.1162/COLI_a_00209

CrossRef Full Text | Google Scholar

26. Kartsaklis D, Sadrzadeh M, Pulman S. A unified sentence space for categorical distributional-compositional semantics: theory and experiments. In: Proceedings of 24th International Conference on Computational Linguistics (COLING 2012). Mumbai: Posters (2012). p. 549–58.

Google Scholar

27. Kartsaklis D, Kalchbrenner N, Sadrzadeh M. Resolving lexical ambiguity in tensor regression models of meaning. In: Proceedings of the 52nd Annual Meeting of the Association for Computational Linguistics, ACL 2014, June 22-27, 2014, Volume 2: Short Papers. Baltimore, MD (2014). p. 212–7. doi: 10.3115/v1/p14-2035

CrossRef Full Text | Google Scholar

28. Kartsaklis D, Sadrzadeh M. Prior disambiguation of word tensors for constructing sentence vectors. In: Proceedings of Conference on Empirical Methods in Natural Language Processing (EMNLP), Stroudsburg, PA: Association for Computational Linguistics (2013). p. 1590–601.

Google Scholar

29. Kartsaklis D, Sadrzadeh M. A study of entanglement in a categorical framework of natural language. In: Proceedings of the 11th Workshop on Quantum Physics and Logic (QPL). Kyoto (2014). doi: 10.4204/eptcs.172.17

CrossRef Full Text | Google Scholar

30. Mikolov T, Chen K, Corrado G, Dean J. Efficient estimation of word representations in vector space. arXiv preprint arXiv:13013781 (2013).

Google Scholar

31. Mikolov T, Sutskever I, Chen K, Corrado GS, Dean J. Distributed representations of words and phrases and their compositionality. In: Burges CJC, Bottou L, Welling M, Ghahramani Z, Weinberger KQ, editors. Advances in Neural Information Processing Systems 26, New York, NY: Curran Associates, Inc., (2013). p. 3111–9.

Google Scholar

32. Milajevs D, Kartsaklis D, Sadrzadeh M, Purver M. Evaluating neural word representations in tensor-based compositional settings. In: Proceedings of the 2014 Conference on Empirical Methods in Natural Language Processing (EMNLP). Stroudsburg, PA: Association for Computational Linguistics (2014). p. 708–19. doi: 10.3115/v1/D14-1079

CrossRef Full Text | Google Scholar

33. Kartsaklis D, Sadrzadeh M. A compositional distributional inclusion hypothesis. In: Logical Aspects of Computational Linguistics. Celebrating 20 Years of LACL (1996-2016) - 9th International Conference, LACL 2016, Nancy (2016). p. 116–33. doi: 10.1007/978-3-662-53826-5_8

CrossRef Full Text | Google Scholar

34. Kartsaklis D, Sadrzadeh M. Distributional inclusion hypothesis for tensor-based composition. In: COLING 2016, 26th International Conference on Computational Linguistics, Proceedings of the Conference: Technical Papers, Osaka, Japan. Stroudsburg, PA: Association for Computational Linguistics (2016).

Google Scholar

35. Clark S, Coecke B, Sadrzadeh M. The frobenius anatomy of relative pronouns. In: 13th Meeting on Mathematics of Language (MoL), Stroudsburg, PA: Association for Computational Linguistics (2013). p. 41–51.

Google Scholar

36. Sadrzadeh M, Clark S, Coecke B. Forbenius anatomy of word meanings I: subject and object relative pronouns. J Logic Comput. (2013) 23:1293–317. doi: 10.1093/logcom/ext044

CrossRef Full Text | Google Scholar

37. Sadrzadeh M, Clark S, Coecke B. Forbenius anatomy of word meanings 2: possessive relative pronouns. J Logic Comput. (2014) 26:785–815.

Google Scholar

38. Hedges J, Sadrzadeh M. A generalised quantifier theory of natural language in categorical compositional distributional semantics with Bialgebras. CoRR (2016) abs/1602.01635. Available online at: http://arxiv.org/abs/1602.01635

Google Scholar

39. Sadrzadeh M. Quantifier scope in categorical compositional distributional semantics. In: Kartsaklis D, Lewis M, Rimell L, editors. Proceedings of the 2016 Workshop on Semantic Spaces at the Intersection of NLP, Physics and Cognitive Science, 11th June 2016. vol. 221 of Electronic Proceedings in Theoretical Computer Science. Glasgow: Open Publishing Association (2016). p. 49–57. doi: 10.4204/eptcs.221.6

CrossRef Full Text | Google Scholar

40. Balkır E, Sadrzadeh M, Coecke B. Distributional sentence entailment using density matrices. In: LNCS Proceedings of the first International Conference on Topics in Theoretical Computer Science (TTCS) 2015, Tehran, Iran, Revised Selected Papers, Berlin; Heidelberg: Springer International Publishing (2016). p. 1–22.

41. Balkir E, Kartsaklis D, Sadrzadeh M. Sentence entailment in compositional distributional semantics. In: International Symposium on Artificial Intelligence and Mathematics (ISAIM), Florida (2016).

Google Scholar

42. Bankova D, Coecke B, Lewis M, Marsden D. Graded entailment for compositional distributional semantics. arXiv preprint arXiv:160104908 (2016).

Google Scholar

43. Salton G, Wong A, Yang CS. A vector space model for automatic indexing. Commun ACM (1975) 18:613–20. doi: 10.1145/361219.361220

CrossRef Full Text | Google Scholar

44. Rubenstein H, Goodenough JB. Contextual correlates of synonymy. Commun ACM (1965) 8:627–33. doi: 10.1145/365628.365657

CrossRef Full Text | Google Scholar

45. Lapesa G, Evert S. A large scale evaluation of distributional semantic models: parameters, interactions and model selection. Trans Assoc Comput Linguist. (2014) 2:531–45.

Google Scholar

46. Bullinaria JA, Levy JP. Extracting semantic representations from word co-occurrence statistics: a computational study. Behav Res Methods (2007) 39:510–26. doi: 10.3758/BF03193020

PubMed Abstract | CrossRef Full Text | Google Scholar

47. Turney PD. Similarity of semantic relations. Comput Linguist. (2006) 32:379–416. doi: 10.1162/coli.2006.32.3.379

CrossRef Full Text | Google Scholar

48. Curran J. From Distributional to Semantic Similarity. School of Informatics, Edinburgh: University of Edinburgh (2004).

Google Scholar

49. Lin D. Automatic retrieval and clustering of similar words. In: Proceedings of the 17th international conference on Computational linguistics-Volume 2, Stroudsburg, PA: Association for Computational Linguistics (1998). p. 768–74. doi: 10.3115/980432.980696

CrossRef Full Text | Google Scholar

50. Landauer T, Dumais S. A solution to Plato's problem: the latent semantic analysis theory of acquision, induction, and representation of knowledge. Psychol Rev. (1997) 104:211–40. doi: 10.1037/0033-295X.104.2.211

CrossRef Full Text | Google Scholar

51. Geffet M, Dagan I. The distributional inclusion hypotheses and lexical entailment. In: Proceedings of the 43rd Annual Meeting on Association for Computational Linguistics. ACL '05. Stroudsburg, PA: Association for Computational Linguistics (2005). p. 107–14. doi: 10.3115/1219840.1219854

CrossRef Full Text | Google Scholar

52. Weeds J, Weir D, McCarthy D. Characterising measures of lexical distributional similarity. In: Proceedings of the 20th International Conference on Computational Linguistics. COLING '04, Stroudsburg, PA: Association for Computational Linguistics (2004). doi: 10.3115/1220355.1220501

CrossRef Full Text | Google Scholar

53. Kelly GM, Laplaza ML. Coherence for compact closed categories. J Pure Appl Algebra (1980) 19:193–213. doi: 10.1016/0022-4049(80)90101-2

CrossRef Full Text | Google Scholar

54. Preller A, Lambek J. Free compact 2-categories. Math Struct Comput Sci. (2007) 17:309–40. doi: 10.1017/S0960129506005901

CrossRef Full Text | Google Scholar

55. Carboni A, Walters RFC. Cartesian bicategories. I. J Pure Appl Algebra (1987) 49:11–32. doi: 10.1016/0022-4049(87)90121-6

CrossRef Full Text | Google Scholar

56. McCurdy M. Graphical methods for Tannaka duality of weak bialgebras and weak Hopf algebras. Theory Appl Categor. (2012) 26:233–80.

Google Scholar

57. Bonchi F, Sobocinski P, Zanasi F. Interacting bialgebras are Frobenius. In: Proceedings of FoSSaCS 2014. vol. 8412. Berlin; Heidelberg: Springer (2014) p. 351–65. doi: 10.1007/978-3-642-54830-7_23

CrossRef Full Text | Google Scholar

58. Frobenius FG. Theorie der hyperkomplexen Größen. Preussische Akademie der Wissenschaften Berlin: Sitzungsberichte der Preußischen Akademie der Wissenschaften zu Berlin, Berlin: Reichsdr (1903).

59. Barwise J, Cooper R. Generalized quantifiers and natural language. Linguist Philos. (1981) 4:159–219. doi: 10.1007/BF00350139

CrossRef Full Text | Google Scholar

60. Joyal A, Street R. The geometry of tensor calculus, I. Adv Math. (1991) 88:55–112. doi: 10.1016/0001-8708(91)90003-P

CrossRef Full Text | Google Scholar

61. Preller A. From Sentence to Concept, a Linguistic Quantum Logic. LIRMM (2011). RR-11019. Available online at: http://hal-lirmm.ccsd.cnrs.fr/lirmm-00600428

Google Scholar

62. Widdows D. Geometry and Meaning. Center for the Study of Language and Information/SRI, Stanford University (2004).

63. Van Rijsbergen CJ. The Geometry of Information Retrieval. Cambridge: Cambridge University Press (2004). doi: 10.1017/CBO9780511543333

CrossRef Full Text | Google Scholar