- Dietrich Stauffer Computational Physics Lab, Departamento de Física, Universidade Federal do Piauí, Teresina, Brazil
Here, the critical properties of kinetic continuous opinion dynamics model are studied on (4, 6, 12) and (4, 82) Archimedean lattices. We obtain pc and the critical exponents from Monte Carlo simulations and finite size scaling. We found out the values of the critical points and Binder cumulant that are pc = 0.086(3) and for (4, 6, 12); and pc = 0.109(3) and for (4, 82) lattices and also the exponent ratios β/ν, γ/ν, and 1/ν are, respectively: 0.23(7), 1.43(5), and 0.60(3) for (4, 6, 12); and 0.149(4), 1.56(4), and 0.94(4) for (4, 82) lattices. Our new results disprove of the Grinstein criterion.
1. Introduction
In 1986 Galam introduced the use of local majority rules to study voting systems as bottom-up democratic voting in hierarchical structures [1], see also the references [2–4]. Although sociophysics has been rejected by some physicists in the eighties [5], it is has become today an active and promising area of research for interdisciplinary physicists [6, 7].
In this same context, in 1982, de Oliveira [8] proposed a non-equilibrium model called Majority Vote Model (MVM). On two-dimensional lattices it shows critical phenomena with critical exponents ν, β, and γ, as for [8–10] the equilibrium Ising model [11, 12], in agree with a hypothesis of Grinstein et al. [13].
In 2012 Biswas et al. [14] proposed a kinetic model of opinion formation. This model kinetic continuous opinion dynamics (KCOD) presents mutual interactions between the individual i, j that can be both positive and negative. In this model the fraction of negative interactions is represented by a parameter p in order to characterize the different types of distributions for the mutual interactions. The results of the continuous version the KCOD model, obtained through numerical simulations indicate the existence of a universal continuous phase transition at p = pc with exponents of mean field (νd = 2.00(1), β = 0.50(1), and γ = 1.00(1)).
Similar to this KCOD model is the one of Deffuant et al. [15], where each person i selects another person j to talk to (no lattice) and both move their opinion toward that of the other person. For the Krause-Hegselmann model [16], each person averages over the opinions of the others in the population, again no lattice. While these two models use continuous opinions, those in the Sznajd model [17] usually are Ising-like (+1 or −1) and restricted to a square lattice with four nearest neighbors. Two Sznajd people happening to agree in their opinion convince all their six neighbors of this opinion. In all these models one may start from a random distribution of opinions and then check if the opinions all converge to one consensus, two opposing camps of opinions, or a fragmentation into many opinion clusters [18–20].
Recently, Mukherjee and Chatterjee [21] studied the KCOD model on square and cubic lattices (2D and 3D). Their numerical results indicate that the same critical behavior of the KCOD model and the Ising model in the corresponding dimensions.
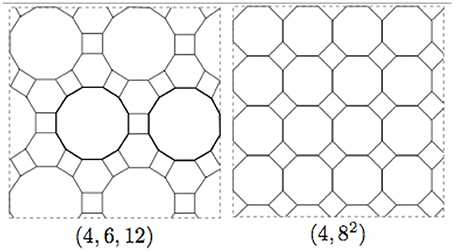
In this work, we studied the KCOD on two Archimedean lattices—namely, (4, 6, 12), and (4, 82)—through extensive Monte Carlo simulations. Pictures of the (4, 6, 12) and (4, 82) AL are shown in Figure 1. The AL are vertex transitive graphs that can be embedded in a plane such that every face is a regular polygon. Kepler showed that there are exactly 11 such graphs. The AL are labeled according to the sizes of faces incident to a given vertex. The face sizes are sorted, starting from the face for which the list is the smallest in lexicographical order. In this way, the square lattice gets the name (4, 4, 4, 4) (abbreviated to (44)), honeycomb is called (63), and Kagome is (3, 6, 3, 6). Here, we also compared our results with those of the MVM made on (3, 4, 6, 4) and (34, 6) AL.
One of our goals, besides finding the critical exponents of the KCOD model on (4, 6, 12) and (4, 82) AL, is to verify the Grinstein et al. criterion [13], for non-equilibrium stochastic spin systems with up-down symmetry on (4, 6, 12) and (4, 82) AL belong to the same universality class as the Ising model on (44) as suggested by Grinstein et al. [13]. Here, we also compared our results with those of the MVM on (4, 6, 12) and (4, 82) [22].
2. Definition and Simulation
The KCOD model [14] is defined by a set of individuals with continuous opinion variables oi(t), where the opinion of a person i at time t, takes the values in the interval [−1, +1], is situated on every node of the (4, 6, 12) and (4, 82) AL with N = 12L2 sites for (4, 6, 12) and N = 4L2 sites for (4, 82). In a population of N individuals, opinions change out of pair-wise interactions via mutual influences/couplings μij as:
The pairs i, j are unrestricted, meaning the original model is defined on a fully-connected graph, giving a mean-field-like limit (infinite range interactions). The pairwise interaction implies no sum over the index j. with real random couplings μij. Agent i updates his/her opinion via Equation (1) by interacting with agent j and is influenced by the coupling μij. The opinions are limited to −1 ≤ oi(t) ≤ 1. If the opinion value of an individual become higher (lower) than +1 (−1), then it is set equal to +1 (−1). This bound, along with Equation (1), defines the dynamics of the model. Here, μij is a continuous random variable defined in the range [−1, +1], i.e., it takes a random real value in the range [−1, 0] or ([0, 1]) with probability p or (1−p). In other words, the disorder parameter p denotes the fraction of negative pairwise interactions. The average opinion measures the ordering in the system. As a function of the fraction p of negative interactions a symmetry breaking transition occurs between an ordered and a disordered phase: below a certain value pc of the parameter p, the system is ordered (giving a non zero value of the opinion O, defined in the following), while it is disordered above pc (O = 0).
The critical properties of model we are interested in are the order parameter O, the order parameter fluctuations (susceptibility) OF and the reduced fourth-order cumulant of the O, namely here by O4, defined as
where 〈⋯ 〉 stands for time averages, computed at the steady states. Nrun independent simulations are averaged over.
The quantities O, OF, and O4 depend on the disorder parameter p and obey
(finite-size scaling) with β, γ, and ν as the usual critical exponents, fo(x), fof(x), fo4(x) as the finite-size scaling functions and
as the scaling variable. Thus, the size dependence of O and OF gives us the exponents β/ν and γ/ν, respectively. The maximum of susceptibility also scales as Lγ/ν. Moreover, the value of p* for which the susceptibility has a maximum scales with L as
Therefore, Equations (4c) and (5) give the exponent 1/ν. The effective dimensionality, Deff, is given by the hyperscaling hypothesis
Monte Carlo simulations were made on (4, 6, 12) and (4, 82) AL with various systems of size N = 768, 3,072, 12,288, 49,152, and 196,608 for (4, 6, 12) and N = 256, 1,024, 4,096, 16,384, 65,536, and for (4, 82) AL. We use 2 × 105 Monte Carlo steps (MCS) to make the system reach the steady state, and then the time averages are estimated over the next 3 × 105 MCS. One MCS is accomplished after N attempts to update the opinions of agents i and j, considering the evolution Equations (1) and (2). The results are averaged over Nrun (500 ≤ Nrun ≤ 2, 000) independent simulation runs for each lattice and for given set of parameters (p, N).
3. Results and Discussion
Figure 2 displays the dependence of the opinion O, OF, and O4 on the disorder parameter p, obtained from simulations on (4, 6, 12) and (4, 82) AL with N ranging from N = 256 to 196,608 sites. The shape of O(p), OF, and O4 curves, for a given value of L, indicate the occurrence of a second-order phase transition in the system. The phase transition occurs at the value of the critical disorder parameter pc. Such critical disorder parameter pc is estimated as the point where the curves of the Binder cumulant O4 for different system sizes N intercept each other [23]. The corresponding value of O4 is represented by . Then, we obtain pc = 0.086(3) and ; pc = 0.109(3) and for (4, 6, 12), and (4, 82) AL, respectively.
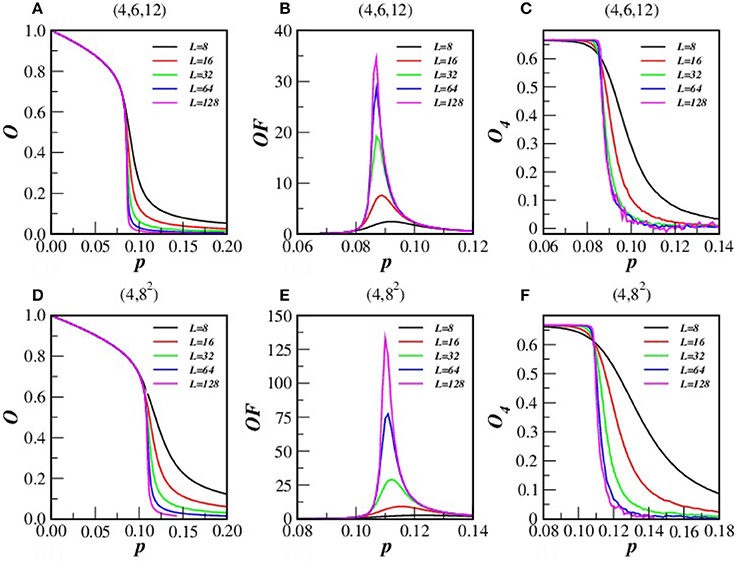
Figure 2. (Color on-line) O, OF, and O4 vs. p, for sizes L = 23, 24, 25, 26 and 27 and N = 12L2 (for 4, 6, 12) AL (first line) and N = 4L2 sites for (4, 82) AL (second line).
The results obtained from Figures 3–6 and used in Figure 7 are summarized in Table 2.
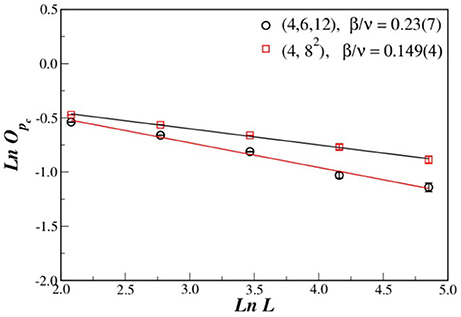
Figure 3. Log-log plot of the dependence of the opinion O* = O(pc) on the linear system size L. Fitting data, we obtained the estimation for the critical ratio β/ν.
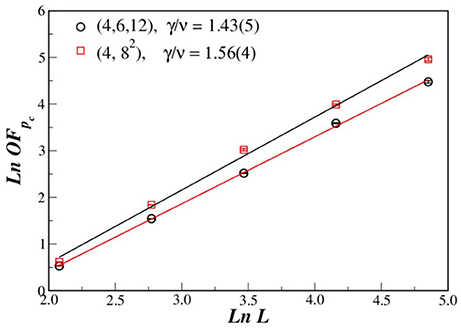
Figure 4. Log-log plot of the OF at pc vs. L for (4, 6, 12), and (4, 82) AL. Fitting data, we obtained the estimation for the critical ratio γ/ν.
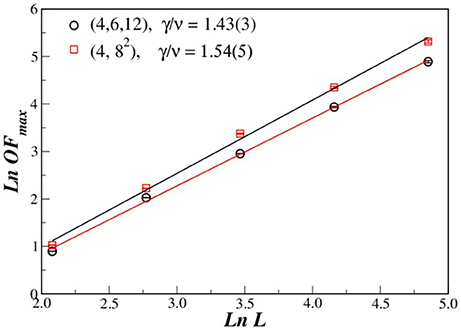
Figure 5. OF at pχmax(N) vs. L for (4, 6, 12) and (82), AL. Fitting data, we obtained another estimation for the critical ratio γ/ν.
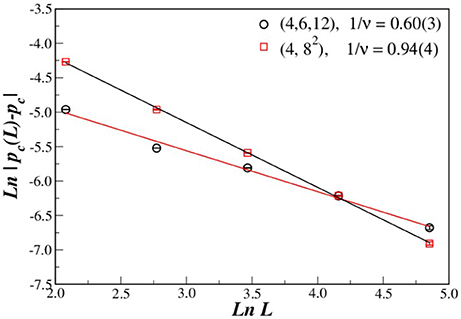
Figure 6. Plot of ln |pc(L) − pc| vs. the linear system size L for (4, 6, 12) and (4, 82) AL. Fitting data, we obtained the estimation for the critical exponent 1/ν.
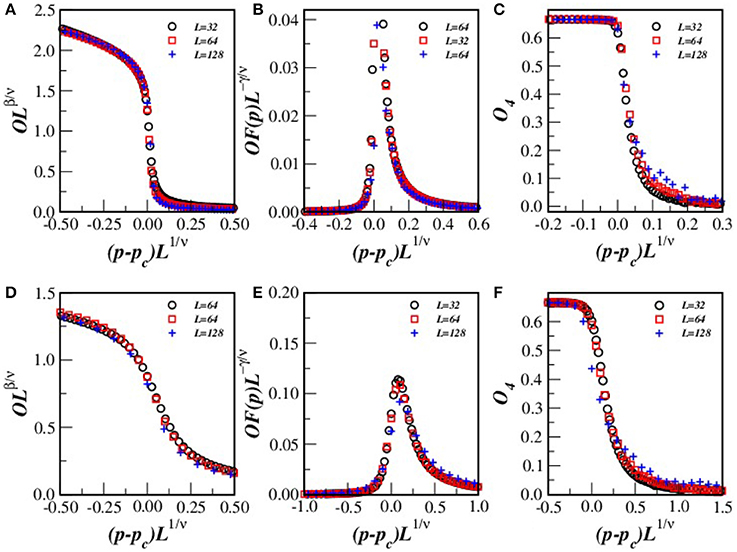
Figure 7. (Color on-line) Data collapse of the opinion O, OF, and O4 shown in Figure 2 for L = 32, 64, and 128 (4, 6, 12) and (4, 82) AL. The exponent ratios used here were β/ν = 0.23(7), γ/ν = 1.43(5), and 1/ν = 0.60(3) for (4, 6, 12), and β/ν = 0.149(4), γ/ν = 1.56(4), and 1/ν = 0.94(4) for (4, 82) AL.
The excellent curve collapses Figure 7 for distinct system sizes corroborates our estimated values for pc and exponent ratios β/ν, γ/ν and 1/ν.
The resulting critical exponents and disorder parameters are collected in Table 2. One can also see that the exponent ratios β/ν, γ/ν, 1/ν are similar to MVM, Table 1, and are different from the Ising model contrary to the Grinstein's hypothesis [13]. They are different from β/ν = 0.125 and γ/ν = 1.75 obtained for a d = 2 lattices, but obey hyperscaling relation (within the error bars). Equation (6) yields effective dimensionality of systems Deff = 1.89(6) for (4, 6, 12) and Deff = 1.76(7) for (4, 82). The effective dimensionalities of KCOD on our two AL are close to those for MVM on (4, 6, 12) AL (Deff = 1.78(7)) and on (4, 82) AL (Deff = 1.83(6)). The results of simulations are collected in Table 2.
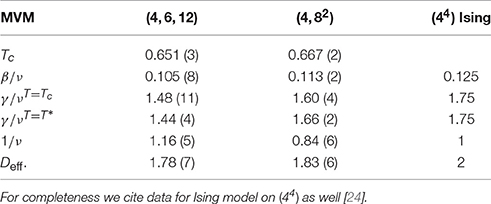
Table 1. Critical temperatures, exponents and effective dimensionalities for MVM on (4, 6, 12) and (4, 82) AL [22].
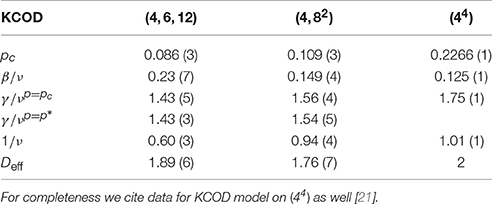
Table 2. Critical parameter, exponents and effective dimension for KCOD model on (4, 6, 12) and (4, 82).
4. Conclusion
We studied a non-equilibrium KCOD model through extensive Monte Carlo simulations on (4, 6, 12) and (4, 82) AL. On these lattices, the KCOD model shows a second-order phase transition. Our Monte Carlo simulations suggest that the effective dimensionality Deff is close to two, i.e., that hyperscaling relation 2β/ν + γ/ν ≈ 2 may be valid.
Finally, we remark that the critical exponents γ/ν, β/ν, and 1/ν for KCOD on (4, 6, 12) and (4, 82) AL are similar to the MVM model on (4, 6, 12) and (4, 82) AL [22], see Tables 1, 2. Therefore, this model not belong to the Ising universality class [24] and the hypothesis of Grinstein has been disproved.
Author Contributions
The author confirms being the sole contributor of this work and approved it for publication.
Conflict of Interest Statement
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
FL is grateful to Dietrich Stauffer for stimulating discussions and for critical reading of the manuscript. He also acknowledges the support the system SGI Altix 1350 the computational park CENAPAD, UNICAMP-USP, SP-BRASIL.
References
1. Galam S. Majority rule, hierarchical structures, and democratic totalitarianism: a statistical approach. J Math Psychol. (1986) 30:426–34; earlier Galam S, Gefen Y, Shapir Y. Sociophysics: a new approach of sociological collective behaviour. I. mean-behaviour description of a strike. J Math Sociol. (1982) 9:1–13. doi: 10.1080/0022250X.1982.9989929
2. Galam S. Social paradoxes of majority rule voting and renormalization group. J Stat Phys. (1990) 61: 943–51. doi: 10.1007/BF01027314
3. Fortunato S, Macy M, Redner S. Editorial. J Stat Phys. (2013) 151:1–8. doi: 10.1007/s10955-013-0703-2
4. Galam S. The drastic outcomes from voting alliances in three-party democratic voting (1990 –> 2013). J Stat Phys. (2013) 151:46–68. doi: 10.1007/s10955-012-0641-4
5. Galam S. Sociophysics: a personal testimony. Phys A (2004) 336:49–55. doi: 10.1016/j.physa.2004.01.009
6. Stauffer D. A biased review of sociophysics. J Stat Phys. (2013) 151:9–20. doi: 10.1007/s10955-012-0604-9
7. Galam S. Sociophysics: A Physicist's Modeling of Psycho-political Phenomena. New York, NY: Springer (2012). doi: 10.1007/978-1-4614-2032-3
8. de Oliveira MJ. Isotropic majority-vote model on a square lattice. J Stat Phys. (1992) 66:273–81. doi: 10.1007/BF01060069
9. Santos MA, Teixeira S. Anisotropic voter model. J Stat Phys. (1995) 78:963–70. doi: 10.1007/BF02183696
10. Crochik L, Tomé T. Entropy production in the majority vote model. Phys Rev E (2005) 72:057103–7. doi: 10.1103/PhysRevE.72.057103
11. Hasenbusch M. Monte Carlo studies of the three-dimensional Ising model in equilibrium. Int J Mod Phys C (2001) 12:911–1009. doi: 10.1142/S0129183101002383
12. Binney JJ, Dowrick NJ, Fisher AJ, Newman MEJ. A Theory of Critical Phenomena. An Introduction to the Renormalization Group. Oxford: Clarendon Press (1992).
13. Grinstein G, Jayaprakash C, He Y. Statistical mechanics of probabilistic cellular automata. Phys Rev Lett. (1985) 55:2527–30. doi: 10.1103/PhysRevLett.55.2527
14. Biswas S, Chatterjee A, Sen P. Disorder induced phase transition in kinetic models of opinion dynamics. Phys A (2012) 391:3257–65. doi: 10.1016/j.physa.2012.01.046
15. Deffuant G, Amblard F, Weisbuch G, Faure T. How can extremism prevail? A study based on the relative agreement interaction model. J Artif Soc Soc Simul. (2002) 5:1–26.
16. Hegselmann R, Krause U. Opinion dynamics and bounded confidence models, analysis and simulation. J Artif Soc Soc Simul. (2002) 5:1–32.
17. Sznajd-Weron K, Sznajd J. Opinion evolution in closed community. Int J Mod Phys C (2000) 11:1157–65. doi: 10.1142/S0129183100000936
18. Costa Filho RN, Almeida MP, Andrade JS Jr, Moreira JE. Scaling behavior in a proportional voting process. Phys Rev E (1999) 60:1067–8. doi: 10.1103/PhysRevE.60.1067
19. Araripe LE, Costa Filho RN, Herrmann HJ, Andrade JS Jr. Pluraty voting: the statistical laws of democracy in Brazil. Int J Mod Phys C (2006) 17:1809–13. doi: 10.1142/S0129183106010200
20. Araripe LE, Costa Filho RN. Role of parties in the vote distribution of proportional elections. Phys A (2009) 388:4167–70. doi: 10.1016/j.physa.2009.06.023
21. Mukherjee S, Chatterjee A. Disorder induced phase transition in an opinion dynamics model: results in 2 and 3 dimensions. Phys Rev E (2016) 94:062317–22. doi: 10.1103/PhysRevE.94.062317
22. Welington F, Lima S. Nonequilibrium model on Archimedean lattices. Cent Eur J Phys. (2014) 12:185–91. doi: 10.2478/s11534-014-0435-1
Keywords: Monte Carlo simulation, critical exponents, phase transition, non-equilibrium
PACS numbers: 05.10.Ln, 05.70.Fh, 64.60.Fr
Citation: Lima FWS (2017) Kinetic Continuous Opinion Dynamics Model on Two Types of Archimedean Lattices. Front. Phys. 5:47. doi: 10.3389/fphy.2017.00047
Received: 27 June 2017; Accepted: 19 September 2017;
Published: 29 September 2017.
Edited by:
Antonio F. Miguel, University of Évora, PortugalReviewed by:
Unjong Yu, Gwangju Institute of Science and Technology, South KoreaRaimundo Nogueira Costa Filho, Federal University of Ceará, Brazil
Copyright © 2017 Lima. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Francisco W. S. Lima, ZndzbGltYUBnbWFpbC5jb20=
 Francisco W. S. Lima
Francisco W. S. Lima