- 1Institute of Radiology, University Hospital Erlangen, Erlangen, Germany
- 2Medical Physics in Radiology, German Cancer Research Center, Heidelberg, Germany
Nuclear magnetic resonance (NMR) diffusion measurements can be used to probe porous structures or biological tissues by means of the random motion of water molecules. The short-time expansion of the diffusion coefficient in powers of t1/2, where t is the diffusion time related to the duration of the diffusion-weighting magnetic field gradient profile, is universally connected to structural parameters of the boundaries restricting the diffusive motion. The t1/2-term is proportional to the surface to volume ratio. The t-term is related to permeability and curvature. The short time expansion can be measured with two approaches in NMR-based diffusion experiments: First, by the use of diffusion encodings of short total duration and, second, by application of oscillating gradients of long total duration. For oscillating gradients, the inverse of the oscillation frequency becomes the relevant time scale. The purpose of this manuscript is to show that the oscillating gradient approach is blind to the t-term. On the one hand, this prevents fitting of permeability and curvature measures from this term. On the other hand, the t-term does not bias the determination of the t1/2-term in experiments.
Introduction
This article builds on and extends a previous article [1], which investigated the term linear in time of the short-time expansion of the diffusion coefficient [2–5] which is given by:
where D0 is the free diffusion coefficient, S/V is the surface-to-volume ratio, κ is the surface permeability, ϱ is the surface relaxivity, is a mean curvature term, d is the spatial dimension, and t is the observation time. This universal expansion is valuable, since it connects a measurable quantity, i.e., D(t), to structural parameters of barriers restricting the diffusive motion.
Using magnetic resonance diffusion experiments [6–9], information about the diffusive motion of spin-bearing particles can be encoded into the signal by using diffusion-weighting magnetic field gradient pulses. Regarding the diffusion time t linked to the total duration of the diffusion-weighting gradient profile, one often considers the long-time and short-time limit. In the first case, the limit of long diffusion time, detailed information about the porous structure of the investigated material can be obtained [10–12] such as actual pore shapes [13–15]. On the other hand, D(t) can be measured in the short-time limit to obtain the structural parameters in Equation (1). For this purpose, a pair of bipolar gradient pulses is applied to achieve diffusion encoding [16]. In the short gradient pulse approximation [6, 17], the measured diffusion coefficient in such experiments is D(t) (Equation 1). If the gradient pulses cannot be considered to be short, Equation (1) must be modified to take into account the effect of the gradient pulse duration and of the temporal evolution of the gradients G(t) [18–22]:
Here, the influence of the temporal gradient profile is expressed solely by the constants c1 and c2, which can be computed from G(t), so that an elegant decoupling takes place. Note that surface relaxation is neglected in Equation (2) and in the remainder of the manuscript, thus avoiding the difficulties in the mathematical treatment [23], and that t is the total duration of the diffusion gradients in Equation (2).
In Laun et al. [1], it was shown that c2 can be tuned to values between 0 and 1. Tuning c2 to zero can be advantageous, for example, if the aim of the experiment is to measure the -term without bias from the t-term.
A striking result [24–30] is that the short-time expansion is moreover valid for the diffusion spectrum 𝔇(ω), or , that can be measured by the use of oscillating gradients. Note that 𝔇app(τ) and Dapp(t) are different functions as outlined in more detail below. Then Equation (1) can be cast in a similar form for the diffusion spectrum, where t is replaced by the duration τ of one gradient oscillation:
The constants Cn in Equation (3) are printed in capital letters because they differ, in general, from the constants cn of Equation (2) as will be described below.
Equations (2) and (3) were successfully applied in experiments to obtain information about the first order term and thus about the surface-to-volume ratio [27, 28, 31–37]. The thereto necessary constants C1 were derived for some gradient waveforms such as the bipolar waveform and oscillating gradients [18, 27, 29, 38].
The aim of the work at hand is to investigate the constant C2. For this purpose, Equation (3) is derived starting from Equation (1).
Materials and Methods
Numerical simulations were performed as in Laun et al. [1]1. The diffusion coefficient Dapp(t) and the diffusion spectrum 𝔇app(τ) [using the signal decrease as recalled in Equation (A13) in Appendix A (Supplementary Material)] were computed using the multiple correlation function (MCF) approach [22, 39–45] (using Equation 114 in Grebenkov [42]). The MCF approach decomposes the magnetization into the eigenfunctions of the Laplace operator. One important parameter is the number Nλ of employed eigenfunctions, which should be sufficiently large to ensure numerical accuracy. In the presented results, the accuracy was verified by increasing Nλ and checking whether numerical results remained unchanged. A detailed description of the MCF approach is beyond the scope of this article, but can be found in Grebenkov and Grebenkov [46, 47], for example.
The following closed domains were considered: slab, cylinder, sphere, “bi-slab” (see Figure 1). The bi-slab domain consists of three parallel planes. The inner plane is permeable, while the two outer ones are impermeable. Particles only reside within the volume between the two impermeable slabs. The radii of cylinder and sphere were 5 μm, the separation of the slabs was 10 μm, and the separation of the planes of the bi-slab domain was 10 μm (thus the bi-slab domain was in total 20 μm wide). The free diffusion coefficient D0 was set to 1 μm2/ms. The boundaries were fully reflecting except for the inner wall of the bi-slab domain, which had a permeability of 50 μm/s. Nλ was 100 for the bi-slab domain, 500 for slab domain and cylinder, and 200 for the sphere. Oscillating cosine gradients were simulated with a total duration Tcos of 0.05, 0.1, and 0.5 s. The number of oscillations N was varied in twenty steps. For bipolar gradients, δ was set to 10−3 ms and t was varied between 0.1 and 15 ms.
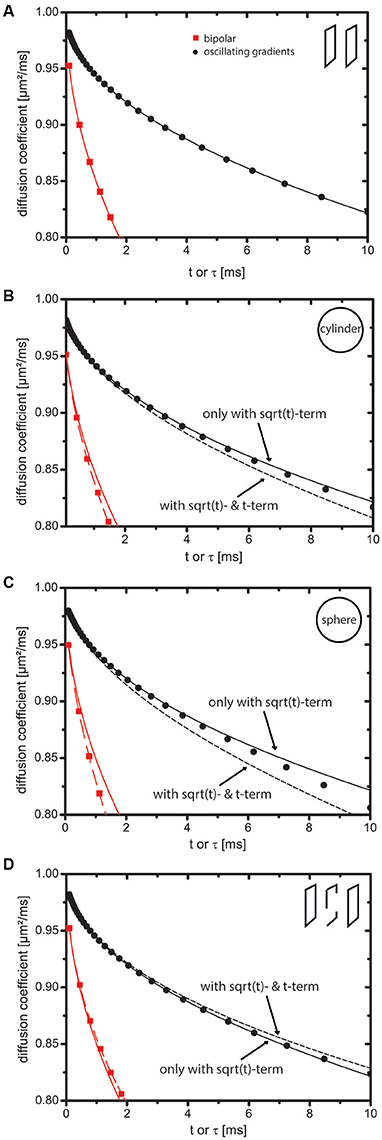
Figure 1. Impact of the t-term on the short-time expansion of the diffusion coefficient. Markers indicate values obtained by numerical simulations. Solid lines represent the short-time expansion to order and dotted lines represent it to order t. Red square markers represent bipolar gradients (i.e., Dapp(t)) and black circular markers represent oscillating cosine gradients (i.e., 𝔇app(τ)). (A) Slab domain. The t-term is zero because curvature and permeability of the sample are zero. (B–D) Cylinder, sphere, and bi-slab. In case of oscillating cosine gradients, the t-term is zero, because C2 is zero. For this reason, the markers stay close to the solid line in contrast to the markers indicating the bipolar gradients, which stay close to the dotted line. Tcos was 500 ms.
Additionally, the difference between simulated diffusion coefficients and first order short time expansion was calculated. This difference is labeled ΔD in the plots and represents or .
Results
Derivation of the t-Term for Oscillating Gradients
First, a shorthand-notation for Equation (2) is introduced:
with the coefficients
and so on (with c0 = 1).
As outlined in Appendix A (Supplementary Material), the short-time expansion for the position correlation function that generates an experimentally detectable signal attenuation reads:
with t21 = t2 − t1, where the brackets 〈…〉 denote the expectation value. Note that the terms and where neglected in Equation (5) because they do not contribute to the signal attenuation. Equation (5) can be related to the diffusion spectrum 𝔇(ω) (see Appendix A in Supplementary Material) via:
This Fourier integral exists (see Appendix B in Supplementary Material):
and thus by inserting Equation (7) in Equation (6), one finds:
Note that the gamma function Γ makes the constants cn increase swiftly at larger n. Defining the time parameter τ = t/n, entailing ω = 2π/τ, one finds:
with 𝔇app(τ) being identical to 𝔇(ω) except for taking a different argument. 𝔇app(τ) has exactly the form of Equation (3) as desired and one can read off the coefficients Cn directly: C1 = 3/8 and C2 = 0. Note that the value of C1 was reported previously (e.g., in Novikov and Kiselev [29]). The vanishing of C2 has not been reported so far to our knowledge.
Using the expression for M1, one finds:
It is interesting to calculate the coefficients c1 and c2 for a short-time cosine gradient with one oscillation [with methods as described, e.g., in Laun et al. [1] and references therein]. We find c1 = 3·(4π FresnelC(2) + 3 FresnelS(2))/16/π ≈ 0.428 and c2 = 0. These values bear great similarity to C1 ≈ 0.375 and C2 = 0. It should be noted that c2 of oscillating cosine gradients with any number of oscillations equals zero because they are “flow-compensated,” i.e., because their first moment vanishes [1].
Validation with Simulations
Figure 1 displays Dapp(t) and 𝔇app(τ). Markers indicate simulation results using the MCF approach and lines represent the short-time expansion. For Dapp(t), solid lines equal and dotted lines equal . For 𝔇app(τ), solid lines equal and dotted lines equal . The term shall represent a reasonable “guess” for the t-term with an effective diffusion time , where the coefficient C2 was set to one. The intention is to visualize a line with C2 ≠ 0, although this term does not occur in reality. Some remarks on effective diffusion times can be found in Appendix C (Supplementary Material).
For the slab domain (Figure 1A), Mn>1 = 0 holds true (see [42]). Hence, Figure 1A does not display a dotted line and markers stay close to the solid lines.
In Figures 1B,C (cylinder, sphere) and Figure 1D (bi-slab), it is clearly visible that the markers for the bipolar gradients (with c2 = 1 ≠ 0) stay close to the dotted lines indicating the importance of the t-term. The markers of the oscillating cosine gradients stay close to the solid line indicating that the t-term does not influence 𝔇app(τ). Owing to higher order terms, deviations between the short-time expansion and markers are present at larger t.
Figure 2 shows ΔD, i.e., the difference between simulated diffusion coefficients and first order short time expansion. The dotted line represents the t-term, i.e., M2c2t for the bipolar gradients. For the oscillating gradients, the black dotted line shall represent an educated guess for the t-term, i.e., , as in Figure 1.
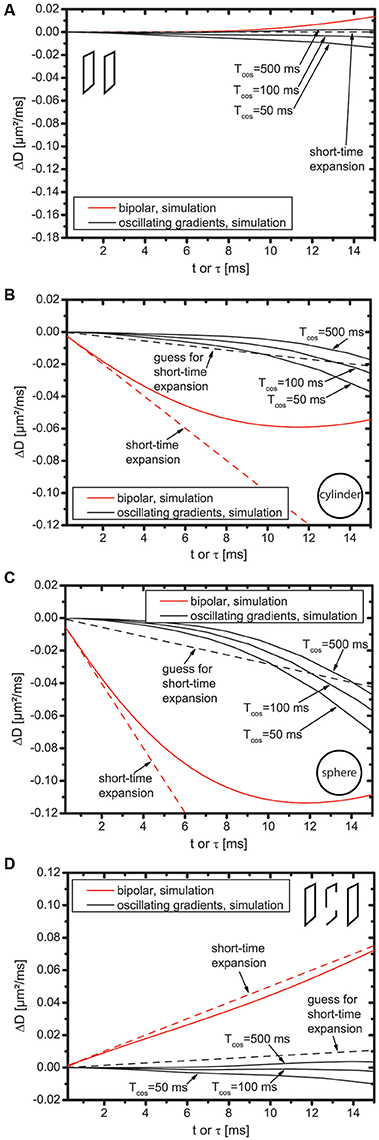
Figure 2. Difference between simulated diffusion coefficients and first order short time diffusion expansion for slab domain (A), cylinder (B), sphere (C), and bi-slab (D).
First, the bipolar gradients displayed in Figure 2 are discussed (displayed in red color). For the slab domain (Figure 2A), the dotted line is flat because M2 = 0. However, deviations of ΔD from zero are well visible for t > 10 ms. This does not result from the influence of higher order terms because all higher order terms are zero. It rather indicates the breakdown of the short-time expansion. For cylinder, sphere, and bi-slab (Figures 2B–D), the slope of ΔD is identical to that of the dotted line at t = 0, but starts deviating already roughly at t = 2 ms indicating that either higher order terms are needed or, again, that the short-time expansion breaks down. This deviation is more pronounced for cylinder and sphere than for the bi-slab.
Next, the oscillating gradients in Figure 2 are discussed (displayed in black color). For cylinder, sphere, and bi-slab, ΔD does have zero slope at t = 0 and does not follow the dotted line for any of these domains, which supports the finding that C2 = 0. This holds true for Tcos = 500 ms, but also for reduced total duration of the oscillating gradients, i.e., for smaller Tcos. The difference of ΔD between Tcos = 500 ms and Tcos = 50 ms is smaller than 0.015 μm2/ms for all domains at τ = 10 ms, which is roughly equally large as the guessed t-term, but an order of magnitude smaller than the -term. Thus, for the considered domains, Tcos = 50 ms still appears to be well suited for investigations of the -term, even with as few as five oscillations.
Discussion
The main result of this work is that oscillating cosine gradients are blind with respect to the t-term of the short-time expansion of the apparent diffusion coefficient.
Oscillating gradients and extensions [48–51] have been used in several research studies [27, 28, 32, 35, 38, 52–65], among them applications to human brains in vivo [66]. Comparing oscillating gradients to pulsed gradients, the advantage of the oscillating gradients is that the obtainable b-value is higher allowing the assessment of shorter times. This is particularly useful if strong gradient amplitudes are not available or if the structure of interest is too small. The disadvantage is the need for longer echo times entailing decreased signal-to-noise ratio due to transversal relaxation, which also entails a longer acquisition time.
As oscillating gradients are blind to the t-term, estimates of S/V as in Reynaud et al. [36] are not biased by this term, but, obviously, the membrane permeability, for example, cannot be estimated using the t-term. This is in line with the findings by Li et al. [67], who reported that the membrane permeability has little effect on oscillating gradient derived diffusion coefficients at high frequencies. This is presumably not a major limitation given the smallness of the t-term that is visible in Figures 1, 2, which makes a fit challenging. The permeability information must have some influence on 𝔇app(τ) at long τ; otherwise diffusion in the bi-slab would have to be identical to that of a single slab domain of double size. Therefore, the estimation of membrane permeability using oscillating gradients might in principle be possible.
As different versions of Equations (10) and (11) can be found in the literature, a comparison is worthwhile. Equation (10) is identical to Equation 10 of the article by Novikov and Kiselev [29]. Except for a small deviation, which may be due to numerics, Equation (10) is also identical to Equation (3) of the article by Xu et al. [35], but, to our understanding, not to the respective equations in an earlier article [27]. In general, care must be taken concerning the definition of τ. For example, Zielinski et al. [38] use the definition τZielinski = τ/2, which is closer to the classical timing definitions of CPMG echo trains than our definition. Considering this difference in definitions, their respective coefficient C1 for the CPMG condition as stated in their Equation (6) is almost identical to 3/8, which is in agreement with the finding that the difference between C1 of CPMG and cosine gradients should be almost negligible as stated in section 3.3 of Novikov and Kiselev [29]. Further, we found our coefficient C1 to be a factor of six smaller than the one stated in Equation 14 in the article by Stepišnik et al. [28]. This difference was noted by the authors themselves and in Novikov and Kiselev [29].
Interestingly, the disappearance of the t-term in the Mitra expansion of Equation (3) using oscillating gradients is due to its disappearance in 𝔇(ω), or 𝔇app(2π/τ), respectively. Thus, optimizing oscillating gradient profiles instead of using, for example, just cosine gradients, which was a successful approach in other regards [68, 69], does not help to make the t-term reappear in the signal attenuation.
In practice, diffusion measurements use spin echoes and hence two gradients at both sides of the refocusing pulse (as in Baron and Beaulieu [66]). This effectively introduces an extra variable, i.e., the separation of two gradients, which can affect the spectrum of diffusion gradients. When interpreting oscillating gradient experiments, this effect must be taken into account.
A limitation of the presented simulations is that they cannot prove the disappearance of the t-term. In principle, a very small t-term might be present and go unnoticed.
In conclusion, oscillating gradients are blind to the t-term and hence no bias in fits of the surface-to-volume ratio arises from the t-term.
Author Contributions
FL performed the simulations and initial computations. TK and MU were involved in the design of the evaluations. TK, AN, KD, and FL were involved in implementation and testing of the MCF code and of the mathematical derivations.
Funding
Financial support by the DFG (grant numbers SFB TRR 125/2 R01 and KU 3362/1-1) is gratefully acknowledged.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
The handling Editor declared a past co-authorship with the authors TK and FL.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2017.00056/full#supplementary-material
Footnotes
1. ^A considerable overlap of the Methods sections with the corresponding sections of the earlier article is present.
References
1. Laun FB, Kuder TA, Zong F, Hertel S, Galvosas P. Symmetry of the gradient profile as second experimental dimension in the short-time expansion of the apparent diffusion coefficient as measured with NMR diffusometry. J Magn Reson. (2015) 259:10–9. doi: 10.1016/j.jmr.2015.07.003
2. Mitra PP, Sen PN, Schwartz LM, Ledoussal P. Diffusion propagator as a probe of the structure of porous-media. Phys Rev Lett. (1992) 68:3555–8. doi: 10.1103/PhysRevLett.68.3555
3. Mitra PP, Sen PN, Schwartz LM. Short-time behavior of the diffusion-coefficient as a geometrical probe of porous-media. Phys Rev B. (1993) 47:8565–74. doi: 10.1103/PhysRevB.47.8565
4. Sen PN, Schwartz LM, Mitra PP, Halperin BI. Surface relaxation and the long-time diffusion coefficient in porous media: periodic geometries. Phys Rev B Condens Matter. (1994) 49:215–25. doi: 10.1103/PhysRevB.49.215
5. Sen PN. Time-dependent diffusion coefficient as a probe of geometry. Concepts Magn Reson Part A. (2003) 23:1–21. doi: 10.1002/cmr.a.20017
6. Callaghan PT. Translational Dynamics and Magnetic Resonance. New York, NY: Oxford University Press (2011).
7. Jones DK. Diffusion MRI: Theory, Methods, and Applications. New York, NY: Oxford University Press (2011).
8. Laun FB, Fritzsche KH, Kuder TA, Stieltjes B. Introduction to the basic principles and techniques of diffusion-weighted imaging. Radiologe (2011) 51:170–9. doi: 10.1007/s00117-010-2057-y
9. Freitag MT, Bickelhaupt S, Ziener C, Meier-Hein K, Radtke JP, Mosebach J, et al. Selected clinically established and scientific techniques of diffusion-weighted MRI. In the context of imaging in oncology. Radiologe (2016) 56:137–47. doi: 10.1007/s00117-015-0066-6
10. Novikov DS, Jensen JH, Helpern JA, Fieremans E. Revealing mesoscopic structural universality with diffusion. Proc Natl Acad Sci USA. (2014) 111:5088–93. doi: 10.1073/pnas.1316944111
11. Sigmund EE, Novikov DS, Sui D, Ukpebor O, Baete S, Babb JS, et al. Time-dependent diffusion in skeletal muscle with the random permeable barrier model (RPBM): application to normal controls and chronic exertional compartment syndrome patients. NMR Biomed. (2014) 27:519–28. doi: 10.1002/nbm.3087
12. Lemberskiy G, Rosenkrantz AB, Veraart J, Taneja SS, Novikov DS, Fieremans E. Time-dependent diffusion in prostate cancer. Invest Radiol. (2017b) 52:405–11. doi: 10.1097/RLI.0000000000000356
13. Laun FB, Kuder TA, Wetscherek A, Stieltjes B, Semmler W. NMR-based diffusion pore imaging. Phys Rev E Stat Nonlin Soft Matter Phys. (2012) 86:021906. doi: 10.1103/PhysRevE.86.021906
14. Kuder TA, Bachert P, Windschuh J, Laun FB. Diffusion pore imaging by hyperpolarized xenon-129 nuclear magnetic resonance. Phys Rev Lett. (2013). 111:028101. doi: 10.1103/PhysRevLett.111.028101
15. Demberg K, Laun FB, Windschuh J, Umathum R, Bachert P, Kuder TA. Nuclear magnetic resonance diffusion pore imaging: experimental phase detection by double diffusion encoding. Phys Rev E. (2017) 95:022404. doi: 10.1103/PhysRevE.95.022404
16. Stejskal EO, Tanner JE. Spin diffusion measurements: spin echoes in the presence of a time-dependent field gradient. J Chem Phys. (1965) 42:288–92. doi: 10.1063/1.1695690
17. Stejskal EO. Use of spin echoes in a pulsed magnetic-field gradient to study anisotropic, restricted diffusion and flow. J Chem Phys. (1965) 43:3597–603. doi: 10.1063/1.1696526
18. De Swiet TM, Sen PN. Decay of nuclear magnetization by bounded diffusion in a constant field gradient. J Chem Phys. (1994) 100:5597–604. doi: 10.1063/1.467127
19. Fordham EJ, Gibbs SJ, Hall LD. Partially restricted diffusion in a permeable sandstone: observations by stimulated echo PFG NMR. Magn Reson Imaging. (1994) 12:279–84. doi: 10.1016/0730-725X(94)91536-9
20. Fordham EJ, Mitra PP, Latour LL. Effective diffusion times in multiple-pulse PFG diffusion measurements in porous media. J Magn Reson Ser A. (1996) 121:187–92. doi: 10.1006/jmra.1996.0159
21. Sen PN, Andre A, Axelrod S. Spin echoes of nuclear magnetization diffusing in a constant magnetic field gradient and in a restricted geometry. J Chem Phys. (1999) 111:6548–55. doi: 10.1063/1.480009
22. Axelrod S, Sen PN. Nuclear magnetic resonance spin echoes for restricted diffusion in an inhomogeneous field: methods and asymptotic regimes. J Chem Phys. (2001) 115:6878–95. doi: 10.1063/1.1356010
23. Grebenkov DS. Multiple Correlation function approach: rigorous results for simple geometries. Diff Fundam. (2007a) 5:1–34. Available online at: http://diffusion.uni-leipzig.de/contents_vol5.html; http://ul.qucosa.de/landing-page/?tx_dlf[id]=http%3A%2F%2Fubl.qucosa.de%2Fapi%2Fqucosa%253A14264%2Fmets
24. Gross B, Kosfeld R. Anwendung der spin-echo-methode der messung der selbstdiffusion. Messtechnik (1969) 77:171–7.
25. Stepišnik J. Analysis of Nmr self-diffusion measurements by a density-matrix calculation. Physica (1981) 104:350–64. doi: 10.1016/0378-4363(81)90182-0
26. Stepišnik J. Time-dependent self-diffusion by NMR spin-echo. Physica B (1993) 183:343–50. doi: 10.1016/0921-4526(93)90124-O
27. Parsons EC, Does MD, Gore JC. Temporal diffusion spectroscopy: theory and implementation in restricted systems using oscillating gradients. Magn Reson Med. (2006) 55:75–84. doi: 10.1002/mrm.20732
28. Stepišnik J, Lasic S, Mohoric A, Sersa I, Sepe A. Spectral characterization of diffusion in porous media by the modulated gradient spin echo with CPMG sequence. J Magn Reson. (2006) 182:195–9. doi: 10.1016/j.jmr.2006.06.023
29. Novikov DS, Kiselev VG. Surface-to-volume ratio with oscillating gradients. J Magn Reson. (2011) 210:141–5. doi: 10.1016/j.jmr.2011.02.011
30. Sukstanskii A. L. Exact analytical results for ADC with oscillating diffusion sensitizing gradients. J Magn Reson. (2013) 234:135–40. doi: 10.1016/j.jmr.2013.06.016
31. Latour LL, Svoboda K, Mitra PP, Sotak CH. Time-dependent diffusion of water in a biological model system. Proc Natl Acad Sci USA. (1994) 91:1229–33. doi: 10.1073/pnas.91.4.1229
32. Schachter M, Does MD, Anderson AW, Gore JC. Measurements of restricted diffusion using an oscillating gradient spin-echo sequence. J Magn Reson. (2000) 147:232–7. doi: 10.1006/jmre.2000.2203
33. Vogt C, Galvosas P, Klitzsch N, Stallmach F. Self-diffusion studies of pore fluids in unconsolidated sediments by PFG NMR. J Appl Geophys. (2002) 50:455–67. doi: 10.1016/S0926-9851(02)00195-7
34. Parsons EC, Does MD, Gore JC. Modified oscillating gradient pulses for direct sampling of the diffusion spectrum suitable for imaging sequences. Magn Reson Imaging. (2003) 21:279–85. doi: 10.1016/S0730-725X(03)00155-3
35. Xu JZ, Xie JP, Jourquin J, Colvin DC, Does MD, Quaranta V, et al. Influence of cell cycle phase on apparent diffusion coefficient in synchronized cells detected using temporal diffusion spectroscopy. Magn Reson Med. (2011) 65:920–6. doi: 10.1002/mrm.22704
36. Reynaud O, Winters KV, Hoang DM, Wadghiri YZ, Novikov DS, Kim SG. Surface-to-volume ratio mapping of tumor microstructure using oscillating gradient diffusion weighted imaging. Magn Reson Med. (2016b) 76:237–47. doi: 10.1002/mrm.25865
37. Lemberskiy G, Baete SH, Cloos MA, Novikov DS, Fieremans E. Validation of surface-to-volume ratio measurements derived from oscillating gradient spin echo on a clinical scanner using anisotropic fiber phantoms. MR Biomed. (2017a). 30:e3708. doi: 10.1002/nbm.3708
38. Zielinski LJ, Hurlimann MD. Probing short length scales with restricted diffusion in a static gradient using the CPMG sequence. Jo Magn Reson. (2005) 172:161–7. doi: 10.1016/j.jmr.2004.10.006
39. Caprihan A, Wang LZ, Fukushima E. A multiple-narrow-pulse approximation for restricted diffusion in a time-varying field gradient. J Magn Reson Series A. (1996) 118:94–102. doi: 10.1006/jmra.1996.0013
40. Callaghan PT. A simple matrix formalism for spin echo analysis of restricted diffusion under generalized gradient waveforms. J Magn Reson. (1997) 129:74–84. doi: 10.1006/jmre.1997.1233
41. Barzykin AV. Theory of spin echo in restricted geometries under a step-wise gradient pulse sequence. J Magn Reson. (1999) 139:342–53. doi: 10.1006/jmre.1999.1778
42. Grebenkov DS. NMR survey of reflected Brownian motion. Rev Modern Phys. (2007b) 79:1077–137. doi: 10.1103/RevModPhys.79.1077
43. Grebenkov DS. Analytical solution for restricted diffusion in circular and spherical layers under inhomogeneous magnetic fields. J Chem Phys. (2008a) 128:134702. doi: 10.1063/1.2841367
44. Özarslan E, Shemesh N, Basser PJ. A general framework to quantify the effect of restricted diffusion on the NMR signal with applications to double pulsed field gradient NMR experiments. J Chem Phys. (2009) 130:104702. doi: 10.1063/1.3082078
45. Laun FB. Restricted diffusion in NMR in arbitrary inhomogeneous magnetic fields and an application to circular layers. J Chem Phys. (2012) 137:044704. doi: 10.1063/1.4736849
46. Grebenkov DS. Laplacian eigenfunctions in NMR. I. A numerical tool. Concepts Magn Reson A. (2008b) 32A:277–301. doi: 10.1002/cmr.a.20117
47. Grebenkov DS. Laplacian eigenfunctions in NMR. II. Theoretical advances. Concepts Magne Resona A. (2009) 34A:264–96. doi: 10.1002/cmr.a.20145
48. Shemesh N, Westin CF, Cohen Y. Magnetic resonance imaging by synergistic diffusion-diffraction patterns. Phys Rev Lett. (2012) 108:058103. doi: 10.1103/PhysRevLett.108.058103
49. Shemesh N, Alvarez GA, Frydman L. Measuring small compartment dimensions by probing diffusion dynamics via Non-uniform Oscillating-Gradient Spin-Echo (NOGSE) NMR. J Magn Reson. (2013) 237:49–62. doi: 10.1016/j.jmr.2013.09.009
50. Lundell H, Sonderby CK, Dyrby TB. Diffusion weighted imaging with circularly polarized oscillating gradients. Magn Reson Med. (2015) 73:1171–6. doi: 10.1002/mrm.25211
51. Shemesh N, Alvarez GA, Frydman L. (2015). Size distribution imaging by non-uniform oscillating-gradient spin echo (NOGSE) MRI. PLoS ONE 10:e0133201. doi: 10.1371/journal.pone.0133201
52. Does MD, Parsons EC, Gore JC. Oscillating gradient measurements of water diffusion in normal and globally ischemic rat brain. Magn Reson Med. (2003) 49:206–15. doi: 10.1002/mrm.10385
53. Aggarwal M, Jones MV, Calabresi PA, Mori S, Zhang JY. Probing mouse brain microstructure using oscillating gradient diffusion MRI. Magn Reson Med. (2012) 67:98–109. doi: 10.1002/mrm.22981
54. Xu JZ, Li K, Smith RA, Waterton JC, Zhao P, Chen HD et al. Characterizing tumor response to chemotherapy at various length scales using temporal diffusion spectroscopy. PLoS ONE (2012) 7:e41714. doi: 10.1371/journal.pone.0041714
55. Ianus A, Siow B, Drobnjak I, Zhang H, Alexander DC. Gaussian phase distribution approximations for oscillating gradient spin echo diffusion MRI. J Magn Reson. (2013) 227:25–34. doi: 10.1016/j.jmr.2012.11.021
56. Aggarwal M, Burnsed J, Martin LJ, Northington FJ, Zhang JY. Imaging neurodegeneration in the mouse hippocampus after neonatal hypoxia-ischemia using oscillating gradient diffusion MRI. Magn Reson Med. (2014) 72:829–40. doi: 10.1002/mrm.24956
57. Li H, Gore JC, Xu JZ. Fast and robust measurement of microstructural dimensions using temporal diffusion spectroscopy. J Magn Reson. (2014) 242:4–9. doi: 10.1016/j.jmr.2014.02.007
58. Portnoy S, Fichtner ND, Dziegielewski C, Stanisz MP, Stanisz GJ. In vitro detection of apoptosis using oscillating and pulsed gradient diffusion magnetic resonance imaging. NMR Biomed. (2014) 27:371–80. doi: 10.1002/nbm.3070
59. Van AT, Holdsworth SJ, Bammer R. In vivo investigation of restricted diffusion in the human brain with optimized oscillating diffusion gradient encoding. Magn Reson Med. (2014) 71:83–94. doi: 10.1002/mrm.24632
60. Wu D, Martin LJ, Northington FJ, Zhang JY. Oscillating gradient diffusion MRI reveals unique microstructural information in normal and hypoxia-ischemia injured mouse brains. Magn Reson Med. (2014) 72:1366–74. doi: 10.1002/mrm.25441
61. Xu JZ, Li H, Harkins KD, Jiang XY, Xie JP, Kang H, et al. Mapping mean axon diameter and axonal volume fraction by MRI using temporal diffusion spectroscopy. Neuroimage (2014) 103:10–9. doi: 10.1016/j.neuroimage.2014.09.006
62. Li H, Jiang XY, Wang F, Xu JZ, Gore JC. Structural information revealed by the dispersion of ADC with frequency. Magn Reson Imaging (2015) 33:1083–90. doi: 10.1016/j.mri.2015.06.009
63. Drobnjak I, Zhang H, Ianus A, Kaden E, Alexander DC. PGSE, OGSE, and sensitivity to axon diameter in diffusion MRI: insight from a simulation study. Magn Reson Med. (2016) 75:688–700. doi: 10.1002/mrm.25631
64. Jiang XY, Li H, Xie JP, Zhao P, Gore JC, Xu JZ. Quantification of cell size using temporal diffusion spectroscopy. Magn Reson Med. (2016) 75:1076–85. doi: 10.1002/mrm.25684
65. Reynaud O, Winters KV, Hoang DM, Wadghiri YZ, Novikov DS, Kim SG. Pulsed and oscillating gradient MRI for assessment of cell size and extracellular space (POMACE) in mouse gliomas. NMR Biomed. (2016a) 29:1350–63. doi: 10.1002/nbm.3577
66. Baron CA, Beaulieu C. Oscillating gradient spin-echo (OGSE) diffusion tensor imaging of the human brain. Magn Reson Med. (2014) 72:726–36. doi: 10.1002/mrm.24987
67. Li H, Jiang XY, Xie JP, McIntyre JO, Gore JC, Xu JZ. Time-dependent influence of cell membrane permeability on MR diffusion measurements. Magn Reson Med. (2016) 75:1927–34. doi: 10.1002/mrm.25724
68. Drobnjak I, Siow B, Alexander DC. Optimizing gradient waveforms for microstructure sensitivity in diffusion-weighted MR. J Magn Reson. (2010) 206:41–51. doi: 10.1016/j.jmr.2010.05.017
Keywords: magnetic resonance imaging, diffusion, short-time limit, surface-to-volume ratio, gradient profile, oscillating gradients
Citation: Laun FB, Demberg K, Nagel AM, Uder M and Kuder TA (2017) On the Vanishing of the t-term in the Short-Time Expansion of the Diffusion Coefficient for Oscillating Gradients in Diffusion NMR. Front. Phys. 5:56. doi: 10.3389/fphy.2017.00056
Received: 03 August 2017; Accepted: 24 October 2017;
Published: 14 November 2017.
Edited by:
Sune Nørhøj Jespersen, Aarhus University, DenmarkReviewed by:
Valerij G. Kiselev, Universitätsklinikum Freiburg, GermanyJunzhong Xu, Vanderbilt University, United States
Copyright © 2017 Laun, Demberg, Nagel, Uder and Kuder. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Tristan A. Kuder, dC5rdWRlckBka2Z6LmRl
 Frederik B. Laun
Frederik B. Laun Kerstin Demberg
Kerstin Demberg Armin M. Nagel1
Armin M. Nagel1 Tristan A. Kuder
Tristan A. Kuder