- 1Centre d'Imagerie Biomédicale, École Polytechnique Fédérale de Lausanne, Lausanne, Switzerland
- 2Department of Neurosurgery, Zablocki VA Medical Center, Medical College Wisconsin, Milwaukee, WI, United States
Diffusion MRI is arguably the method of choice for characterizing white matter microstructure in vivo. Over the typical duration of diffusion encoding, the displacement of water molecules is conveniently on a length scale similar to that of the underlying cellular structures. Moreover, water molecules in white matter are largely compartmentalized which enables biologically-inspired compartmental diffusion models to characterize and quantify the true biological microstructure. A plethora of white matter models have been proposed. However, overparameterization and mathematical fitting complications encourage the introduction of simplifying assumptions that vary between different approaches. These choices impact the quantitative estimation of model parameters with potential detriments to their biological accuracy and promised specificity. First, we review biophysical white matter models in use and recapitulate their underlying assumptions and realms of applicability. Second, we present up-to-date efforts to validate parameters estimated from biophysical models. Simulations and dedicated phantoms are useful in assessing the performance of models when the ground truth is known. However, the biggest challenge remains the validation of the “biological accuracy” of estimated parameters. Complementary techniques such as microscopy of fixed tissue specimens have facilitated direct comparisons of estimates of white matter fiber orientation and densities. However, validation of compartmental diffusivities remains challenging, and complementary MRI-based techniques such as alternative diffusion encodings, compartment-specific contrast agents and metabolites have been used to validate diffusion models. Finally, white matter injury and disease pose additional challenges to modeling, which are also discussed. This review aims to provide an overview of the current state of models and their validation and to stimulate further research in the field to solve the remaining open questions and converge toward consensus.
Diffusion weighted MRI (DWI) is unique in its ability to detect brain microstructure non-invasively. Characterization of white matter microstructure using DWI has shown high sensitivity to changes associated with normal brain development and aging and to the wide array of neurological diseases, injuries, and potential treatments. DWI is an excellent probe of microstructure, whose characteristic features are on the same length scale as the micrometer-scale displacement of water molecules. However, it remains an indirect probe, because extracting quantitative metrics that characterize the underlying tissue microstructure requires modeling of the DWI signal. Decisions regarding model choice and fitting procedures have considerable influence on the accuracy, reliability, and validity of the extracted metrics.
This review first presents an overview of current white matter models “in circulation” and exposes their common features and individual limitations (Part 1), noting that the discussion is restricted to long-time limit diffusion models, where axons are modeled as sticks. Next, efforts to validate models in the normal white matter using complementary techniques are discussed (Part 2), followed by a brief discussion of the additional challenges related to modeling of the diseased tissue (Part 3). Future directions of research are highlighted at every step.
Models
Two complementary approaches have emerged for extracting information about the tissue microstructure from the diffusion signal: signal representations and tissue models.
Signal representations—sometimes also referred to as “statistical models”—aim at empirically describing the diffusion signal behavior in a given voxel without assumptions about the underlying tissue. Thus, they are applicable to any tissue type, healthy or diseased, but the estimated parameters lack specificity and remain an indirect characterization of microstructure.
Tissue models, on the other hand, assume a given (schematic) geometry—a “picture” of the underlying tissue [1]. The analytical expression of the diffusion signal in the chosen environment is fit to the diffusion data, which allows the estimation of the relevant parameters of the microstructure. Tissue models can potentially provide greater specificity and interpretation of biologically-relevant parameters, but only if the assumption is met that the chosen model accurately captures all of the relevant features of the tissue, i.e., all those that effectively and substantially impact the diffusion signal in a given acquisition range.
In this section, we will first briefly review examples of signal representations, in order to reinforce the distinction with modeling. We will then review major biophysical models of white matter, with clear identification of their main assumptions and estimated parameters.
Signal Representations
The most widespread signal representation is the cumulant expansion [2–4], which relies on an expansion of the logarithm of the signal in polynomials up to a given order in b—i.e., a Taylor series:
where D is the diffusion coefficient and K the kurtosis. Or, in tensor form:
where D is the rank-2 diffusion tensor, W is the rank-4 kurtosis tensor, is the mean diffusivity and g is the direction of the applied diffusion weighting.
Diffusion tensor imaging (DTI) is thus an expansion up to the first order in b, valid for low diffusion weighting (b ≪ 1/(DK)) [5]. It is important to stress that DTI does not assume that the tissue is a Gaussian medium (K = 0)—which is reputedly not true for biological tissue, but rather that it is indistinguishable from a Gaussian medium when b ≪ 1/(DK).
Naturally, going beyond this low b-value regime and estimating the kurtosis of the diffusion probability distribution function—i.e., by how much it deviates from a Gaussian distribution—provides information about tissue complexity that is complementary to DTI metrics [2].
In order to estimate the six independent components of the diffusion tensor, the minimal required data is one b = 0 (unweighted) image and six non collinear directions on a single diffusion weighting, or “shell.” The additional estimation of the 15 independent components of the kurtosis tensor requires a minimal acquisition of one b = 0 image and 21 measurements distributed over 2 shells. The choice of the shell b-values is a trade-off between accuracy—they should be as low as possible, since the Taylor expansion is valid for bD → 0 — and precision—they should be as high as admittedly possible to limit the impact of noise [6]. This trade-off value is typically around b = 1 ms/μm2 for DTI and b = 2 ms/μm2 for DKI, in vivo. Largely improved algorithms for unbiased estimation of the diffusion and kurtosis tensors have been developed [7]. It is also noteworthy that fitting the kurtosis tensor greatly improves the accuracy of the diffusion tensor estimation [8]. Extending the series to the sixth order cumulant (in b3) increases the accuracy of the kurtosis estimation, albeit with a penalty on precision [9].
Since no assumption is made about the tissue structure, metrics derived from the diffusion tensor, such as mean diffusivity and fractional anisotropy are used extensively for brain and body tissue characterization in a wide variety of conditions [10, 11]. DKI metrics, such as mean kurtosis, are also increasingly used as complementary biomarkers to DTI metrics in a large panel of applications [12–17]. With acquisition acceleration options available on most clinical scanners, and new reduced acquisition schemes [18, 19], DKI is expected to become more and more widespread.
Other signal representations than the cumulant expansion are of course possible. Yablonskiy et al. [20] proposed to introduce a distribution of diffusion coefficients ρ(D) in the tissue, which can theoretically be estimated by inverse Laplace transform:
However, because the inverse Laplace transform is a mathematically ill-posed problem, in practice some functional form is assumed for ρ(D) and its characteristic parameters estimated [20, 21]. Moreover, the estimated distribution does not mirror the actual distribution of diffusion coefficients in the tissue unless the measurement is performed in a very strong diffusion weighting regime (qlc ≫ 1, where q is the amount of spatial phase-warping introduced and lc is the diffusion distance) [9, 22]. Thus, this approach remains an empirical description of the diffusion-weighted signal and falls in the category of signal representations rather than biophysical models.
The departure from Gaussianity can also be captured empirically as a “stretched exponential” expression of the diffusion signal [23]:
The stretched exponential function has later been associated with the theory of anomalous diffusion, which represents a departure from Brownian motion (〈x2 〉 ∝t), by several groups [24–26]. A comprehensive discussion on the implications of such a theory for biological tissue can be found in Kiselev [9] and Novikov et al. [1]. Although devoid of biophysical meaning, the stretching parameter α is largely used in the literature for tumor delineation and characterization [27–30].
Another example of signal representation is the expansion of the diffusion signal using harmonic oscillator basis functions (Hermite polynomials), as proposed by Özarslan et al. [31], a method dubbed mean apparent propagator (MAP-MRI). In addition to the reconstruction of a diffusion tensor, the method allows the estimation of the return-to-origin probability, which is sensitive to compartment sizes, and of non-Gaussianity indices, indicative of tissue complexity. The data required for MAP-MRI can be acquired in under 10 min on a clinical scanner [32].
Biophysical Models of White Matter
The first attempts at modeling the diffusion signal as multi-compartmental can be attributed to Latour et al. [33] in red blood cells and Szafer et al. [34] who modeled “tissue” as cuboids on a regular lattice, surrounded by extracellular medium. Building on their work, Stanisz et al. [35] proposed the first white matter model based on electron micrographs of bovine optic nerve. In their model, axons were represented as prolate ellipsoids and glial soma as spheres, the extracellular space constituting the third compartment. The model also accounted for membrane permeability of axons and glial cells. The authors noted that the nine-parameter model required a wide range of diffusion times and gradient strengths, and that even with extensive data, the goodness of fit remained unsatisfactory. They also underlined that releasing some of the assumptions and increasing the number of parameters would make the fit unstable. Twenty years later, those insights are still very much topical.
At long diffusion times, the diffusion distance across the axon becomes constant (it is limited by the axon diameter) and the diffusivity tends to zero: axons can thus be modeled as infinitely long “sticks” (cylinders with zero radius). The first group to introduce the stick geometry was Behrens et al. [36] and assumed that water in and around the axons similarly diffused only in the fiber direction with a second compartment of free, isotropically diffusing water. Shortly after, Kroenke et al. [37] used a biophysical model of isotropically oriented sticks to characterize the diffusion of N-acetyl aspartate (NAA) in the neurites. A similar description to Behrens' of two compartments was later adopted by Jespersen et al. [38], who also formulated for the first time the clear goal of estimating dendrite density—i.e., a specific biomarker of the microstructure—in vivo, using diffusion MRI modeling.
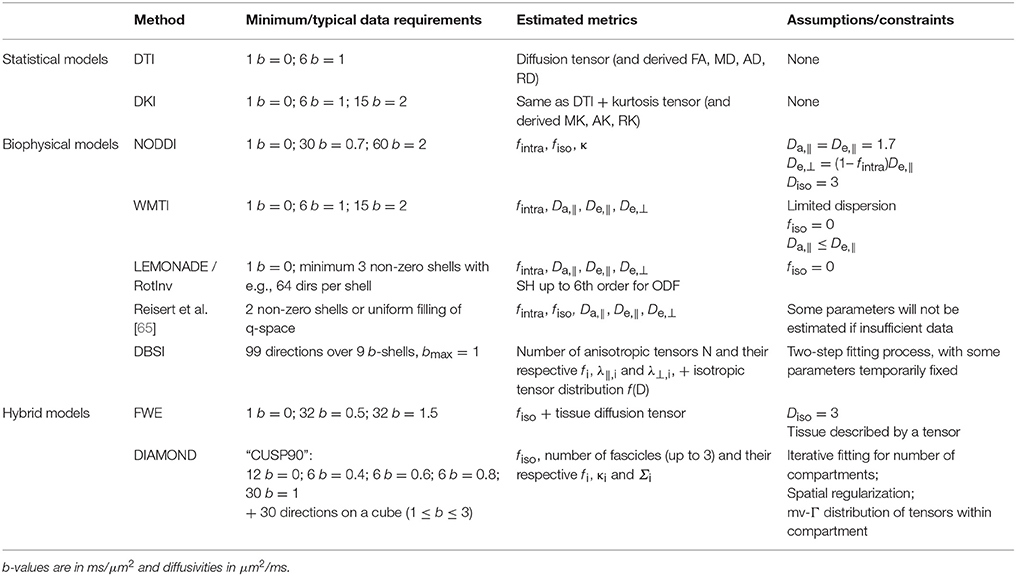
Building on these initial works, most white matter models “in use” today rely on the same common picture: water signal is assumed to originate from two or three non-exchanging compartments, each weighted by their relative volume fractions (Figure 1).
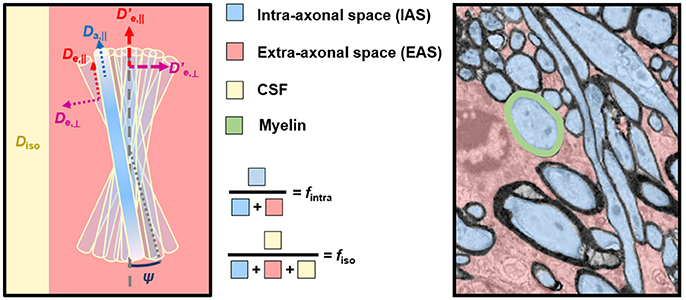
Figure 1. Correspondence between model compartments (Left) and tissue components (Right). (Left) Schematic of a typical three-compartment model with relevant parameters. De,|| and De,⊥ are local extra-axonal diffusivities, and and , are apparent extra-axonal diffusivities, depending how the model defines them. (Right) Cross-sectional electron microscopy image of a white matter bundle. Adapted from Mikula and Denk [39] with permission. While myelin is present in WM, it is absent from DWI models due to its short T2.
The first compartment is the collection of axons, which are modeled as infinitely long sticks, and whose collective orientations are characterized by some orientation distribution function (ODF). Water diffusivity inside each axon is Da,|| along the axon and zero perpendicular to it. The parametrization of the ODF varies between models.
The second compartment is the extra-axonal space which, by exclusion, includes features not explicitly ascribed to the axonal space, including extracellular water, cell somas, and glial cells, all assumed to be in fast exchange. This compartment is modeled as Gaussian anisotropic, with axial and radial diffusivities De,|| and De,⊥, respectively. These extra-axonal diffusivities are either defined locally in proximity of a coherent axon sub-bundle with the resulting signal response convolved with the ODF, or as apparent extra-axonal diffusivities over the entire voxel (indicated with a “prime” symbol in Figure 1 and hereafter, for disambiguation).
The third compartment, if included, is modeled as Gaussian isotropic, with a diffusivity Diso. If it represents freely diffusing water such as cerebrospinal fluid (CSF), Diso (Dfree) is set to 3 μm2/ms in vivo. If it represents water with a negligible diffusivity in all directions, often referred to as “still water,” and non-exchanging with the extracellular space, Diso = 0. The parametrization, constraints, and nomenclature of Diso vary between models.
Modeling necessarily comes with a level of simplification, since the entire biological complexity certainly cannot be rendered. The most difficult part of the modeling task is perhaps figuring out which features of the microstructure are relevant to the voxel-averaged diffusion signal and should be represented in the model, and which ones can be omitted without violating assumptions or accuracy. For a more detailed discussion on coarse-graining and effective medium theory, we direct the reader to a very comprehensive review by Novikov et al. [1].
In what follows, we will briefly review the main white matter models that have, for the most part, emerged in the last decade and that share the common features outlined above. While many different diffusion models and corresponding applications have been proposed, this review will only focus on models of tissue microstructure pertaining to the brain and spinal cord and in the long-time limit where axons are modeled as sticks. We also neglect potential measures of permeability between compartments, though they could have substantial impact on modeling, especially in the case of pathologies [40].
NODDI
The tissue model in Neurite Orientation Dispersion and Density Imaging (NODDI) matches exactly the cartoon in Figure 1 [41]. It is a three-compartment model fully described by seven parameters: two volume fractions (f intra and f iso), four diffusivities (Da,||, De,||, De,⊥, and Diso) and the orientation dispersion, modeled by a Watson distribution of concentration parameter κ. The latter can be related to the angular spread via
where ψ is the angle between an axon and the main diffusion orientation in the voxel. In order to stabilize the fitting procedure, NODDI constrains all diffusivity values, effectively leaving only the two volume fractions and the orientation dispersion to be estimated, i.e., the underlying geometry. The model assumptions are as follows:
The popularity of NODDI is indisputable, with applications to a very large panel of brain alterations and pathologies [42–48]. However, there are important assumptions within NODDI related to its design that have strong implications to its specificity.
NODDI imposes assumptions on the intrinsic diffusivities to the point of fixing Da,|| and De,|| to the same predetermined value for all tissues (Equation 5). First, any deviation from these fixed values can bias the remaining parameters and they will lose their desired specificity. Substantial changes in diffusivity, such as that occurring in cerebral ischemia, for example, will impart a false change in orientation dispersion, neurite density, or CSF partial volume that does not accurately capture the underlying tissue pathology—as will be discussed in more detail in the third part of this review. The decision to fix the axial intra- and extra-axonal diffusivities equal to one another is another assumption that can lead to unpredictable effects. Recent work has shown that fixing Da,|| = De,|| masks a fundamental property of multi-compartment models, namely the multiplicity of mathematical solutions [49, 50]. Indeed, it has been shown that, if all parameters in the fitting procedure are released, namely f intra, Da,||, De,||, De,⊥, and κ (ignoring the CSF compartment), there are two distinct solutions to the parameter estimation problem, both within biologically plausible ranges (Figure 2). The two solutions of a two-compartment model can roughly be described as one where Da,|| < De,||, and another where Da,|| > De,||. Establishing which inequality is biologically valid is an active field of research, with most studies pointing toward Da,|| > De,||. This will be covered in detail in the second part of the review. Finally, the tortuosity approximation that relates De,|| and De,⊥ (Equation 6) has been shown not to hold for tight packings of axons [51].
Figure 2. NODDIDA optimization landscape reveals the existence, in the full 5-parameter space, of two disconnected minima, each surrounded by a pipe-like ensemble of low objective function values. Shown are 3D isosurfaces of the objective function F(f, Da,||, κ). (Aa) F calculated with (De,||; De,⊥) = (2.10; 0.74) and SNR = ∞, thus containing the true global minimum. (Ab) F calculated with (De,||; De,⊥) = (0.32; 0.85) and SNR = ∞, thus containing the second local minimum of the 5D minimization problem. (Ac) The same as (Aa), but SNR = 50. (Ad) The same as (Ab), but SNR = 50. The theoretical minimum of F along each pipe is identified by a black bullet. Noise can displace the effective minimum along the pipe very far from the true one (see Ac). Figure taken from Jelescu et al. [49], with permission.
WMTI
White Matter Tract Integrity (WMTI) is a two-compartment model of sticks embedded in a Gaussian anisotropic extra-axonal medium [52]. The tissue can be described as a combination of two Gaussian compartments (intra- and extra-axonal) each characterized by a tensor ( and ) which can be directly derived from the overall diffusion and kurtosis tensors and [53]. In any direction j,
This approach by-passes inherent limitations associated with non-linear fitting (local minima and long computation time): the linear estimation of the diffusion and kurtosis tensors is followed by a direct derivation of the WMTI model parameters. The quadratic expression in Equation (9) demonstrates, as previously mentioned, that for a two-compartment model, there are two mathematical solutions, where either Da,|| < De,||, or Da,|| > De,||. Establishing which inequality is biologically valid is an active field of research, which will be covered in detail in the second part of the review.
In WMTI, the authors had chosen the inequality Da,|| < De,|| to solve the system (which is the opposite of the inequality that seems to hold from recent work), hence:
WMTI has been used in studies of a large variety of conditions, with substantial validation efforts using animal models of altered myelin [12, 13, 54–58].
In WMTI, the collection of axons is modeled as a Gaussian compartment, which is an assumption that only holds if the axons are highly aligned in a single bundle. Fieremans and colleagues estimated a maximum orientation dispersion of 30° for this approximation to hold, in the case of coplanar dispersion only. The validity of the approximation for three-dimensional dispersion has not been evaluated. Thus, while WMTI captures changes in diffusivities, it is best applied to regions of highly aligned single fiber bundles as per the recommendations. A more recent approach consists in deriving the WMTI equations assuming a Watson distribution of axons, like in NODDI, thus alleviating one of the strongest assumptions of WMTI [59]. The authors then further use time dependent functional forms of model parameters to evaluate which of the two possible solutions is the biologically valid one.
Another limitation is that since WMTI is based on the kurtosis model, it is restricted to the low b-value regime which could lead to some bias, although this may also be advantageous for compatibility with clinical hardware systems.
Rotationally Invariant Features: LEMONADE & co.
In a two-compartment model, estimating compartment diffusivities and orientation dispersion of axons simultaneously is problematic and prone to bias, hence requiring fixed parameter assumptions (NODDI) or limitations to coherent fibers only (WMTI). Loosening these constraints to achieve greater specificity comes at the expense of a larger number of parameters to be estimated in the model, which is problematic for non-linear fitting. In particular, allowing for a complex ODF quickly increases the number of parameters. NODDI for example also has a declination that uses a Bingham rather than Watson distribution (2 free parameters) [60]. Jespersen and colleagues modeled the ODF using a spherical harmonic expansion up to L = 2 (5 free parameters) [38] and later L = 4 (14 free parameters) [61].
For the purpose of extracting a reliable ODF for tractography, several groups had modeled the diffusion signal as a convolution between the response of a perfectly aligned fascicle (axons and their immediate extra-axonal space) pointing in direction n, and the fiber ODF P(n) [62–64]:
Equation 13 factorizes in the spherical harmonics basis, thus separating the estimation of the scalar parameters of the kernel K from that of the ODF parameters. Recently, Novikov et al. [50] and Reisert et al. [65] have exploited this property to estimate the scalar parameters of a two-compartment kernel separately from the ODF:
The approach of Novikov et al. [50] can be decomposed into two steps. The first step relies on solving an algebraic system of equations which relates the kernel parameters to the signal moments. More specifically, using “low b-value” data (e.g., bmax = 2.5 ms/μm2), the scalar parameters and a few basis-independent ODF parameters pl can be directly derived from the first moments of the diffusion signal (up to 6th order) in a similar fashion to which WMTI uses direct relationships between model parameters and cumulants up to the 4th order. This method was dubbed LEMONADE (Linearly Estimated Moments provide Orientations of Neurites And their Diffusivities Exactly), and requires diffusion data distributed over 3 non-zero b shells. Circumventing issues related to non-linear fitting, LEMONADE provides estimates for f intra, Da,||, De,||, De,⊥, and , which gives an estimate of the orientation dispersion in a similar way to κ from the Watson distribution. The spherical harmonic expansion of the ODF can then be fully reconstructed up to L = 6. In a second step, all available data (including high b-values) can be exploited to minimize the rotationally invariant (RotInv) energy function of the system, using the LEMONADE estimates as initialization values. In other words, the projections of the scalar kernel onto Legendre polynomials, weighted by rotational invariants of the ODF, are fitted to rotational invariants of the spherical harmonics decomposition of the signal, in a least-squares sense.
LEMONADE provides further evidence for the existence of two mathematical solutions to the two-compartment model and that, in principle, the degeneracy can be lifted with robust measurements up the 3rd order in b. In practice, solution selection based on noisy data remains challenging and should be validated independently.
The approach of Reisert et al. [65] relies on machine learning to estimate the model parameters. A choice of plausible parameter values is made using insight from isotropic diffusion weighting results, as will be discussed in Validating Microstructural Features. This method also allows renouncing to the determination of specific parameters of the model when data proves insufficient.
The remaining assumptions behind these two methods are: the existence of only two compartments (intra- and extra-axonal), the consistency of kernel parameters across all fascicles in the voxel (e.g., all axons in the voxel have the same diffusivity Da,||), and axial symmetry of the elementary fiber response (kernel).
By contrast to these two approaches, the method described by Kaden et al. [66] based on the spherical mean technique is similar in spirit, in the sense that it factors out the fiber ODF, but it only exploits the lowest order rotational invariant and the estimation of the scalar kernel is constrained by Da,|| = De,|| and by the tortuosity approximation for the extra-axonal space (Equation 6).
DBSI
Another model was proposed with the intent of covering regions of multiple fiber crossings; this model is DBSI (Diffusion Basis Spectrum Imaging) [67], and its general formulation is the following:
where the tissue is described as a collection of NAniso axially symmetric anisotropic tensors (each with unknown fraction f i, axial and radial diffusivities D||, i and D⊥,i and orientation ni) and a continuous spectrum f (D) of isotropic diffusion tensors. The anisotropic tensors represent water inside and just outside myelinated and unmyelinated axons of varied directions, while the continuum of isotropic tensors represents water in cells, sub-cellular structures, and edematous water.
The DBSI fitting procedure is complex and details can be found in Wang et al. [67]. Briefly, it is a two-step process where first the number of anisotropic tensors and their principal orientations are estimated. These parameters are then fixed in the second step of the procedure, which aims at estimating f i, D||, i, and D⊥,i for each anisotropic tensor, as well as f (D). This is achieved by optimizing f i and f (D) for recursively chosen combinations of D||, i and D⊥,i and finally selecting the combination providing a global minimum.
DBSI has been applied to a variety of pathologies [68–72], but has not been extensively validated outside of the originating group. Given the unfavorable fitting landscape in a comparatively much simpler model such as NODDIDA [49], especially in the presence of limited signal-to-noise ratio (SNR) (Figure 2), the reliability of DBSI model estimates remains to be clarified. Moreover, the biophysical interpretation of the continuous distribution of diffusion coefficients f (D) is also problematic, as explained in connection with Equation (3).
Hybrid Models
Hybrid models are based on a combination of biophysical modeling and signal representations.
Free Water Elimination (FWE)
The motivation of the free water elimination technique is to separate CSF contamination from “brain tissue” diffusion properties. The overall signal is separated into an isotropic component of free diffusion (Dfree) and a single diffusion tensor representing the rest of the tissue signal (Dtissue). This approach was first proposed by Pierpaoli and Jones [73] using a comprehensive q-space acquisition (107 directions over 8 shells, bmax = 1.2 ms/μm2). Its potential advantages are the extraction of a free water map (as a new biomarker), improved tissue tensor estimation, and benefits for fiber tracking. The direct correspondence between “free water” and CSF is however not straightforward.
Its application was further extended to single-shell DTI data by Pasternak et al. [74]. Naturally, estimating a system which includes a tensor and an isotropic compartment from single-shell data is an underdetermined problem. To circumvent this issue, Pasternak and colleagues initially imposed additional constraints: spatial regularization and tighter upper and lower bounds on the tissue volume fraction, dependent on tissue diffusivities. This constrained implementation has been applied to a variety of conditions [75–78].
While the intention of making the method applicable to the most widespread acquisition scheme (i.e., single shell) is understandable, the ill-posed nature of the mathematical problem and the issue of constraints has been recognized by the authors, who proposed incorporation of an additional low b-value shell for accuracy and stability [79]. The initial, more conventional, multi-shell approach proposed by Pierpaoli and Jones has also been reintroduced in parallel by Hoy et al. [80]. The latter work included simulations showing that in the absence of a CSF compartment, fitting the FWE model indeed overestimated tissue FA. Later work by the same group compared the FWE technique to the more standard FLAIR-DTI approach where the CSF signal was directly suppressed at the acquisition stage [81, 82]. They reported similar performance between the two techniques in WM tracts where CSF contamination was expected to be high (i.e., fornix and corpus callosum), but unlike FLAIR-DTI, the FWE technique resulted in greater FA and reduced diffusivity measures even in tissues without CSF partial volume effects (e.g., cingulum). The proposed explanation that the “free water” signal arises from the extracellular space [79] highlights the complications of assigning a single tensor to a “tissue” compartment which is known to exhibit non-Gaussian behavior.
DIAMOND
A new hybrid model, termed DIAMOND (DIstribution of 3D Anisotropic MicrOstructural eNvironments in Diffusion-compartment imaging) [83] has recently been proposed. It expands on the concept of distribution of diffusion coefficients introduced by Yablonskiy et al. [20], by accounting for several discrete compartments (biophysical modeling), each withholding a continuous distribution of diffusion tensors (statistical modeling). In mathematical terms:
where Np is the number of compartments (or spin populations), each with its associated volume fraction, and Pκi, Σi(D) is the distribution of diffusion tensors within the compartment, chosen to be a multi-variate Gamma distribution of shape parameter κ and scale parameter Σ. The diffusion tensors are symmetric positive definite matrices [Sym+(3)].
Starting from the generic expression in Equation (16), three types of particular compartments are considered and their presence in each voxel is evaluated using model selection techniques. The three types of compartments are free isotropic (attributed to CSF), restricted isotropic (attributed to water in glial cells) and water in and around white matter fascicles.
In practice, DIAMOND uses an iterative approach in defining the number of compartments in each voxel. The optimization begins with a freely-diffusing compartment and zero fascicles, and the number of fascicles is gradually increased up to three—the higher complexity is retained only if the general error of the model is significantly reduced compared to the previous simpler model. Spatial regularization of voxel parameters is also used. While the goodness of fit has been extensively used in the past to choose which model is most appropriate for describing the data [84, 85], recent insights into the topology of the fitting landscape for a two-compartment model (Figure 2) advises against relying solely on such metrics for model selection [49, 50].
As an extension of the concept of continuous distribution of diffusion coefficients (Equation 3), DIAMOND also inherits from its associated issues, discussed in the section on Signal Representations.
Microstructure metrics estimated using DIAMOND will need to be subjected to substantial validation studies in the near future. Recent work on traumatic brain injury in the mouse suggests that DIAMOND, as any higher order model, is more sensitive than DTI in detecting differences, but a more thorough validation of specificity against histology remains to be performed [86].
Summary
Main approaches for deriving quantities from the diffusion weighted signal include signal representations (also known as statistical models), biophysical models of white matter, and hybrid models that contain features of both approaches. Table 1 summarizes the properties of each of these approaches. Essentially, single-shell diffusion MRI data only enables the estimation of a single diffusion tensor for the voxel, i.e., DTI. Any other more complex analysis that accounts for non-Gaussian diffusion effects in the tissue requires at least two non-zero b-shells, each with sampling along a minimum number of directions.
Biophysical models come with the promise of characterizing tissue microstructure with improved specificity. However, their intrinsic assumptions have the potential to introduce bias. Nearly all models outperform DTI in capturing tissue diffusion properties, but this is a very low benchmark. Biophysical models need to be increasingly compared to one another, and to higher order signal representations such as DKI, to understand convergent model properties likely to be successful in broad applications [57, 65, 87, 88]. Their reliability in the case of pathological tissue also needs thorough investigation.
Validating Diffusion Models
Most biophysical diffusion models share at least partial similarity with one another with respect to their common geometry, as represented in Figure 1. This section will review validation efforts for each of the model features (compartment volume fractions, axon orientation dispersion, and compartment diffusivities). While many validation studies have been performed for DTI, the goal is to emphasize results in the context of biophysical models and how well their derived parameters reflect the true biology of interest. The first two sub-sections focus on method validation using either computer simulations or phantoms, while the following ones discuss the validation of quantitative estimates for each microstructural feature of white matter.
Computational Simulations
Simulating the random walk of diffusing spins within simple or complex environments is often the first step to establish a connection between derived estimates of physical features and their ground truth values. Simulations have been used where analytic solutions are difficult or impossible, and their use is so common that it is impossible to list them here. Notable examples are those that have also released accompanying software packages [89–92]. Synthetic geometries, which are typically composed of cylindrical axons, have been used to model the effects of axon diameter, packing, volume fractions, permeability, and other features that can be easily modulated synthetically, and these have in turn been performed under many different simulated experimental conditions such as modulation of diffusion times, gradient waveform shapes, signal to noise ratios, and other features that would be difficult or time-consuming to perform experimentally. As the diffusion models have evolved to include more complex features such as bending, crossing, and asymmetric fiber orientations, simulations have followed suit and implemented similar physical features. In addition to purely fiber models, other notable examples include complex axonal geometries to demonstrate the effects of swelling [93], beading [94], undulation [95], and other features. Geometrical substrates derived from tissue specimens [96] have been also demonstrated recently, although these remain challenging due to the difficulties in obtaining high-resolution, 3D images of tissues and their subsequent conversion to physical substrates. As 3D microscopy and connectomic techniques push for high resolution and large-scale imaging of brain tissues at microscopic resolutions, parallel advances in relating diffusion indices with more realistic models will likely follow. Importantly, the fidelity of the simulation geometry to the true underlying biology is a major concern. To the extent possible, these should encompass realistic and accurate distributions of axon diameters consistent with histological reports, random packing as opposed to a regular lattice, and other physical features that have been validated in tissue preparations. Although geometrical models are simplistic, simulations ensure that the estimated parameters are at least accurate and precise with respect to known ground truth features, and if this criteria is not met, acceptable performance in real tissues is likely compromised.
Phantoms
Ground truth hardware phantoms have been developed to estimate relevant parameters and calibrate multi-center studies. Ideally, phantoms mimicking WM structure possess certain desirable qualities most notably being tubular hollow structures with diameters approximating those of axons. Another desirable feature is to organize axon-like structures in different configurations that mimic complex features such as dispersed and crossing fibers. Intrinsic diffusivity of the filling material may also be considered, as well as magnetic susceptibility of the scaffolding material. Vegetables with tubular structures or domains, such as celery, asparagus, and chives, have been routinely used to demonstrate the effects of anisotropic diffusion, but these substances are clearly not amenable to long-term or cross-center studies, and phantoms with high consistency and longevity were sought. Most hardware phantoms have so far been developed for the purpose of optimizing DTI acquisitions or validating tractography rather than microstructure models. Textile fiber phantoms were developed with the scope of easily mimicking bending or dispersed fibers but their diameters typically far exceed the range of axons and they are of course not hollow [97]. Microcapillaries have the advantage of producing both an intra-axonal and an extra-axonal space to be filled [98–100], and most recent designs display somewhat more realistic diameters between 9 and 20 microns [101]. However, while crossing bundles can be designed, within each bundle the capillaries are highly aligned, which is a limitation for modeling true white matter.
Two types of phantoms have so far been developed for the purpose of validating higher order diffusion models. Fieremans et al. proposed a phantom of tightly packed solid fibers of Dyneema and compared the measured signal to simulations for diffusion, kurtosis and time dependence [102–104]. While it used reasonable diameters (20 μm) the drawback was that it only modeled the extra-axonal space. Better magnetic susceptibility matching between water and the Dyneema material can be achieved using magnesium chloride [105]. A complementary phantom design of the intra-axonal space has recently been proposed using co-electrospun fibers that produce a hollow honeycomb-like arrangement and a distribution of diameters of about 9.5 μm [106]. The ideal phantom for diffusion microstructure model validation would mimic both intra- and extra-axonal water with diameters matching those of white matter axons, randomly packed to appropriate volume fractions, and orientation dispersion. Clearly, it is challenging to meet all of these conditions simultaneously.
The advantages of phantoms are well recognized and aim to be standardized instruments for calibration of MRI experiments and assessments of multi-site variability. The disadvantages include sophisticated chemistry, limited availability to materials and specialized equipment, and non-standardization. Despite these current limitations, the role of consistent and widely-accepted phantoms has been well-recognized [107]. With the push for reproducibility and precision medicine, physical phantoms will continue to emerge as a solution to multi-center and multi-vendor diffusion MRI data acquisition and modeling.
Validating Microstructural Features
Fiber Orientation and Dispersion
Diffusion MRI and its associated models offer the unique ability to track fiber pathways non-invasively. Diffusion tractography has been widely used in research settings to probe structural connectivity in health and disease and has seen success in clinical scenarios. Most notably, tractography has been used to identify fiber pathways during tumor resection [108] or other neurosurgical applications [109]. Tractography is based on the coherence in fiber orientation between adjacent voxels and is therefore fundamentally based on the accuracy of the estimated fiber orientation within each voxel. Validation efforts to demonstrate the accuracy of diffusion MRI have typically focused on applications to tractography, but these findings are also pertinent to microstructural modeling to derive local (i.e., voxel level) estimates of fiber orientations and dispersion. While the diffusion tensor models a single fiber orientation within each voxel, several methods have been developed to provide a comprehensive estimate of the number and distribution of fiber orientations within each voxel [64, 110], each with their own implications for tractography. Although, they have potential applications to tractography [111–113], diffusion MRI microstructural models aim to estimate intra-voxel orientation dispersion as its own unique feature to reveal interesting characteristics of the healthy, developing, or diseased brain.
Validating the intravoxel fiber dispersion, or ODF, is typically accomplished through imaging of the tissues using light microscopy or similar modalities and deriving quantities reflecting the neurite orientations (Figure 3). Thus, there is a more direct relationship between diffusion MRI quantities and those measured from histological samples than for volume fractions (see following section) because fiber orientations are largely unaffected by fixation and can be reliably measured in tissues with relative ease. Among the first examples to conduct direct validation studies, manual segmentation of axons in stained tissue white matter sections were compared to DTI and Diffusion Spectrum Imaging (DSI) estimates [117]. A variety of automated image processing techniques have been used to derive the angular orientation profiles of stained tissues, permitting large-scale automated analysis of tissue specimens [118–127]. These methods generally fall into classes of algorithms that use pattern-matching, Fourier analysis, or edge detection. Pattern matching attempts to identify discrete fibers within the image to build a full distribution of fiber dispersion. On the other hand, Fourier analysis and structure tensor analysis instead use the texture of the images to derive angular profiles of edges or spectral content. Structure tensor analysis has been particularly attractive since its interpretation is analogous to the diffusion tensor. Typically, the histological specimens were limited by two-dimensional samples, but the structure tensor analysis has also been extended to 3D sections using confocal imaging [128, 129]. Collectively, the results from these studies all demonstrate a consistent and expected finding that while DTI fails to capture the full complexity of the underlying fiber orientation distributions, diffusion models that include dispersion as a feature better reflect the underlying structures. However, most studies thus far have validated orientation in tractography-driven approaches that focus solely on retrieving orientation without regard for diffusivities and volume fractions and do not fall into the category of microstructure models.
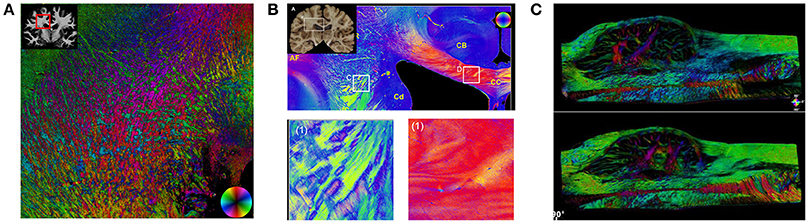
Figure 3. Fiber Orientation Measurements in Fixed Tissues. Examples of fiber orientation measurements in human brain specimens. Structure tensor analysis (A) uses a digital texture analysis method to detect fiber orientations in stained sections imaged with bright-field or fluorescence microscopy. Both polarized light imaging (B) and polarization-sensitive optical coherence tomography (C) exploit the intrinsic birefringence of myelin to obtain fiber orientations. Sections in (A) [114] and (B) [115] (reproduced under the Creative Commons Attribution License) are from the human brain white matter, and (C) [116] from the human medulla oblongata (with permission).
Stained histological sections for validation have several disadvantages and potential complications and confounds. Tissue processing and cutting can lead to distortion or artifacts, and histological staining may also be complicated by staining irregularity or artifacts. Moreover, sectioning, staining, and imaging large volumes at high magnification is very time consuming [130]. Although the brains and spinal cords of small animals can be captured with most laboratory microscopes, imaging large-scale tissues at high resolution such as human brain slices may require custom equipment and high-performance computing. Advances in large-scale microscopic imaging of fixed tissues have circumvented some of the issues with traditional sectioning and staining by using blockface imaging and intrinsic contrasts. Myelin exhibits the property of birefringence [131] which permits imaging of fiber architecture in fixed but unstained tissue sections. Somewhat analogous to diffusion encoding, rotating the polarization angle along different directions enables the estimation of fiber orientations in both 2D and 3D to examine human brain sections in their entirety [115, 132, 133]. Blockface microscopy, which consists of repeated imaging of the exposed surface of a tissue cut using serial sectioning, has also emerged as a powerful tool for large-scale imaging. Notably, compared to traditional sectioning, blockface imaging reduces distortions and the full process can be automated [116, 134, 135]. Modalities such as two-photon microscopy [136] or optical coherence tomography [137, 138] also image up to tens of microns below the surface and can provide contiguous 3D images of large tissue. Many of the whole-specimen imaging techniques developed for local neuron connectomic studies [139–141] have demonstrated utility when coupled with diffusion MRI [142].
Direct histological examination with microscopy has consistently demonstrated that white matter tracts are not strictly composed of uniform bundles. Even in the corpus callosum, an intravoxel dispersion of ~18–20 degrees is consistently evident from rodent [117], and human samples [118, 143]. In the gray matter, Jespersen et al. demonstrated strong agreement between the estimated neurite orientation distributions and histological staining [144].
Volume Fractions or Neurite Density
The ability of diffusion MRI to monitor axon content in the brain and spinal cord has demonstrated wide ranging utility in a variety of applications across normal development, aging, injury, and disease. Unlike fiber orientation, which is generally preserved in fixed tissues, the relative volume fractions are perturbed during fixation and processing which has made non-MR measurements somewhat biased and inconsistent. It is important to first distinguish the true physical cellular fractions obtained from microscopy or other non-MRI methods from those reported from diffusion MRI models. In the brain, the extracellular volume fraction is typically around 20% [145], but traditional tissue fixation and processing artificially reduces this to ~2–5% [146]. In white matter, the axoplasm constitutes ~25–30% of the physical space in white matter tissues [147], myelin constitutes ~20–30% [147, 148], and glial cell bodies and processes constitute ~30–40% [147]. Recent extracellular space-preserving methods of fixation support the approximation of 15–20% extracellular space [149] and indicate that axonal volumes are relatively unaffected by the method of fixation [150]. In typical diffusion MRI experiments, the signal from water associated with myelin has a negligible contribution to the overall signal due to its short T2 and is therefore routinely ignored in diffusion models. Diffusion MRI measures of compartment signal fractions are commonly referred to as neurite density or axonal volume fraction. Since density implies axonal counts and axonal volume fraction is ambiguous due to the myelin volume fraction, the term axonal water fraction (AWF) is a more precise terminology. Thus, derived from physical measurements alone, the AWF in healthy WM should be ~33% [147, 148]. However, to further complicate things, the relative fractions of the remaining “MR-visible” compartments are also weighted by their respective T2's.
Several studies have compared MR-derived axon water fractions with direct histologic preparations of the same samples. Estimates of the intra-axonal volume fractions from DWI models consistently emerge around 40–60% [38, 151], which is generally in line with histologic estimates although slightly higher than estimated from microscopy [152]. Jespersen et al. demonstrated agreement between neurite density estimates from DWI and quantitative microscopy, notably using both ex vivo DWI and histology [38, 61], and others have shown similarly strong relationships [153], although lower fractions have been noted in some samples [154]. Correlations (or absence thereof) between diffusion-derived and electron microscopy (EM)-derived metrics have also helped further establish the selective sensitivity of biomarkers derived from diffusion modeling to different features. For example, using WMTI, AWF has been shown to correlate with axon volume fraction but not with the g-ratio derived from EM, while De,⊥ correlated with the g-ratio but not the with axon volume fraction [56]. Measures of AWF have also been combined with MRI measures of myelin content to estimate myelin g-ratio in vivo, which compared favorably to that derived from EM [155, 156]. However, a strong correlation is not necessarily proof of parameter specificity. Notably, axon fractions derived from microscopy typically correlate very strongly with radial diffusivity (RD) derived from the diffusion tensor [61].
Compartment-Specific Diffusivities
Diffusivities of the various modeled cellular compartments are both critical features that form the basis for diffusion models, and have been arguably the most difficult to validate. Alternative methods to NMR for measuring the self-diffusion coefficient of water are not available, and NMR-based measurements include signals from all compartments. In order to circumvent this issue and gain information about compartment-specific diffusivities, alternative approaches have been proposed: the use of model systems, endogenous compartment-specific metabolites, exogenous compartment-specific probes and tracers, signal suppression in a given compartment, exploiting alternative encoding methods, analyzing time-dependent properties, and combining diffusion methods with other contrasts (T2). Early studies examined compartment-specific diffusivities to glean insight into the nature of diffusion in the nervous system, with a particular focus on the biophysical basis of changes in cerebral ischemia. More recently, as highlighted in Part 1, a two-compartment model of diffusion shows a degeneracy that only an independent determination of compartment diffusivities can lift.
Model systems using invertebrates with large axons were first used to identify the source of anisotropy in the nervous system [157], demonstrating that biological membranes were the primary determinants of diffusion restriction/hindrance. These studies measured the intrinsic intra-axonal diffusivity, demonstrating it was ~70–80% that of pure water [158, 159]. Hence, these studies set the stage showing that intra-axonal diffusion was largely unrestricted along the axon, and the axonal membrane serves as a considerable barrier to diffusion perpendicular to the fibers.
Endogenous MRI-detectable tracers to assess diffusion primarily include metabolites detected through proton magnetic resonance spectroscopy (MRS). These include NAA, creatine, choline, and myo-inositol. NAA is a neuronal-specific metabolite and a surrogate marker of the intra-axonal space in white matter. Although, the neuronal specificity of NAA has recently been called into question since it was found to be also localized in myelin [160], the influence of myelin-associated NAA on the MR signal remains unclear and diffusion of NAA has so far been used to probe intra-axonal diffusion. Kroenke et al. [37] performed diffusion-weighted MRS in the human corpus callosum and rat brain, demonstrating that in vivo the Da,|| of NAA was ~50% (0.36 μm2/ms) of that of an aqueous solution and Da,⊥ was effectively zero. Similar results were shown for NAA in the human brain and in a peripheral nerve preparation [161, 162]. Ronen et al. [143], accounting for both the macro- and microscopic curvature of the human corpus callosum, measured a slightly larger Da,|| (0.51 μm2/ms) putting it in the range of 60–70% of aqueous NAA. Palombo et al. [163] have also demonstrated diffusion of NAA and other metabolites can be modeled as occurring in long, cylindrical fibers, having a Da,|| of 0.33 μm2/ms. The diffusion weighted signals of other metabolites were also fit well by assuming long cylindrical processes [163–165]. Since metabolites have differences in molecular size, affinity to charged surfaces, and potential ambiguity in compartment selectivity, the intra-axonal diffusivity of water cannot be unequivocally extrapolated from metabolite diffusivities. However, these studies and those in experimental preparations are consistent with the intra-axonal water diffusivity being 60–80% of its temperature-matched aqueous diffusivity.
Exogenous MRI-detectable tracers, most notably injectable agents used in animal models, have also been used to probe the diffusivity of specific environments. Non-proton probes have been used to selectively probe either the extracellular space (sodium-based [166]), the intracellular space (cesium-based [167]) or each of them separately (fluorine-based [168]). The diffusivity of extracellular proton-based agents such as mannitol, phenylphosphonate, and polyethylene glycols has also been investigated using diffusion spectroscopy [169]. Often though, the compartment specificity is not perfect and transmembrane exchange is a complicating factor [170]. Nonetheless, using these approaches, it has been suggested that the diffusivities in the intra- and extracellular environments for molecules of these sizes are approximately similar to one another. It should be noted though that these measurements were typically limited to the apparent diffusion coefficient (ADC) in rat gray matter, and should rather be interpreted as: the traces of the diffusion tensors in the intra- and extracellular environments are approximately similar to one another.
Compartment selectivity can be also achieved by suppressing the extracellular water signal using exogenous tracers. Intracerebroventricular infusion of a gadolinium-based contrast agent causes the T2 of the extracellular space to decrease, effectively suppressing its contribution during signal acquisition. Following measurements in the rat gray matter, Silva et al. reported similar ADCs with and without the suppression, which supports the idea of comparable diffusion traces in the intra- and extracellular environments for water molecules as well [171]. Recently, this experiment was replicated in the rat corpus callosum in a direction-specific manner and concluded that Da,|| ≥ De,|| [172].
Non contrast-based alternatives using non-conventional diffusion encoding have also provided insight into how axial compartment diffusivities compare. A double diffusion encoding (DDE) sequence was recently used to exploit Da,⊥ = 0 and suppress the extra-axonal signal using a strong initial diffusion gradient perpendicular to the spinal cord, with the results suggesting Da,|| ≈ De,|| [173]. Isotropic diffusion weighting has been used by two independent groups to show that isotropic kurtosis is negligible in most brain structures, including white matter tracts [174, 175], whereby the traces of the intra- and extra-axonal compartments were similar. This recurrent observation implied the Da,|| ≥ De,|| solution of the two-compartment model was valid. Most recently, Jespersen et al. have shown also that the time-dependence for compartment-specific diffusivities in a Watson-WMTI model is physically acceptable only for Da,|| ≥ De,||, albeit in fixed rat spinal cord [59]. The inclusion of compartment T2's in the LEMONADE model also suggested likewise [176]. Thus, evidence from a variety of experiments has generally favored Da,|| ≥ De,||, although true independent validation is still lacking.
Validation of Model Parameter Choices
The choice and accuracy of diffusion model parameters can be gleaned from these validation studies. The first observation is that, for clinical diffusion times, the long-time limit applies and intra-axonal diffusion perpendicular to a single fiber (Da,⊥) is effectively zero: thus the “stick” model of axons is generally appropriate for axon diameters in the central nervous system, as has also been demonstrated recently [177]. Second, under this stick model assumption, the orientations of fibers examined histologically are reasonably well-approximated by diffusion models that account for dispersion or crossing-fibers, but it should be noted that most of these studies have not jointly considered dispersion along with simultaneous estimates of other microstructural properties. Third, the intra-axonal parallel diffusivity (Da,||) is ~60–80% of the temperature-matched aqueous solution of the same molecule (Dfree). Fourth, in the healthy white matter, the intra-axonal parallel diffusivity Da,|| is likely faster than the extra-axonal diffusivity De,||, although not substantially.
Parameter Choice in the Injured and Diseased White Matter
In the healthy white matter, diffusion models have converged to a relatively uniform set of parameters as described previously, which has been proposed as the universal model of white matter diffusion. To avoid model overfitting, each of the biophysical model variants neglects, constrains, or holds fixed certain parameters while leaving others free to fit to the data. Importantly, while these constraints have nuanced effects in the healthy brain and spinal cord, there is still considerable disparity and disagreement about the necessary and relevant model parameters in the injured or diseased brain. A complication arises in which the pathologies of different injuries or diseases may be different from one another and are likely to evolve over time and therefore, since there is no consistent pathology, there is unlikely to be a diffusion model that universally captures it. Moreover, while a specific pathology can lead to predictable diffusion MRI outcomes, many different pathologies can lead to the same diffusion behavior. Furthermore, single pathologies rarely occur in isolation. While the diffusion model parameters themselves are independent, there are often strong correlations between pairs of diffusion parameters and specific pathological features.
Diffusion MRI has been applied to nearly every brain and spinal cord disease or injury. DTI represents the overwhelming majority of studies related to validation, yet many investigators have conducted comprehensive studies to relate biophysical model parameters with the gold-standard techniques. While a comprehensive review of all of the different disease and injury categories is beyond the scope here, highlighting specific examples will shed light on the issues.
Cerebral Ischemia
The most common clinically useful application of diffusion MRI is in the detection of acute cerebral ischemia [178, 179]. Within minutes of the onset, diffusion within the infarct is decreased by approximately one half. Although the precise mechanism has been debated, it is closely related to the loss of membrane polarization, ion imbalance, and cell swelling characteristic of acute ischemia [180]. Compartment-specific tracer studies have indicated that the intracellular and extracellular compartments exhibit similar decreases in diffusion [168, 171], while others have shown that intracellular diffusivity decreases substantially while the extracellular diffusivity experiences a somewhat lesser decrease [167]. The extracellular decrease is consistent with a reduction in the extracellular space and increase in tortuosity that leads to decreased diffusivity in that compartment [33], while the intracellular decrease is consistent with neurite beading [94, 181]. Oscillating gradient measurements in the rat brain have demonstrated that restrictions caused by ischemia occur on the scale of several microns typical of cell sizes [182]. The reduced diffusion in stroke can also relate to a larger fraction of highly restricted diffusion [183, 184] which may be compatible with a still water compartment (Diso = 0). Clearly, as the injured tissue degenerates, multiple coincident pathologies exist and the interpretation of diffusion MRI changes becomes increasingly more complex. For example, both NODDI and WMTI have been applied to acute human stroke, with contrasting results. WMTI demonstrated a large reduction in Da,|| in coherent fiber pathways, with lesser reductions in De,|| (under the assumption Da,|| < De,||) consistent with neurite beading hypothesis [13]. On the other hand, NODDI applied to human stroke demonstrated pronounced increases in the estimated orientation dispersion [42]. Although these differences may be related to the time after onset, animal models reveal almost no changes to neurite organization in the acute aftermath [185]. Thus, the model assumptions of NODDI of fixed diffusivities appear to cause misleading interpretations when those assumptions are strongly violated.
Demyelination and Myelin Disorders
Demyelination and other myelin disorders, despite having hallmark pathologies of myelin loss, degeneration, or dysfunction, also typically exhibit multiple overlapping pathologies. Particularly in the acute inflammatory phases of the disease or model, myelin pathologies are accompanied by microglia and astrocyte activation and proliferation [186], and axonal injury is also prominent in some models of multiple sclerosis or optic neuritis [187]. Thus, multiple confounding pathologies present significant challenges of both specificity and sensitivity in relation to diffusion models. A chemical model of demyelination induced through cuprizone toxicity has been used by many groups to validate diffusion and other MRI markers related to specific pathologies. Using the WMTI framework, Guglielmetti et al. [12] demonstrated a prominent reduction in Da,|| during the acute inflammatory phase, while a reduced AWF was observed throughout the remyelination and recovery period. Jelescu et al. [56] showed that the axonal fraction assessed with electron microscopy correlated with AWF derived from WMTI, while the g-ratio correlated with De,⊥. In a model of hypomyelination, Kelm et al. [58] demonstrated strong correlations between axonal fractions obtained from histology and MRI, again using WMTI, but no significant correlations between other WMTI parameters and histology measures were found. Using the DBSI framework, Wang et al. [67] demonstrated strong correlations between axial diffusivity (a DBSI parameter related to Da,||) and axon integrity, radial diffusivity (a parameter related to De,⊥), and myelinated axons, and cell ratio (a parameter related to Diso) and histological cell counts, with similar findings reported in the experimental autoimmune encephalomyelitis [72] and optic neuritis [68] animal models. However, most disease models examined previously with DTI [188, 189] demonstrated strong associations between many of the microscopy measures and quantitative diffusion MRI measures, thus strong correlations are not an indicator of specificity. These studies highlight the challenges of diffusion MRI-based biomarkers since many different pathologies can give rise to similar diffusion signatures and separate pathologies rarely occur in isolation from one another. Moreover, it is worth reiterating that diffusion is an indirect marker of the entire water content of the voxel, and while high specificity is desired, the reliability, sensitivity, and clinical usefulness of these techniques will also be paramount.
Summary
Diffusion MRI is uniquely sensitive to microscopic tissue features that are nearly impossible to achieve through other means. However, diffusion MRI is intrinsically limited since it is an indirect measure of tissue microstructure and relies on inferences from models and estimation of relevant parameters. A plethora of approaches have emerged. The biologically-inspired models have many similarities although each has different inherent assumptions and algorithms. Consequently, validating diffusion models and derived parameters is necessary to demonstrate accuracy, and has relied on various approaches. Simulations and phantoms have a role in demonstrating the accuracy and precision to a known ground truth and can identify sources of error and effects of violating the underlying assumptions. The predominant approach to validate diffusion MRI models is optical imaging of fixed tissue specimens since it offers a direct assessment of the physical features of the tissues and their true biological complexity. An increasing body of literature has demonstrated that diffusion models which account for intra-voxel fiber dispersion are generally good approximations to the underlying white matter fiber organization. Estimates of axonal volume fraction with diffusion MRI are also approximately consistent with histological measurements when accounting for potential bias of fixation and tissue processing. The intrinsic diffusivities of the intra- and extra-axonal compartments are more challenging to validate independently since they can only be measured using NMR itself, and alternative diffusion encodings seem promising in providing the sought validation. In the injured and diseased white matter, considerable ambiguity still exists in the choice of model parameters along with their imposed constraints. Critically, the range of possible pathologies is likely to be too complex to be accurately captured with a single universal model and avoid over-fitting. Validation studies will be important to establish disease and pathology specific applications. Ultimately, the goal of diffusion MRI modeling is to provide a clinically meaningful insight for diagnosis and treatment efficacy.
Author Contributions
All authors listed have made a substantial, direct, and intellectual contribution to the work, and approved it for publication.
Funding
IJ acknowledges support from the Centre d'Imagerie Biomédicale (CIBM) of the University of Lausanne (UNIL), the Swiss Federal Institute of Technology Lausanne (EPFL), the University of Geneva (UniGe), the Centre Hospitalier Universitaire Vaudois (CHUV), the Hôpitaux Universitaires de Genève (HUG) and the Leenaards and the Jeantet Foundations. MDB acknowledges support from the Craig H. Neilsen Foundation (297024), the US Department of Veterans Affairs Rehabilitation Research and Development Service (Merit Review Award I01 RX001497), and the Bryon Riesch Paralysis Foundation.
Conflict of Interest Statement
IJ is a co-inventor on U.S. Patent Application No. 15/156250, pending. “System, method and computer-accessible medium for determining brain microstructure parameters from diffusion magnetic resonance.”
The other author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
1. Novikov DS, Jespersen SN, Kiselev VG, Fieremans E. Quantifying brain microstructure with diffusion MRI: Theory and parameter estimation. arXiv:1612.02059 [physics.bio-ph] (2016a).
2. Jensen JH, Helpern JA, Ramani A, Lu H, Kaczynski K. Diffusional kurtosis imaging: the quantification of non-gaussian water diffusion by means of magnetic resonance imaging. Magn Reson Med. (2005) 53:1432–40. doi: 10.1002/mrm.20508
3. Kiselev VG. The cumulant expansion: an overarching mathematical framework for understanding diffusion NMR. In: Jones DK, editor. Diffusion MRI: Theory, Methods, and Applications. Oxford: Oxford University Press (2010), p. 152–68.
4. Van Kampen NG. Stochastic Processes in Physics and Chemistry. 3rd edn. North Holland, North Holland (2007).
5. Basser PJ, Mattiello J, LeBihan D. Estimation of the effective self-diffusion tensor from the NMR spin echo. J Magn Reson B. (1994) 103:247–54. doi: 10.1006/jmrb.1994.1037
6. Jones DK. Precision and accuracy in diffusion tensor magnetic resonance imaging. Top Magn Reson Imaging (2010) 21:87–99. doi: 10.1097/RMR.0b013e31821e56ac
7. Veraart J, Sijbers J, Sunaert S, Leemans A, Jeurissen B. Weighted linear least squares estimation of diffusion MRI parameters: strengths, limitations, and pitfalls. Neuroimage (2013) 81:335–46. doi: 10.1016/j.neuroimage.2013.05.028
8. Veraart J, Poot DH, Van Hecke W, Blockx I, Van der Linden A, Verhoye M, et al. More accurate estimation of diffusion tensor parameters using diffusion Kurtosis imaging. Magn Reson Med. (2011) 65:138–45. doi: 10.1002/mrm.22603
9. Kiselev VG. Fundamentals of diffusion MRI physics. NMR Biomed. (2017) 30:e3602. doi: 10.1002/nbm.3602
10. Mori, S (editor). Chapter 11: Application studies. In: Introduction to Diffusion Tensor Imaging. Amsterdam: Elsevier Science B.V (2007), p. 149–61.
11. Van Hecke W, Emsell L, Sunaert S. Diffusion Tensor Imaging - A Practical Handbook. 1st ed. New York, NY: Springer-Verlag (2016).
12. Guglielmetti C, Veraart J, Roelant E, Mai Z, Daans J, Van Audekerke J, et al. Diffusion kurtosis imaging probes cortical alterations and white matter pathology following cuprizone induced demyelination and spontaneous remyelination. Neuroimage (2016) 125:363–77. doi: 10.1016/j.neuroimage.2015.10.052
13. Hui ES, Fieremans E, Jensen JH, Tabesh A, Feng W, Bonilha L, et al. Stroke assessment with diffusional kurtosis imaging. Stroke (2012) 43:2968–73. doi: 10.1161/STROKEAHA.112.657742
14. Jensen JH, Helpern JA. MRI quantification of non-Gaussian water diffusion by kurtosis analysis. NMR Biomed. (2010) 23:698–710. doi: 10.1002/nbm.1518
15. Kochunov P, Rowland LM, Fieremans E, Veraart J, Jahanshad N, Eskandar G, et al. Diffusion-weighted imaging uncovers likely sources of processing-speed deficits in schizophrenia. Proc Natl Acad Sci USA. (2016) 113:13504–9. doi: 10.1073/pnas.1608246113
16. Paydar A, Fieremans E, Nwankwo JI, Lazar M, Sheth HD, Adisetiyo V, et al. Diffusional kurtosis imaging of the developing brain. AJNR Am J Neuroradiol. (2014) 35:808–14. doi: 10.3174/ajnr.A3764
17. Rosenkrantz AB, Padhani AR, Chenevert TL, Koh DM, De Keyzer F, Taouli B, et al. Body diffusion kurtosis imaging: basic principles, applications, and considerations for clinical practice. J Magn Reson Imaging (2015) 42:1190–1202. doi: 10.1002/jmri.24985
18. Hansen B, Lund TE, Sangill R, Jespersen SN. Experimentally and computationally fast method for estimation of a mean kurtosis. Magn Reson Med. (2013) 69:1754–60. doi: 10.1002/mrm.24743
19. Hansen B, Shemesh N, Jespersen SN. Fast imaging of mean, axial and radial diffusion kurtosis. Neuroimage (2016) 142:381–93. doi: 10.1016/j.neuroimage.2016.08.022
20. Yablonskiy DA, Bretthorst GL, Ackerman JJ. Statistical model for diffusion attenuated MR signal. Magn Reson Med. (2003) 50, 664–9. doi: 10.1002/mrm.10578
21. Grinberg F, Farrher E, Ciobanu L, Geffroy F, Le Bihan D, Shah NJ. Non-Gaussian diffusion imaging for enhanced contrast of brain tissue affected by ischemic stroke. PLoS ONE (2014) 9:e89225. doi: 10.1371/journal.pone.0089225
22. Novikov DS, Kiselev VG. Effective medium theory of a diffusion-weighted signal. NMR Biomed. (2010) 23:682–97. doi: 10.1002/nbm.1584
23. Bennett KM, Schmainda KM, Bennett RT, Rowe DB, Lu H, Hyde JS. Characterization of continuously distributed cortical water diffusion rates with a stretched-exponential model. Magn Reson Med. (2003) 50:727–34. doi: 10.1002/mrm.10581
24. Ingo C, Magin RL, Colon-Perez L, Triplett W, Mareci TH. On random walks and entropy in diffusion-weighted magnetic resonance imaging studies of neural tissue. Magn Reson Med. (2014) 71:617–27. doi: 10.1002/mrm.24706
25. Palombo M, Gabrielli A, De Santis S, Cametti C, Ruocco G, Capuani S. Spatio-temporal anomalous diffusion in heterogeneous media by nuclear magnetic resonance. J Chem Phys. (2011) 135:034504. doi: 10.1063/1.3610367
26. Zhou XJ, Gao Q, Abdullah O, Magin RL. Studies of anomalous diffusion in the human brain using fractional order calculus. Magn Reson Med. (2010) 63:562–9. doi: 10.1002/mrm.22285
27. Bai Y, Lin Y, Tian J, Shi D, Cheng J, Haacke EM, et al. Grading of gliomas by using monoexponential, biexponential, stretched exponential diffusion-weighted MR imaging and diffusion kurtosis MR imaging. Radiology (2016) 278:496–504. doi: 10.1148/radiol.2015142173
28. Lai V, Lee VH, Lam KO, Sze HC, Chan Q, Khong PL. Intravoxel water diffusion heterogeneity MR imaging of nasopharyngeal carcinoma using stretched exponential diffusion model. Eur Radiol. (2015) 25:1708–13. doi: 10.1007/s00330-014-3535-9
29. Liu X, Zhou L, Peng W, Wang H, Zhang Y. Comparison of stretched-Exponential and monoexponential model diffusion-Weighted imaging in prostate cancer and normal tissues. J Magn Reson Imaging (2015) 42:1078–85. doi: 10.1002/jmri.24872
30. Mazaheri Y, Afaq A, Rowe DB, Lu Y, Shukla-Dave A, Grover J. Diffusion-weighted magnetic resonance imaging of the prostate: improved robustness with stretched exponential modeling. J Comput Assist Tomogr. (2012) 36:695–703. doi: 10.1097/RCT.0b013e31826bdbbd
31. Özarslan E, Koay CG, Shepherd TM, Komlosh ME, Irfanoglu MO, Pierpaoli C, et al. Mean apparent propagator (MAP) MRI: a novel diffusion imaging method for mapping tissue microstructure. Neuroimage (2013) 78:16–32. doi: 10.1016/j.neuroimage.2013.04.016
32. Avram AV, Sarlls JE, Barnett AS, Ozarslan E, Thomas C, Irfanoglu MO, et al. Clinical feasibility of using mean apparent propagator (MAP) MRI to characterize brain tissue microstructure. Neuroimage (2016) 127:422–34. doi: 10.1016/j.neuroimage.2015.11.027
33. Latour LL, Svoboda K, Mitra PP, Sotak CH. Time-dependent diffusion of water in a biological model system. Proc Natl Acad Sci USA. (1994) 91:1229–33. doi: 10.1073/pnas.91.4.1229
34. Szafer A, Zhong J, Gore JC. Theoretical model for water diffusion in tissues. Magn Reson Med. (1995) 33:697–712. doi: 10.1002/mrm.1910330516
35. Stanisz GJ, Szafer A, Wright GA, Henkelman RM. An analytical model of restricted diffusion in bovine optic nerve. Magn Reson Med. (1997) 37:103–11. doi: 10.1002/mrm.1910370115
36. Behrens TE, Woolrich MW, Jenkinson M, Johansen-Berg H, Nunes RG, Clare S, et al. Characterization and propagation of uncertainty in diffusion-weighted MR imaging. Magn Reson Med. (2003) 50:1077–88. doi: 10.1002/mrm.10609
37. Kroenke CD, Ackerman JJ, Yablonskiy DA. On the nature of the NAA diffusion attenuated MR signal in the central nervous system. Magn Reson Med. (2004) 52:1052–59. doi: 10.1002/mrm.20260
38. Jespersen SN, Kroenke CD, Ostergaard L, Ackerman JJ, Yablonskiy DA. Modeling dendrite density from magnetic resonance diffusion measurements. Neuroimage (2007) 34:1473–86. doi: 10.1016/j.neuroimage.2006.10.037
39. Mikula S, Denk W. High-resolution whole-brain staining for electron microscopic circuit reconstruction. Nat Methods (2015) 12:541–6. doi: 10.1038/nmeth.3361
40. Lampinen B, Szczepankiewicz F, van Westen D, Englund E, Sundgren PC, Lätt J, et al. Optimal experimental design for filter exchange imaging: apparent exchange rate measurements in the healthy brain and in intracranial tumors. Magn Reson Med. (2017) 77:1104–14. doi: 10.1002/mrm.26195
41. Zhang H, Schneider T, Wheeler-Kingshott CA, Alexander DC. NODDI: practical in vivo neurite orientation dispersion and density imaging of the human brain. Neuroimage (2012) 61:1000–16. doi: 10.1016/j.neuroimage.2012.03.072
42. Adluru G, Gur Y, Anderson JS, Richards LG, Adluru N, DiBella EV. Assessment of white matter microstructure in stroke patients using NODDI. Conf Proc IEEE Eng Med Biol Soc. (2014) 2014:742–5. doi: 10.1109/EMBC.2014.6943697
43. Churchill NW, Caverzasi E, Graham SJ, Hutchison MG, Schweizer TA. White matter microstructure in athletes with a history of concussion: comparing diffusion tensor imaging (DTI) and neurite orientation dispersion and density imaging (NODDI). Hum Brain Mapp. (2017) 38:4201–11. doi: 10.1002/hbm.23658
44. Kunz N, Zhang H, Vasung L, O'Brien KR, Assaf Y, Lazeyras F, et al. Assessing white matter microstructure of the newborn with multi-shell diffusion MRI and biophysical compartment models. Neuroimage (2014) 96, 288–99. doi: 10.1016/j.neuroimage.2014.03.057
45. Okita G, Ohba T, Takamura T, Ebata S, Ueda R, Onishi H, et al. Application of neurite orientation dispersion and density imaging or diffusion tensor imaging to quantify the severity of cervical spondylotic myelopathy and assess postoperative neurological recovery. Spine J. (2017). doi: 10.1016/j.spinee.2017.07.007. [Epub ahead of print].
46. Schneider T, Brownlee W, Zhang H, Ciccarelli O, Miller DH, Wheeler-Kingshott CG. Sensitivity of multi-shell NODDI to multiple sclerosis white matter changes: a pilot study. Funct Neurol. (2017) 32:97–101. doi: 10.11138/FNeur/2017.32.2.097
47. Slattery CF, Zhang J, Paterson RW, Foulkes, AJM, Carton A, Macpherson K, et al. ApoE influences regional white-matter axonal density loss in Alzheimer's disease. Neurobiol Aging (2017) 57:8–17. doi: 10.1016/j.neurobiolaging.2017.04.021
48. Wen Q, Kelley DA, Banerjee S, Lupo JM, Chang SM, Xu D, et al. Clinically feasible NODDI characterization of glioma using multiband EPI at 7 T. Neuroimage Clin. (2015) 9:291–9. doi: 10.1016/j.nicl.2015.08.017
49. Jelescu IO, Veraart J, Fieremans E, Novikov DS. Degeneracy in model parameter estimation for multi-compartmental diffusion in neuronal tissue. NMR Biomed. (2016a) 29, 33–47. doi: 10.1002/nbm.3450
50. Novikov DS, Veraart J, Jelescu IO, Fieremans E. Mapping orientational and microstructural metrics of neuronal integrity with in vivo diffusion MRI. arXiv:1609.09144 (2016b).
51. Novikov DS, Fieremans E. Relating extracellular diffusivity to cell size distribution and packing density as applied to white matter. In: Proc Intl Soc Mag Reson Med. Melbourne, VIC (2012). p. 1829.
52. Fieremans E, Jensen JH, Helpern JA. White matter characterization with diffusional kurtosis imaging. Neuroimage (2011) 58:177–88. doi: 10.1016/j.neuroimage.2011.06.006
53. Fieremans E, Novikov DS, Jensen JH, Helpern JA. Monte Carlo study of a two-compartment exchange model of diffusion. NMR Biomed. (2010) 23:711–24. doi: 10.1002/nbm.1577
54. Benitez A, Fieremans E, Jensen JH, Falangola MF, Tabesh A, Ferris SH, et al. White matter tract integrity metrics reflect the vulnerability of late-myelinating tracts in Alzheimer's disease. Neuroimage Clin. (2013) 4:64–71. doi: 10.1016/j.nicl.2013.11.001
55. de Kouchkovsky I, Fieremans E, Fleysher L, Herbert J, Grossman RI, Inglese M. Quantification of normal-appearing white matter tract integrity in multiple sclerosis: a diffusion kurtosis imaging study. J Neurol. (2016) 263:1146–55. doi: 10.1007/s00415-016-8118-z
56. Jelescu IO, Zurek M, Winters KV, Veraart J, Rajaratnam A, Kim NS, et al. In vivo quantification of demyelination and recovery using compartment-specific diffusion MRI metrics validated by electron microscopy. Neuroimage (2016b) 132:104–14. doi: 10.1016/j.neuroimage.2016.02.004
57. Kamiya K, Hori M, Irie R, Miyajima M, Nakajima M, Kamagata K, et al. Diffusion imaging of reversible and irreversible microstructural changes within the corticospinal tract in idiopathic normal pressure hydrocephalus. Neuroimage Clin. (2017) 14:663–71. doi: 10.1016/j.nicl.2017.03.003
58. Kelm ND, West KL, Carson RP, Gochberg DF, Ess KC, Does MD. Evaluation of diffusion kurtosis imaging in ex vivo hypomyelinated mouse brains. Neuroimage (2016) 124:612–26. doi: 10.1016/j.neuroimage.2015.09.028
59. Jespersen SN, Olesen JL, Hansen B, Shemesh N. Diffusion time dependence of microstructural parameters in fixed spinal cord. Neuroimage (2017). doi: 10.1016/j.neuroimage.2017.08.039. [Epub ahead of print].
60. Tariq M, Schneider T, Alexander DC, Gandini Wheeler-Kingshott CA, Zhang H. Bingham-NODDI: mapping anisotropic orientation dispersion of neurites using diffusion MRI. Neuroimage (2016) 133, 207–23. doi: 10.1016/j.neuroimage.2016.01.046
61. Jespersen SN, Bjarkam CR, Nyengaard JR, Chakravarty MM, Hansen B, Vosegaard T, et al. Neurite density from magnetic resonance diffusion measurements at ultrahigh field: comparison with light microscopy and electron microscopy. Neuroimage (2010) 49:205–16. doi: 10.1016/j.neuroimage.2009.08.053
62. Anderson AW. Measurement of fiber orientation distributions using high angular resolution diffusion imaging. Magn Reson Med. (2005) 54:1194–206. doi: 10.1002/mrm.20667
63. Dell'Acqua F, Rizzo G, Scifo P, Clarke RA, Scotti G, Fazio F. A model-based deconvolution approach to solve fiber crossing in diffusion-weighted MR imaging. IEEE Trans Biomed Eng. (2007) 54:462–72. doi: 10.1109/TBME.2006.888830
64. Tournier JD, Calamante F, Gadian DG, Connelly A. Direct estimation of the fiber orientation density function from diffusion-weighted MRI data using spherical deconvolution. Neuroimage (2004) 23:1176–85. doi: 10.1016/j.neuroimage.2004.07.037
65. Reisert M, Kellner E, Dhital B, Hennig J, Kiselev VG. Disentangling micro from mesostructure by diffusion MRI: a Bayesian approach. Neuroimage (2017) 147:964–75. doi: 10.1016/j.neuroimage.2016.09.058
66. Kaden E, Kelm ND, Carson RP, Does MD, Alexander DC. Multi-compartment microscopic diffusion imaging. Neuroimage (2016) 139:346–59. doi: 10.1016/j.neuroimage.2016.06.002
67. Wang Y, Wang Q, Haldar JP, Yeh FC, Xie M, Sun P, et al. Quantification of increased cellularity during inflammatory demyelination. Brain (2011) 134:3590–601. doi: 10.1093/brain/awr307
68. Chiang CW, Wang Y, Sun P, Lin TH, Trinkaus K, Cross AH, et al. Quantifying white matter tract diffusion parameters in the presence of increased extra-fiber cellularity and vasogenic edema. Neuroimage (2014) 101:310–9. doi: 10.1016/j.neuroimage.2014.06.064
69. Lin TH, Chiang CW, Perez-Torres CJ, Sun P, Wallendorf M, Schmidt RE, et al. Diffusion MRI quantifies early axonal loss in the presence of nerve swelling. J Neuroinflammation (2017) 14:78. doi: 10.1186/s12974-017-0852-3
70. Murphy RK, Sun P, Xu J, Wang Y, Sullivan S, Gamble P, et al. Magnetic resonance imaging biomarker of axon loss reflects cervical spondylotic myelopathy severity. Spine (2016) 41:751–6. doi: 10.1097/BRS.0000000000001337
71. Sun P, Murphy RK, Gamble P, George A, Song SK, Ray WZ. Diffusion assessment of cortical changes, induced by traumatic spinal cord injury. Brain Sci. (2017) 7:E21. doi: 10.3390/brainsci7020021
72. Wang X, Cusick MF, Wang Y, Sun P, Libbey JE, Trinkaus K, et al. Diffusion basis spectrum imaging detects and distinguishes coexisting subclinical inflammation, demyelination and axonal injury in experimental autoimmune encephalomyelitis mice. NMR Biomed. (2014c) 27:843–52. doi: 10.1002/nbm.3129
73. Pierpaoli C, Jones DK. Removing CSF contamination in brain DT-MRIs by using a two-compartment tensor model. In: Proc Intl Soc Mag Reson Med. Kyoto (2004). p. 1215.
74. Pasternak O, Sochen N, Gur Y, Intrator N, Assaf Y. Free water elimination and mapping from diffusion MRI. Magn Reson Med. (2009) 62:717–30. doi: 10.1002/mrm.22055
75. Albi A, Pasternak O, Minati L, Marizzoni M, Bartres-Faz D, Bargallo N, et al. Free water elimination improves test-retest reproducibility of diffusion tensor imaging indices in the brain: a longitudinal multisite study of healthy elderly subjects. Hum Brain Mapp. (2017) 38:12–26. doi: 10.1002/hbm.23350
76. Bergamino M, Pasternak O, Farmer M, Shenton ME, Hamilton JP. Applying a free-water correction to diffusion imaging data uncovers stress-related neural pathology in depression. Neuroimage Clin. (2016) 10:336–42. doi: 10.1016/j.nicl.2015.11.020
77. Oestreich LK, Pasternak O, Shenton ME, Kubicki M, Gong X, McCarthy-Jones S, et al. Abnormal white matter microstructure and increased extracellular free-water in the cingulum bundle associated with delusions in chronic schizophrenia. Neuroimage Clin. (2016) 12:405–14. doi: 10.1016/j.nicl.2016.08.004
78. Ofori E, Pasternak O, Planetta PJ, Li H, Burciu RG, Snyder AF, et al. Longitudinal changes in free-water within the substantia nigra of Parkinson's disease. Brain (2015) 138:2322–31. doi: 10.1093/brain/awv136
79. Pasternak O, Shenton ME, Westin CF. Estimation of extracellular bold from regularized multi-shell diffusion MRI. Med Image Comput Comp Assist Interv. (2012) 15:305–12. doi: 10.1007/978-3-642-33418-4_38
80. Hoy AR, Koay CG, Kecskemeti SR, Alexander AL. Optimization of a free water elimination two-compartment model for diffusion tensor imaging. Neuroimage (2014) 103:323–33. doi: 10.1016/j.neuroimage.2014.09.053
81. Chou MC, Lin YR, Huang TY, Wang CY, Chung HW, Juan CJ, et al. FLAIR diffusion-tensor MR tractography: comparison of fiber tracking with conventional imaging. AJNR Am J Neuroradiol. (2005) 26:591–7.
82. Hoy AR, Kecskemeti SR, Alexander AL. Free water elimination diffusion tractography: a comparison with conventional and fluid-attenuated inversion recovery, diffusion tensor imaging acquisitions. J Magn Reson Imaging (2015) 42:1572–81. doi: 10.1002/jmri.24925
83. Scherrer B, Schwartzman A, Taquet M, Sahin M, Prabhu SP, Warfield SK. Characterizing brain tissue by assessment of the distribution of anisotropic microstructural environments in diffusion-compartment imaging (DIAMOND). Magn Reson Med. (2016) 76:963–77. doi: 10.1002/mrm.25912
84. Ferizi U, Schneider T, Panagiotaki E, Nedjati-Gilani G, Zhang H, Wheeler-Kingshott CA, et al. A ranking of diffusion MRI compartment models with in vivo human brain data. Magn Reson Med. (2014) 72:1785–92. doi: 10.1002/mrm.25080
85. Panagiotaki E, Schneider T, Siow B, Hall MG, Lythgoe MF, Alexander DC. Compartment models of the diffusion MR signal in brain white matter: a taxonomy and comparison. Neuroimage (2012) 59, 2241–54. doi: 10.1016/j.neuroimage.2011.09.081
86. Scherrer B, Qiu J, Hashim J, Afacan O, Wu Y, Marcotrigiano M, et al. Diffusion compartment imaging reveals microstructural injuries in a mouse model of mild traumatic brain injury. In: Proc Intl Soc Mag Reson Med. Honolulu, HI (2017). p. 286.
87. Jelescu IO, Veraart J, Adisetiyo V, Milla SS, Novikov DS, Fieremans E. One diffusion acquisition and different white matter models: how does microstructure change in human early development based on WMTI and NODDI? Neuroimage (2015) 107:242–56. doi: 10.1016/j.neuroimage.2014.12.009
88. Wang S, Peterson DJ, Wang Y, Wang Q, Grabowski TJ, Li W, et al. Empirical comparison of diffusion kurtosis imaging and diffusion basis spectrum imaging using the same acquisition in healthy young adults. Front Neurol. (2017) 8:118. doi: 10.3389/fneur.2017.00118
89. Balls GT, Frank LR. A simulation environment for diffusion weighted MR experiments in complex media. Magn Reson Med. (2009) 62, 771–8. doi: 10.1002/mrm.22033
90. Hall MG, Alexander DC. Convergence and parameter choice for Monte-Carlo simulations of diffusion MRI. IEEE Trans Med Imaging (2009) 28:1354–64. doi: 10.1109/TMI.2009.2015756
91. Mingasson T, Duval T, Stikov N, Cohen-Adad J. AxonPacking: an open-source software to simulate arrangements of axons in white matter. Front. Neuroinform. (2017) 11:5. doi: 10.3389/fninf.2017.00005
92. Yeh CH, Schmitt B, Le Bihan D, Li-Schlittgen JR, Lin CP, Poupon C. Diffusion microscopist simulator: a general Monte Carlo simulation system for diffusion magnetic resonance imaging. PLoS ONE (2013) 8:e76626. doi: 10.1371/journal.pone.0076626
93. Landman BA, Farrell JA, Smith SA, Reich DS, Calabresi PA, van Zijl PC. Complex geometric models of diffusion and relaxation in healthy and damaged white matter. NMR Biomed. (2010) 23:152–62. doi: 10.1002/nbm.1437
94. Budde MD, Frank JA. Neurite beading is sufficient to decrease the apparent diffusion coefficient after ischemic stroke. Proc Natl Acad Sci USA. (2010) 107:14472–7. doi: 10.1073/pnas.1004841107
95. Nilsson M, Latt J, Stahlberg F, van Westen D, Hagslatt H. The importance of axonal undulation in diffusion MR measurements: a Monte Carlo simulation study. NMR Biomed. (2012) 25:795–805. doi: 10.1002/nbm.1795
96. Panagiotaki E, Hall MG, Zhang H, Siow B, Lythgoe MF, Alexander DC. High-fidelity meshes from tissue samples for diffusion MRI simulations. Med. Image Comput. Comp. Assist. Interv. (2010) 13(Pt 2):404–11. doi: 10.1007/978-3-642-15745-5_50
97. Perrin M, Poupon C, Rieul B, Leroux P, Constantinesco A, Mangin JF, et al. Validation of q-ball imaging with a diffusion fibre-crossing phantom on a clinical scanner. Philos Trans R Soc Lond B Biol Sci. (2005) 360:881–91. doi: 10.1098/rstb.2005.1650
98. Kim SJ, Choi CG, Kim JK, Yun SC, Jahng GH, Jeong HK, et al. Effects of MR parameter changes on the quantification of diffusion anisotropy and apparent diffusion coefficient in diffusion tensor imaging: evaluation using a diffusional anisotropic phantom. Korean J Radiol. (2015) 16:297–303. doi: 10.3348/kjr.2015.16.2.297
99. Oida T, Nagahara S, Kobayashi T. Acquisition parameters for diffusion tensor imaging to emphasize fractional anisotropy: phantom study. Magn Reson Med Sci. (2011) 10:121–128. doi: 10.2463/mrms.10.121
100. Tournier JD, Yeh CH, Calamante F, Cho KH, Connelly A, Lin CP. Resolving crossing fibres using constrained spherical deconvolution: validation using diffusion-weighted imaging phantom data. Neuroimage (2008) 42:617–25. doi: 10.1016/j.neuroimage.2008.05.002
101. Komlosh ME, Benjamini D, Barnett AS, Schram V, Horkay F, Avram AV, et al. Anisotropic phantom to calibrate high-q diffusion MRI methods. J Magn Reson. (2017) 275:19–28. doi: 10.1016/j.jmr.2016.11.017
102. Burcaw LM, Fieremans E, Novikov DS. Mesoscopic structure of neuronal tracts from time-dependent diffusion. Neuroimage (2015) 114:18–37. doi: 10.1016/j.neuroimage.2015.03.061
103. Fieremans E, De Deene Y, Delputte S, Ozdemir MS, Achten E, Lemahieu I. The design of anisotropic diffusion phantoms for the validation of diffusion weighted magnetic resonance imaging. Phys Med Biol. (2008a) 53:5405–19. doi: 10.1088/0031-9155/53/19/009
104. Fieremans E, De Deene Y, Delputte S, Özdemir MS, D'Asseler Y, Vlassenbroeck J, et al. Simulation and experimental verification of the diffusion in an anisotropic fiber phantom. J. Magn Reson. (2008b) 190:189–99. doi: 10.1016/j.jmr.2007.10.014
105. Farrher E, Lindemeyer J, Grinberg F, Oros-Peusquens A.-M, Shah NJ. Concerning the matching of magnetic susceptibility differences for the compensation of background gradients in anisotropic diffusion fibre phantoms. PLoS ONE (2017) 12:e0176192. doi: 10.1371/journal.pone.0176192
106. Hubbard PL, Zhou FL, Eichhorn SJ, Parker GJ. Biomimetic phantom for the validation of diffusion magnetic resonance imaging. Magn Reson Med (2015) 73:299–305. doi: 10.1002/mrm.25107
107. Palacios EM, Martin AJ, Boss MA, Ezekiel F, Chang YS, Yuh EL, et al. Toward precision and reproducibility of diffusion tensor imaging: a multicenter diffusion phantom and traveling volunteer study. AJNR Am J Neuroradiol. (2017) 38:537–45. doi: 10.3174/ajnr.A5025
108. Nimsky C, Ganslandt O, Hastreiter P, Wang R, Benner T, Sorensen AG, et al. Preoperative and intraoperative diffusion tensor imaging-based fiber tracking in glioma surgery. Neurosurgery (2005) 56:130–7; discussion: 138. doi: 10.1227/01.NEU.0000144842.18771.30
109. Johansen-Berg H, Behrens TE. Just pretty pictures? What diffusion tractography can add in clinical neuroscience. Curr Opin Neurol. (2006) 19:379–385. doi: 10.1097/01.wco.0000236618.82086.01
110. Tuch DS, Reese TG, Wiegell MR, Wedeen VJ. Diffusion MRI of complex neural architecture. Neuron (2003) 40:885–95. doi: 10.1016/S0896-6273(03)00758-X
111. Christiaens D, Reisert M, Dhollander T, Sunaert S, Suetens P, Maes F. Global tractography of multi-shell diffusion-weighted imaging data using a multi-tissue model. Neuroimage (2015) 123:89–101. doi: 10.1016/j.neuroimage.2015.08.008
112. Daducci A, Dal Palu A, Descoteaux M, Thiran JP. Microstructure informed tractography: pitfalls and open challenges. Front Neurosci (2016) 10:247. doi: 10.3389/fnins.2016.00247
113. Reisert M, Kiselev VG, Dihtal B, Kellner E, Novikov DS. MesoFT: unifying diffusion modelling and fiber tracking. Med Image Comput Comp Assist Interv. (2014) 17:201–8. doi: 10.1007/978-3-319-10443-0_26
114. Budde MD, Annese J. Quantification of anisotropy and fiber orientation in human brain histological sections. Front Integr Neurosci. (2013a) 7:3. doi: 10.3389/fnint.2013.00003
115. Axer M, Strohmer S, Gräßel D, Bücker O, Dohmen M, Reckfort J, et al. Estimating fiber orientation distribution functions in 3D-Polarized Light Imaging. Front. Neuroanat. (2016) 10:40. doi: 10.3389/fnana.2016.00040
116. Wang H, Zhu J, Reuter M, Vinke LN, Yendiki A, Boas DA, et al. Cross-validation of serial optical coherence scanning and diffusion tensor imaging: a study on neural fiber maps in human medulla oblongata. Neuroimage (2014b) 100:395–404. doi: 10.1016/j.neuroimage.2014.06.032
117. Leergaard TB, White NS, de Crespigny A, Bolstad I, D'Arceuil H, Bjaalie JG, et al. Quantitative histological validation of diffusion MRI fiber orientation distributions in the rat brain. PLoS ONE (2010) 5:e8595. doi: 10.1371/journal.pone.0008595
118. Budde MD, Annese J. Quantifying anisotropy and fiber orientation in human brain histological sections. Front Integr Neurosci. (2013b) 7:3. doi: 10.3389/fnint.2013.00003
119. Budde MD, Frank JA. Examining brain microstructure using structure tensor analysis of histological sections. Neuroimage (2012) 63:1–10. doi: 10.1016/j.neuroimage.2012.06.042
120. Choe AS, Stepniewska I, Colvin DC, Ding Z, Anderson AW. Validation of diffusion tensor MRI in the central nervous system using light microscopy: quantitative comparison of fiber properties. NMR Biomed. (2012) 25:900–8. doi: 10.1002/nbm.1810
121. Gangolli M, Holleran L, Hee Kim J, Stein TD, Alvarez V, McKee AC, et al. Quantitative validation of a nonlinear histology-MRI coregistration method using generalized Q-sampling imaging in complex human cortical white matter. Neuroimage (2017) 153:152–67. doi: 10.1016/j.neuroimage.2017.03.059
122. Grussu F, Schneider T, Yates RL, Zhang H, Wheeler-Kingshott, CAMG, DeLuca GC, et al. A framework for optimal whole-sample histological quantification of neurite orientation dispersion in the human spinal cord. J. Neurosci. Methods (2016) 273:20–32. doi: 10.1016/j.jneumeth.2016.08.002
123. Hansen B, Flint JJ, Heon-Lee C, Fey M, Vincent F, King MA, et al. Diffusion tensor microscopy in human nervous tissue with quantitative correlation based on direct histological comparison. Neuroimage (2011) 57:1458–65. doi: 10.1016/j.neuroimage.2011.04.052
124. Mitter C, Jakab A, Brugger PC, Ricken G, Gruber GM, Bettelheim D, et al. Validation of in utero tractography of human fetal commissural and internal capsule fibers with histological structure tensor analysis. Front. Neuroanat. (2015) 9:164. doi: 10.3389/fnana.2015.00164
125. Mollink J, Kleinnijenhuis M, Cappellen van Walsum, AMV, Sotiropoulos SN, Cottaar M, Mirfin C, et al. Evaluating fibre orientation dispersion in white matter: comparison of diffusion MRI, histology and polarized light imaging. Neuroimage (2017) 157:561–74. doi: 10.1016/j.neuroimage.2017.06.001
126. Nazaran A, Wisco JJ, Hageman N, Schettler SP, Wong A, Vinters HV, et al. Methodology for computing white matter nerve fiber orientation in human histological slices. J Neurosci Methods (2016) 261:75–84. doi: 10.1016/j.jneumeth.2015.11.023
127. Seehaus A, Roebroeck A, Bastiani M, Fonseca L, Bratzke H, Lori N, et al. Histological validation of high-resolution DTI in human post mortem tissue. Front Neuroanat. (2015) 9:98. doi: 10.3389/fnana.2015.00098
128. Khan AR, Cornea A, Leigland LA, Kohama SG, Jespersen SN, Kroenke CD. 3D structure tensor analysis of light microscopy data for validating diffusion MRI. Neuroimage (2015) 111:192–203. doi: 10.1016/j.neuroimage.2015.01.061
129. Schilling K, Janve V, Gao Y, Stepniewska I, Landman BA, Anderson AW. Comparison of 3D orientation distribution functions measured with confocal microscopy and diffusion MRI. Neuroimage (2016) 129:185–97. doi: 10.1016/j.neuroimage.2016.01.022
130. Annese J. The importance of combining MRI and large-scale digital histology in neuroimaging studies of brain connectivity and disease. Front Neuroinform. (2012) 6:13. doi: 10.3389/fninf.2012.00013
131. de Campos Vidal B, Mello ML, Caseiro-Filho AC, Godo C. Anisotropic properties of the myelin sheath. Acta Histochem. (1980) 66:32–9. doi: 10.1016/S0065-1281(80)80079-1
132. Axer H, Beck S, Axer M, Schuchardt F, Heepe J, Flucken A, et al. Microstructural analysis of human white matter architecture using polarized light imaging: Views from neuroanatomy. Front Neuroinform. (2011a) 5:28. doi: 10.3389/fninf.2011.00028
133. Axer M, Amunts K, Grässel D, Palm C, Dammers J, Axer H, et al. A novel approach to the human connectome: ultra-high resolution mapping of fiber tracts in the brain. Neuroimage (2011b) 54:1091–101. doi: 10.1016/j.neuroimage.2010.08.075
134. Wang H, Lenglet C, Akkin T. Structure tensor analysis of serial optical coherence scanner images for mapping fiber orientations and tractography in the brain. J Biomed Optics (2015) 20:036003. doi: 10.1117/1.JBO.20.3.036003
135. Wang H, Zhu J, Akkin T. Serial optical coherence scanner for large-scale brain imaging at microscopic resolution. Neuroimage (2014a) 84:1007–1017. doi: 10.1016/j.neuroimage.2013.09.063
136. Oh SW, Harris JA, Ng L, Winslow B, Cain N, Mihalas S, et al. A mesoscale connectome of the mouse brain. Nature (2014) 508:207–14. doi: 10.1038/nature13186
137. Magnain C, Augustinack JC, Reuter M, Wachinger C, Frosch MP, Ragan T, et al. Blockface histology with optical coherence tomography: a comparison with Nissl staining. Neuroimage (2014) 84:524–33. doi: 10.1016/j.neuroimage.2013.08.072
138. Srinivasan VJ, Radhakrishnan H, Jiang JY, Barry S, Cable AE. Optical coherence microscopy for deep tissue imaging of the cerebral cortex with intrinsic contrast. Opt Express (2012) 20:2220–39. doi: 10.1364/OE.20.002220
139. Denk W, Horstmann H. Serial block-face scanning electron microscopy to reconstruct three-dimensional tissue nanostructure. PLoS Biol. (2004) 2:e329. doi: 10.1371/journal.pbio.0020329
140. Dodt HU, Leischner U, Schierloh A, Jährling N, Mauch CP, Deininger K, et al. Ultramicroscopy: three-dimensional visualization of neuronal networks in the whole mouse brain. Nat Methods (2007) 4:331–6. doi: 10.1038/nmeth1036
141. Mikula S, Binding J, Denk W. Staining and embedding the whole mouse brain for electron microscopy. Nat Methods (2012) 9:1198–201. doi: 10.1038/nmeth.2213
142. Chang EH, Argyelan M, Aggarwal M, Chandon T. SS, Karlsgodt KH, Mori S, et al. The role of myelination in measures of white matter integrity: combination of diffusion tensor imaging and two-photon microscopy of CLARITY intact brains. Neuroimage (2017) 147:119–24. doi: 10.1016/j.neuroimage.2016.11.068
143. Ronen I, Budde M, Ercan E, Annese J, Techawiboonwong A, Webb A. Microstructural organization of axons in the human corpus callosum quantified by diffusion-weighted magnetic resonance spectroscopy of N-acetylaspartate and post-mortem histology. Brain Struct Funct. (2014) 219:1773–85. doi: 10.1007/s00429-013-0600-0
144. Jespersen SN, Leigland LA, Cornea A, Kroenke CD. Determination of axonal and dendritic orientation distributions within the developing cerebral cortex by diffusion tensor imaging. IEEE Trans Med Imaging (2012) 31:16–32. doi: 10.1109/TMI.2011.2162099
145. Sykova E, Nicholson C. Diffusion in brain extracellular space. Physiol Rev. (2008) 88:1277–340. doi: 10.1152/physrev.00027.2007
146. Cragg B. Preservation of extracellular space during fixation of the brain for electron microscopy. Tissue Cell (1980) 12:63–72. doi: 10.1016/0040-8166(80)90052-X
147. Perge JA, Koch K, Miller R, Sterling P, Balasubramanian V. How the optic nerve allocates space, energy capacity, information. J Neurosci. (2009) 29:7917–28. doi: 10.1523/JNEUROSCI.5200-08.2009
148. Ong HH, Wright AC, Wehrli SL, Souza A, Schwartz ED, Hwang SN, et al. Indirect measurement of regional axon diameter in excised mouse spinal cord with q-space imaging: simulation and experimental studies. Neuroimage (2008) 40:1619–32. doi: 10.1016/j.neuroimage.2008.01.017
149. Pallotto M, Watkins PV, Fubara B, Singer JH, Briggman KL. Extracellular space preservation aids the connectomic analysis of neural circuits. Elife (2015) 4:e08206. doi: 10.7554/eLife.08206
150. Korogod N, Petersen CC, Knott GW. Ultrastructural analysis of adult mouse neocortex comparing aldehyde perfusion with cryo fixation. Elife (2015) 4:e05793. doi: 10.7554/eLife.05793
151. Grussu F, Schneider T, Zhang H, Alexander DC, Wheeler-Kingshott CA. Neurite orientation dispersion and density imaging of the healthy cervical spinal cord in vivo. Neuroimage (2015) 111:590–601. doi: 10.1016/j.neuroimage.2015.01.045
152. Chklovskii DB, Schikorski T, Stevens CF. Wiring optimization in cortical circuits. Neuron (2002) 34:341–7. doi: 10.1016/S0896-6273(02)00679-7
153. Sepehrband F, Clark KA, Ullmann JF, Kurniawan ND, Leanage G, Reutens DC, et al. Brain tissue compartment density estimated using diffusion-weighted MRI yields tissue parameters consistent with histology. Hum Brain Mapp. (2015) 36:3687–702. doi: 10.1002/hbm.22872
154. Golabchi FN, Brooks DH, Hoge WS, De Girolami U, Maier SE. Pixel-based comparison of spinal cord MR diffusion anisotropy with axon packing parameters. Magn Reson Med. (2010) 63:1510–9. doi: 10.1002/mrm.22337
155. Duval T, Le Vy S, Stikov N, Campbell J, Mezer A, Witzel T, et al. g-Ratio weighted imaging of the human spinal cord in vivo. Neuroimage (2017) 145:11–23. doi: 10.1016/j.neuroimage.2016.09.018
156. Stikov N, Campbell JS, Stroh T, Lavelee M, Frey S, Novek J, et al. In vivo histology of the myelin g-ratio with magnetic resonance imaging. Neuroimage (2015) 118:397–405. doi: 10.1016/j.neuroimage.2015.05.023
157. Beaulieu C. The basis of anisotropic water diffusion in the nervous system - a technical review. NMR Biomed. (2002) 15:435–55. doi: 10.1002/nbm.782
158. Takahashi M, Hackney DB, Zhang G, Wehrli SL, Wright AC, O'Brien WT, et al. Magnetic resonance microimaging of intraaxonal water diffusion in live excised lamprey spinal cord. Proc Natl Acad Sci USA. (2002) 99:16192–6. doi: 10.1073/pnas.252249999
159. Beaulieu C, Allen PS. Water diffusion in the giant axon of the squid: implications for diffusion-weighted MRI of the nervous system. Magn Reson Med. (1994) 32:579–83. doi: 10.1002/mrm.1910320506
160. Nordengen K, Heuser C, Rinholm JE, Matalon R, Gundersen V. Localisation of N-acetylaspartate in oligodendrocytes/myelin. Brain Struct Funct. (2015) 220:899–917. doi: 10.1007/s00429-013-0691-7
161. Ellegood J, Hanstock CC, Beaulieu C. Diffusion tensor spectroscopy (DTS) of human brain. Magn Reson Med. (2006) 55:1–8. doi: 10.1002/mrm.20777
162. Ellegood J, McKay RT, Hanstock CC, Beaulieu C. Anisotropic diffusion of metabolites in peripheral nerve using diffusion weighted magnetic resonance spectroscopy at ultra-high field. J Magn Reson. (2007) 184:20–28. doi: 10.1016/j.jmr.2006.09.008
163. Palombo M, Ligneul C, Valette J. Modeling diffusion of intracellular metabolites in the mouse brain up to very high diffusion-weighting: diffusion in long fibers (almost) accounts for non-monoexponential attenuation. Magn Reson Med. (2017) 77:343–50. doi: 10.1002/mrm.26548
164. Najac C, Branzoli F, Ronen I, Valette J. Brain intracellular metabolites are freely diffusing along cell fibers in grey and white matter, as measured by diffusion-weighted MR spectroscopy in the human brain at 7 T. Brain Struct Funct. (2016) 221:1245–1254. doi: 10.1007/s00429-014-0968-5
165. Najac C, Marchadour C, Guillermier M, Houitte D, Slavov V, Brouillet E, et al. Intracellular metabolites in the primate brain are primarily localized in long fibers rather than in cell bodies, as shown by diffusion-weighted magnetic resonance spectroscopy. Neuroimage (2014) 90:374–380. doi: 10.1016/j.neuroimage.2013.12.045
166. Goodman JA, Kroenke CD, Bretthorst GL, Ackerman JJ, Neil JJ. Sodium ion apparent diffusion coefficient in living rat brain. Magn Reson Med. (2005) 53:1040–1045. doi: 10.1002/mrm.20444
167. Goodman JA, Ackerman JJ, Neil JJ. Cs + ADC in rat brain decreases markedly at death. Magn Reson Med. (2008) 59:65–72. doi: 10.1002/mrm.21418
168. Duong TQ, Ackerman JJ, Ying HS, Neil JJ. Evaluation of extra- and intracellular apparent diffusion in normal and globally ischemic rat brain via 19F NMR. Magn Reson Med. (1998) 40:1–13. doi: 10.1002/mrm.1910400102
169. Duong TQ, Sehy JV, Yablonskiy DA, Snider BJ, Ackerman JJ, Neil JJ. Extracellular apparent diffusion in rat brain. Magn Reson Med. (2001) 45:801–10. doi: 10.1002/mrm.1108
170. Ackerman JJ, Neil JJ. The use of MR-detectable reporter molecules and ions to evaluate diffusion in normal and ischemic brain. NMR Biomed. (2010) 23:725–33. doi: 10.1002/nbm.1530
171. Silva MD, Omae T, Helmer KG, Li F, Fisher M, Sotak CH. Separating changes in the intra- and extracellular water apparent diffusion coefficient following focal cerebral ischemia in the rat brain. Magn Reson Med. (2002) 48:826–37. doi: 10.1002/mrm.10296
172. Jelescu IO, Kunz N, Da Silva AR, Gruetter R. Intra- and extra-axonal axial diffusivities in the white matter: which one is faster? In: Proc. Intl. Soc. Mag. Reson Med. Honolulu, HI (2017). p. 281.
173. Skinner NP, Kurpad SN, Schmit BD, Tugan Muftuler L, Budde MD. Rapid in vivo detection of rat spinal cord injury with double-diffusion-encoded magnetic resonance spectroscopy. Magn Reson Med. (2017) 77:1639–49. doi: 10.1002/mrm.26243
174. Dhital B, Kellner E, Reisert M, Kiselev VG. Isotropic diffusion weighting provides insight on diffusion compartments in human brain white matter in vivo. In: Proc Intl Soc Mag Reson Med. Toronto, ON (2015). p. 2788.
175. Szczepankiewicz F, Lasic S, van Westen D, Sundgren PC, Englund E, Westin CF, et al. Quantification of microscopic diffusion anisotropy disentangles effects of orientation dispersion from microstructure: applications in healthy volunteers and in brain tumors. Neuroimage (2015) 104:241–52. doi: 10.1016/j.neuroimage.2014.09.057
176. Veraart J, Novikov DS, Fieremans E. TE dependent Diffusion Imaging (TEdDI) distinguishes between compartmental T2 relaxation times. Neuroimage (2017). doi: 10.1016/j.neuroimage.2017.09.030. [Epub ahead of print].
177. Veraart J, Fieremans E, Novikov DS. Universal power-law scaling of water diffusion in human brain defines what we see with MRI. arXiv:1609.09145 [physics.bio-ph] (2016).
178. Le Bihan D, Johansen-Berg H. Diffusion MRI at 25: exploring brain tissue structure and function. Neuroimage (2012) 61:324–41. doi: 10.1016/j.neuroimage.2011.11.006
179. Moseley ME, Cohen Y, Mintorovitch J, Chileuitt L, Shimizu H, Kucharczyk J, et al. Early detection of regional cerebral ischemia in cats: comparison of diffusion- and T2-weighted MRI and spectroscopy. Magn Reson Med. (1990) 14:330–46. doi: 10.1002/mrm.1910140218
180. Benveniste H, Hedlund LW, Johnson GA. Mechanism of detection of acute cerebral ischemia in rats by diffusion-weighted magnetic resonance microscopy. Stroke (1992) 23:746–54. doi: 10.1161/01.STR.23.5.746
181. Baron CA, Kate M, Gioia L, Butcher K, Emery D, Budde M, et al. Reduction of diffusion-weighted imaging contrast of acute ischemic stroke at short diffusion times. Stroke (2015) 46:2136–41. doi: 10.1161/STROKEAHA.115.008815
182. Does MD, Parsons EC, Gore JC. Oscillating gradient measurements of water diffusion in normal and globally ischemic rat brain. Magn Reson Med. (2003) 49:206–215. doi: 10.1002/mrm.10385
183. Brugieres P, Thomas P, Maraval A, Hosseini H, Combes C, Chafiq A, et al. Water diffusion compartmentation at high b values in ischemic human brain. AJNR Am J Neuroradiol. (2004) 25, 692–8.
184. Niendorf T, Dijkhuizen RM, Norris DG, van Lookeren Campagne M, Nicolay K. Biexponential diffusion attenuation in various states of brain tissue: implications for diffusion-weighted imaging. Magn Reson Med. (1996) 36:847–57. doi: 10.1002/mrm.1910360607
185. Li P, Murphy TH. Two-photon imaging during prolonged middle cerebral artery occlusion in mice reveals recovery of dendritic structure after reperfusion. J Neurosci. (2008) 28:11970–9. doi: 10.1523/JNEUROSCI.3724-08.2008
186. Lucchinetti C, Bruck W, Parisi J, Scheithauer B, Rodriguez M, Lassmann H. Heterogeneity of multiple sclerosis lesions: implications for the pathogenesis of demyelination. Ann Neurol. (2000) 47:707–17. doi: 10.1002/1531-8249(200006)47:6<707::AID-ANA3>3.0.CO;2-Q
187. Trapp BD, Peterson J, Ransohoff RM, Rudick R, Mork S, Bo L. Axonal transection in the lesions of multiple sclerosis. N Engl J Med. (1998) 338:278–85. doi: 10.1056/NEJM199801293380502
188. Budde MD, Xie M, Cross AH, Song SK. Axial diffusivity is the primary correlate of axonal injury in the experimental autoimmune encephalomyelitis spinal cord: a quantitative pixelwise analysis. J Neurosci. (2009) 29:2805–13. doi: 10.1523/JNEUROSCI.4605-08.2009
Keywords: diffusion MRI, white matter, modeling, microstructure, tissue compartments
Citation: Jelescu IO and Budde MD (2017) Design and Validation of Diffusion MRI Models of White Matter. Front. Phys. 5:61. doi: 10.3389/fphy.2017.00061
Received: 28 September 2017; Accepted: 10 November 2017;
Published: 28 November 2017.
Edited by:
Julien Valette, Commissariat à l'Energie Atomique et aux Energies Alternatives (CEA), FranceReviewed by:
Valerij G. Kiselev, Universitätsklinikum Freiburg, GermanySilvia Capuani, Consiglio Nazionale Delle Ricerche (CNR), Italy
Copyright © 2017 Jelescu and Budde. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Ileana O. Jelescu, aWxlYW5hLmplbGVzY3VAZXBmbC5jaA==
Matthew D. Budde, bWRidWRkZUBtY3cuZWR1
 Ileana O. Jelescu
Ileana O. Jelescu Matthew D. Budde
Matthew D. Budde