The Holographic F Theorem

1. Introduction

In even dimensional quantum field theories, natural candidates for quantifying the number of degrees of freedom are provided by the coefficients of the conformal anomalies of the stress energy tensor at fixed points. The strongest results concerning such a quantification of the degrees of freedom, and the reduction in the number of degrees of freedom along a renormalization group flow, were derived in the famous work of Zamolodchikov [1]. Zamolodchikov demonstrated the existence of a c-quantity in two dimensional unitary quantum field theories; this c-quantity decreases monotonically along a renormalization group flow and coincides with the coefficient of the trace anomaly at fixed points.

Considerable progress has been made in recent years in generalizing Zamolodchikov's work to quantum field theories in four dimensions, most notably the proof by Schwimmer and Komargodski [2] that the a-anomaly coefficient at an infra-red fixed point is always strictly less than the value of the a-anomaly coefficient at the ultra-violet fixed point. The situation in odd dimensions has long been mysterious, however, since the trace of the stress energy tensor automatically vanishes in odd dimensional conformal field theories and thus one needs to propose an alternate measure of the degrees of freedom.

In a three-dimensional quantum field theory, the F quantity is defined in terms of the renormalized partition function of the theory on a three-sphere $Z_{S^3}$ as:

$\begin{array}{cc}F=-\ln Z_{S^3};& (1)\end{array}$

F gives the free energy on the three-sphere. The conjectured F-theorem [3, 4] states that F is positive in a unitary quantum field theory; F is stationary at a fixed point; F_UV ≥ F_IR for UV and IR fixed points and F decreases monotonically along an RG flow. Evidence in favor of the F theorem has been presented in a number of works. In Jafferis et al. [3] it was shown in a number of ${N}=2$ theories that F_IR < F_UV; examples included holographic theories described by AdS₄ × Y₇ M theory solutions in which the partition function is [5]:

$\begin{array}{cc}F=N^{\frac{3}{2}}\sqrt{\frac{2{\pi }^6}{27\text{Vol}(Y_7)}}& (2)\end{array}$

where Vol(Y₇) is the volume of the Sasaki-Einstein manifold Y₇ and N is the number of colors in the dual theory.

Many subsequent papers have provided additional evidence that F_IR < F_UV in holographic and field theory models. For example, Klebanov et al. [4] considered relevant double trace deformations: given an operator Φ in a CFT of dimension Δ₋ such that 1/2 ≤ Δ₋ ≤ 3/2, deforming the CFT by Φ² causes an RG flow to an IR fixed point where Φ has dimension Δ₊ = 3−Δ₋.

The evidence for stationarity and monotonic decrease of the F quantity along an RG flow is somewhat weaker. Arguments for stationarity are based on the fact that F is extremized with respect to the R charges of an IR CFT [6] and (holographically) with respect to the parameters of the Sasaki-Einstein manifold Y₇ [3, 7, 8]. For monotonic decrease, it was shown in Klebanov et al. [4] that the free energy decreases monotonically along weakly relevant flows, while [9] argued that the volume of the compact manifold should increase monotonically along an RG flow in holographic examples, implying monotonic decrease of F. In Freedman and Pufu [10] it was shown that F decreases along certain supersymmetric RG flows of deformations of the ABJM theory.

In a conformal field theory, the partition function on the three sphere is related to the (finite terms) in the entanglement entropy for a disk region in flat space by the Casini-Huerta-Myers map [11]. If the finite contribution to the entanglement entropy of a disk region in the ground state of the CFT is:

$\begin{array}{cc}S=-2\pi ℱ,& (3)\end{array}$

then ${F}$ corresponds precisely to the F quantity, i.e., ${F}$ is conjectured to be positive and to decrease monotonically along an RG flow. The F theorem has hence also been explored using entanglement entropy, see for example [12–14]. Ambiguities in defining the finite contributions can be dealt with by working with the UV finite mutual information [15] or by using renormalized entanglement entropy [16, 17]. There is however evidence that the renormalized entanglement entropy thus defined is not stationary at a fixed point [18].

In this paper we show that the F quantity does not decrease for holographic RG flows associated with deformations by single trace operators of dimension Δ such that 3/2 < Δ < 5/2. Therefore, the strong version of the F theorem, decrease of F under all relevant deformations, is false. Note that in all our examples a weaker version of the F theorem, F_UV ≥ F_IR > 0, is still satisfied.

2. Holographic RG Flows

We begin by discussing holographic realizations of RG flows on curved manifolds. We work in Euclidean signature with a bulk action:

$\begin{array}{cc}{I}_E=-\frac{1}{16\pi G_4}{\displaystyle \int d^4}x\sqrt{g}\left(R-\frac{1}{2}{(\partial \varphi )}^2+V(\varphi )\right),& (4)\end{array}$

where G₄ is the Newton constant, which in a top-down holographic model is related to the number of colors as $1/G_4~N^{3/2}$, as in (2). We consider solutions of the equations of motion such that:

$\begin{array}{cc}d{s}^2=d{w}^2+e^{2{A}(w)}d{s}_{{\Omega }_3}^2& (5)\end{array}$

where Ω₃ is a homogeneous space with Ricci scalar ${R}$ and the scalar field ϕ depends only on the radial coordinate w. We will be interested in the case of a unit radius three sphere for which ${R}=6$. The equations of motion are then given by:

$\begin{array}{cc}\begin{array}{l}\ddot{\varphi }+3\stackrel{.}{{A}}\dot{\varphi }=-V^{\prime }(\varphi );\\ -\frac{ℛ}{6}{e}^{-2{A}}-{\frac{1}{4}\left(\dot{\varphi }\right)}^2=\stackrel{\mathrm{..}}{{A}}.\end{array}& (6)\end{array}$

These equations reduce to the case of flat domain walls when ${R}=0$.

We work perturbatively in the scalar field and assume that the potential has the following analytic expansion in ϕ around an AdS background:

$\begin{array}{cc}V(\varphi )=6-\frac{1}{2}{M}^2{\varphi }^2+\cdots & (7)\end{array}$

In what follows we solve the field equations to quadratic order in ϕ, taking into account the backreaction onto the metric to this order. In anti-de Sitter the warp factor is:

$\begin{array}{cc}{A}(w)\equiv {{A}}_0(w)=\log (\sinh (w)).& (8)\end{array}$

Working to quadratic order in the scalar field, the change in the warp factor is quadratic in the scalar field, and therefore to the order required the scalar field equation is that in AdS, i.e.

$\begin{array}{cc}\ddot{\varphi }+3\coth w\dot{\varphi }=M^2\varphi .& (9)\end{array}$

This equation can be solved exactly (see below) and asymptotically near the conformal boundary. The latter can be expressed as:

$\begin{array}{cc}\begin{array}{l}\varphi =e^{({\Delta }_{+}-3)w}{\varphi }_{(0)}+e^{({\Delta }_{+}-5)w}{\varphi }_{(2)}+\cdots \\ +e^{-{\Delta }_{+}w}{\tilde{\varphi }}_{(0)}+e^{(-{\Delta }_{+}-2)w}{\tilde{\varphi }}_{(2)}+\cdots \end{array}& (10)\end{array}$

where

$\begin{array}{cc}{\varphi }_{(2)}=\frac{3(3-{\Delta }_{+})}{(5-2{\Delta }_{+})}{\varphi }_{(0)}{\tilde{\varphi }}_{(2)}=\frac{3{\Delta }_{+}}{(2{\Delta }_{+}-1)}{\tilde{\varphi }}_{(0)}.& (11)\end{array}$

Here we implicitly assume that Δ₊ is neither 3/2 nor 5/2, since in these cases terms proportional to w arise in the expansion. (These cases can be straightforwardly analyzed but we do not include details in what follows.)

One can then use the other equation of motion to solve for the warp factor up to quadratic order in the scalar field. Letting:

$\begin{array}{cc}{A}={{A}}_0+a& (12)\end{array}$

then

$\begin{array}{cc}\ddot{a}-\frac{2}{{\sinh }^{2}w}a=-\frac{1}{4}{\dot{\varphi }}^2.& (13)\end{array}$

The onshell action is divergent for asymptotically locally AdS solutions, but the divergences may be removed by using the asymptotic solutions of the field equations to regulate the bulk action and adding appropriate covariant counterterms, i.e., the renormalized action [19].

$\begin{array}{cc}{I}_{\text{ren}}=I_E+I_{\text{ct}}& (14)\end{array}$

is finite. The AdS/CFT dictionary implies that the F quantity is calculated from the renormalized action in the limit in which the dual theory is well-described by supergravity.

Working to quadratic order in the scalar field ϕ the required counterterms to render the action finite are [19]:

$\begin{array}{cc}\begin{array}{l}{I}_{\text{ct}}=\frac{1}{8\pi G_4}{\displaystyle \int d^3}x\sqrt{h}(-K+2+\frac{1}{2}{ℛ}_h\\ +\frac{1}{4}(3-{\Delta }_{+}){\varphi }^2+\frac{({\Delta }_{+}-3)}{16(2{\Delta }_{+}-5)}{ℛ}_h{\varphi }^2)\end{array}& (15)\end{array}$

where K is the extrinsic curvature (this is the standard Gibbons-Hawking-York term) and ${{R}}_h$ is the Ricci scalar for the boundary metric h. We define Δ₊ in terms of the mass as:

$\begin{array}{cc}{\Delta }_{+}=\frac{3}{2}+\frac{1}{2}\sqrt{9+4M^2}& (16)\end{array}$

and we assume that $\frac{3}{2}\le {\Delta }_{+}\le 3$. For Δ₊ ≥ 5/2, Δ₊ is the dimension of the operator dual to the scalar field of mass M². In the mass range:

$\begin{array}{cc}-\frac{9}{4}\le M^2\le -\frac{5}{4}& (17)\end{array}$

two quantizations are possible [20]; we will discuss this situation below. In (15) we do not include counterterms which depend on derivatives of the scalar field (see [19]), since the scalar fields under consideration are homogeneous.

Note that the last counterterm in (15) is only required for Δ₊ > 5/2. The corresponding divergence becomes logarithmic at Δ₊ = 5/2 and in this case the value of the renormalized action can be adjusted by finite counterterms, so the F quantity is inherently scheme dependent. Correspondingly F is also scheme dependent for the Δ₋ quantization of the same mass, i.e., Δ₋ = 1/2. No finite counterterms arise for other values of Δ₊ in the range of interest, although working to cubic order in the scalar field finite counterterms would arise at integral values of Δ₊; these can be fixed by requiring supersymmetry [10].

In the mass range −9/4 ≤ M² ≤ −5/4, two quantizations are possible:

$\begin{array}{cc}{\Delta }_{\pm }=\frac{3}{2}\pm \frac{1}{2}\sqrt{9+4M^2}& (18)\end{array}$

with 1/2 ≤ Δ₋ ≤ 3/2 and 3/2 ≤ Δ₊ ≤ 5/2. As discussed in Papadimitriou [21], the evaluation of the renormalized action by adding covariant counterterms is not affected by whether the dual operator has dimension Δ₊ or Δ₋. The difference arises in the identification of the functional that generates correlation functions for the dual operator. For the Δ₊ quantization, the coefficient ϕ₍₀₎ in (10) acts as the source for the dual operator. The renormalized action (14) is a functional of this coefficient and acts as the generating functional for the dual operator.

For the Δ₋ quantization, the renormalized action (14) is still a functional of the coefficient ϕ₍₀₎ in (10) but this coefficient is not the operator source. As discussed in Papadimitriou [21], following [20, 22], the correct generating functional is obtained by a Legendre transformation. Let us define the Legendre transformation as:

$\begin{array}{cc}\tilde{I}[{\varphi }_{(0)},{\psi }_{(0)}]=I_{\text{ren}}[{\varphi }_{(0)}]+{\displaystyle \int d^3}x\sqrt{g_{(0)}}{\varphi }_{(0)}{\psi }_{(0)}& (19)\end{array}$

where g₍₀₎ is the boundary metric. Then extremizing gives:

$\begin{array}{cc}{\tilde{I}}_{\text{ren}}[{\psi }_{(0)}]=\tilde{I}[{\varphi }_{(0)}^{\ast }({\psi }_{(0)}),{\psi }_{(0)}]& (20)\end{array}$

where

$\begin{array}{cc}{\frac{\delta I_{\text{ren}}[{\varphi }_{(0)}]}{\delta {\varphi }_{(0)}}|}_{{\varphi }_{(0)}^{\ast }}+{\psi }_{(0)}=0& (21)\end{array}$

defines ${\varphi }_{(0)}^{*}({\psi }_{(0)})$. Here Ĩ_ren[ψ₍₀₎] is identified as the renormalized generating functional of correlation functions of the operator of dimension Δ₋.

In the case at hand, we work perturbatively in the scalar field and thus the onshell renormalized action necessarily has the form:

$\begin{array}{cc}{I}_{\text{ren}}[{\varphi }_{(0)}]=(I_0+I_2{\varphi }_{(0)}^2+\cdots ),& (22)\end{array}$

where I₀ and I₂ are numerical coefficients. (Recall that ϕ₍₀₎ is homogeneous and therefore does not depend on the sphere coordinates.) The Legendre transformed action is then given by:

$\begin{array}{cc}\tilde{I}[{\varphi }_{(0)},{\Psi }_{(0)}]=(I_0+I_2{\varphi }_{(0)}^2+\cdots )+{\varphi }_{(0)}{\Psi }_{(0)},& (23)\end{array}$

where we denote:

$\begin{array}{cc}{\Psi }_{(0)}\equiv {\displaystyle \int d^3}x\sqrt{g_{(0)}}{\psi }_{(0)}.& (24)\end{array}$

Extremizing, we obtain:

$\begin{array}{cc}2I_2{\varphi }_{(0)}+{\Psi }_{(0)}=0& (25)\end{array}$

and hence

$\begin{array}{cc}{\tilde{I}}_{\text{ren}}[{\Psi }_{(0)}]=I_0-I_2{\varphi }_{(0)}^2+\cdots =I_0-\frac{1}{4I_2}{\Psi }_{(0)}^2+\cdots & (26)\end{array}$

In the Δ₊ quantization, ϕ₍₀₎ acts as the source for the dual operator and therefore (22) gives the free energy to quadratic order in the source. In the Δ₋ quantization, Ψ₍₀₎ acts as the source for the dual operator and (26) gives the free energy to quadratic order in the source. The quadratic terms have different signs in the two quantizations: if I₂ > 0 the free energy on the S³ increases for deformations by the Δ₊ quantization operator and decreases for deformations by the Δ₋ quantization operator, and vice versa. For M² = −9/4, the two quantizations coincide; note however that one needs to treat this case separately, as the above formulae degenerate.

3. Evaluation of Free Energy

Having determined the renormalized free energy functional we now consider exact regular solutions of the field equations, to quadratic order in the scalar field. To the required order we can solve the scalar field equation in the anti-de Sitter background. The scalar field solution may be found analytically in terms of regularized hypergeometric functions ₂${\tilde{F}}_1(a,b,c,z)$ as:

$\begin{array}{cc}\begin{array}{l}\varphi =\frac{{\varphi }_{(0)}{\sinh }^{\Delta }(w)}{2\sqrt{2}\Gamma (3-\Delta )}\Gamma \left(\frac{5}{2}-\Delta \right)\\ [C{(w)}^{3/2}{(C(w)+2)}^{\Delta }\Gamma {(3-\Delta )}_2{\tilde{F}}_1\left(-\frac{1}{2},\frac{3}{2},\frac{5}{2}-\Delta ,-\frac{1}{2}C(w)\right)\\ -C{(w)}^{\Delta }{(C(w)+2)}^{3/2}\Gamma {(\Delta )}_2{\tilde{F}}_1\left(-\frac{1}{2},\frac{3}{2},\Delta -\frac{1}{2};-\frac{1}{2}C(w)\right)]\\ C(w)=\coth w-1,\end{array}& (27)\end{array}$

This solution can conveniently be rewritten as:

$\begin{array}{cc}\begin{array}{l}\varphi =\frac{{\varphi }_{(0)}\Gamma \left(\frac{5}{2}-{\Delta }_{+}\right)}{2\sqrt{2}\Gamma (3-{\Delta }_{+})}{\left(U-1\right)}^{(3-{\Delta }_{+})/2}{\left(U+1\right)}^{{\Delta }_{+}/2}\\ [\Gamma {(3-{\Delta }_{+})}_2{\tilde{F}}_1\left(-\frac{1}{2},\frac{3}{2},\frac{5}{2}-{\Delta }_{+},\frac{1}{2}(1-U)\right)\\ -{\left(\frac{U-1}{U+1}\right)}^{{\Delta }_{+}-\frac{3}{2}}\Gamma {({\Delta }_{+})}_2{\tilde{F}}_1\left(-\frac{1}{2},\frac{3}{2},{\Delta }_{+}-\frac{1}{2},\frac{1}{2}(1-U)\right)]\\ U=\frac{1}{u}=\coth w\end{array}& (28)\end{array}$

where we have imposed regularity throughout the bulk and chosen the overall normalization of the solution to agree with the definition of ϕ₍₀₎ given in (10). Thus, ϕ₍₀₎ is the source for the operator deforming the dual conformal field theory.

We note further that the general solution can be written in terms of associated Legendre functions $P_{\nu }^{\mu }(z)$ and $Q_{\nu }^{\mu }(z)$ as:

$\begin{array}{cc}\varphi =\frac{1}{{\sinh }^{\frac{3}{2}}(w)}\left({\varphi }_1{P}_{\frac{1}{2}}^{\Delta -\frac{3}{2}}(\coth (w))+{\varphi }_2{Q}_{\frac{1}{2}}^{\Delta -\frac{3}{2}}(\coth (w))\right),& (29)\end{array}$

where ϕ₁ and ϕ₂ are computable constants, expressible in terms of ϕ₍₀₎. However, both these functions are complex since coth(w) ≥ 1 and therefore the solution needs to be re-expressed in terms of two manifestly real functions. Standard identities can be used to extend the associated Legendre functions to arguments greater than unity, specifically:

$\begin{array}{cc}{P}_{\nu }^{\mu }(z)=\frac{{(z+1)}^{\mu /2}}{{(z-1)}^{\mu /2}}{}_2{\tilde{F}}_1\left(-\nu ,\nu +1,1-\mu ,\frac{1}{2}(1-z)\right)& (30)\end{array}$

$\begin{array}{cc}\begin{array}{l}{Q}_{\nu }^{\mu }(z)=\frac{\pi }{2}\frac{1}{\sin (\pi \mu )}{e}^{\mu \pi i}[\frac{{(z+1)}^{\mu /2}}{{(z-1)}^{\mu /2}}{}_2{\tilde{F}}_1\left(-\nu ,\nu +1,1-\mu ;\frac{1}{2}(1-z)\right)\\ -\frac{\Gamma (\nu +\mu +1)}{\Gamma (\nu -\mu +1)}\frac{{(z-1)}^{\mu /2}}{{(z+1)}^{\mu /2}}{}_2{\tilde{F}}_1\left(-\nu ,\nu +1,1+\mu ,\frac{1}{2}(1-z)\right)].\end{array}& (31)\end{array}$

Note that the distinct ways of expressing the scalar field solutions are useful for different purposes. The regularity and asymptotic expansions are most easily extracted from (27) and (29) while (28) is most convenient for the subsequent numerical calculations.

As w → 0,

$\begin{array}{cc}\varphi \to {\varphi }_{\text{IR}}\left(1+\frac{1}{5}{M}^2{w}^2+\cdots \right)& (32)\end{array}$

where

$\begin{array}{cc}{\varphi }_{\text{IR}}=\frac{1}{4\sqrt{\pi }}\Gamma (\frac{5}{2}-{\Delta }_{+})\Gamma ({\Delta }_{+})\cos (\pi {\Delta }_{+}){\varphi }_{(0)}& (33)\end{array}$

and consequently the change in the warp factor behaves as:

$\begin{array}{cc}a\to -\frac{M^4}{250}{\varphi }_{\text{IR}}^2{w}^4+\cdots & (34)\end{array}$

as w → 0, i.e., the geometry in the deep interior approaches (Euclidean) AdS₄ in spherical coordinates, and therefore the RG flow ends on an IR fixed point. For such an IR fixed point, the free energy as computed from the renormalized action is:

$\begin{array}{cc}{F}_{IR}=\frac{\pi }{2G_4}\left(1-\frac{1}{12}{M}^2{\varphi }_{\text{IR}}^2\right)& (35)\end{array}$

which clearly satisfies F_IR < F_UV: the free energy for the UV fixed point is given by ϕ_IR = 0.

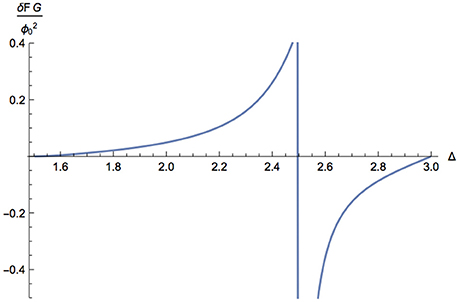
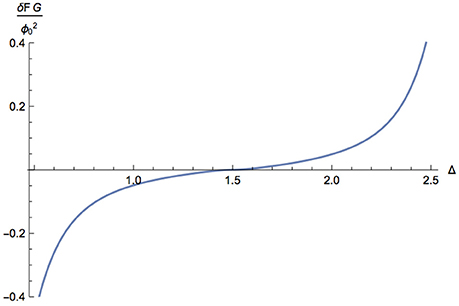
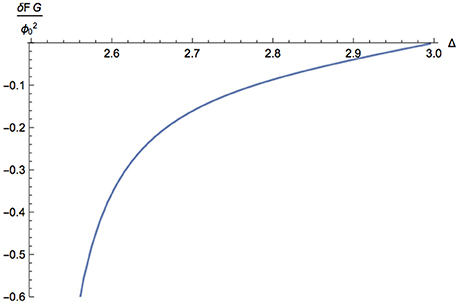
To calculate the free energy for the RG flow, we need to solve numerically for the warp factor and thus for the renormalized onshell action. To carry out the numerics we work with a compactified radial coordinate u = tanhw for all the calculations. Plotted in Figures 1–3 are the changes in the free energy normalized by the scalar source and the Newton constant: we define δF as:

$\begin{array}{cc}\delta F=F({\varphi }_{(0)})-F(0)\equiv F({\varphi }_{(0)})-\frac{\pi }{2G_4},& (36)\end{array}$

where implicitly we use the appropriate source for Δ < 3/2. Note that δF measures the difference between the free energy computed to quadratic order in the source, F(ϕ₍₀₎), and the free energy of the background with no scalar field, F(0). The latter is given by the free energy associated with AdS₄, computed via the renormalized action.

FIGURE 1

Figure 1. The change in the renormalized free energy, normalized by $G_N/{\varphi }_{(0)}^2$, for $\frac{3}{2}<\Delta <3$.

The first figure, Figure 1, shows the free energy computed using the standard Δ₊ quantization of the scalar field, which is applicable for Δ₊ ≥ 3/2. Note that the free energy is ill-defined for Δ = 5/2, as we discussed above, since its value depends on the choice of finite counterterms and hence the renormalization scheme chosen.

In the second figure, Figure 2, we zoom in on the region of 1/2 < Δ < 5/2. For 1/2 < Δ < 3/2, the free energy is computed using the Δ₋ quantization, i.e., by the Legendre transform of the action discussed earlier. In the third figure, Figure 3, we zoom in on the region of 5/2 < Δ < 3, to demonstrate that the change of free energy is indeed zero for Δ = 3. i.e., exactly marginal deformations.

FIGURE 2

Figure 2. The change in the renormalized free energy for $\frac{1}{2}<\Delta <\frac{5}{2}$.

FIGURE 3

Figure 3. The change in the renormalized free energy for $\frac{5}{2}<\Delta <3$.

To summarize the results of our numerical work: the change in the free energy vanishes to quadratic order in the source for Δ = 3/2 and for exactly marginal operators. The change in the free energy is positive for 3/2 < Δ < 5/2, with the corresponding change in the free energy for 1/2 < Δ < 3/2 therefore being negative. The general arguments given above, relating Δ₊ and Δ₋ quantizations, indicated that the change in the free energy would be positive for one of the two quantizations in the mass range where both quantizations are possible. Our explicit numerical results indicate that it is for 3/2 < Δ < 5/2 that the postulated F theorem is violated.

We should note that a related sign change at Δ = 3/2 was found in Berenstein and Miller [23]. This paper calculated one point functions of the deformation operator under relevant deformations, both holographically and using conformal perturbation theory. The sign of this one point function, which is related to the sign of δF found above, indeed changes at Δ = d/2.

4. Conclusions

Working to quadratic order in the operator source, deformations by operators of dimensions 3/2 < Δ < 5/2 lead to increases in the F quantity, although the corresponding IR fixed points still satisfy F_IR < F_UV. Note that we have worked only to quadratic order and changes in the F quantity to higher order in the source would depend on the interactions in the theory.

The F theorem would be satisfied in a holographic theory that contains no operators of dimensions 3/2 < Δ < 5/2, but generically such operators do exist. In particular, it is well-known that in four-dimensional ${N}=8$ gauged supergravity there are 35 Δ₋ = 1 scalar operators and 35 Δ₊ = 2 pseudoscalars corresponding to the 70 scalars with M² = −2, i.e., both quantizations arise [24]. (The pseudoscalar nature of the Δ₊ quantization does not affect the arguments given here.) However, for the supersymmetric RG flows in consistent truncations of ${N}=8$ analyzed in Freedman and Pufu [10] the F quantity does decrease: in this setup supersymmetry does not allow a single real scalar (in the Euclidean) corresponding to a Δ₊ = 2 operator to be switched on. A complete proof of the F theorem would effectively restrict the allowed holographic theories, i.e., it would throw theories such as those considered here into the swampland.

Now let us return to the relationship between the F quantity and the entanglement entropy of a disk entangling region. One can use holographic renormalization techniques to define renormalized entanglement entropy [25]. The renormalized entanglement entropy of disk regions in theories deformed by relevant operators agrees with the behavior of the F quantity found above: F increases for RG flows by operators of dimension 3/2 < Δ < 5/2 (see also [26]).

Our results do not contradict [3, 7, 8]: these works showed that F is extremal within the parameter spaces of putative conformal field theories. In the holographic setups, an AdS₄ factor is assumed and the volume of the compactifying Sasaki-Einstein is extremized. This analysis does not imply that F is decreased under relevant deformations which change the geometry away from AdS₄. The scalar field ϕ and the change in the warp factor a do not decrease monotonically along the flow but this does not in itself contradict the arguments of [9]. From a top-down perspective scalar fields in four-dimensional gauged supergravity theories arise not just from breathing modes of the compact manifold, but also from the four-form flux in eleven dimensions.

In two dimensions one defines the Zamolodchikov c-function c(g_i, μ) in terms of the coupling constants g_i and the energy scale μ. Here implicitly we have defined F as a renormalized quantity, dependent on UV data for coupling constants of the relevant operators. It would be interesting to explore whether one could sharply define an F function with explicit dependence on the energy (i.e., radial) scale holographically. One natural way to do this would be to rewrite the source ϕ₍₀₎ in terms of the bulk scalar field ϕ(w), and interpret w as the energy scale.

Finally, there has been considerable recent interest in how much supersymmetry is required to determine uniquely partition functions on even-dimensional spheres [27]. In three dimensions, an analogous question arises at quadratic order in the source for conformal field theories deformed by operators of dimensions 1/2 and 5/2.

Author Contributions

The authors of this paper contributed equally in all aspects of the preparation of this manuscript.

Funding

This work was supported by the Science and Technology Facilities Council. This project has received funding from the European Union Horizon 2020 research and innovation programme under the Marie Sklodowska-Curie grant agreement No. 674896.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The reviewer TR and handling Editor declared their shared affiliation.

References

1. Zamolodchikov AB. Irreversibility of the flux of the renormalization group in a 2D field theory. JETP Lett. (1986) 43:730–2.

Google Scholar

2. Komargodski Z, Schwimmer A. On renormalization group flows in four dimensions. J High Energy Phys. (2011) 1112:099. doi: 10.1007/JHEP12(2011)099

CrossRef Full Text | Google Scholar

3. Jafferis DL, Klebanov IR, Pufu SS, Safdi BR. Towards the F-theorem: N=2 field theories on the three-sphere. J High Energy Phys. (2011) 06:102. doi: 10.1007/JHEP06(2011)102

CrossRef Full Text | Google Scholar

4. Klebanov IR, Pufu SS, Safdi BR. F-theorem without supersymmetry. J High Energy Phys. (2011) 10:038. doi: 10.1007/JHEP10(2011)038

CrossRef Full Text | Google Scholar

5. Herzog CP, Klebanov IR, Pufu SS, Tesileanu T. Multi-matrix models and tri-sasaki einstein spaces. Phys Rev D (2011) 83:046001. doi: 10.1103/PhysRevD.83.046001

CrossRef Full Text | Google Scholar

6. Jafferis DL. The exact superconformal R-symmetry extremizes Z. J High Energy Phys. (2012) 1205:159. doi: 10.1007/JHEP05(2012)159

CrossRef Full Text | Google Scholar

7. Martelli D, Sparks J. The large N limit of quiver matrix models and Sasaki-Einstein manifolds. Phys Rev D (2011) 84:046008. doi: 10.1103/PhysRevD.84.046008

CrossRef Full Text | Google Scholar

8. Cheon S, Gang D, Kim S, Park J. Refined test of AdS4/CFT3 correspondence for N=2,3 theories. J High Energy Phys. (2011) 1105:027. doi: 10.1007/JHEP05(2011)027

CrossRef Full Text | Google Scholar

9. Gulotta DR, Herzog CP, Pufu SS. From necklace quivers to the F-theorem, operator counting, and T(U(N)). J High Energy Phys. (2011) 1112:077. doi: 10.1007/JHEP12(2011)077

CrossRef Full Text | Google Scholar

10. Freedman DZ, Pufu SS., The holography of F-maximization. J High Energy Phys. (2014) 1403:135. doi: 10.1007/JHEP03(2014)135

CrossRef Full Text | Google Scholar

11. Casini H, Huerta M, Myers RC. Towards a derivation of holographic entanglement entropy. J High Energy Phys. (2011) 05:036. doi: 10.1007/JHEP05(2011)036

CrossRef Full Text | Google Scholar

12. Klebanov IR, Pufu SS, Sachdev S, and Safdi BR. Entanglement entropy of 3-d conformal gauge theories with many flavors. J High Energy Phys. (2012) 05:036. doi: 10.1007/JHEP05(2012)036

CrossRef Full Text | Google Scholar

13. Casini H, Huerta M. On the RG running of the entanglement entropy of a circle. Phys Rev. (2012) D85:125016. doi: 10.1103/PhysRevD.85.125016

CrossRef Full Text

14. Klebanov IR, Nishioka T, Pufu SS, Safdi BR. On shape dependence and RG flow of entanglement wntropy. J High Energy Phys. (2012) 07:001. doi: 10.1007/JHEP07(2012)001

CrossRef Full Text

15. Casini H, Huerta M, Myers RC, and Yale A. Mutual information and the F-theorem. J High Energy Phys. (2015) 1510:003. doi: 10.1007/JHEP10(2015)003

CrossRef Full Text | Google Scholar

16. Liu H, Mezei M. A refinement of entanglement entropy and the number of degrees of freedom. J High Energy Phys. (2013) 04:162. doi: 10.1007/JHEP04(2013)162

CrossRef Full Text | Google Scholar

17. Liu H, Mezei M. Probing renormalization group flows using entanglement entropy. J High Energy Phys. (2014) 01:098. doi: 10.1007/JHEP01(2014)098

CrossRef Full Text | Google Scholar

18. Klebanov IR, Nishioka T, Pufu SS, Safdi BR. Is renormalized entanglement entropy stationary at RG fixed points?. J High Energy Phys. (2012) 10:058. doi: 10.1007/JHEP10(2012)058

CrossRef Full Text | Google Scholar

19. de Haro S, Skenderis K, Solodukhin SN. Holographic reconstruction of spacetime and renormalization in the AdS/CFT correspondence. Commun Math Phys. (2001) 217:595–622. doi: 10.1007/s002200100381

CrossRef Full Text | Google Scholar

20. Klebanov IR, Witten E. AdS/CFT correspondence and symmetry breaking. Nucl Phys. (1999) B556:89–114. doi: 10.1016/S0550-3213(99)00387-9

CrossRef Full Text | Google Scholar

21. Papadimitriou I. Non-supersymmetric membrane flows from fake supergravity and multi-trace deformations. J High Energy Phys. (2007) 02:008. doi: 10.1088/1126-6708/2007/02/008

CrossRef Full Text | Google Scholar

22. Witten E. multitrace operators, boundary conditions, and AdS / CFT correspondence. arXiv:hep-th/0112258.

23. Berenstein D, Miller A. Conformal perturbation theory, dimensional regularization, and AdS/CFT correspondence. Phys Rev. D (2014) 90:086011. doi: 10.1103/PhysRevD.90.086011

CrossRef Full Text | Google Scholar

24. Hawking SW. The boundary conditions for gauged supergravity. Phys Lett. B (1983) 126:175. doi: 10.1016/0370-2693(83)90585-3

CrossRef Full Text | Google Scholar

25. Taylor M, Woodhead W. Renormalized entanglement entropy. J High Energy Phys. (2016) 1608:165. doi: 10.1007/JHEP08(2016)165

CrossRef Full Text | Google Scholar

26. Nishioka T. Relevant perturbation of entanglement entropy and stationarity. Phys Rev D (2014) 90:045006. doi: 10.1103/PhysRevD.90.045006

CrossRef Full Text | Google Scholar

27. Gomis J, Hsin PS, Komargodski Z, Schwimmer A, Seiberg N, Theisen S. Anomalies, conformal manifolds, and spheres. J High Energy Phys. (2016) 1603:022. doi: 10.1007/JHEP03(2016)022

CrossRef Full Text | Google Scholar