- School of Mathematical Sciences, University of Electronic Science and Technology of China, Chengdu, China
The phenomenon of asset heterogeneity is widespread in human society. However, it is unclear what roles heterogeneous assets play in the evolution of cooperation of the collective-risk society. In this paper, we thus introduce asset heterogeneity into a threshold public goods game with collective-risk, and we divide the population into the rich and the poor according to individual assets. We show that asset heterogeneity hinders public cooperation no matter whether the temptation to defect is high or low. We find that cooperation collapses in the conditions of low risk, the high gap between the rich and the poor, and high threshold. Besides, the increment of individual assets can significantly enhance the level of public cooperation even the conditions for the evolution of cooperation are strongly harsh. Our work is instructive to a better understanding of the emergence of cooperation in the risky society with heterogeneous assets.
1. Introduction
The emergence and maintenance of cooperative behavior is fundamental for a society to thrive [1–17]. However, cooperation is often threatened by selfish individuals who only concern the short-time interests [18–20]. Not surprisingly, if all individuals' goal is to maximize their own fitness regardless of the consequences which might have for the whole population, then there will be a dilemma of cooperation in our society [21–28]. One typical dilemma underlying the tragedy of commons is described by the public goods game (PGG) [29–35]. In the PGG, an individual will obtain a higher payoff by contributing nothing, no matter what the other players do. Therefore, rational players have no incentive to contribute, instead they choose to free ride on the benefits produced by others. Although the PGG illustrates that defection is the evolutionary stable strategy and cooperators are prone to be exploited, abundant examples of altruistic behavior exist in animal and human society [36–39].
In order to solve this inconsistency, the PGG model has been extended by adding the risk of a collective failure to ensure the emergence of cooperative behavior [40–44]. Besides, several mechanisms have been proposed in the past decades for supporting the emergence of public cooperation [45–65].
However, these mentioned works assumed that all individuals have been treated as equivalent in all respects, in sharp contrast with real-life situations, in which diversity is ubiquitous. Indeed, our modern societies are grounded in great diversity, in which some individuals play radically different roles depending on their social positions [66–79]. Until recently, such heterogeneity has attracted considerable attention. For example, one research assumed that resource heterogeneity may enable cooperators to spread and persist if the temptation to defect is not too large [80]. Some other researches assumed that players may participant in PGG with different wealth distributions [70, 81, 82]. More specifically, Wang et al. [70] showed that participants with lower initial wealth may choose to cooperate only if all the rich are cooperators. Subsequently, Vasconcelos et al. [82] studied the evolution of cooperation in two different scenarios, namely, with wealth inequality and without wealth inequality, and showed that the former leads to more global cooperation than the latter.
Interestingly, previous researches involving wealth inequality always consider that individuals have been provided with dichotomic initial wealth before participating in the PGG [32, 70, 82]. Indeed in the real world, acquired wealth can only be regarded as a part of personal assets, such as the wage earnings. However, the implications of heterogeneous assets for cooperation have so far remained unexplored. Since uneven distributions of personal assets are ubiquitous, it remains unclear how evolutionary stable levels of cooperation are influenced by asset heterogeneity.
In this study, we thus introduce asset heterogeneity in a threshold public goods game (TPGG) with collective risk to investigate how cooperation evolves. Specifically, we first explore the impact of asset heterogeneity on social cooperation in the conditions of low and high temptation to defect, and find that asset heterogeneity can hinder cooperation no matter whether the temptation to defect is high or low. Then we study the role of increased asset values in social cooperation at the same asset heterogeneity level, and observe that the gradual increase of assets significantly promotes the emergence of cooperative behavior. Finally, we verify how social cooperation depends on other important parameters, such as risk, threshold, and the proportion of the poor.
2. Model and Method
We consider the collective-risk dilemma game in a well-mixed population. We divide the individuals into the poor and the rich, where the fraction of the poor in the population is p. We assume that each rich individual has an initial asset ar and each poor individual has an initial asset ap(ar > ap). Each individual y either pays a cost c as a cooperator with strategy sy = 1 or pays nothing as a defector with strategy sy = 0. Denote the proportion of rich cooperators, poor cooperators, rich defectors, and poor defectors as xr, xp, yr, and yp, respectively. Then xr + yr = 1 − p and xp + yp = p. The collective target will be reached if the total amount of individuals who choose to contribute to the common pool reaches the threshold T. Thus each individual can gain the benefit b, such that the payoff is py = b − csy. However, if the collective target is not reached, all the individuals within the group lose their investment and the assets with probability r. Accordingly, the payoff of individual y with strategy Sy in group having i cooperators can be written as:
where θ(u) = 0 if u < 0 and θ(u) = 1 otherwise. Besides, φ = 1 denotes that the participant is rich, and φ = 0 indicates he is poor.
We further apply a replicator system for the dynamic analysis, based on preferentially imitating strategies of the more successful individuals [83–86]. Unless otherwise specified, problem formulation and modeling are presented in Supplementary Material S1. Results are proved analytically in Supplementary Materials S2, S3.
3. Results
We begin by showing the stationary distribution and the gradient of selection for different parameters of asset heterogeneity ap/ar and of asset ar. As shown in Figure 1, for low ar (for example, ar = 2), when the gap between the rich and the poor is relatively large, there are nine fixed points but only two are stable (Figure 1A), and the stability analysis of equilibria can be found in Supplementary Material S3.2.2(9). We find that the basin of attraction of the stable equilibrium indicating that most of the poor and all the rich are cooperators, is larger than that of another stable point denoting full defection. As ap/ar increases, the higher location stable fixed point moves toward full cooperation and the basin of attraction of full defection rapidly shrinks closely to zero (see Figures 1A–C). For intermediate ar (for example, ar = 10), we find that the tendency of individuals to choose defection shrinks as the gap between the rich and the poor shrinks (see Figures 1D–F). For even larger ar (for example, ar = 50), individuals no matter whether they are the rich or the poor do have a higher expected loss than the cost of cooperation (Figures 1G–I). Particularly, there are very few individuals who choose to defect when the gap between the rich and the poor is not obvious (Figure 1I), and the specific theoretical analysis can be seen in Supplementary Material S3.2.2(10).
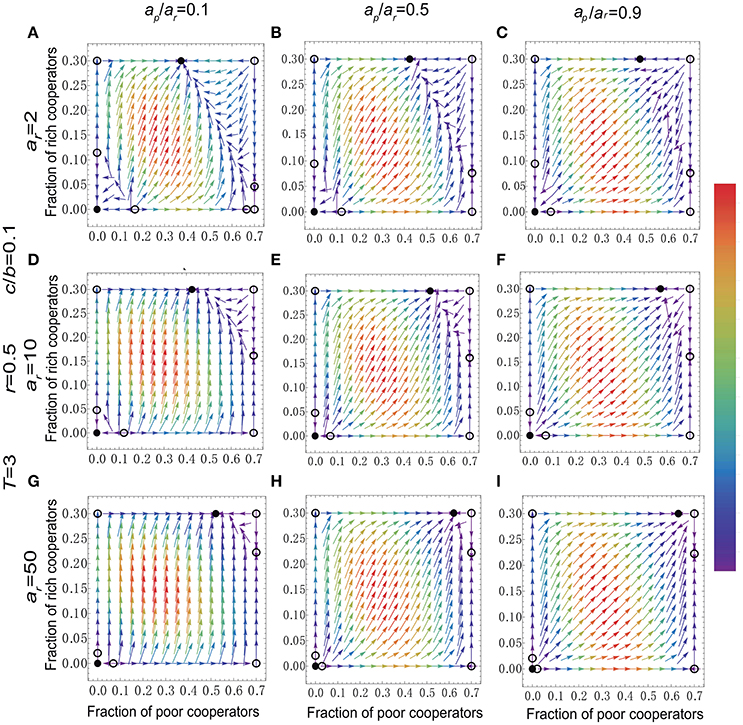
Figure 1. (Color online) Stationary fraction of cooperators and gradient of selection for different levels of asset heterogeneity ap/ar and of assets (A–I). In each panel, open and filled circles denote unstable and stable fixed points, respectively. The curved arrows show the so-called gradient of selection, which provides the most likely direction of evolution. For each arrow, we use a continuous color bar associated with the likelihood of such a transition (red lines denote the highest speed of transition while purple lines represent the lowest speed of transition). The initial assets for the rich and the poor individuals are (A) ar = 2 and ap = 0.2; (B) ar = 2 and ap = 1; (C) ar = 2 and ap = 1.8; (D) ar = 10 and ap = 1; (E) ar = 10 and ap = 5; (F) ar = 10 and ap = 9; (G) ar = 50 and ap = 5; (H) ar = 50 and ap = 25; (I) ar = 50 and ap = 45. Other parameters values are N = 6, T = 3, r = 0.5, p = 0.7, and c/b = 0.1.
Then we explore the effect of asset heterogeneity on cooperation when the temptation to defect is high. In Figure 2, we find that the main conclusions in Figure 1 are not changed. Concretely, the growth of ap/ar can promote the poor to contribute to the common pool even personal assets are significantly low. Besides, the proportion of cooperators increases with personal assets, regardless of whether the gap between the rich and the poor is high or low. But, more importantly, the inhibitory effect of asset heterogeneity on cooperative behavior still exists.
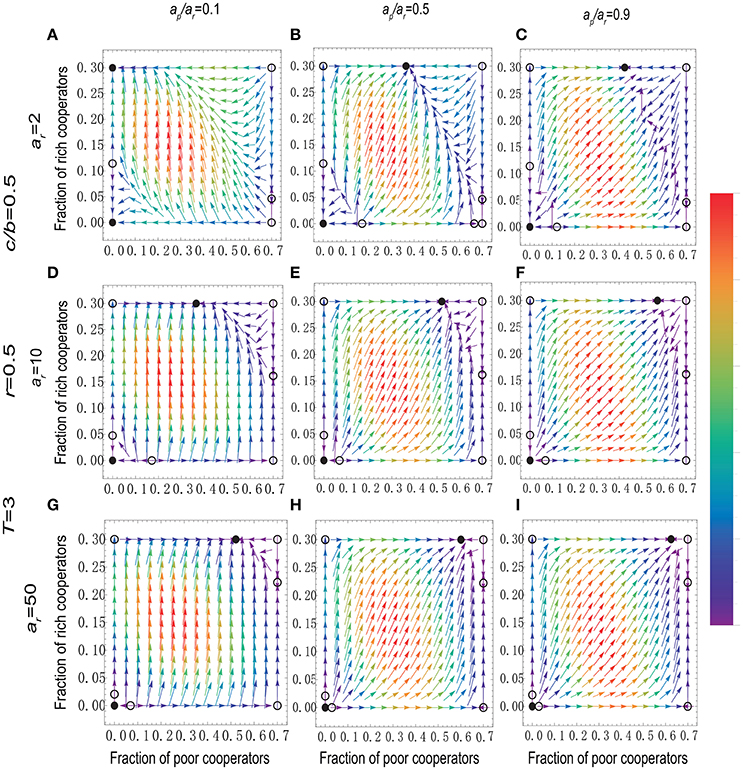
Figure 2. (Color online) Stationary fraction of cooperators and gradient of selection for different values of ap/ar and ar when the temptation to defect is high (A–I). The initial assets for the rich and the poor individuals are (A) ar = 2 and ap = 0.2; (B) ar = 2 and ap = 1; (C) ar = 2 and ap = 1.8; (D) ar = 10 and ap = 1; (E) ar = 10 and ap = 5; (F) ar = 10 and ap = 9; (G) ar = 50 and ap = 5; (H) ar = 50 and ap = 25; (I) ar = 50 and ap = 45; Other parameters values are N = 6, T = 3, r = 0.5, p = 0.7, and c/b = 0.5.
In what follows, we present that public cooperation can be destroyed in the conditions of high gap between the rich and the poor and a relatively high threshold T at a low r value. From Figure 3 we can see there is only one stable point which represents full defection (more detailed analysis of equilibria is presented in Supplementary Materials S2, S3.2.1(3)). Indeed, in this case, low risk causes individuals to worry less about losing all their assets when the target is not reached. Besides, the high gap between the rich and the poor makes the poor reluctant to contribute. Not only that, the rich will be also no longer willing to cooperate if they need to complete a relatively high target.
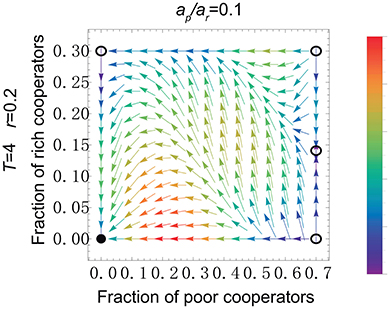
Figure 3. (Color online) Stationary fraction of cooperators and gradient of selection for low values of risk r and asset heterogeneity ap/ar, together with a relatively high threshold T. And the initial assets for the rich and the poor individuals are ar = 2 and ap = 0.2. Other parameters: N = 6, T = 4, p = 0.7, r = 0.2, and c/b = 0.1.
In Figure 3 we mainly study the effects of relatively high threshold value on cooperation in the specific conditions. However, it remains of interest to show how different combinations of threshold and asset heterogeneity affect the stationary distribution. As shown in Figure 4, for low value of T (top row), we can see that the system can converge to the state where all the rich and nearly half of the poor choose to contribute when the gap between the rich and the poor is large (Figure 4A), and for more details see Supplementary Materials S2, S3.1(8). What's more, we find that the proportion of the poor cooperators increases with ap/ar (see Figures 4A–C). When T takes an intermediate value (second row), the basin of attraction of full defection state increases with increasing T. Specially, when T is sufficiently large (third row), for low ap/ar, there are three stable fixed points, and the newly added one located at the top left represents that all the rich are cooperators but the poor cooperators cannot survive (see Figure 4G and Supplementary Material S3.2.1(9)). But this stable equilibrium will disappear when we increase the value of ap/ar.
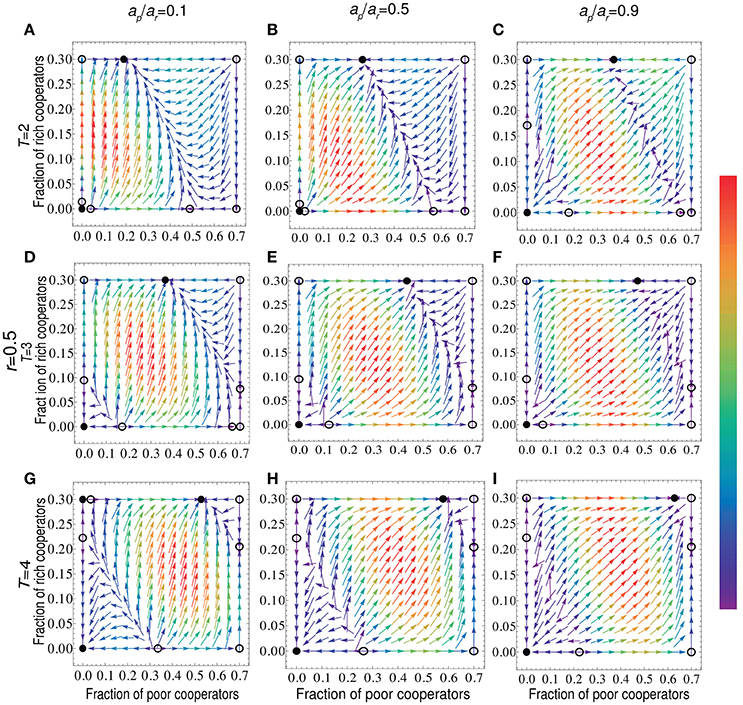
Figure 4. (Color online) Stationary fraction of cooperators and gradient of selection for different values of ap/ar and T. For r = 0.5, the threshold values are T = 2 (A–C), T = 3 (D–F), and T = 4 (G–I). The initial asset for the rich is 2, while the initial asset for the poor is respectively set to 0.2 (left column), 1 (middle column), and 1.8 (right column). Other parameters are p = 0.7, N = 6, and c/b = 0.1.
Furthermore, we investigate how risk values influence the stationary fraction of cooperators at an intermediate threshold value, as shown in Figure 5. We find that for a relatively small ap/ar (for example, ap/ar = 0.1), the poor cooperators cannot survive when r is low (see Figure 5A and Supplementary Material S3.2.2(3)). In fact, the expected loss for the poor is less than the cost of cooperation. This adverse situation will be reversed if we enhance the value of risk r (see Figure 5D and Supplementary Material S3.2.2(9)). More specifically, the growth of the risk leads to the higher location stable point moving toward full cooperation (see Figure 5G and Supplementary Material S3.2.2(10)). Besides, the effect of asset heterogeneity on cooperation is consistent with our above conclusion, namely, narrowing the gap between the rich and the poor can promote public cooperation (see Figures 5G–I).
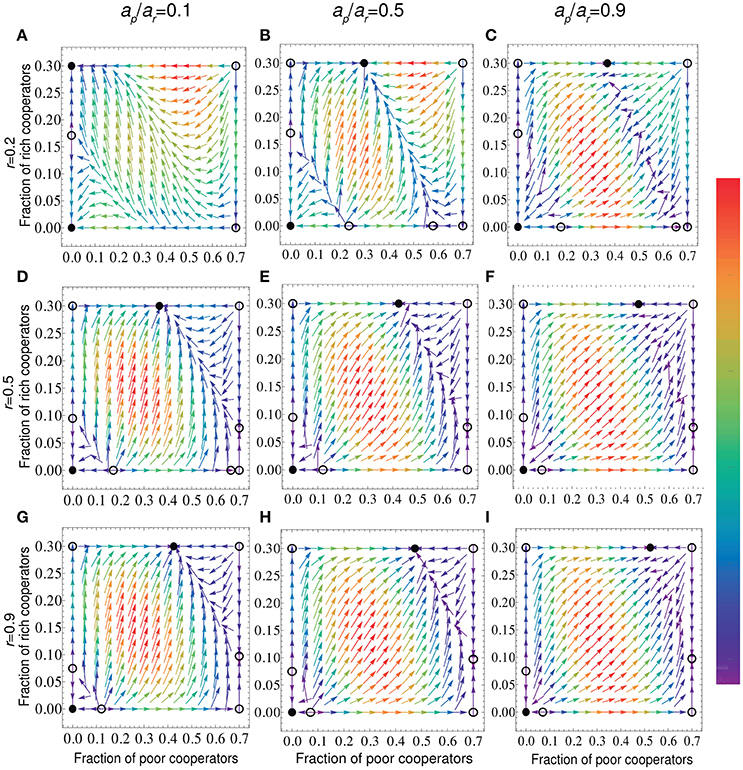
Figure 5. (Color online) Stationary fraction of cooperators and gradient of selection for different values of risk r and the asset ratio of the poor and the rich ap/ar (A–I). And the initial assets for the rich and the poor are respectively ar = 2, ap = 0.2, 1, 1.8 corresponding to ap/ar = 0.1, 0.5, 0.9. Other parameters: N = 6, T = 3, p = 0.7, and c/b = 0.1.
In order to study how the fraction of cooperators depends on the proportion of the poor p, we show the stationary distribution of cooperators as a function of the proportion of the poor p at r = 0.5 and T = 3 for three different values of ap/ar in Figure 6. For a low p (top row), all the poor will choose to free ride even the gap between the rich and the poor is significantly small (see Figures 6A–C). Besides, it is obvious that not all the rich are enthusiastic to contribute, which means that there exist free-riders among the rich if they constitute the vast majority of the group. For an intermediate value of p (second row), the poor cooperators can survive, and beyond that, as ap/ar increases, the proportion of the poor cooperators increases as well [more details can be found in Supplementary Material S3.1(10)]. For much larger p (third row), we can find that the stable point in the upper left corner will disappear when ap/ar is significantly high [see Figures 6G–I and Supplementary Material S3.2.2(6) and (8)].
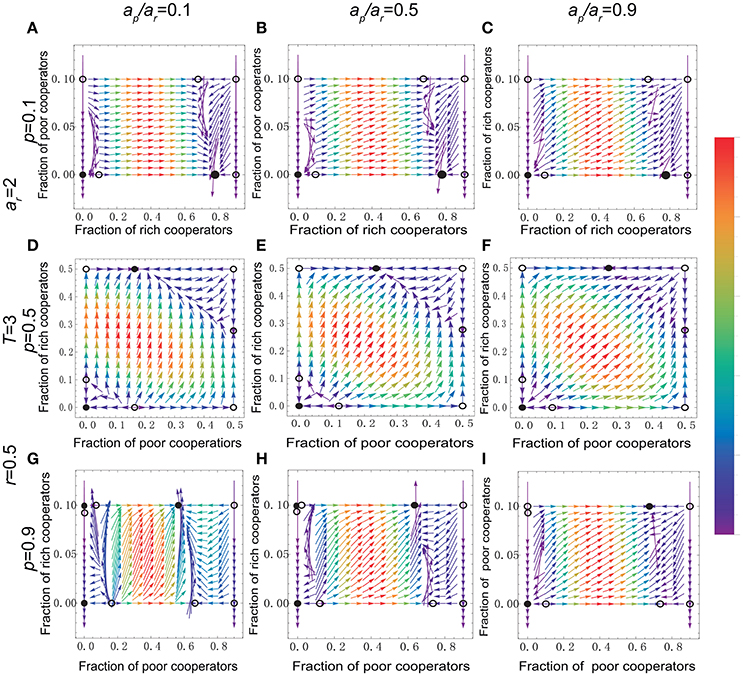
Figure 6. (Color online) Stationary fraction of cooperators and gradient of selection for different values of ap/ar and different proportion of the poor p. The proportions of the poor are respectively p = 0.1 (A–C), p = 0.5 (D–F), and p = 0.9 (G–I). And the initial assets for the rich and the poor individuals are respectively ar = 2, ap = 0.2, 1, 1.8 corresponding to ap/ar = 0.1, 0.5, 0.9. Other parameters: N = 6, T = 3, r = 0.5, and c/b = 0.1.
As also shown in Figure 6, the proportion of the poor p acts an important factor in supporting cooperation. More specifically, when p is particularly small, the change of asset heterogeneity will not have any effect on cooperation. When the proportions of the poor and the rich in the group are the same, then the poor cooperators can survive. At the same time, the region of attraction of full defection has a slight expansion in comparison with a smaller p. As p continues to increase, the poor account for 90 percent of the population. Then the contributions from the rich are far from meeting the target. In order to prevent their assets from losing, the majority of the poor will contribute to the common pool. Besides, narrowing the gap between the rich and the poor can effectively reduce the occurrence of defection as long as the proportion of the poor is not too small.
4. Discussion
We have introduced asset heterogeneity in the collective-risk social dilemma game, and intensively studied its effects on the evolution of public cooperation. We have been motivated by the fact that an uneven distribution of personal assets is surprisingly common in human societies, as well as by the fact that recent research on a similar variant of the collective-risk social dilemma game in a well-mixed population has shown that heterogeneous wealth distributions can affect public cooperation [70]. By considering personal asset rather than wealth, we mainly investigate the effects of asset heterogeneity on cooperation. Our research reveals that asset heterogeneity hinders cooperation no matter whether the temptation to defect is high or low. In addition, four important parameters have been considered in our work, namely, personal assets, threshold, risk, and the proportion of the poor. Specifically, we have shown that the increment of personal assets and risk can both significantly promote social cooperation [43, 44]. Furthermore, the cooperation level increases with the growth of the poor proportion. But a small number of the rich will no longer enthusiastic to contribute when the rich make up a large proportion of the population. Our model also shows an interesting phenomenon: an increase in threshold can contribute to the increase of poor cooperators. However, in some special conditions, a higher threshold can destroy cooperation.
Temptation to defect has been seen as a key factor for exploring the effect of heterogeneity on cooperation in recent years [80, 87, 88]. Kun and Dieckmann [80] have revealed that resource heterogeneity leads to decreased level of cooperation once when the temptation to defect is significantly lowered, otherwise, heterogeneity facilitates the maintenance of cooperation. Unlike previous study, however, our model introduces threshold and the risk of collective failure into the public goods game, and shows that asset heterogeneity can hinder cooperation no matter whether the temptation to defect is high or low (see Figures 1, 2).
Besides, it is worth noting that the impacts of the increment of the threshold value on public cooperation are two-sided. On the one hand, the growth of the threshold enlarges the region of attraction of full defection. On the other hand, it enhances the proportion of poor cooperators (see Figure 4). In addition, social cooperation will collapse at low risk, high poverty gap, and high threshold (see Figure 3). Recently, the effects of the threshold value have been studied theoretically and experimentally [72, 82, 89]. Vasconcelos et al. [82], for instance, verified that threshold uncertainty has a disruptive effect on cooperation when all individuals in the group are equivalent, but they neglected the presence of wealth inequality. Our model proves that, in the specific conditions, a larger target value will destroy cooperation in a risky society with heterogeneous assets.
As we said earlier, our model is inspired partly by the realistic situation, in which it is relatively straightforward to come up with examples where our model could apply. One widely considered example is the problem of climate change. The Paris climate agreement aims at holding global warming to well below 2°C and to “pursue efforts” to limit it to 1.5°C [90]. To accomplish this, countries, no matter whether developed countries or developing countries, have submitted national plans that spell out their intentions for addressing the climate change challenge. Nevertheless, targets and actions for reducing greenhouse gas (GHG) emissions are core components [91, 92]. Therefore, it is of greatest importance for countries to set a measurable emission reduction target. Besides, the action by all countries is effective in averting climate catastrophes, thus it is also a challenge for policy makers to enhance the level of cooperation among different countries. Our research may contribute to a better understanding of the emergence of cooperative behavior in risk society with heterogeneous assets, and thus may provide some insights to how to solve the climate change problem in the realistic world including developed and developing countries.
Author Contributions
LL performed the research. LL and XC designed the research and wrote the paper.
Funding
This research was supported by the National Natural Science Foundation of China (Grants No. 61503062).
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2017.00067/full#supplementary-material
References
1. Chen X, Wang L. Promotion of cooperation induced by appropriate payoff aspirations in a small-world networked game. Physi Rev E. (2008) 77:017103. doi: 10.1103/PhysRevE.77.017103
2. Perc M, Szolnoki A. Coevolutionary games–a mini review. BioSystems (2010) 99:109–25. doi: 10.1016/j.biosystems.2009.10.003
3. Fowler JH, Christakis NA. Cooperative behavior cascades in human social networks. Proc Natl Acad Sci USA. (2010) 107:5334–8. doi: 10.1073/pnas.0913149107
4. Wu B, Altrock PM, Wang L, Traulsen A. Universality of weak selection. Phys Rev E. (2010) 82:046106. doi: 10.1103/PhysRevE.82.046106
5. Wu B, Zhou D, Fu F, Luo Q, Wang L, Traulsen A. Evolution of cooperation on stochastic dynamical networks. PLoS ONE (2010) 5:e11187. doi: 10.1371/journal.pone.0011187
7. Fu F, Nowak MA, Hauert C. Invasion and expansion of cooperators in lattice populations: Prisoner's dilemma vs. snowdrift games. J Theor Biol. (2010) 266:358–66. doi: 10.1016/j.jtbi.2010.06.042
8. Wang J, Wu B, Ho DWC, Wang L. Evolution of cooperation in multilevel public goods games with community structures. EPL (2011) 93:650–67. doi: 10.1209/0295-5075/93/58001
9. Cong R, Wu B, Qiu Y, Wang L. Evolution of cooperation driven by reputation-based migration. PLoS ONE (2012) 7:e35776. doi: 10.1371/journal.pone.0035776
10. Szolnoki A, Perc M. Conditional strategies and the evolution of cooperation in spatial public goods games. Soc Sci Electron Publ. (2012) 85(2 Pt 2):026104. doi: 10.1103/PhysRevE.85.026104
11. Szolnoki A, Perc M. Information sharing promotes prosocial behaviour. New J Phys. (2013) 15:1–5. doi: 10.1088/1367-2630/15/5/053010
12. Wu T, Fu F, Dou P, Wang L. Social influence promotes cooperation in the public goods game. Phys A. (2014) 413:86–93. doi: 10.1016/j.physa.2014.06.040
13. Chen X, Tatsuya S, Matja P. Evolution of public cooperation in a monitored society with implicated punishment and within-group enforcement. Sci Rep. (2015) 5:17050. doi: 10.1038/srep17050
14. Szolnoki A, Perc M. Competition of tolerant strategies in the spatial public goods game. New J Phys. (2016) 18:083021. doi: 10.1088/1367-2630/18/8/083021
15. Wang Z, Bauch CT, Bhattacharyya S, DOnofrio A, Manfredi P, Perc M, et al. Statistical physics of vaccination. Phys Rep. (2016) 664:1–113. doi: 10.1016/j.physrep.2016.10.006
16. Cong R, Li K, Wang L, Zhao Q. Cooperation induced by wise incentive allocation in spontaneous institution. EPL (2016) 115:38002. doi: 10.1209/0295-5075/115/38002
17. Perc M, Jordan JJ, Rand DG, Wang Z, Boccaletti S, Szolnoki A. Statistical physics of human cooperation. Phys Rep. (2017) 687:1–51. doi: 10.1016/j.physrep.2017.05.004
18. Porter ME. From competitive advantage to corporate strategy. Harv Bus Rev (1989) 5:43–59. doi: 10.1007/978-1-349-20317-8_17
19. Fischbacher U, Gächter S, Fehr E. Are people conditionally cooperative? Evidence from a public goods experiment. Econ Lett. (2001) 71:397–404. doi: 10.1016/S0165-1765(01)00394-9
20. Battiston F, Perc M, Latora V. Determinants of public cooperation in multiplex networks. New J Phys. (2017) 19:073017. doi: 10.1088/1367-2630/aa6ea1
21. Dawes RM. Social dilemmas. Annu Rev Psychol. (1980) 31:169–93. doi: 10.1146/annurev.ps.31.020180.001125
22. Kollock P. Social dilemmas: the anatomy of cooperation. Sociology (1998) 24:183–214. doi: 10.1146/annurev.soc.24.1.183
23. Fu F, Chen X, Liu L, Long W. Social dilemmas in an online social network: the structure and evolution of cooperation. Phys Lett A. (2007) 371:58–64. doi: 10.1016/j.physleta.2007.05.116
24. Szolnoki A, Perc M. Resolving social dilemmas on evolving random networks. EPL (2009) 86:30007. doi: 10.1209/0295-5075/86/30007
25. Szolnoki A, Chen X. Cooperation driven by success-driven group formation. Phys Rev E. (2016) 94:042311. doi: 10.1103/PhysRevE.94.042311
26. Perc M. Phase transitions in models of human cooperation. Phys Lett A. (2016) 380:2803–8. doi: 10.1016/j.physleta.2016.06.017
27. Li K, Szolnoki A, Cong R, Wang L. The coevolution of overconfidence and bluffing in the resource competition game. Sci Rep. (2016) 6:21104. doi: 10.1038/srep21104
28. Wang Z, Jusup M, Wang RW, Shi L, Iwasa Y, Moreno Y, et al. Onymity promotes cooperation in social dilemma experiments. Sci Adv. (2017) 3:e1601444. doi: 10.1126/sciadv.1601444
29. Hardin G. The tragedy of the commons. Science (1968) 162:1243–8. doi: 10.1126/science.162.3859.1243
30. Field BC. Governing the commons: the evolution of institutions for collective action by elinor ostrom. Am Polit Sci Assoc. (1990) 8:569–9.
31. Wang Z, Murks A, Du WB, Rong ZH, Perc M. Coveting thy neighbors fitness as a means to resolve social dilemmas. J Theor Biol. (2011) 277:19–26. doi: 10.1016/j.jtbi.2011.02.016
32. Tanimoto J. Fundamentals of Evolutionary Game Theory and its Applications. Tokyo: Springer (2015).
33. Wang Z, Kokubo S, Jusup M, Tanimoto J. Universal scaling for the dilemma strength in evolutionary games. Phys Life Rev. (2015) 14:1–30. doi: 10.1016/j.plrev.2015.04.033
34. Du J, Wu B, Wang L. Aspiration dynamics and the sustainability of resources in the public goods dilemma. Phys Lett A. (2016) 380:1432–6. doi: 10.1016/j.physleta.2016.02.039
35. Perc M. High-performance parallel computing in the classroom using the public goods game as an example. Eur J Phys. (2017) 38:045801. doi: 10.1088/1361-6404/aa6a0e
37. Chase ID. Cooperative and noncooperative behavior in animals. Am Nat. (1980) 115:827–57. doi: 10.1086/283603
38. Gintis H, Bowles S, Boyd R, Fehr E. Explaining altruistic behavior in humans. Evol Hum Behav. (2003) 24:153–72. doi: 10.1016/S1090-5138(02)00157-5
39. Fehr E, Fischbacher U. The nature of human altruism. Nature (2003) 425:785–91. doi: 10.1038/nature02043
40. Wang J, Fu F, Wu T, Wang L. Emergence of social cooperation in threshold public goods games with collective risk. Phys Rev E. (2009) 80:016101. doi: 10.1103/PhysRevE.80.016101
41. Santos FC, Pacheco JM. Risk of collective failure provides an escape from the tragedy of the commons. Proc Natl Acad Sci USA. (2011) 108:10421–5. doi: 10.1073/pnas.1015648108
42. Du J, Wu B, Wang L. Evolution of global cooperation driven by risks. Phys Rev E. (2012) 85(5 Pt 2):056117. doi: 10.1103/PhysRevE.85.056117
43. Chen X, Szolnoki A, Perc M. Risk-driven migration and the collective-risk social dilemma. Phys Rev E. (2012) 86:036101. doi: 10.1103/PhysRevE.86.036101
44. Chen X, Zhang Y, Huang TZ, Perc M. Solving the collective-risk social dilemma with risky assets in well-mixed and structured populations. Phys Rev E. (2014) 90:052823. doi: 10.1103/PhysRevE.90.052823
45. Hackett S, Schlager E, Walker J. The role of communication in resolving commons dilemmas: experimental evidence with heterogeneous appropriators. J Environ Econ Manage. (1994) 27:99–126. doi: 10.1006/jeem.1994.1029
46. Milinski M, Semmann D, Krambeck HJ. Reputation helps solve the ‘tragety of the commons’. Nature (2002) 415:424–6. doi: 10.1038/415424a
47. Szabó G, Hauert C. Evolutionary personer's dilemma games with voluntary participation. Phys Rev E. (2002) 66:062903. doi: 10.1103/PhysRevE.66.062903
48. Hauert C, De Monte S, Hofbauer J, Sigmund K. Volunteering as red queen mechanism for cooperation in public goods games. Science (2002) 296:1129–32. doi: 10.1126/science.1070582
49. Nowak MA. Five rules for the evolution of cooperation. Science (2006) 314:1560–3. doi: 10.1126/science.1133755
50. Rockenbach B, Milinski M. The efficient interaction of indirect reciprocity and costly punishment. Nature (2006) 444:718–23. doi: 10.1038/nature05229
51. Fu F, Hauert C, Nowak MA, Wang L. Reputation-based partner choice promotes cooperation in social networks. Phys Rev E. (2008) 78:026117. doi: 10.1103/PhysRevE.78.026117
52. Wang Z, Perc M. Aspiring to the fittest and promotion of cooperation in the prisoner's dilemma game. Phys Rev E. (2010) 82:021115. doi: 10.1103/PhysRevE.82.021115
53. Tavoni A, Dannenberg A, Kallis G, Löschel A. Inequality, communication, and the avoidance of disastrous climate change in a public goods game. Proc Natl. Acad Sci USA. (2011) 108:11825–9. doi: 10.1073/pnas.1102493108
54. Sasaki T, Unemi T. Replicator dynamics in public goods games with reward funds. J Theor Biol. (2011) 287:109. doi: 10.1016/j.jtbi.2011.07.026
55. Szolnoki A, Szabó G, Perc M. Phase diagrams for the spatial public goods game with pool punishment. Phys Rev E. (2011) 83(3 Pt 2):036101. doi: 10.1103/PhysRevE.83.036101
56. Sasaki T, Brännström A, Dieckmann U, Sigmund K. The take-it-or-leave-it option allows small penalties to overcome social dilemmas. Proc Natl Acad Sci USA. (2012) 109:1165–9. doi: 10.1073/pnas.1115219109
57. Perc M, Szolnoki A. Self-organization of punishment in structured populations. New J Phys. (2012) 14:43013–25. doi: 10.1088/1367-2630/14/4/043013
58. Szolnoki A, Perc M. Effectiveness of conditional punishment for the evolution of public cooperation. J Theor Bioly. (2013) 325:34–41. doi: 10.1016/j.jtbi.2013.02.008
59. Sasaki T, Uchida S. The evolution of cooperation by social exclusion. Proc R Soc B Biol Sci. (2012) 280:20122498. doi: 10.1098/rspb.2012.2498
60. Wang Z, Szolnoki A, Perc M. Rewarding evolutionary fitness with links between populations promotes cooperation. J Theor Biol. (2014) 349:50–6. doi: 10.1016/j.jtbi.2014.01.037
61. Chen X, Szolnoki A, Perc M. Probabilistic sharing solves the problem of costly punishment. New J Phys. (2014) 16:083016. doi: 10.1088/1367-2630/16/8/083016
62. Sasaki T, Uchida S, Chen X. Voluntary rewards mediate the evolution of pool punishment for maintaining public goods in large populations. Sci Rep. (2015) 5:8917. doi: 10.1038/srep08917
63. Li K, Cong R, Wu T, Wang L. Social exclusion in finite populations. Phys Rev E. (2015) 91:042810. doi: 10.1103/PhysRevE.91.042810
64. Liu L, Chen X, Szolnoki A. Competitions between prosocial exclusions and punishments in finite populations. Sci Rep. (2017) 7:46634. doi: 10.1038/srep46634
65. Szolnoki A, Chen X. Alliance formation with exclusion in the spatial public goods game. Phys Rev E. (2017) 95:052316. doi: 10.1103/PhysRevE.95.052316
66. Szolnoki A, Szabó G. Cooperation enhanced by inhomogeneous activity of teaching for evolutionary Prisoner's Dilemma games. EPL (2006) 77:30004. doi: 10.1209/0295-5075/77/30004
67. Perc M, Szolnoki A. Social diversity and promotion of cooperation in the spatial prisoner's dilemma game. Phys Rev E. (2008) 77(1 Pt 1):011904. doi: 10.1103/PhysRevE.77.011904
68. Santos FC, Santos MD, Pacheco JM. Social diversity promotes the emergence of cooperation in public goods games. Nature (2008) 454:213–6. doi: 10.1038/nature06940
69. Perc M, Wang Z. Heterogeneous aspirations promote cooperation in the prisoner's dilemma game. PLoS ONE (2010) 5:e15117. doi: 10.1371/journal.pone.0015117
70. Wang J, Fu F, Wang L. Effects of heterogeneous wealth distribution on public cooperation with collective risk. Phys Rev E. (2010) 82:016102. doi: 10.1103/PhysRevE.82.016102
71. Wang J, Wu B, Chen X, Wang L. Evolutionary dynamics of public goods games with diverse contributions in finite populations. Phys Rev E. (2010) 81:056103. doi: 10.1103/PhysRevE.81.056103
72. Milinski M, Röhl T, Marotzke J. Cooperative interaction of rich and poor can be catalyzed by intermediate climate targets. Clim Change (2011) 109:807–14. doi: 10.1007/s10584-011-0319-y
73. Santos FC, Pinheiro FL, Lenaerts T, Pacheco JM. The role of diversity in the evolution of cooperation. J Theor Biol. (2012) 299:88–96. doi: 10.1016/j.jtbi.2011.09.003
74. Perc M. Does strong heterogeneity promote cooperation by group interactions? New J Phys. (2012) 13:123027–37. doi: 10.1088/1367-2630/13/12/123027
75. Sun L, Yang HX, Chen SM, Chen YS. Heterogeneous aspirations promote cooperation in the public goods game. Int J Modern Phys C. (2013) 24:1250089. doi: 10.1142/S0129183112500891
76. Chen X, Perc M. Optimal distribution of incentives for public cooperation in heterogeneous interaction environments. Front Behav Neurosci. (2014) 8:248. doi: 10.3389/fnbeh.2014.00248
77. Nishi A, Shirado H, Rand DG, Christakis NA. Inequality and visibility of wealth in experimental social networks. Nature (2015) 526:426–9. doi: 10.1038/nature15392
78. Chen X, Szolnoki A. Individual wealth-based selection supports cooperation in spatial public goods games. Sci Rep. (2016) 6:32802. doi: 10.1038/srep32802
79. Qin J, Chen Y, Kang Y, Perc M. Social diversity promotes cooperation in spatial multigames. EPL (2017) 118:18002. doi: 10.1209/0295-5075/118/18002
80. Kun Á, Dieckmann U. Resource heterogeneity can facilitate cooperation. Nat Commun. (2013) 4:2453. doi: 10.1038/ncomms3453
81. Buckley E, Croson R. Income and wealth heterogeneity in the voluntary provision of linear public goods. J Pub Econ. (2006) 90:935–55. doi: 10.1016/j.jpubeco.2005.06.002
82. Vasconcelos VV, Santos FC, Pacheco JM, Levin SA. Climate policies under wealth inequality. Proc Natl Acad Sci USA. (2014) 111:2212–6. doi: 10.1073/pnas.1323479111
83. Schuster P, Sigmund K. Replicator dynamics. J Theor Biol. (1983) 100:533–8. doi: 10.1016/0022-5193(83)90445-9
84. Hofbauer J, Sigmund K. Evolutionary Games and Population Dynamics. Cambridge: Cambridge University Press (1998).
85. Ohtsuki H, Nowak MA. The replicator equation on graphs. J Theor Biol. (2006) 243:86–97. doi: 10.1016/j.jtbi.2006.06.004
86. Nowak MA. Evolutionary Dynamics: Exploring the Equations of Life. Cambridge: Harvard University Press (2006).
88. Santos FC, Pacheco JM, Lenaerts T. Evolutionary dynamics of social dilemmas in structured heterogeneous populations. Proc Natl. Acad Sci USA. (2006) 103:3490. doi: 10.1073/pnas.0508201103
89. Barrett S, Dannenberg A. Climate negotiations under scientific uncertainty. Proc Natl Acad Sci USA. (2012) 109:17372–6. doi: 10.1073/pnas.1208417109
90. Rogelj J, Den Elzen M, Höhne N, Fransen T, Fekete H, Winkler H, et al. Paris agreement climate proposals need a boost to keep warming well below 2 C. Nature (2016) 534:631–9. doi: 10.1038/nature18307
91. Mendelsohn R, Dinar A, Williams L. The distributional impact of climate change on rich and poor countries. Environ Dev Econ. (2006) 11:159–78. doi: 10.1017/S1355770X05002755
Keywords: asset heterogeneity, collective-risk, threshold public goods game, individual assets, public cooperation
Citation: Liu L and Chen X (2018) Evolution of Public Cooperation in a Risky Society with Heterogeneous Assets. Front. Phys. 5:67. doi: 10.3389/fphy.2017.00067
Received: 30 September 2017; Accepted: 07 December 2017;
Published: 04 January 2018.
Edited by:
Matjaž Perc, University of Maribor, SloveniaReviewed by:
Zhen Wang, Hong Kong Baptist University, Hong KongJun Tanimoto, Kyushu University, Japan
Copyright © 2018 Liu and Chen. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Xiaojie Chen, eGlhb2ppZWNoZW5AdWVzdGMuZWR1LmNu
 Linjie Liu
Linjie Liu Xiaojie Chen
Xiaojie Chen