- 1Institute for Theoretical Solid-State Physics, KIT, Karlsruhe, Germany
- 2Department of Physical Chemistry, Chalmers University of Technology, Gothenburg, Sweden
This work has shown the way to put the formal statistical-mechanical basement under the hotly debated notion of enthalpy-entropy compensation. The possibility of writing down the universal equation of state based upon the statistical mechanics is discussed here.
Introduction
The present communication is based upon the work of an outstanding Viennese-born USA-American physical chemist, Dr. Georg(e) Augustus Linhart (1885–1951) [1–11] and aims at demonstrating its fundamental significance, in an attempt to bridge the gap between Linhart's approach and those introduced and followed by other colleagues. In fact, this report is the sequel to our most recent publications on this theme [12–15], and our work is still going on, but we would greatly appreciate presenting some preliminary results herewith.
We realize that submitting such a manuscript to a modern physical journal ought to be running a gauntlet—both for the authorship and for the readership. The present author would greatly appreciate to revitalize a number of well-forgotten ideas expressed long time ago by “widely unknown” colleagues, and this warrants the novelty of the communication at hand.
Specifically, Dr. Linhart could have managed to formally infer the “notoriously magic” Boltzmann-Planck logarithmic formula connecting the entropy notion with some Probability. Linhart's idea was to employ the Bayesian approach to clarify the physical sense of the latter, and he successfully solved the problem by demonstrating that the “Probability” is in effect nothing else than just a handy algebraic function of the absolute temperature, and it is this way that it could have become possible to start building up the physically sound statistical mechanics. To our regret, Dr. Linhart had no chance to complete his seminal work, and this communication ought to represent one of the steps in our already active project aiming at the revitalization of his legacy.
In analyzing Dr. Linhart's published and unpublished work, we have encountered a totally fresh, unconventional and, howbeit, fully professional line of sight as concerns thermodynamics. Further, in thoroughly digging the available literature we have encountered works by a non-negligible number of colleagues, who were consistently following strikingly similar trains of thoughts. This has clearly suggested that trying to combine the details of the latter ones might definitely be throughout fruitful. Hence, by choosing the word “unconventional” here we would greatly appreciate attracting the attention of the young professional readership in the first place.
Results and Discussion
Dr. Linhart could not only manage to formally prove the ingenious Boltzmann-Planck guess that entropy is proportional to the natural logarithm of some fancy probability. He could also clarify the physical sense of the latter in demonstrating that it ought to be a handy algebraic function of the absolute temperature [1–3, 6].
In our works [12, 15] we have shown that Linhart's representation of the heat capacity at constant volumes, CV, as an algebraic function of the absolute temperature might not only lead to the formal inference of the Boltzmann-Planck formula, but also to revealing the actual physical sense of the fancy probability variable under the natural logarithm's sign. It also occurs to be possible to introduce the “Bayesian Statistical Mechanics” upon such a ground, which is not in contradiction with the conventional one, but definitely extending the applicability scope of the latter.
Here we would greatly appreciate presenting some further formal proof of the above statement.
Entropy-Enthalpy Compensation at the Tip of Pen
In the works [12, 15] we could have derived handy mathematical expressions for the entropy, internal energy—and therefore for the Helmholtz free energy—as functions of the absolute temperature and demonstrated that the actual statistical properties of the systems under consideration ought to obey the Beta probability distribution. This way it is throughout possible to treat mathematically formally and rigorously the ubiquitous fuzzy aspects of the problem under study.
Meanwhile, the next important theoretical problem is to how might we treat further important thermodynamic functions, namely, the enthalpy—and therefore the Gibbs free energy?
It is well known [16, 17] that enthalpy is connected with the heat capacity at constant pressures, Cp, which might well be approximated by CV, but solely at low and intermediate temperatures, whereas at higher temperatures there are always discrepancies between the both. The actual reason for such a behavior has been thoroughly studied both empirically and computationally, and the point is that CV gets anyway saturated at approximately Dulong-Petit level, whereas Cp is still noticeably temperature-dependent (see e.g., [1–3, 6, 18, 19] and the references therein).
This urges us to look in for the physical sense of the enthalpy notion in much more detail.
The interconnections between the CV and Cp are well known as well (cf. e.g., [20]). Specifically, to work with an intensive property, we first define the specific heat capacity
Here C stands for the heat capacity of some physical-chemical system of interest, being built-up by a definite material; m is the mass of this system, whereas ρ and V are the corresponding density and volume, respectively. With this in mind, we might speak of the following basic relationship, first of all:
Here α stands for the thermal expansion/compression coefficient, whereas βT is isothermal compressibility, p–pressure, T–absolute temperature. Moreover, there is ratio cp/cV as well
Here βS stands for the adiabatic/isentropic compressibility, S is the entropy.
Further, in general terms, the enthalpy change ought to be expressed as follows:
Taking into account (Equations 1–3), we get:
Of considerable interest would be evaluating how enthalpy is dependent on the absolute temperature. With this in mind, first we would like to neglect the pressure dependence of enthalpy, in considering the case of the ideal gas. Otherwise, to avoid working with basically ideal systems, we might wish to consider some realistic isobaric situation. Then, dp = 0, implying that in our considerations we might control from outside the pressure imposed on our system, and wish now to ensure that the pressure imposed on our system is constant. This way, we might recast Equation (5) as follows:
As we do know from Linhart's work what the temperature dependence of cV should be, of our primary interest is to correctly assign the temperature dependences of both the isothermal and the adiabatic compressibility.
In the literature we might fetch an extended row of papers dealing with this topic thoroughly and in detail (cf. e.g., [21–42] and the references therein). After taking into account this entire information, we dare to conclude that whereas the adiabatic compressibility might largely be considered a linear function of temperature, the isothermal compressibility is dependent on temperature in a much more non-trivial way, namely:
In these relationships, the temperature is in Kelvin, whereas isothermal compressibility is in (J · cm−3)−1.
The work [26] shows that the both relationships given by Equation (7) properly guarantee satisfactory fitting the relevant experimental results, while using the exponential expression leads to noticeably better results than employing the algebraic equation. On the other hand, to our mind, the exponential functional dependence is much more difficult to treat theoretically, while the latter one enables us to evaluate and analyze the anti-derivative of Equation (6) in a straightforward way.
This is why we employ the algebraic formulation in our present work, implying that it delivers a handy functional approximation to the exponential one. That the latter one is possessed of the better numeric properties renders our conclusions a rather reasonable approximation.
With this in mind we shall present here our result, with sending the readership to the mathematical Appendix here for all the necessary technical details.
To sum up, we adopt here the relative absolute temperature like in our work [12], x ≡ T/Tref, where Tref is some reference temperature, the physical sense of which we shall clarify. Bearing this in mind; we arrive at the following result for the isobaric temperature dependence of enthalpy, Hp (“2F1” denotes below the conventional Gaussian hypergeometric function 2F1 (a, b; c, z)):
Analyzing Equation (8) enables to recast it in the following approximate form (see the Appendix in Supplementary Material for the technical details):
One striking feature might be of immediate interest, namely the similarity of the functional expressions of the enthalpy and entropy's temperature dependencies. Indeed, Linhart's result for the entropy's temperature dependence dictates [1–3, 6, 12] that
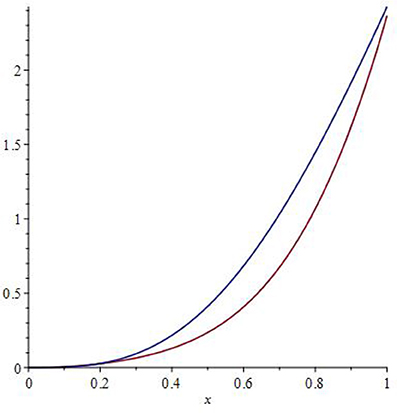
Here C∞ stands for the limiting heat capacity (C∞ ≅ 3NAkB ≡ 3R, where NA is the Avogadro number, kB−the Boltzmann's constant and R−the universal gas constant) [1–12]. Figure 1 depicts typical behavior of entropy and enthalpy vs. temperature, and one can immediately recognize the convergent behavior of the both up to the value of x = 1, after which the graphs diverge.
Hence, it is throughout possible to interpret this as an enthalpy-entropy compensation (EEC), whereas x = 1, that is, T = Tref defines the so-called “enthalpy-entropy compensation temperature” Tc, that is, Tref ≡ Tc (see e.g., [43–52] and the references therein).
Noteworthy, the approximate considerations here (cf. Figure 1) support our conclusion that the generic functional form of the EEC ought to be rather non-linear, although linear function still appears to be a rather good approximation for the EEC anyway (for details, see [44, 45] and the references therein).
Howbeit, in the work [12] we discussed a possibility of interpreting the temperature values Tref as points of some “hidden zero-order phase transition.” Such a conclusion is firmly supported by finding a discontinuity at x = 1 in the temperature dependencies of the internal energy U(T) and, accordingly, in the Helmholtz free energy F(T), without revealing it in the temperature dependencies of both CV(T) and S(T).
Interestingly in this respect, according to our isobaric analysis above, the temperature dependence of the Gibbs' free energy G(T) does not exhibit any discontinuities for the whole range of x values from zero to unity:
Noteworthy, this is a very interesting result, for our earlier elementary thermodynamic consideration of the EEC phenomenon reveals a definite interrelationship between the Helmholtz' and Gibbs' free energies [51].
Meanwhile, the both free energy types are possessed of quite different mathematical properties, and therefore ought to reveal two quite different sides of one and the same phenomenon.
Indeed, the first idea coming to mind would be that although the enthalpy notion does contain the internal energy notion, adding the pV product to the latter ought to remove the discontinuity in the U as a function of T. This means that the absolute temperature dependence of the pV product does somehow compensate the discontinuity in the U(T). In more mathematical and physical detail we would like to analyze and discuss this point in the mathematical Appendix in Supplementary Material.
This train of thoughts brings us immediately to the old and good poser of writing the equation of state, as here we have just arrived at the fundamental problem of properly describing correlations among volume/density, pressure and temperature.
Universal Equation of State
After reading the above headline our readership might immediately exclaim: Stop, there is but still no universal equation of state, see any serious handbook of thermodynamics (e.g., [53]).
Indeed, we open this book and read in its Chapter 6 on the Page 280 as follows:
“If we only had a general relation that perfectly described P = P(V, T) for all the chemicals in the universe, it could be combined with the tools in this chapter to compute any property required by the energy and entropy balances. At present, no such perfect equation exists. This means that we need to understand what makes it so difficult to develop such an equation and how the various available equations can be applied in various situations to achieve reasonable and continuously improving estimates.”
Without going in for answering the question as to “what makes it so difficult to develop such an equation?”—This exciting topic will be discussed in a separate publication—we just give here the pointer to the ingenious works by Swedish colleagues Dr. Nils Engelbrektsson (1875–1963) and Karl Alexius Franzén (1882–1967), who had answered this poser quite positively and very constructively. Specifically, Dr. Engelbrektsson could have inferred such an equation by analyzing in detail the fundamental principles of thermodynamics, whereas Mr. Franzén could have successfully checked Dr. Engelbrektsson's inferences experimentally and proven their complete validity. Back in 1920 they both have published their seminal results as a separate book in Swedish, but until now nobody had anywhere come to pay attention to this publication. Dr. Engelbrektsson had devoted his whole life in working on the formulation of the basic thermodynamics, being also an interesting publicist as a hobby aside of this. His works might now be fetched in the Swedish National Library, and we would greatly appreciate presenting here his full publication list [54–68].
May the above be considered an answer to our poser in such a case? In our opinion, not to 100%, for Dr. Engelbrektsson was not studying interrelationships between thermodynamics and statistical mechanics. Instead, Dr. Linhart could have solely managed to show the way of developing the statistical mechanics in connection with thermodynamics, and thus duly pursuing Prof. Dr. J. W. Gibbs' train of thoughts. This is why; to answer the above poser we would actually need bridging the gap between Linhart and Engelbrektsson's approaches.
Still, our picture would be largely incomplete, if we would not mention here the works by another outstanding theoretical physicist, who was working in Germany: Prof. Dr. Max Bernhard Weinstein (1852–1918). Prof. Dr. Weinstein is presently known solely as a harsh censor of A. Einstein's approach to the relativity theory, whereas in fact, he was one of the serious and productive multitalented workers in the fields of theoretical metrology, physics and natural philosophy. Here we would like to present the full list of his works (the publications in the periodic media as well as monographs, including both his original works and German translations of the classical physical treatises) [69–101]. As it is apparent from his publication list, among other important problems, Prof. Dr. Weinstein was productively working on the formulation of the equation of state. These works by him have been noticed and taken into detailed consideration by Dr. Engelbrektsson.
Apart from the above, of immense interest for us here ought to be Prof. Dr. Weinstein's immense and productive efforts in the fields of thermodynamics and statistical mechanics' foundations. Specifically, to be mentioned are Prof. Weinstein's criticism of the then vogue in connection with the so-called “Third Basic Law of Thermodynamics” and the reaction to it from the scientific community [102, 103], as well as Prof. Weinstein's grounded, constructive criticism of Ludwig Boltzmann's approach to the statistical thermodynamics [104] (noteworthy, Prof. Weinstein has published this work under the pseudonym of “Mr. F. Cohen”), as well as the immediate reaction to this publication by Max Planck (revealing but not much more than his outrage and voluntarism in this particular case) [105].
Meanwhile, as we know now, Dr. Linhart could mathematically formally infer the famous, but mostly guessed Boltzmann-Planck formula S = kB· ln W. He had demonstrated that revealing the important details of the function S ≡ S(T), where T is the absolute temperature, leads to the conclusion that S(0) = 0. As it is throughout possible to infer the latter fact in the mathematically rigorous way, it immediately loses its truly fabulous context of some Basic and Fundamental Natural Law…This interesting theme will be discussed elsewhere in detail.
Conclusions and Future Prospects
To sum up, here we could show that the Bayesian Statistical Mechanics initiated by Dr. Linhart allows us to put the rational statistical-mechanical basement under the phenomenon of the valid enthalpy-entropy compensation hotly debated till nowadays. Recently, we have carried out a detailed overview and thoroughly discussed the possible implications of the valid enthalpy-entropy compensation at the molecular level [106].
Following this direction, it becomes in principle possible to approach the problem of statistically-mechanically deriving the universal equation of state, and we have demonstrated here, how this might be accomplished for a particular case of an isobaric system, where the externally applied pressure might be reliably controlled. Meanwhile, Dr. Engelbrektsson had already inferred the truly universal equation of state, whereas Mr. Franzén could successfully check its validity in the pertinent experiments. Still, Dr. Engelbrektsson was employing a unique thermodynamic approach, without any application to statistical mechanics. Prof. Dr. Weinstein has approached solving the latter problem, but all the mentioned colleagues had no more lifetimes to accomplish their seminal task.
Therefore, we might conclude that ultimately writing down the universal equation of state based upon the statistical mechanics ought to be throughout possible, if we would manage to properly synthesize the approaches by G. A. Linhart, N. Engelbrektsson and M. B. Weinstein. Writing down such a form of the universal equation of state would definitely open us the way to pertinent and handy mechanistic analyses of the whole wealth of interesting and important physical-chemical-biological events at the molecular level.
Author Contributions
ES is the sole author of this work and confirms that he meets the following authorship criteria.
• Substantial contributions to the conception or design of the work; or the acquisition, analysis, or interpretation of data for the work;
• Drafting the work or revising it critically for important intellectual content;
• Final approval of the version to be published; and
• Agreement to be accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved.
Conflict of Interest Statement
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2018.00002/full#supplementary-material
References
1. Linhart GA. The relation between entrophy and probability. The integration of the entropy equation. J Am Chem Soc. (1922) 44:140–2. doi: 10.1021/ja01422a017
2. Linhart GA. Correlation of entropy and probability. J Am Chem Soc. (1922) 44:1881–6. doi: 10.1021/ja01430a005
3. Linhart GA. Additions and corrections - correlation of entropy and probability. J Am Chem Soc. (1922) 44:2968–9. doi: 10.1021/ja01433a609
4. Linhart GA. The Relation between Chronodynamic Entropy Time. Riverside, CA: Occasional Papers of Riverside Junior College (1929).
5. Linhart GA. Note on the absorption of oxygen by sheets of rubber. J Phys Chem. (1932) 36:1908–11. doi: 10.1021/j150337a003
6. Linhart GA. Correlation of heat capacity, absolute temperature and entropy. J Chem Phys. (1933) 1:795–8. doi: 10.1063/1.1749247
7. Linhart GA. The application of the law of mathematical probability to the behavior of gases in their pressure-volume-temperature relations. J Phys Chem. (1932) 37:645–53. doi: 10.1021/j150347a009
8. Linhart GA. Interpretation of the pressure-volume-temperature relations of single and composite gases. J Phys Chem. (1933) 38:1091–7. doi: 10.1021/j150359a010
9. Linhart GA. Mathematical relation between turbulence and depth of the ocean. Am Math Monthly (1935) 42:224–7. doi: 10.2307/2302101
10. Linhart GA. Penetration of solar and cosmic rays into fresh water lakes. J Phys Chem. (1935) 40:113–9. doi: 10.1021/j150370a014
11. Linhart GA. General Laws of Dynamics Their Application. Riverside, CA: Occasional Papers of Riverside Junior College (1938).
12. Starikov EB. Many faces of entropy or Bayesian statistical mechanics. Chem Phys Chem. (2010). 11:3387–94. doi: 10.1002/cphc.201000583
13. Starikov EB. George Augustus Linhart–As a “Widely Unknown” Thermodynamicist. World J Cond Matt Phys. (2012) 2:101–16. doi: 10.4236/wjcmp.2012.22018
14. Starikov EB. ‘Entropy is Anthropomorphic’: does this lead to interpretational devalorisation of entropy-enthalpy compensation? Chem Month. (2013) 144:97–102. doi: 10.1007/s00706-012-0837-y
15. Starikov EB. Statistical mechanics in Bayesian representation: how it might work and what ought to be the probability distribution behind it. In: Proceedings of the SEE-Mie Conference, Taken Place at the City of Tsu (2015). Available online at: https://www.researchgate.net/publication/281030679
17. Moran MJ, Shapiro HN. Fundamentals of Engineering Thermodynamics. Chichester: John Wiley & Sons (2006).
18. Xie J, de Gironcoli S, Baroni S, Scheffler M. First-principles calculation of the thermal properties of silver. Phys Rev B (1999) 59:965–9. doi: 10.1103/PhysRevB.59.965
19. Irons FE. New method for reducing the general formula for lattice specific heat to the Einstein and Nernst-Lindemann approximations. Canad J Phys. (2003) 81:1015–36. doi: 10.1139/p03-069
20. Gaskell DR. Introduction to the Thermodynamics of Materials, 5th Edn. New York, NY: Taylor & Francis (2009).
22. Lynch JW Jr. Calculation of the Heat Capacities of Molecular Liquids. Ph.D. Thesis, Georgia Institute of Technology (1951).
23. Nasekovskii AP. Temperature dependence of thermal expansion coefficient of crystals with cubic syngony. Sov Phys J. (1967) 10:50–52.
24. Nasekovskii AP. Temperature dependence of the thermal-expansion coefficient of certain polycrystalline materials. Sov Phys J. (1969) 12:45–8.
25. Brelvi SW, O'Connell JP. Corresponding states correlations for liquid compressibility and partial molal volumes of gases at infinite dilution in liquids. AICHE J. (1972) 18:1239–43.
26. Brostow W, Maynadier P. Temperature dependence of the isothermal compressibility of liquids. High Temp. Sci. (1979) 11:7–21.
27. Gekko K, Noguchi H. Compressibility of globular proteins in water at 25°C. J Phys Chem. (1979) 83:2706–14.
28. Brostow W, del Rocio Enriquez EM, Espiritu AL. Isobaric expansivity of liquids and its dependence on temperature. Mater Chem Phys. (1983) 8:541–52. doi: 10.1016/0254-0584(83)90003-2
29. Kagaya HM and Soma T. Temperature dependence of the linear thermal expansion coefficient for Si and Ge. Phys Status Solidi B (1985) 129:K5–8. doi: 10.1002/pssb.2221290149
30. Dymond JH, Malhotra R. Densities of n-alkanes and their mixtures at elevated pressures. Int J Thermophys. (1987). 8:541–55.
31. Huang YH, O'Connell JP. Corresponding states correlation for the volumetric properties of compressed liquids and liquid mixtures. Fluid Phase Equilibria (1987) 37:75–84.
32. Gekko K, Hasegawa Y. Effect of temperature on the compressibility of native globular proteins. J Phys Chem. (1989) 93:426–29.
33. Asaoka K, Kuwayama N. Temperature dependence of thermal expansion coefficient for palladium-based binary alloy. Dental Mater J. (1990) 9:47–57.
34. Attwood D, Mosquera V, Rey C, Garcia M. Temperature dependence of molar volume and adiabatic compressibility of aqueous solutions of an amphiphilic phenothiazine drug. J Coll Interf Sci. (1991) 147:316–20. doi: 10.1016/0021-9797(91)90163-3
35. Kohler F, Van Nhu N. The Temperature dependence of the isothermal compressibility of liquids along the Orthobaric curve. J Mol Liquids (1992) 52:97–108. doi: 10.1016/0167-7322(92)80098-3
36. Kumar M, Upadhyay SP. Analysis of the thermal expansion coefficient and its temperature dependence for alkali halides. Phys Status Solidi B (1994) 181:55–61. doi: 10.1002/pssb.2221810106
37. Wang F, Saeki S, Yamaguchi T. Temperature and pressure dependence of thermal expansion coefficient and thermal pressure coefficient for amorphous polymers. Polymer (1997) 38:3485–92. doi: 10.1016/S0032-3861(96)00910-X
38. Cibulka I, Takagi T. P-ρ-T Data of Liquids: Summarization and Evaluation. 6. Nonaromatic Hydrocarbons (Cn, n ≥ 5) except n-Alkanes C5 to C16. J Chem Eng Data (1999) 44:1105–28.
39. Dubiel M, Brunsch S, Tröger L. Temperature dependence of thermal expansion coefficient of silver nanoparticles and of bulk material determined by EXAFS. J Synchrotron Rad. (2001) 8:539–41. doi: 10.1107/S0909049500016666
40. Gu M, Sun CQ. A Rule for the Thermally Induced Bond Expansion. In: Science Paper Online; Physics, Paper 154, Shanghai. (2007).
41. Sluyters JH, Sluyters-Rehbach M. Arrest as a general property of the Supercooled liquid state. J Phys Chem B (2016) 120:3735–45. doi: 10.1021/acs.jpcb.6b01766
42. Sluyters JH, Sluyters-Rehbach M. Deviation from van't Hoff behavior of solids at low temperature. ACS Omega (2017) 2:2317–25. doi: 10.1021/acsomega.7b00169
43. Starikov EB, Nordén B. Enthalpy-entropy compensation – A phantom or something useful? J Phys Chem B (2007) 111:14431–5. doi: 10.1021/jp075784i
44. Starikov EB, Nordén B. Physical rationale behind the nonlinear enthalpy-entropy compensation in DNA duplex stability. J Phys Chem B (2009) 113:4698–707. doi: 10.1021/jp8089424
45. Starikov EB, Nordén B. DNA duplex length and salt concentration dependence of enthalpy-entropy compensation parameters for DNA melting. J Phys Chem B (2009) 113:11375–7. doi: 10.1021/jp903924j
46. Starikov EB, Nordén B. Entropy-enthalpy compensation may be a useful interpretation tool for complex systems like protein-DNA complexes: an appeal to experimentalists. Appl Phys Lett. (2012) 100:193701. doi: 10.1063/1.4714726
47. Starikov EB, Nordén B. Entropy–enthalpy compensation as a fundamental concept and analysis tool for systematical experimental data. Chem Phys Lett. (2012) 538:118–20. doi: 10.1016/j.cplett.2012.04.028
48. Starikov EB, Nordén B. Entropy-enthalpy compensation: is there an underlying microscopic contribution to mechanism? In: Mendez-Vilas A, editor. Current Microscopy Advances in Science and Technology, vol. 2. Badajoz: Formatex Research Center (2012). p. 1492–1503.
49. Starikov EB. Valid entropy–enthalpy compensation: fine mechanisms at microscopic level. Chem Phys Lett. (2013) 564:88–92. doi: 10.1016/j.cplett.2013.02.016
50. Starikov EB. Entropy–enthalpy compensation and its significance – in particular for nanoscale events. J Appl Sol Chem Model. (2013) 2:126–35. doi: 10.6000/1929-5030.2013.02.02.7
51. Starikov EB. Valid entropy-enthalpy compensation: its true physical-chemical meaning. J Appl Sol Chem Model. (2013) 2:240–5.
52. Starikov EB. ‘Meyer-Neldel Rule’: true history of its development and its intimate connection to classical thermodynamics. J Appl Sol Chem Model. (2014) 3:15–31.
53. Richard Elliott J, Lira CT. Introductory Chemical Engineering Thermodynamics. Englewood Cliffs, NJ: Prentice Hall International Series in Physical and Chemical Engineering Sciences (2012).
54. Engelbrektsson N. Meddelande Till Matematiska Kongressen i Stockholm. Lund: Håkan Ohlssons Boktryckeri (1909).
55. Engelbrektsson N. K. Läroverksöfverstyrelsen och Lärarepersonligheten. Göteborg: A. Lindgren & Söner (1911).
56. Engelbrektsson N. K. Vetenskaps- och Vitterhetssamhället i Göteborg och det Vetenskapliga Initiativet. Lund: Håkan Ohlssons boktryckeri (1911).
59. Engelbrektsson N. Entropieekvationens Integrationsteorem och Kontaktsprincipen. Lund: Håkan Ohlssons Boktryckeri (1916).
60. Engelbrektsson NI. Über die Bestimmtheit des zweiten Hauptsatzes der Thermodynamik. Lösung mittels des zweiten Hauptsatzes von Problemen bei denen der Entropiesatz keine bestimmte Lösung gibt. (Anwendung: Herleitung der Temperaturfunktion des Dampfdruckes. Analytische Definition des kritischen Zustandes bei Substanzen). II. Zusammenhang zwischen Wärmefunktionen bei einer Substanz, die einem thermischen Prozess unterworfen ist und dem unveränderlichen Gewicht der Substanz. (Anwendung: Herleitung des Gesetzes von Dulong-Petit und der Regel von Trouton). Lund: Håkan Ohlssons Boktryckeri (1917).
61. Engelbrektsson N. Termodynamikens Grunddrag, Appendix: Verification of Engelbrektsson's Equation (the Rational Equation of State of Bodies) for Saturated and Unsaturated Vapors, Liquids at Finite and Infinite Pressures, and Isotropic Solids – by Karl Franzén. Lund: Håkan Ohlssons Boktryckeri (1920).
62. Engelbrektsson N. The Phase Limit Motor as Heat Engine in Cases of Boiling or Melting. Göteborg: A. Lindgren & Söner (1926).
63. Engelbrektsson N. Expansion by Heat Regarded as a Function of the Phase Limit Motor. Göteborg: A. Lindgren & Söner (1927).
64. Engelbrektsson N. The Integral Form for the Integrability Condition of the Entropy Equation. Göteborg: A. Lindgren & Söner: (1928).
65. Engelbrektsson N. A Thermodynamic Study: The Deduction of the Form of the Thermometry. Göteborg: A. Lindgren & Söner (1928).
66. Engelbrektsson N. A Thermodynamic Study: The Deduction of the Forms for Gas-Expansion Solid-Expansion at Small Pressures. Göteborg: A. Lindgren & Söner (1928).
67. Engelbrektsson N. Notiz von dem Entwicklungsgang Meiner Thermodynamischen Arbeiten. Göteborg: A. Lindgren & Söner (1935).
68. Engelbrektsson N. Akademisk Matematik Eller Mitt Räkneinstrument – Ett Dilemma; Academical Thermodynamics or My Heat Engine Form – A Dilemma. Helsingfors: Centraltryckeriet (1948).
69. Maxwell JC, Weinstein B. Lehrbuch der Electricität und des Magnetismus: in zwei Bänden. Autorisierte deutsche Übersetzung von B. Weinstein. Berlin: Springer (1883) (German Translation by M. B. Weinstein).
70. Fourier JBJ, Weinstein B. Analytische Theorie der Wärme. Dt. Ausgabe von Dr. B. Weinstein. Berlin: Springer (1884) (German Translation by M. B. Weinstein).
74. Weinstein B, Privat-Dozent an der Universität zu Berlin und Hilfsarbeiter bei der Kaiserlichen Normal-Eichung-Kommission. Handbuch der Physikalischen MaaßBestimmungen. Erster Band. Die Beobachtungsfehler, ihre Rechnerische Ausgleichung und Untersuchung. Berlin: Axel Springers Verlag (1886).
75. Weinstein B. Kapillaritäts-Untersuchungen und ihre Verwerthung bei der Bestimmung der alkoholometrischen Normale. Berlin: Axel Springers Verlag (1889).
76. Weinstein B. Über die Bestimmung von Aräometern mit besonderer Anwendung auf die Feststellung der deutschen Urnormale für Alkoholometer. Berlin: Axel Springers Verlag (1890).
77. Weinstein B. Physik und Chemie. Gemeinsätzliche Darstellung ihrer Erscheinungen und Lehren. Berlin: Axel Springers Verlag (1898).
78. Weinstein B. Die Erdströme im Deutschen Reichstelegraphengebiet und ihr Zusammenhang mit den Erdmagnetischen Erscheinungen. Braunschweig: Friedrich Vieweg und Sohn (1900).
79. Weinstein B. Denken und Träumen. Dichtungen. Berlin: Ferdinand Dümmlers Verlagsbuchhandlung (1901).
80. Weinstein B. Einleitung in die Höhere Mathematische Physik. Berlin: Ferdinand Dümmlers Verlagsbuchhandlung (1901).
81. Weinstein B. Thermodynamik und Kinetik der Körper. I. Band: Allgemeine Thermodynamik und Kinetik, und die Theorie der idealen und wirklichen Gase und Dämpfe. Braunschweig: Friedrich Vieweg und Sohn (1901).
82. Weinstein B. Thermodynamik und Kinetik der Körper. II. Band: Absolute Temperatur. Die Flüssigkeiten – die festen Körper. Thermodynamische Statik und Kinetik. Die (nichtverdünnten) Lösungen. Braunschweig: Friedrich Vieweg und Sohn (1903).
83. Weinstein B. Entropie und innere Reibung. In: Meyer S, editor. Festschrift Ludwig Boltzmann Gewidmet zum Sechzigsten Geburtstage 20. Leipzig: Verlag von Johann Ambrosius Barth (1904). p. 510–17.
84. Weinstein B. Thermodynamik und Kinetik der Körper. III. Band, I. Halbband: Die Verdünnten Lösungen. Die Dissoziation – Thermodynamik der Elektrizität (Erster Theil). Braunschweig: Friedrich Vieweg und Sohn (1905).
85. Weinstein B. Die Philosophischen Grundlagen der Wissenschaften. Vorlesungen Gehalten an der Universität Berlin. Leipzig; Berlin: Druck und Verlag von B. G. Teubner (1906).
86. Weinstein B. Thermodynamik und Kinetik der Körper. III. Band, II. Halbband: Thermodynamik der Elektrizität (Zweiter Theil) – Elektrochemie. Braunschweig: Friedrich Vieweg und Sohn (1908).
87. Weinstein B. Entstehung der Welt und der Erde nach Sage und Wissenschaft. Leipzig; Berlin: Verlag von B. G. Teubner (1908).
88. Weinstein MB. Welt- und Lebensanschauungen Hervorgegangen aus Religion, Philosophie und Naturerkenntnis. Leipzig: Verlag von Johann Ambrosius Barth (1910).
89. Weinstein MB. Die Physik der bewegten Materie und die Relativitätstheorie. Dem Andenken Hermann Minkowskis. Leipzig: Verlag von Johann Ambrosius Barth (1913).
90. Weinstein B. Zu Minkowskis Mechanik. Die Weltkonstante, die Systemmechanik. Ann Phys. (1914) 348:929–54.
91. Weinstein MB. Kräfte und Spannungen- Das Gravitations- und Strahlenfeld. Braunschweig: Friedrich Vieweg und Sohn (1914).
92. Weinstein MB. Die Relativitätslehre und die Anschauung von der Welt. Himmel Erde (1914) 26:1–14.
94. Weinstein MB. Über Die Innere Reibung der Gase. I. Der erste Reibungskoeffizient. Ann Phys. (1916) 355:601–54.
95. Weinstein MB. Über die innere Reibung der Gase. II. Der zweite Reibungskoeffizient, die Gustav Kirchhoff'schen thermodynamisch-hydrodynamischen Gleichungen, die Maxwell'sche Gastheorie. Ann Phys. (1916) 355:796–814.
98. Weinstein MB. Das Nernst'sche Theorem und die Wärmeausdehnung fester Stoffe. Ann Phys. (1917) 357:218–20.
100. Weinstein MB. Das Nernst'sche Theorem und die Wärmeausdehnung fester Stoffe. Ann Phys. (1917) 358:47–8.
101. Weinstein MB. Zur Prüfung der Annahmen über die thermodynamischen Potentiale. Ann Phys. (1918) 360:497–526.
103. Weinstein MB. Zu Hrn. Epsteins Bemerkungen über das Nernst'sche Theorem. Ann Phys. (1917) 359:79–80.
104. Cohen F. Zur kinetischen Gastheorie: Eine kritische Untersuchung. Physikalische Zeitschrift (1909) 10:138–40, 196–7.
105. Planck M. Zur kinetischen Gastheorie: Eine kritische Untersuchung. Physikalische Zeitschrift (1909) 10:195–6.
106. Starikov EB, Nordén B. Entropy-enthalpy compensation: is there an underlying microscopic mechanism? In: Méndez-Vilas A, editor. Current Microscopy Contributions to Advances in Science and Technology (2012). p. 1492–1503. Available online at: http://www.formatex.info/microscopy5/book/1492-1503.pdf
Keywords: entropy, enthalpy, compensation, equation of state, thermodynamics
Citation: Starikov EB (2018) Bayesian Statistical Mechanics: Entropy-Enthalpy Compensation and Universal Equation of State at the Tip of Pen. Front. Phys. 6:2. doi: 10.3389/fphy.2018.00002
Received: 03 July 2017; Accepted: 15 January 2018;
Published: 06 February 2018.
Edited by:
Ramesh L. Gardas, Indian Institute of Technology Madras, IndiaReviewed by:
Naved I. Malek, Sardar Vallabhbhai National Institute of Technology Surat, IndiaSugata Chowdhury, National Institute of Standards and Technology, United States
Copyright © 2018 Starikov. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Evgeni B. Starikov, c3Rhcmlrb3dAdGZwLnVuaS1rYXJsc3J1aGUuZGU=
 Evgeni B. Starikov
Evgeni B. Starikov