Initiation of Rotors by Fast Propagation Regions in Excitable Media: A Theoretical Study

We study the effect of geometry of a fast propagation region (FPR) in an excitable medium on the rotor initiation using a generic two-dimensional reaction-diffusion model. We find that, while the flat boundary of a rectangularly shaped FPR may block the propagation of the excitation wave, a large local curvature at the rounded corners of the FPR would prevent the blockage and thus initiate a rotor. Our simulations demonstrate that the prerequisites for the rotor initiation are the degree of the heterogeneity, its shape and size. These results may explain the incidence of arrhythmias by local heterogeneities induced, for example, by a cardiac tissue remodeling.

1. Introduction

Rotors, also known as spiral waves, are observed in many systems, including the Belousov-Zhabotinsky chemical reactions [1–4], autocatalytic reactions of carbon monoxide on a platinum surface [5], aggregations of Dictyostelium discoideum amoebae [6], Xenopus oocytes [7], disinhibited mammalian neocortex [8], chicken retina [9], and especially cardiac tissue [10, 11]. Rotors, resulting in reentries in heart tissue, are known to cause cardiac arrhythmias and even sudden death [12–14]. To understand the mechanism of the rotor initiation and to eliminate the consequential malignant arrhythmias, the effects of the electrophysiological heterogeneity are thought to be one of the major causes and have attracted much attention [15–20].

Destabilization of wave fronts and the subsequent initiation of reentrant excitation can result from both intrinsic and dynamical heterogeneity. For example, a possible result of a multiple pacing of cardiac tissue is a dynamically induced heterogeneities of repolarization leading to a destabilization of a propagating wave and initiation of a self-sustained activity [21–25]. The heterogeneities of the electrical coupling and automaticity also might lead to the appearance of fragmented ectopic waves [26]. Furthermore, the boundary layer between the well-coupled and uncoupled cardiac tissues would create a rich set of phenomena associated with self-organized spiral waves and ectopic waves [27]. Transient rotors could be also initiated in complicated and rare situations [28, 29]. An abrupt transition of the coupling gradient would block the wave propagation, but nearby parts with a smooth transition would not and therefore cause a reentry. The wave blockage was also found in a model of human ventricular tissue due to an abrupt transition of the anisotropic coupling [30].

As exemplary mentioned above, there are many situations, which can lead to the initiation of a self-sustained excitation wave. One novel scenario, which was found recently in a generic model for the excitable system, is that a region with the fast propagation of an excitation wave might cause a unidirectional block of the wave propagation [31]. This unidirectional block is realized based on a phenomenon termed source-sink mismatch in the cardiology literature [32]. The further study demonstrated that rotors could be nucleated in the presence of a localized fast propagation region (FPR) after application of one stimulus only [33]. It was shown also that various geometrical factors play an important role in rotor initiation [34].

Here we show that in the two-dimensional medium the flat boundary of a rectangularly shaped FPR may block the propagation of the outside excitation wave. However, a large local curvature at the rounded corner of the FPR would prevent the blockage and thus let the outside excitation penetrate into the FPR causing a rotor initiation. We demonstrate that the rotor initiation critically depends on the size of the FPR and the degree of the heterogeneity. If the FPR size is below a certain threshold, the initiated rotor would vanish eventually when it approaches the medium's boundary. The critical size of the FPR depends on the degree of the heterogeneity.

2. Model and Method

Although some aspects of the complex electrical activity in the cardiac tissue need to be studied using the reaction-diffusion equations with the detailed ionic channel model, many general spatiotemporal features of cardiac dynamics can be reproduced by a relatively simple but universal two-component system as follows

$\begin{array}{ll}\frac{\partial u}{\partial t}=\nabla ·(D\nabla u)-AF(u,v),& (1)\end{array}$

$\begin{array}{ll}\frac{\partial v}{\partial t}=ϵG(u,v),& (2)\end{array}$

where u and v are the activator and inhibitor, respectively. The local kinetics of u and v are specified by the nonlinear functions F(u, v) and G(u, v). Let us consider a widely-used computationally-efficient model proposed by Barkley [35]. In this generic model, the two nonlinear functions read as

$\begin{array}{ll}F(u,v)=u(u-1)\left(u-\frac{v+b}{a}\right),& (3)\end{array}$

$\begin{array}{cc}G(u,v)=\{\begin{array}{cc}(u-v)& u\ge v,\\ k_{ϵ}(u-v)& u<v.\end{array}& (4)\end{array}$

To simulate a relatively quick recovery of the excitability after a pulse generation, the original Barkley model is slightly modified by introducing an additional parameter k_ϵ > 1.

The propagation wave velocity in the Barkley model is proportional to $\sqrt{DA}$. Spatial heterogeneity of the parameters D and A can result in creation of FPR capable to initiate spiral waves [33, 34].

Below a FPR is considered to be a rounded rectangular region of the length L with two rounded corners of the radius R, as illustrated in Figure 1A. Inside this region, the values of D and/or A are larger than outside. It is inserted into a square shaped medium of size 450 × 450 in space unit, and the no-flux boundary conditions at the boundaries are implied. The parameters a = 1, b = 0.44, ϵ = 0.00011 and k_ϵ = 10 are fixed in our simulations. We use the explicit finite difference method in the Cartesian coordinates. The staircase approximation is used at the rounded corner. The spatial step dx = 0.3, and the time step dt = 0.01, when R ≥ 15. The finer spatial and time steps are used for smaller R. For instance, dx = 0.2 and dt = 4.44 × 10⁻³, when R = 10, and dx = 0.1 and dt = 1.11 × 10⁻³, when R = 5.

FIGURE 1

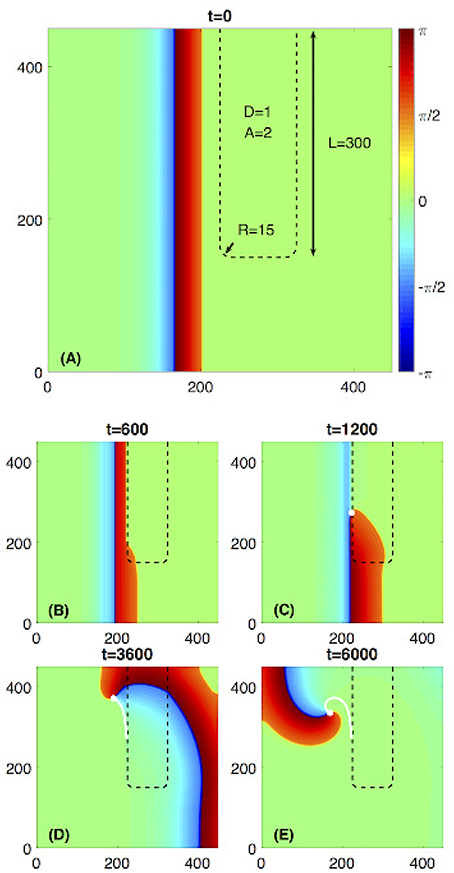
Figure 1. Rotor initiated due to a rectangularly shaped fast propagation region (FPR). (A) The FPR marked by a black dashed line has length L = 300 and two rounded corners with the radius of R = 15. Within the FPR D = 1, A = 2 and outside the FPR D = 1 and A = 1. A plane wave propagates from the left toward the FPR. (B) The wave is blocked at the flat boundary of the FPR but penetrates into it at the rounded corner. (C–E) A rotor is initiated and stably rotates. The white dot and line are the rotors phase change point (PCP) and its trajectory, respectively.

The variables u and v in Equations (1)-(4) are vary within the range 0 < u < 1 and 0 < v < a−2b. The spatiotemporal dynamics of u and v is represented in Figures 1–4, 6, 7 by color-coded distribution of the excitation phase ϕ, where −π < ϕ < π. The phase is defined as ϕ = α + 3π/4, in which an angle α is determined by the direction of the vector with components (u − 1/2) and (v − a/2 + b)/(a − 2b) on the (u, v) phase plane. According to this definition, ϕ = 0 corresponds to the resting state of the medium (green areas in Figures 1–4, 6, 7), narrow yellow (dark blue) regions represent the wave front (wave back), and red areas correspond to a wave plateau, whereas blue ones represent the refractory regions.

3. Results

3.1. Rotor Initiated from a Rectangularly Shaped FPR

To illustrate the phenomenon of the rotor initiation from a rounded rectangular heterogeneous region, we set L = 300, R = 15, as shown in Figure 1. Inside this region D = 1 and A = 2, while outside D = 1 and A = 1. Due to an increased value of A, this rounded rectangular region could be considered as a FPR since the propagation velocity inside it is larger than outside. For such parameter choice, the flat boundary of the FPR would unidirectionally block a plane wave propagating through the medium outside FPR. However, the local curvature at the rounded corner of the FPR 1/R ≈ 0.067 is large enough to prevent the blockage and let the excitation penetrate into the FPR. Then, a phase change point (PCP) emerges, and a self-sustained rotor is initiated. The process is similar to the scenario described in Zykov et al. [33, 34].

However, if the local curvature at the rounded corner of the FPR is below some critical value, as illustrated in Figure 2, there would be no penetration into the FPR at the corner. Thus, the FPR would act for propagating waves as an obstacle. The transient rotor starts to circulate around the FPR and vanishes eventually when it approaches the medium boundary. The critical value of the corner curvature depends on D and A within the FPR.

FIGURE 2

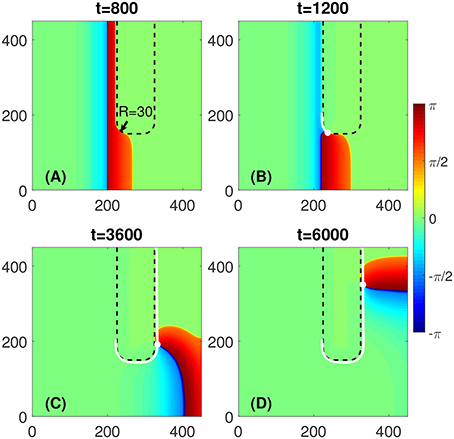
Figure 2. No wave penetration occurs at the rounded corner of a FPR if R is above some critical value. (A) No penetration is observed at the corner of radius R = 30, as an example. (B–D) The PCP (white dot) would travel along the FPR boundary and vanishes eventually, as shown by its trajectory (white line). Other parameters are the same as in Figure 1.

Another scenario appears when the values of D and/or A within the FPR are below some critical values. As illustrated in Figure 3, in this case, the flat boundary of the FPR would not block the propagating wave. The plane wave would become curved, propagates through the FPR, and vanishes eventually when it reaches the medium's boundary. No self-sustained rotors are initiated.

FIGURE 3

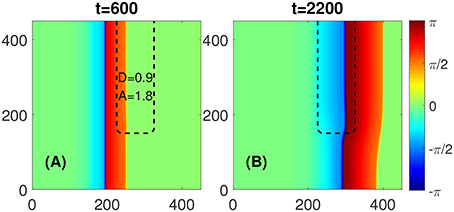
Figure 3. No blockage occurs at the flat boundary of a FPR if D and/or A inside it are below some critical values. (A) No PCP would emerge for D = 0.9 and A = 1.8, as an example. (B) A slightly deformed plane wave propagates through the FPR and disappears at the right boundary of the medium. Other parameters are the same as in Figure 1.

3.2. Critical Length of a Rectangularly Shaped FPR

For a given D and A within the FPR, its length L is also a critical parameter to initiate a self-sustained rotor. If L is shorter than a certain critical length, as illustrated in Figure 4, the PCP would approach the medium boundary and vanishes eventually. After the PCP has disappeared, a curved wave propagates through the medium and vanishes at its boundary. Thus, no rotors are initiated.

FIGURE 4

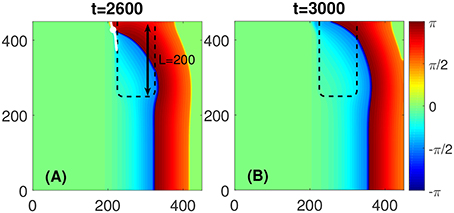
Figure 4. No stably rotating rotor appears if L is shorter than a critical length. (A) Although a PCP would be initiated like in the case shown in Figures 1A–C, the PCP (white dot) would be too close to the medium boundary and vanishes eventually, as shown by its trajectory (white line). (B) After the PCP vanishing the curved wave would propagate to the right boundary of the medium, and no stably rotating rotor would exist. The FPR length L = 200 and other parameters are the same as in Figure 1.

We investigate in detail the critical length of the FPR needed to initiate a self-sustained rotor and determine the boundaries of the non-penetration and non-blockage regions for various A and D, as shown in Figure 5. Here the radius of the rounded corner is fixed as R = 15. As shown in Figure 5A, the non-penetration occurs when D and/or A are above some critical values, and the non-blockage occurs when D and/or A are below other critical values. Between these two boundaries, the initiation of a self-sustained rotor is possible with the color-coded critical length L_c of the rounded rectangular FPR. The larger D and/or A are, the shorter L_c would be.

FIGURE 5

Figure 5. (A) The phase diagram shows the regions of non-penetration, non-blockage, and rotor initiation due to the FPR with critical length L_c for different values of D and A but fixed R = 15. (B) The detailed dependence of L_c on A for fixed D = 1 and different R. (C) The detailed dependence of L_c on D for fixed A = 2 and different R.

This dependence of L_c on D and A is further confirmed in Figures 5B,C, where we show how L_c shrinks as D or A increases for different corner radius R. Figures 5B,C also demonstrate how L_c changes as R increases.

We also investigate the impact of the width of the rectangular FPR. The simulation results show that the FPR width has no significant effect on the rotor initiation if it is larger than 2R.

4. Analysis

To analyze the conditions for the rotor initiation by a rounded rectangular FPR, we simplify the two-component reaction-diffusion equations by taking ϵ = 0 and setting v = 0. In this limiting case, the initial Equations (1)–(4) can be reduced to

$\begin{array}{ll}\frac{\partial u}{\partial t}=\nabla ·(D\nabla u)-Au(u-1)\left(u-\frac{b}{a}\right).& (5)\end{array}$

This equation describes a bistable extended system, where the resting state u = 0, the excited state u = 1, and the unstable steady state u = b/a exist. The value β = b/a is the excitation threshold. The bistable equation has been widely used to analyze the propagation of the wave front when ϵ ≪ 1 [36]. It is also useful to establish fundamental mechanism behind the blockage and penetration at the FPR boundary.

4.1. Analysis of the Non-blockage and Non-penetration Boundary

To analyze the conditions for the blockage of the initial plane wave at the flat boundary of the FPR, we could further simplify Equation (5) to consider a stationary wave profile for a one-dimensional bistable system as follows

$\begin{array}{ll}\frac{d}{dx}\left(D(x)\frac{du}{dx}\right)-A(x)u(u-1)(u-\beta )=0,& (6)\end{array}$

where A(x) = 1, D(x) = 1 for x ≤ 0 and A(x) = A, D(x) = D for x > 0. The boundary conditions and the continuity conditions at x = 0 read as

$\begin{array}{l}u{|}_{x=-\infty }=1,u{|}_{x=\infty }=0,\\ \frac{du}{dx}{\left|{}_{x=-\infty }=\frac{du}{dx}\right|}_{x=\infty }=0,& (7)\end{array}$

$\begin{array}{cc}\frac{du}{dx}{\left|{}_{x=-0}=D\frac{du}{dx}\right|}_{x=+0}.& (8)\end{array}$

Multiplying Equation (6) by du/dx, integrating over x from −∞ to 0 and from 0 to ∞, using Equations (7) and (8), we obtain the following equation

$\begin{array}{ll}{\displaystyle {\int }_1^{u(0)}}u(u-1)(u-\beta )du=DA{\displaystyle {\int }_0^{u(0)}}u(u-1)(u-\beta )du,& (9)\end{array}$

which determines the value of u(0) at the point of the parameter jump as a function of the product DA. Note that the front could be stopped only if u(0) < β. Thus, the Equation (9) for u(0) = β gives the critical value of the product DA, above which the propagation blockage could be observed. Therefore, the non-blockage boundary in the phase diagram has an analytical form as follows

$\begin{array}{ll}DA<\frac{(1-{\beta }^2){(1-\beta )}^2}{{\beta }^3(2-\beta )}.& (10)\end{array}$

This expression represents a modification of another one mentioned already in Zykov et al. [33, 34]. It looks more simple because of the normalized values of the parameters A = 1 and D = 1 in the part of the medium outside an FPR. This normalization performed by rescaling of time and space variables in Equation (5) is made without loss of generality. It is worth to note also that this expression generalizes a similar analysis for the case of a steep rise of the parameter D under constant value of A performed earlier in Pauwelussen [37] and Mornev [38].

It is important to stress that the obtained analytical expression (10) gives a very precise estimate of the non-blockage boundary obtained by numerical computations illustrated by Figure 5A. The deviations do not exceed one percent.

To analyze the conditions to prevent wave penetration at the rounded corner of the FPR, we look in detail into the process of the (non-)penetration, as illustrated in Figure 6A. The initial plane wave would become curved at the rounded corner of the FPR. It is analogous to a circular wave penetrating into a circular FPR with a radius r, as shown in Figure 6B.

FIGURE 6

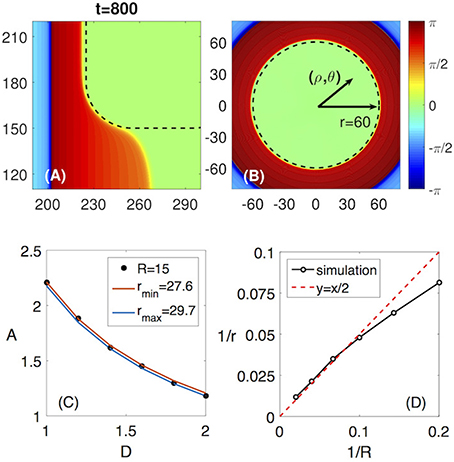
Figure 6. Analogy between the non-penetration at the corner of a rectangularly shaped FPR and the non-penetration of a circular wave into a circular shaped FPR. (A) The non-penetration at the rounded corner of the FPR (zoomed from Figure 2A). (B) A circular wave blocked by the circular shaped FPR of the radius r = 60. (C) The non-penetration boundaries for the rectangularly shaped FPR for R = 15 (black dots) and for the circular wave and the circular shaped FPR with the radii r_min = 27.6 (red line) and r_max = 29.7 (blue line). (D) The dependence of 1/r = 1/(2R) is proofed to be valid for a large range of R.

To verify the analogy, we compare the non-penetration boundaries for the rounded rectangular FPR with the circular FPR in a A − D diagram. As shown in Figure 6C, the non-penetration boundary for the rectangularly shaped FPR with the corner radius of R is located between two curves corresponding to non-penetration boundaries for the circular FPR with the radius r_min and r_max, as shown in Figure 6C. Note, that in a vicinity of the rounded corner the boundary curvature jumps from zero to 1/R. Hence, it is natural to assume that the non-penetration boundaries for the circular FPR with the curvature about an averaged curvature of the rounded corner, 1/r ≈ 1/(2R), will approximate the non-penetration boundary for the rounded rectangular FPR. This approximation is working well for 10≤R≤50, as demonstrated in Figure 6D.

Therefore, we can use the results of the simulations for the circular FPR and the radius relation r ≈ 2R to approximate the non-penetration boundary for the rounded rectangular FPR. Since the circular FPR in the polar coordinates (ρ, θ) has a rotational symmetry, this allows us to transform the two-dimensional Equations (1) and (2) to the one-dimensional ones as follows

$\begin{array}{ll}\frac{\partial u}{\partial t}=\frac{1}{\rho }\frac{\partial }{\partial \rho }\left(D(\rho )\rho \frac{\partial u}{\partial \rho }\right)-A(\rho )F(u,v),& (11)\end{array}$

$\begin{array}{ll}\frac{\partial v}{\partial t}=ϵG(u,v).& (12)\end{array}$

This one-dimensional equations considerably simplifies the analysis. The corresponding computations have been performed by use of the explicit finite difference method with the spatial step dρ = 0.3 and the time step dt = 0.005. In order to simulate a circular wave approaching a circular shaped FPR, a part of the medium with ρ > ρ_ext is assumed to be in the excited state at t = 0, as illustrated in Figure 6B.

4.2. Analysis of the Critical Length L_c of a Rounded Rectangular FPR

To understand the mechanism behind the dependence of L_c on the characteristics of the FPR, i.e., D, A and R, we separate L_c into three parts, as shown in Figure 7. The first part is the distance from the rounded corner of the FPR, where the penetration of the excitation starts, to the position where the PCP emerges for the first time. This part, named L_exc, should be determined by the characteristics of the FPR since it describes the propagation of the excitation inside the FPR. The second part is the distance from the initial position of the PCP to the highest position in its trajectory. This part, named L_r, describes the range of the PCP trajectory along the FPR but located outside the FPR. This trajectory part should be practically independent of the FPR characteristics. The third part is the distance from the highest PCP position in its trajectory to the top medium boundary. This part, named L_min, should be above some minimum distance toward the top medium's boundary. Otherwise, the PCP would be too close to the boundary and vanishes eventually. The value of L_min should only depend on the given characteristics of the medium outside the FPR, and thus is fixed in our simulations. Therefore, the value of L_c is the sum of L_min and L_r, which are fixed, and L_exc, which is determined by D and A inside the FPR, and R at the FPR corner.

FIGURE 7

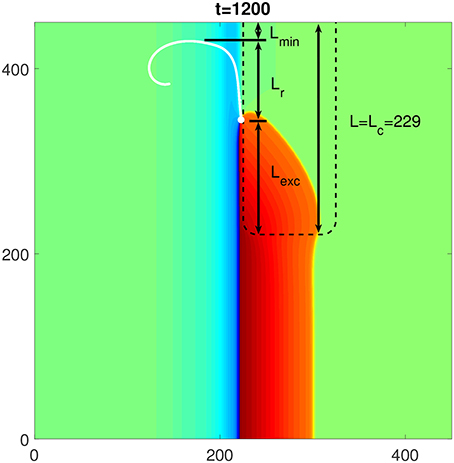
Figure 7. The composition of the critical length L_c of a rectangularly shaped FPR to initiate a rotor. The white dot and line are the initial location and the following trajectory of the PCP, respectively. Three components of L_c are: L_min which describes the minimum distance of a persistent PCP from the top medium boundary, L_r which describes the vertical range of the PCP trajectory in the medium outside the FPR, and L_exc which describes the propagation of the penetrated excitation within the FPR. The FPR length L = L_c = 229 and other parameters are the same as in Figure 1.

Hence, L_exc is the only part which is varied and depends on D, A, and R. Its value may read as

$\begin{array}{ll}{L}_{exc}={\displaystyle {\int }_{t_p}^{t_r}}{c}_{v}dt,& (13)\end{array}$

where t_p is the time when the penetration of the excitation at the rounded corner of the FPR starts, t_r is the time when the PCP initially emerges, and c_v is the propagation velocity of the excitation along the flat border of the FPR. As shown in Figure 8, t_r remains constant for different sets of D, A, and R, while t_p varies. The velocity c_v changes with time and also depends on D, A, and R.

FIGURE 8

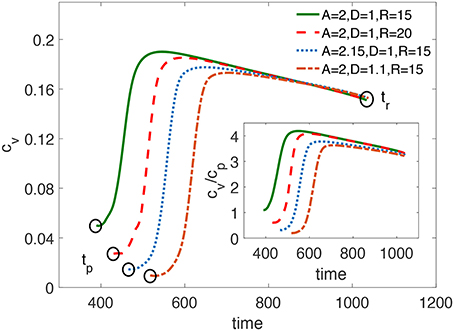
Figure 8. The propagation speed c_v of the penetrated excitation along the vertical flat boundary of a FPR over time. t_p is the time when the penetration at the FPR corner starts. t_r is the time when the PCP initially emerges. Larger D, A, or R lead to a delayed t_p, but nearly the same t_r. The subfigure shows the change of the ratio between c_v and c_p over time, where c_p is the plane wave velocity for the medium's parameters established inside the FPR.

Based on these results, three conclusions can be made. First, larger D, A, or R would delay t_p. Second, t_r is nearly the same in all cases since it is determined by the time when the wave back of the plane wave reaches the left flat boundary of the FPR. Therefore, it is determined by the fixed characteristics of the medium outside the FPR. Third, for the most part of the trajectory, c_v is larger than the plane wave velocity c_p in a homogeneous medium where the parameters D and A are the same as inside the FPR, as shown in the subfigure of Figure 8. Obviously, c_v is accelerated since the value of the activator u > 0 in the vicinity of the left flat boundary of the FPR due to a diffusive influence of the blocked plane wave. Such increase of the propagation velocity is a general effect in bistable models of one-dimensional excitable media if ahead of the wave front the activator value exceeds the resting state [39]. In the context of a flame propagation, which also can be described by Equation (6), this phenomenon is named as preheating effect [40].

4.2.1. Mechanism of Delay of t_p

The delay of t_p occurs at the rounded corner of a FPR. As shown above, the penetration of the plane wave into the rounded corner with the radius of R is analogous to the penetration of a circular wave into a circular FPR with the radius r ≈ 2R. Thus, considering the analogy and just focusing on the propagation of the excitation wave front, we could use the bistable version of Equations (11) and (12) to investigate the variation of u at the rounded FPR corner with time. The bistable equation for the circular FPR expressed in the polar coordinates (ρ, θ) reads as

$\begin{array}{ll}\frac{\partial u}{\partial t}=\frac{1}{\rho }\frac{\partial }{\partial \rho }\left(D(\rho )\rho \frac{\partial u}{\partial \rho }\right)-A(\rho )u(u-1)(u-\beta ).& (14)\end{array}$

Using the finite difference method with space step Δρ, at the circular FPR boundary r = 2R, Equation (14) could be expanded as

$\begin{array}{l}\frac{{\partial u|}_r}{\partial t}=\frac{1}{r\Delta {\rho }^2}[{D|}_{r+\Delta \rho /2}\left(r+\Delta \rho /2\right)\left({u|}_{r+\Delta \rho }-{u|}_r\right)\\ -{D|}_{r-\Delta \rho /2}(r-\Delta \rho /2)\left({u|}_r-{u|}_{r-\Delta \rho }\right)]\\ -{A|}_r{u|}_r\left({u|}_r-1\right)\left({u|}_r-\beta \right),& (15)\end{array}$

where

$\begin{array}{l}\begin{array}{l}D{|}_{r+\Delta \rho /2}=\frac{1}{2}(D{|}_{r+\Delta \rho }+D{|}_r)=\frac{1}{2}(1+D),\\ D{|}_{r-\Delta \rho /2}=\frac{1}{2}(D{|}_r+D{|}_{r-\Delta \rho })=\frac{1}{2}(D+D)=D,\\ A{|}_r=A.\end{array}\end{array}$

When the circular wave reaches the circular FPR boundary at r, we have u|_r−Δρ < u|_r < u|_r+Δρ, and u|_r is still smaller than the excitation threshold β. Thus, u|_r(u|_r − 1)(u|_r − β) > 0. Then we can divide the right hand side of Equation (15) into two terms. The term which would cause an increase of u|_r with time is named as the source term. It reads as

$\begin{array}{ll}\frac{1}{\Delta {\rho }^2}\frac{1+D}{2}\left(1+\frac{\Delta \rho }{2r}\right)(u{|}_{r+\Delta \rho }-u{|}_r).& (16)\end{array}$

The other term which would cause a decrease of u|_r with time is named the sink term. It reads as

$\begin{array}{ll}-& \frac{1}{\Delta {\rho }^2}D\left(1-\frac{\Delta \rho }{2r}\right)(u{|}_r-u{|}_{r-\Delta \rho })\\ -& Au{|}_r(u{|}_r-1)(u{|}_r-\beta ).& (17)\end{array}$

From the above expressions of two terms, we find that larger D would enhance the source term (Equation 16) but enhances the sink term (Equation 17) even more. Larger A would not affect the source term but enhance the sink term. Larger r, i.e., 2R in the analogy, would reduce the source term, but enhance the sink term.

Therefore, the conclusion is that the larger D, A and R are, the stronger the sink term would be, and the later u|_r reaches the excitation threshold. This is the cause of the delay of the start time of the excitation penetration near the corner of the rounded rectangular FPR, i.e., t_p in Equation (13). As shown in Figure 9, the numerical simulation results prove our explanation of the delay effect by plotting the value of u at the corner of the rounded rectangular FPR with time.

FIGURE 9

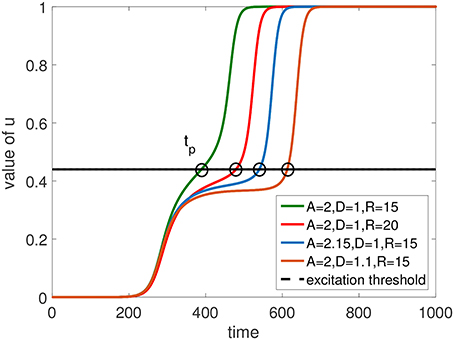
Figure 9. Temporal dynamics of the value of u at the junction point between the flat boundary and the corner of a rectangularly shaped FPR. An increase of D, A, or R inside the FPR delays the time t_p when the excitation threshold is reached.

4.2.2. Influence of “Preheating” on c_v

Inside the rounded rectangular FPR, the accelerating effect on the propagation velocity c_v occurs near its vertical flat boundary. When the initial plane wave is blocked at the flat boundary, although it does not penetrate inside the FPR, it yet increases the value of u in a vicinity of the FPR boundary. This is quite similar to a preheating effect in the flame propagation when the fuel temperature ahead of the flame front is increased [39, 40]. This “preheated” medium would accelerate the propagation velocity c_v of the excitation wave front along the vertical flat boundary of the FPR.

The mechanism of the accelerated wave front could be analytically understood from Equation (5) for the bistable distributed system. If a preheated part of the FPR near its flat boundary is assumed as a nearly one-dimensional medium, we can establish a comoving frame as z = x + ct, where c is the propagation velocity of the wave front. Thus, Equation (5) would be simplified as

$\begin{array}{ll}D{u}_{zz}-c{u}_z-Au(u-1)(u-\beta )=0.& (18)\end{array}$

The preheating effect increases the value of u to some preheated state u_p, and makes the excitation start from u_p > 0 instead of the resting state u = 0. Based on the theory described in Keener and Sneyd [36], the propagation velocity of the excitation wave front could be expressed as

$\begin{array}{ll}c(u_p)=\frac{{\int }_{u_p}^{1}Au(1-u)(u-\beta )du}{{\int }_{-\infty }^{\infty }{u}_z^{2}dz}=\frac{{\int }_{u_p}^{\beta }Au(1-u)(u-\beta )du+{\int }_{\beta }^{1}Au(1-u)(u-\beta )du}{{\int }_{-\infty }^{\infty }{u}_z^{2}dz}.& (19)\end{array}$

The analytical expressions of Equation (19) would be obtained for two limiting cases. The first one is the unpreheated case at which u_p is equal to the resting state. That gives

$\begin{array}{ll}c(0)=\sqrt{DA/2}(1-2\beta ).& (20)\end{array}$

The second is the fully preheated case at which u_p is equal to the excitation threshold β. This gives

$\begin{array}{ll}c(\beta )=\sqrt{DA/2}(1+\beta ).& (21)\end{array}$

The above two analytical expressions apparently demonstrate that c(β) > c(0), since β > 0.

We also investigate the preheated propagation velocity in the numerical simulations of Equation (5). As shown in Figure 10, the numerical results elucidate the acceleration of the propagation velocity c(u_p) as a function of the preheated state u_p. The analytical results from Equations (20) and (21) perfectly describe both limiting cases following from these numerical data.

FIGURE 10

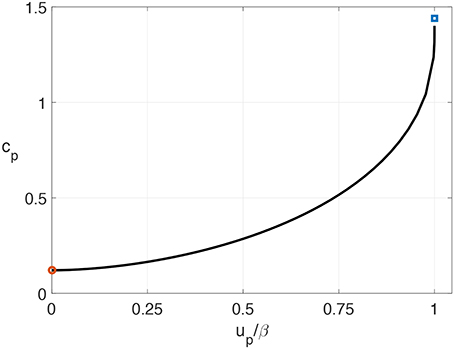
Figure 10. The propagation speed c_p corresponding to the preheated state u = u_p. The values of D = 1 and A = 2 are taken as an example. The solid line represents the numerical simulation results in a one-dimensional medium described by Equation (5). The value of u ahead of the wave front is set to be u_p. The open circle and square are the analytic results from Equations (20) and (21) at the limiting cases of u_p = 0 and u_p = β, i.e., the resting state and the excitation threshold, respectively.

5. Conclusions and Applications

Our results demonstrate that a self-sustained rotor could be initiated from the spatial heterogeneity, i.e., a rectangularly shaped FPR. We use a generic model to parameterize the heterogeneity with three parameters D, A, and R. In the D − A diagram at a given R, the region of the rotor initiation is located between the non-blockage and non-penetration regions. The two boundaries of the rotor initiation region could be estimated by the analytical equation for the bistable distributed system and the simulations in a one-dimensional medium for a circular FPR, respectively. We also show that to initiate the self-sustained rotor the length of the rounded rectangular FPR should be larger than the critical L_c. The critical value L_c depends on the parameters D and A, within the FPR, as well as on the radius R of a rounded corner.

Our findings in the generic model might be applicable to describe the electrophysiological dynamics of cardiac tissue. Indeed, the distribution of transmembrane potential V in a two-dimensional tissue could be described by the reaction-diffusion equation as follows [41]

$\begin{array}{ll}\frac{\partial V}{\partial t}=\frac{1}{\chi C_m}\nabla (\sigma ·\nabla V)-\frac{I_{ion}(V,\overrightarrow{h})}{C_m},& (22)\end{array}$

$\begin{array}{ll}\frac{\partial \overrightarrow{h}}{\partial t}=g(V,\overrightarrow{h}),& (23)\end{array}$

where χ is the surface-to-volume ratio of the cardiac cells, C_m is the membrane capacitance, σ is the tensor of electric conductivity, and I_ion is the sum of ion channel currents. Intensity of each separate current is determined by corresponding component of the vector $\overrightarrow{h}$. Equations (22) and (23) can be generalized into a two-component reaction-diffusion system as follows

$\begin{array}{ll}\frac{\partial V}{\partial t}=\nabla (D·\nabla V)-\frac{I_{ion}(V,h)}{C_m},& (24)\end{array}$

$\begin{array}{ll}\frac{\partial h}{\partial t}=g(V,h),& (25)\end{array}$

where the effective diffusion coefficient tensor D = σ/χC_m and the description of the ion currents is reduced to a scalar value h. In an isotropic tissue, we can simplify the tensors σ and thus D to be scalars. Thus, the reduced system which describes electrophysiological properties of the cardiac tissue looks similar to the reaction-diffusion model we use.

Nowadays many detailed models of human atria incorporate both structural and electrophysiological heterogeneities leading to differences in conduction velocity between the neighboring regions [42–44]. It is also well known that atrial fibrosis in the aging heart can result in spatial variations in the electrical conductivity of a part of the cardiac muscle [45]. If some regions within this part remain unchanged, they can resemble fast propagation regions introduced in our model. Note, that a similar nonhomogeneity in the electrical conductivity can appear, for instance, when fresh stem cells aggregates implanted in strongly remodeled cardiac tissue form gap junctions with adult cardiac myocytes [46]. Moreover, some cardiac diseases cause ion channel remodeling [47]. This remodeling can be represented as a variation of the term I_ion in Equation (22). This is to some extent equivalent to a variation of the parameter A in our model. If this remodeling occurs non-uniformly in space, one can expect the creation of some spots with a negligible variation of this parameter in comparison to its strong decrease in the surrounding regions. Thus, nonhomogeneous remodeling can results in a creation of fast propagation regions considered in this study.

Of course, the model used above is aimed to reproduce only most generic features of electrical activity in myocardial tissue. Investigation of specific dynamical features can be done by application of more detailed models widely used in the literature [48–50]. It is important to note that our recent results based on the Fenton-Karma model [48] indicate that all scenarios of rotor initiation obtained with the Barkley model are perfectly reproducible [33]. An obvious reason for this is that the restitution of action potential duration in detail reproduced in the Fenton-Karma model plays only a restricted role in the described scenarios, where spiral waves are generated after application of a single excitation stimulus. Of course, the following dynamics of the initiated rotors is strongly influenced by many other factors and specific features of cardiac tissue, which are not reproduced in the framework of the generic model used in the study.

Therefore, computer simulations of a real tissue in the framework of much more detailed models and most importantly experimental investigations definitely can help to verify the role of the observed scenario for generation of cardiac arrhythmias.

Author Contributions

All authors conceived of the presented idea. XG, AK, VZ performed the computations. All authors discussed the results and contributed to the final manuscript.

Funding

This work was supported by the National Natural Science Foundation of China under Grants No. 11447026 and No. 11705114, the Max Planck Society, the German Center for Cardiovascular Research (DZHK), and Grant DFG-SFB937 Collective Behavior of Soft and Biological Matter.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

1. Winfree AT. Spiral waves of chemical activity. Science (1972) 175:634–6. doi: 10.1126/science.175.4022.634

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Agladze KI, Krinsky, VI. Multi-armed vortices in an active-chemical medium. Nature (1982) 296:424–6. doi: 10.1038/296424a0

CrossRef Full Text | Google Scholar

3. Ouyang Q, Flesselles JM. Transition from spirals to defect turbulence driven by a convective instability. Nature (1996) 379:143–6. doi: 10.1038/379143a0

CrossRef Full Text | Google Scholar

4. Vanag VK, Epstein IR. Inwardly rotating spiral waves in a reaction-diffusion system. Science (2001) 294:835–7. doi: 10.1126/science.1064167

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Jakubith S, Rotermund HH, Engel W, Vonoertzen A, Ertl G. Spatiotemporal concentration patterns in a surface-reaction - propagating and standing waves, rotating spirals, and turbulence. Phys Rev Lett. (1990) 65:3013–6. doi: 10.1103/PhysRevLett.65.3013

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Sawai S, Thomason PA, Cox EC. An autoregulatory circuit for long-range self-organization in Dictyostelium cell populations. Nature (2005) 433:323–6. doi: 10.1038/nature03228

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Lechleiter J, Girard S, Peralta E, Clapham D. Spiral calcium wave-propagation and annihilation in xenopus-laevis oocytes. Science (1991) 252:123–6. doi: 10.1126/science.2011747

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Huang XY, Troy WC, Yang Q, Ma HT, Laing CR, Schiff SJ, et al. Spiral waves in disinhibited mammalian neocortex. J Neurosci. (2004) 24:9897–902. doi: 10.1523/JNEUROSCI.2705-04.2004

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Yu Y, Santos LM, Mattiace LA, Costa ML, Ferreira LC, Benabou K, et al. Reentrant spiral waves of spreading depression cause macular degeneration in hypoglycemic chicken retina. Proc Natl Acad Sci USA (2012) 109:2585–9. doi: 10.1073/pnas.1121111109

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Davidenko JM, Pertsov AV, Salomonsz R, Baxter W, Jalife J. Stationary and drifting spiral waves of excitation in isolated cardiac-muscle. Nature (1992) 355:349–51. doi: 10.1038/355349a0

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Gray RA, Pertsov AM, Jalife J. Spatial and temporal organization during cardiac fibrillation. Nature (1998) 392:75–8.

PubMed Abstract | Google Scholar

12. Carmelite E, Vereecke J. Cardiac Cellular Electrophysiology. New York, NY: Springer (2002).

13. Jalife J. Ventricular fibrillation: mechanisms of initiation and maintenance. Annu Rev Physiol. (2000) 62:25–50. doi: 10.1146/annurev.physiol.62.1.25

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Karma A. Physics of cardiac arrhythmogenesis. Annu Rev Condens Matt Phys. (2013) 4:313–37. doi: 10.1146/annurev-conmatphys-020911-125112

CrossRef Full Text | Google Scholar

15. Luther S, Fenton FH, Kornreich BG, Squires A, Bittihn P, Hornung D, et al. Low-energy control of electrical turbulence in the heart. Nature (2011) 475:235–9. doi: 10.1038/nature10216

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Alonso S, Bar M. Reentry near the percolation threshold in a heterogeneous discrete model for cardiac tissue. Phys Rev Lett. (2013) 110:158101. doi: 10.1103/PhysRevLett.110.158101

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Gao X, Zhang H. Mechanism of unpinning spirals by a series of stimuli. Phys Rev E (2014) 89:062928–32. doi: 10.1103/PhysRevE.89.062928

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Quail T, Shrier A, Glass L. Spiral symmetry breaking determines spiral wave chilarity. Phys Rev Lett. (2014) 113:158101. doi: 10.1103/PhysRevLett.113.158101

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Feng X, Gao X, Tang JM, Pan JT, Zhang H. Wave trains induced by circularly polarized electric fields in cardiac tissues. Sci Rep. (2015) 5:13349–57. doi: 10.1038/srep13349

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Kazbanov IV, ten Tusscher KHWJ, Panfilov AV. Effects of heterogeneous diffuse fibrosis on arrhythmia dynamics and mechanism. Sci Rep. (2016) 6:20835. doi: 10.1038/srep20835

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Fenton FH, Cherry EM, Hastings HM, Evans SJ. Multiple mechanisms of spiral wave breakup in a model of cardiac electrical activity. Chaos (2002) 12:852–92. doi: 10.1063/1.1504242

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Cherry EM, Fenton FH. Suppression on alternans and conduction blocks despite steep APD restitution: electrotonic, memory, and conduction velocity restitution effects. Am J Physiol Heart Circ Physiol. (2004) 286:H2332–41. doi: 10.1152/ajpheart.00747.2003

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Gelzer ARM, Koller ML, Otani NF, Fox JJ, Enyeart MW, Hooker GJ, et al. Dynamic mechanism for initiation of ventricular fibrillation in vivo. Circulation (2008) 118:1123–9. doi: 10.1161/CIRCULATIONAHA.107.738013

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Bueno-Orovio A, Hanson BM, Gill JS, Taggart P, Rodriguez B. In vivo human left-to-right ventricular differences in rate adaptation transiently increase pro-arrhythmic risk following rate acceleration. PLoS ONE (2012) 7:e52234. doi: 10.1371/journal.pone.0052234

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Bueno-Orovio A, Cherry EM, Evans SJ, Fenton FH. Basis for the unduction of tissue-level phase-2 reentry as a repolarization disorder in the Brugada syndrome. BioMed Res Int. (2015) 2015:197586. doi: 10.1155/2015/197586

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Pumir A, Arutunyan A, Krinsky V, Sarvazyan N. Genesis of ectopic waves: role of coupling, automaticity, and heterogeneity. Biophys J. (2005) 89:2332–49. doi: 10.1529/biophysj.105.061820

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Biktashev VN, Arutunyan A, Sarvazyan NA. Generation and escape of local waves from the boundary of uncoupled cardiac tissue. Biophys J. (2008) 94:3726–38. doi: 10.1529/biophysj.107.117630

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Zemlin CW, Pertsov AM. Bradycardic onset of spiral wave re-entry: structural substrates. Europace (2007) 9:59–63. doi: 10.1093/europace/eum205

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Zemlin CW, Mitrea GB, Pertsov AM. Spontaneous onset of atrial fibrillation. Physica D (2009) 238:969–75. doi: 10.1016/j.physd.2008.12.004

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Kudryashova NN, Kazbanov IV, Panfilov AV, Agladze KI. Conditions for waveblock due to anisotropy in a model of human ventricular tissue. PLoS ONE (2015) 10:e0141832–849. doi: 10.1371/journal.pone.0141832

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Gao X, Zhang H, Zykov VS, Bodenschatz E. Stationary propagation of a wave segment along an inhomogeneous excitable stripe. New J Phys. (2014) 16:033012–28. doi: 10.1088/1367-2630/16/3/033012

CrossRef Full Text | Google Scholar

32. Rudy Y. Reentry-insights from theoretical simulations in a fixed pathway. J Cardiovasc Electrophysiol. (1995) 6:294–312. doi: 10.1111/j.1540-8167.1995.tb00402.x

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Zykov V, Krekhov A, Bodenschatz E. Fast propagation regions cause self-sustained reentry in excitable media. Proc Natl Acad Sci USA (2017) 114:1281–6. doi: 10.1073/pnas.1611475114

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Zykov V, Krekhov A, Bodenschatz E. Geometrical factors in propagation block and spiral wave initiation. Chaos (2017) 27:093923. doi: 10.1063/1.4999473

PubMed Abstract | CrossRef Full Text | Google Scholar

35. Barkley D. A model for fast computer-simulation of waves in excitable media. Physica D (1991) 49:61–70. doi: 10.1016/0167-2789(91)90194-E

CrossRef Full Text | Google Scholar

36. Keener J, Sneyd J. Mathematical Physiology. New York, NY: Springer Science+Business Media (2009).

Google Scholar

37. Pauwelussen JP. Nerve impulse propagation in a branching nerve system: a simple model. Physica (1981) 4D:67–88. doi: 10.1016/0167-2789(81)90005-1

CrossRef Full Text | Google Scholar

38. Mornev OA. Elements of optics of autowaves. In: Krinsky VI, editor. Self-Organization: Autowaves and Structures Far from Equilibrium Springer Series in Synergetics, Vol. 28, Berlin; Heidelberg: Springer (1984). p. 111–8.

Google Scholar

39. Zykov VS. Simulation of Wave Processes in Excitable Media. New York, NY: Manchester University Press (1987).

Google Scholar

40. Dikici B, Pantoya ML, Levitas V. The effect of pre-heating on flame propagation in nanocomposite thermites. Combustion Flame (2010) 157:1581–5. doi: 10.1016/j.combustflame.2010.04.014

CrossRef Full Text | Google Scholar

41. Qu ZL, Hu G, Garfinkel A, Weiss JN. Nonlinear and stochastic dynamics in the heart. Phys Rep. (2014) 543:61–162. doi: 10.1016/j.physrep.2014.05.002

PubMed Abstract | CrossRef Full Text | Google Scholar

42. Seemann G, Höper C, Sachse FB, Dössel O, Holden AV, Zhang H. Heterogeneous three-dimensional anatomical and electrophysiological model of human atria. Philos Trans R Soc A (2006) 364:1465–81. doi: 10.1098/rsta.2006.1781

PubMed Abstract | CrossRef Full Text | Google Scholar

43. Xie Y, Garfinkel A, Camelliti P, Kohl P, Weiss JN. Effects of fibroblast-myocyte coupling on cardiac conduction and vulnerability to reentry: a computational study. Heart Rhythm (2009) 6:1641–9. doi: 10.1016/j.hrthm.2009.08.003

PubMed Abstract | CrossRef Full Text | Google Scholar

44. Sanchez C, Bueno-Orovio A, Pueyo E, Rodriguez B. Atrial fibrillation dynamics and ionic block effects in six heterogeneous human 3D virtual atria with distinct repolarization dynamics. Front Bioeng Biotechnol. (2017) 5:29. doi: 10.3389/fbioe.2017.00029

PubMed Abstract | CrossRef Full Text | Google Scholar

45. Rother J, Richter C, Turco L, Knocj F, Mey I, Luther S, et al. Crosstalk of cardiomyocytes and fibroblasts in co-cultures. Open Biol. (2015) 5:150038. doi: 10.1098/rsob.150038

PubMed Abstract | CrossRef Full Text | Google Scholar

46. Smit NW, Coronel R. Stem cells can form gap junctions with cardiac myocytes and exert pro-arrhythmic effects. Front Physiol. (2014) 5:419–26. doi: 10.3389/fphys.2014.00419

PubMed Abstract | CrossRef Full Text | Google Scholar

47. Nattel S. Effects of heart disease on cardiac ion current density versus current amplitude: important conceptual subtleties in the language of arrhythmogenic ion channel remodeling. Circul Res. (2008) 102:1298–300. doi: 10.1161/CIRCRESAHA.108.178087

PubMed Abstract | CrossRef Full Text | Google Scholar

48. Fenton F, Karma A. Vortex dynamics in three-dimensional continuous myocardium with fiber rotation: filament instability and fibrillation. Chaos (1998) 8:20–47. doi: 10.1063/1.166311

CrossRef Full Text | Google Scholar

49. Faber GM, Rudy Y. Action potential and contractility changes in [Na(+)](i) overloaded cardiac myocytes: a simulation study. Biophys J. (2000) 78:2392–404. doi: 10.1016/S0006-3495(00)76783-X

PubMed Abstract | CrossRef Full Text | Google Scholar

50. Bueno-Orovio A, Cherry E, Fenton F. Minimal model for human ventricular action potentials in tissue. J Theor Biol. (2008) 253:544–60. doi: 10.1016/j.jtbi.2008.03.029

PubMed Abstract | CrossRef Full Text | Google Scholar