A Theoretical Approach to Norm Ecosystems: Two Adaptive Architectures of Indirect Reciprocity Show Different Paths to the Evolution of Cooperation

Indirect reciprocity is one of the basic mechanisms to sustain mutual cooperation, by which beneficial acts are returned, not by the recipient, but by third parties. This mechanism relies on the ability of individuals to know the past actions of others, and to assess those actions. There are many different systems of assessing others, which can be interpreted as rudimentary social norms (i.e., views on what is “good” or “bad”). In this paper, impacts of different adaptive architectures, i.e., ways for individuals to adapt to environments, on indirect reciprocity are investigated. We examine two representative architectures: one based on replicator dynamics and the other on genetic algorithm. Different from the replicator dynamics, the genetic algorithm requires describing the mixture of all possible norms in the norm space under consideration. Therefore, we also propose an analytic method to study norm ecosystems in which all possible second order social norms potentially exist and compete. The analysis reveals that the different adaptive architectures show different paths to the evolution of cooperation. Especially we find that so called Stern-Judging, one of the best studied norms in the literature, exhibits distinct behaviors in both architectures. On one hand, in the replicator dynamics, Stern-Judging remains alive and gets a majority steadily when the population reaches a cooperative state. On the other hand, in the genetic algorithm, it gets a majority only temporarily and becomes extinct in the end.

Introduction

Cooperative relationships such as I-help-you-because-you-help-me relations can often be found in both biological systems and human societies. Cooperative behaviors are obviously essential to make societies effective and smooth. However, evolutionary biologists and social scientists have long been puzzled about the origin of cooperation. Recently, scientists from a variety of fields such as economics, mathematics and physics have been tackling the puzzle using tools developed in each discipline.

According to a thorough review published from statistical physics viewpoints recently [1], there have been numerous contributions from physicists to this area for the past decade. In those researches, diverse methods to handle many interacting particles developed in statistical physics are used to investigate interactions of biological and social elements.

Following the context of the physics literature, in this paper, we deal with interactions of “social norms.” Social norms are interpreted as views on what is “good” or “bad” and play an essential role in indirect reciprocity based on reputation systems. Indirect reciprocity is known as one of the main mechanisms for the emergence of cooperation. It has a long history and has been amply documented in human populations [2–12]. One feature of indirect reciprocity is that helpful acts are returned, not by the recipient as in direct reciprocity, but by third parties [13–15]. To decide helpful acts therefore needs information on others, who can be possible recipients in the future.

As mentioned in Nowak and Sigmund [16], there are two main motivations to pursue the investigation of indirect reciprocity. One concerns the evolution of human communities: how can cooperation emerge in villages and small-scale societies? (see for instance [17, 18]) The other motivation is related to the recent rapid growth of anonymous interactions on a global scale, made possible by the spread of communication networks on the internet: how can cheating be avoided in on-line trading [19]? In both cases, simple, robust methods for assessing others, i.e., social norms are necessary.

Vast studies on indirect reciprocity in the framework of evolutionary game theory have discovered various types of norms or assessment rules that enhance the evolution of cooperation in the modern society with highly mobile interactions. Theoretically, assuming that the same norm is adopted by all members of a population, Ohtsuki and Iwasa have shown that only eight out of 4,096 resulting possible norms lead to a stable regime of mutual cooperation. These are said to be the “leading eight” [20, 21]. In this context, “stable” means that the corresponding population cannot be invaded by other action rules. However, this does not settle the issue on whether the focal norm can be invaded by other norms (i.e., assessment rules) or not.

Many theoretical studies also considered another stability criterion. Those studies focus on whether the corresponding population cannot be invaded by or can invade into unconditional strategies such as perfect cooperators and perfect defectors [21–24]. Clearly, these previous studies do not allow us to fully compare different norms either.

If one wants to analyze the evolution of even the simplest system of morals, one has to consider the interaction of several assessment rules in a population. Some studies meet the theme. For example, comparing Simple-Standing with Stern-Judging, both members of the leading eight, is an important task to explore a champion of the assessment rules using second-order information. Uchida and Sigmund [25] analyzed the competition of these two different rudimentary norms and established significant findings.

Despite the theoretical developments of Uchida and Sigmund [25] on analyzing multiple rules, its approach cannot describe a mixture of more than a few rules. Real society, however, comprises a melting pot of various norms that interact with each other. Therefore an imperative next step of studies on indirect reciprocity would be to develop an analytical tool which can deal with “norm ecosystems” in which more than a few norms coexist, interact and compete. Although some insights have been derived in a research using individual-based simulations [26], a new theoretical approach may capture co-evolution of diverse norms more in detail.

Therefore the main focus of the present paper is in developing a systematic analytical methodology with which entanglements of all sixteen norms using second-order information can be formulated in an equation system. Extending the methodology proposed by Uchida and Sigmund [25], we see that the key problem, i.e., determining the average payoff of each norm surrounded by other norms to determine its fitness, comes down to a linear problem (i.e., a task of solving an inhomogeneous linear equation system). Thus it is computationally feasible to calculate the payoffs even when to deal with mixture of many norms. Uchida and Sigmund [25] treated a special case of the linear problem analyzed here.

The authors' development is useful not only for rigorous analysis of norm ecosystems, but also helps compare different “adaptive architectures.” Here an adaptive architecture means a way for individuals to adapt to their environments. In this paper, we take up the two representative architectures, replicator dynamics and genetic algorithm. Although these architectures are popular in the literature, they are studied independently in different domains and their comparison in the framework of evolutionary game theory has not yet been done because there has been no technical method developed to capture all strategies in a norm space at once as the study of genetic algorithm requires. Our approach offers a first opportunity to theoretically analyze a comparison of replicator dynamics and genetic algorithm in evolutionary game theory.

The analysis reveals that the two representative adaptive architectures show different paths to the evolution of cooperation. We find that Stern-Judging, one of the best studied norms in the literature, plays important but different roles in both cases [25, 27, 28]. In the replicator dynamics, Stern-Judging remains alive and gets a majority whenever the population reaches a cooperative state. On the other hand, in the genetic algorithm, it gets a majority just before cooperation rate starts rising but becomes extinct after the cooperation has been accomplished.

In the next section, we describe the model ecosystem, derive the equation to analyze it and introduce the adaptive architectures. Then we present the results and discuss them.

Materials and Methods

Game, Norm, and Payoff

An infinitely large, well-mixed population of individuals (or players) is considered. From time to time, one potential donor and one potential recipient are chosen at random from the population and they engage in a donation game: the donor decides whether to help the recipient at a personal cost c. If the donor chooses to help, the recipient receives a benefit b > c; otherwise the recipient obtains nothing. Each individual in the population experiences such decision makings many times both as a donor and as a recipient [29–31]. From here on, we denote the action “help” by “1” and “refuse” by “0.”

Individuals in the population have the ability to observe and assess others following their assessment rules (or social norms). Here “assess” means that players label other players “good” or “bad” according to their actions as a donor in their last interactions. The images of players are also denoted by “1” (for “good”) and “0” (for “bad”). The assessment is done privately but the information needed for the assessment is so easily accessed that all individuals have the same information (on private information see for example [29–31]).

A donor determines whether or not to help the recipient, depending on the current image of the donor (i.e., whether the recipient is labeled as 1 or 0). If the recipient is viewed as 1 in the eyes of the potential donor, the recipient will be given help, otherwise the recipient will not be offered a help. Note that we do not assume any kind of error in the model because this is a first attempt to describe competitions of all norms in the focal norm space (for the role of errors, see [32–34]). Moreover, we assume that all individuals are trustful, therefore, initially good.

The social norms in this present research are at most of second order, i.e., they take the image of the recipient as well as the action of the donor into consideration. Denoting the action of the donor by α ∈ {0, 1} and the image of the recipient by β ∈ {0, 1}, the new image of the donor after the game from the view point of some norm is a binary function of α and β: β^new = f(α, β) ∈ {0, 1}. Hence a second order norm can be identified by a four bit (f(1, 1), f(1, 0), f(0, 1), f(0, 0)).There are 16 possible norms and we number them by defining that i = f(1, 1)2³ + f(1, 0)2² + f(0, 1)2¹ + f(0, 0)2⁰ + 1. The 16 norms include some well-studied norms in the literature: the 9th norm (1000) is known as Shunning (SH), the 10th norm (1001) is called Stern-Judging (SJ), the 13th norm (1100) Image-Scoring (IS) (which is of first order) and the 14th norm (1101) Simple-Standing (SS). The first norm (0000) and the last one (1111) are unconditional norms and called AD and AC, respectively.

We denote by x_i the frequency of individuals that follow social norm $i(\sum _{i=1}^{16}{x}_i=1)$. Note that individuals using the same norm have the same opinion on others, since all individuals have the same information without errors.

As individuals play the game, the images of the individuals gradually change. At the equilibrium of images, the average payoff of individuals with norm i depends on the frequencies of the other norms in the population and on how many individuals are good. The average payoff P_i at the equilibrium of images is in fact given by

$\begin{array}{ll}{P}_i={\displaystyle \sum _{j=1}^{16}}{x}_j(s_{ji}b-s_{ij}c),& (1)\end{array}$

where s_ij is the probability that a random player with norm i has a good image of a random player with norm j. We call $s_{ij}{\in \left[0,1\right]}^{16\times 16}$ the “image matrix.” Thus specifying the image matrix provides the average payoff with the frequencies x_j fixed. The outline of the calculation for the image matrix is shown in the Results section (The full information on the calculation is found in the Supplementary Material).

Adaptive Architectures

The players adaptively switch their assessment rules, aiming at more payoffs. We examine two different switching processes: adaptive changes due to social learning by imitation described by the replicator dynamics and those changes of norms modeled by the genetic algorithm.

Replicator Dynamics

In case of replicator dynamics, an individual occasionally has a chance to change its norm by imitating another individual (i.e., adopting its norm as a model). The probability that an individual (with norm i) is chosen as a model is proportional to the norm's frequency x_i and that model's fitness F_i = F + P_i. Here, F is a baseline fitness (the same for all) and will be set to c in all simulations (We also normalize F_i in simulations.).

With some probability, an individual selects a norm totally at random and adopts that norm. This occurs due to mutation. The resulting dynamics is given by the replicator-mutation equation $\dot{x_i}=x_i\left(P_i-\overline{P}\right)+\mu \left(\frac{1}{16}-x_i\right)$, where $\overline{P}=\sum _{k=1}^{16}{x}_k{P}_k$ is the average payoff in the population (see [35]) and μ is a parameter that measures strength of mutation. In fact, we use the discretized version of replicator dynamics to compare with genetic algorithm: $x_i(t+dt)=x_i(t)+dt{x}_i(t)(P_i(t)-\overline{P}(t))+dt\mu \left(\frac{1}{16}-x_i(t)\right)$.

Genetic Algorithm

In case of genetic algorithm, an individual decomposes a norm into a collection of bits and changes its norm “bit-wise” by imitating the norms of two randomly selected individuals (called parents) [36]. Following [26], the probability that an individual with norm i is selected as a parent is proportional to the norm's frequency x_i and the square of the fitness of norm i (rule 1).

After parents have been chosen [now, the norms of the parents are j = (a, b, c, d) and k = (e, f, g, h), respectively], a crossover is uniformly performed: the first bit of the child's norm is either “a” or “e” with the same probability and the second bit “b” or “f” and so on. The uniform crossover generates the norms (a, b, c, d), (a, b, c, h)…(e, f, g, d), (e, f, g, h) with the same probability, which is 1/16 (rule 2).

From rules 1 and 2, we can derive the probability that any norm i = (p, q, r, s) is generated at the next generation (which we denote by w_i). However, due to mutation, a bit of the generated norm can be flipped with probability μ. Note that μ in the RD and that in the GA have different meanings. We assume that at most one bit can be inverted because of the small mutation probability. Thus the probability that none of 4 bits is flipped is 1 − 4μ. Therefore the probability that norm i = (p, q, r, s) is actually generated is v_i = (1 − 4μ)w_i + μI. Here I is the total of the probabilities that the neighboring norms (1 − p, q, r, s), (p, 1 − q, r, s), (p, q, 1 − r, s), (p, q, r, 1 − s) are generated before mutation.

The frequency of norm i at the next generation t + dt is given by x_i(t + dt) = (1 − dt)x_i(t) + dtv_i, where dt is the proportion of individuals that change their norms between the generations t and t + dt.

Replicator Dynamics with Multiple Models

In addition to the ordinary adaptive architectures well-studied in the literature mentioned above, we consider two other adaptive architectures that are modified versions of the conventional replicator dynamics and the genetic algorithm, respectively. The first one is replicator dynamics with multiple models.

In this adaptive architecture, an individual learns each bit of its norm independently from probably different models. The probability that an individual having norm j = (p, q, r, s) flips its first bit is proportional to the average fitness of such individuals that follow a norm the first bit of which is 1 − p. This fitness is given by $\sum _{V\in X_1}{x}_V{F}_V$. Here X₁ is the set of norms whose first bit is 1 − p (i.e., norms of the form (1 − p, *, *, *)) and F_V is the normalized fitness of V. Then for instance, the probability that the individuals change their norm from j = (p, q, r, s) to k = (1 − p, q, r, s) is given by $\sum _{V\in X_1}{x}_V{F}_V(1-\sum _{V\in X_2}{x}_V{F}_V)(1-\sum _{V\in X_3}{x}_V{F}_V)$ $(1-\sum _{V\in X_4}{x}_V{F}_V)$. In this formula, for example, the second term $(1-\sum _{V\in X_2}{x}_V{F}_V)$ is the probability that the individual does not flip its second bit. By considering all possibilities, we can calculate the in-flow to norm j from norm i (w_ij) and out-flow from j to i (w_ji). Then the increase rate of norm j is given by $\sum _i(x_i{w}_{ij}-x_j{w}_{ji})$.

As in ordinary replicator-mutation dynamics, we also include a mutation term in addition to the switching process described above. But here, we assume that mutation occurs “bit-wise” as assumed in genetic algorithm. That is, by μ, we denote the probability that each bit is flipped by mutation. Then the in-flow to j due to mutation is given by $\mu \sum _k{x}_i$ with k being 4 neighboring norms of j (i.e., the hamming-distances between the 4 norms j are 1.) and the out-flow from j by 4μx_j.

The resulting dynamics is given by $\dot{x_j}=\sum _i(x_i{w}_{ij}-x_j{w}_{ji})+\mu (\sum _k{x}_i-4x_j).$ Note that “4μ” in this dynamics corresponds to “μ” in the ordinary replicator-mutation dynamics. As for other adaptive architectures, we use discretized version of the dynamics.

Genetic Algorithm with a Single Parent

The other one is genetic algorithm with a single parent. In this architecture, only one individual is chosen as the unique parent of an individual. Then the child copies the norm of the parent. That is, the child adopts the entire norm of the single parent. Mutation effects and the probability that an individual is chosen as a parent are calculated in the same way as in the ordinary genetic algorithm mentioned above.

All four corresponding evolution equations depend on expected payoffs. We assume that images are always at equilibrium at each time step of the evolution equations. Under this assumption in the next section, we derive the equation system to specify image matrices (thus expected payoffs of norms) and show time evolutions of norms based on the above mentioned adaptive architectures.

Results

Image Matrix

Images of individuals change in time as well as frequencies of norms. But we assume that the time scale of the changes of images is much faster than that of norm changes. As a result, images are always at equilibrium and norm frequencies are treated as constant in estimating image matrices, as is assumed in the literature (See [37]).

To calculate image matrix s_ij, we introduce “image profile” $s_{e_1{e}_2{e}_3\dots e_{16}}^{(j)}\in {\left[0,1\right]}^{2^{16}}$, which is the joint probability distribution in terms of the images of a random player with norm j from the viewpoints of all norms. Thus the value of $s_{e_1{e}_2{e}_3\dots e_{16}}^{(j)}$ is the probability that a random player with norm j is labeled an image e₁ ∈ {0, 1} from the first norm and e₂ from the second norm, …, and e₁₆ from the 16^th norm. Note that, since the first norm is unconditional AD, the probability that e₁ = 1 is zero. Thus $s_{e_1=1,e_2{e}_3\dots e_{16}}^{(j)}=0$. Similarly, $s_{e_1{e}_2{e}_3\dots e_{16}=0}^{(j)}=0$.

The image profile is a joint probability distribution and contains the finest probabilistic information about the system. For example, the image matrix is interpreted as the marginal distribution:

$\begin{array}{ll}{s}_{ij}={\displaystyle \sum _{e_1{e}_2\dots e_{i-1}{e}_{i+1}\dots e_{16}}}{s}_{e_1{e}_2\dots {ẽ}_i\dots e_{16}}^{(j)},& (2)\end{array}$

with ẽ_i = 1.

Now we define the joint distribution in the whole population by

$\begin{array}{ll}{R}_{f_1{f}_2\dots f_{16}}={\displaystyle \sum _{j=1}^{16}}{x}_j{s}_{f_1{f}_2\dots f_{16}}^{(j)},& (3)\end{array}$

which gives the proportion of those individuals in the whole population, who are labeled image f₁ from the viewpoint of the first norm and f₂ from the second norm, f₃ from the third norm and so on. Since R_f1f2…f16 is a probability distribution, there is a constraint on R_f1f2…f16:

$\begin{array}{ll}{\displaystyle \sum _{f_1{f}_2\dots \dots f_{16}}}{R}_{f_1{f}_2\dots f_{16}}=1.& (4)\end{array}$

According to our analysis, it is possible to derive the equation system that yields the values of all image profiles $s_{e_1{e}_2\dots e_{16}}^{(j)}$(the joint probability distribution). More concretely, we can find an expression of $s_{e_1{e}_2\dots e_{16}}^{(j)}$as a linear function of R_f1f2…f16. Then inserting those relations between $s_{e_1{e}_2\dots e_{16}}^{(j)}$ and R_f1f2…f16into Equations (3) and (4), we can have an inhomogeneous linear equation system for R_f1f2…f16. Solving this equation system yields the values of $s_{e_1{e}_2\dots e_{16}}^{(j)}$, because $s_{e_1{e}_2\dots e_{16}}^{(j)}$is expressed as a function of R_f1f2…f16. See the supplementary material for the details of the derivation.

We remark that the equation system with respect to R_f1f2…f16 includes 2¹⁶ − 1 unknowns in principle, but the fact that the equation system contains some trivial variables such as R_f1f2…f16 = 0 with f₁ = 1 or f₁₆ = 0 reduces the dimension of the equation system.

Moreover, the case where f₁₃ = f_(1,1,0,0) = 1 indicates that action C has been taken. In this case, the following conditions must be satisfied: f_(1,1,0,1) = f_(1,1,1,0) = 1 and f_(0,0,1,1) = f_(0,0,0,1) = f_(0,0,1,0) = 0. The situations in which the above conditions are broken never happen. For those situations, R_f1f2…f16 = 0.

Similarly if f₁₃ = f_(1,1,0,0) = 0, which implies that action D has been chosen, then f_(0,1,0,0) = f_(1,0,0,0) = 0 and f_(0,0,1,1) = f_(0,1,1,1) = f_(1,0,1,1) = 1. Therefore R_f1f2…f16 = 0 for the situations where the above condition is not satisfied.

As a result the dimension of the equation system reduces to 2⁹ − 1, which can computationally be handled.

Note that the solution depends on the frequencies of norms in the population. In Figure 1, we can compare an image matrix obtained by an individual simulation with an image matrix calculated by the above mentioned method with all frequencies equal: x_i = 1/16. We see that the simulation and the analytic method generate parallel results.

FIGURE 1

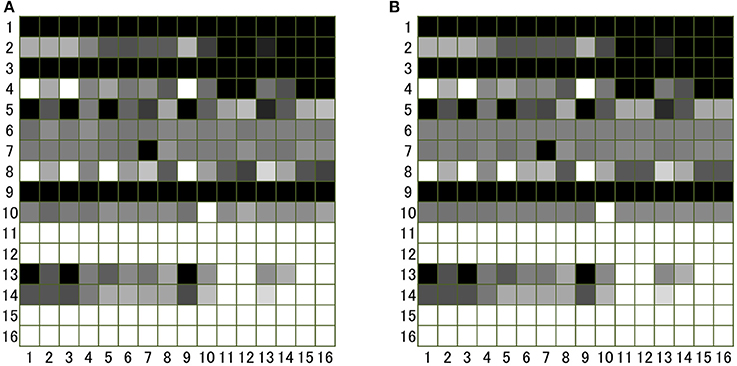
Figure 1. Image matrix s_ij (i, j = 1, …16) produced by (A) an individual based simulation and (B) the analytical method described in the text. In order to generate (A), an individual simulation with 3,200 agents was run (each norm has 200 individuals). In the simulation, each individual plays the donation game as the donor 100 times on average with different randomly chosen recipients (i.e., 320,000 games in total). This number of games is large enough for the process to reach the equilibrium. After each game, all individuals, following their own norms, assess the donor and label “1” or “0” to the individual. After 320,000 games, the number of individuals with norm j of whom the individuals with i has image “1” is counted and the number is divided by 200 (total number of individuals with j) to obtain s_ij. The value of s_ij is shown in gray scale, in which white corresponds to “1,” and black to “0”.

Time Evolutions of Norms

Frequencies of norms in a population change in time, based on its adaptive architecture. The equations describing such changes depend on payoffs. Therefore the calculating image matrices by the above mentioned method makes it possible to investigate the evolution of multiple norms caused by both switching processes, replicator dynamics and genetic algorithm.

In Figure 2A, we show a typical pattern of time evolutions of norms produced by (ordinary) replicator-mutation dynamics for a case where cooperation is achieved. Figure 2B shows its initial part (the first 100 steps). Similarly in Figure 3, a time series produced by (ordinary) genetic algorithm (for a case where cooperation is reached) and its initial part (the first 30 steps) are displayed. We note that whether or not the population evolves to cooperation depends on initial conditions. It can happen that a population evolves into non-cooperative states in both architectures. In this paper, we discuss typical situations in which cooperation is achieved.

FIGURE 2

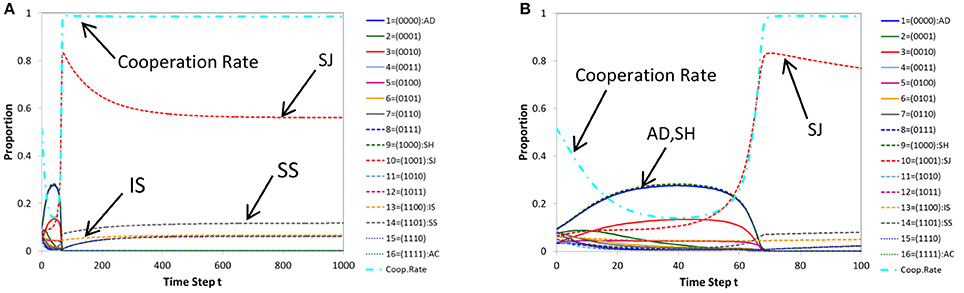
Figure 2. A typical pattern of time evolution of norms' frequencies and the cooperation rate in the population generated by replicator dynamics (A) and its initial part (the first 100 steps) (B) for a case where cooperation is achieved. Parameters: c = 1, b = 7, μ = 0.05, dt = 0.2.

FIGURE 3

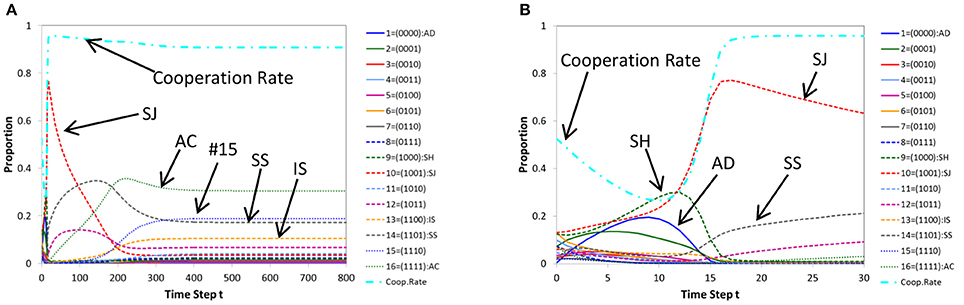
Figure 3. A typical pattern of time evolution of norms' frequencies and the cooperation rate in the population generated by genetic algorithm (A) and its initial part (the first 30 steps) (B) for a case where cooperation is achieved. Parameters: c = 1, b = 7, μ = 0.01, dt = 1.

As Figures 2B, 3B show, initial parts of both architectures are similar, in that the cooperation rate declines at first as defective norms such as AD (blue solid line) and Shunning (SH; green dashed line) pervade in the population. But they gradually decrease and alternatively the frequency of Stern-Judging (SJ; red dashed line) rises. In parallel, the cooperation rate increases.

However the long-term behavior of Stern-Judging differs in both architectures. In replicator dynamics, Stern-Judging gets a majority after defective norms have disappeared and cooperation has been realized. This trend after the transition between non-cooperative states and cooperative states is preserved stably (Figure 2A). In genetic algorithm, Stern-Judging gets a majority during the transition but it becomes extinct when cooperation has been achieved.

Generally, from Figure 3A, we see that genetic algorithm prefers tolerant norms to strict norms in cooperative states. In fact, after cooperation has been established, AC (the 16th norm; green dotted line) gets a majority and the 15th norm (blue dotted line) is the second best, then the 14th (Simple-Standing = SS; gray dashed line) and the 13th (Image-Scoring = IS; yellow dashed line). The more tolerant a norm is, the higher the frequency of the norm becomes in the population.

But this is not true for replicator dynamics. In replicator dynamics, Stern-Judging (red dashed line) is the best, Simple-Standing (gray dashed line) is the second best and Image Scoring (yellow dashed line) is the third. All these norms are well-known in the literature. Note that in both architectures, Image-Scoring survives in the long run. This is a significant finding since, in literature, Image-Scoring is known as an unstable strategy [32] and is not included in the leading eight [21].

Figure 4A shows a typical pattern of time evolutions of norms produced by replicator dynamics with multiple models for a case where cooperation is achieved. Its initial part (the first 500 steps) is shown in Figure 4B. We see that the evolutionary path is similar to that of ordinary genetic algorithm (Figure 3) rather than ordinary replicator dynamics (Figure 2). Conversely, a typical pattern of time evolutions of norms produced by genetic algorithms with a single parent (Figures 5A,B) is similar to that of ordinary replicator dynamics. Thus in Figure 4, Stern-Judging becomes extinct and in Figure 5, Stern-Judging gets a majority in the end.

FIGURE 4

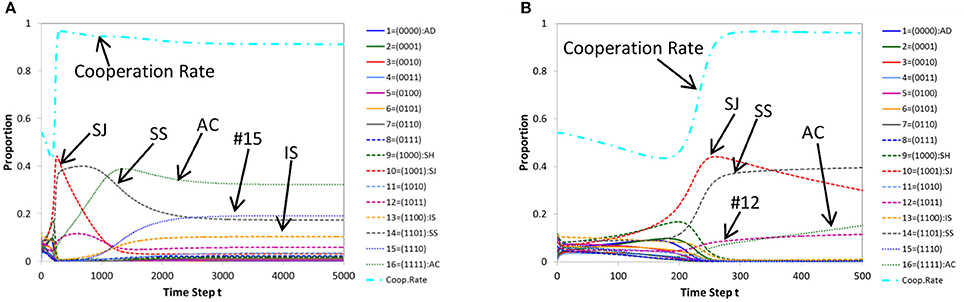
Figure 4. A typical pattern of time evolution of norms' frequencies and the cooperation rate in the population generated by replicator dynamics with multiple models (A) and its initial part (the first 500 steps) (B) for a case where cooperation is achieved. Parameters: c = 1, b = 7, μ = 0.005, dt = 0.2.

FIGURE 5

Figure 5. A typical pattern of time evolution of norms' frequencies and the cooperation rate in the population generated by genetic algorithm with a single parent (A) and its initial part (the first 60 steps) (B) for a case where cooperation is achieved. Parameters: c = 1, b = 7, μ = 0.01, dt = 1.

Discussion

In the last section we found that the norm ecosystems based on different architectures show similarity and dissimilarity. Although the norm ecosystems investigated here are complex systems, their analyses enable us to gain deep understanding of a simple single norm. For instance, an unstable norm, Image-Scoring, evolves and survives in the melting pot of competing norms regardless of architectures individuals are based on. This insight cannot be obtained if we solely analyze the single norm.

The main difference of the two representative architectures (ordinary replicator dynamics and genetic algorithm) appears in the roles of Stern-Judging, whose local stability is well-studied in the literature. The analysis revealed that Stern-Judging wins the competition against other norms and stays alive in ordinary replicator dynamics even after cooperation is achieved. That is, Stern-Judging is not only locally stable but can evolve from a mixture of diverse norms and gets a majority in the end as far as ordinary replicator dynamics is assumed. In this sense, we say that Stern-Judging plays the role of a “leading” norm in the framework of replicator dynamics.

This norm also plays a vital role in genetic algorithm since it gets a majority just before the cooperation rate starts rising. This occurs because Stern-Judging can defeat defective norms such as AD or Shunning and can increase its frequency in defective states. In other words, Stern-Judging kick-starts the evolution toward cooperation. In Yamamoto et al. [26], in which genetic algorithm is adopted as an adaptive architecture, it is reported that cooperation cannot evolve without Stern-Judging. However it is not a stable leading norm because it becomes extinct after cooperation has been achieved. Thus Stern-Judging takes a role of a “go-between” (defective states and cooperative states) in genetic algorithm.

But why do these architectures show such different results? What is the essential difference between the two? In genetic algorithm, individuals divide norms into smaller parts (bits) and learn the parts more or less independently (from its mother and father). So we can call the learning process “analytic.” For individuals with genetic algorithm, the first bit of a norm represents pro-sociality of the norm, the second bit tolerance, the third anti-sociality and the fourth intolerance (i.e., punitive nature) and they imitate each aspect of their parents, respectively.

On the other hand, individuals based on (ordinary) replicator dynamics do not analyze norms into parts but treat norms as a whole. The learning process based on replicator dynamics can therefore be called “synthetic.” And whether or not the adaptive architecture is analytic or synthetic has a large impact on the results.

In fact, we modified genetic algorithm so that an individual learns how to assess others from only one parent (i.e., the norm is not divided into parts), and we obtained similar results as ordinary replicator dynamics. Moreover we extended replicator dynamics so that an individual decomposes norms into four bits and imitates each part of different models. As a result, we found similar results as ordinary genetic algorithm (with two parents). From these results, we can conclude that whether Stern-Judging can survive in a long run in cases where cooperation is achieved does not depend on switching processes (i.e., whether replicator dynamics is assumed or genetic algorithm is used). But it relies on whether norms are treated as a whole or “bit-wise” in the corresponding switching processes.

In spite of the findings mentioned so far, we have to remark that much remains to be studied. The model studied in this present research especially has many limitations, which offers some tasks for future research from physics perspectives. First of all, we omitted implementation errors in the model to simplify the analysis. Whether and how errors change the results is interesting and necessary research yet to be done.

Moreover we assumed well-mixed populations in the analysis and ignored the effects of structured populations and group formations on cooperative behaviors of individuals. Recently interactions between heterogeneity of populations and reciprocal behaviors are investigated from physics viewpoints. For example, Nax et al. [38] studied interactions among groups and found that how important roles Image-Scoring plays for cooperation to emerge relative to “group scoring” depends on the population size. And Szolnoki et al. [39] introduced facilitators, a special type of players, on interaction networks and showed that the facilitators reveal the optimal interplay between information exchange and reciprocity. These studies provide evidence that structured populations in fact affect reciprocal functions. Inversely, some papers showed that indirect reciprocity affects population structures. For instance, it is reported that indirect reciprocity can function as a boosting mechanism of group formation and in-group favoritism, which is another aspect of cooperation [40–43].

Another factor that is out of scope in this research is the imperfectness of information. From the players' viewpoint, although the same interaction can be interpreted differently by players with distinct norms, different individuals that share the same norm always have the same opinion since all individuals are based on the same information in the model. In the literature, the imperfectness of information has been studied in several ways [29, 30, 33, 44–46] and examining the effect of such imperfectness may lead us to understand the moral ecosystem more deeply. Obviously this present paper is just a first step to theoretically investigate the competition and cooperation among multiple norms.

Author Contributions

All authors conceived and designed the project. SU built and analyzed the model and wrote the manuscript. All authors discussed the results, helped draft and revise the manuscript, and approved the submission.

Funding

Part of this work was supported by JSPS (Grants-in-Aid for Scientific Research) 15KT0133 (HY), 16H03120 (HY), 17H02044 (HY), 16H03120 (IO), 26330387 (IO), 17H02044 (IO) and the Austrian Science Fund (FWF) P27018-G11 (TS).

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

SU wishes to thank Voltaire Cang for his useful comments.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2018.00014/full#supplementary-material

References

1. Perc M, Jordan JJ, Rand DG, Wang Z, Boccaletti S, Szolnoki A. Statistical physics of human cooperation. Phys Rep. (2017) 687:1–51. doi: 10.1016/j.physrep.2017.05.004

CrossRef Full Text | Google Scholar

2. Ellison G. Cooperation in the Prisoner's Dilemma with anonymous random matching. Rev Econ Stud. (1994) 61:567–88. doi: 10.2307/2297904

CrossRef Full Text | Google Scholar

3. Kandori M. Social norms and community enforcement. Rev Econ Stud. (1992) 59:63–80. doi: 10.2307/2297925

CrossRef Full Text | Google Scholar

4. Okuno-Fujiwara M, Postlewaite A. Social norms and random matching games. Games Econ Behav. (1995) 9:79–109. doi: 10.1006/game.1995.1006

CrossRef Full Text | Google Scholar

5. Pollock GB, Dugatkin LA. Reciprocity and the evolution of reputation. J Theor Biol. (1992) 159:25–37. doi: 10.1016/S0022-5193(05)80765-9

CrossRef Full Text

6. Rosenthal RW. Sequences of games with varying opponents. Econometrica (1979) 47:1353–66. doi: 10.2307/1914005

CrossRef Full Text | Google Scholar

7. Yamagishi T, Jin N, Kiyonari T. Bounded generalized reciprocity: ingroup boasting and ingroup favouritism. Adv Group Process. (1999) 16:161–97.

8. Camerer C, Fehr E. When does “economic man” domiate social behaviour? Science (2006) 311:47–52. doi: 10.1126/science.1110600

CrossRef Full Text | Google Scholar

9. Bolton G, Katok E, Ockenfels A. Cooperation among strangers with limited information about reputation. J Public Econ. (2005) 89:1457–68. doi: 10.1016/j.jpubeco.2004.03.008

CrossRef Full Text | Google Scholar

10. Seinen I, Schram A. Social status and group norms: indirect reciprocity in a repeated helping experiment. Eur Econ Rev. (2001) 50:581–602. doi: 10.1016/j.euroecorev.2004.10.005

CrossRef Full Text | Google Scholar

11. Wedekind C, Milinski M. Cooperation through image scoring in humans. Science (2000) 288:850–52. doi: 10.1126/science.288.5467.850

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Wedekind C, Braithwaite VA. The long-term benefits of human generosity in indirect reciprocity. Curr Biol. (2002) 12:1012–15. doi: 10.1016/S0960-9822(02)00890-4

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Alexander RD. The Biology of Moral Systems. New York, NY: Aldine de Gruyter (1987).

Google Scholar

14. Sugden R. The Economics of Rights, Cooperation and Welfare. Oxford: Basil Blackwell (1986).

15. Trivers R. The evolution of reciprocal altruism. Q Rev Biol. (1971) 46:35–57. doi: 10.1086/406755

CrossRef Full Text | Google Scholar

16. Nowak MA, Sigmund K. Evolution of indirect reciprocity. Nature (2005) 437:1292–98. doi: 10.1038/nature04131

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Santos FC, Pacheco JM. Social norms of cooperation in small-scale societies. PLoS Comput Biol. (2016) 12:e1004709. doi: 10.1371/journal.pcbi.1004709

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Sasaki T, Yamamoto H, Okada I, Uchida S. The evolution of reputation-based cooperation in regular networks. Games (2017) 8:1. doi: 10.3390/g8010008

CrossRef Full Text | Google Scholar

19. Diekmann A, Jann B, Przepiorka W, Wehrli S. Reputation formation and the evolution of cooperation in anonymous online markets. Am Sociol Rev. (2014) 79:65–85. doi: 10.1177/0003122413512316

CrossRef Full Text | Google Scholar

20. Ohtsuki H, Iwasa Y. How should we define goodness? – Reputation dynamics in indirect reciprocity. J Theor Biol. (2004) 231:107–20. doi: 10.1016/j.jtbi.2004.06.005

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Ohtsuki H, Iwasa Y. The leading eight: social norms that can maintain cooperation by indirect reciprocity. J Theor Biol. (2006) 239:435–44. doi: 10.1016/j.jtbi.2005.08.008

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Brandt H, Sigmund K. The logic of reprobation: assessment and action rules for indirect reciprocation. J Theor Biol. (2004) 231:475–86. doi: 10.1016/j.jtbi.2004.06.032

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Ohtsuki H, Iwasa Y. Global analyses of evolutionary dynamics and exhaustive search for social norms that maintain cooperation by reputation. J Theor Biol. (2007) 244:518–31. doi: 10.1016/j.jtbi.2006.08.018

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Sasaki T, Okada I, Nakai Y. The evolution of conditional moral assessment in indirect reciprocity. Sci Rep. (2017) 7:41870. doi: 10.1038/srep41870

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Uchida S, Sigmund K. The competition of assessment rules for indirect reciprocity. J Theor Biol. (2010) 263:13–19. doi: 10.1016/j.jtbi.2009.11.013

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Yamamoto H, Okada I, Uchida S, Sasaki T. A norm knockout method on indirect reciprocity to reveal indispensable norms. Sci Rep. (2017) 7:44146. doi: 10.1038/srep44146

CrossRef Full Text | Google Scholar

27. Chalub F, Santos FC, Pacheco JM. The evolution of norms. J Theor Biol. (2006) 241:233–40. doi: 10.1016/j.jtbi.2005.11.028

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Pacheco JM, Santos FC, Chalub F. Stern-judging: a simple, successful norm which promotes cooperation under indirect reciprocity. PLoS Comput Biol. (2006) 2:e178. doi: 10.1371/journal.pcbi.0020178

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Uchida S. Effect of private information on indirect reciprocity. Phys Rev E (2010) 82:036111. doi: 10.1103/PhysRevE.82.036111

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Uchida S, Sasaki T. Effect of assessment error and private information on stern-judging in indirect reciprocity. Chaos Solitons Fractals (2013) 56:175–80. doi: 10.1016/j.chaos.2013.08.006

CrossRef Full Text | Google Scholar

31. Ohtsuki H, Iwasa Y, Nowak MA. Reputation effects in public and private interactions. PLoS Comput Biol. (2015) 11:e1004527. doi: 10.1371/journal.pcbi.1004527

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Brandt H, Sigmund K. The good, the bad and the discriminator – errors in direct and indirect reciprocity. J Theor Biol. (2006) 239:183–94. doi: 10.1016/j.jtbi.2005.08.045

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Takahashi N, Mashima R. The importance of subjectivity in perceptual errors on the emergence of indirect reciprocity. J Theor Biol. (2006) 243:418–36. doi: 10.1016/j.jtbi.2006.05.014

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Seki M, Nakamaru M. A model for gossip-mediated evolution of altruism with various types of false information by speakers and assessment by listeners. J Theor Biol. (2016) 407:90–105. doi: 10.1016/j.jtbi.2016.07.001

PubMed Abstract | CrossRef Full Text | Google Scholar

35. Hofbauer J, Sigmund K. Evolutionary Games and Population Dynamics. Cambridge: Cambridge University Press (1998).

Google Scholar

36. Holland J. Adaptation in Natural and Artificial Systems. Ann Arbor: University of Michigan Press (1975).

Google Scholar

37. Sigmund K. The Calculus of Selfishness. Princeton: University Press (2010).

Google Scholar

38. Nax HH, Perc M, Szolnoki A, Helbing D. Stability of cooperation under image scoring in group interactions. Sci Rep. (2015) 5:12145. doi: 10.1038/srep12145

PubMed Abstract | CrossRef Full Text | Google Scholar

39. Szolnoki A, Perc M, Mobilia M. Facilitators on networks reveal optimal interplay between information exchange and reciprocity. Phys Rev E (2014) 89:042802. doi: 10.1103/PhysRevE.89.042802

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Oishi K, Shimada T, Ito N. Group formation through indirect reciprocity. Phys Rev E (2013) 87:030801. doi: 10.1103/PhysRevE.87.030801

CrossRef Full Text | Google Scholar

41. Masuda N. Ingroup favoritism and intergroup cooperation under indirect reciprocity based on group reputation. J Theor Biol. (2012) 311:8–18. doi: 10.1016/j.jtbi.2012.07.002

PubMed Abstract | CrossRef Full Text | Google Scholar

42. Nakamura M, Masuda N. Groupwise information sharing promotes ingroup favoritism in indirect reciprocity. BMC Evol Biol. (2012) 12:213. doi: 10.1186/1471-2148-12-213

PubMed Abstract | CrossRef Full Text | Google Scholar

43. Fu F, Tarnita CE, Christakis NA, Wang L, Rand DG, Nowak MA. Evolution of in-group favoritism. Sci Rep. (2012) 2:460. doi: 10.1038/srep00460

PubMed Abstract | CrossRef Full Text | Google Scholar

44. Nowak MA, Sigmund K. The dynamics of indirect reciprocity. J Theor Biol. (1998) 194:561–74. doi: 10.1006/jtbi.1998.0775

PubMed Abstract | CrossRef Full Text | Google Scholar

45. Mohtashemi M, Mui L. Evolution of indirect reciprocity by social information: the role of trust and reputation in evolution of altruism. J Theor Biol. (2003) 223:523–31. doi: 10.1016/S0022-5193(03)00143-7

PubMed Abstract | CrossRef Full Text | Google Scholar

46. Nakamaru M, Kawata M. Evolution of rumors that discriminate lying defectors. Evol Ecol Res. (2004) 6:261–83.

Google Scholar