Influence of the Size and Curvedness of Neural Projections on the Orientationally Averaged Diffusion MR Signal

Neuronal and glial projections can be envisioned to be tubes of infinitesimal diameter as far as diffusion magnetic resonance (MR) measurements via clinical scanners are concerned. Recent experimental studies indicate that the decay of the orientationally-averaged signal in white-matter may be characterized by the power-law, Ē(q) ∝ q⁻¹, where q is the wavenumber determined by the parameters of the pulsed field gradient measurements. One particular study by McKinnon et al. [1] reports a distinctively faster decay in gray-matter. Here, we assess the role of the size and curvature of the neurites and glial arborizations in these experimental findings. To this end, we studied the signal decay for diffusion along general curves at all three temporal regimes of the traditional pulsed field gradient measurements. We show that for curvy projections, employment of longer pulse durations leads to a disappearance of the q⁻¹ decay, while such decay is robust when narrow gradient pulses are used. Thus, in clinical acquisitions, the lack of such a decay for a fibrous specimen can be seen as indicative of fibers that are curved. We note that the above discussion is valid for an intermediate range of q-values as the true asymptotic behavior of the signal decay is Ē(q) ∝ q⁻⁴ for narrow pulses (through Debye-Porod law) or steeper for longer pulses. This study is expected to provide insights for interpreting the diffusion-weighted images of the central nervous system and aid in the design of acquisition strategies.

1. Introduction

Diffusion-sensitized magnetic resonance acquisitions have been employed to recover the microscopic building blocks of complex nervous tissue. Simplified models exploiting the compartmentalized structure of the tissue are instrumental in this endeavor. Water molecules in the intra- and extra-cellular spaces have been envisioned to form separate compartments with different signal characteristics [2]. The intracellular signal is also thought to represent the superposition of contributions from cells of different types, shapes, and orientations [3]. The same argument has been employed even for a single neuron wherein each neurite has been considered to comprise a collection of straight compartments [4]. Such representation of neurites as slender cylinders distributed in random orientations within the voxel is perhaps the model most relevant to the current study.

The diameter of neurites, and in fact all neural projections, is so small that diffusion in the transverse plane may be negligible. More explicitly, a cylinder with the same diameter as a neurite would not suffer any signal loss in a typical clinical diffusion MRI measurement when the diffusion gradients are applied in the direction perpendicular to the cylinder's axis. This justifies assigning zero value to transverse diffusivity for molecules confined in the cylinder. Such behavior [5] was indeed observed for N-acetyl-L-aspartate (NAA) diffusion in the brain [6] and have been employed for water in recent models [7].

In this work, we consider the pulsed field gradient measurement introduced by Stejskal and Tanner [8] featuring diffusion encoding gradients G of duration δ, whose leading edges are separated from each other by duration Δ (see Figure 1A for the effective gradient waveform). We define q = γδG, where γ is the gyromagnetic ratio and note that for sufficiently small values of q = |q|, the signal for each compartment can be approximated with a Gaussian, i.e.,

$\begin{array}{ll}E(q)\approx e^{-q^{⊺}Vq}.& (1)\end{array}$

Considering the form (Equation 1) of the signal, V can be referred to as the signal decay tensor¹. The geometric parameters of the compartment have typically a complicated relation to V; the exact form of such relation is dictated by the temporal parameters (δ and Δ) of the diffusion encoding pulse sequence. For axially symmetric V, we shall denote by v_∥ and v_⊥ the eigenvalues of V associated with directions parallel and perpendicular to the symmetry axis, respectively.

FIGURE 1

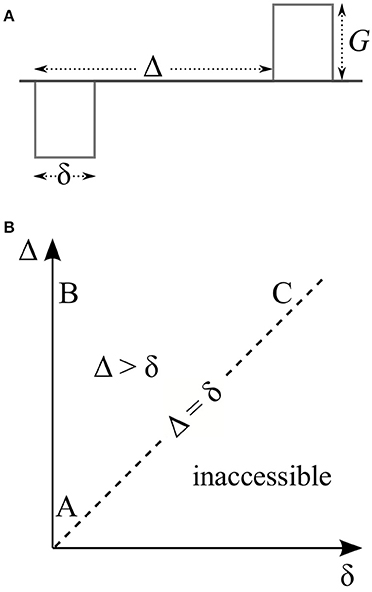
Figure 1. (A) Stejskal and Tanner's pulsed field gradient experiment features a pair of rectangular gradient pulses of duration δ whose leading edges are separated by Δ. (B) The timing parameters of this experiment lie on or above the dashed line since the separation of the two pulses (Δ) has to be at least as long as the duration of each of them (δ). Thus, the experiment has three distinct regimes (labeled A, B, and C) based on whether these timing parameters are short or long. These are the three regimes that exhibit all interesting features of the signal. The same features are expected to be observed to various degrees in the intermediate region between these three regimes.

Our focus in this work is the orientationally-averaged signal, which can be obtained by computing the “isotropic component” of the signal, as was referred to in Özarslan and Basser [10] and actually estimated as a byproduct of the q-space signal representation in Özarslan et al. [11]. Alternatively, the signal values measured over all gradient directions at a particular q-value can be averaged [12, 13] so that any dependence on the direction of the gradient vector is lost. Repeating this procedure for all q-values reduces the data collected over the three-dimensional q-space into a one-dimensional profile, which does not contain any information on ensemble (macroscopic) anisotropy². The estimated signal profile represents the decay for the so-called “powdered” specimen, which contains an isotropic distribution of each and every compartment in the original specimen [19, 20]. The orientationally-averaged signal for axisymmetric compartments, each of which contributes according to Equation (1), is thus the same as the signal for an isotropic ensemble of such compartments, and is given by [6, 21, 22]

$\begin{array}{ll}\overline{E}(q)=\frac{\sqrt{\pi }{e}^{-q^2{v}_{\perp }}\text{ erf}(q\sqrt{v_{\parallel }-v_{\perp }})}{2q\sqrt{v_{\parallel }-v_{\perp }}}.& (2)\end{array}$

This expression predicts a squared exponential decay in general. However, if signal loss is limited to only the fiber direction (v_⊥ = 0), a much slower decay emerges. A power law of the form Ē ∝ q⁻¹, to be specific. Therefore, the appearance of this particular power-law can be used as an indicator of vanishing transverse diffusivity, in other words, the signal decay tensor V being of rank 1. We note that the problem of characterizing the orientationally averaged signal is considerably more complicated when Equation (1) cannot be used to represent the compartmental signal; addressing this issue is one of our goals in this study.

The Ē ∝ q⁻¹ decay alluded to above was recently reported in white matter [1, 23]. These studies have found that in white-matter-dominated regions of the brain, the orientationally averaged signal exhibits a decay ~q^−c with an exponent c close to 1, in support of cylindrical neural projections as remarked above. In gray-matter-dominated regions, McKinnon et al.[1] have observed a larger exponent c ≈ 1.8 ± 0.2. They proposed that the apparent breakdown of the cylinder model may indicate a significantly larger permeability of the cellular membranes in gray matter vs. white matter. Here, we investigate an alternative hypothesis. Namely, the departure of the exponent c from 1 can well be due to impermeable but curved projections. To assess this point, we studied the influence of neural projections' size and shape on the orientationally-averaged diffusion MR signal. Due to the large variability in the geometric features of the neural cells, all temporal regimes of the Stejskal-Tanner sequence were considered, and the problem was studied both in the small-q regime as well as at larger q-values for which Equation (1) and thus Equation (2) are inaccurate.

Investigation of power-like tails in the diffusion MR signal goes back to Köpf et al.[24], where large values of the wave vector were achieved using a fringe field method. A range of exponents (roughly between −1.8 and −4.6) were observed across various nonneural tissue types, as well as stretched exponential behavior, which was ascribed to fractional Brownian motion. In a subsequent study, Yablonskiy et al.[25] predicted an exponent of −2 for specimens featuring compartments with a distribution of diffusivities. Jian et al.[26] considered a parametric tensor distribution, which suggested a signal decay with a general power-law tail. These studies, however, observe or predict the signal decay for measurements along a single direction. As for the orientationally (powder) averaged signal, a quite general statement regarding an asymptotic power-law decay in the diffusion MR signal is the Debye-Porod law [27]. Here, the orientationally averaged signal measured using narrow pulses is predicted to follow a q⁻⁴ tail under quite general considerations. In our discussion, we take up apparent violations of this.

Although the influence of fiber curvature on the MR signal has been considered [28–33] in various contexts, to our knowledge, this is the first study to provide explicit expressions for the signal decay for diffusion along a general parametrized curve and study its effect on the orientationally averaged signal.

In the next section, we provide explicit expressions for the MR signal for diffusion on curves in three distinct temporal regimes of the Stejskal-Tanner measurement. In the subsequent section, we discuss the implications of our theoretical findings as they relate to the morphology of neural cells and recent experimental observations. The article is concluded following a brief discussion of what observed power-law tails in the powder averaged signal may represent in that context, as well as from the perspective of the Debye-Porod law.

2. Compartmental and Orientationally-Averaged Signal for Diffusion Along Curves

The effective gradient waveform of a traditional Stejskal-Tanner measurement is shown in Figure 1A. In this work, we consider three distinct regimes of this pulse sequence based on whether δ and Δ are short or long. These regimes are indicated by the letters A, B, and C on the δ-Δ plane in Figure 1B. We note that the essential features of the signal at these three extreme situations are exhibited to some extent for more general timing values, i.e., within the interior of the triangle whose vertices are at A, B, and C.

The relevant size parameters of a simplified neural projection (ignoring branchings and other features such as beading patterns [34]) are: its contour length denoted by ℓ, its radius of gyration R_g, its characteristic curvature radius R_c, and the radius of the projection's cross-section R₀. These parameters are illustrated for a representative projection in Figure 2. As mentioned in Introduction, R₀ is typically so small that qR₀ ≪ 1 for clinical MRI; this justifies representing the neurites and glial projections via one-dimensional curves. Thus, we shall consider diffusion taking place on a curve $r(s)={(r_1(s),r_2(s),r_3(s))}^{⊺}$ parameterized by its arclength s, where 0 ≼ s ≼ ℓ.

FIGURE 2

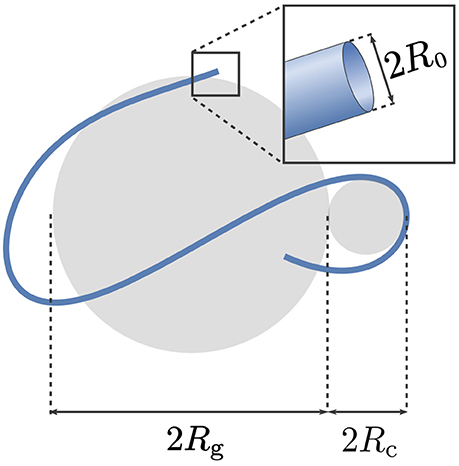
Figure 2. The relevant size parameters of a simplified neural projection (ignoring branchings and other features such as beading patterns [34]) are: its contour length denoted by ℓ, its radius of gyration R_g, the characteristic radius of curvature R_c, and the radius of the projection's cross-section R₀.

2.1. Regime A: Short Diffusion-Time

In the first case, diffusion is observed for such a short time that the hindrances have not been encountered. This condition implies that the pulse durations are short as well. In fact, when $D\Delta \ll R_{\text{c}}^2$, spins spread so little that even the most curved point along the projection seems like a straight segment³. Thus, the compartmental signal occurs as the average, over the curve, of the signals originating from the tangents of the curve:

$\begin{array}{ll}E(q)=\frac{1}{\ell }{\displaystyle {\int }_0^{\ell }\text{d}}s{e}^{-D\Delta q^{⊺}\widehat{t}(s){\widehat{t}}^{⊺}(s)q},& (3)\end{array}$

where

$\begin{array}{ll}\widehat{t}(s)=\frac{\text{d}r(s)}{\text{d}s}& (4)\end{array}$

is the unit tangent to the curve.

As shown in Appendix A (see the Supplementary Material), the very small-q behavior of the orientationally-averaged signal (q²DΔ ≪ 1) is given by Ē(q) ≈ e^−q2DΔ/3. Thus, the decay rate is determined solely by the (intracellular) diffusivity, and bears no geometric feature of the neural arborization in this regime.

For a more general analysis involving larger q-values, one can still employ Equations (1, 2) as follows. We are interested in the orientational average of the compartmental signal in Equation (3), i.e.,

$\begin{array}{ll}\overline{E}(q)=\frac{1}{\ell }{\displaystyle {\int }_0^{\ell }\text{d}}s\langle e^{-D\Delta q^{⊺}\widehat{t}(s){\widehat{t}}^{⊺}(s)q}\rangle ,& (5)\end{array}$

where the order of integration and orientational averaging, indicated by the angular brackets, was changed. However, the expression within the angular brackets is of the Gaussian form (Equation 1) with a rank-1 decay tensor whose non-vanishing eigenvalue is DΔ. Consequently, the signal for the powdered specimen is given through Equation (2) by setting v_⊥ = 0, and v_∥ = DΔ to be

$\begin{array}{ll}\overline{E}(q)=\frac{\sqrt{\pi }\text{ erf}(q\sqrt{D\Delta })}{2q\sqrt{D\Delta }}.& (6)\end{array}$

Clearly, for larger q-values, the orientationally-averaged signal decay in regime A is proportional to q⁻¹ irrespective of the shape of the curve as long as $R_{\text{c}}^2\gg D\Delta$. It can be observed that Equation (5) has the form of a signal arising from a uniform orientational distribution of “sticks”. Hence the emergence of q⁻¹ at large q-values can be justified alternatively by Veraart et al.'s arguments [23].

2.1.1. Incorporating Curvature Effects

The above expression holds when the diffusion distance is much smaller than R_c as pointed out earlier. Here, we would like to generalize this expression to larger timing parameters, Δ and δ, to allow for the possibility that the diffusion distance during the course of the experiment is long enough for the molecules to traverse an approximately circular arc along the curve. Moreover, we assume that there is a single characteristic radius of curvature that represents the effective curvedness of the entire projection. This characteristic curvature is denoted by R_c.

Let $E_{\text{arc}}(\widehat{n},\phi ,q)$ denote the signal for a single such arc, where $\widehat{n}$ is the unit vector normal to its plane and φ is the polar coordinate of the center of the arc in a cylindrical reference frame oriented along $\widehat{n}$. The orientationally averaged signal can then be written as the average of $E_{\text{arc}}(\widehat{n},\phi ,q)$, over all possible realizations of a single arc, i.e.,

$\begin{array}{ll}\overline{E}(q)=\frac{1}{4\pi }{\displaystyle {\int }_{S_2}\text{d}}\widehat{n}\frac{1}{2\pi }{\displaystyle {\int }_0^{2\pi }\text{d}}\phi E_{\text{arc}}(\widehat{n},\phi ,q),& (7)\end{array}$

where S₂ denotes the unit sphere. The second average simply defines the signal for a full circle of radius R_c. If we denote by $E_{\text{circ}}(\widehat{n},q)$ the signal for such a circle whose plane has the normal vector $\widehat{n}$, the orientationally averaged signal can be expressed as

$\begin{array}{ll}\overline{E}(q)=\frac{1}{4\pi }{\displaystyle {\int }_{S_2}\text{d}}\widehat{n}{E}_{\text{circ}}(\widehat{n},q).& (8)\end{array}$

Due to its axial symmetry, the signal for the circle has the functional dependence $E_{\text{circ}}(\widehat{n}·\widehat{q},q)$, where $\widehat{q}=q/q$. Since $\widehat{n}·\widehat{q}$ is invariant under exchange of the unit vectors $\widehat{n}$ and $\widehat{q}$, one is free to replace the integration variable above with $\widehat{q}$ and fix $\widehat{n}$ instead [19]. With the variable θ defined through $\widehat{n}·\widehat{q}=cos\theta$, we moreover note that since there is no motion and hence no signal attenuation in the direction along $\widehat{n}$, the integrand's functional dependence may further be reduced to E_circ(qsinθ), namely, the signal obtained when a q-vector of magnitude qsinθ is applied in the plane of the circle. Upon taking these observations into account, we obtain

$\begin{array}{ll}\overline{E}(q)={\displaystyle {\int }_0^{\pi /2}\text{d}}\theta \text{ sin }\theta E_{\text{circ}}(q\text{ sin }\theta ).& (9)\end{array}$

2.1.1.1. Narrow pulses

First, we shall consider the scenario involving narrow pulses, i.e., $D\delta \ll R_c^2$, but allow for the possibility that $D\Delta \approx R_c^2$. For arbitrary Δ, the signal for a full circle is given by Özarslan et al. [28]

$\begin{array}{ll}{E}_{\text{circ}}(q)=J_0{(q{R}_c)}^2+2{\displaystyle \sum _{n=1}^{\infty }{e}^{-n^{2}D\Delta /R_c^2}}{J}_n{(q{R}_c)}^2,& (10)\end{array}$

where J_n denotes the nth order Bessel function. This expression yields, via Equation (9), the orientationally-averaged signal to be

$\begin{array}{ll}\begin{array}{l}\overline{E}(q)=J_0(2q{R}_c)+\frac{\pi }{2}\left[J_1(2q{R}_c)H_0(2q{R}_c)-J_0(2q{R}_c)H_1(2q{R}_c)\right]\\ +2{\displaystyle \sum _{n=1}^{\infty }{e}^{-n^{2}D\Delta /R_c^2}}\frac{{(q{R}_c)}^{2n}}{(2n+1)!}\\ {}_1{F}_2\left(n+\frac{1}{2};n+\frac{3}{2},2n+1;-q^2{R}_c^2\right),\end{array}& (11)\end{array}$

where H_α is the Struve function of order α and ₁F₂ represents the generalized hypergeometric function. We note that this orientationally averaged signal in the narrow pulse regime has the asymptotic behavior

$\begin{array}{ll}\overline{E}(q)~\frac{\sqrt{\pi }\text{erf}(q\sqrt{D\Delta })}{2q\sqrt{D\Delta }}+\frac{{(D\Delta )}^2{q}^2{e}^{-D\Delta q^2}}{6R_c^2}-{O}(R_c^{-4}).& (12)\end{array}$

This expression contains the curvature-related correction to Equation (6), which is valid for straight fibers, and suggests that curvature induced effects are rather limited for the case of narrow pulses, as the Ē(q) ∝ q⁻¹ dependence is unaffected at larger q-values.

2.1.1.2. Longer pulse durations

To investigate the influence of longer pulse durations, we numerically evaluated the integral in Equation (9) using Simpson's rule [35]. We adapted the multiple correlation (MCF) framework to the problem of diffusion on a circle. The details of this procedure are provided in Appendix B (see the Supplementary Material).

In Figure 3, we illustrate the signal decay curves at different pulse durations. In these simulations, the DΔ value was set equal to $R_c^2$; during a time interval of duration Δ, the spread of molecules on the circle is about 80°. When the pulse duration is short, we verified that the decay obeys the expressions in Equations (11) and (12) (results not shown). The power-law, E(q) ∝ q⁻¹, which is valid in the narrow pulse regime does not prevail when the pulses are prolonged.

FIGURE 3

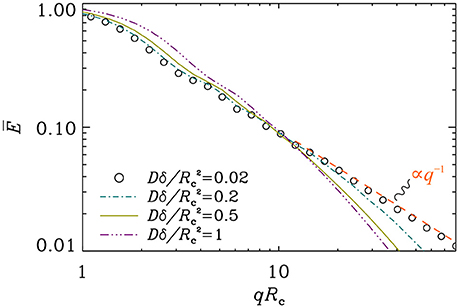
Figure 3. Signal attenuation curves for different values of the pulse duration. The separation of pulses was taken so that $D\Delta =R_c^2$. The q⁻¹ decay, visible at short pulse durations, disappears as the pulses are prolonged.

2.2. Regime B: Long Diffusion-Time and Narrow Pulses

When diffusion is probed via a pair of impulses (or, when $D\delta \ll R_{\text{c}}^2$) separated from each other by a duration long enough for the molecules to reach all points within the curve, i.e., DΔ ≫ ℓ², the signal is given simply by the expression $E(q)=|\tilde{\rho }(q){|}^2$, where $\tilde{\rho }(q)$ is the Fourier transform of the density

$\begin{array}{ll}\rho (r)=\frac{1}{\ell }{\displaystyle {\int }_0^{\ell }\text{d}}s\delta (r-r(s)),& (13)\end{array}$

which is uniform along the curve. The orientationally averaged signal decay is thus obtained by averaging $|\tilde{\rho }(q){|}^2$, and is given by

$\begin{array}{ll}\overline{E}(q)=\frac{1}{{\ell }^2}{\displaystyle {\int }_0^{\ell }\text{d}}s{\displaystyle {\int }_0^{\ell }\text{d}}{s}^{\prime }\frac{\sin \left[q|r(s)-r(s^{\prime })|\right]}{q|r(s)-r(s^{\prime })|}.& (14)\end{array}$

This expression is referred to as the Debye scattering equation [36], which is widely utilized in studies employing small angle scattering experiments for characterizing the structure of polymers. The essential features of the resulting Ē(q) curve are well-understood [37, 38]. As shown in Appendix A (see the Supplementary Material), the small-q regime (qR_g ≪ 1, the “Guinier regime” of scattering experiments) is described by the relationship $Ē(q)\approx e^{-{(q{R}_{\text{g}})}^2/3}$. As for larger q-values, such studies indicate that depending on the structure of the polymer, different sections of the curve could be characterized by different power-laws. For example, Gaussian chains undergo q⁻² decay, while fractional exponents are obtained for curves exhibiting fractality. Perhaps the most relevant finding, however, is that wormlike structures (i.e., those characterized by a so-called persistence length over which the polymer is likely to retain its direction) are characterized by a decay ∝ q⁻¹ at q-values about the reciprocal of the chain's persistence length [39]. Thus, even a class of non-straight structures exhibit q⁻¹ decay in Regime B.

2.3. Regime C: Long Pulse-Duration

For the traditional Stejskal-Tanner measurement utilizing a pair of identical pulses in opposite directions, the compartmental signal has the form

$\begin{array}{ll}E={\langle e^{-iq·\left({\xi }_2-{\xi }_1\right)}\rangle }_{\text{paths}},& (15)\end{array}$

where the averaging is performed over all trajectories, with

$\begin{array}{ll}{\xi }_n=\frac{1}{\delta }{\displaystyle {\int }_{t_n}^{t_n+\delta }r}(t)\text{d}t& (16)\end{array}$

being the center of mass coordinate [40] of the fragment of trajectory coinciding with each pulse (t₁ = 0 and t₂ = Δ). Therefore, the MR signal (Equation 15) elicited by flat gradient pulses is not sensitive to the Brownian trajectories instant by instant but only in a time averaged sense.

In the limit Dδ/ℓ² → ∞, the two random variables lose correlation and the explicit dependence on Δ disappears, leading to the signal intensity [40]

$\begin{array}{ll}E={\left|{\tilde{p}}_{\text{cm}}(q,\delta )\right|}^2,& (17)\end{array}$

where

$\begin{array}{ll}{\tilde{p}}_{\text{cm}}(q,\delta )={\displaystyle \int p_{\text{cm}}}(\xi ,\delta )e^{-iq·\xi }\text{ d}\xi & (18)\end{array}$

is the Fourier transform of the center of mass distribution. Moreover, in this limit, the distribution for the random variable ξ approaches a Gaussian due to the central limit theorem [41]⁴. Consequently, the signal (Equation 17) also approaches a quadratic exponential form, encoding no more structural information than the variance of p_cm(ξ, δ). Whether the domain is an irregularly curved fiber or a much more regular shape like a sphere, its fine structural features will find no representation in the signal acquired this way, since the length of the time averaging (pulse) has suppressed all short-scale (high q) variation encoded in the cumulants higher than the second.

Hence, the compartmental signal has the form Equation (1). Here, though, V is the variance tensor for the center of mass coordinate (Equation 16) for a trajectory of (long) duration δ. This variance can be calculated for diffusion along a general continuous curve following Mitra and Halperin's [40] derivation in the case of slab geometry, with slight modifications. One finds

$\begin{array}{ll}\begin{array}{l}{V}_{ij}=\frac{2}{D\delta }{\displaystyle {\int }_0^{\ell }\text{d}}s{r}_i(s){\displaystyle {\int }_0^{\ell }\text{d}}{s}^{\prime }{r}_j(s^{\prime })\{B_2\left(\frac{|s-s^{\prime }|}{2\ell }\right)+B_2\left(\frac{s+s^{\prime }}{2\ell }\right)\\ +\frac{{\ell }^2}{3D\delta }\left[B_4\left(\frac{|s-s^{\prime }|}{2\ell }\right)+B_4\left(\frac{s+s^{\prime }}{2\ell }\right)\right]\},\end{array}& (19)\end{array}$

where B_n(·) denotes the nth order Bernoulli polynomial, and Dδ/ℓ² ≫ 1. Here, the exponentially decaying terms are ignored as their contribution is negligible at even moderate durations. The details of the derivation of the above expression is provided in Appendix A (see the Supplementary Material). We note that alternative representations of the final result (Equation 19) can be given in terms of polylogarithmic or Hurwitz zeta functions. We verified that Equation (19) correctly reproduces Mitra and Halperin's expression [40] in the same regime for the slab geometry, i.e., for a straight line.

As were in the previous cases, the signal decay tensor for long pulse duration is not rank-1 for a general curve. However, unlike in previous regimes, the compartmental signal decay is truly Gaussian. Consequently, the orientationally averaged signal in this regime suffers q⁻¹ decay if and only if the fibers are straight.

3. Results and Discussion

3.1. Summary

The above findings can be summarized as follows: For narrow pulses ($D\delta \ll R_{\text{c}}^2,{\ell }^2$) in regimes A and B, the orientationally averaged signal exhibits a slow q⁻¹ tail for large q for diffusion along curved as well as straight 1 dimensional structures. As the pulse duration is prolonged, as we have studied for regime A, the slow q⁻¹ tail gives way to a steeper drop for substantially curved fibers, by which we mean $R_{\text{c}}\lesssim \sqrt{D\delta }$. Indeed, the signal may be expected to bear less features of diffusion along a 1D structure and more of diffusion in a 3D domain (i.e., a steep decay), since a long pulse serves to average the motion of the spin carriers over a length $~\sqrt{D\delta }$ along the path curved in 3D space. Fibers much shorter than the averaging length ($\ell \ll \sqrt{D\delta }$) fall into regime C and may contribute to an exponent of −1 in the orientationally averaged signal only if they are straight (R_c ≫ ℓ).

3.2. Clinical Relevance

An important question to ask is: What regime is the most relevant for clinical MR examinations of the brain? There is no clear answer to this question, essentially because of the extremely wide variability in the size and shapes of cells within the brain [44]⁵. Consequently, it is impossible to suggest that diffusion within all neural cells takes place in a single experimental regime. We can, nonetheless, argue that regime B is the least relevant one as it is impossible to meet the narrow pulse condition along with the long diffusion time condition when δ ≈ Δ as in clinical acquisitions performed at larger (in a practical sense) b-values, where b = q²(Δ−δ/3). The diffusion distance $\sqrt{2D\Delta }$ is expected to be about 10–20 μm in such acquisitions, which will place longer ($\ell \gg \sqrt{D\Delta }$) arborizations toward regime A while the shorter ($\ell \ll \sqrt{D\Delta }$) ones will tend to exhibit features of regime C. If the longer structures furthermore exhibit curvature radii safely above the “averaging length” ($R_{\text{c}}\gg \sqrt{D\delta }$), the q⁻¹ signature will be possible to observe over a range of large q-values without requiring strict straightness, as demonstrated in Figure 3. For structures whose radii of curvature are small ($R_{\text{c}}\lesssim \sqrt{D\delta }$) the appearance of the slow decay q⁻¹ becomes sensitive to curvature, and is not retained for as wide a range of q-values (see Figure 4). At the extreme end of the spectrum, for structures so short that $\ell \ll \sqrt{D\delta }$, entering into regime C, no curvature is tolerated if the tail q⁻¹ is to appear. These considerations will have to be revisited if one measures the diffusion of molecules other than water, due to differences in their diffusion characteristics [48–50].

FIGURE 4

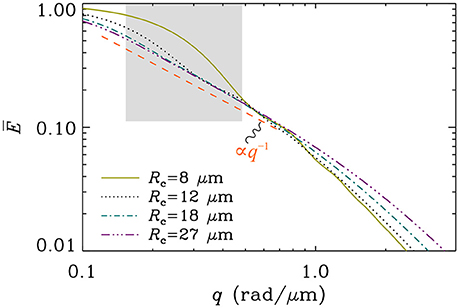
Figure 4. Simulation of the orientationally averaged signal for diffusion along an arc of various curvature radii. The contour length was taken to be infinite so that the results for Regime A are employed. The timing parameters were taken to be clinically realistic for high b-value acquisitions (δ = 50 ms and Δ = 60 ms), and the diffusion coefficient was set to D = 3 μm²/ms. The gray box depicts roughly the range of b-values between 1 and 10 ms/μm². It is seen that the larger the curvature radius, the wider the range over which the exponent −1 can be observed. Conversely, below a cutoff determined by the averaging length $\sqrt{D\delta }$, a steeper decay of the signal becomes very prominent.

3.3. On Experimental Findings

In light of the above deliberations, we can revisit the experimental observations of McKinnon et al. [1] who have reported the powder averaged signals stemming from various brain regions dominated by white- or gray-matter. In white-matter regions, they have measured a decay q^−c for large q with c values in the neighborhood c ≈ 1.1 ± 0.1, whereas in gray-matter regions, the decay was significantly faster, with c ≈ 1.8 ± 0.2. Concerning the faster decay observed in gray-matter, they propose an explanation based on permeability differences in white and gray-matter regions. If one assumes impermeable membranes, as we did in this study, the following alternative interpretation seems adequate: In white-matter, the observation of the tail q⁻¹ is compatible with regimes A and C, suggesting a substantial presence of fibers that fall into these regimes. The former implies long fibers ($\ell \gg \sqrt{D\Delta }$) that could in fact be modestly curved (as long as $R_c\gg \sqrt{D\delta }$ remains valid). The latter implies short fibers ($\ell \ll \sqrt{D\delta }$) that are straight. In gray-matter regions, the loss of the slow q⁻¹ decay suggests that the signal originates predominantly from fibers that fall outside these descriptions, i.e., exhibiting strong curvature ($R_{\text{c}}\lesssim \sqrt{D\delta }$). Indeed, gray-matter is rich in dendrites and unmyelinated axons, which will exhibit a fair amount of bending distributed across any voxel. The gray box in Figure 4 depicts roughly the q range used in McKinnon et al.'s study, where it is seen that while modest curvatures do exhibit the exponent −1 for a while, strong curvature yields a steeper decay for most of the range.

Another potential explanation involves glial cells, which constitute a substantial portion of all neural cells. Similar to neurons, glial cells exhibit an extraordinary level of diversity in their size and shape throughout the brain. Their relative number and distribution is the subject of ongoing debate [51]. Thus, an accurate assessment of their influence on the detected diffusion MR signal is infeasible at this time. It is known, however, that the glial cells tend to be smaller than neurons, they lack axons, and many of them are star-shaped [52]. These structural features tend to disfavor the emergence of a q⁻¹ decay. However, recent studies have suggested that the glial cells are significantly more prevalent in cerebral white-matter compared to gray-matter [53]. Thus, it can be argued that their contribution to the overall MR signal must be rather limited. We note that the vast variation in neuronal and glial morphology along with the reported regional differences justify future studies performed at high spatial resolutions, for understanding the influence of compositional variations on the diffusion MR signal.

3.4. Immobile Water

The detected orientationally-averaged signal would typically include contributions from many different compartments besides the neural projections, including extracellular matrix, cell bodies, and molecules trapped within very small regions (e.g., within certain organelles, between myelin layers, etc.). Among these, molecules diffusing relatively freely (for instance, between the neural processes) are expected to yield a decay rate faster than q⁻¹ so that much of their contribution is expected to disappear at larger q values. Conversely, there would be no significant loss of signal for truly restricted particles. Presence of a substantial portion of signal originating from such compartments as well as noise-induced bias associated with employing magnitude-valued data would make the decay appear slower [54, 55] than q⁻¹. The decay exponent c ≈ 1.1 ± 0.1 reported by McKinnon et al.[1] suggests that contributions from such immobile spins could be negligible in their acquisitions. This can be attributed [23] to the relatively short transverse relaxation times those spins are expected to have, along with the long echo times employed at larger q-value acquisitions via clinical scanners.

3.5. A Possible Error

One may be tempted to employ Equation (1) for the compartmental signal, as it always has a Gaussian form for sufficiently small q values, and then to attribute the emergence of the q⁻¹ behavior of the orientationally averaged signal through Equation (2) to the rank of the decay tensor V being 1. However, this may be permissible for large q only in regime C. This attribution would therefore be erroneous for large q in regimes A and B. Specifically, in regimes A and B, the q range in which Equation (1) applies is similar to the q range in which the orientational average (Equation 2) exhibits a Gaussian tail no matter the rank of the tensor V (see Appendix A in the Supplementary Material). Thus, the q⁻¹ behavior is not a consequence of the signal decay tensor having rank 1. Importantly, such behavior naturally emerges at larger q-values in regimes A and B for reasonable shapes of neural projections.

3.6. Debye-Porod Law

The powder averaged signal may be envisioned as having originated from a porous specimen which is macroscopically isotropic, in which case one expects an asymptote of the form q⁻⁴ due to the Debye-Porod law [27] (see Appendix C in the Supplementary Material), while a steeper decay is predicted for longer pulses as the process approaches a Gaussian (Regime C). Since this behavior arises from quite general considerations, the observation of a tail of q⁻¹ appears questionable. Indeed, the observed power is most likely valid only in an intermediate range, as opposed to the strict q → ∞ limit. The asymptotic expansion, whose leading term gives the Debye-Porod law, contains terms that decay faster than any pure power (e.g., exponential). These terms may very well exhibit decays slower than q⁻⁴ over a certain stretch of q-values, before the Debye-Porod asymptote takes over, which happens when q begins to compete with the inverse length of the smallest dimension of the pore geometry. Alas, the q values used in McKinnon et al.'s experiments are of the order 0.1μm⁻¹ which is far from large enough compared to the inverse length scale of 1μm⁻¹ afforded by the axon diameter.

3.7. Unaccounted Factors

One of the hallmarks of neuronal morphology is the axonal and dendritic branchings [56], which are not accounted for in our treatment of diffusion on curves. Although an accurate assessment of the influence of branchings could be achieved via careful numerical studies [57], the insight gained from our description above can be employed to some extent for making some predictions. For long structures, each branch can be considered a separate segment along which diffusion takes place. Thus, the presence of branchings would not impact the formulation for projections in regime A. However, since the total contour length can be considerably increased in the presence of branchings, it may be more difficult to satisfy the long pulse duration condition of regime C. When this condition is met, however, the rank of the signal decay tensor would almost certainly be greater than one. In other words, detecting q⁻¹ decay in regime C would be nearly impossible for smaller cells unless most arborizations run parallel within a narrow cylindrical region.

The detected MR signal is known to be dependent on factors other than those accounted for in this work. Among these, spatial heterogeneity of magnetic susceptibility within the tissue have been reported to influence the diffusion decay [58, 59] as well. In fact, suppressing [60] or taking advantage [61, 62] of effects due to susceptibility variations is an active area of research. We note that the presence of internal gradients could be investigated as yet another mechanism that could explain the reported features in the orientationally averaged signal; doing so would require an extension of existing studies relating the diffusion MR signal to microscopic perturbations in susceptibility [63, 64].

4. Conclusion

In an attempt to interpret new experimental findings, we studied the influence of diffusion along parameterized curves on orientationally-averaged diffusion MR signal. We examined the problem in three distinct temporal regimes of the Stejskal-Tanner experiment and investigated the appearance of a slow decay. We have found that for smaller cells, the q⁻¹ decay of the orientationally-averaged signal is predicted only for straight fibers. This decay is more general for cells with longer projections, while it fades away for curvy structures as the pulse duration of the gradient sequence increases. Finally, we stressed that the q⁻¹ decay could represent an intermediate range as the true asymptotic behavior is governed by a steeper attenuation. The findings of this paper are expected to provide insight into the link between the diffusion weighted MR acquisitions and geometry of the neural cells.

Author Contributions

EÖ conceptualized the problem, and performed the main derivations. EÖ and CY developed and refined the theory, performed the numerical simulations, and wrote the manuscript. MH and HK provided inputs to the theory while C-FW provided guidelines. All authors collaborated in bringing the manuscript to its final state.

Funding

This study was supported by the Swedish Foundation for Strategic Research AM13-0090, the Swedish Research Council CADICS Linneaus research environment, the Swedish Research Council 2015-05356 and 2016-04482, Linköping University Center for Industrial Information Technology (CENIIT), VINNOVA/ITEA3 13031 BENEFIT, and National Institutes of Health P41EB015902, R01MH074794, P41EB015898.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2018.00017/full#supplementary-material

Footnotes

1. ^We note that the decay tensor is closely related to an apparent diffusion tensor (ADT) whose time-dependence has been shown to be sufficient for describing (approximately-)Gaussian diffusion via general gradient waveforms [9]. In this study, it proves convenient to employ the V-tensor, which encapsulates all dependencies other than that on the q-vector.

2. ^Yet another approach would involve employing alternative gradient waveforms for isotropic diffusion weighting [14–18]. However, we do not discuss such sequences here because of the complicated dependence of the signal intensity on the gradient waveform.

3. ^The “most curved point” should be taken with a grain of salt. Even though, mathematically, the approximations in this regime would require a diffusion length $\sqrt{D\Delta }$ much smaller than the smallest radius of curvature along the curve, R_c is not such a strict measure. Rather, it is the minimal radius of curvature that the curve exhibits along a portion of it significant enough to influence the signal.

4. ^This non-obvious statement, whose rigorous proof can be found in mathematics literature [42], was instrumental in our identification of an effective potential for restricted diffusion [43].

5. ^A collection of neuron images for various species and anatomical regions can be found in the Neuromorpho database, which can be accessed through its web site, http://www.neuromorpho.org. For a recent review on the findings based on this database, see Parekh and Ascoli [45]. We also note [46] wherein the authors employ the approach taken in Jespersen et al. [47] on this database to relate the neuronal morphology in gray-matter to the MR signal at very low diffusion sensitivity.

References

1. McKinnon ET, Jensen JH, Glenn GR, Helpern JA. Dependence on b-value of the direction-averaged diffusion-weighted imaging signal in brain. Magn Reson Imaging (2017) 36:121–7. doi: 10.1016/j.mri.2016.10.026

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Assaf Y, Freidlin RZ, Rohde GK, Basser PJ. New modeling and experimental framework to characterize hindered and restricted water diffusion in brain white matter. Magn Reson Med. (2004) 52:965–78. doi: 10.1002/mrm.20274

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Stanisz GJ, Szafer A, Wright GA, Henkelman RM. An analytical model of restricted diffusion in bovine optic nerve. Magn Reson Med. (1997) 37:103–11.

PubMed Abstract | Google Scholar

4. Jespersen SN, Kroenke CD, Østergaard L, Ackerman JJH, Yablonskiy DA. Modeling dendrite density from magnetic resonance diffusion measurements. NeuroImage (2007) 34:1473–86. doi: 10.1016/j.neuroimage.2006.10.037

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Behrens TEJ, Woolrich MW, Jenkinson M, Johansen-Berg H, Nunes RG, Clare S, et al. Characterization and propagation of uncertainty in diffusion-weighted MR imaging. Magn Reson Med. (2003) 50:1077–88. doi: 10.1002/mrm.10609

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Kroenke CD, Ackerman JJH, Yablonskiy DA. On the nature of the NAA diffusion attenuated MR signal in the central nervous system. Magn Reson Med. (2004) 52:1052–9. doi: 10.1002/mrm.20260

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Zhang H, Schneider T, Wheeler-Kingshott CA, Alexander DC. NODDI: practical in vivo neurite orientation dispersion and density imaging of the human brain. NeuroImage (2012) 61:1000–16. doi: 10.1016/j.neuroimage.2012.03.072

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Stejskal EO, Tanner JE. Spin diffusion measurements: spin echoes in the presence of a time-dependent field gradient. J Chem Phys. (1965) 42:288–92.

Google Scholar

9. Jensen JH. Sufficiency of diffusion tensor in characterizing the diffusion MRI signal to leading order in diffusion weighting. NMR Biomed. (2014) 27:1005–7. doi: 10.1002/nbm.3145

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Özarslan E, Basser PJ. Microscopic anisotropy revealed by NMR double pulsed field gradient experiments with arbitrary timing parameters. J Chem Phys. (2008) 128:154511. doi: 10.1063/1.2905765

PubMed Abstract | CrossRef Full Text

11. Özarslan E, Koay CG, Shepherd TM, Komlosh ME, İrfanoğlu MO, Pierpaoli C, et al. Mean apparent propagator (MAP) MRI: a novel diffusion imaging method for mapping tissue microstructure. NeuroImage (2013) 78:16–32. doi: 10.1016/j.neuroimage.2013.04.016

PubMed Abstract | CrossRef Full Text

12. Kaden E, Kruggel F, Alexander DC. Quantitative mapping of the per-axon diffusion coefficients in brain white matter. Magn Reson Med. (2016) 75:1752–63. doi: 10.1002/mrm.25734

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Szczepankiewicz F, Westin CF, Knutsson H. A measurement weighting scheme for optimal powder average estimation. Proc Intl Soc Mag Reson Med. (2017) 26:3345.

14. Mori S, van Zijl PC. Diffusion weighting by the trace of the diffusion tensor within a single scan. Magn Reson Med. (1995) 33:41–52.

PubMed Abstract | Google Scholar

15. Wong EC, Cox RW, Song AW. Optimized isotropic diffusion weighting. Magn Reson Med. (1995) 34:139–43.

PubMed Abstract | Google Scholar

16. Eriksson S, Lasič S, Topgaard D. Isotropic diffusion weighting in PGSE NMR by magic-angle spinning of the q-vector. J Magn Reson. (2013) 226:13–18. doi: 10.1016/j.jmr.2012.10.015

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Westin CF, Knutsson H, Pasternak O, Szczepankiewicz F, Özarslan E, van Westen D, et al. Q-space trajectory imaging for multidimensional diffusion MRI of the human brain. NeuroImage (2016) 135:345–62. doi: 10.1016/j.neuroimage.2016.02.039

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Lampinen B, Szczepankiewicz F, Møartensson J, van Westen D, Sundgren PC, Nilsson M. Neurite density imaging versus imaging of microscopic anisotropy in diffusion MRI: a model comparison using spherical tensor encoding. NeuroImage (2017) 147:517–31. doi: 10.1016/j.neuroimage.2016.11.053

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Özarslan E. Compartment shape anisotropy (CSA) revealed by double pulsed field gradient MR. J Magn Reson. (2009) 199:56–67. doi: 10.1016/j.jmr.2009.04.002

PubMed Abstract | CrossRef Full Text

20. Lawrenz M, Finsterbusch J. Double-wave-vector diffusion-weighted imaging reveals microscopic diffusion anisotropy in the living human brain. Magn Reson Med. (2013) 69:1072–82. doi: 10.1002/mrm.24347

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Yablonskiy DA, Sukstanskii AL, Leawoods JC, Gierada DS, Bretthorst GL, Lefrak SS, et al. Quantitative in vivo assessment of lung microstructure at the alveolar level with hyperpolarized 3He diffusion MRI. Proc Natl Acad Sci USA (2002) 99:3111–6. doi: 10.1073/pnas.052594699

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Anderson AW. Measurement of fiber orientation distributions using high angular resolution diffusion imaging. Magn Reson Med. (2005) 54:1194–206. doi: 10.1002/mrm.20667

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Veraart J, Fieremans E, Novikov DS. Universal power-law scaling of water diffusion in human brain defines what we see with MRI. arXiv 1609.09145. (2016).

Google Scholar

24. Köpf M, Corinth C, Haferkamp O, Nonnenmacher TF. Anomalous diffusion of water in biological tissues. Biophys J. (1996) 70:2950–8.

PubMed Abstract

25. Yablonskiy DA, Bretthorst GL, Ackerman JJH. Statistical model for diffusion attenuated MR signal. Magn Reson Med. (2003) 50:664–9. doi: 10.1002/mrm.10578

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Jian B, Vemuri BC, Özarslan E, Carney PR, Mareci TH. A novel tensor distribution model for the diffusion-weighted MR signal. NeuroImage (2007) 37:164–76. doi: 10.1016/j.neuroimage.2007.03.074

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Sen PN, Hürlimann MD, de Swiet TM. Debye-Porod law of diffraction for diffusion in porous media. Phys Rev B (1995) 51:601–4.

PubMed Abstract | Google Scholar

28. Özarslan E, Koay CG, Basser PJ. Remarks on q-space MR propagator in partially restricted, axially-symmetric, and isotropic environments. Magn Reson Imaging (2009) 27:834–44. doi: 10.1016/j.mri.2009.01.005

PubMed Abstract | CrossRef Full Text

29. Nørhøj Jespersen S, Buhl N. The displacement correlation tensor: microstructure, ensemble anisotropy and curving fibers. J Magn Reson. (2011) 208:34–43. doi: 10.1016/j.jmr.2010.10.003

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Nilsson M, Lätt J, Støahlberg F, van Westen D, Hagslätt H. The importance of axonal undulation in diffusion MR measurements: a Monte Carlo simulation study. NMR Biomed. (2012) 25:795–805. doi: 10.1002/nbm.1795

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Reisert M, Kellner E, Kiselev VG. About the geometry of asymmetric fiber orientation distributions. IEEE Trans Med Imaging (2012) 31:1240–9. doi: 10.1109/TMI.2012.2187916

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Pizzolato M, Wassermann D, Boutelier T, Deriche R. Exploiting the phase in diffusion MRI for microstructure recovery: Towards axonal tortuosity via asymmetric diffusion processes. In: International Conference on Medical Image Computing and Computer-Assisted Intervention (Cham: Springer International Publishing) (2015). p. 109–16.

Google Scholar

33. Cetin S, Özarslan E, Unal G. Elucidating intravoxel geometry in diffusion-MRI: asymmetric orientation distribution functions (AODFs) revealed by a cone model. In: International Conference on Medical Image Computing and Computer-Assisted Intervention (Cham: Springer International Publishing) (2015). p. 231–8.

Google Scholar

34. Budde MD, Frank JA. Neurite beading is sufficient to decrease the apparent diffusion coefficient after ischemic stroke. Proc Natl Acad Sci USA (2010) 107:14472–7. doi: 10.1073/pnas.1004841107

PubMed Abstract | CrossRef Full Text | Google Scholar

35. Press WH, Teukolsky SA, Vetterling WT, Flannery BP. Numerical Recipes in C: The Art of Scientific Computing. Cambridge: Cambridge Press (1992).

36. Debye P. Zerstreuung der röntgenstrahlen. Ann Phys. (1915) 46:809–24.

Google Scholar

37. Glatter O, Kratky O (eds.). Small Angle X-Ray Scattering. London: Academic Press (1982).

38. Feigun LA, Svergun DI. Structure Analysis by Small-Angle X-Ray and Neutron Scattering. New York, NY: Springer Science + Business Media (1987).

39. des Cloizeaux J. Form factor of an infinite Kratky-Porod chain. Macromolecules (1973) 6:403–7.

Google Scholar

40. Mitra PP, Halperin BI. Effects of finite gradient-pulse widths in pulsed-field-gradient diffusion measurements. J Magn Reson A (1995) 113:94–101.

Google Scholar

41. Neuman CH. Spin echo of spins diffusing in a bounded medium. J Chem Phys. (1974) 60:4508–11.

Google Scholar

42. Baxter JR, Brosamler GA. Energy and the law of the iterated logarithm. Math Scand. (1976) 38:115–36.

Google Scholar

43. Özarslan E, Yolcu C, Herberthson M, Westin CF, Knutsson H. Effective potential for magnetic resonance measurements of restricted diffusion. Front Phys. (2017) 5:68. doi: 10.3389/fphy.2017.00068

CrossRef Full Text

44. Schoonover C. Portraits of the Mind. New York, NY: Abrams (2010).

45. Parekh R, Ascoli GA. Quantitative investigations of axonal and dendritic arbors: development, structure, function, and pathology. Neuroscientist (2015) 21:241–54. doi: 10.1177/1073858414540216

PubMed Abstract | CrossRef Full Text | Google Scholar

46. Hansen MB, Jespersen SN, Leigland LA, Kroenke CD. Using diffusion anisotropy to characterize neuronal morphology in gray matter: the orientation distribution of axons and dendrites in the NeuroMorpho.org database. Front Integr Neurosci. (2013) 7:31. doi: 10.3389/fnint.2013.00031

PubMed Abstract | CrossRef Full Text | Google Scholar

47. Jespersen SN, Leigland LA, Cornea A, Kroenke CD. Determination of axonal and dendritic orientation distributions within the developing cerebral cortex by diffusion tensor imaging. IEEE Trans Med Imaging (2012) 31:16–32. doi: 10.1109/TMI.2011.2162099

PubMed Abstract | CrossRef Full Text | Google Scholar

48. Najac C, Branzoli F, Ronen I, Valette J. Brain intracellular metabolites are freely diffusing along cell fibers in grey and white matter, as measured by diffusion-weighted MR spectroscopy in the human brain at 7 T. Brain Struct Funct. (2016) 221:1245–54. doi: 10.1007/s00429-014-0968-5

PubMed Abstract | CrossRef Full Text | Google Scholar

49. Palombo M, Ligneul C, Najac C, Le Douce J, Flament J, Escartin C, et al. New paradigm to assess brain cell morphology by diffusion-weighted MR spectroscopy in vivo. Proc Natl Acad Sci USA (2016) 113:6671–6. doi: 10.1073/pnas.1504327113

PubMed Abstract | CrossRef Full Text | Google Scholar

50. Palombo M, Ligneul C, Valette J. Modeling diffusion of intracellular metabolites in the mouse brain up to very high diffusion-weighting: diffusion in long fibers (almost) accounts for non-monoexponential attenuation. Magn Reson Med. (2017) 77:343–50. doi: 10.1002/mrm.26548

PubMed Abstract | CrossRef Full Text

51. Hilgetag CC, Barbas H. Are there ten times more glia than neurons in the brain? Brain Struct Funct. (2009) 213:365–6. doi: 10.1007/s00429-009-0202-z

PubMed Abstract | CrossRef Full Text | Google Scholar

52. Purves D, Augustine GJ, Fitzpatrick D, Katz LC, LaMantia AS, McNamara JO, et al. (eds.). Neuroscience, 2nd Edn. Sunderland, MA: Sinauer Associates (2001).

53. Herculano-Houzel S, Lent R. Isotropic fractionator: a simple, rapid method for the quantification of total cell and neuron numbers in the brain. J Neurosci. (2005) 25:2518–21. doi: 10.1523/JNEUROSCI.4526-04.2005

PubMed Abstract | CrossRef Full Text | Google Scholar

54. Koay CG, Özarslan E, Basser PJ. A signal transformational framework for breaking the noise floor and its applications in MRI. J Magn Reson. (2009) 197:108–19. doi: 10.1016/j.jmr.2008.11.015

PubMed Abstract | CrossRef Full Text | Google Scholar

55. Özarslan E, Shepherd TM, Koay CG, Blackband SJ, Basser PJ. Temporal scaling characteristics of diffusion as a new MRI contrast: findings in rat hippocampus. NeuroImage (2012) 60:1380–93. doi: 10.1016/j.neuroimage.2012.01.105

PubMed Abstract | CrossRef Full Text

56. Cajal SR. Histologie Du Systeme Nerveux De L'Homme Et Des Vertebretes. Paris: Maloine (1911).

57. Van Nguyen D, Grebenkov D, Le Bihan D, Li JR. Numerical study of a cylinder model of the diffusion MRI signal for neuronal dendrite trees. J Magn Reson. (2015) 252:103–13. doi: 10.1016/j.jmr.2015.01.008

PubMed Abstract | CrossRef Full Text | Google Scholar

58. Palombo M, Gabrielli A, De Santis S, Capuani S. The γ parameter of the stretched-exponential model is influenced by internal gradients: validation in phantoms. J Magn Reson. (2012) 216:28–36. doi: 10.1016/j.jmr.2011.12.023

PubMed Abstract | CrossRef Full Text

59. Caporale A, Palombo M, Macaluso E, Guerreri M, Bozzali M, Capuani S. The γ-parameter of anomalous diffusion quantified in human brain by MRI depends on local magnetic susceptibility differences. NeuroImage (2017) 147:619–31. doi: 10.1016/j.neuroimage.2016.12.051

PubMed Abstract | CrossRef Full Text | Google Scholar

60. Zheng G, Price WS. Suppression of background gradients in (B0 gradient-based) NMR diffusion experiments. Concept Magn Reson A (2007) 30:261–77. doi: 10.1002/cmr.a.20092

CrossRef Full Text | Google Scholar

61. Song YQ, Ryu S, Sen PN. Determining multiple length scales in rocks. Nature (2000) 406:178–81. doi: 10.1038/35018057

PubMed Abstract | CrossRef Full Text | Google Scholar

62. Álvarez GA, Shemesh N, Frydman L. Internal gradient distributions: a susceptibility-derived tensor delivering morphologies by magnetic resonance. Sci Rep. (2017) 7:3311. doi: 10.1038/s41598-017-03277-9

PubMed Abstract | CrossRef Full Text

63. Pathak AP, Ward BD, Schmainda KM. A novel technique for modeling susceptibility-based contrast mechanisms for arbitrary microvascular geometries: the finite perturber method. NeuroImage (2008) 40:1130–43. doi: 10.1016/j.neuroimage.2008.01.022

PubMed Abstract | CrossRef Full Text | Google Scholar

64. Kurz FT, Kampf T, Buschle LR, Schlemmer HP, Bendszus M, Heiland S, et al. Generalized moment analysis of magnetic field correlations for accumulations of spherical and cylindrical magnetic perturbers. Front Phys. (2016) 4:46. doi: 10.3389/fphy.2016.00046

CrossRef Full Text | Google Scholar

65. Tanner JE, Stejskal EO. Restricted self-diffusion of protons in colloidal systems by the pulsed-gradient, spin-echo method. J Chem Phys. (1968) 49:1768–77.

Google Scholar

66. Robertson B. Spin-echo decay of spins diffusing in a bounded region. Phys Rev. (1966) 151:273–7.

Google Scholar

67. Barzykin AV. Theory of spin echo in restricted geometries under a step-wise gradient pulse sequence. J Magn Reson. (1999) 139:342–53. doi: 10.1006/jmre.1999.1778.575

PubMed Abstract | CrossRef Full Text | Google Scholar

68. Grebenkov DS. NMR survey of reflected Brownian motion. Rev Mod Phys. (2007) 79:1077–137. doi: 10.1103/RevModPhys.79.1077

CrossRef Full Text | Google Scholar

69. Özarslan E, Shemesh N, Basser PJ. A general framework to quantify the effect of restricted diffusion on the NMR signal with applications to double pulsed field gradient NMR experiments. J Chem Phys. (2009b) 130:104702. doi: 10.1063/1.3082078

PubMed Abstract | CrossRef Full Text

70. Grebenkov DS. Analytical solution for restricted diffusion in circular and spherical layers under inhomogeneous magnetic fields. J Chem Phys. (2008) 128:134702. doi: 10.1063/1.2841367

PubMed Abstract | CrossRef Full Text | Google Scholar

71. Torrey HC. Bloch equations with diffusion terms. Phys Rev. (1956) 104:563–5.

Google Scholar

72. Hörmander L. The Analysis of Linear Partial Differential Operators I, (Distribution Theory and Fourier Analysis), 2nd Edn. Berlin: Springer-Verlag (1990).

73. Yolcu C, Memiç M, Şimşek K, Westin CF, Özarslan E. NMR signal for particles diffusing under potentials: from path integrals and numerical methods to a model of diffusion anisotropy. Phys Rev E (2016) 93:052602.

PubMed Abstract | Google Scholar