One-Dimensional Multi-Channel Photonic Crystal Resonators Based on Silicon-On-Insulator With High Quality Factor

Introduction

Modern Silicon fabrication technology has advanced remarkably over the last two decades, demonstrating an unprecedented level of photonic integration [1–7]. Particular attention is paid to different types of photonic devices based on one-dimensional, two-dimensional and three-dimensional photonic crystals with a consequent variation of layers of different refractive indices in these (various) directions [4–6]. Development of integrated compact multi-channel filters in particular, for applications including communication systems [8, 9], multifunctional sensing [10–12] and spectral imaging detection [13] is an active area of research in this field. Vertically etched silicon one-dimensional photonic crystals (1D PhCs) have attracted particular interest, due to their easy fabrication and integration onto a chip with in-plane light propagation [14–16]. Other advantages of these structures are the possibility of tuning their optical properties [17–19], as well as their ease of adoption for micro/nano-fluidic devices [20–22].

These advantages have resulted in the development of a variety of opto-electronic devices, including multimode filters for wavelength division multiplexing (WDM) as well as opto-fluidic devices for biochemical and biomedical sensing. The desired characteristics for these devices are high quality factor (Q), large modulation depth, also known as extinction ratio (E.R), high selectivity, high out-of-band rejection, low power attenuation, low insertion losses and a small footprint, see, for example, Reed [6]. The use of vertical 1D PhCs for sensing is particularly important for the near- and mid-infrared regions and may be extended in future to the far-infrared and even the THz regions [1–3, 7, 23]. Another attraction of these structures is that the delivery of chemical or biological substances into the air gaps can be performed via standard “flow-over” (see, for example [24]) and “flow-through” approaches. The latter method is achieved by pumping through the channels as well as by capillary action [25–27]. Simulations of three vertical silicon/air 1D PhC Fabry-Perot resonant cavities with different architectures and fluidic functionalities were discussed in Surdo and Barillaro [28]. The impact of cavity order and 1D PhC micromirror reflectivity on their biosensing performance is analyzed. Results on the surface sensitivity, the limit of detection and the range of linearity of the devices are reported.

For effective frequency separation, multimode filters are used. These are fabricated by creating a cavity of extended size in a Fabry-Perot (FP) resonator, as well as by using cascaded and coupled resonators [17, 29–31]. These cascaded structures consist of separate FP filters connected in series. Changing the optical properties of individual filters does not affect the properties of the neighboring filters [29–31]. The use of PhC technology can remarkably improve the tuning capability of individual channels within these filters and optical switches for WDM optical interconnect applications. PhC technology can also reduce the footprint and provide an easier integration process [32]. Tunable multichannel PhC filters rely on the tuneability of the refractive index, n, of several periods within the periodic photonic structure, allowing the formation of coupled resonators, via thermotuning, electrotuning and a photorefractive effect [33–37]. These devices allow fine-tuning of individual channels in the filter system, by, for example, varying the temperature or applying an electric or magnetic field.

The development of integrated compact multi-channel optical filters is a rapidly developing area. Coupled microresonators are used in waveguide structures [38] and ring resonators [39], which can be tuned by injecting carriers with Δn < 10⁻⁴, resulting in a relatively small tunable range. By using liquid crystals with a larger range of Δn, up to 0.4, tuning of the resonance modes has been significantly extended, for example, in a cascade resonator [29]. In Cos et al. [40] the design of an optical equalizer, or tunable filter, is proposed, with the possibility of changing the shape of the interference bands by changing n within different periods of the 1D PhC structure.

The optical properties of a system of two coupled Fabry-Perot microresonators were investigated theoretically in Kaliteevski [41], where the interaction of localized photon states is considered, leading to a splitting of the optical modes of the system. In this study, the coupling parameter, the reflection, R, of the common mirror, is identified, characterizing the interaction force between the modes. A decrease in R led to an increase in the splitting of the peaks in the spectrum. By using coupled FP resonators and exploiting the possibility of individual tuning of n in each resonator, a 1D PhC structure with two defects and various options to control the position of the doublet of resonance modes was investigated in Tolmachev et al. [42].

In this study, we propose a novel design for a multichannel integrated filters based on silicon-on-insulator (SOI) photonic crystal concepts and optofluidics technology. By infiltrating specific periods of a 1D PhC with a reconfigurable liquid filler, an efficiently coupled Fabry-Pérot micro-resonator (Figure 1) can be realized in which the wide stop band (SB) is used for frequency channel separation. Using a coupled triple-cavity 1D PhC filter operated using the third SBs, we have demonstrated refractive index control within individual cavities using a reconfigurable fluid, enabling independent fine tuning of each channel in the system by an applied voltage. By applying a voltage to one of the cavities, a triplet resonance is achieved with a significant increase in the Q factor for one of the resonance peaks.

FIGURE 1

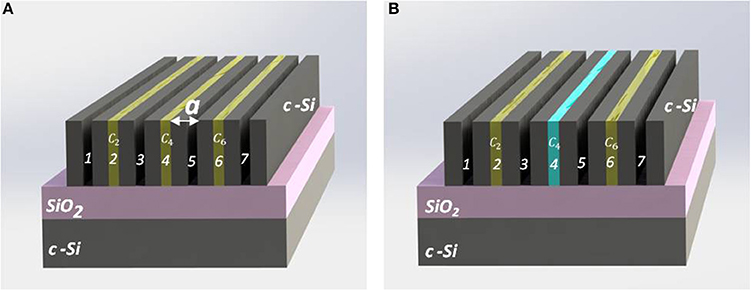
Figure 1. (A) Schematic diagram of 1D PhC based on a Si-air structure with three central air channels (c2, c4, and c6) infiltrated with a nematic liquid crystal (LC) of tunable refractive index, n_c. (B) Schematic diagram of 1D PhC in which the refractive index of the central cavity n_c4 is changed without changing n_c in the edge cavities, giving a new sequence of n_c. The notation ɑ stands for the lattice constant of the 1D PhC and is equal to a sum of the thicknesses of crystalline Si (c-Si) rib, d_Si, and the air (or LC) channel, d_air.

Simulations

Coupled Fabry-Perot Resonators With Tunable Triple Mode Capability

In this section, we describe the optical properties of 1D PhCs based on a Si-air structure with three central air channels infiltrated with an LC of tunable refractive index, n_c. These structures form three coupled FP resonators with triple-defect modes within the photonic SBs. The optical properties of these structures were estimated using a transfer matrix method (TMM), see for details [26].

The introduction of 3 cavities, infiltrated with a filler of tunable n_c, to a 1D PhC, leads to the formation of triple conjugated FP resonators, Figure 1A. The transfer matrix for 3-coupled resonators (M_3CR) can be written as

$\begin{array}{cc}\begin{array}{l}{\text{M}}_{\text{3CR}}=\text{H}{\left(\text{LH}\right)}^{mBr}{\text{L}}_{\text{c2}}\left[{\left(\text{HL}\right)}^{mo}\text{H}\right]{\text{L}}_{\text{c4}}\left[{\left(\text{HL}\right)}^{mo}\text{H}\right]{\text{L}}_{\text{c6}}\\ [\left(\text{HL}\right){\left(\text{HL}\right)}^{mB}H,\end{array}& (1)\end{array}$

where H – stands for the matrix of the high-refractive index component and L—the matrix of the low-refractive index component, c₂, c₄ and c₆—refer to the resonator cavities (2, 4, and 6), mBr—the number of periods for the Bragg mirror and mo—the number of periods for the internal mirror. The refractive index of the air is taken as n_air = 1, while the data for the dispersion of Si, n_Si(v), were taken from Salzberg and Villa [43]. For our calculations, we use various combinations of n_c in the FP-resonator cavities, with parallel or cross-tuning in the range 1.5–1.7. From the large range of possible n_c available, we selected four specific cases which may be of practical interest for different applications. The calculations were performed for the following geometrical parameters of a 1D PhC: d_Si = 0.718 μm and d_air = 2.5 μm (i.e., a = 3.218 μm) and mBr = mo = 1.

Parallel Tuning of Triplet FP Resonator

In the initial state, when the filler in all three cavities of the resonator have n_c = 1.585 (Figure 2a), a triplet of defect modes appears in the spectrum of the 1st SB, Figure 2c—bottom spectrum. The distance between the peak positions in this triplet is Δv ≈ 40 cm⁻¹, the linewidth, i.e., the full width at half-maximum, FWHM, for the edge and central peaks is = 2.5 and 5.5 cm⁻¹ respectively, and the Q-factors for each peak are 420 and 190, respectively.

FIGURE 2

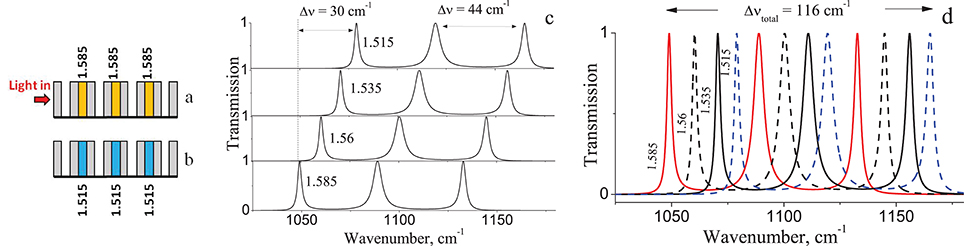
Figure 2. Schematic diagram of three coupled resonators with tuning of n_c of the filler from (a) 1.585 to (b) 1.515; (c) parallel tuning of the triplet mode with Δν = 30 cm⁻¹ for the 1st SB, (d) the full range of 12 resonance peaks with Δν_total = 116 cm⁻¹. The numbers beside the peaks are the refractive indices, n_c, of the filler liquid in the resonator cavities.

When n_c in all three cavities is decreased from 1.585 to 1.515 (Figure 2b), the triplet as a whole experiences a blue shift by Δv = 30 cm⁻¹ (Figure 2c—top spectrum), or in relative units by Δv/Δn_c = 429 cm⁻¹/RIU, where RIU stands for refractive index unit. Taking into account the linewidth of the peaks and the distance between them, equal to Δv ≈ 40 cm⁻¹, as well as the possibility of changing the values of n_c to a high degree of accuracy, it is possible to obtain other triplets occupying different positions in the spectrum. Thus, it is possible to achieve tuning of 4 triplets, with 12 resonant peaks in total, covering the range Δv_total = 116 cm⁻¹ (Figure 2d).

The tuning effect can be increased by using higher order SBs. To obtain non-overlapping peaks, it is possible to use an almost full range of n_c variation in the range 1.5–1.7, Figure 3A. Calculations show that in the 3st SB the linewidth of the peaks remains the same as in the 1st SB, viz. 2.5 cm⁻¹ for the edge peaks and 4.5 cm⁻¹ for the central peak. The distance between the two nearest peaks is 40 cm⁻¹ and the tuning range increased 5-fold from 30 to 167 cm⁻¹, Figure 3B. The relative tuning was Δv/Δn_c = 835 cm⁻¹/RIU, a 2-fold increase. We note that 12 resonant peaks were obtained using only four possible values of n_c in the range 1.5–1.7, including the lowest and the highest n_c values. However, to obtain the maximum number of non-overlapping peaks, further fine tuning of the n_c values within this range is required.

FIGURE 3

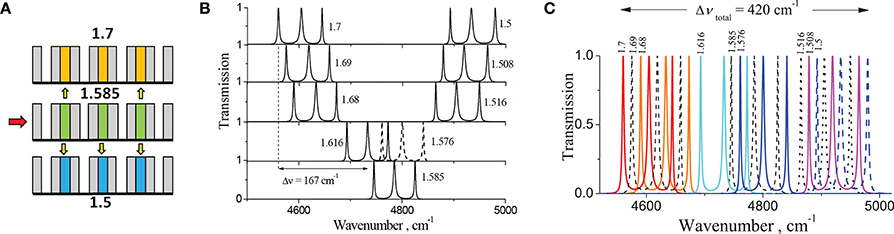
Figure 3. (A) Schematic diagram illustrating n_c tuning in resonator cavities, (B) nine triple peaks in the spectra of the 3rd SB with parallel tuning of the n_c filler from 1.5 to 1.7, (C) the full range of 27 resonance peaks with Δv_total = 420 cm⁻¹. Numbers beside the peaks correspond to the values of n_c for the fillers in all three cavities of the resonators.

The spectrum in Figure 3B (bottom spectrum) shows only one triplet for n_c = 1.585, whereas in all other spectra in this Figure, two triplets are shown for the larger and smaller values of n_c to save space. Figure 3C shows the positions of all 27 peaks in the range Δv_total = 420 cm⁻¹, exhibiting good resolution between the peaks. As in the case of double resonators [41, 42] the central position of the resonance peaks in the 3rd SB, with a linewidth of w_3SB ≈ 600 cm⁻¹, made it possible to use over 2/3 of the SB to create a wide range of tunable resonances within it. In contrast, for the 1st SB, only 15% of the width of the band, w_1SB ≈ 770 cm⁻¹, can be used in this manner.

Tuning of the Edge Peaks in the Triplet

Other options for triplet tuning are available. The initial state of the resonators is described by the following sequence of n_c: 1.515–1.515–1.515, Figure 4a. The calculated transmission spectrum, T, for the 1st SB is shown in Figure 4d. The n_c of the central cavity is changed to 1.585 without changing n_c in the edge cavities, giving a new sequence of n_c: 1.515–1.585–1.515 (Figure 4b) with the corresponding spectrum shown in Figure 4e.

FIGURE 4

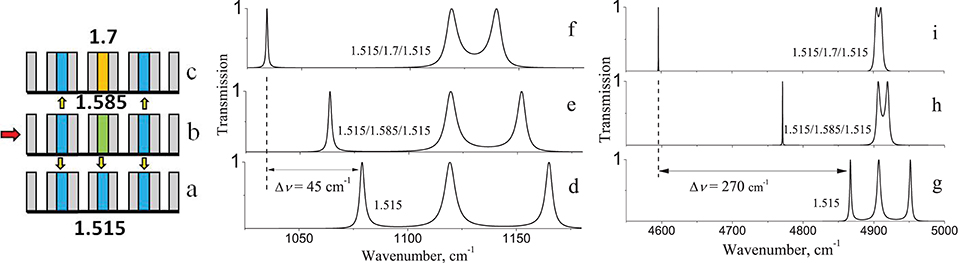
Figure 4. (a–c) Schematic diagram illustrating tuning of n_c in one of the three cavities of the resonator. Triplet peaks with tuning of the n_c filler from 1.5 to 1.7 in the central cavity with splitting of the triplet into doublet and mono-peaks in the spectra of the 1st SB (d–f) and 3rd SB (g–i). The numbers correspond to the value of n_c of the filler in the resonator cavities.

Finally, by changing n_c in the central cavity to 1.7, Figure 4c, we obtain the spectrum shown in Figure 4f. The result of this tuning is a red shift of two edge defect modes at Δv = 45 cm⁻¹. In relative units, the shift is small, i.e., Δv/Δn_c = 225 cm⁻¹/RIU, and the central mode within the triplets remains stationary.

This is more clearly manifested in the 3rd SB shown in Figures 4g–i. Indeed, splitting of the triplet into a double peak (doublet) and a single peak (mono-peak) occurred, and, as seen in Figure 4i, both peaks in the doublet merge to form a single broadened peak, while the monopeak is narrowed greatly. Formation of the doublet structure is explained by the interaction between two resonators with identical resonant frequencies. These are the two extreme cavities, with n_c = 1.515, connected through a central resonator. Its resonant frequency, with a change of n_c2 to 1.585 and then to 1.7, differs from the frequency of the resonators forming a doublet. For the initial state, the central resonator was in resonance with the edge cavities and it's intrinsic frequency begins to increase as n_c increases. This, in turn, reduces the interaction between the resonances in the edge cavities, due to the appearance of a reflector at their intrinsic frequency, ultimately greatly weakening their interaction, resulting in minimal peak splitting in the doublet (Figure 4i). From Figures 4g–i, the total shift as a result of the tuning is Δv = 270 cm⁻¹, which is significant if expressed in relative units, viz. Δν/Δn_c = 1,350 cm⁻¹/RIU. In addition, the quality factor, Q = v_res/Δv, where v_res is the resonance peak position and Δv is the linewidth, is significantly increased from 1,400 to 21,200 for the left peaks in Figures 4g,i respectively.

Let us now consider the following tuning option utilizing the 3rd SB: n_c in the edge cavities unchanged and equal to 1.6, while the n_c of the central cavity (n_c2) changes to a larger or smaller value from n_c, that is, n_c2 = ± Δn, where Δn = 0.035. A schematic of the n_c changes is shown in Figures 5a–c. Figure 5d shows the original triplet, obtained in the 3rd SB with splitting of the peaks by Δν = 40 cm⁻¹ for the original state with n_c = 1.6 in all 3 cavities of the resonator. Furthermore, by increasing or decreasing n_c by Δn = 0.006, 0.017, and 0.035, different triplets were obtained, as presented in Figures 5e–g. As a result, the position of the central peak on the graphs remains unchanged while peak splitting is observed. With increased n_c2 the edge peaks are red shifted, while with decreasing n_c2 the peaks are blue shifted.

FIGURE 5

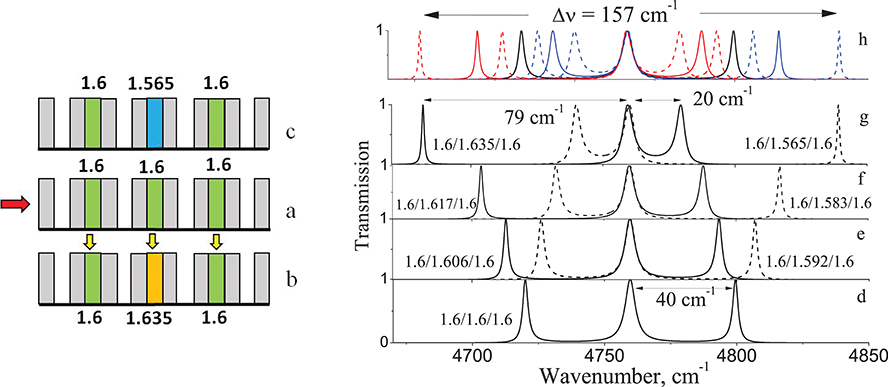
Figure 5. (a–c) Tuning of the n_c filler in the central cavity only: (d–g) 7 triplets in the 3rd SB, realized with different n_C2 (shown by numbers at the peaks) with a fixed central peak and tuned lateral (edge) resonances, (h) summing peaks for all states of n_c.

In addition, the nature of the peak splitting of the triplet changes. For example, increasing n_c to 1.635, the left peak splits more strongly (Δv = 79 cm⁻¹), while the right peak approaches the central peak (Δv = 20 cm⁻¹). This situation is analogous to the effect shown in Figures 4g–i, where splitting of the triplet into a doublet and a mono-peak was observed. This was explained by a weakening of the interaction of the coupled resonators caused by different n_c values within the cavities. Thus, by selecting a more appropriate combination of n_c values, (Figures 5a–c), it is possible to obtain well-separated transmission peaks in the interval Δv_total = 157 cm⁻¹ as shown in Figure 5h. So, it is possible to tune 7 different peak pairs with one common unchanged transmission channel, that is, 15 channels in total.

Summarizing the results from the data shown in Figures 4g–i, 5d–h, we conclude that changes in the triplet with increasing Δn between the cavities are more pronounced in the 3rd SB when compared with the 1st SB, allowing edge tuning to provide a larger range of transmission channels.

Tuning of the Central Peak in the Triplet

Another option for triplet tuning was investigated, that of changing n_c simultaneously in all 3 cavities. The variation of n_c was carried out according to the schematic shown in Figures 6a–c. For the initial state n_c in the cavities (1.6/1.6/1.6), the triplet in the 1st SB is shown in Figure 6d. A decrease of n_c4 to 1.57 was made in the central cavity of the resonator, with a simultaneous increase of n_c2 and n_c6 to 1.625. This state (1.625 / 1.57 / 1.625) is depicted in Figure 6b. Since n_c in the resonators now changes in opposite directions, we refer to this situation as cross-tuning. The original triplet calculated is shown in Figure 6d with another triplet obtained using an intermediate value of n_c. Also included are triplets obtained by reverse tuning of n_c in the resonators, as shown in the schematic in Figure 6c.

FIGURE 6

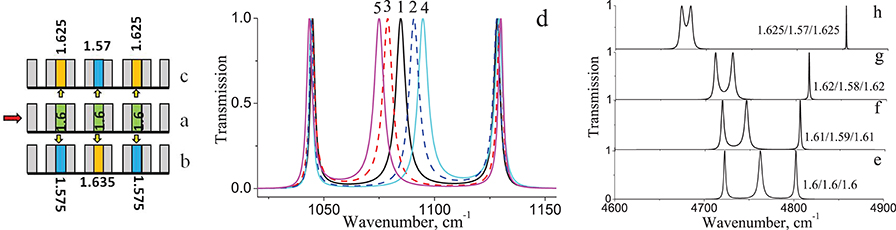
Figure 6. (a–c) Schematic diagram illustrating cross-tuning of the n_c filler, (d) 5 triplets in the 1st SB with fixed edge peaks and a tunable central peak, (e–h) the original triplet and 3 triplets in the 3rd SB, demonstrating the split into a doublet and a mono-peak. Numbers at the peaks are the values of n_c for the fillers in the cavities of the resonators. In panel (d) the numbers beside the curves correspond to the following set of n_c: 1 – 1.6/1.6/1.6; 2 – 1.585/1.62/1.585; 3 – 1.615/1.58/1.615; 4 – 1.575/1.63/1.575; 5 – 1.625/1.57/1.625.

From Figure 6d, the positions of the side peaks remain practically the same for the 5 triplets obtained, while the central peak experiences a red shift as the n_c2 of the central cavity decreases. This is the opposite case to the tuning effect for a single peak in a classical FP resonator. In a single peak in a classical FP resonator, a decrease in the optical thickness of the cavity results in the resonance peak experiencing a blue shift. Examining this effect for the 3st SB in Figures 6e–h, it is apparent that as the cross-sectional change in n_c increases, resonance effects split the triplet into a doublet and a mono-peak, as observed earlier, see Figure 4. Indeed, the central peak of the triplet in this case experiences a red shift. Thus, for the 3rd SB, performing cross-tuning of n_c in the cavities enables control of the doublet structure, shifting it to the red. The edge cavities with the same refractive index are responsible for the appearance of the doublet structure. n_c in this case increases, leading to a redshift of the doublet, and the central peak responsible for its creation. This redshift is apparent in Figures 6e–h.

It should be noted that because of strong splitting due to cross-tuning of n_c in the cavities in the 3rd SB, the side peaks in the triplet cannot be fixed, as was possible in the 1st SB. Attempts to realize a similar resonator, i.e., fixed edge channels—tuning of the central channel, for the well-divided peaks in the 3rd SB failed, even when changing the values of n_c by small amounts.

The results of simulations demonstrating the tuning of triple FP resonances with suppression of the edge peaks are described in the Supplementary Materials section and shown in Supplementary Figure S1.

Experiment

Results and Discussions

Prototypes of integrated triple-cavity PhC filters were designed and fabricated on a Silicon-On-Insulator (SOI) platform. The triple-channel resonator device was fabricated on a <100> p-type SOI wafer with a silicon device layer thickness of 4.5 μm and a 1 μm thick buried oxide layer, Supplementary Figure S2 in Supplementary Material. Electron-Beam Lithography followed by plasma etching was used to fabricate the nano-scale structures with a lattice constant of 1600 nm and a Si wall thickness of 1040 nm. These design parameters for the 1D PhC structures were selected in order to create triple resonances in the telecommunication wavelength range after infiltration of the 2nd, 4th, and 6th grooves with a nematic liquid crystal filler E7, Figure 7a. This liquid crystal was chosen mainly because of its high birefringence, n_e – n_o = 0.21, where n_e and n_o correspond to the extraordinary and ordinary refractive indices respectively, as well as a wide nematic temperature range (from −10^oC to 59^oC). Electrical isolation of the 2nd, 4th, and 6th grooves of the 1D PhC was achieved by dry-etching the micro-channels across the chip, Supplementary Figure S3 in Supplementary Material. One cone-shape cavity is designed for the easy infiltration of these grooves with LC E7, Figure 7a. A 500 nm layer of aluminum was deposited by sputtering for the contact pads. Optical lithography followed by a wet etch process was used to define the contact pads, as shown in Figure 7a. Finally, U-grooves with a depth of 60 μm were etched from both sides of the nano-structure for easier integration of the optical fibers and direct coupling to the device (Figures 7b,c).

FIGURE 7

Figure 7. SEM images of the fabricated (a) SOI-based chip with integrated triple-coupled defect photonic crystal filter with connected microfluidic channels to the 2nd, 4th, and 6th periods (clearly indicated beside the output channels) and metal contact pads (circles), and (b) closer view of the defect-free 1D PhC with three-channels connected to the 2nd, 4th, and 6th grooves for infiltration purposes. (c) Schematic representation of light coupling with optical fibers integrated on-chip using U-grooves from both sides of the PhC structure.

By applying a voltage to the aluminum contact pads, different orientations of the LC molecules were obtained in the individual grooves, allowing manipulation of the refractive index in the 2nd, 4th, and 6th grooves and, consequently, with the transmission channels as described earlier in the Simulations section. In Figure 8, the electro-optical effect obtained for three channels is demonstrated with crossed-polarized optical microscopy. The black stripes are silicon electrodes, orange lines are air grooves and light stripes are grooves filled with a LC, Figure 8. A rectangular pulse train is applied to the three channels, alternating between 0 and 10 V, with a pulse duration of τ_p = 1 ms and a frequency of f _p = 100 Hz. The applied voltage causes the Fredericks transition to occur in the LC in the grooves, as demonstrated by the change in color of the groove stripes. The effect of the applied voltage on all three FP channels individually or simultaneously is demonstrated clearly in the video uploaded in the Supplementary Material section.

FIGURE 8

Figure 8. Polarized Optical Microscope images showing a top view of the channels: (a) no applied electric field (0 V), (b) under applied electric field of 10 V to the 4th central channel, (c) under applied electric field of 10 V to the 2nd and the 6th channels and (d) under applied electric field of 10 V to all three channels. Note: Applied voltage indicated by numbers (0 and 10) in Volts.

A demonstration of the appearance of the full set of resonance peaks within the 1st and 3rd SBs under applied voltage was not possible in this work due to limitations in the wavenumber range available for measurements in our fiber-coupling set-up. However, a shift of the resonance peak position by the applied electric field of different strength (and, therefore, by fine-tuning of n_c) was demonstrated by us earlier [44], see also a schematic illustration of this effect shown in Supplementary Figure S4 in Supplementary Material section. In Tolmachev et al. [44], we presented the results of TMM simulations for a single-cavity FP resonator, filled with LC E7, over a wide IR spectral range. The experimental verifications of these calculations were provided using FTIR microspectroscopy.

On-chip in-situ transmission testing of the device with an electric field applied to the micro-fluidic cavities was performed in the geometry demonstrated in Figure 7c (see also Supplementary Figure S5 in Supplementary Material). Light from the Yeniast Tunics T100S tunable laser source in the range 1,540–1,630 nm was coupled into the chip on the left-hand side. The transmitted signal was collected from the right-hand side, using standard optical fibers. Output power was measured using an optical spectrum analyser (OSA), Yenista Optics FP002417 OSA. The schematic of this set-up is shown in Supplementary Material section.

The device was electrically driven by terminating probes on the contact pads during the transmission measurements using a customized Microtech 2 probe coupler. Device transmission characteristics were initially assessed with no voltage applied to the channels, as in Figure 8a. In Figure 9A we demonstrate the realization of a triple resonance mode obtained with a spontaneously aligned LC in the grooves with an average refractive index of 1.68. The simulated resonance peaks obtained at 1,589.4, 1,608 and 1,629.6 nm demonstrate a Q factor of the order of 1,130 with a total resonance wavelength spacing of 40.2 nm. Under an applied AC voltage of 10V, the refractive index of c₄ channel is decreased to 1.458. This results in the formation of a doublet at 1,607.6 and 1,617 nm and a single resonance peak at 1,562.4 nm, with a significant increase of the Q factor to 3,720, see Figure 9B and Supplementary Figure S6 in Supplementary Material. Under applied voltage, this peak is shifted by 27 nm from its original position at 1,589.4 nm, as shown in Figure 9A with no voltage applied. The fitted n_c value corresponds to a homeotropic alignment of rod-like LC molecules perpendicular to the Si walls (see Supplementary Figure S4d in Supplementary Material), expected to occur with an applied electric field across the 1D PhC groove channels, see, for example, page 516 in Perova et al. [26] and Tolmachev et al. [44]. This experimental result demonstrates for the first time, electrically controllable, ultra-high sensitivity of a single resonance device based on the triple cavity Fabry-Pérot system. The LC filler in the 2nd and 6th cavities can be replaced by any other liquid filler analyte or gas with arbitrary refractive index, while the electrically tunable 4th central cavity can be used as a highly-sensitive reference liquid. The nematic LC E7 can demonstrate a relatively high-quality factor and sensitivity for high-order stop-bands in particular.

FIGURE 9

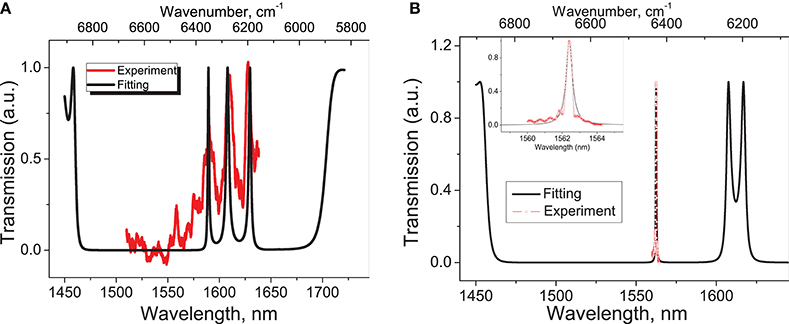
Figure 9. Simulated (black) and experimental (red) transmission spectra of (A) triple resonance system with refractive index of LC filler of n_c = 1.68 in 2nd, 4th, and 6th grooves and (B) single resonance system realized by application of 10V to the 4th groove and reduction of refractive index to n_c = 1.458. A magnified view of the single resonance peak can be found in the inset figure.

We note that for SOI electro-optical devices, that required a fast tuning of the refractive index of liquid crystal, the LC E7 is not very suitable, since its operation time is in the range of milliseconds. However, the other nematic LCs like, for example, 5CB and CCN-47 not only characterized by their high birefringence but also demonstrate an impressive electro-optical switching time in the range of 30–50 nanoseconds, as recently was demonstrated under specific experimental conditions in Geis et al. [45] and Borshch et al. [46]. In addition to that, it was shown during the last decade that some new type of liquid crystal molecules (for example, banana-shaped or bent-core LCs) can demonstrate also fast switching time at microseconds/nanoseconds level [47, 48].

Conclusions

In this paper, we propose a novel design for multichannel integrated devices based on SOI photonic crystal concepts and optofluidic technology. By infiltrating specific periods of a 1D PhC with a reconfigurable liquid filler of different refractive indices, n_c, an efficiently coupled Fabry-Pérot micro-resonators can be realized. Various combinations of n_c in the cavities of the FP resonators with parallel and cross-tuning in the range 1.5–1.7 are investigated by simulations using the transfer matrix method. With parallel tuning of n_c in all three cavities, a large number of narrow triple resonance peaks can be obtained within the wide stop-bands of different order in the infrared range of spectra. Simulations of cross-tuning of n, reveal splitting of the triple resonance peaks into a doublet and a single peak with significantly enhanced quality factor, Q = 21,200.

Prototype devices were fabricated with three central cavities infiltrated with LC E7. Simulations of the electro-optical and optical properties of these devices were confirmed experimentally using polarized optical microscopy and spectroscopic measurements using fiber-coupling. Tuning of the refractive index of the filler in all three cavities simultaneously or individually was confirmed by electro-optical measurements. These structures may have application to WDM devices in the near IR to THz range, depending on the geometry. Spectroscopic measurements, performed over a limited near-IR spectral range, verified the presence of the triple resonance peaks within the 3rd stop-band in the absence of an applied electric field in the grooved channels. Application of an electric field to one of the three channels, using a voltage of 10 V, caused a shift of the low-frequency peak and a substantial increase of the quality factor to Q = 3,720. This suggests that these devices could form the basis of coupled FR resonators for application in refractive index sensing and for ultra-narrow optical filters in the infrared range.

Author Contributions

TP, VT, and AB: conceived the idea; VT, AB, and JF: performed device design and simulation; TP and AB: participated in device fabrication; AB and JF: performed near-IR measurements; TP, VT, AB, and JF: wrote the manuscript. All authors were involved in the analysis of the results and revision of the manuscript.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

We acknowledge financial support from: The Engineering and Physical Sciences Research Council (EPSRC) of the United Kingdom via the EPSRC (Grant No. EP/L015331/1 and Grant No. EP/N035569/1) and the Royal Society International Exchange Grant 2015/R3. The microfluidic structures were fabricated at Tyndall National Institute under the Science Foundation Ireland NAP368 and NAP94 programs. The part of this research at the Ioffe Institute was supported by the Russian Federal Agency of Scientific Organizations.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2018.00033/full#supplementary-material

References

1. Soref R. The past, present, and future of silicon photonics. IEEE J Sel Top Quantum Electron (2006) 12:1678–87. doi: 10.1109/JSTQE.2006.883151

CrossRef Full Text | Google Scholar

2. Soref R. Mid-infrared photonics in silicon and germanium. Nature Photon. (2010) 4:495–7. doi: 10.1038/nphoton.2010.171

CrossRef Full Text | Google Scholar

3. Soref R. Group IV photonics for the mid infrared. Proc SPIE (2013) 8629:862902. doi: 10.1117/12.2013769

CrossRef Full Text | Google Scholar

4. Wehrspohn RB, Kitzerow HS, Busch K. Nanophotonic Materials: Photonic Crystals, Plasmonics, and Metamaterials. Weinheim: Wiley-VCH (2008).

Google Scholar

5. Vivien L, Pavesi L. Handbook of Silicon Photonics. Boca Raton, FL: CRC Press (2013).

Google Scholar

6. Reed GT. Silicon Photonics: The State of the Art. West Sussex: Wiley (2008).

Google Scholar

7. Hu T, Dong B, Luo X, Liow TY, Song J. Silicon photonic platforms for mid-infrared applications. Photon Res. (2017) 5:417. doi: 10.1364/PRJ.5.000417

CrossRef Full Text | Google Scholar

8. Yariv A, Yeh P. Photonics: Optical Electronics in Modern Communications, Oxford: Oxford University Press (2007).

Google Scholar

9. Li Q, Soltani M, Yegnanarayanan S, Adibi A. Design and demonstration of compact, wide bandwidth coupled-resonator filters on a silicon-insulator platform. Opt Express (2009) 17:2247–54. doi: 10.1364/OE.17.002247

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Shu X, Chisholm K, Felmeri I, Sugden K. Highly sensitive transverse load sensing with reversible sampled fiber Bragg gratings. Appl Phys Lett. (2003) 83:3003–5. doi: 10.1063/1.1618367

CrossRef Full Text | Google Scholar

11. Armani AM, Kulkarni RP, Fraser SE, Flagan RC, Vahala KJ. Label-free, single-molecule detection with optical microcavities. Science (2007) 317:783–7. doi: 10.1126/science.1145002

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Marquez S, Alvarez M, Plaza JA, Villanueva LG, Dominguez C, Lechuga LM. Asymmetrically coupled resonators for mass sensing. J Appl Phys. (2017) 111:113101. doi: 10.1063/1.5003023

CrossRef Full Text | Google Scholar

13. Lin J, Tong Q, Lei Y, Xin Z, Wei D, Zhang X, et al. Electrically tunable infrared filter based on a cascaded liquid-crystal Fabry–Perot for spectral imaging detection. Appl Opt. (2017) 56:1925–9. doi: 10.1364/AO.56.001925

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Tolmachev VA, Perova TS, Astrova EV, Volchek BZ, Vij JK. Vertically etched silicon as 1-D photonic crystal. Phys Status Solidi A (2003) 197:544–8. doi: 10.1002/pssa.200306561

CrossRef Full Text | Google Scholar

15. Barillaro G, Strambini LM, Annovazzi-Lodi V, Merlo S. Optical characterization of high-order 1-D silicon photonic crystals. IEEE J Sel Top Quantum Electron (2009) 15:1359. doi: 10.1109/JSTQE.2009.2017278

CrossRef Full Text | Google Scholar

16. St-Gelais R, Poulin A, Peter YA. Advances in modelling, design, and fabrication of deep-etched multilayer resonators. J Lightwave Technol. (2012) 30:1900–8. doi: 10.1109/JLT.2012.2191136

CrossRef Full Text | Google Scholar

17. Yi Y, Bermel P, Wada K, Duan X, Joannopoulos JD, Kimerling LC. Tunable multichannel optical filter based on silicon photonic band gap materials actuation. Appl Phys Lett. (2002) 81:4112–4. doi: 10.1063/1.1525072

CrossRef Full Text | Google Scholar

18. Lipson A, Yeatman EM. A 1-D photonic band gap tunable optical filter in (110) silicon. J Microelectromech Syst. (2007) 16:521–7. doi: 10.1109/JMEMS.2007.892894

CrossRef Full Text | Google Scholar

19. Masson J, St -Gelais R, Poulin A, Peter YA. Tunable fiber laser using a MEMS-based in plane Fabry-Perot filter. IEEE J Quantum Electron. (2010) 46:1313–9. doi: 10.1109/JQE.2010.2050299

CrossRef Full Text | Google Scholar

20. Zhao Y, Zhao X, Gu Z. Photonic crystals in bioassays. Adv Funct Mater. (2010) 20:2970–88. doi: 10.1002/adfm.201000098

CrossRef Full Text | Google Scholar

21. Surdo S, Merlo S, Carpignano F, Strambini LM, Trono C, Giannetti A, et al. Optofluidic microsystems with integrated vertical one-dimensional photonic crystals for chemical analysis. Lab Chip (2012) 12:4403–15. doi: 10.1039/c2lc40613f

PubMed Abstract | CrossRef Full Text | Google Scholar

22. St-Gelais R, Masson J, Peter YA. All-silicon integrated Fabry-Perot cavity for volume refractive index measurements in microfluidic system. Appl Phys Lett. (2009) 94:243905. doi: 10.1063/1.3152286

CrossRef Full Text | Google Scholar

23. Lavchiev VM, Jakoby B. Photonics in the mid-infrared: challenges in single-chip integration and absorption sensing. IEEE J Select Top Quantum Electron. (2017) 23:8200612. doi: 10.1109/JSTQE.2016.2619330

CrossRef Full Text | Google Scholar

24. Mazzini G, Carpignano F, Surdo S, Aredia F, Panini N, Torchio M, et al. 3D Silicon microstructures: a new tool for evaluating biological aggressiveness of tumor cells. IEEE Trans Nanobiosci. (2015) 14:797–805. doi: 10.1109/TNB.2015.2476351

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Surdo S, Carpignano F, Strambini LM, Merlo S, Barillaro G. Capillarity-driven (self -powered) one-dimensional photonic crystals for refractometry and (bio)sensing applications. RSC Adv. (2014) 4:51935–41. doi: 10.1039/C4RA09056J

CrossRef Full Text | Google Scholar

26. Perova T, Tolmachev V, Berwick K. Chapter XI: Design of composite and multi-component one-dimensional photonic crystal structures based on silicon. In: Granitzer P, Rumpf K, editors. Nanostructured Semiconductors: From Basic Research to Applications. Singapore: Pan Stanford Publishing Pte. Ltd. (2014). 453–526.

27. Hogan BT, Dyakov S, Brennan LJ, Younesy S, Perova TS, Gun'ko YK, et al. Dynamic in-situ sensing of fluid-dispersed 2D materials integrated on microfluidic Si chip. Sci Rep. (2017) 7:42120. doi: 10.1038/srep42120

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Surdo S, Barillaro G. On the performance of label-free biosensors based on vertical one-dimensional photonic crystal resonant cavities. Opt Express (2015) 23:9192–201. doi: 10.1364/OE.23.009192

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Zheng Z, Yang G, Li H, Liu X. Three-stage Fabry–Perot liquid crystal tunable filter with extended spectral range. Optics Express (2011) 19:2158–64. doi: 10.1364/OE.19.002158

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Shabtay G, Eidinger E, Zalevsky Z, Mendlovic D, Marom E. Tunable birefringent filters – optimal iterative design. Opt Express (2002) 10:1534–41. doi: 10.1364/OE.10.001534

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Aharon O, Abdulhalim I. Tunable optical filter having a large dynamic range. Opt Lett. (2009) 34:2114–6. doi: 10.1364/OL.34.002114.

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Zhao X, Yang Y, Chen Z, Wang Y, Fei H, Deng X. Ultra-wide tuning single channel filter based on one-dimensional photonic crystal with an air cavity. J Semicond. (2017) 38:023004. doi: 10.1088/1674-4926/38/2/023004

CrossRef Full Text | Google Scholar

33. Hu X, Liu Z, Gong Q. Tunable multichannel filter in photonic crystal heterostructure containing permeability-negative materials. Phys Lett A (2008) 372:333–9. doi: 10.1016/j.physleta.2007.07.029

CrossRef Full Text | Google Scholar

34. Yun SS, Lee JH. A micromachined in-plane tunable optical filter using the thermo-optic effect of crystalline silicon. J Micromech Microeng. (2003) 13:721–5. doi: 10.1088/0960-1317/13/5/326

CrossRef Full Text | Google Scholar

35. Pruessner MW, Stievater TH, Rabinovich WS. In-plane microelectromechanical resonator with integrated Fabry–Pérot cavity. Appl Phys Lett. (2008) 92:081101. doi: 10.1063/1.2883874

CrossRef Full Text | Google Scholar

36. Barrios CA, Almeida VR, Panepucci RR, Schmidt BS, Lipson M. Compact silicon tunable fabry-perot resonator with low power consumption. IEEE Photon Technol Lett. (2004) 16:506–8. doi: 10.1109/LPT.2003.822251

CrossRef Full Text | Google Scholar

37. Baldycheva A, Tolmachev VA, Berwick K, Perova TS. Multi-channel Si-liquid crystal filter with fine tuning capability of individual channels for compensation of fabrication tolerances. Nanosci Res Lett. (2012) 7:387. doi: 10.1186/1556-276X-7-387

PubMed Abstract | CrossRef Full Text | Google Scholar

38. O'Brien D, Settle MD, Karle T, Michaeli A, Salib M, Krauss TF. Coupled photonic crystal heterostructure nanocavities. Opt Express (2007) 15:1228–33. doi: 10.1364/OE.15.001228

PubMed Abstract | CrossRef Full Text | Google Scholar

39. Vahala KJ. Optical microcavities. Nature (2003) 424:839–46. doi: 10.1038/nature01939

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Cos J, Ferre-Borrull J, Pallares J, Marsal LF. Tunable Fabry–Pérot filter based on one-dimensional photonic crystals with liquid crystal components. Opt Commun. (2009) 282:1220–5. doi: 10.1016/j.optcom.2008.11.074

CrossRef Full Text | Google Scholar

41. Kaliteevski MA. Optical properties of a system of two coupled vertical microcavities. Technol Phys. (1998) 43:565–8.

42. Tolmachev VA, Baldycheva AV, Perova TS. Coupled microresonator structures. In: Book of Abstracts of VII International Conference on Fundamental Problems in Optics. St.-Petersburg: ITMO University (2012). p. 340–1.

43. Salzberg CD, Villa JJ. Infrared refractive indexes of silicon, germanium and modified selenium glass. J Opt Soc Am. (1957) 47:244–6. doi: 10.1364/JOSA.47.000244

CrossRef Full Text

44. Tolmachev VA, Melnikov VA, Baldycheva AV, Berwick K, Perova TS. Electrically tunable Fabry-Pérot resonator based on microstrcutured Si containing liquid crystal. Prog Electromagn Res. (2012) 122:293–309. doi: 10.2528/PIER11091506

CrossRef Full Text | Google Scholar

45. Geis MW, Molnar RJ, Turner GW, Lyszczarz TM, Osgood RM, Kimball BR. 30 to 50 ns liquid-crystal optical switches. In: Proceedings Volume 7618, Emerging Liquid Crystal Technologies V. San Francisco, CA (2010).

PubMed Abstract | Google Scholar

46. Borshch V, Shiyanovskii S.V, Lavrentovich OD. Nanosecond electro-optic switching of a liquid crystal. Phys Rev Lett. (2013) 111:1–5. doi: 10.1103/PhysRevLett.111.107802

CrossRef Full Text

47. Jakli AI. Fast Switching Electro-Optical Devices Using Banana-Shaped Liquid Crystals. US Patent 7782438 (2010).

48. Jakli AI. Liquid crystals of the twenty-first century – nematic phase of bent-core molecules. Liquid Cryst Rev. (2013) 1:65–82. doi: 10.1080/21680396.2013.803701

CrossRef Full Text | Google Scholar