Sociophysics Analysis of the Dynamics of Peoples' Interests in Society

Introduction

In the present age, where consumer behavior remains on record through the internet, the purchase and action records of numerous consumers are available. Analyses reveal that there are many cases, where it is possible to incorporate natural science methodology, such as physics, apart from conventional social science. Therefore, sociophysics, which studies society using physics, has developed significantly, of late [1, 2]. In this paper, we present certain results based on sociophysics for analyzing and forecasting social phenomena, and the possibility of applying it for marketing, etc., using the voice of the society recorded in blogs and Twitter as data. Sociophysics is a new frontier of physics alongside economic physics; however, if vast amounts of data are available, the methodology of physics that has been the subject of experimental data on natural phenomena can also be applied to social science. Nowadays, we can use the vast stock of digital data on human communication as the observation data of real society [3–6]. Therefore, sociophysics is progressing rapidly.

As a sociophysics theory for analyzing society based on social media writing, a mathematical model for the hit phenomenon has been developed by Ishii et al. [7]. Here, mathematical equation inspired from physics are used to explain people's interest due to the influence of advertisement and communication with other people. Ishii et al. [7] utilized the effects of advertisement and verbal communication to form a model that successfully predicted the outcome of each film, which was screened. For the analysis of the film market in marketing science, although several researches use regression analysis [8–15], it is very difficult to analyze the dynamics of consumers, using this analysis.

In the mathematical theory of the hit phenomenon, the effect of advertisement and the propagation of reputation and rumors by human communication are incorporated into the statistical physics of human dynamics. The propagation of information, reputation, and rumors has been studied in several works. For example, the SIR model is a simple mathematical model for epidemics [16], which is applicable not only to the spread of infectious diseases but also to the spread of information. The equations of the SIR model are as follows:

$\begin{array}{l}\frac{dS}{dt}=-\beta S(t)I(t),\\ \frac{dI}{dt}=\beta S(t)I(t)-\gamma I(t),\\ \frac{dR}{dt}=\gamma I(t),\end{array}$

where, S is the number of susceptible, I is the number of infectious, and R is the recovered individuals. In the case of information spread, S indicates the non-adopters, I are the contagious adopters, and R are the non-contagious adopters.

The other famous model for the spread of information is the Bass model [17, 18]. The equation of the Bass model is as follows:

$\begin{array}{l}\frac{dN(t)}{dt}=a\left(m-N(t)\right)+b\left(m-N(t)\right)N(t),\end{array}$

where m is the total number of people and N(t) is the number of adopters. The first term of the equation indicates a constant propensity to adopt, independent of the number of customers, who have adopted the innovation before time, t. The second term is proportional to the number of customers, who have already adopted the innovation by t; this term represents the extent of favorable exchange of word-of-mouth (WOM) communication between the innovators and the other adopters of the new product.

There are several problems in the above two models. In the SIR model, the spread of information is assumed to happen as communication between an adopter and non-adopter, and the mass media effects are not included. Moreover, the exchange of WOM communication is assumed to be proportional to the number of adopters. In the Bass model, it is assumed that once a consumer adopts a new product, he influences other non-adopters to adopt the product at all later times. In order to overcome these disadvantages, the Bass-SIR model was presented [19].

Another similar mathematical model for calculating the spread of information is the opinion dynamics model by Galam [1] based on the Ising model of statistical physics. It is considered that accumulation of the opinions of individuals (agents) is similar to the mathematical model of the hit phenomenon, considering the interaction between people. In Galam's opinion dynamics model, a variable, c_i = ±1, represents the choice of agents, I, with Yes = 1 and No = −1. Galam expressed the group conflict function, G, as

$\begin{array}{l}G=J{\displaystyle \sum _{i,j}}{c}_i{c}_j+S{\displaystyle \sum _i}{c}_i+{\displaystyle \sum _i}{S}_i{c}_i,\end{array}$

where the first term corresponds to the direct communication between people and the second to the external field effect. The third term can correspond to more complex communication. This model is applied to the modern politics [20].

Our approach is different. Here, we use the mathematical model of the hit phenomenon [7], where the intention of people for a certain topic is calculated. In this model, the calculated intention is not on/off. Thus, the value of the intention in the mathematical model of the hit phenomena has no upper limit. The upper-limit value of the intentions of N people is not N. On the contrary, for the SIR model, the Bass model, or the model of Galam, the calculated value of each person is on/off or in-between on and off; the upper limit is unity and is N for N persons. Hence, in the mathematical model of the hit phenomenon, the calculated intention of an adopter can increase to a very large value far beyond unity, depending on mass media advertisement and communication, although the upper limit of each adopter is unity for the SIR model, Bass model, and the opinion dynamics model of Galam.

The target of the mathematical model of the hit phenomenon is the “hits” phenomenon. The hits on social media are similar to the burst phenomenon, which is found to evolve through non-Poissonian dynamics [21]. The similarity between the burst and hit phenomena is that specific topics that are referred to widely, occur frequently in the social media. The difference is that the burst phenomenon is spontaneous, whereas the hit phenomenon is artificially drawn. Nonetheless, the hit and burst phenomena are similar, and the study of the hit phenomenon is useful for the research of the burst phenomenon.

There many investigations on the hit phenomenon, other than our works [22–34]. In contrast to other works on the hit pheonomenon, in our model, the effect of advertisements, and the propagation of reputation and rumors by human communication are incorporated into the statistical physics of human dynamics. The mathematical model has been applied to the motion picture business in the Japanese market, and the calculations have been compared to the reported revenue and observed number of blog posts for each film. Furthermore, in several recent papers, it has been shown that the theory is not only applicable to the box office, but also to other social entertainment, such as local events [35], animated dramas on TV [36], the “general election” of the Japanese girl-group, AKB48 [37], online music [38], plays [39], music concerts [40, 41], Japanese stage actors [42], Kabuki players of the nineteenth century [43], and TV drama [44]. In these works, an extended mathematical theory of the hit phenomena was used to apply the model to general entertainment in society. Thus, it is very natural to use this theory for the prediction of the motion picture business.

In this paper, after screening a movie/ drama and expanding the topic of the social incident using the mathematical model of the hit phenomenon, which is modified slightly from the original model of Ishii et al. [7], we analyze the result of the mathematical model of the hit phenomenon for the analysis and prediction of social dynamics.

Theory

Mathematical Model of the Hit Phenomenon

The mathematical model of the hit phenomenon within a society is presented as a stochastic process of the interaction of human dynamics as in the many-body theory in physics [7]. In this model, we assume that the intentions of humans in society are affected by three mechanisms: advertisement, communication with friends, and rumor. Advertisements are the external forces for each person in society. Communication with friends is called the direct communication effect and is considered as interaction with the intentions of friends. The rumor effect is considered as interaction among three persons and called indirect communication, as described in Galam [1]. In the model, we use only the time distribution of the advertisement budget as the input, and the WOM represented by posts on social network systems (SNS) is used as the observed data for comparison with the calculated results. The parameters in the model are adjusted in comparison with the calculation and observed SNS posting data.

Here, we introduce the intention of a person, “i,” as I_i(t), where this quantity is assumed to be a real number and proportional to the number of posting in a blog or Twitter. Although I_i(t) itself is not expected to be measured directly in experiments or in social media analysis, we expect that it to be proportional to the number of postings on the internet. According to Ishii et al. [7], we express the equation of the intention of each person using the exponential form as

$\begin{array}{ll}\frac{d{I}_i(t)}{dt}=-a{I}_i(t)+{\displaystyle \sum _j}{D}_{ij}{I}_j(t)+{\displaystyle \sum _j}{\displaystyle \sum _k}{P}_{ijk}{I}_j(t)I_k(t)+f_i(t),& (1)\end{array}$

where D_ij, P_ijk, and f_i(t) are the coefficient of direct communication, coefficient of indirect communication, and the random external force effect for a person, i, respectively. As we consider the above equation for every consumer, i = 1, …, N_p. Considering the effect of direct communication, indirect communication, and the decline of the audience, we obtain the above equation for the mathematical model of the hit phenomenon. The advertisement and publicity effect for each person can be described as the mean field value of the random external force effect, <f_i(t)>. Here, it is assumed that people's height of interest, I (t), attenuates exponentially. Although this is known to occur in movies and as mentioned in Allsop et al. [3], attention to events and anniversaries is known to attenuate as per the power function [45, 46]. In the case of social interest, we attenuate the intermediate between the exponential and power functions [47], but here we adopt exponential decay.

Generally, information spreads through WOM, which sometimes has a significant effect on the spread of topics. The WOM effect can be distinguished into two types: WOM direct from friends and indirect WOM as rumors. We call the WOM effect between friends “direct communication” because customers obtain information directly from their friends. In previous marketing theories based on the Bass model [17, 18], communication from the adopter to non-adopter alone are generally are taken into account. Here, in this paper, we include the communication between non-adopters, in addition. We consider here that person, i, hears information from person, j. The probability per unit time for the information to affect the purchase intention of person, i, can be noted as D_ijI_j(t), where I_j(t) is the purchase intention of person, j, and D_ij is the coefficient of direct communication. Thus, we can describe the effect of direct communication as follows:

$\begin{array}{l}{\displaystyle \sum _{j=1}^N}{D}_{ij}{I}_j(t),\end{array}$

where the summation is done without j = i.

In this paper, the rumor is called indirect communication. In this form of communication, a person hears a rumor while chatting on the street, overhearing a conversation from the next table in a restaurant or on a train, or finds the rumor in blogs or on Twitter. To construct a mathematical model, we focus on a person, who listens to a conversation happening around him/her. We consider that person, i, overhears the conversation between person, j, and person, k. The strength of the effect of the conversation of j and k can be described as D_jkI_j(t)I_k(t). The probability per unit time for the conversation between j and k to affect the purchase intention of person, i, is defined as Q_ijkD_jkI_j(t)I_k(t), where Q_ijk is the coefficient of indirect effect to i. Thus, the indirect communication coefficient can be defined as P_ijk = Q_ijkD_jk.

Equation (1) is for individuals; however, it is not convenient for analysis. Thus, we consider the ensemble average of the purchase intention of individuals, as follows:

$\begin{array}{ll}\langle I(t)\rangle =\frac{1}{N}{\displaystyle \sum _i}{I}_i(t).& (2)\end{array}$

Considering the effect of direct and indirect communication, and the decline of the audience, we obtain the above equation for the mathematical model of the hit phenomenon. The advertisement and publicity effect for each person can be described by the random effect, f_i(t).

For the ensemble average of Equation (1), we obtain for the left-hand side,

$\begin{array}{ll}\langle \frac{d{I}_i(t)}{dt}\rangle =\frac{1}{N}{\displaystyle \sum _i}\frac{d{I}_i(t)}{dt}=\frac{d}{dt}\left(\frac{1}{N}{\displaystyle \sum _i}{I}_i(t)\right)=\frac{d\langle I\rangle }{dt}.& (3)\end{array}$

For the right-hand side, the ensemble average of the first, second, and third are as follows:

$\begin{array}{ll}\langle -a{I}_i\rangle =-a\frac{1}{N}{\displaystyle \sum _i}{I}_i(t)=-a\langle I(t)\rangle ,& (4)\end{array}$

$\begin{array}{l}\langle {\displaystyle \sum _j}{D}_{ij}{I}_j(t)\rangle =\langle {\displaystyle \sum _j}D{I}_j(t)\rangle =\frac{1}{N}{\displaystyle \sum _i}{\displaystyle \sum _j}D{I}_j(t)\\ ={\displaystyle \sum _i}D\frac{1}{N}{\displaystyle \sum _j}{I}_j(t)=ND\langle I(t)\rangle ,& (5)\end{array}$

$\begin{array}{l}\langle {\displaystyle \sum _j}{\displaystyle \sum _k}{P}_{ijk}{I}_j(t)I_k(t)\rangle =\langle P{\displaystyle \sum _j}{\displaystyle \sum _k}{I}_j(t)I_k(t)\rangle \\ =\frac{1}{N}{\displaystyle \sum _i}P{\displaystyle \sum _j}{\displaystyle \sum _k}{I}_j(t)I_k(t)\\ ={\displaystyle \sum _i}P\frac{1}{N}{\displaystyle \sum _j}{\displaystyle \sum _k}{I}_j(t)I_k(t)\\ =NP{\displaystyle \sum _i}\frac{1}{N}{\displaystyle \sum _j}{I}_j(t)\frac{1}{N}{\displaystyle \sum _k}{I}_k(t)\\ =N^{2}P{\langle I(t)\rangle }^2,& (6)\end{array}$

where we assume that the coefficients of the direct and indirect communication can be approximated by

$\begin{array}{l}{D}_{ij}\cong D,\\ P_{ijk}{D}_{jk}=p_{ijk}\cong P\end{array}$

under the ensemble average.

For the fourth term, which is the random effect term, we consider that the random effect can be divided into two parts: the collective and individual effects:

$\begin{array}{ll}{f}_i(t)=\langle f(t)\rangle +\Delta f_i(t),& (7)\end{array}$

$\begin{array}{ll}\langle f_i(t)\rangle =\frac{1}{N}{\displaystyle \sum _i}{f}_i(t)=\langle f(t)\rangle ,& (8)\end{array}$

where Δf_i(t) is the deviation of the individual external effects from the collective effect, 〈f(t)〉. Thus, we consider here that the collective external effect term, 〈f(t)〉, corresponds to the advertisements and publicity, for the persons in society. The deviation term, Δf_i(t), corresponds to the deviation effect from the collective advertisement and publicity effect for individuals, which can be assumed to be

$\begin{array}{ll}\langle \Delta f_i(t)\rangle =\frac{1}{N}{\displaystyle \sum _i}\Delta f_i(t)=0.& (9)\end{array}$

Taking the above ensemble average of Equation (1), we obtain the following form as the intention of society as a collective mode:

$\begin{array}{ll}\frac{d\langle I(t)\rangle }{dt}=-a\langle I(t)\rangle +D\langle I(t)\rangle +P{\langle I(t)\rangle }^2+{{\displaystyle \sum }}_{\xi }{C}_{\xi }{A}_{\zeta }(t),& (10)\end{array}$

where Nd = D and N²h = P. The detailed derivation is shown in Allsop et al. [3]. We represent the external effect as $\langle f(t)\rangle =\sum _{\xi }{C}_{\xi }{A}_{\zeta }(t)$. Hereafter, we denote 〈I(t)〉 as I(t). Equation (10) is modified slightly from the original model in Ishii et al. [7]. In the original mathematical model for the hit phenomenon, direct and the indirect communication are distinguished as the roles of known and unknown people, respectively, for a certain topic. Thus, in the original model, five parameters are to be determined for direct and indirect communication. Moreover, in the original model, we assume different parameters for the before-open and after-open periods. Thus, at least 10 parameters need to be adjusted in the original model, for the communication effects. In the model of this paper, for simplicity, we do not distinguish between known and unknown people for the topic of concern. Hence, the number of parameters that should be adjusted using real data are only two, D and P. The decay rate, a, in Equation (10) can be assumed to be 0.5, which is same as that in the original model [7]. The strength of each media, C_ξ, should be determined separately. Thus, if the number of media is one, the number of parameters that should be adjusted using real data is only three.

In the following calculation, coefficients C, D, and P are determined such that the calculated value according to the Equation (10) coincides with the daily change in the observed tweet number; the Monte Carlo method is used, and the details are available in Ishii et al. [7], as given below.

The advertisement and publicity effects are included in A_ξ(t), which is treated as an external force. The index, ξ, sums up the mass media exposures. The WOM, represented by posts on SNSs, such as blogs or Twitter, is used as the observed data, which can be compared with the calculated results of the model. The unit of time is a day.

The advertisement and publicity effects are obtained from M Data Co. Ltd (http://mdata.tv/en/) as the TV metadata of real-time advertisement and publicity on television for a certain topic. TV metadata includes text data containing the summary of TV programs and commercials with time stamp. M Data records them immediately after broadcast. It captures TV metadata by verifying the aired content with human eyes and ears. This metadata contains the summary of the broadcast contents, performer's name, brand name, company name, place name, and duration of exposure. The WOM, represented by posts on SNSs, are observed using the social media analysis tool, Kuchikomi @ Kakaricyo by Hottolink Co. Ltd (https://www.hottolink.co.jp/english/).

Parameter Estimation

For reliability, we introduce the “R-factor” (reliability factor), which is well-known in the field of low-energy electron diffraction (LEED) [48]. In LEED experiments, the experimentally observed curve of the current vs. voltage is compared to the corresponding theoretical curve, using the R-factor.

For our purpose, we define the R-factor as follows:

$\begin{array}{ll}R=\frac{{\displaystyle \sum _i}{\left(f(i)-g(i)\right)}^2}{{\displaystyle \sum _i}\left[f^2(i)+g^2(i)\right]},& (11)\end{array}$

where f(i) and g(i) correspond to the calculated I(t) and the observed number of blog posts or tweets, respectively. The smaller the value of R, the better are the functions, f and g. Thus, we use a stochastic method to search for the parameter set that minimizes R. This random number technique is similar to the Metropolis method [49], which we have used previously [7]. In the actual calculation, we change each parameter within 10% of its value, using the random number per turn. We perform such calculations for more than one-hundred-thousand turns, similar to the Metropolis method for molecular dynamics. For the molecular dynamics, we try to obtain the parameter configuration that gives the lowest total energy. In our case, we try to obtain the parameter configuration with the least R-factor.

In the real calculation, for adjusting parameters C_ξ, D, and P, the local minimum trapping, as in the first principle calculation in material physics, needs to be avoided. There are several ways to determine the minimum condition, including the steepest descent, equation of motion method, and conjugate gradient method. Even in the actual first principle calculation or density functional theory, local minimum trapping needs to be avoided. In this paper, we only calculate, using several initial values in a Metropolis-like method to avoid local minimum trapping. To check the accuracy of the parameter adjustment, we use the R-factor value. For every calculation shown in this paper, the R-factor is below 0.01.

Although parameters C_ξ, D, and P in Equation (10) can be considered as functions of time, we retain C_ξ, D, and P as constant values to examine whether Equation (10) can be applied to any social phenomena.

Results

In this section, we present the analysis results of social-media posts, using the mathematical model of the hit phenomenon. The actual analysis of the direct and indirect communication are presented, which are critical in the mathematical model of the hit phenomenon. Other examples include Japanese group events, reputation of popular videos, and the results before the conclusion of event-ticket reservation.

Case A

In Figure 1, the mathematical model of the hit phenomenon is applied to a “Case A.” Our target is Japanese Famous Food WOM of “Case A.” The horizontal axis in the figure represents the date from 2014/1/1 to 2014/12/31. The peaks in the figure correspond to the number of daily exposures on Blog and the internet of “Case A.” As can be seen, our calculation results demonstrate that the number of social media posts are measured with sufficient precision. Thus, the mathematical model of the hit phenomenon can be applied to Japanese Famous Food WOM of “Case A.”

FIGURE 1

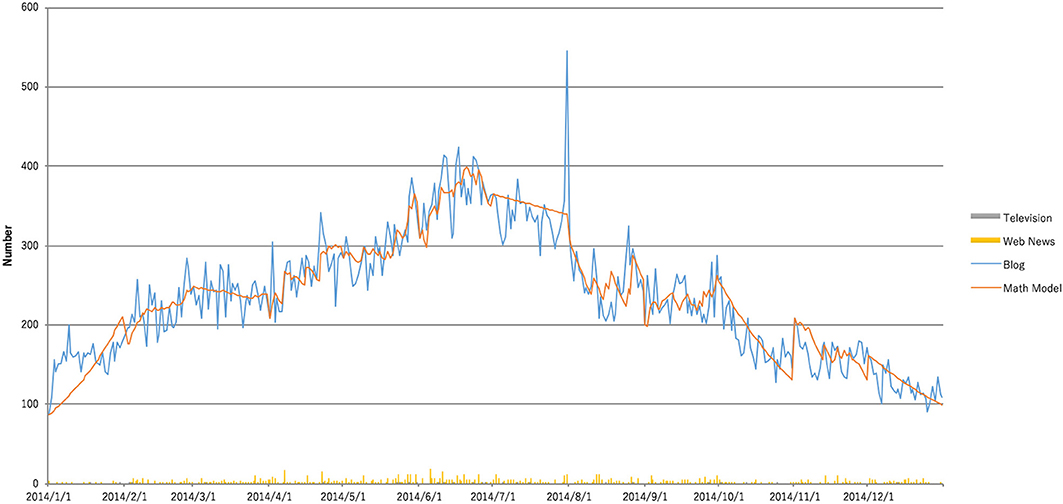
Figure 1. Calculated and observed data for Japanese Famous Food WOM of “Case A” in 2014/1/1–2014/12/31. The histograms are the daily total advertisements on TV (Green) and the internet (Purple). The blue curve corresponds to the observed number of daily Blog postings and the red curve is our calculation.

Case B

A movie example is shown in Figure 2, our calculation for the American movie, “Case B” (2015), is depicted [50]. The histogram indicates the number of seconds of exposure by advertisement or publicity on television. Excluding small fluctuations, the calculation result matches with the number of Twitter postings accurately. Thus, the mathematical model of the hit phenomenon can be used for movies, as well.

FIGURE 2

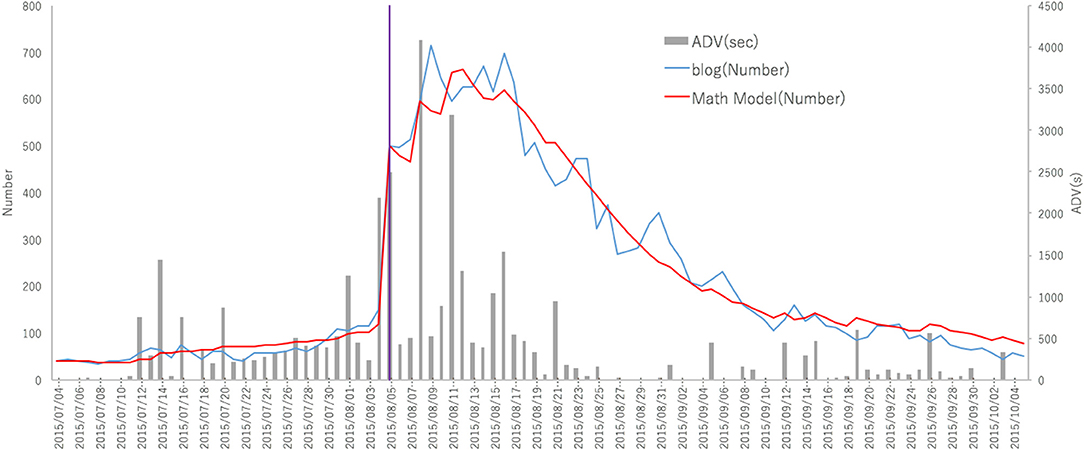
Figure 2. Calculated and observed data for the movie, “Case B” in Japan. The histogram indicates [ADV (s)] is the number of daily exposures on TV information about “Case B” in seconds. The blue curve corresponds to the observed number of daily Twitter postings and the red curve is our calculation.

Strong Indirect Communication

In the analysis, we present an example, where indirect communication, which is a characteristic action in the mathematical model of the hit phenomenon, has significant effect. According to the mathematical-model analysis of the hit phenomenon, several movies show large indirect communication. The results for movies, “Case C” and “Case D,” are depicted in Figure 3. The calculation result by the mathematical model of the hit phenomenon matches well with the number of blog posts. Considerable indirect communication enhances the movie's reputation.

FIGURE 3

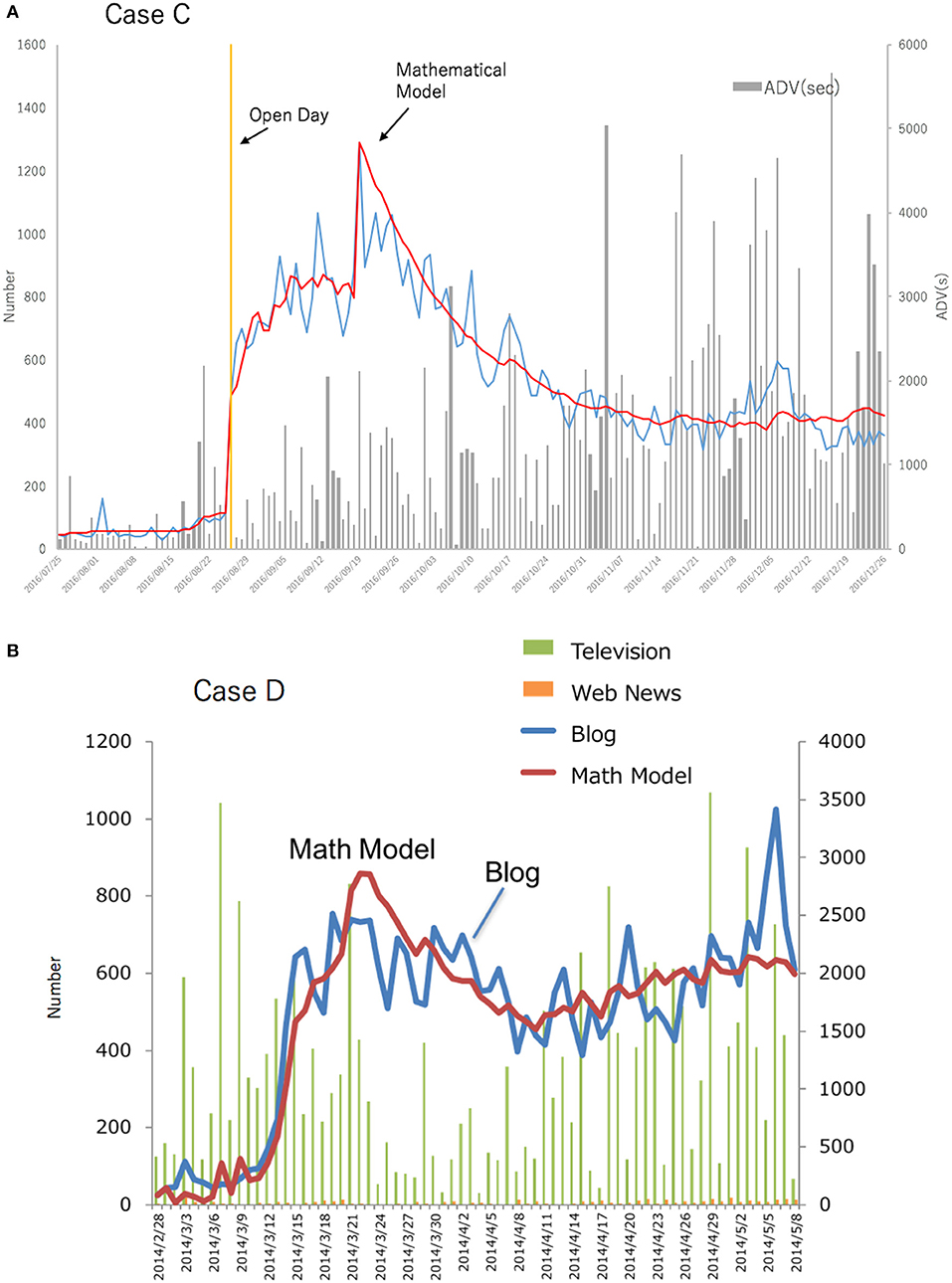
Figure 3. Reputation of films (A) “Case C” and (B) “Case D” based on analysis using the mathematical model of the hit phenomenon. The line chart is the number of daily blog posts and the corresponding calculated values. The histogram (Case C) indicates [ADV (s)] is the number of daily exposures on TV information about “Case C” in seconds. And The histogram (Case D) indicates [ADV (s)] is the number of daily exposures on TV (Green) and the internet (Orange).

Another typical break is “Case E,” a Japanese Tarent who became a hit in September 2016. Figure 4 shows the analysis of the reputation of “Case E” using the number of blog posts, which are calculated using the mathematical model of the hit phenomenon. The calculation agrees well with the actual measurement [50].

FIGURE 4

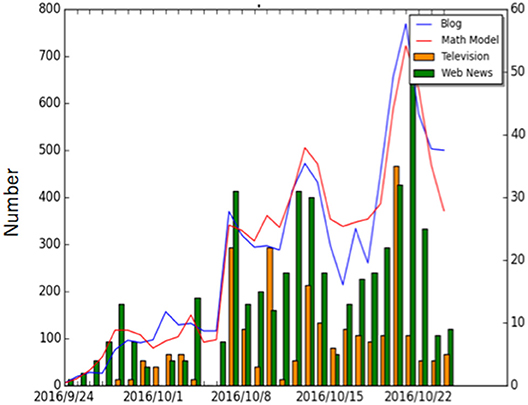
Figure 4. Analysis of “Case E.” The red curve is our calculation using the model, the blue curve is the observed daily number of postings in blogs, in Japanese language, and the histograms are the daily total advertisements on TV (Orange) and the internet (Green).

Figure 5 compares the coefficients determined, before and after the day influencer introduced the video. The strength, “P,” of the indirect communication significantly increased, after introduction. Response to media exposure also increased considerably. Thus, it is considered that an explosive epidemic appears as an increase in the strength, “P,” of the indirect communication.

FIGURE 5

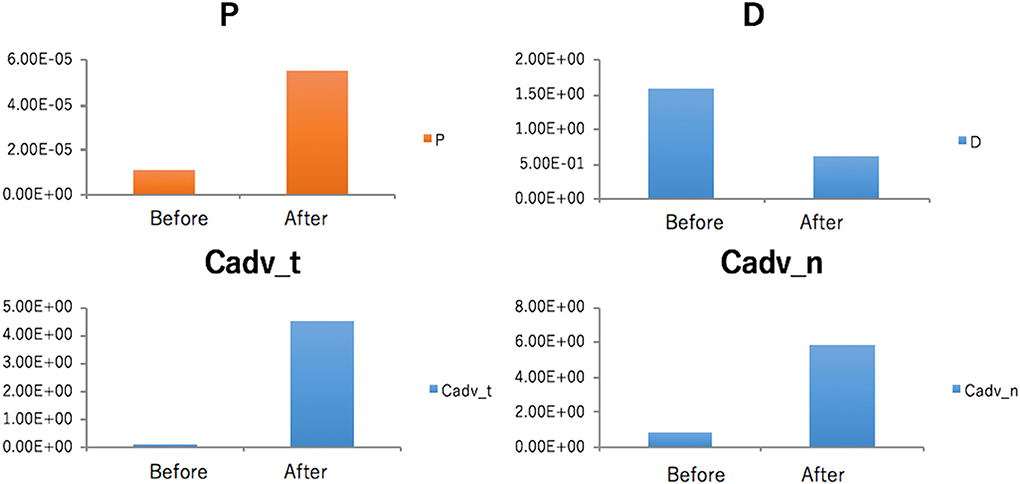
Figure 5. Observed parameters “P,” “D,” and C_adv for TV, and C_adv for the internet, as per the calculations in of Figure 4.

On the other hand, the direct communication strength, “D,” is rather weak. Although this movie was spreading through breaks, it shows there is no increase in the number of “Case E” 's core interested people. This indicates that even in the midst of an explosive epidemic, the direct communication strength, i.e., the satisfaction of the core interested people is not necessarily increased or limited. We also did a similar calculation on the explosive epidemic for “Pokemon GO” [51].

Direct and Indirect Communication

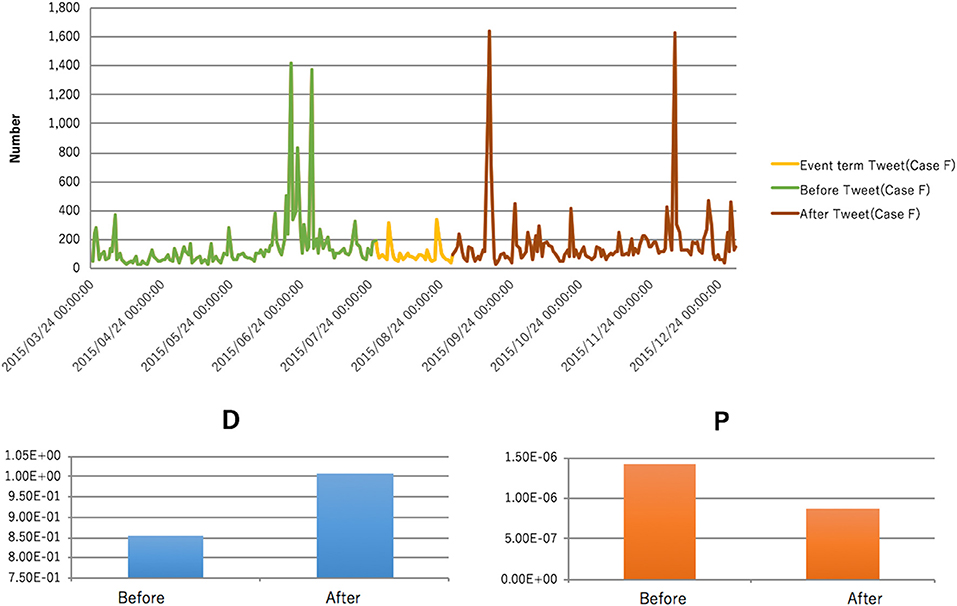
The following example is of the reputation of the Japanese Famous group, “Case F” for event. We analyzed the reputation, before and after event held in summer 2015, using the mathematical model of the hit phenomenon [52]. The result is shown in Figure 6.

FIGURE 6

Figure 6. Analysis of the “Case F,” before and after event in Japan, in the summer of 2016.

Several Famous groups participated in this event and gathered a vast audience. Before event, the indirect communication strength, “P,” was large, whereas that of the direct communication, “D,” increased, after the event. Indirect communication shows the strength with which people, other than the interested people, are interested and direct communication indicates the interest of interested people. In the “Case F,” it appears that those who were interested, before the event, became core interested people of “Case F,” after the event.

In hit contents, indirect communication increases after publication. The “Case E” epidemic is consistent with the increase in break and indirect communication. Hence, the reputation breaks, when indirect communication increases rapidly. Additionally, convergence occurs, when indirect communication decreases.

On the other hand, the strength of direct communication shows the enthusiasm of core interested people but does not imply that there are numerous core interested people. The increase in direct communication, after the event at “Case F,” indicates an increase in the number of enthusiastic interested people. However, the fact that there is no increase in direct communication in the “Case E” indicates that “Case E” is only a topicality and there is no increase in “Case E” 's core interested people.

Discussion

Using the mathematical model of the hit phenomenon, we analyzed the reputations of a movie, a YouTube movie that became a global topic, and the popular event trend in Japanese. Important factors in the mathematical model of the hit phenomenon include the direct communication strength, “D,” the indirect communication strength, “P,” and the coefficient, “C,” of the media response strength.

The results indicate that for the reputation of “Case E” 's movie, the indirect communication strength, “P,” increased, with the world-wide reputation. “P” tends to be large, for hit movies also. Therefore, the indirect communication strength, “P,” was found to be related to the wide propagation of the topic.

On the other hand, the comparison of the reputation, before and after the group event, shows that the direct communication strength, “D,” appears to be the satisfaction level of the support layer.

Hence, “D” indicates whether the current support layer is satisfied, and P indicates the power to acquire a new support layer. This can be said to be effective not only for the analysis of entertainment and marketing strategy but also for political election analysis.

As the mathematical model of the hit phenomenon is a theory of sociophysics, it is possible to describe how a person in society causes interest, and follow the time change of this interest. Therefore, expansion is easy. For example, to determine which among two competing topics shows interest, a theory has already been proposed, which generates two mathematical models of the hit phenomenon simultaneously [53, 54].

In addition, it is possible to solve the influence of social media on the market share of products by the simultaneous theory of the market share, in economics, and the mathematical model of the hit phenomenon [55].

The hits on social media are similar to the burst phenomenon, which evolves through non-Poissonian dynamics.

Conclusion

In this paper, using the mathematical model of the hit phenomenon, which is one of the theories of sociophysics, the rise of topics and convergence in society were calculated, even for movies, and events, and the reputation of a YouTube movie that became a global topic. This establishes that the mathematical model of the hit phenomenon can explain the spread of topics as a social phenomenon. Using this model, it can be determined whether the topic is spread beyond clusters by social dynamics; if the indirect communication is considerable, it becomes a hit. Additionally, it is possible to quantitatively analyze the propagation mechanism of popular topics, using the mathematical model of the hit phenomenon. It may be possible to clarify the mechanism for information propagation as a social epidemic phenomenon, according to the utilization of the corresponding parameter.

Author Contributions

AI consider the model and select the target. YK do actual computation.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

1. Galam S. Sociophysics: A Physicist's Modeling of Psycho-Political Phenomena. Berlin: Springer (2012).

Google Scholar

2. Pentland A. Sociophysics: How Social Networks Can Make Us Smarter. New York, NY: Penguin Books (2015).

3. Allsop DT, Bassett BR, Hoskins JA. Word-of-mouth research: principles and applications. J Advertising Res. (2007) 47:398. doi: 10.2501/S0021849907070419

CrossRef Full Text | Google Scholar

4. Kostka J, Oswald YA, Wattenhofer R. Word of mouth: rumor dissemination in social networks. Lect Notes Comput Sci. (2008) 5058:185–96.

Google Scholar

5. Bakshy E, Hofman JM, Mason WA, Watts DJ. Everyone's an influencer: quantifying influence on twitter. In: Proceedings of the Fourth ACM International Conference on Web Search and Data Mining, New York, NY (2011). p. 65–74.

Google Scholar

6. Jansen BJ, Zhang M, Sobel K, Chowdury A. Twitter power: tweets as electronic word of mouth. J Am Soc Inform Sci Tech. (2009) 60:2169. doi: 10.1002/asi.21149

CrossRef Full Text | Google Scholar

7. Ishii A, Arakaki H, Matsuda N, Umemura S, Urushidani T, Yamagata N, et al. The ‘hit’ phenomenon: a mathematical model of human dynamics interactions as a stochastic process. New J Phys. (2012) 14:063018. doi: 10.1088/1367-2630/14/6/063018

CrossRef Full Text | Google Scholar

8. Elberse, Eliashberg J. Demand and supply dynamics for sequentially released products in international markets: the case of motion pictures. Marketing Sci. (2003) 22:329. doi: 10.1287/mksc.22.3.329.17740

CrossRef Full Text | Google Scholar

9. Liu Y. Word of mouth for movies: its dynamics and impact on box office revenue. J Marketing (2006) 70:74. doi: 10.1509/jmkg.70.3.74

CrossRef Full Text | Google Scholar

10. Duan X, Gu B, Whinston AB. Do online reviews matter? – An empirical investigation of panel data. Decis Support Syst. (2008) 45:1007.

Google Scholar

11. Duan X, Gu B, Whinston AB. J Retailing (2008) 84:233.

12. Zhu M, Lai S. A study about the WOM influence on tourism destination choice. In: Paper Presented at the International Conference on Electronic Commerce and Business Intelligence (ECBI), Bejing (2009).

Google Scholar

13. Goel S, Hofman JM, Lahaie S, Pennock DM, Watts DM. Predicting consumer behavior with web search. Proc Natl Acad Sci USA. (2010) 107:1786. doi: 10.1073/pnas.1005962107

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Karniouchina EV. Impact of star and movie buzz on motion picture distribution and box office revenue. Int J Res Marketing (2011) 28:62. doi: 10.1016/j.ijresmar.2010.10.001

CrossRef Full Text | Google Scholar

15. Eliashberg J, Jonker J-J, Sawhney MS, Wierenga B. MOVIEMOD: an implementable decision-support system for prerelease market evaluation of motion pictures. Marketing Sci. (2000) 19:226–43. doi: 10.1287/mksc.19.3.226.11796

CrossRef Full Text | Google Scholar

16. Kermack WO, McKendrick AG. A contribution to the mathematical theory of epidemics. Proc R Soc Lond Series A (1927) 115:700–21. doi: 10.1098/rspa.1927.0118

CrossRef Full Text | Google Scholar

17. Bass FM. A new product growth for model consumer durables. Manag Sci. (1969) 15:215–27.

Google Scholar

18. Bass FM. Comments on a new product growth for model consumer durables: the bass model. Manag Sci. (2004) 50:1833–40. doi: 10.1287/mnsc.1040.0300

CrossRef Full Text | Google Scholar

19. Fibich G. Bass-SIR model for diffusion of new products. Phys Rev. (2016) E94:032305. doi: 10.1103/PhysRevE.94.032305

CrossRef Full Text | Google Scholar

20. Galam S. The Trump Phenomenon, an Explanation from Sociophysics. arXiv:1609.03933 (2016).

21. Karsai M, Jo H-H, Kaski K. Burstly Human Dynamics. arXiv:1803.025801v1. (2018)

22. Mestyán M, Yasseri T, Kertész J. Early prediction of movie box office success based on wikipedia activity big data. PLoS ONE (2013) 8:e71226. doi: 10.1371/journal.pone.0071226

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Lipizzi C, Iandoli L, Marquez JER. Combining structure, content and meaning in online social networks: the analysis of public's early reaction in social media to newly launched movies. Technol Forecast Soc Change (2016) 109:35–49. doi: 10.1016/j.techfore.2016.05.013

CrossRef Full Text | Google Scholar

24. Tanaka Y, Kurashima T, Fujiwara Y, Iwata T, Sawada H. Inferring latent triggers of purchases with consideration of social effects and media advertisements. In: WSDM'16 Proceedings of the Ninth ACM International Conference on Web Search and Data Mining. New York, NY (2016). p. 543–52.

Google Scholar

25. Golosovsky M, Solomon S. Growing complex network of citations of scientific papers: modeling and measurements. Phys Rev. (2017) E95:012324. doi: 10.1103/PhysRevE.95.012324

CrossRef Full Text | Google Scholar

26. Chakrabarti AS, Sinha S. Hits emerge through self-organized coordination in collective response of free agents. Phys Rev. (2016) E94:042302. doi: 10.1103/PhysRevE.94.042302

CrossRef Full Text | Google Scholar

27. Abdullah N, Salleh S, Dambul R, Hassan D. Behavioral and viewing patterns of cinema-goers in Malaysia. In: Proceedings of 2nd World Conference on Islamic Thoughts & Civilisation. Casuarina. Meru; Ipoh; Perak; Malaysia (2014). p. 876–83.

28. Chakraborti A, Fujiwara Y, Ghosh A, Inoue J, Sinha S. Physicists' approaches to a few economic problems, In: Abergel F, Aoyama H, Chakrabarti B, Chakraborti A, Ghosh A, editors. Econophysics and Data Driven Modelling of Market Dynamics. Cham: New Economic Windows, Springer (2015). p. 237–86.

Google Scholar

29. Kononovicius A. Empirical analysis and agent-based modeling of the Lithuanian Parliamentary Elections. Complexity (2017) 2017:7354642. doi: 10.1155/2017/7354642

CrossRef Full Text | Google Scholar

30. Tajima S, Mita T, Bakkum DJ, Takahashi H, Toyoizumi T. Locally embedded presages of global network bursts. Proc Natl Acad Sci USA. (2017) 114:9517–22. doi: 10.1073/pnas.1705981114

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Abdullah N, Salleh S, Zainodin HJ, Hassan D. Factors relating behavioral patterns on film viewers in East Malaysia. In: Proceedings of INTCESS15-2nd International Conference on Education and Social Sciences. Istanbul (2015). p. 430–7.

32. Kononovicius A. Modeling of the Parties' Vote Share Distributions. arXiv:1709.07655. (2017).

33. Yamamoto K. A simple view of the heavy-tailed sales distributions and application to the box-office grosses of U.S. movies. EuroPhys Lett. (2014) 108:68004.

34. Soh H, Hong JH, Jeong J, Jeong H. Emergence of Long-Term Memory in Popularity. arXiv:1712.02234. (2017).

35. Ishii A, Matsumoto T, Miki S. Revenue prediction of local event using mathematical model of hit phenomena. Prog Theor Phys Suppl. (2012) 194:64. doi: 10.1143/PTPS.194.64

CrossRef Full Text | Google Scholar

36. Ishii A, Furuta K, Oka T, Koguchi H, Uchiyama K. Mathematical model of hit phenomena as a theory for collective motion of human mind in societies. In: Neves-Silva R, Watada J, Phillips-Wren G, Jain LC, Howlett RJ, editors. Ebook: Intelligent Decision Technologies, Frontiers in Artificial Intelligence and Applications, Vol. 255, Amsterdam: IOS Press (2013). p. 267.

Google Scholar

37. Ishii A, Ota S, Koguchi H, Uchiyama K. Quantitative analysis of social popularity of entertainments using mathematical model for hit phenomena for Japanese Pop Girl Group AKB48. In: Proceedings of the 2013 International Conference on Biometrics and Kansei Engineering (ICBAKE2013) New Jersey: IEEE (2013). p. 143–7.

Google Scholar

38. Ishii A, Fujimoto H, Fukumoto W, Koguchi H, Chiyama K. Mathematical model for the hit phenomenon as a stochastic process of interactions of human dynamics and its application to movie and online music market. In: Presentation in WEHIA2012 in Paris. Paris (2013).

39. Kawahata Y, Genda E, Ishii A. Promotion theater company adopting a mathematical model of the hit phenomenon. Adv Sci Technol Lett. (2013) 35:625. doi: 10.14257/astl.2013.35.15

CrossRef Full Text | Google Scholar

40. Kawahata Y, Genda E, Ishii A. Revenue prediction of music concerts using the mathematical model of hit phenomena. In: Proceedings of the 2013 International Conference on Biometrics and Kansei Engineering (ICBAKE2013). New Jersey: IEEE (2013). p. 208–13.

Google Scholar

41. Kawahata Y, Genda E, Ishii A. Analysis of local concerts using Facebook adapting the mathematical model of hit phenomena. Adv Intell Syst Comput. (2014) 273:53. doi: 10.1007/978-3-319-05533-6_6

CrossRef Full Text | Google Scholar

42. Kawahata Y, Genda E, Koguchi H, Uchiyama K, Ishii A. Analysis of mathematical model of hit phenomena stage actors of Japan. Int J Affect Eng. (2014) 13:89. doi: 10.5057/ijae.13.89

CrossRef Full Text | Google Scholar

43. Kawahata Y, Genda E, Ishii A. Possibility of analysis of ‘Big Data’ of Kabuki Play in 19th century using the mathematical model of hit phenomena. In: Proceedings of ACE2013 in Springer LNCS series, Lecture Notes in Computer Science, 8253. Berlin: Springer (2013). p. 656.

Google Scholar

44. Ishii A, Ota S, Tanimura T, Kitao A, Arakaki H, Uchiyama K, et al. Mathematical theory for hit phenomena as a tool to analyze social phenomena using social networks. In: Proceedings of AAMAS2014, ACM Digital Library, New York, NY (2014).

45. Sano Y, Yamada K, Watanabe H, Takayasu H, Takayasu M. Empirical analysis of collective human behavior for extraordinary events in the blogosphere. Phys Rev. (2013) E87:012805. doi: 10.1103/PhysRevE.87.012805

CrossRef Full Text | Google Scholar

46. Sano Y. Empirical Analysis and Modeling of Word Frequency Time Series in Social Media, Doctoral thesis, Tokyo: Tokyo Institute of Technology (2013).

47. Ishii A, Koyabu T. Analysis of behavior of attenuation of social memories on movie and social scandal using sociophysics approach. In: Proceedings of the 47th ISCIE International Symposium on Stochastic Systems Theory and its Applications. Honolulu, Hawaii (2015). p. 204–9.

Google Scholar

48. Pendry JB. Reliability factors for LEED calculations. J Phys. (1980) C13:937. doi: 10.1088/0022-3719/13/5/024

CrossRef Full Text | Google Scholar

49. Metropolis N, Rosenbluth A, Rosenbluth MN, Teller AH, Teller E. Equations of state calculations by fast computing machines. J Chem Phys. (1953) 21:1087. doi: 10.1063/1.1699114

CrossRef Full Text

50. Ishii A, Fukui K. Analysis of ‘Pico Taro’ epidemic using mathematical model of hit phenomenon. In: Presentation at the Japanese Conference of Computational Social Science. Tokyo, Japan (2017).

51. Ishii A, Ajito M, Kawahata Y. Analysis of Pokemon GO using sociophysics approach. In: Proceeding of 2016 IEEE International Conference on BigData, New Jersey (2016). p. 3986–8.

Google Scholar

52. Oda T. Analysis of Fun of Program Using TV Actual Viewing Data, Bachelor thesis, Tottori University, Japan (2017).

53. Ishii A, Sakaidani S, Iwanaga S. Possibility of estimating payoff matrix from model for hit phenomena. Chaos Solitons Fractals (2016) 90:72–80. doi: 10.1016/j.chaos.2016.03.023

CrossRef Full Text | Google Scholar

54. Ishii A, Ajito M. Mathematical model for conflict of topics on social media platform. Evol Inst Econ Rev. in press.

55. Ishii A, Kawahata Y, Goto U. Model of market share affected by social media reputation. J Phys Soc Jpn Conf Proc. (2017) 16:011006. doi: 10.7566/JPSCP.16.011006

CrossRef Full Text | Google Scholar