- 1Department of Mathematics, Dartmouth College, Hanover, NH, United States
- 2Department of Biomedical Data Science, Geisel School of Medicine at Dartmouth, Lebanon, NH, United States
The rise and spread of antibiotic resistance causes worsening medical cost and mortality especially for life-threatening bacteria infections, thereby posing a major threat to global health. Prescribing behavior of physicians is one of the important factors impacting the underlying dynamics of resistance evolution. It remains unclear when individual prescribing decisions can lead to the overuse of antibiotics on the population level, and whether population optimum of antibiotic use can be reached through an adaptive social learning process that governs the evolution of prescribing norm. Here we study a behavior-disease interaction model, specifically incorporating a feedback loop between prescription behavior and resistance evolution. We identify the conditions under which antibiotic resistance can evolve as a result of the tragedy of the commons in antibiotic overuse. Furthermore, we show that fast social learning that adjusts prescribing behavior in prompt response to resistance evolution can steer out cyclic oscillations of antibiotic usage quickly toward the stable population optimum of prescribing. Our work demonstrates that provision of prompt feedback to prescribing behavior with the collective consequences of treatment decisions and costs that are associated with resistance helps curb the overuse of antibiotics.
1. Introduction
Antibiotics have been used primarily as human medicine for the treatment and prevention of bacterial infections for about 80 years; later as a growth promoter applied in animal feeds, for about 65 years [1, 2]. In this period, it has proved itself incredibly powerful to benefit individual patients, to suppress the overall epidemic of diseases and also to expand livestock production [3–5]. However, the wide use of antibiotics in our society is tagged along by the development of resistance, first identified in the 1940's [6–19].
In recent years, the number of new antibiotics approved by the U.S. Food and Drug Administration (FDA) has been dramatically reduced, suggesting an “EROOM” law (a phenomenon in contrast to the Moore's law) [11, 20, 21]. Even worse, the time period of an antibiotic's effectiveness from its introduction to first resistance identified becomes increasingly short (Figure 1A; see data sources in section 1 of the SI, Data Sheet 1). Moreover, superbugs (multi-drug resistant bacteria) such as Methicillin-resistant S. aureus (MRSA) seem to outsmart our efforts to treat infectious diseases [6–8, 12, 13, 16, 22–25]. Antibiotic resistance is associated with worsening mortality and medical costs [26]. As a consequence, we are confronted with antibiotic resistance crisis, at the risk of running out of effective antibiotics for infection treatments [19].
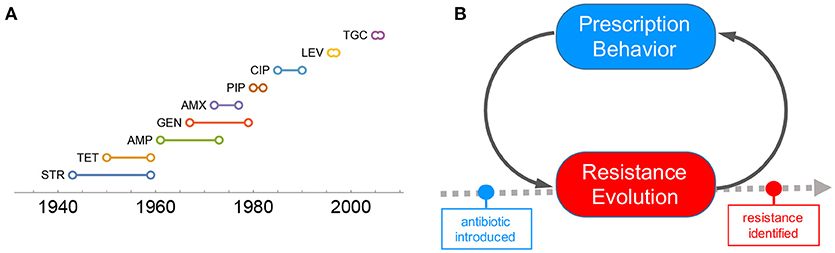
Figure 1. Problem of antibiotic resistance. (A) Timeline plot of resistance emergence for common antibiotics. The time period of an antibiotic's effectiveness from its introduction to first resistance identified becomes increasingly short. (B) Prescribing behavior is one of the driving factors contributing to the fast emergence of resistance. The interaction between resistance evolution and prescripting behavior plays an important role in determining the timeline of resistance emergence.
One of the important factors contributing to the the fast emergence of resistance is overprescribing [27–30]. High demand for antibiotics driven by individual self-interest is not necessarily aligned with the social optimum of antibiotic consumption. Under certain conditions, the overuse of antibiotics can lead to the tragedy of the commons [24, 31–34]. Therefore, it is of significant public health interest to understand and manage antibiotic resistance from this behavioral perspective.
Here, we focus on the interaction of prescription behavior and resistance evolution through a feedback loop (Figure 1B): collective outcomes of prescribing decisions affect the underlying resistance evolution, which in turn influences prescription behavior. The behavior-disease interaction model of this kind is simple yet proof of concept [35–38], and sheds light on how social learning of prescription behavior in response to the underlying evolutionary dynamics of resistance can render population optimum of antibiotic use.
2. Model
Previous work demonstrates that social learning promotes the emergence of institutions for governing the commons [39, 40]. Inspired by this, we will explore how social learning of prescription behavior in response to the underlying evolutionary dynamics of resistance can promote population optimum of antibiotics usage. We will study a behavior-disease interaction model that incorporates a feedback loop between prescription behavior and resistance evolution:
Here, b denotes the birth rate per capita, which is set equal to the death rate d; βs and βm are the transmission rates of the two strains; , , , and are the respective recovery rates of different infection cases (infected with sensitive or resistant strain; untreated or treated); ϵs and ϵm are the effectivenesses of the antibiotics for treating sensitive and resistant infections, respectively. S, I and R are the fractions of susceptible, infected and recovered individuals in the population with , , , and denoting the four infection cases (infected with sensitive or resistant strains, and untreated or treated); Rs and Rm the two recovery cases, respectively. The two parameters μs and μm indicates the mutation rates between the two strains.
As given in the last equation (Equation 1), prescription norm changes in response to the actual payoffs of individual prescribing vs. non-prescribing behavior (fA vs. fB), which are determined by disease prevalence and resistance evolution on the population level [41]. This feedback loop between prescription behavior and resistance evolution constitutes an adaptive social learning process in which the society adjusts antibiotic use in response to the underlying resistance evolution.
We focus on quantifying the extent to which the (over)use of antibiotics would cause the emergence of resistance in the long run (see section 4). To do so, we introduce the parameter θ to denote the presentation rate of infected individuals who bring their condition to a physician's attention and seek antibiotic treatment for their illness (In this regard, the θ value is determined by individual disease awareness and health-seeking behavior). To account for prescribing norm of physicians, we use p to denote the likelihood that each patient at presentation is prescribed antibiotic treatment, 0 ≤ p ≤ 1. Thus, the overall prescribing rate, pθ, mediates the selection pressure on resistance that is attributed to collective consequence of prescription behavior.
3. Results and Discussion
We use the next-generation approach to calculate basic reproductive ratios for both strains, and in closed-form (see section 2 of the SI for details, Data Sheet 1). We assume that resistance is costly in the absence of treatment, but confers an advantage in the presence of treatment; that is, resistance compromises the efficacy of treatment, 0 ≤ ϵm < 1. Comparing and allows us to answer questions of interest, such as predicting whether resistance can evolve in the long run.
For simplicity, we first consider resistance evolution under full treatment (p = 1), in which infected individuals, once seen by medical professionals at their presentation, unvaryingly receive antibiotic treatment. As shown in Figure 2A, we characterize the conditions for resistance evolution in the parameter space (θ, ϵm). For small θ values below a threshold (blue region in Figure 2A), neither can the disease be eradicated, nor can resistance evolve. Disease can be eradicated for high θ and ϵm (yellow region in Figure 2A). However, for combinations of intermediate θ and low ϵm (red region in Figure 2A), resistance evolves and leads to disease escape despite full treatment.
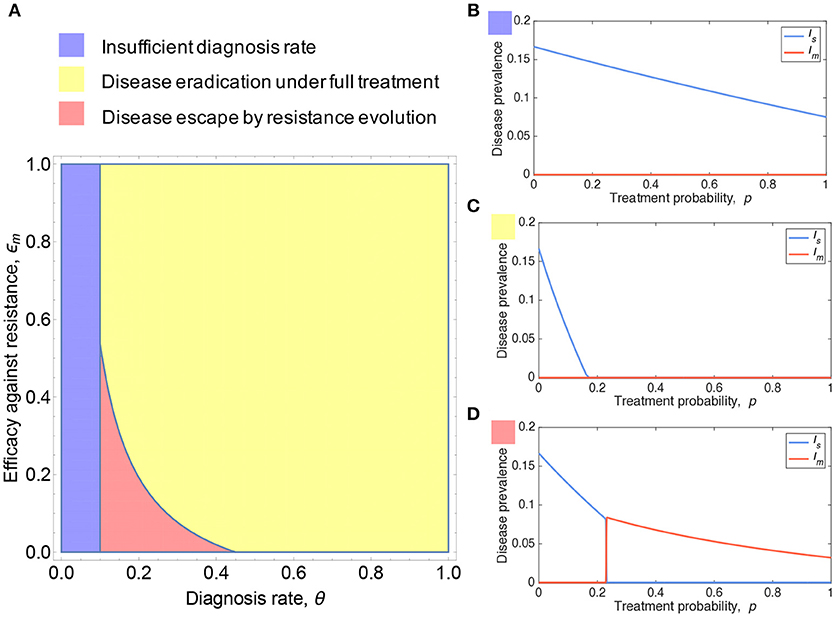
Figure 2. Resistance evolution and antibiotic usage. (A) Shown is the parameter region of presentation rate θ and efficacy against resistance ϵm under which antibiotic resistance can emerge. (B–D) plot the prevalence of sensitive and resistant strains as a function of treatment probability p. Resistance can be favored under sufficiently high treatment coverage and as a consequence, the tragedy of the commons in antibiotic overuse can occur. Parameters: b = 0.1, βs = 0.3, βm = 0.26, , , , ϵs = 1, (A) ϵm = 0, (B) ϵm = 0.6, θ = 0.05, (C) ϵm = 0.8, θ = 0.6, (D) ϵm = 0, θ = 0.2, (B–D) .
To further gain intuitive understanding of how resistance evolution depends on antibiotic use, we plot the disease prevalence with respect to treatment probability p, corresponding to the three scenarios as colored in Figure 2A. The sensitive strain is predominant for all 0 ≤ p ≤ 1, whereas the resistant strain is maintained at low frequency purely by the mutation-selection equilibrium (Figure 2B). Disease can be eradicated for sufficiently high treatment rate and resistance has no chance to evolve (Figure 2C). In Figure 2D, disease eradication is impossible due to the emergence of resistance that greatly comprises the efficacy of treatment; resistance can be selected for p above a critical threshold p > ph (see section 3 of the SI, Data Sheet 1), and as a consequence, the predominant incidence of infections switches from sensitive to resistant strains.
Let us now turn our attention to this last scenario where resistance evolution is inevitable for p > ph. Empirical evidence shows that there exists a threshold in prescription rate above which sustained resistance can cause huge public health crisis [42]. To determine the population optimum of antibiotic use, we need to take into account the impact of resistance on the cost-benefit analysis of antibiotic treatment (Figure 3). The cost of sensitive infection, if treated, can be mitigated. In contrast, resistant infections may greatly exacerbate the overall cost for both treated and untreated cases [43]. Under these conditions, the overall social burden of the disease can be minimized at p = ph (i.e., population optimum). Although the disease prevalence and thus the risk of infection for susceptible individuals can be lowered by overprescribing beyond ph (Figure 3A), the cost associated with resistance is much greater than the benefit, if any, that full treatment could provide (Figure 3B).
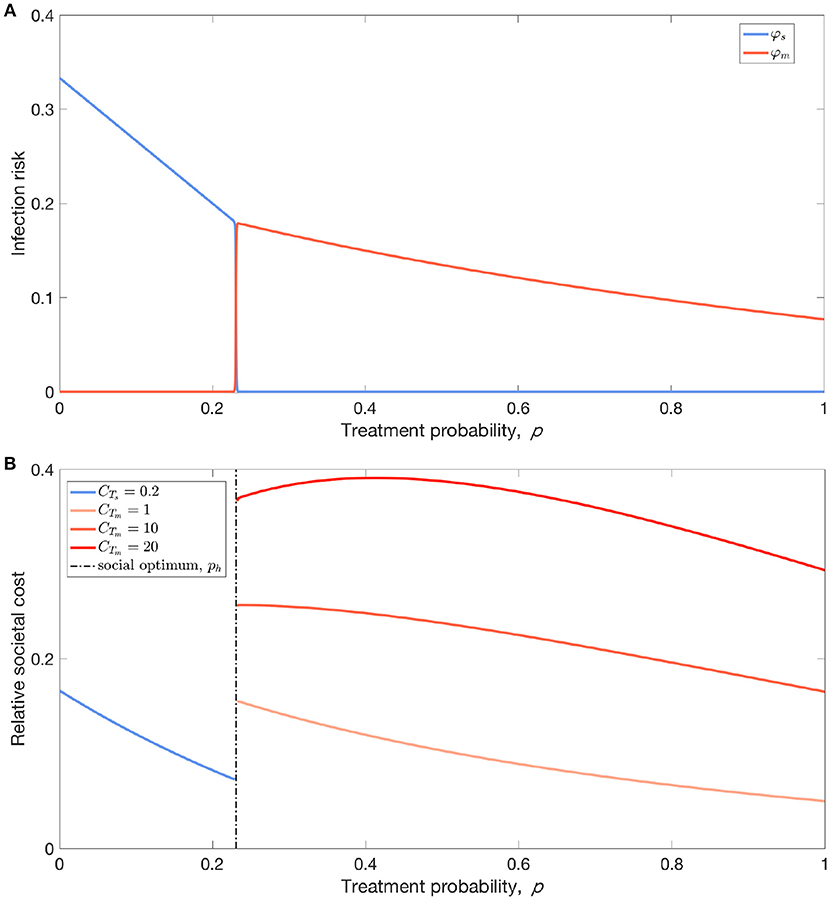
Figure 3. Cost-benefit analysis of antibiotic usage. (A) From the perspective of susceptible individuals, their infection risk reduces with increasing treatment probability (coverage) p, but there exists a threshold of treatment coverage, ph, above which the risk of infection almost exclusively comes from resistant strain instead of sensitive stain. (B) Accounting for the differing costs of treating patients infected with sensitive and resistant strains, the threshold ph corresponds to the social optimum of antibiotic usage: the total societal disease burden is decreasing with p for p < ph, but followed by a surge in the total cost of infection due to resistance. Parameters: (A,B) b = 0.1, βs = 0.3, βm = 0.26, , , , ϵs = 1, ϵm = 0, θ = 0.2, , (B) relative social burden of the disease: CIs = 1, CTs = 0.2, BTs = 0.3, CIm = 2, BTm = 0.1.
Despite these population-level considerations, individual self-interest can cause antibiotic overuse, thereby leading to a tragedy of the commons. This is largely due to the disconnect between individual behavior and population-level resistance in prescribing decision-makings. Therefore, curbing antibiotic overuse requires provision of feedback to individual prescribing behavior with the social costs and consequences of their collective action. In light of this, we investigate whether population optimum of antibiotic use can be reached if the society learns from the collective consequences of treatment decisions and costs that are associated with resistance and accordingly adjusts prescription behavior.
We assume disease dynamics coevolves with a social norm that governs prescription behavior (see section 4 of the SI, Data Sheet 1). We use evolutionary game theory to study the evolution of prescription norm [41, 39]. Prescription norm changes in response to the actual payoffs of individual prescribing vs. non-prescribing behavior, which are determined by disease prevalence and resistance evolution on the population level. This feedback loop between prescription behavior and resistance evolution constitutes an adaptive social learning process in which the society adjusts antibiotic use in response to the underlying resistance evolution.
We find that how swiftly the society responds to the underlying resistance evolution has an impact on the coevolutionary dynamics (Figure 4). Slow social learning leads to prolonged oscillatory dynamics of overprescribing and underprescribing, and thus gives chance for resistance to accumulate and build up in the population, causing resurgences of marked resistance prevalence alternated with sensitive infections (Figure 4A). In stark contrast, fast social learning can help the population steer out cyclic oscillations of antibiotic use due to overcorrection. In this latter case, the society adapts prescription norm so quickly that resistance has no chance to grow into pronounced prevalence as it is outpaced by the change in prescribing behavior. Besides, fast social learning helps the society settle on a social norm that reaches the population optimum of antibiotic use (Figure 4B).
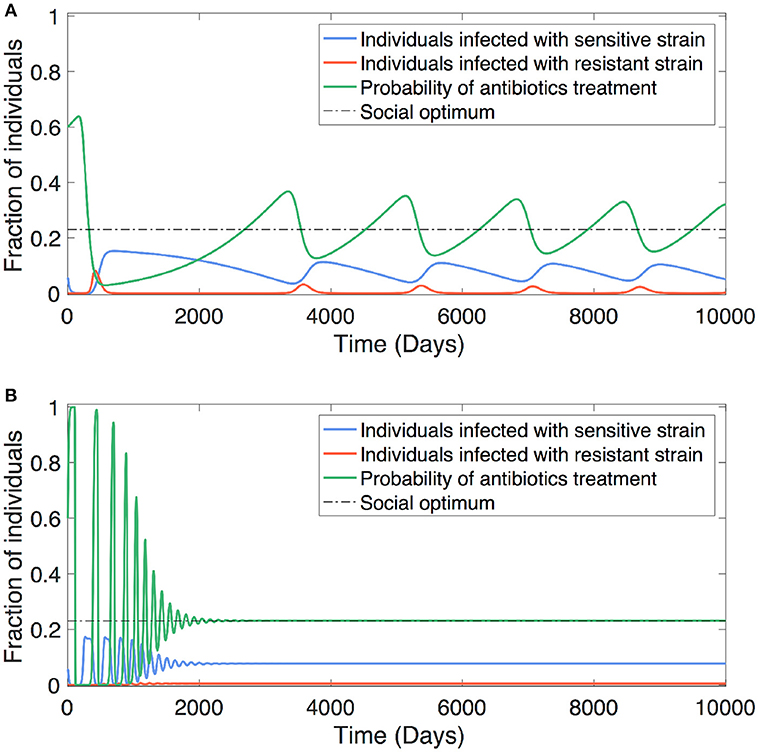
Figure 4. Social learning impacts antibiotic usage. The antibiotic usage behavior can be adjusted in response to the underlying dynamics of resistance evolution. The convergence of optimum antibiotic usage is determined by how promptly the society learns from the collective consequences of treatment decisions and costs that are associated with resistance. (A) Slow learning leads to oscillatory dynamics of antibiotic usage (between overuse and lesser use) together with alternating dominance of resistant and sensitive strains. (B) Fast learning can steer out cyclic oscillations of antibiotic usage due to overcorrection, and therefore helps the society quickly reach socially optimal usage. Parameters: b = 0.1, βs = 0.3, βm = 0.26, , , , ϵs = 1, ϵm = 0, θ = 0.2, , relative social burden of the disease: CIs = 1, CTs = 0.2, BTs = 0.3, CIm = 2, CTm = 20, BTm = 0.1, (A) ω = 0.001, (B) ω = 0.1.
We demonstrate that social learning without centralized institutions can maneuver the population toward a socially optimal policy of prescribing, therefore helping curb the overuse of antibiotics. Our theoretical results are in line with recent trial findings that highlight the importance of provision of social norm feedback in reducing antibiotic overuse [29]. Taken together, in order to reach sustainable use of antibiotics, it is important to promote awareness of the population problem of resistance by providing prompt feedback to prescribing behavior with the social cost of resistance.
Owing to the drastic slowdown of new drug discoveries [21, 44], managing resistance evolution with an emphasis on human factors, as we demonstrate here, seems to be necessary and feasible [45]. Prior studies suggest that the consumption of antibiotics and the patterns in which different agents are deployed directly impact the frequency of resistance and the number of ineffective antibiotics [42, 46, 47]. To inform rational use of antibiotics, efforts should be focused on developing new diagnostic technologies and strategies for reducing the inappropriate use of antibiotics [48], determining the optimal timing of deployment sequence for existing drugs [49, 50], and optimizing combination therapies [51, 52]. Moreover, promoting and enforcing infection control procedures in hospitals can prevent the spread of resistance and mitigate the impact of resistance on society [9, 15, 16, 27, 45, 48, 50, 53, 54]. Along these lines, it is worthwhile for future study to incorporate population structure [55, 56] and multiple drugs [57–59] in the coevolutionary dynamics of prescribing behavior and multi-drug resistance.
The socially optimum use of antibiotics implies a second order of dilemma—not every sickness should be treated, but who on earth deserves the treatment and who would have to forgo? This consideration leads to the ethics dilemma of accessibility of antibiotics, an important topic worthy of further investigation. Reducing antibiotics usage via national guidelines has been found to lead to significant decreases in resistance [46, 47], yet denials or approvals of antibiotic treatment seem to be determined by an arbitrary trade-off between preventing resistance and treating infected patients [20]. With multiple interest groups such as pharmaceutical industry, public institutions as well as patients themselves involved in the problem, it is of fundamental interest to look into the issues of supervising the common pool resources [60–62] and enhancing collaborative efforts through the behavioral perspective [18, 24].
4. Methods and Analysis
We begin our analysis with characterizing the conditions for resistance evolution for given levels of antibiotic use p in the long run.
4.1. Basic Reproductive Ratios
The competition dynamics of sensitive vs. resistant strains is described by the evolutionary epidemiological model, as given in Equation (1). The basic reproductive ratios and of the two strains can be determined by the spectral radius of the next-generation operator FV−1, where F is the reproduction matrix and V the state transition matrix [63–65]. We obtain that
assume that resistance incurs a fitness penalty, so that the transmission rates βs > βm. Despite the fact that laboratory studies revealed a scenario where compensatory evolution (resistant bacteria ameliorating the costs by acquiring fitness-compensatory mutations) and cost-free resistances can slow down the primary driver for reversibility and that co-selection between the resistance mechanism and other selected markers can delay any latent reversibility driven by fitness costs in vitro [66], clinical studies have found that the compensatory adaptation is not effective in vivo, which is in line with our assumption [67]. Theoretical arguments and experimental results, in addition, provide basis for that the fitness costs of resistance is critical to the displacement of resistant strains with sensitive ones [66, 67].
Both and are decreasing functions of p under our model assumptions (see SI, Data Sheet 1). We demonstrate that the graphs of the two basic reproductive numbers will vary with values of their endpoints and (see the SI for details). Without loss of generality, we scrutinize the following three cases: (I) Rs > 1; (II-a) Rs(1) < 1 and Rm(1) < 1; (II-b) Rs(1) < 1 < Rm(1). The case noteworthy in practice is the last one, in which resistant strains predominate and even full treatment can not eradicate the disease.
For a better understanding of the disease dynamics in case (II-b), we perform a further investigation of the relations among those parameters, where the presentation rates θs and θm for the two infected cases are seen as independent. Substituting p = 1 into (2) and (3) and combining with the inequality Rs(1) < 1 < Rm(1), we derive an equivalent condition for case (II-b) to occur:
The values of , , and are given in the SI. Therefore, to get the basic reproductive ratio below 1 and thus control the disease, we need θm to be greater than or ϵm greater than . The two solvents correspond to either patients presenting promptly after infection or introducing potent antibiotics in treatment.
Moreover, let ph be the critical prescribing probability (which can be translated into treatment coverage, namely, the proportion of patients that are prescribed antibiotic treatment) at which the dominance of the two strains switches in case (II-b). For , we derive a simplified form
where ph is referred to as the social optimum of antibiotic use (see details in section 3 of the SI, Data Sheet 1).
4.2. Cost-Benefit Analysis
When p < ph, the sensitive strain dominates and the system converges to an equilibrium, of which we derive a closed form approximation ; when p > ph, the resistant strain dominates, with the system converging to another equilibrium, approximated by . We prove in the SI (Data Sheet 1) that S is increasing while I0 and I0 + It are decreasing with respect to p for both equilibria.
For susceptible individuals, if the sensitive strain dominates, the infection probability at equilibrium is approximately
which can be simplified as . Analogously, if the resistant strain prevails, the infection probability at equilibrium is approximately
Although the actual treatment cost can be determined only after treatment outcomes, it is expected that (1) sensitive strain claims lower sickness and treatment costs while it redounds to greater treatment benefit (CIs < CIm, BTs > BTm and CTs < CTm), (2) treatment of patients with sensitive strains can mitigate the overall cost of infection (CTs − CIs < BTs), and in contrast (3) treatment of patients with resistant strains may exacerbate the overall cost of infection (CTm − CIm > BTm) [43].
When it comes to the population, the total social cost is a piecewise function
Invoking the monotonicity of and , it is easy to verify that the total social cost Csocial is decreasing when p < ph. However, Csocial may not be monotonic when p > ph (see detailed analysis in section 3 of the SI, Data Sheet 1).
4.3. Social Learning
We consider that prescription behavior coevolves with disease dynamics. We regard the problem as a two strategy game, prescribing (denoted as A) vs nonprescribing (B). The evolution of prescribing behavior can be described by:
where p is the frequency of prescribing A and ṗ is referred to as the rate of prescription norm evolution, driven by the time scale parameter of social learning, ω.
The expected payoffs fA and fB are
with
Here λs and λm are the conditional probabilities of individuals being infected with sensitive or resistant strains, respectively.
Denote the fractions of individuals infected with sensitive and resistant strains by Is and Im, respectively ( and ). The behavior of the disease dynamics are described by Is and Im while the prescribing norm is presented by p, all as functions of the time t.
Author Contributions
XC and FF conceived the model, performed analyses, and wrote the manuscript.
Conflict of interest statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
We are grateful for support from the G. Norman Albree Trust Fund, Dartmouth Faculty Startup Fund, Walter & Constance Burke Research Initiation Award and NIH Roybal Center Pilot Grant.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2018.00139/full#supplementary-material
References
1. Jones F, Ricke S. Observations on the history of the development of antimicrobials and their use in poultry feeds. Poultry Sci. (2003) 82:613–17. doi: 10.1093/ps/82.4.613
2. Castanon J. History of the use of antibiotic as growth promoters in European poultry feeds. Poultry Sci. (2007) 86:2466–71. doi: 10.3382/ps.2007-00249
3. Aminov RI. A brief history of the antibiotic era: lessons learned and challenges for the future. Front Microbiol. (2010) 1:134. doi: 10.3389/fmicb.2010.00134
4. Zaffiri L, Gardner J, Toledo-Pereyra LH. History of antibiotics. From salvarsan to cephalosporins. J Investigat Surg. (2012) 25:67–77. doi: 10.3109/08941939.2012.664099
5. Van Boeckel TP, Glennon EE, Chen D, Gilbert M, Robinson TP, Grenfell BT, et al. Reducing antimicrobial use in food animals. Science (2017) 357:1350–2. doi: 10.1126/science.aao1495
6. Garrett L. The Coming Plague: Newly Emerging Diseases in a World Out of Balance. London: Penguin (1994).
8. Walsh C. Molecular mechanisms that confer antibacterial drug resistance. Nature (2000) 406:775. doi: 10.1038/35021219
9. Palumbi SR. Humans as the world's greatest evolutionary force. Science (2001) 293:1786–90. doi: 10.1126/science.293.5536.1786
10. Levy SB. The Antibiotic Paradox: How the Misuse of Antibiotics Destroys Their Curative Power. Cambridge, MA: Da Capo Press (2002).
11. Norrby SR, Nord CE, Finch R, European Society of Clinical Microbiology and Infectious Diseases. Lack of development of new antimicrobial drugs: a potential serious threat to public health. Lancet Infect Dis. (2005) 5:115–9. doi: 10.1016/S1473-3099(05)01283-1
12. Spellberg B, Guidos R, Gilbert D, Bradley J, Boucher HW, Scheld WM, et al. The epidemic of antibiotic-resistant infections: A call to action for the medical community from the Infectious Diseases Society of America. Clin Infect Dis. (2008) 46:155–64. doi: 10.1086/524891
13. Arias CA, Murray BE. Antibiotic-resistant bugs in the 21st century? a clinical super-challenge. N Engl J Med. (2009) 360:439–43. doi: 10.1056/NEJMp0804651
14. Davies J, Davies D. Origins and evolution of antibiotic resistance. Microbiol Mol Biol Rev. (2010) 74:417–33. doi: 10.1128/MMBR.00016-10
15. zur Wiesch PA, Kouyos R, Engelstädter J, Regoes RR, Bonhoeffer S. Population biological principles of drug-resistance evolution in infectious diseases. Lancet Infect Dis. (2011) 11:236–47. doi: 10.1016/S1473-3099(10)70264-4
16. Rossolini GM, Arena F, Pecile P, Pollini S. Update on the antibiotic resistance crisis. Curr Opin Pharmacol. (2014) 18:56–60. doi: 10.1016/j.coph.2014.09.006
18. World Bank Group Drug-resistant Infections: a Threat to Our Economic Future. Discussion Draft Published online (2016).
19. Reardon S. Resistance to last-ditch antibiotic has spread farther than anticipated. Nat News (2017). doi: 10.1038/nature.2017.22140
20. Projan SJ. Why is big Pharma getting out of antibacterial drug discovery? Curr Opin Microbiol. (2003) 6:427–30. doi: 10.1016/j.mib.2003.08.003
21. Scannell JW, Blanckley A, Boldon H, Warrington B. Diagnosing the decline in pharmaceutical R&D efficiency. Nat Rev Drug Discov. (2012) 11(3):191–200. doi: 10.1038/nrd3681
22. Flores PA, Gordon SM. Vancomycin-resistant Staphylococcus aureus: an emerging public health threat. Cleveland Clin J Med. (1997) 64:527–32.
23. Woodford N, Livermore DM. Infections caused by Gram-positive bacteria: a review of the global challenge. J Infect. (2009) 59:S4–S16. doi: 10.1016/S0163-4453(09)60003-7
24. Conly J. Antimicrobial resistance: revisiting the tragedy of the commons. Bull World Health Organ. (2010) 88:797–876. doi: 10.2471/BLT.10.031110
25. Magiorakos AP, Srinivasan A, Carey R, Carmeli Y, Falagas M, Giske C, et al. Multidrug-resistant, extensively drug-resistant and pandrug-resistant bacteria: an international expert proposal for interim standard definitions for acquired resistance. Clin Microbiol Infect. (2012) 18:268–81. doi: 10.1111/j.1469-0691.2011.03570.x
26. Vaughan L, Wise K, Holmes-Maybank K, Charity P. Antibiotic Resistant Threats in the United States. Prevention for Disease Control (2013). Available online at: https://www.cdc.gov/drugresistance/pdf/ar-threats-2013-508.pdf
27. Nyquist AC, Gonzales R, Steiner JF, Sande MA. Antibiotic prescribing for children with colds, upper respiratory tract infections, and bronchitis. JAMA (1998) 279:875–77.
28. Christakis NA, Fowler JH. Commentary–Contagion in prescribing behavior among networks of doctors. Market Sci. (2011) 30:213–16. doi: 10.1287/mksc.1100.0595
29. Hallsworth M, Chadborn T, Sallis A, Sanders M, Berry D, Greaves F, et al. Provision of social norm feedback to high prescribers of antibiotics in general practice: a pragmatic national randomised controlled trial. Lancet (2016) 387:1743–52. doi: 10.1016/S0140-6736(16)00215-4
30. Murshid MA, Mohaidin Z. Models and theories of prescribing decisions: a review and suggested a new model. Pharm Pract (Granada) (2017) 15:990. doi: 10.18549/PharmPract.2017.02.990
31. Hardin G. The tragedy of the commons. J Natl Resour Policy Res. (2009) 1:243–53. doi: 10.1126/science.162.3859.1243
32. Baquero F, Campos J. The tragedy of the commons in antimicrobial chemotherapy. Rev Esp Quimioter. (2003) 16:11–3. Available online at: http://www.seq.es/seq/0214-3429/16/1/11.pdf
33. Foster KR, Grundmann H. Do we need to put society first? The potential for tragedy in antimicrobial resistance. PLoS Med. (2006) 3:e29. doi: 10.1371/journal.pmed.0030029
34. Porco TC, Gao D, Scott JC, Shim E, Enanoria WT, Galvani AP, et al. When does overuse of antibiotics become a tragedy of the commons? PLoS ONE (2012) 7:e46505.
35. Bauch CT. Imitation dynamics predict vaccinating behaviour. Proc R Soc Lond B Biol Sci. (2005) 272:1669–75. doi: 10.1098/rspb.2005.3153
36. Fu F, Rosenbloom DI, Wang L, Nowak MA. Imitation dynamics of vaccination behaviour on social networks. Proc R Soc Lond B Biol Sci. (2011) 278:42–9. doi: 10.1098/rspb.2010.1107
37. Zheng C, Xia C, Guo Q, Dehmer M. Interplay between SIR-based disease spreading and awareness diffusion on multiplex networks. J Parall Distrib Comput. (2018) 115:20–8. doi: 10.1016/j.jpdc.2018.01.001
38. Sanz J, Xia CY, Meloni S, Moreno Y. Dynamics of interacting diseases. Phys Rev X (2014) 4:41005. doi: 10.1103/PhysRevX.4.041005
39. Sigmund K, De Silva H, Traulsen A, Hauert C. Social learning promotes institutions for governing the commons. Nature (2010) 466:861. doi: 10.1038/nature09203
40. Chen X, Szolnoki A. Punishment and inspection for governing the commons in a feedback-evolving game. PLoS Computat Biol. (2018) 14:e1006347. doi: 10.1371/journal.pcbi.1006347
42. Baquero F. Trends in antibiotic resistance of respiratory pathogens: an analysis and commentary on a collaborative surveillance study. J Antimicrob Chemother. (1996) 38(Suppl A):117–32.
43. Roberts RR, Hota B, Ahmad I, Scott RD, Foster SD, Abbasi F, et al. Hospital and societal costs of antimicrobial-resistant infections in a Chicago teaching hospital: implications for antibiotic stewardship. Clin Infect Dis. (2009) 49:1175–84. doi: 10.1086/605630
44. Verhoef TI, Morris S. Cost-effectiveness and pricing of antibacterial drugs. Chem Biol Drug Design. (2015) 85:4–13. doi: 10.1111/cbdd.12417
45. Levin BR. Minimizing potential resistance: a population dynamics view. Clin Infect Dis. (2001) 33(Suppl 3):S161–9. doi: 10.1086/321843
46. Seppala H, Klaukka T, Vuopio-varkila J, Muotiala A, Helenius H, Lager K, et al. The effect of changes in the consumption of macrolide antibiotics on erythromycin resistance in group A streptococci in Finland. N Engl J Med. (1997) 337:441–6.
47. Kristinsson KG. Effect of antimicrobial use and other risk factors on antimicrobial resistance in pneumococci. Microb Drug Resist. (1997) 3:117–23.
49. Wang YC, Lipsitch M. Upgrading antibiotic use within a class: tradeoff between resistance and treatment success. Proc Natl Acad Sci USA. (2006) 103:9655–60. doi: 10.1073/pnas.0600636103
50. McClure NS, Day T. A theoretical examination of the relative importance of evolution management and drug development for managing resistance. Proc R Soc Lond B Biol Sci. (2014) 281:20141861. doi: 10.1098/rspb.2014.1861
51. Bonhoeffer S, Lipsitch M, Levin BR. Evaluating treatment protocols to prevent antibiotic resistance. Proc Natl Acad Sci USA. (1997) 94:12106–11.
52. Cottarel G, Wierzbowski J. Combination drugs, an emerging option for antibacterial therapy. Trends Biotechnol. (2007) 25:547–55. doi: 10.1016/j.tibtech.2007.09.004
53. Smith DL, Levin SA, Laxminarayan R. Strategic interactions in multi-institutional epidemics of antibiotic resistance. Proc Natl Acad Sci USA. (2005) 102:3153–8. doi: 10.1073/pnas.0409523102
54. World Health Organization. Guidelines for the Reatment of Malaria. World Health Organization (2015). Available online at: https://www.who.int/malaria/publications/atoz/9789241549127/en/
55. Leventhal GE, Hill AL, Nowak MA, Bonhoeffer S. Evolution and emergence of infectious diseases in theoretical and real-world networks. Nat Commun. (2015) 6:6101. doi: 10.1038/ncomms7101
56. Chen X, Fu F, Wang L. Influence of different initial distributions on robust cooperation in scale-free networks: a comparative study. Phys Lett A. (2008) 372:1161–7. doi: 10.1371/journal.pone.0171680
57. Lipsitch M, Samore MH. Antimicrobial use and antimicrobial resistance: a population perspective. Emerging Infect Dis. (2002) 8:347. doi: 10.3201/eid0804.010312
58. Donskey CJ, Chowdhry TK, Hecker MT, Hoyen CK, Hanrahan JA, Hujer AM, et al. Effect of antibiotic therapy on the density of vancomycin-resistant enterococci in the stool of colonized patients. N Engl J Med. (2000) 343:1925–32. doi: 10.1056/NEJM200012283432604
59. Enne VI, Livermore DM, Stephens P, Hall LM. Persistence of sulphonamide resistance in Escherichia coli in the UK despite national prescribing restriction. Lancet (2001) 357:1325–8. doi: 10.1016/S0140-6736(00)04519-0
60. Wu T, Fu F, Zhang Y, Wang L. Adaptive role switching promotes fairness in networked ultimatum game. Sci Reports (2013) 3:1550. doi: 10.1038/srep01550
61. Wu T, Fu F, Dou P, Wang L. Social influence promotes cooperation in the public goods game. Phys A Statist Mechan Applic. (2014) 413:86–93. doi: 10.1016/j.physa.2014.06.040
62. Perc M, Jordan JJ, Rand DG, Wang Z, Boccaletti S, Szolnoki A. Statistical physics of human cooperation. Phys Reports (2017) 2:281–93. doi: 10.1016/j.physrep.2017.05.004
63. Heffernan JM, Smith RJ, Wahl LM. Perspectives on the basic reproductive ratio. J R Soc Interf. (2005) 2:281–93. doi: 10.1098/rsif.2005.0042
64. Diekmann O, Heesterbeek J, Roberts M. The Construction of Next-Generation Matrices for Compartmental Epidemic Models. J R Soc Interface (2009) 7:873–85. doi: 10.1098/rsif.2009.0386
65. Hurford A, Cownden D, Day T. Next-generation tools for evolutionary invasion analyses. J R Soc Interface. (2010) 7:561–71. doi: 10.1098/rsif.2009.0448
66. Andersson DI, Hughes D. Antibiotic resistance and its cost: is it possible to reverse resistance? Nat Rev Microbiol. (2010) 8:260. doi: 10.1038/nrmicro2319
Keywords: evolutionary dynamics, game theory, antibiotic resistance, public health, cooperation
Citation: Chen X and Fu F (2018) Social Learning of Prescribing Behavior Can Promote Population Optimum of Antibiotic Use. Front. Phys. 6:139. doi: 10.3389/fphy.2018.00139
Received: 18 October 2018; Accepted: 21 November 2018;
Published: 06 December 2018.
Edited by:
Matjaž Perc, University of Maribor, SloveniaReviewed by:
Xiaojie Chen, University of Electronic Science and Technology of China, ChinaChengyi Xia, Tianjin University of Technology, China
Copyright © 2018 Chen and Fu. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Feng Fu, ZnVmZW5nQGdtYWlsLmNvbQ==
 Xingru Chen
Xingru Chen Feng Fu
Feng Fu