Catalyst-Inspired Charge Carriers for High Energy Density Redox Flow Batteries

We introduce a theoretical design approach aiming at improving energy density of redox flow batteries (RFBs) via the utilization of redox non-innocent ligands capable of stabilizing a metal center in a wide range of oxidation states. Our findings suggest that this promotes the possibility of multiple redox events as well as high open circuit voltages. Specifically, we have proposed two Fe-coordination complexes (I, Fe(^Me2Pytacn)(C₂N₃H₂), and II, Fe(H₂pmen)(C₂N₃H₂)) combining two different types of ligands, i.e., catalyst-inspired scaffolds and triazole ring, which were previously shown to promote high and low oxidation states in transition metals, respectively. These complexes exhibit as many as six theoretical redox events in the full range of charge states +4 → −2, several of which reside within the electrochemical window of acetonitrile. Electronic structure calculations show that the Fe center exhibits oxidation states ranging from the very rare Fe⁴⁺ to Fe¹⁺. Values of the reduction potentials as well as nature of the redox events of both complexes is found to be similar in their high +4 → +1 charge states. In contrast, while exhibiting qualitatively similar redox behavior in the lower 0 → −2 range, some differences in the electronic ground states, delocalization patterns as well as reduction potential values are also observed. The calculated open circuit voltages can reach values of 5.09 and 6.14 V for complexes I and II, respectively, and hold promise to be experimentally accessible within the electrochemical window of acetonitrile expanded by addition of ionic liquids. The current results obtained for these two complexes are intended to illustrate a more general principle based on the simultaneous utilization of two types of ligands responsible for the stabilization of high and low oxidation states of the metal that can be used to design the next-generation charge carriers capable of supporting multi-electron redox and operating in a broad range of charge states, leading to RFBs with greater energy density.

Introduction

The worldwide demand of electricity as a major form of energy is increasing significantly every year [1]. Although renewable energy sources still make up only a small part of the total energy produced in the world, their rapid expansion and utilization leave no doubt that humanity will eventually switch to using them as more environmentally friendly and cost effective choices [2]. However, current renewable energy resources, such as wind, solar, and wave power, are intermittent and require new energy storage solutions to be incorporated on the grid. Utilization of redox flow batteries (RFBs) has recently been recognized as a promising technology for scalable energy storage, ranging from shopping centers, computing/data handling facilities, and factories, to electricity grids [3– 5]^1,2. Unlike traditional batteries, where energy is stored in and limited by the electrodes, non-hybrid RFBs only use the electrodes/cell for the transfer of energy to/from dissolved chemical species that largely reside in external tanks [6]. The rational design scheme ensuring decoupling between power delivery and energy density makes such systems very flexible and scalable [7, 8].

Since the invention of the first RFB system [9], significant progress has been made in their development [10–28]. Current state-of-the-art commercial non-hybrid flow cell technology uses an aqueous acidic electrolyte and one-electron redox couples, e.g., V^II/V^III and V^IV/V^V3,4. On one hand, these RFBs can exhibit unlimited energy capacity simply by using larger electrolyte storage tanks, while also being inherently safe since the electrolyte is aqueous and non-flammable. On the other hand, the energy density in these systems is controlled by the concentration of vanadium, which is an expensive metal also requiring specific conditions for better solubility [29]. Some efficient steps have recently been undertaken with the aim of increasing their energy storage capacity as well as expanding the temperature range, in which they can operate [30]. However, the narrow electrochemical window (EW) of water (1.23 V) prevents accessibility to a large number of redox events, which could appreciably increase the total open circuit voltage (OCV) determined as the difference of the outermost positive and negative redox potentials. Due to the aforementioned shortcomings, it is difficult for these systems to meet both operational and economic requirements for broad market penetration.

In contrast to aqueous systems^1,2[31], non-aqueous RFBs can offer a wider range of working temperature, higher cell voltage, and potentially higher energy density with a small sacrifice in greater solvent toxicity/flammability [3]. Milestone examples of non-aqueous metal-based RFBs include Ru- [32], Fe- [32], U- [33], V- [34, 35], Mn- [36], Cr- [37], Ni- [38], Co- [39], and W [40]-containing systems. It is worthy to note that efforts to develop more efficient electrolytes for non-aqueous RFBs have mostly been empirical, from both theoretical and experimental perspectives, with limited attempts toward the rational design of structural, electronic, and other RFB-relevant properties [41–44]. It is clear that there is an urgent need to develop more affordable and efficient RFBs to meet the world's growing energy storage demands.

To address the challenges of reducing the cost and increasing energy density of RFBs, we implemented a two-pronged approach: (1) develop charge carriers based on iron (Fe) and (2) utilize two different ligand types to stabilize a wide range of complex charge states. Cost will primarily be addressed by using the second most abundant metal in the earth's crust and developing high cycle-life charge carriers. Increased energy density will also facilitate meeting cost charges by reducing the balance of plant costs [4]. The energy density of a RFB is a function of cell potential, the number of electrons stored per molecule, and solubility. Fe complexes are ideal for improving this density since they have demonstrated oxidation states ranging from −2 in Na₂[Fe(CO)₄] [45] to +6 in FeO₄ [46]. Since appropriate ligands are critical to the stability of the aforementioned oxidation states, we propose to use two different types of ligands, one which help stabilize low charge states, the other which helps stabilize high charge states, with the hope of generating high OCV values, leading to RFBs with high energy density.

To address the aforementioned charge carrier performance needs, we designed two complexes (I: Fe(^Me2Pytacn)(C₂N₃H₂) and II: Fe(H₂pmen)(C₂N₃H₂)) shown in Figure 1. First, we theoretically evaluated their ability of maintaining structural integrity in various charge states, surmising that small changes equate to insignificant structural degradation. This is a key factor for the performance of a RFB system as reversibility is important for cycling through charging and discharging. Next, we also assessed redox properties of these complexes by calculating their reduction potentials within a rather extended range of charge states from +4 → −2, thus enabling investigation of structural and electronic changes at extremes as well as assessing the limits of such processes from a thermodynamic standpoint. Mulliken spin density and Adaptive Natural Density Partitioning (AdNDP) analyses were applied to determine the oxidation states of the Fe center and shed light on the nature of redox events (either metal- or ligand-based) at each charge transfer step. Understanding charge distribution may provide further ideas for maximizing redox potentials and stability by ligand tuning with different functional groups of ligands. It is worthy to note that in this work we considered only thermodynamic properties of these complexes that determine the capacity of the RFBs. Indeed, reactivity or transport kinetics may also have impact on the performance but not on the capacity of RFBs.

FIGURE 1

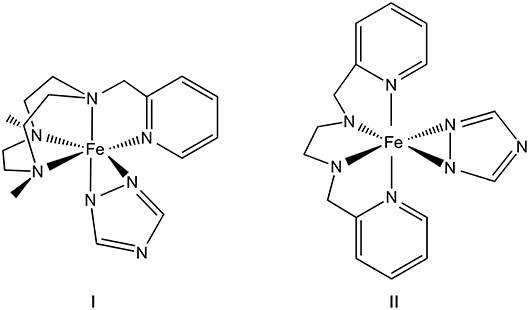
Figure 1. Structures of complex I, Fe(^Me2Pytacn)(C₂N₃H₂); and II, Fe(H₂pmen)(C₂N₃H₂), where ^Me2Pytacn=1-(2'-pyridylmethyl)-4,7-dimethyl-1,4,7-triazacyclononane, H₂pmen=N,N′-bis(2-pyridylmethyl)ethylenediamine, and C₂N₃H₂ = 1,2,4-triazole.

In summary, we found that these complexes exhibit six theoretical redox events in the +4 → −2 range of charge states, while also maintaining their geometrical structures. In the higher charge states +4 → +1, the Fe center is hexacoordinated with two Fe–N_triazole bonds, while only one such bond is found in the lower 0 → −2 charge states of both complexes. Analyses of the spin and charge densities revealed that the oxidation states of the Fe center in both complexes change from the highest +4 to the lowest +1 during the whole charge transfer series. Overall, the redox performance of the two complexes was found to be similar in the +4 → +1 charge states with some differences in the 0 → −2 range. The OCV values, which can potentially be accessed experimentally in the EW of acetonitrile (MeCN) with addition of ionic liquids (ILs), can reach as high as 5.09 and 6.14 V for complexes I and II, respectively.

It is important to mention that the choice of these two specific complexes may not necessarily be ideal given the complexity of a real RFB system, wherein other factors should also be considered, such as transport kinetics, solubility of the active species, reversibility, etc. Instead, in this work we focus on the investigation of the changes in the geometries as well as in the redox properties occurring upon charge transfer within the wide range of charge states. This provides us with an opportunity to assess viability of the proposed principle, which could further be used to design better charge carriers for RFBs. A better understanding of the design principles can help guide the synthesis and selection of charge carrier candidates for the ultimate use in RFBs leading to improved energy storage capacities, cyclability, and lower overall cost.

Methodology

The reduction potentials of the proposed complexes were computed using the revised Born-Haber cycle, described elsewhere [47], in which all reduction steps are referenced to a calculated absolute half-cell potential of a ferrocene couple, i.e., Fc⁰ + Aⁿ → Fc⁺ + Aⁿ⁻¹, as opposed to an experimental standard reference electrode, such as the standard hydrogen electrode (SHE) or the saturated calomel electrode (SCE). This approach has recently been applied in a systematic study of Fe-complexes across a wide range of charge states [48]. All calculations were carried out with Gaussian 09 software package (Version D.01) [49]. The PBE functional [50, 51] was utilized as it does not require the application of a correction term to the theoretical reduction potentials, as suggested previously [47]. Specifically, in contrast to the generalized gradient approximation (GGA) PBE functional, hybrid functionals like B3LYP require a consistent shift (−0.48 V) for various transition metal coordination compounds [47]. It has been shown that the PBE functional provides good results for several early-, middle-, and late-transition metal complexes including Fe complexes with high correlation between calculated and experimental values (R² = 0.97) [47], thus making it possible to predict OCV values. In addition, recent studies [52] have revealed that the PBE functional was less likely to show artificial charge separation in complexes with redox non-innocent ligands. The LANL2DZ effective core potential basis set [53] was employed for Fe, the 6-311G(d) basis set was used for C and N, and 6-31G(d) was used for H atoms. Geometry optimizations of the studied complexes with different spin states (Tables S1, S2) for a particular charge state were performed both in a gas phase and MeCN solvent (dielectric constant is 36.64) using the self-consistent reaction field approach based on the integral equation formalism of the polarized continuum model (PCM) [54–56], as implemented in Gaussian 09 [57]. The geometrical structures obtained in the PCM environment were found to be qualitatively identical to the gas-phase geometries with only minor variations that can be neglected. Frequency calculations were performed to ensure that the optimized geometries represented minima along the potential energy surface for each charge state of both complexes.

To understand electronic structure changes occurring in the +4 → −2 range, we employed Mulliken spin density analysis and the AdNDP [58] electron density partitioning algorithm, which has previously been used to decipher complicated chemical bonding patterns of various transition-metal containing clusters and molecules [59, 60]. Mulliken spin densities of the studied complexes were found to have similar values in both environments (gas-phase or MeCN) at each charge state. Combination of both methods enabled determination of the nature of the redox event (metal- or ligand-based), as well as identification of the oxidation state of the metal center. AdNDP calculations were performed based on a density matrix taken from the NBO5.9 [61, 62] calculations at the same level of theory as the geometry optimizations. The choice of the NBO version was not found to qualitatively affect the results of the AdNDP localization algorithm. Previously, AdNDP was shown to be insensitive to the level of theory or the basis set used [63]. The Molekel 5.4.0.8 program [64] was used for molecular orbitals visualization of the AdNDP results.

Results and Discussion

Proposed Design Principle

As mentioned earlier, the proposed approach is based on the combined utilization of two different types of ligands, which can potentially stabilize complexes both in low and high charge states. Herein, we tested it in the example of two specific compounds I and II (Figure 1). Both designed complexes are composed of two moieties, which were previously shown to be capable of stabilizing transition metals in either low or high oxidation states. By pushing the limit for high oxidation and charge states, which could result in larger values of redox potentials, one can achieve higher OCV values and overall energy density going through all charge states. We chose to exploit two structural motifs, which are used in highly efficient multi-electron water oxidation catalysis [65, 66]. Specifically, ^Me2Pytacn (1-(2′-pyridylmethyl)-4,7-dimethyl-1,4,7-triazacyclononane) and mep (N,N′-dimethyl-N,N′-bis-(2-pyridylmethyl)-ethane-1,2-diamine) ligands were previously used in [Fe(OTf)₂(^Me2Pytacn)] and [Fe(OTf)₂(mep)] complexes, which oxidize water with higher activity than the tetramido macrocyclic ligand complexes [65] known to catalyze various technologically important organic reactions [67, 68]. The most interesting feature of these complexes is their ability to stabilize Fe in its rare high oxidation states of +4 and +5 during the catalytic cycle of water oxidation [65, 66]. Hence, in this work we employed ^Me2Pytacn and H₂pmen ligands (H₂pmen as a lighter analog of mep, in which methyl groups at the imine nitrogens are substituted by hydrogens) as potential candidates to promote high oxidation states of Fe within their high charge states.

Utilization of these tetradentate nitrogen-based ligands leaves two available positions at the metal center, which can be coordinated with some other ligands to stabilize low charge states. Choosing between two monodentate and one bidentate ligand to achieve this goal, the latter one is preferred since the potential loss of even one of the two monodentate ligands may lead to reversibility issues. Hence, we were inspired by the 1,2,4-triphosphacyclopentadienyl bidentate ligand (C₂P₃H₂), which has two phosphorous atoms available for coordination as σ donors, while also being a potential π acceptor due to the presence of π aromatic system. Heavier analog of C₂P₃H₂, i.e., C₂P₃tBu₂ ligand has been previously shown to stabilize low oxidation state transition metal complexes, i.e., [{Sc(C₂P₃tBu₂)₂}₂] was described as a mixed oxidation state complex containing both Sc(I) and Sc(III) centers [69]. To keep the same type of coordinated atoms and bonding interactions around the Fe center, we replaced all P atoms by lighter N atoms, and thus used a 1,2,4-triazole ring (C₂N₃H₂) as a second ligand. Altogether, the resulting complexes I, Fe(^Me2Pytacn)(C₂N₃H₂), and II, Fe(H₂pmen)(C₂N₃H₂), are anticipated to exhibit both high and low oxidation states of the Fe center, thus promoting large theoretical OCV values, while potentially avoiding large structural reorganizations within the charge transfer series.

In attempting to design efficient charge carriers capable of operating within multiple charge states, one also needs to consider the limitation of EW, in which both low and high charge states could be experimentally accessible. In this work, we use MeCN as a solvent of choice due its wide EW, which is greater than that of water thus providing an opportunity to access various redox events. From an experimental standpoint, this solvent is also a good option due to its low viscosity and reasonable cost [70]. As reported previously [71], the EW of MeCN can further be expanded by using various ILs. For instance, introduction of tris(n-hexyl)tetradecylphosphonium trifluorotris(pentafluoroethyl)phosphate ([P₆₆₆₁₄][FAP]) can increase the EW of MeCN from {−2.90 V; 2.60 V} up to {−3.10 V; 3.40 V} [71]. In principle, such expansion can significantly aid in the investigation of compounds that are known to oxidize at high potentials, thus enabling cyclic voltammetry (CV) studies that may otherwise be limited due to the decomposition of the solvent.

Reduction Potentials

Overall, reduction potentials of complex I and II are found to have similar values in their +4 → 0 charge states, whilst some differences are observed at each redox event in the lower 0 → −2 range (Table 1).

TABLE 1

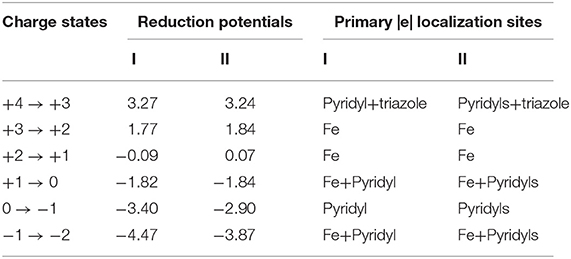
Table 1. Theoretical reduction potentials (in V) of complexes I and II relative to Fc⁰/Fc⁺ in MeCN in the +4 → −2 range of charge states, and their primary electron localization sites within each reduction step.

As expected, both proposed complexes can get oxidized up to the +4 charge state, producing rather high reduction potentials. These findings demonstrate the fact that both ^Me2Pytacn and H₂pmen ligands can indeed act as those capable of stabilizing high charge states, and likely, high oxidation states of Fe. It is important to note that the +4 → +3 reduction event may be experimentally accessible only with the help of ILs, such as [P₆₆₆₁₄][FAP], which could expand the oxidative window of MeCN up to 3.4 V [71]. By comparing the reduction potentials of these two complexes in their lower 0 → −2 charge states, it is clear that complex I has more negative values at each reduction step. As will be shown later, this difference can be explained by the difference in π acceptor capacities of the ligands in these charge states.

Considering the limits of the EW of MeCN [71], the +3 → 0 charge states are expected to be experimentally accessible for both complexes. Expansion of the EW of MeCN by introduction of ILs [71] can help access the +4 → 0 charge states of complex I, and the +4 → −1 charge states of complex II. Overall, considering the OCVs of these complexes in the + 4 → −2 range (Table 2), complex I has the larger value (7.74 vs. 7.11 V). However, considering boundaries of the EW of MeCN (3.59 vs. 3.68 V) or MeCN doped with ILs (5.09 vs. 6.14 V), complex II should be a better candidate to harvest/release more electrons, thus holding promise for RFBs with higher energy densities.

TABLE 2

Table 2. OCV and Σ values of complexes I and II.

We also report the sums of all reduction potentials (∑) within various EWs, which are proportional to the energy density of RFBs. In principle, if it is experimentally possible to connect batteries in series and make use of all reduction potentials within the entire charge transfer series, then even higher voltages can be realized. Specifically, Σ_full value, defined as a sum of all reduction potentials within the +4 → −2 range, can get as high as 13.76 and 14.82 V for complex I and II, respectively. Due to the low reduction potential values associated with the +3 → +2 step, the OCV_MeCN and Σ_MeCN values of these complexes are very similar. In contrast, Σ_MeCN+IL values of complex I (6.95 V) and II (9.89 V) are appreciably higher than their corresponding OCV_MeCN+IL values (5.09 and 6.14 V).

Let us compare OCV values of the studied complexes with the corresponding values of charge carriers employed in commercially available RFB systems. For instance, OCV values of one of the most developed aqueous all-vanadium RFB [72, 73] (1.35 V) or zinc-bromine hybrid RFB (1.85 V) [74], which offers one of the highest cell voltages due to the release of two electrons per atom of zinc, are appreciably lower than that of complex II in the EW of MeCN (OCV_MeCN = 3.68 V). OCV values of aqueous RFBs are principally lower than those of non-aqueous systems because the expanded EW of the organic solvent provides an opportunity to access redox events outside the EW of water. By comparing the OCVs of complexes I and II to the previously reported non-aqueous systems, it is also evident that they are higher than those of M-acetylacetonates, e.g., Ru(acac)₃ (1.75 V) [75], V(acac)₃ (2.20 V) [34], Cr(acac)₃ (3.40 V) [37]. Since complex II has two pyridyl moieties, one should compare it to the previously reported redox potentials of the M(bpy)₃ and M(tpy)₂ complexes (M=Fe, Ru) (vs. Fc⁰/Fc⁺) in the +3 → −1 charge states [76]. Within this range, the OCV value of complex II (4.74 V) is also higher than those of Fe(bpy)₃ (2.71 V [77, 78] and 2.80 V [76]), Ru(bpy)₃ (2.88 V) [79, 80], Fe(tpy)₂ (3.14 V) [76], and Ru(tpy)₂ (3.24 V) [81–83]. Indeed, the expansion of the EW by ILs could further increase the OCV values of all complexes. For example, as seen from Table 1, accessibility of the +4 charge state of complex II can result in the increase of the OCV by 1.4 V, i.e., due to the reduction potential value of the +4 → +3 redox event. Overall, it is clear that the OCV values of the proposed complexes are higher than those of the existing charge carriers, thus justifying the proposed approach. Obviously, due to the high number of redox events accessible within the EW of MeCN expanded by ILs (4 and 5 in the cases of complexes I and II, respectively) as well as their high OCV and Σ values, such systems hold promise for RFBs with high energy densities.

Structural Stability

As mentioned earlier, geometrical stability is a critical aspect of charge carriers needed for reversible redox processes and cyclability of RFBs. Among the wide range of charge states from +4 to −2 being considered, no drastic geometrical changes were observed. Specifically, the oxidative limit of +4 was chosen because complex I was found to exhibit an appreciable structural change at the higher +5 charge state, i.e., oxidation of the triazole ring resulting in the breaking of one of the C–N bonds. The considered anodic limit was set to −2 due to the detachment of the triazacyclononane ligand of complex I at the hypothetical −3 charge state resulting in the complete loss of coordination. Since the geometrical changes for complex I are generally similar to those of complex II (Figure S1), for brevity of discussion Figure 2 illustrates trends of the Fe–N bond distances of complex I for the range of the +4 → −2 charge states. The detailed numbers for both complex I and II are tabulated in Table S3 and all their geometries in each charge state are illustrated in Figures S2, S3.

FIGURE 2

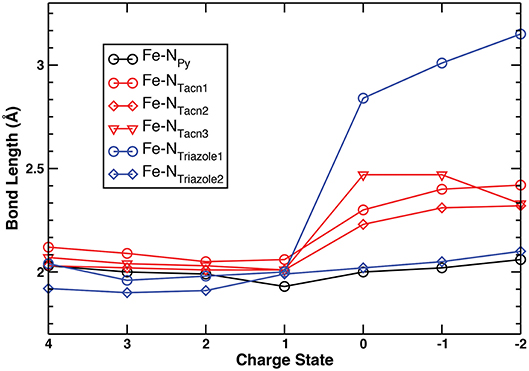
Figure 2. Fe–N bond lengths of the pyridyl, triazacyclononane, and triazole moieties of complex I in the +4 → −2 range of charge states.

No appreciable geometrical changes of any of the Fe–N bonds are observed in the +4 → +1 range of states (Table S3, Figures S1–S3) for both complexes (standard deviation is up to 0.04). At the 0 charge state, one of the nitrogen atoms of the triazole ring tilts away from the metal center within the same plane (2.84 and 2.89 Å for complexes I and II, respectively), thus losing its coordination (Figures S2, S3). However, the bidentate triazole ring remains connected to the metal center with one Fe–N bond, thus avoiding a complete detachment. Such “off” mode of this N atom is preserved across the series upon further reductions with an increasing Fe–N_Triazole1 distance, up to 3.15 Å and 3.16 Å at the −2 charge state for complexes I and II, respectively while maintaining one short Fe–N bond. This increase is accompanied by simultaneous tilting and twisting of the triazole ring out of the initial plane at the lower charge states +1 → −2. At the same time, Fe–N_Triazole2 distance slightly increases although still keeping its coordination with Fe (from 2.02 Å at 0 charge state up to 2.10 Å at −2 for complex I, and from 1.95 Å at 0 charge state up to 2.27 Å at −2 for complex II). The Fe–N_pyridyl distances get only slightly longer in the +1 → −2 charge states (by up to 0.13 and 0.05 Å for complexes I and II, respectively). However, the increases in Fe–N_Tacn bond distances of complex I (by up to 0.46 Å) and Fe–N_En distances in complex II (by up to 0.44 Å) are more pronounced. Nevertheless, the molecular frameworks of both complexes are still preserved even at the extreme −2 state (Figures S2, S3), thus demonstrating that they are potentially capable of restoring their hexacoordinate geometries upon oxidation. Overall, the geometry of complexes I and II can be preserved by switching “on” with bidentate mode in high charge states and switching “off” with monodentate mode in low charge states.

Spin and Charge Density

To gain further insight into the electronic structure changes occurring during the charge transfer within the series, we employed Mulliken spin density analysis (Figure 3, Figure S4, Tables S4, S5) in conjunction with the AdNDP method (Tables S6–S19, Figures S5–S10) for both complexes. Considering trends across the series one can deduce the nature of the redox event (metal- or ligand-based), as well as identify the oxidation state of the metal center.

FIGURE 3

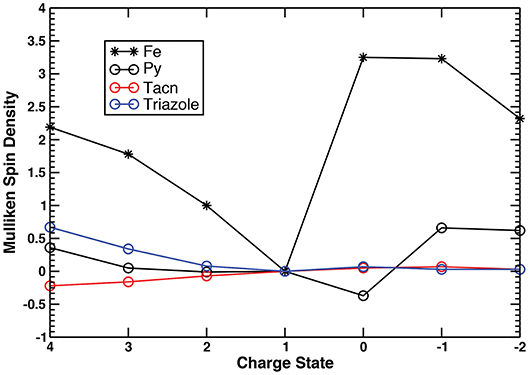
Figure 3. Mulliken spin densities on the metal center, pyridyls, triazacyclononane, and triazole moieties of complex I in the +4 → −2 range of charge states.

Similar changes in the Fe–N bond lengths of both complexes across the +4 → −2 charge states are supported by qualitatively similar electron localization schemes (Table 1, Tables S6–S19). For brevity of discussion, we will focus on complex I to describe its electronic structure changes, while adding remarks on the redox performance of complex II if it is different from that of complex I (see Tables S13–S19 for the detailed description of chemical bonding of complex II). Considering the +1 charge state as a starting point, first we describe a redox behavior in the high (+4 → +1) and, afterwards, in the lower (+1 → −2) charge states. The +1 charge state (referred to as [complex]⁺¹ hereafter) corresponds to the closed-shell low-spin ground state electronic configuration of a Fe²⁺ (3d⁶) system, hence the Mulliken spin densities on all fragments are equal to zero (Tables S4, S5). The occupation numbers (ON) values of the three d-type lone pairs (LPs) on Fe (Figure S5a) are in excellent agreement with this assignment, showing the d^5.76 configuration for complex I (Tables S9, S16). As expected based on the Fe–N bond distances, there are six two-center two-electron (2c−2e) Fe–N σ bonds with high ON values (1.88–1.96 |e|) responsible for the hexacoordinate coordination of Fe (Figure S5c). Besides the 2c−2e C–C and C–H σ bonds, constituting framework of the complex I, there is also one s-type LP on the non-coordinating N atom of the triazole ligand (N_Triazole3) with ON=1.91 |e| (Figure S5b), and six delocalized π bonds with ON=1.91–2.00 |e|, i.e., three six-center two-electron (6c−2e) π bonds found over the pyridyl moiety (Figure S6a) and three five-center two-electron (5c−2e) π bonds over the triazole ring (Figure S6b).

Due to the similar oxidative power of the ^Me2Pytacn and H₂pmen ligands, both complexes exhibit similar redox performances in the +4 → +1 charge states (Table 1). Detachment of one electron from the singlet [complex]⁺¹ (from the d_yz orbital, Figure S5a) produces a doublet [complex]⁺² species with the Fe³⁺ center (d^4.93 configuration, Table S8). The Mulliken spin densities as well as ON values of the AdNDP bonds show no appreciable changes on any other fragments, except for the metal center, hence, the +2 → +1 step is characterized as a pure metal-based reduction event. Further electron detachment produces a triplet [complex]⁺³, where one electron is removed from the d_xy orbital of Fe (Figure S5a), thus resulting in the Fe⁴⁺ metal center with d^3.96 configuration (Table S7). Some increase (0.34 |e|) in Mulliken spin densities on the triazole ring of [complex]⁺³ in comparison to [complex]⁺² is in excellent agreement with the smaller ON values of the s-type LP of N_Triazole3 (1.90 |e| vs. 1.80 |e|) and one of the 5c−2e π bonds (1.84 |e| vs. 1.76 |e|), thus pointing to the partial oxidation of the triazole in [complex]⁺³. Subsequent electron removal slightly changes the d configuration of Fe (d^3.75) keeping the Fe⁴⁺ oxidation state in [complex]⁺⁴. Simultaneous oxidation of pyridyl and triazole fragments is confirmed by both spin and charge density analyses (Tables S4, S6). Specifically, the ON of one of the 6c−2e π bonds with two nodal planes of pyridyl (Figure S6b) drops from 1.92 |e| to 1.66 |e|, and the ON of the LP on N_Triazole3 (Figure S5b) decreases from 1.80 |e| to 1.63 |e|. Similar behavior is observed for complex II at the +4 → +3 step, though its lower values of Mulliken spin density (1.57) and higher d electron configuration on metal center (3.86) at the +4 charge state suggests that the catalyst-inspired ligand of complex I is capable of promoting higher oxidation states of the metal center than complex II (Tables S5, S13). Overall, both complexes hold promise to be stable at high charge states, involving high oxidation states of Fe, thus validating our initial assumptions.

Although exhibiting similar redox performances in the +4 → +1 range, complexes I and II have more differences in their lower charge states +1 → −2. As noted before, addition of one electron to the singlet [complex]⁺¹ results in breaking the Fe–N_triazole1 bond (LP is formed on the N_triazole1 atom instead of the bond, Figure S7b) and small increase of the Fe–N_Tacn distances (Figure 2). This geometric change is associated with the formation of a quartet [complex]⁰ species. The +1 → 0 event is characterized as a simultaneous reduction of the Fe center and pyridyl fragment through the formation of a delocalized bond over the pyridyl fragment and metal center (Figure S7c). The negative value of the Mulliken spin density on pyridyl (−0.37) is due to the polarization effect, in excellent agreement with the increased beta electron density on the pyridyl moiety as well as somewhat increased d electron configuration (d^6.43) on the Fe center, as evident from the AdNDP calculations (Table S10). Thus, [complex]⁰ can be considered as the one with an intermediate oxidation state of Fe, i.e., Fe^2+/1+. Increase of the Fe–N_Tacn distances leads to a more ionic character of bonding between triazacyclononane moiety and the metal center. In fact, the 2c−2e Fe–N_Tacn σ bonds could also be viewed as three direct LPs of N atoms pointing toward Fe (Table S10, Figure S7a). Their ON values are similar to those of the Fe–N_Tacn σ bonds, thus supporting ionic character of this bonding. Importantly, the Fe–N_Tacn bond elongation does not perturb the overall geometry of the complex, thus holding potential for these Fe–N_Tacn σ bonds to be restored upon oxidation. Similar reduction pattern is observed for complex II, although with a low-spin electron configuration (doublet), which exhibits smaller Fe–N bond distance increase at the +1 → 0 step as compared to the complex I (Table S3). As opposed to complex I, complex II exhibits smaller d electron configuration suggesting smaller degree of metal reduction (d^6.23) and larger electron delocalization over the pyridyl moieties. Further reduction of the [complex]⁰ proceeds with the formation of the quintet [complex]⁻¹ species, as confirmed by somewhat increased Fe–N bond distances (Figure 2). Mulliken spin density on the pyridyl moiety (0.66) is associated with its reduction, in agreement with the formation of the additional 6c−1e π* bond (Table S11, Figure S8) over the pyridyl fragment (α electron density). Thus, the 0 → −1 event is characterized as a primary reduction of the pyridyl ligand while still keeping the intermediate oxidation state of Fe between 2+ and 1+ (d^6.62). In contrast, due to the presence of the second pyridyl moiety, complex II at the −1 charge state has two electrons occupying antibonding π* orbitals over the pyridyls (one electron on each, Figure S9). These electrons are antiferromagnetically coupled with two d-electrons of the Fe center, thus resulting in a lower-spin triplet state (Table S18) and formal Fe²⁺ oxidation state (d^5.87). The last reduction event of complex I (−1 → −2) is also accompanied by the simultaneous reduction of Fe (major, population of beta density of the d${}_{\text{z}}^2$ LP of Fe) and pyridyl moiety (minor), resulting in a higher d electron configuration (d^7.39) that accounts for the lowest oxidation state of Fe within the series, i.e., Fe¹⁺. The quartet ground state of the [complex]⁻² stems from the two unpaired d-electrons (${\text{d}}_{\text{xy}}\text{ and }{\text{d}}_{\text{x}}{}^2-{\text{y}}^2$) on Fe and one delocalized 6c−1e π* bond (Table S12). In contrast, complex II has smaller d-electron density on Fe in complex II (d^5.89), and more delocalized bonding via formation of thirteen-center one-electron (13c−1e) π* bond involving two pyridyls and the metal center (Figure S10), while still keeping the formal oxidation state of +2 on Fe (Table S19). Overall, comparing two complexes in their low +1 → −2 charge states, one can see that the combination of the ^Me2Pytacn and triazole ligands of complex I promotes a stabilization of the lower oxidation states of Fe (Fe¹⁺) as compared to complex II, where the H₂pmen and triazole couple can promote only an intermediate Fe^2+/1+ oxidation state. This difference is reflected in the greater negative values of reduction potentials of complex I as compared to complex II in the 0 → −2 charge states.

Summary and Concluding Remarks

Herein, we propose a design principle for charge carriers that could be used in RFBs based on combining ligands capable of stabilizing both high and low oxidation states of metal centers that could promote multiple redox events and high OCV values. The choice of the ligands is based on their ability to stabilize transition metals in unusually high (up to 5+) and low (1+) oxidation states due to the simultaneous presence of the σ donor as well as π acceptor groups. Specifically, two theoretically designed complexes Fe(^Me2Pytacn)(C₂N₃H₂) (I) and Fe(H₂pmen)(C₂N₃H₂) (II), are calculated to exhibit up to four/five redox events within the EW attainable by MeCN with the addition of ILs, such as [P₆₆₆₁₄][FAP]. Spin and charge density analyses confirm the appearance of the high Fe⁴⁺ and low Fe¹⁺ oxidation states in the charge states +4 → −2. Both complexes hold promise to be stable in their highest +4 charge state, though complex I was found to be capable of oxidizing Fe slightly better than complex II. Similar oxidative power of the catalyst-inspired ^Me2Pytacn and H₂pmen ligands explains their comparable redox performance in the high charge states with very similar reduction potential values. Although the nature of the redox events in the lower +1 → −2 is also similar in both complexes, different electronic ground states, delocalization patterns, and oxidation states of Fe are noticed. Due to the smaller number of π acceptor moieties, complex I was found to stabilize lower oxidation states of Fe (Fe¹⁺) than complex II (intermediate Fe^2+/1+) in these states. The difference in the redox behaviors is reflected in the greater negative values of reduction potentials of complex I as compared to complex II in the 0 → −2 charge states. Overall, the OCV values of complexes I and II can reach rather high values (5.09 and 6.14 V in the EW of MeCN expanded by the addition of ILs, i.e., {−3.10 V to 3.40 V}). The OCV values of the proposed systems are found to be significantly higher than those of aqueous systems (such as all-vanadium and zinc-bromide), as well as non-aqueous M-acetylacetonates, such as (Ru(acac)₃, V(acac)₃, Cr(acac)₃), and pyridyl-containing M(bpy)₃ and M(tpy)₂ systems (M=Fe, Ru) in their respective +3 → −1 charge states. No appreciable geometrical changes of any of the Fe–N bonds were observed in the +4 → +1 range of states of both complexes, indicating strong stability of complexes in those states. Switching off one of the two Fe–N_Triazole bonds and elongation of the Fe–N_Tacn and Fe–N_En distances occurred in the lower +1 → −2 range, while still holding potential for these σ bonds to be restored upon oxidation. As a result, these two complexes show promise for the rational design of charge carriers with high OCVs and multiple redox events, thus giving prospects for RFBs high energy density.

It is worth mentioning that although the two novel complexes proposed in this study do exhibit multiple redox events and high OCV values, before they are employed as charge carriers in commercial RFBs, studies of compounds solubility, transport kinetics across the charge states, reversibility, proper membranes, and electrodes, as well as other techno-economical parameters are needed. However, while recognizing the importance of all these factors, in this work we illustrated the viability of the design principle based on the utilization of catalysts-inspired ligands to stabilize high charge states (oxidation states) as well as triazole ligands for stabilizing low oxidation states of the metal center while keeping the molecular framework stable. The proposed approach can serve as a more general guideline for experimentalists to design charge carriers for next-generation RFBs by exploring various combinations of ligands capable of operating in both low and high charge states to produce high OCV values.

Author Contributions

IAP, EB, and PY designed the project, carried out the calculations, analyzed the results, and wrote the manuscript. BD and RM discussed the results and reviewed the manuscript.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

This work was supported by the Laboratory Directed Research and Development (LDRD) program of Los Alamos National Laboratory under project number 20170046DR. This work was supported by the US Department of Energy through the Los Alamos National Laboratory. Los Alamos National Laboratory is operated by Triad National Security, LLC, for the National Nuclear Security Administration of U.S. Department of Energy (Contract No. 89233218CNA000001). IAP acknowledges the support from a Director's Postdoctoral Fellowship and J. Robert Oppenheimer Distinguished Postdoctoral Fellowship at Los Alamos National Laboratory.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2018.00141/full#supplementary-material

Electronic Supplementary Information (ESI). Geometrical changes, Mulliken spin density, detailed AdNDP analyses, relative free energies of complexes with different spin states, and Cartesian coordinates of complexes I and II in the +4 → −2 range of charge states. See doi: 10.1039/x0xx00000x.

Footnotes

1. ^https://redflow.com

2. ^http://www.primuspower.com/en/

3. ^http://www.americanvanadium.com

4. ^https://energy.gildemeister.com/en/

References

1. U. S. Energy Information Administration. Annual Energy Review. Washington, DC: U.S. Department of Energy (2014).

2. International Energy Agency. World Energy Outlook. Paris: International Energy Agency (2012).

3. Gong K, Fang Q, Gu S, Li SFY, Yan Y. Nonaqueous redox-flow batteries: organic solvents, supporting electrolytes, and redox pairs. Energy Environ Sci. (2015) 8:3515–30. doi: 10.1039/C5EE02341F

CrossRef Full Text | Google Scholar

4. Soloveichik GL. Flow batteries: current status and trends. Chem Rev. (2015) 115:11533–58. doi: 10.1021/cr500720t

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Ogunsolu OO, Wang JC, Hanson K. Increasing the open-circuit voltage of dye-sensitized solar cells via metal-ion coordination. Inorg Chem. (2017) 56:11168–75. doi: 10.1021/acs.inorgchem.7b01531

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Huang Q, Wang Q. Next-generation, high-energy-density redox flow batteries. ChemPlusChem (2015) 80:312–22. doi: 10.1002/cplu.201402099

CrossRef Full Text | Google Scholar

7. Yang ZG, Zhang JL, Kintner-Meyer MCW, Lu XC, Choi DW, Lemmon JP, et al. Electrochemical energy storage for green grid. Chem Rev. (2011) 111:3577–613. doi: 10.1021/cr100290v

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Dunn B, Kamath H, Tarascon JM. Electrical energy storage for the grid: a battery of choices. Science (2011) 334:928–35. doi: 10.1126/science.1212741

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Thaller LH. Electrically rechargeable redox flow cells. In: The 9th Intersociety Energy Conversion Engineering Conference Proceedings. San Francisco, CA (1974). p. 924–8.

Google Scholar

10. Ferrigno R, Stroock AD, Clark TD, Mayer M, Whitesides GM. Membraneless vanadium redox fuel cell using laminar flow. J Am Chem Soc. (2002) 124:12930–1. doi: 10.1021/ja020812q

PubMed Abstract | CrossRef Full Text | Google Scholar

11. de Leon CP, Frias-Ferrer A, Gonzalez-Garcia J, Szanto DA, Walsh FC. Redox flow cells for energy conversion. Power Sourc J. (2006) 160:716–32. doi: 10.1016/j.jpowsour.2006.02.095

CrossRef Full Text | Google Scholar

12. Lu YH, Goodenough JB, Kim Y. Aqueous cathode for next-generation alkali-ion batteries. J Am Chem Soc. (2011) 133:5756–9. doi: 10.1021/ja201118f

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Skyllas-Kazacos M, Chakrabarti MH, Hajimolana SA, Mjalli FS, Saleem M. Progress in flow battery research and development. J Electrochem Soc. (2011) 158, R55–79. doi: 10.1149/1.3599565

CrossRef Full Text | Google Scholar

14. Schwenzer B, Zhang JL, Kim S, Li LY, Liu J, Yang ZG. Membrane development for vanadium redox flow batteries. ChemSusChem (2011) 4:1388–406. doi: 10.1002/cssc.201100068

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Wang YR, Wang YG, Zhou HS. ALi–liquid cathode battery based on a hybrid electrolyte. ChemSusChem (2011) 4:1087–90. doi: 10.1002/cssc.201100201

CrossRef Full Text | Google Scholar

16. Weber AZ, Mench MM, Meyers JP, Ross PN, Gostick JT, Liu QH. Redox flow batteries: a review. J Appl Electrochem. (2011) 41:1137–64. doi: 10.1007/s10800-011-0348-2

CrossRef Full Text | Google Scholar

17. Li XF, Zhang HM, Mai ZS, Zhang HZ, Vankelecom I. Ion exchange membranes for vanadium redox flow battery (VRB) applications. Energy Environ Sci. (2011) 4:1147–60. doi: 10.1039/c0ee00770f

CrossRef Full Text | Google Scholar

18. Brushett FR, Vaughey JT, Jansen AN. An all-organic non-aqueous lithium-ion redox flow battery. Adv Energy Mater. (2012) 2:1390–6. doi: 10.1002/aenm.201200322

CrossRef Full Text | Google Scholar

19. Leung P, Li X, Ponce de León C, Berlouis L, Low C, Walsh FC. Progress in redox flow batteries, remaining challenges and their applications in energy storage. RSC Adv. (2012) 2:10125–56. doi: 10.1039/C2RA21342G

CrossRef Full Text | Google Scholar

20. Kim KJ, Park MS, Kim JH, Hwang U, Lee NJ, Jeong G, et al. Novel catalytic effects of Mn₃O₄ for all vanadium redox flow batteries. Chem Commun. (2012) 48:5455–7. doi: 10.1039/c2cc31433a

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Wang W, Xu W, Cosimbescu L, Choi DW, Li LY, Yang ZG. Anthraquinone with tailored structure for a nonaqueous metal–organic redox flow battery. Chem Commun. (2012) 48:6669–71. doi: 10.1039/c2cc32466k

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Braff WA, Bazant MZ, Buie CR. Membrane-less hydrogen bromine flow battery. Nat Commun. (2013) 4:2346. doi: 10.1038/ncomms3346

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Luo QT, Li LY, Wang W, Nie ZM, Wei XL, Li B, et al. Capacity decay and remediation of nafion-based all-vanadium redox flow batteries. ChemSusChem (2013) 6:268–74. doi: 10.1002/cssc.201200730

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Liu J, Zhang JG, Yang ZG, Lemmon JP, Imhoff C, Graff GL, et al. Materials science and materials chemistry for large scale electrochemical energy storage: from transportation to electrical grid. Adv Funct Mater. (2013) 23:929–46. doi: 10.1002/adfm.201200690

CrossRef Full Text | Google Scholar

25. Wang W, Luo QT, Li B, Wei XL, Li LY, Yang ZG. Recent progress in redox flow battery research and development. Adv Funct Mater. (2013) 23:970–86. doi: 10.1007/978-3-642-33596-9

CrossRef Full Text | Google Scholar

26. Shin SH, Yun SH, Moon SH. A review of current developments in non-aqueous redox flow batteries: characterization of their membranes for design perspective. RSC Adv. (2013) 3:9095–116. doi: 10.1039/c3ra00115f

CrossRef Full Text | Google Scholar

27. Gu S, Gong K, Yan EZ, Yan YS. A multiple ion-exchange membrane design for redox flow batteries. Energy Environ. Sci. (2014) 7:2986–98. doi: 10.1039/C4EE00165F

CrossRef Full Text | Google Scholar

28. Huskinson B, Marshak MP, Suh C, Er S, Gerhardt MR, Galvin CJ, et al. A metal-free organic–inorganic aqueous flow battery. Nature (2014) 505:195–8. doi: 10.1038/nature12909

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Shen Y, Xu H, Xu P, Wu X, Dong Y, Lu L. Electrochemical catalytic activity of tungsten trioxide- modified graphite felt toward VO${}_2^{+}$/VO${}_2^{+}$ redox reaction. Electrochim Acta (2014) 132:37–41. doi: 10.1016/j.electacta.2014.03.107

CrossRef Full Text | Google Scholar

30. Li L, Kim S, Wang W, Vijaayakumar M, Nie Z, Chen B, et al. A stable vanadium redox-flow battery with high energy density for large-scale energy storage. Adv Energy Mater. (2011) 1:392–400. doi: 10.1002/aenm.201100008

CrossRef Full Text | Google Scholar

31. Gong K, Xu F, Grunewald JB, Ma X, Zhao Y, Gu S, et al. All-soluble all-iron aqueous redox-flow battery. ACS Energy Lett. (2016) 1:89–93. doi: 10.1021/acsenergylett.6b00049

CrossRef Full Text | Google Scholar

32. Matsuda Y, Tanaka K, Okada M, Takasu Y, Morita M, Matsumurainoue T. A rechargeable redox battery utilizing ruthenium complexes with non-aqueous organic electrolyte. J Appl Electrochem. (1988) 18:909–14. doi: 10.1007/BF01016050

CrossRef Full Text | Google Scholar

33. Yamamura T, Shiokawa Y, Yamana H, Moriyama H. Electrochemical investigation of uranium β-diketonates for all-uranium redox flow battery. Electrochim Acta (2002) 48:43–50. doi: 10.1016/S0013-4686(02)00546-7

CrossRef Full Text | Google Scholar

34. Liu QH, Sleightholme AES, Shinkle AA, Li YD, Thompson LT. Non-aqueous vanadium acetylacetonate electrolyte for redox flow batteries. Electrochem Commun. (2009) 11:2312–5. doi: 10.1016/j.elecom.2009.10.006

CrossRef Full Text | Google Scholar

35. Cappillino PJ, Pratt HD, Hudak NS, Tomson NC, Anderson TM, Anstey MR. Application of redox non-innocent ligands to non-aqueous flow battery electrolytes. Adv Energy Mater. (2014) 4:1300566. doi: 10.1002/aenm.201300566

CrossRef Full Text | Google Scholar

36. Sleightholme AES, Shinkle AA, Liu QH, Li YD, Monroe CW, Thompson LT. Non-aqueous manganese acetylacetonate electrolyte for redox flow batteries. Power Sources J. (2011) 196:5742–5. doi: 10.1016/j.jpowsour.2011.02.020

CrossRef Full Text | Google Scholar

37. Liu QH, Shinkle AA, Li YD, Monroe CW, Thompson LT, Sleightholme AES. Non-aqueous chromium acetylacetonate electrolyte for redox flow batteries. Electrochem Commun. (2010) 12:1634–7. doi: 10.1016/j.elecom.2010.09.013

CrossRef Full Text | Google Scholar

38. Kim JH, Kim KJ, Park MS, Lee NJ, Hwang U, Kim H, et al. Development of metal-based electrodes for non-aqueous redox flow batteries. Electrochem Commun. (2011) 13:997–1000. doi: 10.1016/j.elecom.2011.06.022

CrossRef Full Text | Google Scholar

39. Zhang DP, Lan HJ, Li YD. The application of a non-aqueous bis(acetylacetone)ethylenediamine cobalt electrolyte in redox flow battery. Power Sources J. (2012) 217:199–203. doi: 10.1016/j.jpowsour.2012.06.038

CrossRef Full Text | Google Scholar

40. Pratt HD, Hudak NS, Fang XK, Anderson TM. A polyoxometalate flow battery. Power Sources J. (2013) 236:259–64. doi: 10.1016/j.jpowsour.2013.02.056

CrossRef Full Text | Google Scholar

41. Assary RS, Brushettac FR, Curtiss LA. Reduction potential predictions of some aromatic nitrogen-containing molecules. RSC Adv. (2014) 4:57442–51. doi: 10.1039/C4RA08563A

CrossRef Full Text | Google Scholar

42. Kucharyson JF, Cheng L, Tung SO, Curtiss LA, Thompson LT. Predicting the potentials, solubilities and stabilities of metal-acetylacetonates for non-aqueous redox flow batteries using densi. J Mater Chem A (2017) 5:13700–9. doi: 10.1039/C7TA01285C

CrossRef Full Text | Google Scholar

43. Yang C, Nikiforidis G, Park JY, Choi J, Luo Y, Zhang LS, et al. Designing redox-stable cobalt–polypyridyl complexes for redox flow batteries: spin-crossover delocalizes excess charge. Adv Energy Mater. (2018) 2018:1702897. doi: 10.1002/aenm.201702897

CrossRef Full Text | Google Scholar

44. Sevov CS, Fisher SL. Thompson LT, Sanford MS. Mechanism-based development of a low-potential, soluble, and cyclable multielectron anolyte for nonaqueous redox flow batteries. J Am Chem Soc. (2016) 138:15378–84. doi: 10.1021/jacs.6b07638

CrossRef Full Text | Google Scholar

45. Strong H, Krusic PJ, Fillipo JS. Sodium carbonyl ferrates, Na₂[Fe(Co)₄], Na₂[Fe₂(Co)₈], and Na₂[Fe₃(Co)₁₁]. Bis[μ-Nitrido-Bis(Triphenylphosphorus)(1+)] Undeca-Carbonyltriferrate(2-), [(Ph₃P)₂N]₂[Fe₃(Co)₁₁]. Inorg Synth. (1990) 28:203. doi: 10.1002/9780470132593.ch52

CrossRef Full Text | Google Scholar

46. Huang W, Xing D-H, Lu J-B, Long B, Schwarz W, Li J. How much can density functional approximations (DFA) fail? The extreme case of the FeO₄ species. J Chem Theory Comput. (2016) 12:1525–33. doi: 10.1021/acs.jctc.5b01040

PubMed Abstract | CrossRef Full Text | Google Scholar

47. Roy LE, Jakubikova E, Guthrie MG, Batista ER. Calculation of one-electron redox potentials revisited. is it possible to calculate accurate potentials with density functional methods? J Phys Chem A (2009) 113:6745–50. doi: 10.1021/jp811388w

PubMed Abstract | CrossRef Full Text | Google Scholar

48. Popov IA, Mehio N, Chu T, Davis BL, Mukundan R, Yang P, et al. Impact of ligand substitutions on multielectron redox properties of Fe complexes supported by nitrogenous chelates. ACS Omega (2018) 3:14766–78. doi: 10.1021/acsomega.8b01921

CrossRef Full Text | Google Scholar

49. Frisch MJ, Trucks GW, Schlegel HB, Scuseria GE, Robb MA, Cheeseman JR, et al. Gaussian 09 (Revision D.01). Wallingford, CT: Gaussian, Inc (2009).

50. Perdew JP, Burke K, Ernzerhof M. Generalized gradient approximation made simple. Phys Rev Lett. (1996) 77:3865–8. doi: 10.1103/PhysRevLett.77.3865

PubMed Abstract | CrossRef Full Text

51. Perdew JP, Burke K, Ernzerhof M. Generalized gradient approximation made simple. Phys Rev Lett. (1997) 78:1396. doi: 10.1103/PhysRevLett.78.1396

CrossRef Full Text | Google Scholar

52. Milko P, Iron MA. On the innocence of bipyridine ligands: how well do DFT functionals fare for these challenging spin systems? J Chem Theory Comput. (2014) 10:220–35. doi: 10.1021/ct400913z

PubMed Abstract | CrossRef Full Text | Google Scholar

53. Hay PJ, Wadt WR. Ab initio effective core potentials for molecular calculations. Potentials for K to Au including the outermost core orbitals. J Chem Phys. (1985) 82:299–310. doi: 10.1063/1.448975

CrossRef Full Text | Google Scholar

54. Cancès E. A new integral equation formalism for the polarizable continuum model: theoretical background and applications to isotropic and anisotropic dielectrics. J Chem Phys. (1997) 107:3032.

Google Scholar

55. Mennucci B, Cancès E, Tomasi J. Evaluation of solvent effects in isotropic and anisotropic dielectrics and in ionic solutions with a unified integral equation method: theoretical bases, computational implementation, and numerical applications. J Phys Chem B (1997) 101:10506–17.

Google Scholar

56. Cancès E, Mennucci B. New applications of integral equations methods for solvation continuum models: ionic solutions and liquid crystals. J Math Chem. (1998) 23:309–26.

Google Scholar

57. Scalmani G, Frisch MJ. Continuous surface charge polarizable continuum models of solvation. I. general formalism. J Chem Phys. (2010) 132:114110. doi: 10.1063/1.3359469

PubMed Abstract | CrossRef Full Text | Google Scholar

58. Zubarev DY, Boldyrev AI. Developing paradigms of chemical bonding: adaptive natural density partitioning. Phys Chem Chem Phys. (2008) 10:5207–10. doi: 10.1039/b804083d

PubMed Abstract | CrossRef Full Text | Google Scholar

59. Popov IA, Pan F-X, You X-R, Li L-J, Matito E, Liu C, et al. Peculiar all-metal σ-aromaticity of the [Au₂Sb₁₆]⁴⁻ anion in the solid state. Angew Chem Int Ed. (2016) 55:15344–6. doi: 10.1002/anie.201609497

PubMed Abstract | CrossRef Full Text | Google Scholar

60. Popov IA, Jian T, Lopez GV, Boldyrev AI, Wang L-S. Cobalt-centred boron molecular drums with the highest coordination number in the CoB${}_{16}^{-}$ cluster. Nat Commun. (2015) 6:8654. doi: 10.1038/ncomms9654

CrossRef Full Text | Google Scholar

61. Foster JP, Weinhold F. Natural hybrid orbitals. J Am Chem Soc. (1980) 102:7211–8. doi: 10.1021/ja00544a007

CrossRef Full Text | Google Scholar

62. Weinhold F, Landis C. Valency and Bonding: A Natural Bond Orbital Donor-Acceptor Perspective. Cambridge, UK; New York, NY: Cambridge University Press (2005). doi: 10.1017/CBO9780511614569

CrossRef Full Text | Google Scholar

63. Sergeeva AP, Boldyrev AI. The chemical bonding of Re₃Cl${}_9^{2-}$₉ and Re₃Cl revealed by the adaptive natural density partitioning analyses. Comments Inorg Chem. (2010) 31:2–12. doi: 10.1080/02603590903498639

CrossRef Full Text | Google Scholar

64. Varetto U. Molekel 5.4.0.8. (2009).

Google Scholar

65. Lloret-Fillol J, Codola Z, Garcia-Bosch I, Gomez L, Pla JJ, Costas M. Efficient water oxidation catalysts based on readily available iron coordination complexes. Nat Chem. (2011) 3:807–13. doi: 10.1038/nchem.1140

CrossRef Full Text | Google Scholar

66. Acuña-Parés F, Codolà Z, Costas M, Luis JM, Lloret-Fillol J. Unraveling the mechanism of water oxidation catalyzed by nonheme iron complexes. Chem Eur J. (2014) 20:5696–707. doi: 10.1002/chem.201304367

PubMed Abstract | CrossRef Full Text | Google Scholar

67. Costas M, Mehn MP, Jensen MP, Que L Jr. Dioxygen activation at mononuclear nonheme iron active sites: enzymes, models, and intermediates. Chem Rev. (2004) 104:939–86. doi: 10.1021/cr020628n

PubMed Abstract | CrossRef Full Text | Google Scholar

68. Denisov IG, Makris TM, Sligar SG, Schlichting I. Structure and chemistry of cytochrome P450. Chem Rev. (2005) 105:2253–78. doi: 10.1021/cr0307143

PubMed Abstract | CrossRef Full Text | Google Scholar

69. Clentsmith GKB, Cloke FGN, Green JC, Hanks J, Hitchcock PB, Nixon JF. Stabilization of low-oxidation-state early transition-metal complexes bearing 1,2,4-triphosphacyclopentadienyl ligands: structure of [[Sc(P₃C₂tBu₂)₂]₂]; Sc^II or mixed oxidation state? Angew Chem Int Ed. (2003) 42:1038–41. doi: 10.1002/anie.200390267

CrossRef Full Text | Google Scholar

70. Darling RM, Gallagher KG, Kowalski JA, Haac S, Brushett FR. Pathways to low-cost electrochemical energy storage: a comparison of aqueous and nonaqueous flow batteries. Energy Environ Sci. (2014) 7:3459–77. doi: 10.1039/C4EE02158D

CrossRef Full Text | Google Scholar

71. Buzzeo MC, Hardacre C, Compton RG. Extended electrochemical windows made accessible by room temperature ionic liquid/organic solvent electrolyte systems. ChemPhysChem (2006) 7:176–80. doi: 10.1002/cphc.200500361

PubMed Abstract | CrossRef Full Text | Google Scholar

72. Kazacos M, Skyllas-Kazacos M. Performance characteristics of carbon plastic electrodes in the all-vanadium redox cell. J Electrochem Soc. (1989) 136:2759–60. doi: 10.1149/1.2097588

CrossRef Full Text | Google Scholar

73. Kazacos M, Cheng M, Skyllas-Kazacos M. Vanadium redox cell electrolyte optimization studies. J Appl Electrochem. (1990) 20:463–7. doi: 10.1007/BF01076057

CrossRef Full Text | Google Scholar

74. Bryans D, McMillan BG, Spicer M, Wark A, Berlouis L. Complexing additives to reduce the immiscible phase formed in the hybrid ZnBr₂ flow battery. J Electrochem Soc. (2017) 164:A3342–8. doi: 10.1149/2.1651713jes

CrossRef Full Text | Google Scholar

75. Chakrabarti MH, Roberts EPL, Bae C, Saleem M. Ruthenium based redox flow battery for solar energy storage. Energy Convers Manage. (2011) 52:2501–8. doi: 10.1016/j.enconman.2011.01.012

CrossRef Full Text | Google Scholar

76. England J, Scarborough CC, Weyhermüller T, Sproules S, Wieghardt K. Electronic structures of the electron transfer series [M(bpy)₃]ⁿ, [M(tpy)₂]ⁿ, and [Fe(^tbpy)₃]ⁿ (M = Fe, Ru; n = 3+, 2+, 1+, 0:1–): amössbauer spectroscopic and DFT study. Eur J Inorg Chem. (2012) 4605–21. doi: 10.1002/ejic.201200232

CrossRef Full Text | Google Scholar

77. Rao JM, Hughes MC, Macero J. Further studies on the stabilization of high and low oxidation states in aromatic imine ligand complexes of first row transition metals. I. Substituted bipyridine complexes of cobalt and iron. Inorg Chim Acta (1979) 35:L369–73. doi: 10.1016/S0020-1693(00)93402-9

CrossRef Full Text | Google Scholar

78. Chum HL, Rock M, Murakami NY, Jordan I, Rabockai T. Cyclic voltammetry of iron dimine complexes in acetonitrile. J Electroanal Chem. (1977) 76:277–85. doi: 10.1016/S0022-0728(77)80480-4

CrossRef Full Text | Google Scholar

79. Ohsawa Y, DeArmond MK, Hanck KW, Morris DE, Whitten DG, Neveux PE. Spatially isolated redox orbitals: evidence from low-temperature voltammetry. J Am Chem Soc. (1983) 105:6522–4. doi: 10.1021/ja00359a045

CrossRef Full Text | Google Scholar

80. Saji T, Aoyagui S. Polarographic studies on bipyridines complexes: II. correlation between charge-transfer frequencies and oxidation potentials of tris (2,2′-bipyridine) complexes of iron, ruthenium, osmium, cobalt and chromium. Electroanal Chem Interfac Electrochem. (1975) 60:1. doi: 10.1016/S0022-0728(75)80196-3

CrossRef Full Text | Google Scholar

81. Heath GA, Yellowlees LJ, Braterman PS. Spectro-electrochemical studies on tris-bipyridyl ruthenium complexes; ultra-violet, visible, and near-infrared spectra of the series [Ru(bipyridyl)₃]^2+/1+/0/1−. J Chem Soc Chem Commun. (1981) 1981:287. doi: 10.1039/c39810000287

CrossRef Full Text | Google Scholar

82. Berger RM, McMillin DR. Localized states in reduced and excited-state ruthenium(II) terpyridyls. Inorg Chem. (1988) 27:4245–9. doi: 10.1021/ic00296a032

CrossRef Full Text | Google Scholar

83. Wadman SH, Lutz M, Tooke DM, Spek AL, Harte F, Havenith RWA, et al. Consequences of N,C,N′- and C,N,N′-coordination modes on electronic and photophysical properties of cyclometalated aryl ruthenium(II) complexes. Inorg Chem. (2009) 48:1887–900. doi: 10.1021/ic801595m

PubMed Abstract | CrossRef Full Text | Google Scholar