How T Cells Do the “Search for the Needle in the Haystack”

In the body, a T cell is confronted with millions of antigen-presenting cells (APCs) in the search for potentially harmful antigen. To elicit an appropriate immune response, this search has to be performed as fast and as precise as possible. These two requirements, however, are at odds with each other: fast searches lack accuracy, whereas high fidelity decisions are typically time-consuming. Here, we use the archetypical search for the needle in the haystack as an analogy for the T cell's search problem. We provide a statistical framework to quantitatively estimate the constraints of search strategies for rare instances. Particularly, we propose a solution for balancing the demand for high speed with low error rates. It takes advantage of a two-phase search process, which combines a first rapid scan with a second high-fidelity check. Finally, we provide arguments that support a two-phase search model for identification of antigen-positive APCs by T cells.

Introduction

T cells have evolved to launch specific immune responses when they detect peptides derived from potentially harmful intruders. Such peptides are displayed to T cells on the surface of antigen-presenting cells (APCs) via the major histocompatibility complex (MHC) [1]. A particular cognate peptide-loaded MHC (pMHC) might be present on only very few APCs out of tens of millions in the whole body [2]; conversely only very few down to even single T cells specific for a particular cognate antigen are present in an individual [3, 4]. T cells have thus the need (i) to detect very rare instances against immense background, and (ii) to scan as many APCs as possible in a short time, so that the immune system can react to the intruder as fast as possible.

In other words, T cells are challenged with the classical search problem of a rare event, often referred to as the search for the needle in the haystack. What is more, they have to do their job fast enough to avoid that potentially harmful intruders inflict significant damage on the body.

On the molecular level, a specific T cell receptor (TCR), which is expressed exclusively on the surface of one particular T cell clone, has to bind a given pMHC in order to elicit a T cell response. Binding is then translated into biochemical events in the T cells and eventually into an immune response [1]. Notably, only a small fraction of pMHC molecules—as few as 1 to 5 single molecules—on the surface of APCs actually contains peptides from dangerous intruders; the vast majority of peptides—as many as 200,000 [5, 6]—stems from endogenous components that have been captured and processed by APCs along with foreign ones. Identifying cognate antigen at high fidelity hence imposes a huge challenge: if this process was performed at high speed, it could lead to spurious decisions; on the other hand, if it was performed at high precision it would take a long time.

Here, we want to elaborate on some of the conceptual constraints of this statistical search problem. We show that the search for the needle in the haystack massively benefits from a two-phase search approach, which combines a first rapid scan with a second high-fidelity check. This sheds some light on why certain observed features of the T cell's search for antigen might have evolved in particular ways.

Formulating the Stochastic Problem

In analogy to the search for the needle in the haystack, let us suppose a barn full of hay, and the task is to find the proverbial needle. People may come up with different strategies to perform this search: on one end of the spectrum, there are the structured personalities, who start on one corner and search their way through the whole haystack; on the other end, we have the intuitive searchers who randomly start somewhere, without any clear search strategy. But is there an optimum search strategy? This depends on (i) the search question, (ii) the cost function, and (iii) whether there is prior information available, e.g., on the position of the needle.

i) The search question

Before starting the search, the underlying search question has to be specified. As a matter of fact, there is a variety of questions which may be asked in the context of the needle in the haystack problem. Examples include:

• Is there a needle in the haystack?

• How many needles are in the haystack?

• Is there a specific spatial arrangement of needles within the haystack?

The type of question affects the search strategy: for example, it does not make sense to continue the search after finding the needle, if the first question should be answered. In case of T cell activation, we are just beginning to understand how to phrase the search question: while it is undoubted that T cells integrate signals over time and modulate their response accordingly, the underlying mechanisms are not well-understood [7]. Also the recruitment of APCs into the lymph node [8] as well as potential clustering of pMHC at the cell surface [9] will affect a T cell's search process. In this paper, we restrict ourselves to the analysis of the question about the presence of APCs presenting cognate antigen.

ii) The cost function

Optimization problems can be reduced to the task of minimizing or maximizing the cost function. In our case, there is a variety of cost functions which may be considered:

• The total search time

• The rate of false positives or false negatives

• The precision of the counting result

The search problem gets more complicated, if two or more cost functions should be optimized at the same time. In such a multi-objective optimization problem, there is typically no single solution that simultaneously optimizes all cost functions. In other words, the different cost functions may be conflicting. In many cases, however, it is not important to find the global minima of all cost functions; a value below a certain threshold may be sufficient. This multi-objective optimization problem becomes important below, where we discuss the T cell's challenge to harmonize the conflicting needs for both specific and fast identification of antigen.

iii) Additional information

Prior information helps to focus a search. For example, we may ask the owner of the barn about the number of needles in the haystack, their position, how they are spatially distributed, etc. Also during the search, we may learn more about the organization of the haystack, which allows for updating the prior information and modify our search strategy accordingly. Finally, it could be the case that—during our search—additional needles are thrown into the haystack, making the problem dynamic. For the T cells' search problem, priors such as co-stimulating and co-inhibiting signals [10], or cytokines [11] convey additional information about the nature of potential antigens. This modulates the functional outcome of TCR signaling. In addition, the architecture of lymph nodes and T cell migratory patterns have evolved in a way that maximizes the chances of antigen encounter [4, 12]. Despite their importance in the real live scenario, we will neglect such priors in our discussion, as they would further complicate the line of argumentation without affecting the principal arguments.

Different Search Problems

Following our analogy further, the T cell would correspond to the person, who is searching for the needle—i.e., the cognate antigen—and all APCs together make up the haystack; the body corresponds to the barn (Figure 1). As APCs are separate entities, however, we can modify our search problem by splitting the haystack into smaller haybales, each corresponding to a single APC. The task is now to move through the barn, and to test—bale by bale—whether it contains a needle. The average probability of finding an APC bearing agonist pMHC is given by $p=\frac{M}{N}$, with M the number of APCs bearing agonist pMHC and N the total number of APCs. It should be mentioned here that different mechanisms exist that direct T cells and APCs to lymph nodes during infections [4]; i.e., T cells in lymph nodes have to deal only with a subsample of all APCs in the body. However, since T cells roam multiple lymph nodes during their search for antigen and still interact with a great number of APCs, our assumption appears realistic.

FIGURE 1

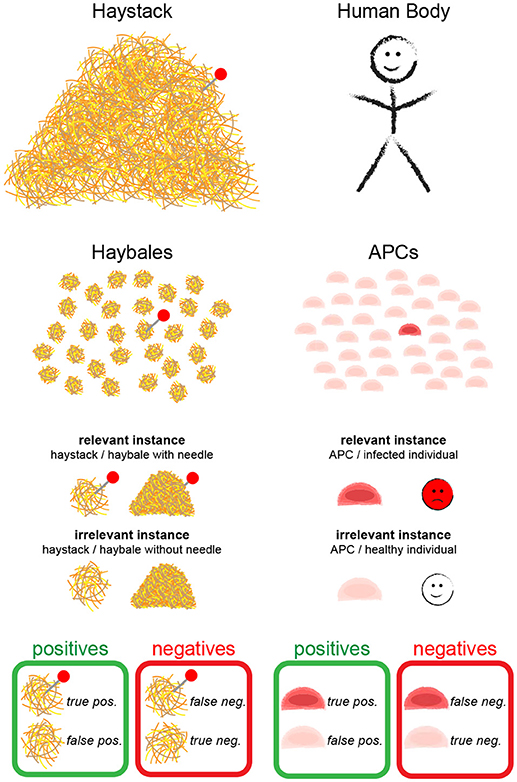
Figure 1. The needle in the haystack problem. Terms and statistical concepts referred to in the text are shown for the hypothetical search of the needle in the haystack (Left) and for the search of a T cell for cognate antigen on APCs (Right).

In the following, we formulate a statistical approach to solve the search for the needle in the haystack. In the main text we confine ourselves to a discussion of the main results; derivations of the formulas are provided as Supplementary Information. During the text, we introduce statistical parameters that are important to quantify the different problems (see Table 1 for an overview). We call a “relevant instance” a scenario which would be detected by an ideal test, and “irrelevant instances” all other cases. Depending on the task, a single haybale—but also the whole haystack—carrying a needle could be a relevant instance.

TABLE 1

Table 1. Statistical parameters.

Let us consider the search question, whether the barn contains haybales with needles. Let the null hypothesis be that there are no haybales with needles; this null hypothesis shall be tested. A straight-forward approach would be an unbiased random search, in which the haybales are classified as needle-positive or -negative. The procedure is stopped after n haybales; if we find k ≥ 1 relevant instances, we reject the null hypothesis, otherwise we keep it.

In order to provide statistically quantifiable arguments, multiple search experiments of this kind shall be performed: we assume many (ideally infinite amounts of) haystacks, some containing haybales with needles, others do not; this experiment allows to determine the four key figures of merit (Figure 1):

• True positives (TP): relevant instances that were correctly detected

• False negatives (FN): relevant instances that were erroneously rejected

• False positives (FP): irrelevant instances that were erroneously detected

• True negatives (TN): irrelevant instances that were correctly rejected

Since no errors for the classification step of single haybales were included up to now, this approach cannot yield any false positive results: if there are no needles, no needles will be detected. In contrast, we might miss haybales containing needles, in particular if they are rare and we do not search long enough. An appropriate measure of the search fidelity is the true positive rate (TPR), also called sensitivity or recall. Maximizing TPR is equivalent to minimizing false negatives, with maximum sensitivity being given by zero false negatives. In other words, at maximum TPR we will find the needle without doubt.

In Figure 2 we show the true positive rate as a function of the number of checked haybales, n, for different values of the probability of finding a relevant instance, p. We neglected here correlations between the haybales, which allowed us to assume a Binomial distribution of events. Naturally, TPR increases with increasing n. Detection becomes unlikely for p ≪ 1, in which case we can approximate TPR ≈ n·p. In other words, for rare relevant instances one needs more checks n, and—hence—longer time for the overall search to reach a similar value of the TPR.

FIGURE 2

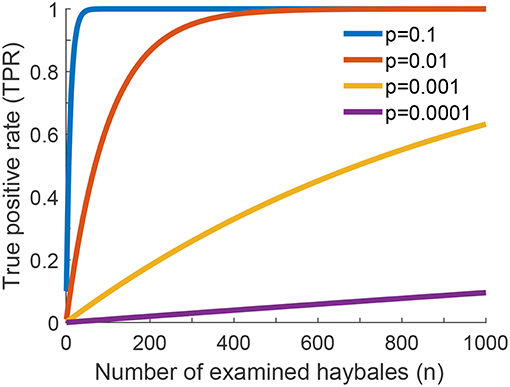
Figure 2. True positive rate (TPR) for one-phase search strategy assuming no errors in the classification of individual haybales. The global true positive rate (TPR) of the search problem as a function of the number of examined haybales for different values of p is shown (see Equation 2 of Supplementary Information). p is the fraction of relevant instances present in the haystack.

Up to now the search problem was unrealistically simple: difficulties arising from the classification of each haybale were not considered so far. In our T cell activation scenario, however, it may well occur that a T cell erroneously classifies irrelevant APCs as relevant or vice versa. To consider such local mistakes, the model gets slightly more complicated: every haybale itself may belong to the group of true positives (it contains a needle, and was correctly detected), false negatives (it contains a needle, but was erroneously rejected), false positives (it does not contain a needle, but was erroneously detected), and true negatives (it does not contain a needle and was correctly rejected). To avoid confusion, we denote with upper case letters the figures of merit of the global search problem (the haystack), with lower case letters the figures of merit of the local search problem (the haybales).

Let us consider the situation, where there are needles present in the haystack. A true positive result of the global search problem is defined as the correct identification of such a haystack, and the true positive rate as the probability to correctly detect such haystacks as being relevant (i.e., containing needles). We can improve the global TPR by increasing the number of local true positives: high numbers of haybales containing needles, and a high yield of correctly detecting them would suffice. On the other hand, however, we can also improve the global TPR by increasing local false positives: the more erroneous detections of needles, the more likely is a positive result of the global search. Let us look at this seemingly contradictory statement in more detail: Apparently, TPR is not the only parameter, which has to be considered when assessing the quality of our search process. For illustrating the diagnostic properties of a binary classifier system, statistics often uses receiver operating characteristic (ROC) curves. For this, a second figure of merit, the false positive rate, is calculated. It captures the likelihood of a global positive detection for the irrelevant case (no needles in the haystack). The idea of a good classifier system is achieving reasonably high TPR, while keeping FPR reasonably low.

In a ROC plot, TPR is plotted vs. FPR for various parameters of the test. In principle, if a test has no discriminative power, the curve follows the diagonal (also called the line of no discrimination). The better the test gets, the further the points locate in the upper half of the plot, with the point (TPR = 1, FPR = 0) representing perfect classification. In contrast, points below the diagonal correspond to classifications worse than random. The ROC curve for our problem is shown in Figure 3A, where we used the number of checked haybales n as parameter. Curves are shown for p = 10⁻⁴ and various values of the local false positive rate fpr. For fpr = 10⁻⁴ the classifier is doing reasonably well, with all data being above the diagonal (blue line). If the local false positive rate is increased, the performance of the classifier declines and the test loses its discriminative power (red line). In contrast, the test performs better when fpr is further reduced. Ultimately, if there were no local false assignments at all (fpr = 0), the curve would follow the y-axis, which would be identical to the case discussed above in the context of Figure 2.

FIGURE 3

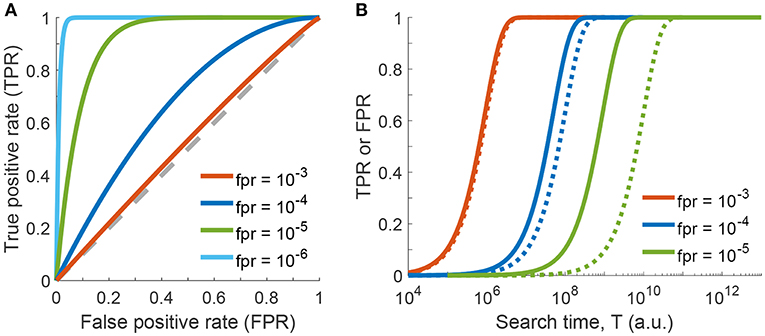
Figure 3. One-phase search strategy, considering errors in classification of individual haybales. (A) Receiver operating characteristic (ROC) curve showing the global true positive rate TPR as a function of the global false positive rate FPR (see Equations 5 and 8 of Supplementary Information). Curves were calculated for p = 10⁻⁴ and various values of local false positive rates fpr by varying the parameter n (the number of checked haybales). The line of no discrimination, i.e., where the test has no discriminative power, is shown as dashed gray line. (B) Global true or false positive rates as a function of search time T (see Equation 16 of Supplementary Information, Δt = 1) are shown for various values of local false positive rates fpr. Global true positive rates (TPR) are shown as solid lines, global false positive rates (FPR) as dotted lines.

Taken together, an appropriate search strategy keeps the local false positive rates low while checking as many haybales as possible. While this strategy appears reasonable, it is not realistic. High global true positive rates do not come for free: we need a considerable number of tested haybales n and hence a rather long overall search time to achieve an appropriate TPR. Even more so, keeping fpr low is not simple in practice: too fast local searches will likely increase fpr.

In the final step of our statistical model, we will now include the search time in our considerations. For the sake of simplicity, let us assume that the time for testing a single haybale scales with fpr⁻¹. This reflects the idea that more time allows for more TCR-pMHC encounters, which improves the fidelity of the decision. Hence, the total time for testing n haybales is given by T = n · Δt/fpr, where Δt denotes the time needed to check a single haybale. Figure 3B shows the resulting global true and false positive rates as a function of time T for different values of the local fpr. On the one extreme, for fpr = 10⁻³ (red curve) the TPR rapidly approaches 1, however, there is no discriminative power against FPR. In other words, the test cannot discriminate between true and false positive events and is therefore useless. On the other end of the spectrum, for fpr = 10⁻⁵ (green curves) discrimination works very well. However, we need more than 5 orders of magnitude longer to achieve the same TPR.

From these considerations, it becomes apparent that in case of extremely low relevant instances, a two-phase search strategy could make sense (Figure 4). In a first quick test phase, TPR is optimized without investing time to keep fpr low. In our picture, n₁ haybales are first superficially screened; the negatives are disregarded, whereas the positives are kept for a second phase, in which the hits of the first phase are scrutinized. The first phase, hence, contains all instances, the second phase only the positives of the first phase.

FIGURE 4

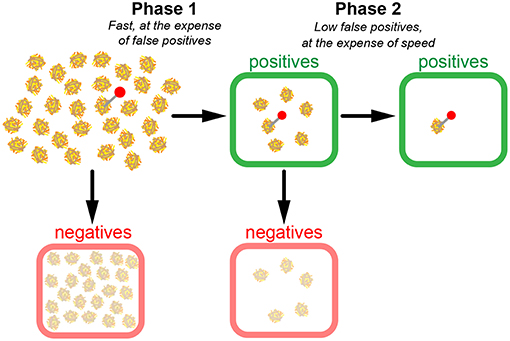
Figure 4. Model of a two-phase search strategy. In a fast first scan (phase 1), candidate haybales are classified as positives (green boxes) or negatives (red boxes). Negatives are discarded and positives are re-evaluated in phase 2. Note the substantial number of false positives after phase 1. However, since much fewer candidates have to be scanned during phase 2, it is possible to conduct a more precise yet still time-efficient scan in phase 2.

The huge difference to the situation before, however, is the altered total time required for coming up with a decision. The duration of the first phase is calculated in the same way as before, T₁ = n₁ · Δt/fpr₁, however, it is performed now at much higher false positive rate and hence carried out much faster. For phase 2, more time has to be invested for keeping the false positive rate low, however, only the positives of phase 1 have to be considered. The two-phase search approach is thus massively faster than the one phase search approach, if we compare the time required for achieving the same figures of merit for TPR and FPR (Figure 5). As an example, we compared the search times of the one-phase and two-phase approaches using the parameters p = 10⁻⁴, $fp{r}_1=10^{-2}$, and $fp{r}_2=10^{-4}$ (two-phase approach), which corresponds to $fpr=fp{r}_1·fp{r}_2=10^{-6}$ for the one-phase approach. The time improvement is an impressive factor of ~5,000 (see Equations 22 and 23 of Supplementary Information).

FIGURE 5

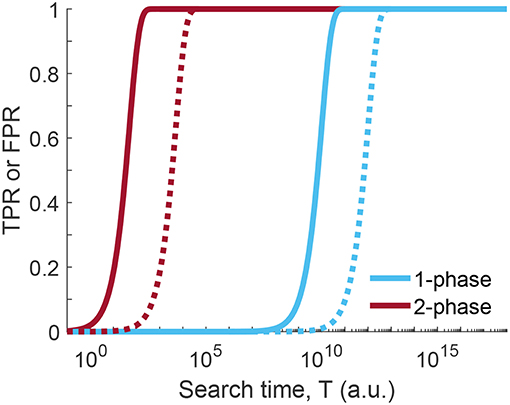
Figure 5. Time comparison of one-phase and two-phase search strategy. True positive rate (TPR, solid line) or false positive rate (FPR, dotted line) for one-phase and two-phase search strategy as a function of the search time T (see Equations 16 and 21 of the one-phase and two-phase search, respectively; Δt = 1). Curves were calculated for p = 10⁻⁴, local false positive rates were set to $fp{r}_1=10^{-2}$ and $fp{r}_2=10^{-4}$ for the two-phase search and $fpr=fp{r}_1·fp{r}_2=10^{-6}$ for the one-phase search, yielding the same figures of merit for TPR and FPR. For the calculation of the total search time T we set Δt = 1. Clearly, less time is needed in case of the two-phase search for the same level of discrimination between TPR and FPR.

Note that one can further improve the speed of the search by stopping, whenever a relevant case was detected in phase 1, and immediately proceed with phase 2. If phase 2 does not confirm the result of phase 1, one continues with phase 1 on the next haybale. While this analogy is closer to the real situation a T cell experiences, there is no substantial difference in the argumentation: The two-phase approach still outperforms the one-phase approach by orders of magnitude.

Finding Cognate Antigens on APCs Instead of Needles in Haystacks

Let us now put our calculations into context with what we know from experiments on the search of T cells for antigen presented by APCs. A human body carries approximately 50 million dendritic cells [2], of which around 10³ to 10⁵ accumulate per lymph node upon infection [13]. On the other hand, a given T cell is specific for only one antigen-bearing APC out of ~10⁵-10⁶ [12]. Together, there is a need to identify approximately one relevant APC out of 10⁴, as we assumed in our calculations by setting p = 10⁻⁴. Also our assumption of a random search appears justified, as T cell migratory behavior within lymph nodes is essentially random [14].

In the lymph node, the typical dwell time of a T cell on a dendritic cell is on the order of 1 min, if no cognate antigen is presented on a dendritic cell [15, 16]. In our terminology, this would correspond to phase 1, where TPR is maximized and fpr is neglected. This process can be achieved at rather high speeds. In practice, for a single T cell-APC encounter we should consider three contributions to this time: (i) the time needed for the T cell to move to the next dendritic cell, which is less than a second [17] and can hence be neglected here. (ii) The time for the TCR to encounter cognate pMHC, which can be of the order of seconds to minutes, depending on TCR and pMHC concentrations and diffusion coefficients. Note that the average encounter time is lowest for purely random TCR distributions. (iii) The time required for reaching a preliminary decision during phase 1. In the model formulation, we assumed this time to be given by Δt/fpr₁.

It is interesting to discuss which approach is used by T cells to make the initial search (phase 1 in our model) most efficient and fast. A number of models are currently discussed, which address how T cells come up with a first decision during phase 1: they include cooperative effects [18, 19], conformational changes of TCR subunits [20, 21], kinetic segregation of the phosphatase CD45 [22, 23], kinetic proofreading [24, 25], and pulling forces [26–28]. In addition, the Krummel lab recently proposed that microvilli on the T cell palpate an APC in search of cognate pMHC [15]. The dynamic nature of these microvilli would facilitate 98% coverage of the APC surface within 1 min. Such a palpating search strategy would be beneficial if pMHC was quite immobile. Of course, the spatial distribution of the TCR also plays an important role in making phase 1 as fast as possible. It was hypothesized for some time that the TCR could be organized in nanoscopic clusters in resting T cells [29–32]. This would lead to cooperativity between TCRs upon ligand binding and/or enhanced rebinding of cognate pMHC within a cluster. However, such a clustered organization would decrease the on-rate of TCR to cognate pMHC and hence the speed to find potentially harmful antigen. Clustering of the TCR is therefore unexpected considering that fast scanning of an APC is one of the main tasks of a T cell. In this respect, we recently provided evidence that the TCR is essentially distributed as monomers and at random on the plasma membrane of T cells interacting with model surfaces [33, 34]. Such a configuration would increase the probability and speed to find cognate pMHC on APCs and thus enhance phase 1. TCR enrichment at the tips of microvilli as the sites of first contact with APCs would further improve recognition at the onset of synapse formation [35].

One of the remaining questions is how phase 2, i.e., scrutinizing the first decision, is brought about. As soon as the T cell discovers cognate antigen on a dendritic cell, massive rearrangements of the surface molecules take place, leading to the formation of the immunological synapse [36], and the cell to cell contact becomes prolonged to hours [37–39]. According to our terminology, we have now entered phase 2: The T cell has encountered antigen of interest, which shall be further scrutinized. Microclusters containing TCR and signaling molecules are formed now [40, 41], which are believed to constitute the basic signaling unit in T cells [42]. They are densely packed with a diverse set of proteins, including, besides the TCR, Lck, the costimulatory molecule CD28, and ZAP-70. According to our model, T cells may occasionally enter phase 2 erroneously after classifying APCs as positive, although they actually lack cognate antigenic peptide; in other words, we would expect non-zero false positive rates. Recent literature indicates that such scenarios indeed happen: TCR microcluster formation was also observed under non-activating conditions [43], and premature interruption of the T cell-APC contact might lead to reversal and/or alteration of T cell commitment to differentiation [7, 44, 45]. Notably, parts of these processes likely start already during phase 1 and acquire additional fidelity via multiple rounds of checks and rechecks during phase 2.

Taken together, considering both the principal search requirements and experimental data it appears likely that T cells do not do the search for the needle in the haystack in a single phase, but rather in several phases. One consequence of our model is the occurrence of false positive classifications at early stages of T cell signaling, which do not progress to full activation. In principle, this could be tested experimentally in single-T cell activation measurements, where T cells are allowed to screen mixtures of APCs with very few relevant and a huge excess of irrelevant APCs. The idea would be to compare the read-out of proximal T cell signaling such as phosphorylated ITAMs (e.g., via quantifying ZAP-70 recruitment to the plasma membrane), TCR or LAT microcluster formation or the presence of Ca²⁺ signals with later signaling events such as transcription factor translocation, cytokine production (e.g. IL-2) [39] and the expression of CD69 [46] or CD25 [47]. According to our model, we would expect T cells to react occasionally with the onset of proximal signaling events, even if an irrelevant APC was contacted. This would allow to determine the local true and false positive rates of the first phase, tpr₁ and fpr₁. The global true and false positive rates TPR and FPR could be determined from the late activation markers. If our proposed model was correct, improved ROC plots for the global rates compared to the local rates should be obtained; particularly, we would expect FPR ≪ fpr₁. In conclusion, the proposed two-phase search approach offers a plausible framework to conceptualize the search for antigen by T cells. Experiments such as the one described above should provide the means to test the proposed hypothesis and possibly help to understand the molecular mechanisms underlying the T cell's search problem.

Author Contributions

All authors listed have made a substantial, direct and intellectual contribution to the work, and approved it for publication.

Funding

This work was supported by the Austrian Science Fund (FWF) projects P 26337-B21, F 6809-N36 (GS), P27941-B28 (FB), and by the Vienna Science and Technology Fund (WWTF) project LS13-030 (GS).

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2019.00011/full#supplementary-material

References

1. Huppa JB, Davis MM. T-cell-antigen recognition and the immunological synapse. Nat Rev Immunol. (2003) 3:973–83. doi: 10.1038/nri1245

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Fearnley DB, Whyte LF, Carnoutsos SA, Cook AH, Hart DNJ. Monitoring human blood dendritic cell numbers in normal individuals and in stem cell transplantation. Blood (1999) 93:728–36.

PubMed Abstract | Google Scholar

3. Jenkins MK, Chu HH, McLachlan JB, Moon JJ. On the composition of the preimmune repertoire of T cells specific for peptide–major histocompatibility complex ligands. Ann Rev Immunol. (2010) 28:275–94. doi: 10.1146/annurev-immunol-030409-101253

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Bajénoff M, Egen JG, Qi H, Huang AYC, Castellino F, Germain RN. Highways, byways and breadcrumbs: directing lymphocyte traffic in the lymph node. Trend Immunol. (2007) 28:346–52. doi: 10.1016/j.it.2007.06.005

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Irvine DJ, Purbhoo MA, Krogsgaard M, Davis MM. Direct observation of ligand recognition by T cells. Nature (2002) 419:845–9. doi: 10.1038/nature01076

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Harding CV, Unanue ER. Quantitation of antigen-presenting cell MHC class II/peptide complexes necessary for T-cell stimulation. Nature (1990) 346:574. doi: 10.1038/346574a0

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Mayya V, Dustin ML. What scales the T cell response? Trends Immunol. (2016) 37:513–22. doi: 10.1016/j.it.2016.06.005

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Girard JP, Moussion C, Förster R. HEVs, lymphatics and homeostatic immune cell trafficking in lymph nodes. Nat Rev Immunol. (2012) 12:762. doi: 10.1038/nri3298

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Jenei A, Varga S, Bene L, Matyus L, Bodnar A, Bacso Z, et al. HLA class I and II antigens are partially co-clustered in the plasma membrane of human lymphoblastoid cells. Proc Natl Acad Sci USA. (1997) 94:7269–74. doi: 10.1073/pnas.94.14.7269

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Chen L, Flies DB. Molecular mechanisms of T cell co-stimulation and co-inhibition. Nat Rev Immunol. (2013) 13:227–42. doi: 10.1038/nri3405

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Curtsinger JM, Mescher MF. Inflammatory cytokines as a third signal for T cell activation. Curr Opin Immunol. (2010) 22:333–40. doi: 10.1016/j.coi.2010.02.013

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Krummel MF, Bartumeus F, Gérard A. T cell migration, search strategies and mechanisms. Nat Rev Immunol. (2016) 16:193. doi: 10.1038/nri.2015.16

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Usherwood EJ, Hogg TL, Woodland DL. Enumeration of antigen-presenting cells in mice infected with sendai virus. J Immunol. (1999) 162:3350–5.

PubMed Abstract | Google Scholar

14. Miller MJ, Wei SH, Cahalan MD, Parker I. Autonomous T cell trafficking examined in vivo with intravital two-photon microscopy. Proc Natl Acad Sci USA. (2003) 100:2604–9. doi: 10.1073/pnas.2628040100

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Cai E, Marchuk K, Beemiller P, Beppler C, Rubashkin MG, Weaver VM, et al. Visualizing dynamic microvillar search and stabilization during ligand detection by T cells. Science (2017) 356:eaal3118. doi: 10.1126/science.aal3118

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Gérard A, Patino-Lopez G, Beemiller P, Nambiar R, Ben-Aissa K, Liu Y, et al. Detection of rare antigen-presenting cells through t cell-intrinsic meandering motility, mediated by myo1g. Cell (2014) 158:492–505. doi: 10.1016/j.cell.2014.05.044

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Fooksman DR, Vardhana S, Vasiliver-Shamis G, Liese J, Blair D, Waite J, et al. Functional anatomy of T cell activation and synapse formation. Ann Rev Immunol. (2010) 28:79–105. doi: 10.1146/annurev-immunol-030409-101308

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Su X, Ditlev JA, Hui E, Xing W, Banjade S, Okrut J, et al. Phase separation of signaling molecules promotes T cell receptor signal transduction. Science (2016) 352:595–9. doi: 10.1126/science.aad9964

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Huang WYC, Yan Q, Lin WC, Chung JK, Hansen SD, Christensen SM, et al. Phosphotyrosine-mediated LAT assembly on membranes drives kinetic bifurcation in recruitment dynamics of the Ras activator SOS. Proc Natl Acad Sci USA. (2016) 113:8218–23. doi: 10.1073/pnas.1602602113

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Swamy M, Beck-Garcia K, Beck-Garcia E, Frederike Hartl A, Morath A, Yousefi OS, et al. A cholesterol-based allostery model of T cell receptor phosphorylation. Immunity (2016) 44:1091–101. doi: 10.1016/j.immuni.2016.04.011

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Xu C, Gagnon E, Call ME, Schnell JR, Schwieters CD, Carman CV, et al. Regulation of T cell receptor activation by dynamic membrane binding of the CD3epsilon cytoplasmic tyrosine-based motif. Cell (2008) 135:702–13. doi: 10.1016/j.cell.2008.09.044

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Davis SJ, van der Merwe PA. The kinetic-segregation model: TCR triggering and beyond. Nat Immunol. (2006) 7:803–9. doi: 10.1038/ni1369

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Chang VT, Fernandes RA, Ganzinger KA, Lee SF, Siebold C, McColl J, et al. Initiation of T cell signaling by CD45 segregation at ‘close contacts.' Nat Immunol. (2016) 17:574–82. doi: 10.1038/ni.3392

PubMed Abstract | CrossRef Full Text | Google Scholar

24. McKeithan TW. Kinetic proofreading in T-cell receptor signal transduction. Proc Natl Acad Sci USA. (1995) 92:5042–6. doi: 10.1073/pnas.92.11.5042

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Lever M, Maini PK, van der Merwe PA, Dushek O. Phenotypic models of T cell activation. Nat Rev Immunol. (2014) 14:619–29. doi: 10.1038/nri3728

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Feng Y, Brazin KN, Kobayashi E, Mallis RJ, Reinherz EL, Lang MJ. Mechanosensing drives acuity of αβ T-cell recognition. Proc Natl Acad Sci USA. (2017) 114:E820–13. doi: 10.1073/pnas.1703559114

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Liu B, Chen W, Brian Evavold D, Zhu C. Accumulation of dynamic catch bonds between TCR and agonist peptide-MHC triggers T cell signaling. Cell (2014) 157:357–68. doi: 10.1016/j.cell.2014.02.053

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Klotzsch E, Gerhard Schütz J. Improved ligand discrimination by force-induced unbinding of the T cell receptor from peptide-MHC. Biophys J. (2013) 104:1670–5. doi: 10.1016/j.bpj.2013.03.023

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Lillemeier BF, Mortelmaier MA, Forstner MB, Huppa JB, Groves JT, Davis MM. TCR and Lat are expressed on separate protein islands on T cell membranes and concatenate during activation. Nat Immunol. (2010) 11:90–6. doi: 10.1038/ni.1832

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Schamel WW, Arechaga I, Risueno RM, van Santen HM, Cabezas P, Risco C, et al. Coexistence of multivalent and monovalent TCRs explains high sensitivity and wide range of response. J Exp Med. (2005) 202:493–503. doi: 10.1084/jem.20042155

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Kumar R, Ferez M, Swamy M, Arechaga I, Maria Rejas T, Jose Valpuesta M, et al. Increased sensitivity of antigen-experienced T cells through the enrichment of oligomeric T cell receptor complexes. Immunity (2011) 35:375–87. doi: 10.1016/j.immuni.2011.08.010

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Pageon SV, Tabarin T, Yamamoto Y, Ma Y, Bridgeman JS, Cohnen A, et al. Functional role of T-cell receptor nanoclusters in signal initiation and antigen discrimination. Proc Natl Acad Sci USA. (2016) 113:E5454–63. doi: 10.1073/pnas.1607436113

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Rossboth B, Arnold AM, Ta H, Platzer R, Kellner F, Huppa JB, et al. TCRs are randomly distributed on the plasma membrane of resting antigen-experienced T cells. Nat Immunol. (2018) 19:821–7. doi: 10.1038/s41590-018-0162-7

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Brameshuber M, Kellner F, Rossboth BK, Ta H, Alge K, Sevcsik E, et al. Monomeric TCRs drive T cell antigen recognition. Nat Immunol. (2018) 19:487–96. doi: 10.1038/s41590-018-0092-4

PubMed Abstract | CrossRef Full Text | Google Scholar

35. Jung Y, Riven I, Feigelson SW, Kartvelishvily E, Tohya K, Miyasaka M, et al. Three-dimensional localization of T-cell receptors in relation to microvilli using a combination of superresolution microscopies. Proc Natl Acad Sci USA. (2016) 113:E5916–24. doi: 10.1073/pnas.1605399113

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Monks CR, Freiberg BA, Kupfer H, Sciaky N, Kupfer A. Three-dimensional segregation of supramolecular activation clusters in T cells. Nature (1998) 395:82–6. doi: 10.1038/25764

PubMed Abstract | CrossRef Full Text | Google Scholar

37. Bousso P, Robey E. Dynamics of CD8+ T cell priming by dendritic cells in intact lymph nodes. Nat Immunol. (2003) 4:579. doi: 10.1038/ni928

PubMed Abstract | CrossRef Full Text | Google Scholar

38. Mempel TR, Henrickson SE, Von Andrian UH. T-cell priming by dendritic cells in lymph nodes occurs in three distinct phases. Nature (2004) 427:154–9. doi: 10.1038/nature02238

PubMed Abstract | CrossRef Full Text | Google Scholar

39. Huang J, Brameshuber M, Zeng X, Xie J, Li QJ, Chien YH, et al. A single peptide-major histocompatibility complex ligand triggers digital cytokine secretion in CD4+ T cells. Immunity (2013) 39:1–12. doi: 10.1016/j.immuni.2013.08.036

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Yokosuka T, Sakata-Sogawa K, Kobayashi W, Hiroshima M, Hashimoto-Tane A, Tokunaga M, et al. Newly generated T cell receptor microclusters initiate and sustain T cell activation by recruitment of Zap70 and SLP-76. Nat Immunol. (2005) 6:1253–62. doi: 10.1038/ni1272

PubMed Abstract | CrossRef Full Text | Google Scholar

41. Campi G, Varma R, Dustin ML. Actin and agonist MHC-peptide complex-dependent T cell receptor microclusters as scaffolds for signaling. J Exp Med. (2005) 202:1031–6. doi: 10.1084/jem.20051182

PubMed Abstract | CrossRef Full Text | Google Scholar

42. Hashimoto-Tane A, Saito T. Dynamic regulation of TCR–microclusters and the microsynapse for T cell activation. Front Immunol. (2016) 7:255. doi: 10.3389/fimmu.2016.00255

PubMed Abstract | CrossRef Full Text | Google Scholar

43. Crites TJ, Padhan K, Muller J, Krogsgaard M, Gudla PR, Lockett SJ, et al. TCR microclusters pre-exist and contain molecules necessary for TCR signal transduction. J Immunol. (2014) 193:56–67. doi: 10.4049/jimmunol.1400315

PubMed Abstract | CrossRef Full Text | Google Scholar

44. Marangoni F, Murooka TT, Manzo T, Kim EY, Carrizosa E, Elpek NM, et al. The transcription factor nfat exhibits signal memory during serial T cell interactions with antigen presenting cells. Immunity (2013) 38:237–49. doi: 10.1016/j.immuni.2012.09.012

PubMed Abstract | CrossRef Full Text | Google Scholar

45. Das J, Ho M, Zikherman J, Govern C, Yang M, Weiss A, et al. Digital signaling and hysteresis characterize Ras activation in lymphoid cells. Cell (2009) 136:337–51. doi: 10.1016/j.cell.2008.11.051

PubMed Abstract | CrossRef Full Text | Google Scholar

46. Simms PE, Ellis TM. Utility of flow cytometric detection of CD69 expression as a rapid method for determining poly- and oligoclonal lymphocyte activation. Clin Diagn Lab Immunol. (1996) 3:301–4.

PubMed Abstract | Google Scholar

47. Shatrova AN, Mityushova EV, Vassilieva IO, Aksenov ND, Zenin VV, Nikolsky NN, et al. Time-dependent regulation of IL-2R α-chain (CD25) expression by TCR signal strength and IL-2-induced STAT5 signaling in activated human blood T lymphocytes. PLoS ONE (2016) 11:2e0167215. doi: 10.1371/journal.pone.0167215

PubMed Abstract | CrossRef Full Text | Google Scholar