Dark-Bright Optical Soliton and Conserved Vectors to the Biswas-Arshed Equation With Third-Order Dispersions in the Absence of Self-Phase Modulation

The form-I version of the new celebrated Biswas-Arshed equation is studied in this work with the aid of complex envelope ansatz method. The equation is considered when self-phase is absent and velocity dispersion is negligibly small. New Dark-bright optical soliton solution of the equation emerge from the integration. The acquired solution combines the features of dark and bright solitons in one expression. The solution obtained are not yet reported in the literature. Moreover, we showed that the equation possess conservation laws (Cls).

1. Introduction

The study of dynamical systems in non-linear physical models plays an important role in optical fibers, electrical transmission lines, plasma physics, mathematical biology, and many more [1]. This is motivated by the capacity to model the behavior of these systems and other under different physical conditions [2]. These systems are represented by non-linear equations. Seeking the exact solutions of non-linear evolution equations has been an interesting topic in mathematical physics, and the solutions of corresponding models are the ways to well describe their dynamics. Several results have been reported in the last few decades [3–24]. The main principle for the existence of solitons in metamaterials, optical fibers, and crystals is the existence of a balance between non-linearity and dispersion. It is obvious that some situations may lead to. Recently, Biswas and Arshed [3] put forward a new model for soliton transmission in optical fibers in the event when self-phase modulation is neglible in the absence of non-linearity.

The third-order model in the absence of self-phase modulation that will be studied in this paper is given by [3, 4]:

$\begin{array}{ll}i{\psi }_t+\alpha {\psi }_{xx}+\gamma {\psi }_{xt}+i[\sigma {\psi }_{xxx}+\delta {\psi }_{xxt}]-i[\text{Ω}{(|\psi {|}^2\psi )}_x+\mu {(|\psi {|}^2)}_x\psi +\theta |\psi {|}^2{\psi }_x]=0.& (1)\end{array}$

The function ψ(x, t) representing the dependent involving t an x which denotes the temporal and spatial components. The first term represents the temporal evolution of the wave, γ represents the(STD) coefficient, α is the coefficient of GVD and σ is the coefficient of the third order dispersion, δ is the coefficient of spatio-temporal 3OD (ST-3OD), Ω is the effect of self-steepening. Finally, μ and θ provide the effect of non-linear dispersion. Dark, bright, combo and singular soliton solutions of Equation (1) have been reported in Biswas and Arshed [3] and Ekici and Sonmezoglu [4]. But to the best of our knowledge, the dark-bright optical soliton and Cls of the equation have not been reported. In this work, this special solution combining the features of dark and bright optical soliton in one expression will be recovered by applying a suitable ansatz. The Cls of the equation will be derived using the multiplier method [8, 9].

2. Dark-Bright Optical Soliton

In order derive the dark-bright soliton solution of the equation, we consider the ansatz solution given by Li et al. [5]:

$\begin{array}{ll}\psi (x,t)=A(x,t)\times e^{i\text{Ψ}(x,t)},& (2)\end{array}$

with

$\begin{array}{ll}\text{Ψ}(x,t)=-kx+\omega t+\text{ν}.& (3)\end{array}$

In Equation (2), Ψ denotes the phase shift, k denotes the wave number, ω represents the frequency and ν is the phase constant. We now utilize the ansatz put forward from Li et al. [5]:

$\begin{array}{ll}\begin{array}{l}A(x,t)=\mathrm{\text{i}}\beta +\text{λ}\mathrm{\text{tanh}}\left[\eta (x-vt)\right]+\mathrm{\text{i}}\rho \mathrm{\text{sech}}\left[\eta (x-vt)\right],\end{array}& (4)\end{array}$

where v represents the velocity and η is the pulse width. In the even when λ → 0 or ρ → 0, the Equation (4) transforms to a bright or dark soliton solution. The intensity of A(x, t) is given by

$\begin{array}{ll}|A(x,t)|={\displaystyle {\left\{{\text{λ}}^2+{\beta }^2+2\beta \rho \text{sech}[\eta (x-vt)]+({\rho }^2-{\text{λ}}^2){\text{sech}}^2[\eta (x-vt)]\right\}}^{\frac{1}{2}}.}\hfill & (5)\end{array}$

The non-linear phase shift ψ_NL is represented by

$\begin{array}{ll}{\psi }_{NL}=\mathrm{\text{arctan}}\left[\frac{\beta +\rho \mathrm{\text{sech}}\left[\eta (x-vt)\right]}{\text{λ}\mathrm{\text{tanh}}\left[\eta (x-vt)\right]}\right].& (6)\end{array}$

Putting Equation (2) into Equation (1) leads to

$\begin{array}{rr}\begin{array}{r}-A(\omega +k(k(\alpha +k\sigma )-(\gamma +k\delta )\omega )+k(\theta +\mu +\text{Ω})|A{|}^2+2i\text{Ω}A{A}_x)-\\ i((-1+k(\gamma +k\delta ))A_t+(k(2\alpha +3k\sigma )-(\gamma +2k\delta )\omega +(\theta +\mu +\text{Ω})|A{|}^2)A_x+\\ i((\gamma +2k\delta )A_{xt}+(\alpha +3k\sigma -\delta \omega )A_{xx}+i(\delta A_{xxt}+\sigma A_{xxx})))=0.\end{array}& (7)\end{array}$

Now, putting Equation(4) into Equation(7), expanding the result and equating the combination of coefficients of sech(τ) and tanh(τ), we acquire the independent parametric equations represented by:

Constants:

$\begin{array}{r}-i\beta (\omega +k(-\gamma \omega +k(\alpha +k\sigma -\delta \omega )+({\beta }^2+{\text{λ}}^2)\\ (\theta +\mu +\text{Ω})))=0,& (8)\end{array}$

sech(τ) :

$\begin{array}{r}-i\rho (\omega +k(-\gamma \omega +k(\alpha +k\sigma -\delta \omega )+(3{\beta }^2+{\text{λ}}^2)\\ (\theta +\mu +\text{Ω})))=0,& (9)\end{array}$

sech²(τ) :

$\begin{array}{l}i(v(-1+k(\gamma +k\delta ))\eta \text{λ}-3k^2\eta \text{λ}\sigma -\eta \text{λ}\\ (-\gamma \omega +({\beta }^2+{\text{λ}}^2)(\theta +\mu +\text{Ω}))+\\ k(-2\alpha \eta \text{λ}+2\delta \eta \text{λ}\omega +\beta ({\text{λ}}^2-3{\rho }^2)(\theta +\mu +\text{Ω})))=0,& (10)\end{array}$

sech³(τ) :

$\begin{array}{r}i\rho (-\alpha {\eta }^2+v(\gamma +2k\delta ){\eta }^2-2\beta \eta \theta \text{λ}+k\theta {\text{λ}}^2-2\beta \eta \text{λ}\mu \\ +k{\text{λ}}^2\mu -k\theta {\rho }^2-k\mu {\rho }^2-3k{\eta }^2\sigma +\\ \delta {\eta }^2\omega -2\beta \eta \text{λ}\text{Ω}+k{\text{λ}}^2\text{Ω}-k{\rho }^2\text{Ω})=0,& (11)\end{array}$

sech⁴(τ) :

$\begin{array}{ll}i\eta \text{λ}(2{\eta }^2(v\delta -\sigma )+(\text{λ}-\rho )(\text{λ}+\rho )(\theta +\mu +\text{Ω}))=0,& (12)\end{array}$

tanh(τ) :

$\begin{array}{r}-\text{λ}(\omega +k(-\gamma \omega +k(\alpha +k\sigma -\delta \omega )+({\beta }^2+{\text{λ}}^2)\\ (\theta +\mu +\text{Ω})))=0,& (13)\end{array}$

tanh(τ)sech(τ) :

$\begin{array}{r}\rho (v(-1+k(\gamma +k\delta ))\eta -3k^2\eta \sigma -2k(\alpha \eta -\delta \eta \omega \\ +\beta \text{λ}(\theta +\mu +\text{Ω}))-\eta (-\gamma \omega +\\ {\text{λ}}^2(\theta +\mu +\text{Ω})+{\beta }^2(\theta +\mu +3\text{Ω})))=0,& (14)\end{array}$

tanh(τ)sech²(τ) :

$\begin{array}{r}(-2\alpha {\eta }^2\text{λ}+2v(\gamma +2k\delta ){\eta }^2\text{λ}+k\theta {\text{λ}}^3+k{\text{λ}}^3\mu -2\beta \eta \theta {\rho }^2\\ -k\theta \text{λ}{\rho }^2-2\beta \eta \mu {\rho }^2-k\text{λ}\mu {\rho }^2-6k{\eta }^2\text{λ}\sigma \\ +2\delta {\eta }^2\text{λ}\omega +({\text{λ}}^2(2\beta \eta +k\text{λ})-(6\beta \eta +k\text{λ}){\rho }^2)\text{Ω})=0,& (15)\end{array}$

tanh(τ)sech³(τ) :

$\begin{array}{ll}\eta \rho (5{\eta }^2(v\delta -\sigma )+(\text{λ}-\rho )(\text{λ}+\rho )(\theta +\mu +3\text{Ω}))=0,& (16)\end{array}$

tanh²(τ)sech(τ) :

$\begin{array}{ll}-i\eta \rho (\eta (-\alpha +v(\gamma +2k\delta )-3k\sigma +\delta \omega )-2\beta \text{λ}\text{Ω})=0,& (17)\end{array}$

tanh²(τ)sech²(τ) :

$\begin{array}{ll}-2i\eta \text{λ}(2{\eta }^2(v\delta -\sigma )+(\text{λ}-\rho )(\text{λ}+\rho )\text{Ω})=0,& (18)\end{array}$

tanh³(τ)sech(τ) :

$\begin{array}{ll}{\eta }^3\rho (-v\delta +\sigma )=0,& (19)\end{array}$

where τ = η(x − vt). From the solution of Equations(8)–(19), we observed that β = 0. but, for a dark-bright optical soliton to exist, we require both ρ ≠ 0 and λ ≠ 0. For the sake of compatibility, we considered the case when ρ = λ from the solutions of Equations(8)–(19). We acquire the velocity as

$\begin{array}{ll}v=-{\rho }^2(\theta +\mu +\text{Ω}),& (20)\end{array}$

the wave number is represented by

$\begin{array}{ll}k=-\frac{\omega }{{\rho }^2(\theta +\mu +\text{Ω})}.& (21)\end{array}$

We also acquire the value of δ and α as

$\begin{array}{ll}\delta =-\frac{\sigma }{{\rho }^2(\theta +\mu +\text{Ω})},& (22)\end{array}$

$\begin{array}{ll}\alpha =-\gamma {\rho }^2(\theta +\mu +\text{Ω}).& (23)\end{array}$

The dark-bright optical soliton to the model reads:

$\begin{array}{c}\psi (x,t)={\displaystyle \{i\text{λ}\mathrm{\text{sech}}\left[\eta (x+t{\text{λ}}^2(\theta +\mu +\text{Ω}))\right]+\text{λ}\mathrm{\text{tanh}}\left[\eta (x+t{\text{λ}}^2(\theta +\mu +\text{Ω}))\right]\}}\\ \times e^{i(\theta +t\omega +\frac{x\omega }{{\text{λ}}^2(\theta +\mu +\text{Ω})})}.& (24)\end{array}$

and the intensity gives

$\begin{array}{ll}\begin{array}{l}|\psi (x,t){|}^2={\text{λ}}^2.\end{array}& (25)\end{array}$

The phase shift is represented by

$\begin{array}{ll}{\psi }_{NL}=\mathrm{\text{arctan}}\left[\frac{\mathrm{\text{sech}}[\eta (x+t{\text{λ}}^2(\theta +\mu +\text{Ω})]}{\mathrm{\text{tanh}}[\eta (x+t{\text{λ}}^2(\theta +\mu +\text{Ω})]}\right].& (26)\end{array}$

The dark-bright soliton Equation (24) represents a soliton combining the features of dark and bright solitons in one expression. The constant β = 0 implies a pronounced “platform” underneath the soliton under non-zero boundary conditions and its asymptotic value approaches λ as |t| → ∞. To analyze the dynamics behavior of the soliton solution Equation (24), we have made numerical evolutions for some perturbations to show the evolution of the dark-bright optical soliton solution. Figures 1-3 shows the profiles surfaces of the dark-bright soliton Equation (24). The obtained soliton Equation (24) possesses the structure of the physical properties of dark and bright optical solitons in the same expression. These solitons appear temporal solitons observed in optical fibers.

FIGURE 1

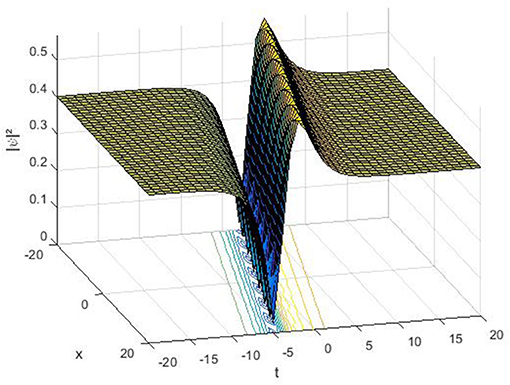
Figure 1. 3D surface of solution Equation(24) by selecting the parameter values of η = 0.1, λ = 0.1, θ = 1, Ω = 0.1.

FIGURE 2

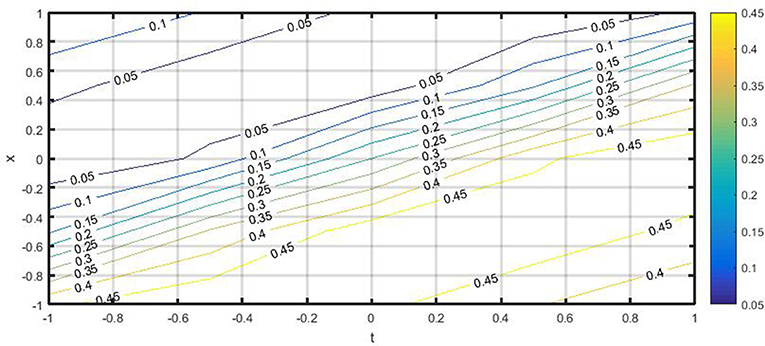
Figure 2. The contour surface of solution Equation (24) by selecting the parameter values of η = 0.1, λ = 0.1, θ = 1, Ω = 0.1.

FIGURE 3

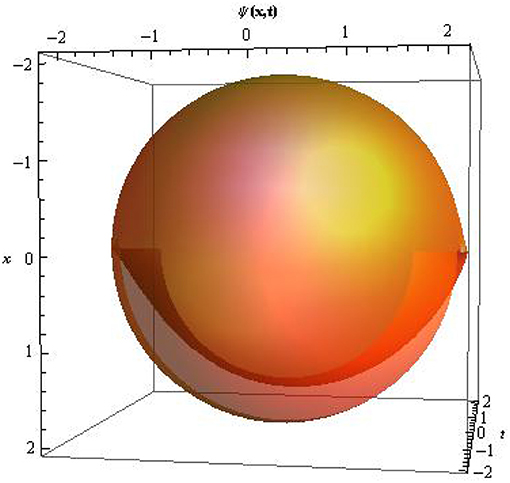
Figure 3. contour plot in spherical coordinates of solution Equation (24) by selecting the parameter values of η = 0.1, λ = 0.1, θ = 1, Ω = 0.1.

3. Conservation Laws

In this part, we will utilize the multiplier to derive the Cls [8, 9]. To achieve this aim, we apply

$\begin{array}{ll}\psi (x,t)=u(x,t)+i\upsilon (x,t),& (27)\end{array}$

to transform Equation (1) to a system of PDEs. Putting Equation (27) into Equation (1), we acquire:

$\begin{array}{ll}\{\begin{array}{l}-{\upsilon }_t+2(\mu +\text{Ω})u\upsilon u_x+(\theta +\text{Ω})u^2{\upsilon }_x+(\theta +2\mu +3\text{Ω}){\upsilon }^2{\upsilon }_x\\ +\gamma u_{xt}+\alpha u_{xx}-\delta {\upsilon }_{xxt}-\sigma {\upsilon }_{xxx}=0.\\ \\ u_t+(-\theta -2\mu -3\text{Ω})u^2{u}_x+(-\theta -\text{Ω}){\upsilon }^2{u}_x-2(\mu +\text{Ω})u\upsilon {\upsilon }_x\\ +\gamma {\upsilon }_{xt}+\alpha {\upsilon }_{xx}+\delta u_{xxt}+\sigma u_{xxx}=0.\end{array}& (28)\end{array}$

Applying the formula for determining equations in [9], we acquires the multipliers of zeroth-order Λ₁(x, t, u, υ), Λ₂(x, t, u, υ) for Equation (1)

$\begin{array}{ll}\begin{array}{l}{\text{Λ}}_1=c_{1}u,\\ {\text{Λ}}_2=c_1\upsilon ,\end{array}& (29)\end{array}$

where c₁ is a constant.

1. If c₁ = 1 in Equation(29), then we have the following multipliers:

$\begin{array}{ll}\begin{array}{l}{\text{Λ}}^1=u,{\text{Λ}}^2=\upsilon .\end{array}& (30)\end{array}$

Subsequently, we acquire the fluxes given by:

$\begin{array}{ll}\begin{array}{l}\begin{array}{l}{\text{T}}^{\text{x}}=\frac{-\delta (u{u}_{xx}-\upsilon {\upsilon }_{xx})}{\sigma },\\ \\ {\text{T}}^{\text{t}}=\frac{u^{3}t{u}_t(3\text{Ω}+2\mu +\theta )+\sigma (u{u}_{xx}+\upsilon {\upsilon }_{xx})}{\sigma }.\end{array}\end{array}& (31)\end{array}$

4. Concluding Remarks

In this article, we have explored a suitable ansatz solution to derive a dark-bright soliton solution of the new celebrated Biswas-Arshed equation. observing the solutions derived in Biswas and Arshed [3] and Ekici and Sonmezoglu [4], we observed that the solution of the equation acquired in this manuscript is new. The method used here has been proved to be efficient in investigating the combined soliton solution of non-linear models. We finally showed that the equation has conservation laws and we reported the conserved vectors. We hope to apply other techniques to extract additional new forms of solutions of the new model in the future.

Author Contributions

All authors listed have made a substantial, direct and intellectual contribution to the work, and approved it for publication.

Funding

This study was Funded by Cankaya University.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

1. Whitham GB. Linear and Nonlinear Waves. New York, NY: John Whiley (1974).

Google Scholar

2. Agrawal GP. Nonlinear Fiber Optics. New York, NY: Academic Press (1995).

Google Scholar

3. Biswas A, Arshed S. Optical solitons in presence of higher order dispersions and absence of self-phase modulation. Optik. (2018) 174:452–9. doi: 10.1016/j.ijleo.2018.08.037

CrossRef Full Text | Google Scholar

4. Ekici M, Sonmezoglu A. Optical solitons with Biswas-Arshed equation by extended trial function method. Optik. (2018) 177:13–20. doi: 10.1016/j.ijleo.2018.09.134

CrossRef Full Text | Google Scholar

5. Li Z, Li L, Tian H. New types of solitary wave solutions for the higher order nonlinear Schrödinger equation, Phys Rev Lett. (2000) 84:4096–9. doi: 10.1103/PhysRevLett.84.4096

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Zhou Q, Zhu Q. Combined optical solitons with parabolic law nonlinearity and spatio-temporal dispersion. J Mod Opt. (2015) 62:483–6. doi: 10.1080/09500340.2014.986549

CrossRef Full Text | Google Scholar

7. Choudhuri A, Porsezian K. Dark-in-the-Bright solitary wave solution of higher-order nonlinear Schrödinger equation with non-Kerr terms. Opt. Commun. (2012) 285:364–7. doi: 10.1016/j.optcom.2011.09.043.

CrossRef Full Text | Google Scholar

8. Anco SC, Bluman G. Direct construction method for conservation laws of partial differential equations Part II: general treatment. Eur J Appl Math. (2002) 13:567–85. doi: 10.1017/S0956792501004661

CrossRef Full Text | Google Scholar

9. Buhe E, Bluman GW. Symmetry reductions, exact solutions, and conservation laws of the generalized Zakharov equations. J Math Phys. (2015) 56:101501. doi: 10.1063/1.4931962

CrossRef Full Text | Google Scholar

10. Jawad MA, Petkovic MD, Biswas A. Modified simple equation method for nonlinear evolution equations. Appl Math Comput. (2010) 217:869–77. doi: 10.1016/j.amc.2010.06.030

CrossRef Full Text | Google Scholar

11. Mirzazadeh M, Eslami M, Biswas A. Soliton solutions to KdV6 equation. Nonlinear Dyn. (2015) 80:387–96. doi: 10.1007/s11071-014-1876-1

CrossRef Full Text | Google Scholar

12. Mirzazadeh M, Mahmood MF, Majid FB, Biswas A, Belic M. Optical solitons in birefringent fibers with riccati equation method. Optoelectron Adv Mat Rapid Commun. (2015) 9:1032–6.

Google Scholar

13. Inc M, Aliyu AI, Yusuf A. optical solitons to the nonlinear Schrödinger's equation with Spatio-temporal dispersion using complex amplitude ansatz. J Mod Opt. (2017) 64:2273–80. doi: 10.1080/09500340.2017.1352047

CrossRef Full Text | Google Scholar

14. Baleanu D, Inc M, Aliyu AI, Yusuf A. Dark optical solitons and conservation laws to the resonance nonlinear Schrödinger equation with Kerr law nonlinearity. Optik. (2017) 147:248–55. doi: 10.1016/j.ijleo.2017.08.080

CrossRef Full Text | Google Scholar

15. Inc M, Aliyu AI, Yusuf A. Solitons and conservation laws to the resonance nonlinear Schrödinger equation with both spatio-temporal and inter-modal dispersions. Optik. (2017) 142:509–22. doi: 10.1016/j.ijleo.2017.06.010

CrossRef Full Text | Google Scholar

16. Inc M, Hashemi MS, Aliyu AI. Exact solutions and conservation laws of the Bogoyavlenskii equation, Acta Phys Polon A. (2018) 133:1133–7. doi: 10.12693/APhysPolA.133.1133

CrossRef Full Text | Google Scholar

17. Aliyu AI, Inc M, Yusuf A, Baleanu D. Symmetry analysis, explicit solutions, and conservation laws of a sixth-order nonlinear ramani equation. Symmetry. (2018) 10:341. doi: 10.3390/sym10080341

CrossRef Full Text | Google Scholar

18. Inc M, Aliyu AI, Yusuf A, Baleanu D. Novel optical solitary waves and modulation instability analysis for the coupled nonlinear Schrödinger equation in monomode step-index optical fibers. Superlattices Microstruct. (2018) 113:745–53. doi: 10.1016/j.spmi.2017.12.010

CrossRef Full Text | Google Scholar

19. Inc M, Aliyu AI, Yusuf A, Baleanu D. Optical solitons, conservation laws and modulation instability analysis for the modified nonlinear Schrödinger's equation for Davydov solitons. J Electromagn Waves Appl. (2018) 32:858–73. doi: 10.1080/09205071.2017.1408499

CrossRef Full Text | Google Scholar

20. Inc M, Aliyu AI, Yusuf A, Baleanu D. Optical solitary waves, conservation laws and modulation instability analysis to the nonlinear Schrödinger's equation in compressional dispersive Alven waves. Optik. (2017) 155:257–66. doi: 10.1016/j.ijleo.2017.10.109

CrossRef Full Text

21. Zhou Q, Mirzazadeh M, Ekici M, Sonmezoglu A. Analytical study of solitons in non-Kerr nonlinear negative-index materials. Nonlinear Dyn. (2016) 86:623–38. doi: 10.1007/s11071-016-2911-1

CrossRef Full Text | Google Scholar

22. Zhou Q. Analytical solutions and modulation instability analysis to the perturbed nonlinear Schrödinger equation. J Mod Opt. (2014) 61:500–3. doi: 10.1080/09500340.2014.897391

CrossRef Full Text

23. Taghizadeh N, Mirzazadeh M, Farahrooz F. Exact solutions of the nonlinear Schrodinger equation by the first integral method. J Math Anal Appl. (2011) 374:549–53. doi: 10.1016/j.jmaa.2010.08.050

CrossRef Full Text | Google Scholar

24. Inc M, Aliyu AI, Yusuf A, Baleanu D. Combined optical solitary waves and conservation laws for nonlinear Chen-Lee-Liu equation in optical fibers. Optik. (2018) 158:297–304. doi: 10.1016/j.ijleo.2017.12.075

CrossRef Full Text | Google Scholar