Minimum Spectral Bandwidth in Echo Seeded Free Electron Lasers

This paper examines the impact of non-linear longitudinal phase distortions on the spectral bandwidth in echo seeded free electron lasers (FELs). It extends the existing theory developed in Hemsing [1] for echo-enabled harmonic generation (EEHG) to include finite laser pulse durations. An analytic expression for the shape of the optimized longitudinal bunching envelope is derived, and is used to determine the laser and electron beam pulse durations that minimize the seeded bandwidth in the presence of arbitrary phase distortions. The time-bandwidth product (TBP) is also derived, and is shown that the TBP and the bandwidth increase by no more than $\sqrt{2}$ from their transform-limited values when the bandwidth is minimized.

Introduction

Externally seeded FELs use lasers to produce coherent high harmonic density modulations (bunching) in relativistic electron beams that are then used for the emission of coherent radiation at short wavelengths. Seeding is useful for overcoming the otherwise noisy output of SASE (self-amplified spontaneous emission) from these beams to generate narrowband FEL radiation. Besides improved longitudinal coherence, external seeding also enables control over the character of the FEL output pulses [2, 3], allowing adjustable coherent bandwidths [4] or the ability to produce multiple, phase locked pulses [5, 6], or multiple colors [7, 8].

Several different external seeding schemes have been proposed, and a few demonstrated (see e.g., [9] and references therein). Relevant specifically to this work, echo-enabled harmonic generation (EEHG) is a scheme that uses two external laser pulses (generally UV wavelengths) to efficiently generate bunching in the electron beam down to soft x-rays [10, 11]. In EEHG, the first laser produces a sinusoidal energy modulation in the electron beam that is typically only a few times the intrinsic slice energy spread. The beam then goes through a strong longitudinally dispersive section that folds over the sinusoids and creates a filamentary phase space structure in the particle distribution. The second laser then modulates the filamented phase space distribution, and a final dispersive section creates high harmonic bunching at short wavelengths in the current distribution. The beam then enters the FEL where coherent light is emitted and exponentially amplified.

A primary goal of seeding schemes is to minimize the FEL bandwidth and produce transform-limited pulses. In principle, the narrowest obtainable bandwidth is given by the inverse electron beam bunch length. In practice however, electron beams in modern FELs have distortions in the longitudinal phase space that mix additional frequencies into the harmonic up-conversion that spoil the purity of the final output spectrum [12–20]. In Hemsing [1] a general method was developed to calculate the impact of beam energy distortions through the broadening they introduce in the bunching spectrum (i.e., the Fourier transform of the current distribution). The broadening width was then used to set limits on the amplitude of common distortions to maintain near transform-limited seeding.

The magnitude, shape, and location of these distortions, within both the electron beam and the laser pulse, is an important factor in the optimization of external seeding schemes. The analysis in Hemsing [1] assumed infinitely long lasers that completely covered the electron beam (e-beam). In this limit, the bunching spectrum is predicted to be highly sensitive to e-beam energy variations because the whole beam contributes to the final spectrum and can have strong nonlinear portions in the head and tail. However, in practice, the seed lasers can be comparable in length to the electron beam or shorter, and positioned longitudinally within the e-beam to avoid seeding in the strong nonlinear portions. Shorter pulses naturally have broader bandwidths, so in order to achieve the narrowest harmonic bunching spectrum, a balance must be found between the transform limited bandwidth of the short laser and the broadening from the nonlinear phase contributions.

Here, using an extension of the formalism in Hemsing [1], we examine this more practically relevant case where the seed laser pulse can vary in duration, and also carry nonlinear temporal phase structures. This allows analysis of the bunching spectrum in the presence of nonlinearity in the electron beam and laser phase. From a general expression for the bandwidth, we show that laser pulses optimized in duration can produce much narrower bunching spectra once the e-beam energy distortions reach a threshold value. We also define the requirements that allow the laser phase to precisely compensate the e-beam distortions to obtain transform limited pulses.

The paper is arranged as follows. We first present an extension to the theory in Hemsing [1] that includes a finite seed laser pulse that produces a modulation with a longitudinal profile given by the function g(z). Under reasonable approximations, the bunching bandwidth can be calculated straightforwardly from g(z), the e-beam distribution f(z), and the combined phase distortions φ(z). Since the spectral-temporal properties in EEHG are inherited primarily from the second laser, we assume the first laser is infinite. Assuming that the EEHG bunching amplitude is optimized, we then derive an analytic expression for g(z) with a Gaussian seed laser. From this we retrieve the well-known m^−1/3 harmonic compression effect, and are able to calculate the transform-limited bandwidth. Arbitrary phase distortions are then included as a Taylor series, and their impacts to each order on the total bandwidth and time-bandwidth product (TBP) are then calculated analytically. We then derive the conditions on the laser pulse length and e-beam length to minimize the bandwidth, and study a few examples.

Mathematical Description

Notation closely follows that of Xiang [11]. Consider an EEHG electron beam transformation of the form,

$\begin{array}{l}{p}_1=p+A_1\text{sin}(k_{1}z)+\text{Δ}{p}_1(z),\\ z_1=z+B_1{p}_1/k_1,\\ p_2=p_1+A_2(z_1)sin\left[k_2{z}_1+{\psi }_2(z_1)\right]+\text{Δ}{p}_2(z_1),\\ z_2=z_1+B_2{p}_2/k_1.& (1)\end{array}$

where the normalized laser modulations are A_{1, 2} = ΔE_{1, 2}/σ_E, normalized dispersions are $B_{1,2}=k_1{R}_{56}^{(1,2)}{\sigma }_E/E$, the slice energy spread is σ_E, and E is the electron beam energy. Here, distinct from the analysis in Hemsing [1], we allow the second laser to have a finite pulse length, A₂(z₁), as well as a longitudinally dependent phase ψ₂(z₁). The first laser, A₁, is assumed to be ideal and infinite in length. Additional energy distortions in the electron beam, Δp₁ and Δp₂, are again modeled as occurring alongside the laser modulations.

The bunching spectrum near the harmonic peak k_E = a_Ek₁ = (n + mK)k₁ is given by

$\begin{array}{c}{b}_{n,m}(k)=e^{-{\xi }_E^2/2}{J}_n(-{\xi }_E{A}_1){\displaystyle \int e^{-iz(k-k_E)+i\phi (z)}}\\ \times f(z)J_m(-a_E{A}_2(z)B_2)dz,& (2)\end{array}$

where ξ_E = nB₁ + a_EB₂ is the EEHG scaling parameter, and f (z) is the longitudinal electron beam distribution function. The beam is assumed to have an uncorrelated Gaussian initial energy distribution. Similar to Hemsing [1], here we utilize the weakly-folding approximation which assumes that the energy structures satisfy B₁dΔp₁/dz ≪ k₁ and are small enough so that they do not lead to large changes in the phase space distribution after the first chicane. We also assume that the longitudinal variations in Δp₂, A₂, and ψ₂ are sufficiently slowly-varying that the full integral can be simplified by replacing z for z₁ in the function arguments. It is also assumed that the system is far from the minimum pulse duration limit [21].

With these approximations, the phase φ(z) captures the combined impact of energy distortions in the electron beam, Δp_{1, 2}, and the phase variation ψ₂ in the second laser,

$\begin{array}{ll}\phi (z)=-{\xi }_E\text{Δ}{p}_1(z)-a_E{B}_2\text{Δ}{p}_2(z)+m{\psi }_2(z).& (3)\end{array}$

The z-dependence of the second laser envelope A₂(z) is still within the argument of the J_m Bessel function, which complicates simple analytic solutions. We therefore search for an ansatz of the form,

$\begin{array}{ll}{J}_m(-a_E{A}_2(z)B_2)=g(z)J_m(-a_E{A}_2{B}_2),& (4)\end{array}$

where the imprint of the slowly-varying laser envelope is captured by the function g(z), determined shortly by approximate expansion. Note that in the limit of an infinitely long laser, g → 1. In anticipation of a Gaussian laser profile, A₂ = A₂(0) is the peak of the modulation.

With $b_{n,m}(k)=\int {\tilde{b}}_{n,m}(z)e^{-ikz}dz$, the longitudinal bunching factor can then be expressed as

$\begin{array}{ll}{\tilde{b}}_{n,m}(z)\approx {\bar{b}}_{n,m}f(z)g(z)e^{i{k}_{E}z+i\phi (z)},& (5)\end{array}$

where f(z)g(z) together form the z-dependent envelope, and ${\bar{b}}_{n,m}=e^{-{\xi }_E^2/2}{J}_n(-{\xi }_E{A}_1)J_m(-a_E{A}_2{B}_2)$ the optimized bunching amplitude [20]. Now the instantaneous spatial bunching frequency is just the z-derivative of the full longitudinal phase,

$\begin{array}{ll}{k}_z(z)=k_E+{\phi }^{\prime }(z).& (6)\end{array}$

The average frequency is then

$\begin{array}{ll}\langle k_z\rangle =\frac{{\displaystyle {\int }_{-\infty }^{\infty }}{k}_z(z){\left[f(z)g(z)\right]}^{2}dz}{{\displaystyle {\int }_{-\infty }^{\infty }}{\left[f(z)g(z)\right]}^{2}dz}=k_E+\text{〈}{\phi }^{\prime }(z)\text{〉},& (7)\end{array}$

and the spectral bandwidth of the harmonic bunching spike is

$\begin{array}{l}{\sigma }_k^2={\sigma }_{k_E}^2+\text{〈}{({\phi }^{\prime })}^2\text{〉}-{\text{〈}{\phi }^{\prime }\text{〉}}^2,\\ ={\sigma }_{k_E}^2+{\sigma }_{{\phi }^{\prime }}^2,& (8)\end{array}$

where the transform-limited bunching bandwidth is [22]

$\begin{array}{ll}{\sigma }_{k_E}^2=\frac{\int {\left[{(fg)}^{\prime }\right]}^{2}dz}{\int {(fg)}^{2}dz}.& (9)\end{array}$

This gives the bandwidth due to the combination of the laser modulation g(z) with the electron beam distribution function f(z). It is dominated by the shorter of the two if they coincide longitudinally. The bandwidth due to the nonlinear phase structures is given by ${\sigma }_{{\phi }^{\prime }}$.

Optimized Modulation

We consider the effect of a Gaussian laser pulse in the second echo modulator on the longitudinal profile of the bunching. This will enable us to calculate an approximate form for g(z), and thus the harmonic compression factor and scaling of the bunching bandwidth in the presence of the phase φ(z). Slippage in the modulator is ignored.

The optimum amplitude of the second laser from time-independent echo theory is $A_2=j_{m,1}^{\prime }/a_E{B}_2$, given by the requirement that J_m(a_EA₂B₂) is peaked, with $j_{m,1}^{\prime }=m+0.8087m^{1/3}$ the first zero of the Bessel function $J_m^{\prime }$. Small relative changes in the bunching due to variations from the optimum modulation are given by [20]

$\begin{array}{ll}\frac{\text{Δ}{\bar{b}}_{n,m}}{{\bar{b}}_{n,m}}=-{\left(\frac{\text{Δ}{A}_2}{A_2}\right)}^2\frac{{(j_{m,1}^{\prime })}^2-m^2}{2},& (10)\end{array}$

where m ≫ 1 is the harmonic of the second laser. Let us assume that the laser modulation envelope has an rms intensity duration σ_L/c,

$\begin{array}{ll}{A}_2(z)=A_2{e}^{-z^2/4{\sigma }_L^2}& (11)\end{array}$

To lowest order near the z = 0 peak, small changes in the laser amplitude vary according to $\text{Δ}{A}_2/A_2=-z^2/4{\sigma }_L^2$. This suggests that the bunching envelope function g(z) can be written as $g(z)\approx 1-{\left(\frac{z^2}{4{\sigma }_L^2}\right)}^2\frac{{(j_{m,1}^{\prime })}^2-m^2}{2}$. Mathematically, this looks like a lowest order expansion about z = 0 for small values of the second term. We posit then, that the functional dependance of g(z) may be modeled as a super-Gaussian distribution that has the same series expansion to lowest order:

$\begin{array}{l}g(z)\approx \text{exp}\left[-{\left(\frac{z^2}{4{\sigma }_L^2}\right)}^2\frac{{(j_{m,1}^{\prime })}^2-m^2}{2}\right]\\ =\text{exp}\left[-\frac{q^2}{2}{\left(\frac{z}{{\sigma }_g}\right)}^4\right]& (12)\end{array}$

where q = Γ(3/4)/Γ(1/4) ≈ 1/3. This form for the z-dependent bunching envelope induced by the laser closely matches exact solutions, as shown in Figure 1. The rms width of |g(z)|² is, to a good approximation,

$\begin{array}{ll}{\sigma }_g\approx \frac{{\sigma }_L}{m^{1/3}}.& (13)\end{array}$

FIGURE 1

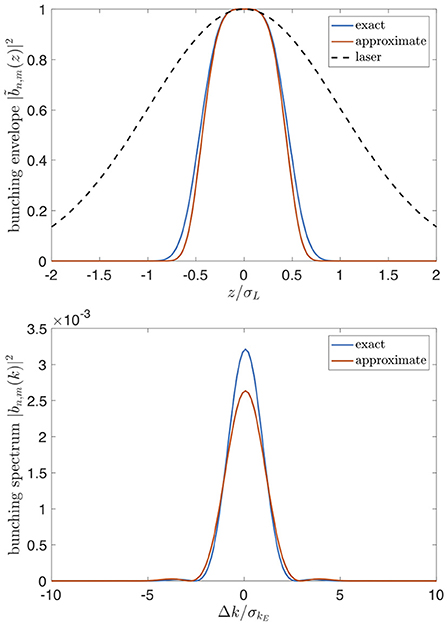
Figure 1. (Top) Bunching envelope and harmonic compression effect for m=50. The approximate super-Gaussian g(z) is slightly narrower than the exact solution. (Bottom) Corresponding frequency spectra.

Thus we recover the m^−1/3 scaling of the harmonic compression effect of the initial laser pulse length [13, 14], where for large harmonics ${(j_{m,1}^{\prime })}^2-m^2\approx 1.62m^{4/3}$. The FWHM has the same scaling but with a different proportionality, ${\text{Δ}}_g\approx \frac{1.4}{m^{1/3}}{\text{Δ}}_L$, where ${\text{Δ}}_L={\sigma }_L\sqrt{8ln2}$ is the FWHM of the seed laser intensity. These scalings are plotted against exact values in Figure 2.

FIGURE 2

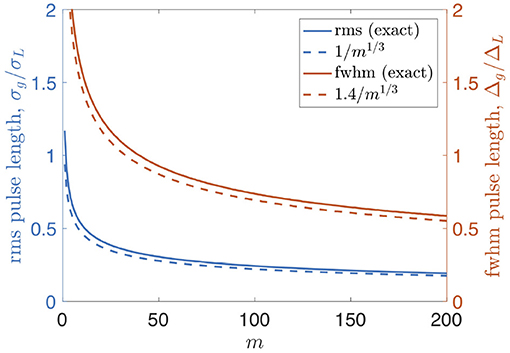
Figure 2. Normalized RMS and FWHM lengths of the bunching envelope from exact numerical calculations (solid lines) and from the super-Gaussian approximation (dashed lines).

Harmonic compression is the result of the high harmonics being increasingly more sensitive to the optimal modulation amplitude to produce bunching, so the longitudinal region of the Gaussian modulation that matches this condition becomes narrowed. The flattened, super-Gaussian form of g(z) is thus characteristic of the optimized bunching envelope for a Gaussian second seed laser. We note that it slightly underestimates the exact longitudinal width of the bunching envelope, as shown in Figures 1, 2. The rms value in (13) is low by about 10%, so the predicted spectral bandwidths can also differ slightly, but the scaling with m still holds.

With an analytic form for g(z) in hand, the transform-limited bandwidth in Equation (9) can be calculated for a specified electron beam distribution f(z). For the sake of simplified calculations, we assume that f(z) has the same, super-Gaussian form as g(z), but with a different rms, σ_z, and properly normalized,

$\begin{array}{ll}f(z)=\frac{2\sqrt{q}}{{\sigma }_z\text{Γ}(1/4)}exp\left[-q^2{\left(\frac{z}{{\sigma }_z}\right)}^4\right].& (14)\end{array}$

The rms transform-limited bandwidth of the bunching spectrum then has simple analytic solution that is approximately (see Supplementary Material),

$\begin{array}{ll}{\sigma }_{k_E}^2\approx \frac{1}{2}{\left(\frac{1}{{\sigma }_z^4}+\frac{1}{2{\sigma }_g^4}\right)}^{1/2}=\frac{1}{2}{\left(\frac{1}{{\sigma }_z^4}+\frac{m^{4/3}}{2{\sigma }_L^4}\right)}^{1/2}.& (15)\end{array}$

Similarly, the rms length of the bunching envelope $|{\tilde{b}}_{n,m}(z){|}^2$ is simply (see Equation 51),

$\begin{array}{ll}{\sigma }_b\approx \frac{1}{\sqrt{3}{\sigma }_{k_E}}.& (16)\end{array}$

Figure 3 shows how σ_kE varies with σ_L for different harmonics. Two limiting regimes can be identified. If the laser is much longer than the beam ${\sigma }_L\gg m^{1/3}{\sigma }_z$, then σ_kE is independent of m and is at its narrowest value. This is the regime studied in Hemsing [1]. In the opposite limit, with g(z) much shorter than the electron beam, the bandwidth grows like m^1/3 because of the harmonic compression effect. Note that the relative bandwidth decreases in this limit like m^2/3,

$\begin{array}{ll}{\sigma }_{{\nu }_E}=\frac{{\sigma }_{k_E}}{k_E}~\frac{{\sigma }_{{\nu }_L}}{m^{2/3}},& (17)\end{array}$

assuming k_E = a_Ek₁ ≈ mk₂, and σ_νL = 1/2σ_Lk₂ is the relative bandwidth of the laser.

FIGURE 3

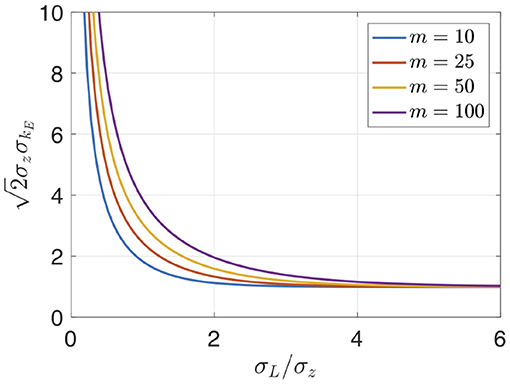
Figure 3. Transform-limited bandwidth σ_kE as a function of laser pulse length σ_L from Equation (15). Because of harmonic compression, the laser pulse length needs to increase slightly with increasing harmonic number to maintain a fixed bandwidth.

In general, the transform-limited bunching bandwidth σ_kE is set by the length of the laser on the electron beam. However, nonlinear phase structures φ(z) introduce additional bandwidth through the term ${\sigma }_{{\phi }^{\prime }}$ in Equation (8). Depending on the origin of the nonlinear phase structures, it may be possible to limit their impact on the total bandwidth by adjusting σ_kE, either with the laser pulse length σ_L or the electron beam length σ_z. In other words, what combination of σ_L or σ_z gives the smallest total bandwidth of the bunching spike σ_k? Consider the example of an electron beam with a quadratic chirp, as shown in Figure 4. On one hand, a narrowband laser with a longer pulse length could work, but it may extend over or add more of the undesirable nonlinearities that add bandwidth during the harmonic up-conversion. Conversely, a short laser pulse is intrinsically broadband, but may be less impacted by the presence of nonlinearities. As we will see, the optimization is straightforward once the phase is known, and the answer depends on the amplitude and source of the non-linearity.

FIGURE 4

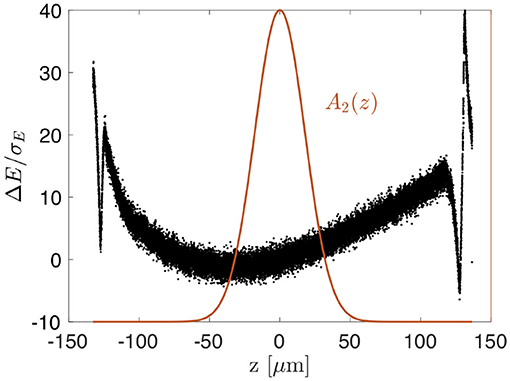
Figure 4. Example electron beam phase space distribution (from FERMI [Allaria, personal communication]) with dominant quadratic structure and higher order structure near the head and tail. The optimized laser pulse length to produce a minimum bandwidth depends on the amplitude of the non-linearities in the beam.

Simple Nonlinear Structure

Without regard to the origin of the nonlinear phase structure (i.e., laser phase ψ₂ or electron beam energy structures Δp_{1, 2}), let us first calculate the impact of generalized phase structures on the bunching bandwidth σ_k. We will then use the results to derive conditions for obtaining the minimum bandwidth.

Arbitrary continuous phase distortions can be expanded in a Taylor series about z = 0. Similar to the temporal phase in laser physics, we can expand the bunching phase φ(z) as,

$\begin{array}{ll}\phi (z)={\displaystyle \sum _{N=1}^{\infty }}\frac{{\varphi }_N}{N!}{z}^N,& (18)\end{array}$

where each ${\varphi }_N={\partial }^N\phi (z)/\partial z^N{|}_{z=0}$ is real. The absolute phase of the pulse ϕ₀ is ignored, as it does not affect the frequency or bandwidth. With Equation (6), the instantaneous frequency is $k_z(z)=k_E+{\varphi }_1+{\varphi }_{2}z+\frac{{\varphi }_3}{2}{z}^2+\dots$ Combined with (7) and (8), the bandwidth ${\sigma }_{{\phi }^{\prime }}^2$ associated with the energy distortions can be calculated analytically up to arbitrary order in N (see Supplementary Material).

Single Phase Term

The analysis is simplified by isolating a single term in the phase expansion,

$\begin{array}{ll}\phi (z)=\frac{{\varphi }_N}{N!}{z}^N.& (19)\end{array}$

The total bunching bandwidth is then written in terms of the nonlinear coefficient ϕ_N, as

$\begin{array}{ll}{\sigma }_k^2={\sigma }_{k_E}^2\left(1+\frac{G_N{\varphi }_N^2}{{\sigma }_{k_E}^{2N}}\right).& (20)\end{array}$

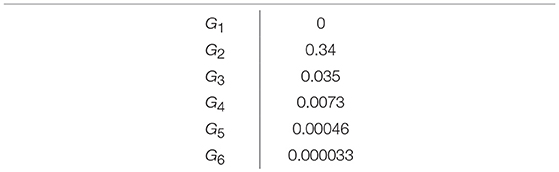
The second term is the excess bandwidth from the phase nonlinearity. The analytic expression for the numerical coefficient G_N is given in the Supplementary Material, and the lowest order numerical values are given in Table 1.

TABLE 1

Table 1. Numerical values of G_N.

The time-bandwidth product (TBP) of the bunching spectrum is the dimensionless product of the rms envelope length (16) and the rms bandwidth (20),

$\begin{array}{ll}TBP={\sigma }_b{\sigma }_k\approx \frac{1}{\sqrt{3}}\sqrt{1+\frac{G_N{\varphi }_N^2}{{\sigma }_{k_E}^{2N}}}.& (21)\end{array}$

Figure 5 plots shows how the TBP is impacted by the different order nonlinear phases. Here we see that larger order longitudinal phase structures have a larger effect on the TBP. This is in contrast to different order spectral phases in which only the even orders broaden the bunching bandwidth [14].

FIGURE 5

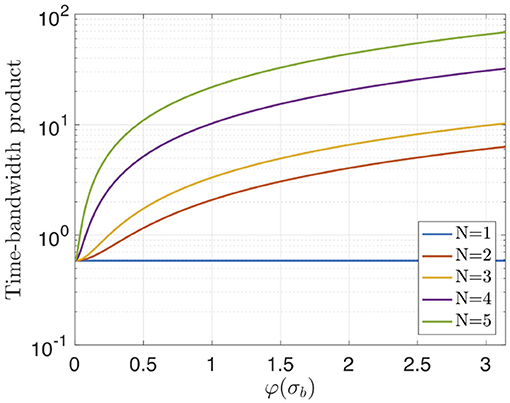
Figure 5. Time-bandwidth product as a function of the phase change over the rms bunching envelope $\phi ({\sigma }_b)={\varphi }_N{\sigma }_b^N/N!$. Results are predicted from Equation (21).

Minimum Bandwidth

With the expression for the bunching bandwidth in (20), it is straightforward to find the values of the laser pulse length or the electron beam length that minimize σ_k in the presence of a phase nonlinearity. In either case this amounts to finding the optimal value of σ_kE for a given ϕ_N. Assuming that ϕ_N is fixed with respect to the parameter being changed, the minimum bandwidth occurs when σ_kE can be adjusted to satisfy,

$\begin{array}{ll}{\sigma }_{k_E}^{2N}={\varphi }_N^2{G}_N(N-1).& (22)\end{array}$

The minimum total bandwidth then scales directly with optimal σ_kE,

$\begin{array}{ll}{({\sigma }_k)}_{min}={\sigma }_{k_E}\sqrt{\frac{N}{N-1}}.& (23)\end{array}$

An example of how the minimum bandwidth varies in general for different amplitude phase distortions is shown in Figure 6.

FIGURE 6

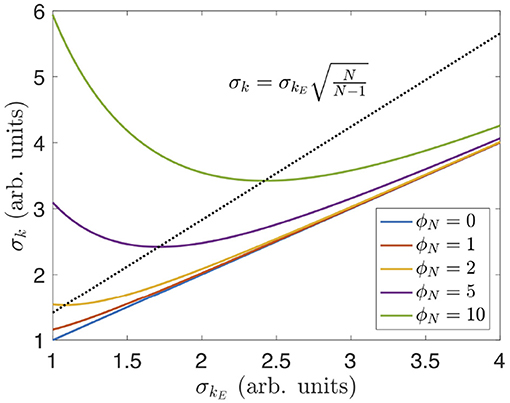
Figure 6. Total bandwidth vs. σ_kE for different N = 2 phase distortions. The minimum total bandwidth follows the dashed curve if ϕ_N is large enough (i.e., if Equation 22 is satisfied). Otherwise the minimum is set by the minimum possible value of σ_kE (σ_kE = 1, in this example for ϕ_N = 0 and 1).

The full expressions for the optimal electron beam length and laser pulse length are given in (60) and (62) the Supplementary Material. Consider the case where the transform-limited laser pulse length can be varied over a fixed length electron beam. If the phase distortion is large enough that ${\varphi }_N^2{G}_N(N-1)\gg 1/{(2{\sigma }_z^2)}^N$, then the laser that minimizes the bandwidth is given by

$\begin{array}{ll}{({\sigma }_L^2)}_{min}=\frac{m^{2/3}}{2\sqrt{2}{\left[{\varphi }_N^2{G}_N(N-1)\right]}^{1/N}}.& (24)\end{array}$

Figure 7 illustrates this scenario. Identical values of the dimensionless phase distortion ${\varphi }_N{\sigma }_z^N=20$ for different orders N show that, as N is increased, shorter and shorter laser pulses are needed to minimize the bandwidth, as given by Equation (24).

FIGURE 7

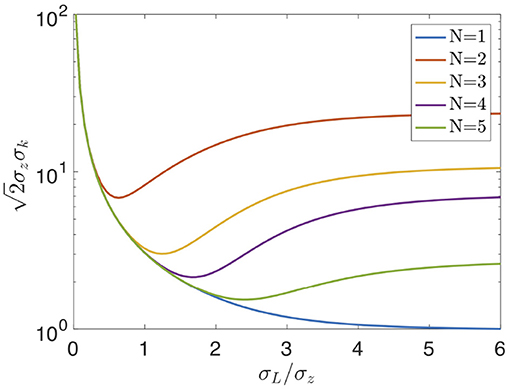
Figure 7. Scaled bunching bandwidth vs. relative laser duration for phase distortions of ${\varphi }_N{\sigma }_z^N=20$ caused by different orders. Harmonic m = 50 is modeled.

Alternatively, if the laser is held fixed and ${\varphi }_N^2{G}_N(N-1)\gg (m^{2/3}/\sqrt{8}{\sigma }_L^2{)}^N$, the optimal electron bunch length is

$\begin{array}{ll}{({\sigma }_z^2)}_{min}=\frac{1}{2{\left[{\varphi }_N^2{G}_N(N-1)\right]}^{1/N}}.& (25)\end{array}$

Note that this is independent of the harmonic, in contrast to the optimal laser pulse length.

The TBP at the minimum bandwidth is,

$\begin{array}{ll}TBP=\frac{1}{\sqrt{3}}\sqrt{\frac{N}{N-1}}.& (26)\end{array}$

It has the same dependence on the order of the phase distortion as σ_k; both approach their transform-limited values as N becomes large. Clearly the lowest order phase distortions have the greatest impact on both. These results shows that, if the phase distortions are described by a single polynomial term, then by proper optimization the TBP and the bandwidth will be no more than $\sqrt{2}$ times the transform-limit.

Inspection of the full expression for the TBP shows that it cannot be minimized simultaneously with the total bandwidth by adjustment of σ_kE alone, though it is possible if ϕ_N is not held fixed.

Quadratic Electron Beam Chirp

In modern FELs, it is common that the electron beam has some residual energy-time correlation in the phase space. These correlations can be the result of wakefields or other collective effects during compression and transport. They may be difficult to remove completely, and may be present at the entrance to the EEHG seeding system, or can develop within the EEHG beam line from collective effects [1]. In either case, their impact on the final bunching bandwidth can be calculated within the present framework and stated constraints.

Consider a purely quadratic energy chirp on the electron beam of the form,

$\begin{array}{ll}\text{Δ}p(z)=h_2{k}_2^2{z}^2.& (27)\end{array}$

The chirp amplitude is characterized by the dimensionless factor h₂. Assuming the second seed laser is transform-limited (ψ₂ = 0), the bunching phase can be written generically as [1],

$\begin{array}{ll}\phi (z)=-\eta \text{Δ}p(z),& (28)\end{array}$

where η = ξ_E or a_EB₂ depending on where the energy distortion occurs, as expressed in Equation (3). The nonlinear coefficient in (19) for N = 2 is then

$\begin{array}{ll}{\varphi }_2=-2\eta h_2{k}_2^2.& (29)\end{array}$

Plugging this into Equation (22) and optimizing the laser pulse length, one can show that if the amplitude of the quadratic beam chirp strongly satisfies

$\begin{array}{ll}{h}_2>\frac{\sqrt{3}}{4\eta {(k_2{\sigma }_z)}^2},& (30)\end{array}$

then the laser pulse length that minimizes the bandwidth is, from Equation (24),

$\begin{array}{ll}{({\sigma }_L)}_{min}\approx \frac{5m^{1/3}}{9k_2\sqrt{\eta h_2}}.& (31)\end{array}$

The corresponding relative bandwidth from Equation (23) is then

$\begin{array}{ll}{({\sigma }_{\nu })}_{min}=\frac{{({\sigma }_k)}_{min}}{k_E}\approx \frac{3\sqrt{\eta h_2}}{2m}.& (32)\end{array}$

Consider the realistic case of electron beams at the FERMI FEL [23] (for example in Figure 4), which can have a quadratic chirp of 30 MeV/ps² upstream of the 260 nm seeding sections. This corresponds to $h_2=2\times 10^{-6}$ for a slice energy spread of σ_E = 0.15 MeV. In this case Equation (30) is satisfied for beams longer than σ_z = 30 μm (100 fs), which is easily the case for the ps-scale beams at FERMI (assuming η = 1/2). The minimum bandwidth setting from (31) requires a laser pulse duration of 250 fs at the 36th harmonic and produces ${({\sigma }_{\nu })}_{min}=4.2\times 10^{-5}$. At the 64th harmonic, a 300 fs laser is optimum to generate ${({\sigma }_{\nu })}_{min}=2.3\times 10^{-5}$.

Linear Laser Frequency Chirp

Similar to quadratic structure on the electron beam, a linear laser chirp in the second seed laser introduces frequency-time correlations that mix into the harmonic up-conversion process and impact the final bunching bandwidth. If the electron beam phase space is flat, the bunching phase φ(z) in Equation (3) is only the laser phase times the harmonic,

$\begin{array}{ll}\phi (z)=m{\psi }_2(z).& (33)\end{array}$

It is useful to separate laser chirps according to whether they are defined in terms of a fixed pulse length as in Siegman [24] or in terms of a fixed bandwidth (e.g., [25]).

Fixed Laser Pulse Length

A linear frequency chirp corresponds to a quadratic phase of the form [24],

$\begin{array}{ll}{\psi }_2(z)=\alpha z^2.& (34)\end{array}$

Assuming the pulse length is fixed, α only affects the laser bandwidth. The quadratic coefficient of the bunching phase is then ϕ₂ = 2mα, and the analysis is the same as with a quadratic e-beam chirp with the replacement $-\eta h_2{k}_2^2=m\alpha$. If both the e-beam and the laser phase have quadratic structure, then their effect on the bunching cancels if $\eta h_2{k}_2^2=m\alpha$.

Fixed Laser Bandwidth

On the other hand, for a fixed-bandwidth laser pulse with rms intensity σ_kL, a linear frequency chirp that changes only the pulse length σ_L corresponds to a phase,

$\begin{array}{ll}{\psi }_2(z)=C{\sigma }_{k_L}^2{z}^2,& (35)\end{array}$

where the chirp is

$\begin{array}{ll}C=\pm \frac{\sqrt{x^2-1}}{x^2},& (36)\end{array}$

and

$\begin{array}{ll}x=\frac{{\sigma }_L}{{\sigma }_{L_0}}=2{\sigma }_L{\sigma }_{k_L}\ge 1,& (37)\end{array}$

is the pulse stretch factor. The laser bandwidth corresponds to transform-limited pulse length, σ_L0 = 1/2σ_kL.

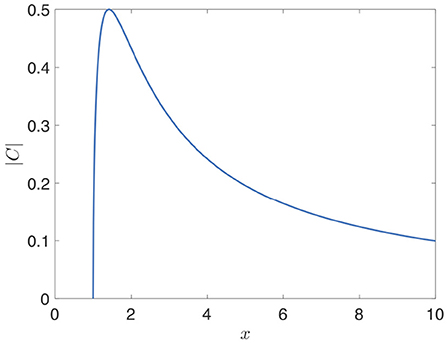
Note that the chirp grows from zero to a maximum of |C| = 1/2 when the pulse length is stretched by $x=\sqrt{2}$, and then decreases to zero as the pulse is stretched further. This is shown in Figure 8. This means that a strongly stretched pulse can have the same small chirp as a barely stretched pulse, even though the pulse lengths are quite different [25]. Wigner distributions of the laser pulses for different values of x are shown in Figure 9.

FIGURE 8

Figure 8. Chirp as a function of stretch factor, x = σ_L/σ_L0. From Equation (36).

FIGURE 9

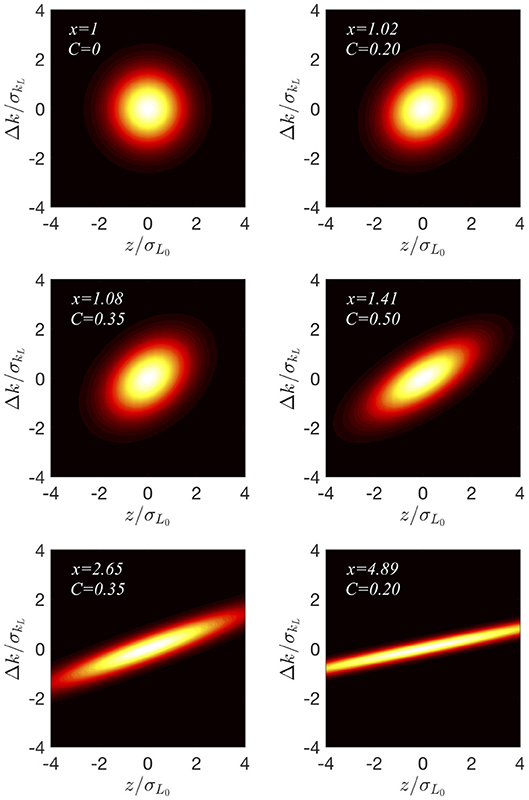
Figure 9. Wigner distributions of a chirped laser pulse with fixed bandwidth with x and C values from Equation (36).

The quadratic coefficient of the bunching phase is,

$\begin{array}{ll}{\varphi }_2=2mC{\sigma }_{k_L}^2.& (38)\end{array}$

The chirp is multiplied by the harmonic. Because the laser pulse length changes, the bandwidth σ_kE is also a function of the stretch factor x,

$\begin{array}{ll}{\sigma }_{k_E}^2=\frac{1}{2}{\left(\frac{1}{{\sigma }_z^4}+\frac{8m^{4/3}{\sigma }_{k_L}^4}{x^4}\right)}^{1/2}.& (39)\end{array}$

Inserting (38) into (22), one can see that if the pulse is stretched such that $\frac{2}{3}{m}^{2/3}(x^2-1)>1$, then there exists a finite length electron beam that minimizes the bandwidth, given approximately by (25),

$\begin{array}{ll}{({\sigma }_z)}_{min}\approx \frac{3^{1/4}}{2{\sigma }_{k_L}\sqrt{mC}}.& (40)\end{array}$

The optimum electron beam length is the smallest at the maximum chirp, C = 1/2, and is also less than σ_L0 unless the harmonic chirp is smaller than one, mC < 1. This can occur for both barely stretched or strongly stretched pulses. The minimum relative bandwidth from Equation (23) is then,

$\begin{array}{ll}{({\sigma }_{\nu })}_{min}=\frac{2{\sigma }_{{\nu }_L}}{3^{1/4}}\sqrt{\frac{C}{m}}.& (41)\end{array}$

Figure 10 shows how the bandwidths evolve for different σ_z.

FIGURE 10

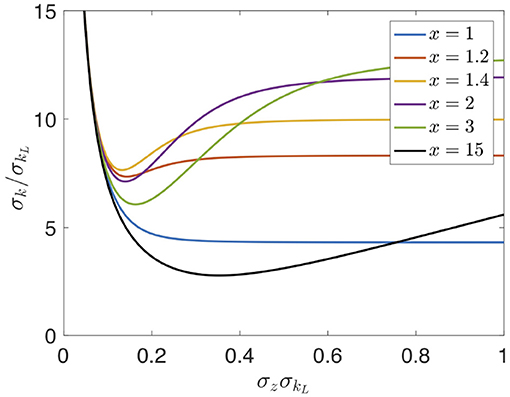
Figure 10. Scaled bandwidth vs. electron beam length for different values of a fixed-badwidth laser stretched with a linear chirp at m = 50.

Note that if the electron beam also has quadratic curvature, the laser chirp can be set to negate the bandwidth broadening if $C=-\eta h_2/m{\sigma }_{{\nu }_L}^2$, similar to [4]. Consider the example of the 4 GeV (σ_E = 0.45 MeV) beam at LCLS-II using EEHG to reach harmonic m = 130 of a 260 nm laser. Assuming σ_z = 15 μm (50 fs), and quadratic electron beam curvature $h_2=1\times 10^{-4}$ in the beam core, the transform-limited laser pulse to minimize the bandwidth from (30) is also 50 fs (assuming η = 1/2). This yields a relative bandwidth from (32) of ${({\sigma }_{\nu })}_{min}\approx 8\times 10^{-5}$. However, chirping the laser slightly $C=-\eta h_2/m{\sigma }_{{\nu }_L}^2\approx -1/4$, (stretching the pulse by about 3%), the bandwidth is reduced by $\sqrt{2}$ and is at the transform limit.

Finally, it is useful to look at a practical example in which the electron beam is long compared to the length of the second laser, irrespective of the chirp (e.g., FERMI). The total relative bandwidth from Equation (20) is then

$\begin{array}{ll}{\sigma }_{\nu }^2\approx \frac{4{\sigma }_{{\nu }_L}^2}{3x^2{m}^{4/3}}\left[1+\frac{3}{4}{m}^{2/3}(x^2-1)\right].& (42)\end{array}$

Inspection reveals that σ_ν grows with increasing x for high harmonics, so the minimum bandwidth is obtained only when the laser chirp is zero. The scaling with the harmonic number clearly differs according to whether the laser is fully compressed or stretched,

$\begin{array}{ll}{\sigma }_v\approx \{\begin{array}{ll}{\sigma }_{v_L}/m^{2/3}\hfill & (x=1)\hfill \\ {\sigma }_{v_L}/m^{1/3}\hfill & (x\gg 1).\hfill \end{array}& (43)\end{array}$

Figure 11 illustrates the bandwidth growth between the two regimes.

FIGURE 11

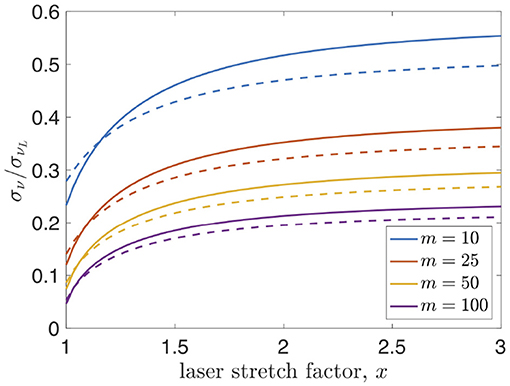
Figure 11. Relative bandwidth as the fixed-bandwidth second laser is stretched for different harmonics, assuming σ_z → ∞. Exact solutions are solid lines, and approximate solutions from Equation (42) are dashed lines. The disagreement with exact solutions is attributed to the super-Gaussian approximation for g(z).

Conclusions

Finite laser pulse length effects in EEHG FEL seeding are investigated. We have derived an approximate super-Gaussian form for the laser modulation g(z) and used it to calculate the spectral bandwidth of the harmonic bunching peak. The effects of nonlinear longitudinal variations in the e-beam energy and the laser temporal phase are studied by way of a general phase term φ(z). From the series expansion, the impact on the bandwidth and the TBP of the different order phase contributions is determined. All orders of the temporal phase contribute, in direct contrast to the spectral phase where the odd orders are negligible. Conditions on obtaining the minimum bandwidth are derived, which is shown to exceed the transform-limited bandwidth by at most $\sqrt{2}$, depending on the order of the nonlinearity.

Author Contributions

The author confirms being the sole contributor of this work and has approved it for publication.

Conflict of Interest Statement

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

This work was supported by the U.S. Department of Energy Contract No. DE-AC02-76SF00515 and the U.S. DOE Office of Basic Energy Sciences under award number 2017-SLAC-100382. The author would like to thank L. Giannessi for helpful discussions.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2019.00035/full#supplementary-material

References

1. Hemsing E. Bunching phase and constraints on echo enabled harmonic generation. Phys Rev Accel Beams. (2018) 21:050702. doi: 10.1103/PhysRevAccelBeams.21.050702

CrossRef Full Text | Google Scholar

2. Allaria E, Appio R, Badano L, Barletta W, Bas-sanese S, Biedron S, et al. Highly coherent and stable pulses from the FERMI seeded free-electron laser in the extreme ultraviolet. Nat Photon. (2012) 6:699. doi: 10.1038/nphoton.2012.233

CrossRef Full Text | Google Scholar

3. Allaria E, Castronovo D, Cinquegrana P, Craievich P, Dal Forno M, Danailov M, et al. Two-stage seeded soft-X-ray free-electron laser. Nat Photon. (2013) 7:913. doi: 10.1038/nphoton.2013.277

CrossRef Full Text | Google Scholar

4. Gauthier D, Ribič PCVR, De Ninno G, Allaria E, Cinquegrana P, Danailov MB, et al. Spectrotemporal shaping of seeded free-electron laser pulses. Phys Rev Lett. (2015) 115:114801. doi: 10.1103/PhysRevLett.115.114801

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Labat M, Joly N, Bielawski S, Szwaj C, Bruni C, Couprie ME. Pulse splitting in short wavelength seeded free electron lasers. Phys Rev Lett. (2009) 103:264801. doi: 10.1103/PhysRevLett.103.264801

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Gauthier D, Ribič PCVR, De Ninno G, Allaria E, Cinquegrana P, Danailov MB, et al. Generation of phase-locked pulses from a seeded free-electron laser. Phys Rev Lett. (2016) 116:024801. doi: 10.1103/PhysRevLett.116.024801

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Petralia A, Anania MP, Artioli M, Bacci A, Bellaveglia M, Carpanese M, et al. Two-color radiation generated in a seeded free-electron laser with two electron beams. Phys Rev Lett. (2015) 115:014801. doi: 10.1103/PhysRevLett.115.014801

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Roussel E, Ferrari E, Allaria E, Penco G, Di Mitri S, Veronese M, et al. Multicolor high-gain free-electron laser driven by seeded microbunching instability. Phys Rev Lett. (2015) 115:214801. doi: 10.1103/PhysRevLett.115.214801

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Hemsing E, Stupakov G, Xiang D, Zholents A. Beam by design: laser manipulation of electrons in modern accelerators. Rev Mod Phys. (2014) 86:897. doi: 10.1103/RevModPhys.86.897

CrossRef Full Text | Google Scholar

10. Stupakov G. Using the beam-echo effect for generation of short-wavelength radiation. Phys Rev Lett. (2009) 102:074801. doi: 10.1103/PhysRevLett.102.074801

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Xiang D, Stupakov G. Echo-enabled harmonic generation free electron laser. Phys Rev ST Accel Beams. (2009) 12:030702. doi: 10.1103/PhysRevSTAB.12.030702

CrossRef Full Text | Google Scholar

12. Huang Z, Ratner D, Stupakov G, Xiang D. Effects of energy chirp on echo-enabled harmonic generation free-electron lasers. In: Proceedings of the 2009 Free-Electron Laser Conference. Liverpool (2009). p. 127.

Google Scholar

13. Stupakov G. SLAC-PUB-14639. Effect of finite pulse length and laser frequency chirp on HGHG and EEHG seeding. SLAC-PUB-14639. (2011)

Google Scholar

14. Ratner D, Fry A, Stupakov G, White W. Laser phase errors in seeded free electron lasers. Phys Rev ST Accel Beams. (2012) 15:030702. doi: 10.1103/PhysRevSTAB.15.030702

CrossRef Full Text | Google Scholar

15. Geloni G, Kocharyan V, Saldin E. Analytical studies of constraints on the performance for eehg fel seed lasers (2011). arXiv:1111.1615.

Google Scholar

16. Penn G. Tech. Rep. NGLS Technical Note 35, LBNL (2012).

17. Zhao ZT, Wang D, Chen JH, Chen ZH, Deng HX, Ding JG, et al. First lasing of an echo-enabled harmonic generation free-electron laser. Nat Photon. (2012) 6:360. doi: 10.1038/nphoton.2012.105

CrossRef Full Text | Google Scholar

18. Penn G. Stable, coherent free-electron laser pulses using echo-enabled harmonic generation. Phys Rev ST Accel Beams. (2014) 17:110707. doi: 10.1103/PhysRevSTAB.17.110707

CrossRef Full Text | Google Scholar

19. Rebernik Ribič P, Roussel E, Penn G, De Ninno G, Giannessi L, Penco G, et al. Echo-enabled harmonic generation studies for the FERMI free-electron laser. Photonics. (2017) 4:19. doi: 10.3390/photonics4010019

CrossRef Full Text | Google Scholar

20. Hemsing E, Garcia B, Huang Z, Raubenheimer T, Xiang D. Sensitivity of echo enabled harmonic generation to sinusoidal electron beam energy structure. Phys Rev Accel Beams. (2017) 20:060702. doi: 10.1103/PhysRevAccelBeams.20.060702

CrossRef Full Text | Google Scholar

21. Penn G, Garcia B, Hemsing E, Marcus G. Constraints on pulse duration produced by echo-enabled harmonic generation. In: Proceedings, 38th International Free Electron Laser Conference, FEL2017. Santa Fe, NM (2018). p. MOP010.

Google Scholar

22. Lilly JM, Olhede SC. Bivariate Instantaneous Frequency and Bandwidth. IEEE Trans Signal Process. (2010) 58:591. doi: 10.1109/TSP.2009.2031729

CrossRef Full Text | Google Scholar

23. Giannessi L, Masciovecchio C. FERMI: present and future challenges. Appl Sci. (2017) 7:640. doi: 10.3390/app7060640

CrossRef Full Text | Google Scholar

24. Siegman A. Lasers. Sausalito, CA: University Science Books (1986).

Google Scholar

25. Huang S, Ding Y, Feng Y, Hemsing E, Huang Z, Krzywinski J, et al. Generating single-spike hard X-ray pulses with nonlinear bunch compression in free-electron lasers. Phys Rev Lett. (2017) 119:154801. doi: 10.1103/PhysRevLett.119.154801

PubMed Abstract | CrossRef Full Text | Google Scholar