Theoretical Platform for Liquid-Crystalline Self-Assembly of Collagen-Based Biomaterials

The collagen triple helix is a ubiquitous biomacromolecule used in acidic aqueous solutions as precursor in the fabrication of artificial compact bone and cornea and in tissue engineering. The primary architecture of these highly structured solid tissues is formed during the cholesteric liquid-crystalline stage of their morphogenesis. The theoretical platform that describes the coupled dynamics of phase-ordering and mass transfer developed, implemented and validated here can be used for optimal material design and plays a significant complementary role to future experimental studies. Based on uniaxiality assumption, we have recently developed and validated a theory for the free energy tailored for acidic collagenous dispersions. Here we significantly expand and generalize our previous study, by including biaxiality since cholesteric phases must have a degree of biaxiality. In this work, we first modify the proposed interchain interaction and excluded-volume contribution by use of the addition theorem for spherical harmonics. Then, the Euler-Lagrange minimization followed by expansion around I/N^* transition allows us to construct the free energy of ordering in terms of the phenomenological Landau–de Gennes formulation. Finally, we use the time-dependent Ginzburg-Landau equations to study the non-Fickian evolution of a single two dimensional cholesteric tactoid through a shallow quench from the isotropic to biphasic region of the phase diagram. Although equilibrium biaxiality is considerably low for these long-pitch cholesterics, we found that during self-assembly the biaxial order parameter achieves significant larger values than the equilibrium value. Additionally, the relaxed director field becomes both onion-like and defect-less, which is consistent with the twisted bipolar structure observed experimentally. The self-assembly simulations demonstrate that the formulated theoretical platform is not only consistent with previous theoretical and experimental studies but also able to be used to explore new routes for non-equilibrium collagen self-assembly. Taken together, this study deepens our understanding of cholesteric (chiral nematic N^*) mesophase in acidic solutions of tropocollagen, and suggests a systematic spatio-temporal model that is capable of being used to extract the engineering principles for processing of these sought-after biomaterials.

Introduction

Type I Collagen is composed of three left-handed polypeptide helices (denoted by [α1(I)]₂ [α2(I)]) twisted together to yield a right-handed triple helix. This rod-shaped biomacromolecule, also known as tropocollagen, commonly has a 1.5 nm bare diameter and 300 nm height. The tropocollagen falls into the class of fibrous proteins and is abundantly found in both soft and hard human's tissues, namely cornea, tendon, cortical bone, and more [1]. Over the past two decades, biomimetic fabrication of collagen-based biomaterials has received considerable attention in view of the abundant critical applications such as artificial bone [2–5] and cornea [6, 7] reconstruction. Moreover, for in-vitro replication of these collagenous biological tissues, there is fortunately no concern about supply because tropocollagen can be readily accessible through mammalian and non-mammalian resources [8]. Consequently, numerous promising applications of biomimetic fabrication of collagenous biomaterials [9–11] in conjunction with the availability of precursor play a central role in the drive to create the bioinspired collagen-based materials.

The structural pattern of tropocollagen rods bestows great structural-relation properties on collagenous biological materials and biomaterials. Furthermore, their structures are analogous with architecture of tropocollagen in liquid-crystalline states [12], hence these materials are called “solid analogs.” This correspondence establishes the role and impact of liquid-crystalline morphogenesis [13–15] and singles out liquid-crystal-based biomimetic material process engineering as a promising route to enhance the quality of collagen-based biomaterials or even to explore new ones [3, 16–19].

Normally, tropocollagen is immiscible in aqueous solutions due to its hydrophobicity. To attain a stable aqueous isotropic phase, which is the starting point of biomimetic fabrication, hydrophobicity of tropocollagen must be reduced by being dispersed in acidic solutions. Basically, numerous amine function groups that are good proton receptors are found along the tropocollagen backbone. Once these functional groups are protonated, the intrachain repulsion causes that, the semi-flexible (worm-like) backbones become uncoiled and essentially rigid rods. The existing interchain repulsion also impedes aggregation, in other words the rods have an effective diameter between two or three times the bare one [20–22]. Finally, due to being charge-carrier rigid rod-like molecules, tropocollagen is capable of exhibiting lyotropic cholesteric phase organization. For example, for an acetic acid concentration of [AC] ≈ 2, 900 mM, a phase transition from isotropic to chiral nematic (N^*) takes places at tropocollagen concentrations of [C] ≈ 88 mg/ml [21].

Although the primary architecture of these versatile biomaterials are formed at the molecular level (i.e., mesophasic stage), the focus has been at the tissue level [23] and studies on molecular level are few [21, 22]. Furthermore, to the best of authors' knowledge, theoretic studies of cholesteric self-assembly of aqueous acidic tropocollagen solutions have not been carried out, which also reflects the case of chiral nematic phase ordering in general [24–26]. To address this gap, we have recently developed, implemented, and validated a theoretical model tailored for self-assembly of tropocollagen dispersed in acidic aqueous solutions [20]. This thermodynamic theory [20], which is based on the uniaxiality assumption, has integrated microscopic mechanisms of mixing entropy and enthalpy, attraction, repulsion, twisting, excluded-volume, and chirality. In the present study, we lift the uniaxiality assumption by generalizing the free energy that includes biaxial effects. This is crucial for cholesteric materials because chiral nematic phase is described by two vectors: the director (n) and the chiral axis (h), additionally cholesterogens are intrinsically biaxial as discussed by Wulf [27] and Wright and Mermin [28]. Incorporation of the biaxial order parameter into the cholesteric self-assembly deserves consideration because biaxiality influences pattern-formation even in nematic mesophase, such as interfacial biaxiality under tangential director orientation [29–32], the biaxial core of singular disclinations [31, 33], and sometimes more pronounced biaxiality under time-dependent conditions than under static equilibrium [34]. For the above reasons we first include biaxiality in the model formulation stage and then focus on its emergence in bulk, defect core, and interfacial regions; which are of significant importance in all structured materials [30, 33, 35–37].

In our previous validated work [20], we showed that our thermodynamic model of acidic collagen solutions captures two key features: (i) the expected chimney diagram predicted by Flory and found experimentally for many lyotropic rod-like liquid-crystalline polymers [38], and (ii) the parabolic bi-phasic funnel in aqueous acidic collagenous solutions under increasing pH, where cholesteric tactoids (drops) emerge from isotropic phases. Study of cholesteric tactoids is important because of three main reasons: (i) tactoid formation process must occur in to chimney and funnel phase diagrams, which are the fingerprint of rod-like macromolecules. Thus, these cholesteric drops are a crucial element in the validation of thermodynamics of rod-shaped rigid macromolecules; (ii) these stable but deformable drops serve a sources of material properties information such as bulk Frank-Oseen-Mermin elasticity [27], novel coupled gradient contributions between nematic order parameter and collagen concentration, and the cholesteric pitch; (iii) characterizing and understanding the emergence, growth, annihilation, and coalescence of tactoids are essential to future developments of collagen-based material processing. To focus on collagen tactoids, as shown in Figure 1, we then target the dynamic of self-assembly through a shallow quench from isotropic phase into the bi-phasic funnel of the previously obtained phase diagram [20]. In contrast to the better known single component monomeric thermotropic tactoids, in the present case concentration is a conserved transport variable that need to be included. For this purpose, we formulate the coupled phase ordering/mass transfer Model C [39, 40] in order to derive the governing equations of collagen self-assembly. Afterward, we impose proper auxiliary conditions (e.g., initial and boundary conditions for the computational domain) on the obtained governing equations to capture a thorough spatio-temporal evolution of a single cholesteric tactoid—see Figure 2. This evolution has two steps: (i) emergence of a cholesteric nucleus in a continuous isotropic phase, (ii) followed by the formation of a stable chiral nematic tactoid coexisting with the isotropic phase.

FIGURE 1

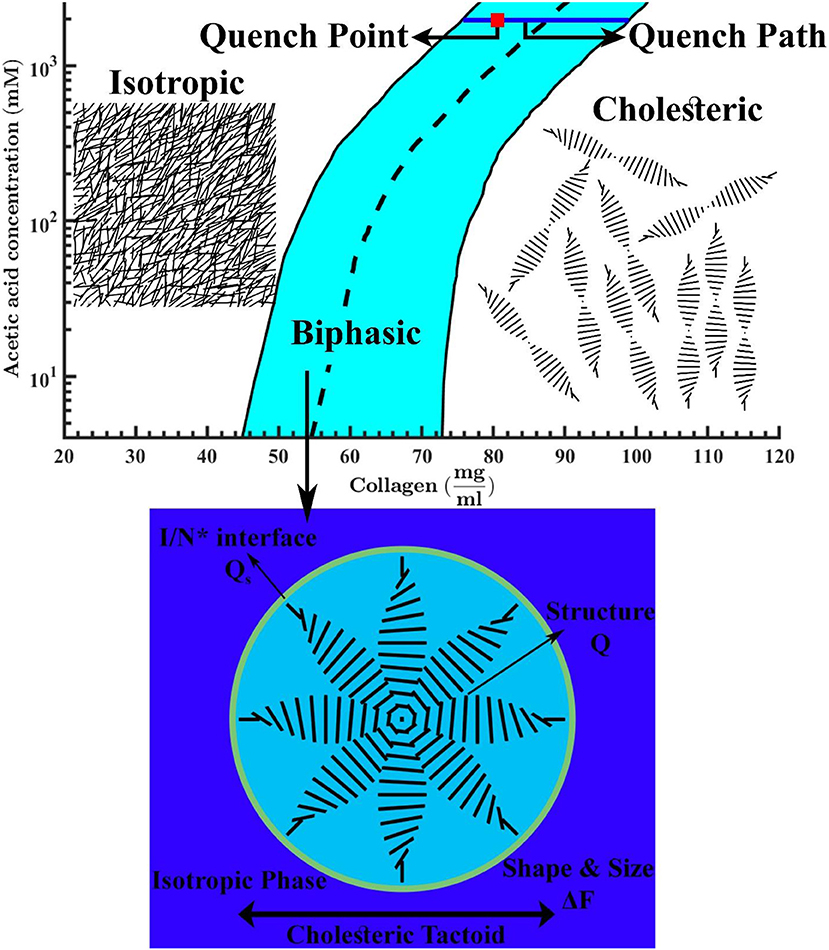
Figure 1. Phase diagram of tropocollagen in acidic aqueous solutions. The black solid lines are binodal curves and the black dashed line is phase transition boundary. The quench point and the evolution path are shown by a red square and a blue solid line, respectively. This figure is adapted from Khadem and Rey [20]. The schematics denote the isotropic phase at low collagen concentrations, a typical micron-sized cholesteric drop in an isotropic bulk at intermediate concentrations, and the chiral nematic (N^*) or cholesteric phase at higher concentrations.

FIGURE 2

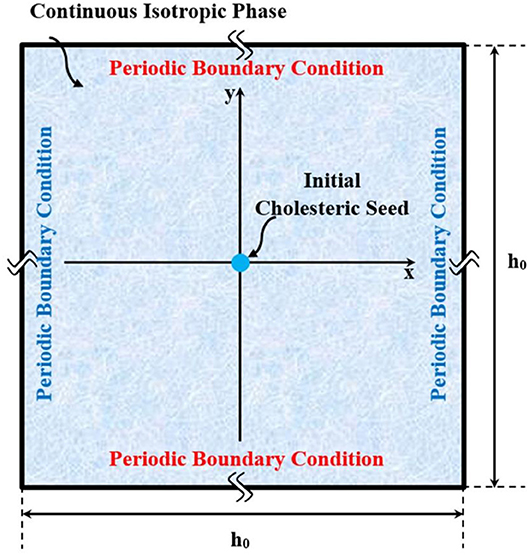
Figure 2. Schematic of the computational domain, in which a small chiral nematic drop is initially seeded, and allowed to naturally grow in coexistence with an isotropic phase.

In this work we restrict simulations to a single collagen tactoid with the aim of contributing to the evolving understanding of chiral phase ordering [24, 25, 41]. The simulations are also restricted to 2D. In principle, 3D spatio-temporal simulations can give a full picture of tactoid formation stages. Yet, from practical viewpoint, the present phase ordering/mass transfer coupled non-linear model with nano-to-micron scales becomes essentially intractable [42]. Furthermore, we have previously shown [43–45] that 2D simulations can provide invaluable predictions, and as discussed later on, in this study the important metrics of size, shape, and structure are not lost when using our 2D simulation box. In particular, we capture bulk disclinations, interfacial anchoring, interfacial biaxiality, growth modes, and self-selected shapes. Hence, this 2D study gives a necessary foundation for future 3D simulations.

The paper is organized as follows. Section Continuum Methodology for Simulation of Liquid-Crystalline Self-assembly of Tropocollagen Dispersed in Acidic Aqueous Solutions presents the methodology used in the formulation of self-assembly, including: (1) Formulation of the free energy for a system consisting of charged cholesterogen dispersed in a mixture of water solvent and mobile ions—see subsections Long-Range Description of Molecular Alignment to Total Free Energy Tailored for Tropocollagen Self-assembly in Acidic Aqueous Solutions. Subsection Long-Range Description of Molecular Alignment defines the Q-tensor. In Free Energy Contributions for Pure Charged Cholesterogens; Incorporation of Biaxial Order Parameter, the free energy of pure charged cholesterogen is developed taking into account the biaxial order parameter. In Mixing Free Energy of Binary Dispersions Consisting a Charged Cholesterogen and Small-Sized Solvent, the obtained free energy is generalized for a mixture of charged cholesterogen and small-sized solvent. In Total Free Energy Tailored for Tropocollagen Self-assembly in Acidic Aqueous Solutions, we discuss and incorporate other free energy contributions involved in the evolution of mesophasic state, such as the elasticity of Frank-Oseen-Mermin [28] and gradient contributions, and formation of the I/N^* interface. Thus, in Total Free Energy Tailored for Tropocollagen Self-assembly in Acidic Aqueous Solutions, the total free energy of system is formulated [2]. Formulation of governing equations along with the appropriate auxiliary conditions for simulation of liquid-crystalline self-assembly in which a cholesteric nucleus of tropocollagen is initially seeded and allowed to spontaneously growth in coexistence with isotropic phase—see subsections Governing Equations for Kinetics of Self-assembly; Orientational Relaxation, and Uphill Diffusion to Computational Details. In Governing Equations for Kinetics of Self-assembly; Orientational Relaxation, and Uphill Diffusion, the governing transport equations (Model C) are formulated. Finally, subsection Computational Details presents the implementation of self-assembly simulation for nucleation and growth of a single cholesteric tactoid coexisting with an isotropic phase. Section Results and Discussions, presents results of emergence and growth of a cholesteric tactoid. Lastly, the conclusions and nomenclature are summarized in sections Conclusions and Nomenclature, respectively.

Continuum Methodology for Simulation of Liquid-Crystalline Self-Assembly of Tropocollagen Dispersed in Acidic Aqueous Solutions

Long-Range Description of Molecular Alignment

The long-range orientational order in a liquid-crystalline phase is parameterized by a second-order symmetric traceless tensor called Q-tensor [14, 15, 46].

$\begin{array}{ll}\text{Q}=S(\text{n}\text{n}\text{ -}\delta /3)+\frac{\text{1}}{3}\text{P}(\text{m}\text{m}\text{ - }\text{l}\text{l})& (1)\end{array}$

where δ is the Kronecker delta. The orientation of a mesogen is characterized by the orthogonal director triad of (n, m, l). The degree of alignment along the uniaxial director, n, and biaxial director, m, are S and P, respectively. Due to the quadrupolar symmetry of Q-tensor, it possesses the salient feature of head-tail invariance of molecular alignment (i.e., n ≡ −n, m ≡ −m, and l ≡ −l). The largest absolute eigenvalue of Q-tensor equals to 2S/3 and the corresponding eigenvector is equivalent of uniaxial director, n. The difference between the absolute medium and smallest eigenvalues is 2P/3 and the eigenvector corresponds to the second largest absolute eigenvalue is biaxial director, m. Thus, in the isotropic and ordered phases, the Q-tensor becomes the 3 × 3 zero matrix, Q = 0, and non-zero matrix, Q ≠ 0, respectively.

The uniaxial and biaxial order parameters are also defined in terms of directors/Q-tensor or the normalized orientational distribution function on the unit sphere, ψ(u), for any given molecular orientation, u:

$\begin{array}{ll}\text{S}={\displaystyle \int {\text{P}}_2\left(\cos (\theta )\right)\psi \left(u\right)\text{ d}\Omega =3n\cdot Q\cdot n/2}& (2)\end{array}$

$\begin{array}{ll}\text{P}={\displaystyle \int \Delta \left(\theta ,\varphi \right)\psi \left(u\right)\text{ d}\Omega =3\left(m\cdot Q\cdot m-1\cdot Q\cdot 1\right)/2}& (3)\end{array}$

dΩ = sin(θ) dθdφ represents a solid angle, and θ and φ are the polar and azimuthal angles. Δ(θ, φ) is defined as 3sin²(θ)cos(2φ)/2. As explained below, P₂(cos(θ)) and Δ(θ, φ) are representative of uniaxiality and biaxiality, respectively. In addition, the normalized distribution function, employed in Equations (2, 3), implies following constraint [47]:

$\begin{array}{ll}{\displaystyle \int }\psi (\text{u})d\Omega =1& (4)\end{array}$

Free Energy Contributions for Pure Charged Cholesterogens; Incorporation of Biaxial Order Parameter

The total dimensionless Helmholtz free energy per particle, $\tilde{\text{F}}$, for a dispersion comprising N_A charged cholesterogens is [20, 48, 49]:

$\begin{array}{l}\tilde{\text{F}}=\frac{\beta \text{F}}{{\text{N}}_{\text{A}}}\text{ = }{\beta \mu }^{\text{o}}(\text{T})-1+\text{ln}{\text{c}}_{\text{A}}\text{+ }\sigma (\psi (\text{u}))\text{ + }{\text{B}}_{\text{2}}(\psi (\text{u}))\\ +\text{M}(\psi (\text{u}))& (5)\end{array}$

where β, ${\mu }^{\text{o}}(\mathrm{\text{T}})$, and c_A stand for thermal energy, standard chemical potential and number density, respectively. The last three terms in Equation (5) account for the contribution of molecular orientation (i.e., uniaxiality and biaxiality) in the mesophasic state. σ(ψ(u)) describes the decrease of orientational entropy upon alignment of the mesogenic molecules.

$\begin{array}{ll}\sigma (\psi (\text{u}))\text{=}\int \psi (\text{u})\text{ln}(\text{4}\pi \psi (\text{u}))\text{d}\Omega & (6)\end{array}$

Since we focus on rod-like rigid mesogen, the second virial approximation is capable of accurately describing the excluded volume effect, given by Odijk [49] and Drwenski et al. [50]:

$\begin{array}{ll}{\text{B}}_2(\psi (\text{u}))={\text{c}}_{\text{A}}{\overline{\upsilon }}_{\text{AA}}\rho (\psi (\text{u}))& (\mathrm{7a})\end{array}$

$\begin{array}{ll}\rho (\psi (\text{u}))=\frac{4}{\pi }\iint \Gamma (\gamma )\psi (\text{u})\psi ({\text{u}}^{\prime })\text{d}\Omega \text{d}{\Omega }^{\prime }& (\mathrm{7b})\end{array}$

$\begin{array}{l}\Gamma (\gamma )=|sin(\gamma )|\\ \times \left\{1+\text{h}\left[-\text{ln}|sin(\gamma )|-\text{ln}(2)+\frac{1}{2}\right]\right\}& (\mathrm{7c})\end{array}$

${\overline{\upsilon }}_{\mathrm{\text{AA}}}$ is the average excluded volume defined as $\pi {\mathrm{\text{D}}}_{\mathrm{\text{eff}}}{\mathrm{\text{L}}}^{\mathrm{\text{2}}}\mathrm{\text{/4}}$ in which L and D_eff denote contour length and effective diameter of tropocollagen. D_eff has a dependence on the bare diameter, D = 1.5 nm, and concentration [20]. To take biaxiality into consideration, in accordance with Drwenski [51, 52] and Matsuyama and Crystals [53], we make use of the addition theorem for spherical harmonics to express the angle between two rods, γ, in terms of the polar, θ, and azimuthal, φ, angles in spherical coordinate:

$\begin{array}{ll}{\text{P}}_2(\text{cos}(\gamma ))={\text{P}}_2(\text{cos}(\theta )){\text{P}}_2(\text{cos}({\theta }^{\prime }))+\Delta (\theta ,\phi )\Delta ({\theta }^{\prime },{\phi }^{\prime })/3& (8)\end{array}$

First term in Equation (8) is independent from azimuthal angle and represents uniaxiality. Second term is related to biaxial contribution and has the dependence on both polar and azimuthal angles.

The intermolecular interaction and angle between rods interchangeably affect each other because the electrostatic repulsion and twisting favors perpendicular orientation while the van der Waals attraction prefers the parallel alignment (i.e., nematic phase) [49, 50, 54]. Hence, based on our previous work [20] and [51], we suggest the net interchain potential expressed by

$\begin{array}{ll}{\text{βU}}_{\text{i}}=\text{β}\left({\text{U}}^{\prime \text{elc}}-{\text{U}}^{\prime \text{MS}}\right){\upsilon }_{\text{A}}{\text{P}}_2\left(\cos \left(\text{γ}\right)\right)& (9)\end{array}$

where υ_A is the volume of an individual rigid rod, ${\upsilon }_{\mathrm{\text{A}}}=\pi {\mathrm{\text{D}}}_{\mathrm{\text{eff}}}^2\mathrm{\text{L/4}}$. U'^elc and U'^MS are parameters of electrostatic repulsion and a positive constant, respectively. The contribution of intermolecular interaction, M(ψ(u)), is then obtained by taking average over all possible rod configurations [20]:

$\begin{array}{ll}\text{M}(\psi (\text{u}))=\frac{3}{2}\beta \text{U}{\text{c}}_{\text{A}}{\upsilon }_{\text{A}}^{\text{2}}\text{Q}\text{:}\text{Q}& (10)\end{array}$

U = U^elc − U^MS is called the potential of the orientation-dependent intermolecular interactions where U^elc and U^MS are the strength of electrostatic repulsion and Maier-Saupe constant that is a positive constant independent of temperature. Note that Q:Q is related to uniaxial and biaxial order parameters by 2(S²+P²/3)/3.

We note that the effective diameter reflects the intermolecular repulsion, or to put it another way, the effective thickness of the attached ions on the backbone of tropocollagen. This effective thickness is called double-layer thickness, ακ^-1 [49, 50]:

$\begin{array}{ll}{\text{D}}_{\text{eff}}=\text{D}+{\alpha \kappa }^{\text{-1}}& (11)\end{array}$

α and κ^-1, which are defined as follows, are parameter of double-layer thickness and Debye screening length, respectively:

$\begin{array}{l}\alpha ={\text{lnA}}^{\text{′}}+{\gamma }_{\text{E}}+\text{ln}(2)-\frac{1}{2}\\ -\frac{4}{\text{π}}{\left[\left|\sin \left(\text{γ}\right)\right|\text{Ei}\left(-\frac{{\text{A}}^{\prime }}{\left|\sin \left(\text{γ}\right)\right|}\right)\right]}_{\text{i}}& (\mathrm{12a})\end{array}$

$\begin{array}{ll}\text{A}\prime =\text{A}\frac{{\text{e}}^{\text{κD}}}{\text{κD}},\text{A}=2\text{π}{\Lambda }^2{\text{λ}}_{\text{B}}\text{D}& (\mathrm{12b})\end{array}$

$\begin{array}{ll}{\left[\text{f}\left(u,u^{\prime }\right)\right]}_{\text{i}}=\frac{1}{16{\text{π}}^2}{\displaystyle \int {\displaystyle \int \text{f}\left(u,u^{\prime }\right)\text{d}\Omega \text{d}{\Omega }^{\prime }}}& (\mathrm{12c})\end{array}$

$\begin{array}{ll}{\text{κ}}^{-1}={\left(8{\text{πλ}}_{\text{B}}{\text{N}}_{\text{avo}}\in \right)}^{-1/2}& (\mathrm{12d})\end{array}$

$\begin{array}{ll}\in =\frac{1}{2}{\displaystyle \sum _{\text{i}}{\text{m}}_{\text{i}}{\text{Z}}_{\text{i}}^2}& (12e)\end{array}$

where λ_B, N_avo, ϵ, m, Z, Ei(•), γ_E, and Λ are the Bjerrum length, Avogadro's number, ionic strength, molar concentration, charge number, the exponential integral defined as $\mathrm{\text{Ei}}(\mathrm{\text{x}})\mathrm{\text{=}}-{\text{∫}}_{\mathrm{\text{-x}}}^{\text{∞}}\mathrm{\text{exp}}(\mathrm{\text{-t}})/\mathrm{\text{t }}\mathrm{\text{dt}}$, Euler constant equals to 0.5772, and linear charge density. A detailed account of parameters' values, their selection and physical significance and physical properties for aqueous acidic collagen I solutions is given in Khadem and Rey [20].

Mixing Free Energy of Binary Dispersions Consisting a Charged Cholesterogen and Small-Sized Solvent

The mixing free energy of the binary solution is given by Matsuyama and Kato [48]

$\begin{array}{ll}\text{F}=\text{Δ}{\text{F}}_{\text{mixing}}({\text{N}}_{\text{A}},{\text{N}}_{\text{I}})={\text{F}}^{\text{s}}({\text{N}}_{\text{A}},{\text{N}}_{\text{I}})-{\text{F}}^{\text{s}}({\text{N}}_{\text{A}},0)-{\text{F}}^{\text{s}}(0,{\text{N}}_{\text{I}})& (13)\end{array}$

where ${\text{F}}^{\text{s}}({\text{N}}_{\text{A}},{\text{N}}_{\text{I}})$, ${\text{F}}^{\text{s}}({\text{N}}_{\text{A}},0)$ and ${\text{F}}^{\text{s}}(0,{\text{N}}_{\text{I}})$ are free energies of solution, pure anisotropic component dispersed in isotropic state and isotropic component, respectively. Thus, in this subsection, we shall first derive the free energy of solution, and then formulate the mixing free energy of a binary dispersion by use of Equation (13).

Substituting Equations (7, 10) into Equation (5) leads to the free energy of pure charged chiral nematic rods. The free energy for binary mixture of charged chiral mesogen and small-sized solvent (water in our case)—denoted by subscript A and I, respectively—is then formulated as

$\begin{array}{l}\text{β}{\text{F}}^{\text{s}}={\text{N}}_{\text{A}}{\beta \mu }_{\text{A}}^{\text{o}}+{\text{N}}_{\text{I}}{\beta \mu }_{\text{I}}^{\text{o}}-{\text{N}}_{\text{A}}-{\text{N}}_{\text{I}}+{\text{N}}_{\text{A}}\text{ln}{\text{c}}_{\text{A}}+{\text{N}}_{\text{I}}\text{ln}{\text{c}}_{\text{I}}+{\text{N}}_{\text{A}}\sigma \\ (\psi (\text{u}))+{\overline{\upsilon }}_{\text{AA}}{\text{N}}_{\text{A}}{\text{c}}_{\text{A}}\rho (\psi (\text{u}))+2{\overline{\upsilon }}_{\text{AI}}{\text{N}}_{\text{I}}{\text{c}}_{\text{A}}+{\overline{\upsilon }}_{\text{II}}{\text{N}}_{\text{I}}{\text{c}}_{\text{I}}\\ +{\text{N}}_{\text{A}}\beta \text{U}{\text{c}}_{\text{A}}{\upsilon }_{\text{A}}^2\left(\text{S}{(\psi (\text{u}))}^2+\frac{1}{3}\text{P}{(\psi (\text{u}))}^2\right)& (14)\end{array}$

Equation (14) is not usable unless the unknown normalized distribution function, ψ(u), is known. To formulate the normalized distribution function, the total free energy of system subjected to the normalizing constraint, given by Equation (4), is minimized using Euler-Lagrange method. This minimization yields an irreducible algebraic integral equation expressed by

$\begin{array}{l}\text{ln}(4\pi \psi (\theta ,\phi ))={\eta }^{\text{′}}-2\text{βU}{\text{c}}_{\text{A}}{\upsilon }_{\text{A}}^2\left\{\text{S}{\text{P}}_2(\text{cos}(\theta ))+\frac{1}{3}\text{P}\Delta (\theta ,\phi )\right\}\\ -\frac{8}{\text{π}}{\overline{\upsilon }}_{\text{AA}}{\text{c}}_{\text{A}}{\displaystyle \int \text{Γ}\left(\text{γ}\right)\text{ψ}\left({\text{θ}}^{\prime },\phi \right)\text{d}{\text{Ω}}^{\prime }}& (15)\end{array}$

Simplicity of free energy expression is essential since our ultimate objective is the self-assembly simulation which in itself is computationally complex. A heavy computational load is expected because the self-assembly process covers a wide range of length scale (i.e., ranging from nano- to macro-scale) and it may go through a variety of complex microscopic mechanisms [41, 55–59]. Thus, to improve tractability, we expand the functional part of Equation (15), Γ(γ), in terms of the second Legendre polynomial by use of Equation (8):

$\begin{array}{l}\Gamma (\gamma )\approx \frac{\pi }{4}-\frac{5\pi }{32}\left(1-\frac{11}{8}\text{h}\right)\\ \left\{{\text{P}}_2(\text{cos}(\theta )){\text{P}}_2(\text{cos}({\theta }^{\prime }))+\frac{1}{3}\Delta (\theta ,\phi )\Delta ({\theta }^{\prime },{\phi }^{\prime })\right\}& (16)\end{array}$

Having substituted Equation (16) into Equation (15), the normalized distribution function is obtained:

$\begin{array}{ll}\text{ψ}(\text{θ},\text{φ})=\frac{\text{exp}\left(\text{W}\left\{\text{S}{\text{P}}_2(\text{cos}(\theta ))+\text{P}\Delta (\theta ,\text{φ})/3\right\}\right)}{{\text{I}}_{00}}& (17)\end{array}$

where the I₀₀ is a definite integral defined as

$\begin{array}{ll}{\text{I}}_{00}(\text{S},\text{P},\text{W})={\displaystyle \underset{0}{\overset{1}{\text{∫}}}}{\displaystyle \underset{0}{\overset{1}{\text{∫}}}}\text{exp}(\text{W}\{\text{S}{\text{P}}_2(\text{x})+\text{P}\Delta (\text{x},\text{y})/3\})\text{ dxdy}& (18)\end{array}$

W is known as the net cholesteric potential, which is similar to Khadem and Rey [20] and can be parameterized as

$\begin{array}{ll}\text{W}={\text{α}}_{\text{w}}{\varphi }_{\text{A}}& (\mathrm{19a})\end{array}$

$\begin{array}{ll}{\text{α}}_{\text{w}}=\frac{5}{4}\left(1-\frac{11}{8}\text{h}\right)\frac{\text{L}}{{\text{D}}_{\text{eff}}}-\frac{\text{π}}{2}{\text{D}}_{\text{eff}}^2\text{βUL}& (\mathrm{19b})\end{array}$

ϕ_A is the effective volume fraction and $\text{h}={(\kappa {\text{D}}_{\text{eff}})}^{-1}$. α_W is assumed to only be dependent on concentration of acid throughout the evolution—a reasonable assumption because α_W is mainly affected by concentration of acid [20].

Next the mixing free energy, Equations (20a–c), is obtained by use of Equations (13, 14, 17). Detailed account of such algebraic derivation are given in Khadem and Rey [20] and Odijk [48]. Note that hereafter, for convenience, we use ϕ to represent the effective volume fraction of tropocollagen—it can be related to the concentration of tropocollagen in units of mg of tropocollagen pre ml of solution by C = ϕ/α_c where α_c is a unit conversion factor. The dimensionless mixing free energy density is:

$\begin{array}{ll}{\tilde{\text{f}}}_{\text{mxing}}={\tilde{\text{f}}}_{\text{iso}}+{\tilde{\text{f}}}_{\text{h}}& (\mathrm{20a})\end{array}$

$\begin{array}{ll}{\tilde{\text{f}}}_{\text{iso}}=\frac{\varphi \text{ln}(\varphi )}{\text{n}}+(1-\varphi )\text{ln}(1-\varphi )+\chi \varphi (1-\varphi )& (\mathrm{20b})\end{array}$

$\begin{array}{ll}{\tilde{\text{f}}}_{\text{h}}=\frac{\varphi }{\text{n}}\left[\frac{3}{4}\text{W}\text{Q}:\text{Q}-\text{ln}({\text{I}}_{00}(\text{W},\text{S},\text{P}))\right]& (\mathrm{20c})\end{array}$

where n stands for number of segments on tropocollagen backbone. ${\tilde{\text{f}}}_{\mathrm{\text{iso}}}$ and ${\tilde{\text{f}}}_{\mathrm{\text{h}}}$ describe different physics; the former explains the phase separation which is the well-known Flory-Huggins equation and the latter controls the phase transition (i.e., homogenous contribution). In the absence of biaxiality, P = 0, the obtained mixing free energy, Equations (20a–c), is reduced to the validated free energy functional given in Khadem and Rey [20] which was validated with experimental data of tropocollagen and with previous theoretical studies. It is worth mentioning that with further assumptions the obtained free energy density leads to the formulation given in Matsuyama and Kato [48] as well as the well-established theory of Onsager—see ESI of Khadem and Rey [20] for further discussion. For numerical tractability, similar to Matsuyama [51] and Matsuyama and Kato [48], we make use of a Taylor expansion in vicinity of I/N^* to expand Equation (20c) in a power series of order parameters, SⁱP^j–the resulting polynomial is the phenomenological Landau-de Gennes (LdG) theory [60]:

$\begin{array}{ll}{\tilde{\text{f}}}_{\text{h}}=\frac{\text{a}}{2}\text{Tr}({\text{Q}}^2)-\frac{\text{b}}{3}\text{Tr}({\text{Q}}^3)+\frac{\text{c}}{4}{\left(\text{Tr}({\text{Q}}^2)\right)}^2& (\mathrm{21a})\end{array}$

$\begin{array}{ll}\text{a}(\varphi )=\frac{3}{2}\frac{{\alpha }_{\text{w}}}{\text{n}}\left(1-\frac{{\alpha }_{\text{w}}\varphi }{5}\right){\varphi }^2& (\mathrm{21b})\end{array}$

$\begin{array}{ll}\text{b}(\varphi )=\frac{9}{70}\frac{{\alpha }_{\text{w}}^3}{\text{n}}{\varphi }^4& (\mathrm{21c})\end{array}$

$\begin{array}{ll}\text{c}(\varphi )=\frac{{\alpha }_{\text{w}}}{10}\text{b}\varphi & (\mathrm{21d})\end{array}$

Although self-assembly simulations by use of the Equations (21a–d) is appreciably more tractable than with Equation (20c), it should be noted that the used expansion may affect the accuracy of simulations in the cases of deep quenches. However, this study only focuses on the self-assembly of shallow quenches into biphasic region which is a narrow region around I/N^* boundary, see Figure 1.

An order-disorder phase transition takes place if and only if W = α_Wϕ = α_Wα_cC > 5 to make the coefficient of second invariant of Q-tensor, a, negative. The derived LdG coefficients satisfy two general theoretical expectations; (1) the first-order phase transition (i.e., B ≠ 0), and (2) two minima correspond to isotropic and ordered phases (i.e., A<0 and C>0) [46]. Furthermore, in the cholesteric phase, W can be about 10, and under such conditions the proposed LdG coefficients becomes similar to the well-established lyotropic LCP Doi's model, were b ≈ c [14, 15, 61].

Total Free Energy Tailored for Tropocollagen Self-Assembly in Acidic Aqueous Solutions

In addition to ${\tilde{\text{f}}}_{\mathrm{\text{mxing}}}$ which is capable of describing phase separation and an order–disorder phase transition, for constructing the total free energy of mesogenic solutions, the contributions of gradients should be taken to account [62–64]:

$\begin{array}{ll}{\tilde{\text{F}}}_{\text{net}}={\displaystyle \underset{\tilde{\text{V}}}{\int }}\left({\tilde{\text{f}}}_{\text{iso}}+{\tilde{\text{f}}}_{\text{h}}+{\tilde{\text{f}}}_{\text{e}}+{\tilde{\text{f}}}_{\text{cg}}+{\tilde{\text{f}}}_{\text{c}}\right)\text{d}\tilde{\text{V}}& (\mathrm{22a})\end{array}$

$\begin{array}{l}{\tilde{\text{f}}}_{\text{e}}=\frac{1}{2}{\left(\frac{\text{ξ}}{{\text{h}}_0}\right)}^2[{\left[\tilde{\nabla }\times \text{Q}+4\pi \left(\frac{{\text{h}}_0}{{\text{p}}_{\infty }}\right)\text{Q}\right]}^2\\ +\left(\frac{{\text{L}}_2}{{\text{L}}_1}\right){\left[\tilde{\nabla }·\text{Q}\right]}^2]& (\mathrm{22b})\end{array}$

$\begin{array}{ll}{\tilde{\text{f}}}_{\text{cg}}=\frac{1}{2}{\tilde{\text{L}}}_{\varphi }{\left(\tilde{\nabla }\varphi \right)}^2& (\mathrm{22c})\end{array}$

$\begin{array}{ll}{\tilde{\text{f}}}_{\text{c}}={\tilde{L}}_{\varphi -\text{Q}}\left(\tilde{\nabla }\varphi \right)·\left(\tilde{\nabla }·\text{Q}\right)& (\mathrm{22d})\end{array}$

$\xi =\sqrt{{\text{a}}^3{\text{L}}_1\beta }$ is the coherence length in which a³ stands for the volume of each lattice unit and L_i are elastic constants. $\tilde{\nabla }={\text{h}}_0\nabla$ is dimensionless gradient in which ${\text{h}}_0$ denotes a macroscopic length scale and the spatial domain is scaled by ${\text{h}}_0$, ${\tilde{\text{L}}}_{\varphi }={\text{L}}_{\varphi }{\text{a}}^3\beta /{\text{h}}_0^2$ and ${\tilde{\text{L}}}_{\varphi -\text{Q}}={\text{L}}_{\varphi -\text{Q}}{\text{a}}^3\beta /{\text{h}}_0^2$ where L_ϕ is cost of interfacial formation and L_ϕ−Q represents coupling constant. The total free energy as well as the evolution of chiral nematic phase for tropocollagen are mesoscopic because it retains both microscopic length scale, ξ, in a nanometer range and macroscopic length scale, h₀, in the range of micrometers.

Governing Equations for Kinetics of Self-Assembly; Orientational Relaxation, and Uphill Diffusion

Simulations of pattern-formation in fibrous composites, including collagen-based tissues, were first carried out by De Luca and Rey [61, 64, 65]. Their approaches were based on diffusionless evolution of mesophase, and capable of predicting macroscopic architecture of these materials to a great extent. However, recent studies have revealed the imperative role of diffusion in accurately capturing the growth of order-disorder interface [43, 45]. Hence, for the purpose of realistic self-assembly modeling, in this subsection, we formulate the spatio-temporal evolution of tropocollagen in which the Q-tensor augmented with a mass transfer equation.

The cholesteric micro-structures in collagenous biomaterials are formed through the liquid-crystalline self-assembly stage. Two simultaneous mesoscopic mechanisms govern this thermodynamically driven assembly. First, mass transfer mechanism allows tropocollagen macromolecules to diffuse into cholesteric phase (i.e., tropocollagen-rich phase) from isotopic phase (i.e., tropocollagen-lean phase). The mentioned demixing is known as uphill or non-Fickian diffusion and reduces the total free energy of system. Second, orientational relaxation mechanism induces cholesteric architecture inside the formed high-concentration domain. To describe these two phenomena; two coupled fields are required. First, the conserved scalar field of concentration, C, or equivalently volume fraction, ϕ, governing the phase separation. Secondly, the non-conserved tensorial field of Q-tensor by which the orientation of tropocollagen biomacromolecules is primarily specified. The spatio-temporal evolution of {Q, ϕ } is found using the time-dependent Ginzburg–Landau (TDGL) formalism, also known as model C in Hohenberg and Halperin classification [39, 40]. The dimensionless form of model C adjusted for self-assembly simulation reads [17, 61, 64, 66, 67]:

$\begin{array}{ll}\frac{\partial \text{Q}}{\partial \tilde{\text{t}}}=-\frac{1}{{\left(1-3\text{Tr}({\text{Q}}^2)/2\right)}^2}{\left(\frac{\delta {\tilde{\text{F}}}_{\text{net}}}{\delta \text{Q}}\right)}^{\left[\text{s}\right]}& (\mathrm{23a})\end{array}$

$\begin{array}{ll}\frac{\partial \varphi }{\partial \tilde{t}}={\tilde{\text{M}}}_{\varphi }\tilde{\nabla }·\left(\left[\text{I}+\text{Q}\right]·\tilde{\nabla }\frac{\delta {\tilde{\text{F}}}_{\text{net}}}{\delta \varphi }\right)& (\mathrm{23b})\end{array}$

$\delta {\tilde{\text{F}}}_{\text{net}}/\delta \text{Q}$ represents functional derivative. $\tilde{\text{t}}$ is dimensionless time defined as $\tilde{\text{t}}=\text{ t}{\text{M}}_{\text{Q}}/({\text{a}}^3\beta )$where t is time, ${\tilde{\text{M}}}_{\varphi }={\text{M}}_{\varphi }/({\text{M}}_{\text{Q}}{\text{h}}_0^2)$in which the mobilities of Q and ϕ are M_Q and M_ϕ, respectively. Additionally, the superscript [s] indicates that the functional derivative must be symmetric traceless in order to be consistent with the nature of Q-tensor—for any given second rank tensor T^[s] = (T + T^t)/2 − Tr(T)δ/3 where superscript t denotes transpose.

The system given in Equations (23a,b) is a set of six coupled non-linear PDEs. Equation (23a) accounts for the spatio-temporal evolutions of the orientational tensor order parameter. This equation is the compact tensorial form of five independent second-order PDEs. Furthermore, Equation (23b) is a fourth-order PDE, known as the Cahn-Hilliard equation, to describe the concentration field by which the chiral nematic and isotropic phases gradually evolve through the uphill diffusion mechanism.

Computational Details

Here we elaborate on the simulation of nucleation and growth of an isolated cholesteric tactoid in a continuous isotropic phase. This simulation consists of a diffusional phenomenon coupled with structural relaxation. The general schematic representation of this implementation is illustrated in Figure 2.

As above mentioned, the biomimetic formation of collagen-based tissues starts with dissolving tropocollagen in acidic aqueous solutions to obtain the isotropic phase. In such condition, a nucleus is thermodynamically allowed to grow, providing its radius is greater than a critical value. In that case, as a single tactoid grows, the tropocollagen rods diffuse from collagen-lean phase to collagen-rich phase, in turn, the isotopic and cholesteric phases become depleted from and enriched in tropocollagen, respectively. The diffusion of tropocollagen from lean phase (isotropic phase) to rich phase (cholesteric phase) continues till a point where the chemical potentials of two phases become identical.

As illustrated in the Figure 2, we consider the bulk of system as a square with [−0.5 0.5] × [−0.5 0.5] normalized by h₀. Each pair of sides are subjected to the periodic boundary condition. Initially Q = 0 and the phase is isotropic. Afterwards, an initial cholesteric tactoid is seeded by a circular Gaussian distribution with FWHM (full width at half maximum of Gaussian function) greater than the critical drop diameter. The seeding is expressed:

$\begin{array}{l}{\text{Q}|}_{t=0}=\left[S_{\text{e}}({\text{n}}_{\text{e}}{\text{n}}_{\text{e}}-\delta /3)+\frac{1}{3}{\text{P}}_{\text{e}}({\text{m}}_e{\text{m}}_e-{\text{l}}_{\text{e}}{\text{l}}_{\text{e}})\right]\\ \times {\text{e}}^{-\frac{1}{2}\left({\left(\frac{\text{x}-{\text{x}}_0}{{\sigma }_{\text{x}}}\right)}^2+{\left(\frac{\text{y}-{\text{y}}_0}{{\sigma }_{\text{y}}}\right)}^2\right)}+\Xi & (\mathrm{24a})\end{array}$

$\begin{array}{l}{\varphi |}_{t=0}=({\varphi }_{\text{ch}}-{\varphi }_{\text{iso}})\times {\text{e}}^{-\frac{1}{2}\left({\left(\frac{\text{x}-{\text{x}}_0}{{\sigma }_{\text{x}}}\right)}^2+{\left(\frac{\text{y}-{\text{y}}_0}{{\sigma }_{\text{y}}}\right)}^2\right)}\\ +{\varphi }_{\text{iso}}+\Xi & (\mathrm{24b})\end{array}$

Ξ and Ξ, that are, respectively, a second rank symmetric traceless random tensor and scalar random number, are included in the modeling to represent the fluctuations existing in a real system. The subscript e indicates the equilibrium condition given by:

$\begin{array}{ll}{\text{n}}_{\text{e}}=\left[\begin{array}{ccc}0& \text{cos}\left(\frac{2\pi }{{\text{p}}_{\infty }}\text{x}\right)& \text{sin}\left(\frac{2\pi }{{\text{p}}_{\infty }}\text{x}\right)\end{array}\right]& (\mathrm{25a})\end{array}$

$\begin{array}{ll}{\text{m}}_{\text{e}}=\left[\begin{array}{ccc}0& -\text{sin}\left(\frac{2\pi }{{\text{p}}_{\infty }}\text{x}\right)& \text{cos}\left(\frac{2\pi }{{\text{p}}_{\infty }}\text{x}\right)\end{array}\right]& (\mathrm{25b})\end{array}$

In accordance with l = n × m, l_e is computed as [0 0 1]. Equations (24a,b, 25a,b) describe a nucleus whose center placed at position (x₀, y₀) at a concentration equivalent to the effective volume fraction of ϕ_ch. For convenience, we choose the center at (x = 0, y = 0). The concentration of tropocollagen from the center, which is a cholesteric phase, gradually decreases along the radius to the concentration of continuous isotropic phase, ϕ_iso. This approach for simulating the initial nucleus was adapted from Wincure and Rey [30, 31, 33]. In order to make sure that the initial drop is sufficiently large, we choose the σ_x = σ_y = σ and obtain σ in way that FWHM equals two times the critical diameter: $\text{FWHM}=2\sqrt{2ln2}\sigma =2{\text{D}}_{\text{c}}=4{\text{R}}_{\text{c}}$. Classical Nucleation theory [68] provides a rough estimation of the critical radius of a drop as expressed by ${\text{R}}_{\text{c}}=|2{\gamma }_{\text{i}}/\left({\text{c}}_{\text{A}}\Delta {\mu }^{\text{iso}-\text{Cho}}\right)|$ in which γ_i and Δμ^iso−Cho are the interfacial tension and the chemical potential difference between isotropic and cholesteric phase [68, 69]. Additionally, Equation (24b) yields the quenched concentration as ϕ_q = ∬_CD ϕ|_{t = 0} dxdy/∬_CD dxdy in which CD denotes the entire system (computational domain). Consequently, ϕ_iso plays an appreciable role in the size of tactoid because its value affects the initial amount of tropocollagen existing in the system.

Furthermore, the total conservation of mass is imposed by:

$\begin{array}{ll}\frac{\text{d}}{\text{dt}}{\displaystyle \underset{\text{CD}}{\int }}\varphi \text{dxdy = 0}& (26)\end{array}$

Simulation parameters used in this study are summarized in Table 1—also readers are referred to the Khadem and Rey [20] for detailed account of parameters selection in order to accurately capture the available experimental data.

TABLE 1

Table 1. The material properties and parameter values used in the present paper.

Although the ${\tilde{\text{L}}}_{\varphi -\text{Q}}$, ${\tilde{\text{L}}}_{\varphi }$, and L₂/L₁ have not been documented for tropocollagen, we choose common values which satisfy the energy transformation constraint [70–72]:

$\begin{array}{ll}\frac{{\left({\tilde{\text{L}}}_{\varphi -\text{Q}}\right)}^2}{{\tilde{\text{L}}}_{\varphi }\times ({\text{L}}_{\text{2}}/{\text{L}}_1)}<1& (27)\end{array}$

Equations (24a,b) in conjunction with the above-explained conditions are solved with an adaptive finite elements technique with biquadratic basis functions (General PDE solver of COMSOL Multi-physics 5.3a). Furthermore, to acquire the acceptable spatial resolution, we considered at least 50 elements per pitch which resulted in nearly 10⁴ triangular elements, and temporal resolution was carried out by the Backward Euler method. Convergence, accuracy, and stability were checked using standard techniques—for further information on the method and solution approach, please see the accompanying Supplementary Material.

Results and Discussions

In this section, the dynamics of mesophasic evolution and the resulting equilibrium configuration for a shallow quench from the isotropic phase into the cholesteric phase in the presence of one small cholesteric seed are given and discussed (see Figures 1, 2).

Figures 3a–d show snapshots of a growing tactoid corresponding to dimensionless times 0, 900, 960, and 1,100, respectively. Figure 3a shows the initial condition of a small chiral nematic drop seeded in a large isotropic phase area. Note that only a small section of the computational domain, in which the self-assembly is supposed to take place, is shown in Figure 3. The computational domain is actually chosen as a fairly large square with length of h₀ = 100 μm in order to make sure that the existing amount of tropocollagen in the system is sufficient for formation of a single cholesteric tactoid with diameter of the order of 30 μm—as experimentally observed [21]. The size of initial seed must be greater than a critical value in order for the drop to grow based on the mechanism of uphill diffusion, otherwise downhill diffusion takes place and the initial drop is dissolved in isotropic phase.

FIGURE 3

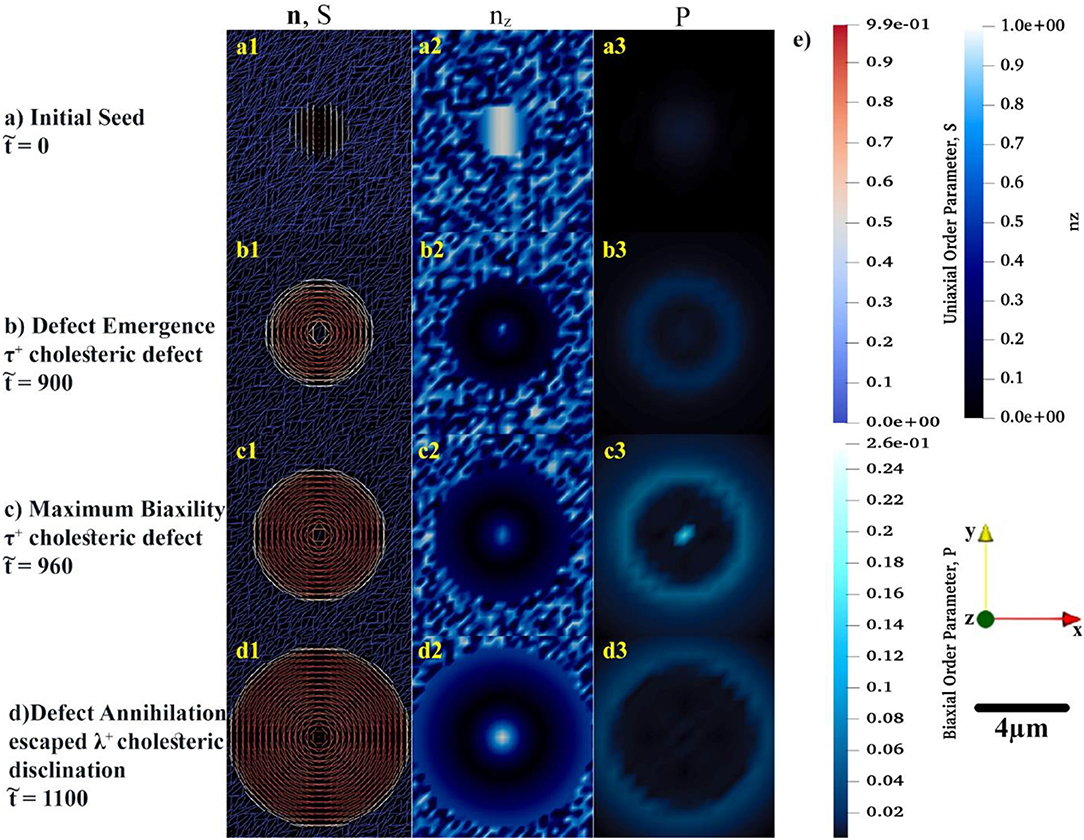
Figure 3. The spatial distributions of order parameters, S and P, in conjunction with the director configuration at the early growth of cholesteric tactoid shown in (a–d). In the first column, the uniaxial configuration, n, of tropocollagen macromolecules are represented by rods whose color (blue to red) shows the uniaxial order parameter, S. To complete the understanding about the configuration of rods in xy-plane, in the second column, the z component of n is shown by use of a monochromatic blue spectrum. In last column, the monochromatic cyan denotes the variation of biaxial order parameter during the time evolution. (e) Illustrating the color bars for S, n_z, and P, the used coordination of system and length-scale bar.

Although the initial configuration of rods is chosen as twisting around x-axis, see Figure 3a1, the rods prefer to be aligned in a concentric configuration, as shown in Figure 3b1. During the early growth of the tactoid, rods attempt to radially twist—the helicoidal axes are along the radii of the circular tactoid. Yet, rods placed at the center of drop exhibit orientational frustration. This frustration emerges in $\tilde{\text{t}}=900$, Figure 3b1, and yields a τ⁺¹ cholesteric defect. As the tactoid grows, the central rods resolve the orientational frustration with an escaped configuration (see Figure 3d1) known as a non-singular λ⁺¹ cholesteric disclination. These important predictions may be difficult to be captured experimentally due to intrinsic size length scale resolutions when using optical methods [73–75].

Figures 3a2–d2 show the z component of uniaxial director, n. The figures show that the central director regions evolves slower and lags the radial helix formation that results in tangential interfacial orientation experimentally observed for tropocollagen tactoids [37]. The tangential orientation minimizes the interfacial free energy at n.k = 0 where k is the interfacial normal vector. This tangential configuration, n.k = 0, emerges when the coupling coefficient, ${\tilde{\text{L}}}_{\varphi -\text{Q}}$<0 [21, 71, 72, 76]. The structure of the 2D tactoid is a radial helix, with tangential interface orientation at the edge and non-singular escape orientation at its center.

Of particular interest to this study is incorporation and analysis of biaxial order parameter during the evolution of the cholesteric tactoid. In the third column of Figures 3a3–d3, the spatial variation of biaxial order parameter, P, is shown in the early stages of growth. The biaxial order parameter becomes particularly noticeable at the interface and at the defect core. Thus, we found that although the equilibrium biaxiality for rod-like macromolecules is small [27, 51], during the phase ordering it takes a larger value than its equilibrium; the difference between dynamical and equilibrium values for biaxiality may be up to three orders of magnitude.

In the course of time, the Q-tensor is relaxed, mass transfer ceases and the structure equilibrates, as shown in Figure 4. As depicted in Figures 4a1,b, the equilibrium configuration of tropocollagen rods becomes concentric, also known as onion-like. This defectless configuration, which has a non-singular λ⁺¹ cholesteric disclination at its center, thoroughly matches with the xy-cross-section of Twisted Bipolar Structure (TBS) given in Sec et al. [77]. Moreover, the experimental POM image reported in Gobeaux et al. [21] confirms TBS for the 3D tropocollagen tactoids. Consequently, the resulting 2D configuration, shown in Figures 3, 4, is consistent with experimental observation. Figure 4a1 shows that the size of tactoid is also consistent with experimental results given in Gobeaux et al. [21]. As can be seen, the diameter of tactoid contains three pitches that each of which has a length of 10 μm. Therefore, the tactoid shape becomes a nearly 30 μm spherulite. Figure 4c represents the equilibrium concentration field. Although a gradient of concentration exists in the interface, the drop remains intact and stable in the isotropic phase. This feature verifies that the growth of cholesteric tactoid is according to the mechanism of uphill diffusion. Figure 4d demonstrates that the equilibrium biaxial order parameter P in the interface is nearly 0.04, however its value sharply decreases to 10⁻⁴ confirmed by previous theoretical studies [27, 51].

FIGURE 4

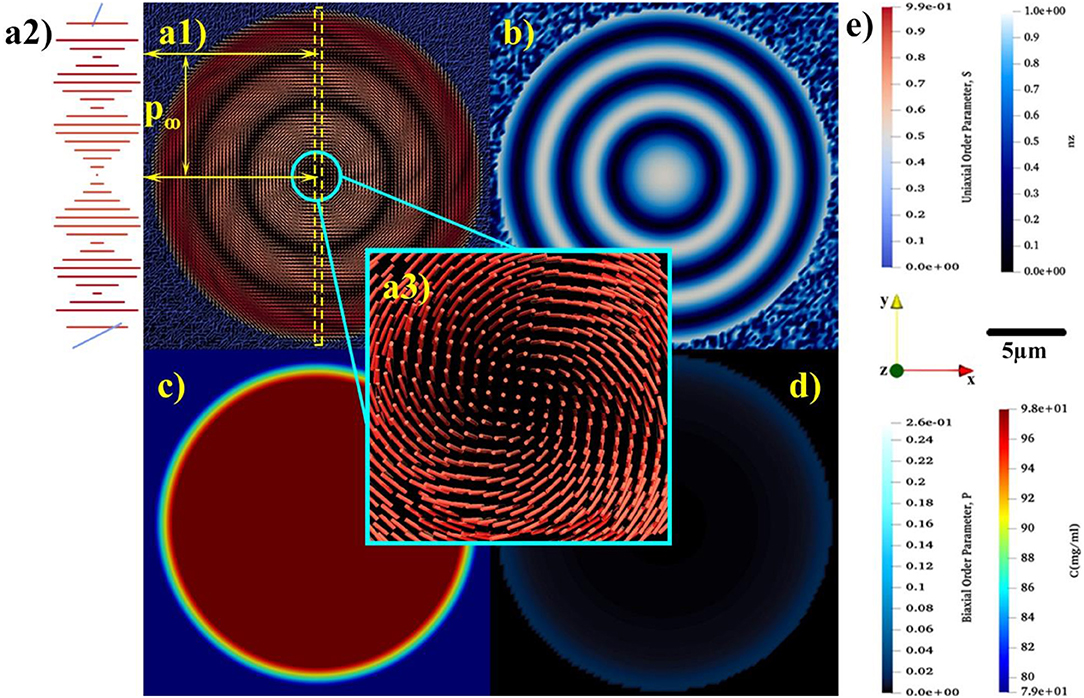
Figure 4. The equilibrium spatial distributions of (a1) uniaxial order parameter, S, and the relaxed uniaxial director, n, (b) z component of uniaxial director, (c) concentration, and (d) biaxial order parameter, P. (a2) showing the magnified rotation of tropocollagen placed in the yellow dash-line box. (a3) indicating the non-singular escaped λ⁺¹ disclination emerges at the center of tactoid. (e) Representing the color bars for S, n_z, P, and C, the used coordination of system and length-scale bar.

Through the entire evolution we find: (1) the interfacial uniaxial order parameter is approximately S_c = 0.39 that is quite close to the critical uniaxial order parameter reported in Khadem and Rey [20] and Gobeaux et al. [21]; (2) The biaxial order parameter at the tactoid's interface is at all times greater than in the interior. The only exception is during initial defect nucleation where biaxiality pronouncedly appears at the core and edge of the 2D drop.

According to the principle of minimum free energy, the kinetic of a spontaneous process follows a path over which the free energy progressively decreases and ends up in a minimum at equilibrium. Figure 5 illustrates the averaged free energy contributions through the phase ordering process of tropocollagen dispersed in the constant concentration of 2.9 M acetic acid. These spatial averages are defined as

$\begin{array}{ll}{\overline{\text{F}}}_{\text{i}}\left(\tilde{\text{t}}\right)={\displaystyle \underset{\text{CD}}{\iint }{\tilde{\text{f}}}_{\text{i}}}\cdot \text{dxdy}/{\displaystyle \underset{\text{CD}}{\iint }\text{dxdy}};\text{ i}\in \left\{\text{iso},\text{ h},\text{ e},\text{ cg},\text{ c}\right\}& (28)\end{array}$

The formation of the single cholesteric drop is the interplay of five free energy contributions. The entropic and enthalpic contributing factors in isotropic phase separation are described by Flory-Huggins theory, ${\tilde{\text{f}}}_{\mathrm{\text{iso}}}$. The LdG theory, ${\tilde{\text{f}}}_{\mathrm{\text{h}}}$, also accounts for the homogeneous effect of phase transition. The spatial averages of these contributions are shown by ${\bar{\text{F}}}_{\mathrm{\text{iso}}}$ and ${\bar{\text{F}}}_{\mathrm{\text{h}}}$, respectively. The monotonic decrease in ${\bar{\text{F}}}_{\mathrm{\text{iso}}}$ and ${\bar{\text{F}}}_{\mathrm{\text{h}}}$ shows that the phase separation and phase ordering are energetically favorable. In addition, it emphasizes on the lyotropic nature of phase ordering in acidic collagenous dispersions; rods are spontaneously accumulated in cholesteric phase, in turn, removed from the isotropic phase. Hence, ${\bar{\text{F}}}_{\mathrm{\text{net}}}$ which is the summation of all contributions, is considerably affected by contributions of phase separation and phase ordering.

FIGURE 5

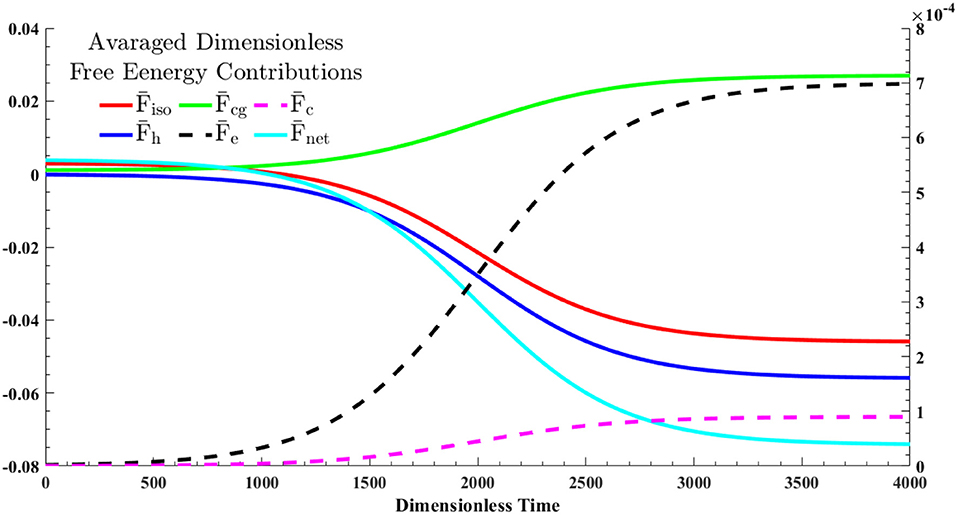
Figure 5. The dynamics of the averaged free energy contributions, given in Equation (28), through a shallow quench from an isotropic state into cholesteric phase—the quench point and evolution path are shown in Figure 1. The solid lines correspond to the left y-axis and dash lines should be referred to the right y-axis.

In spite of these energetically favorable contributions, formation of I/N^* interface and cholesteric configuration inside the tactoid require energy costs which are reflected as penalty terms in the net free energy; see Equations (22a–d). The green solid line in Figure 5, ${\bar{\text{F}}}_{\mathrm{\text{cg}}}$, depicts the cost of interface formation (i.e., mass gradient zone shown in the Figure 4c). This cost is nearly 40 percent of the energy reduction in either phase separation, ${\bar{\text{F}}}_{\mathrm{\text{iso}}}$, or phase ordering, ${\bar{\text{F}}}_{\mathrm{\text{h}}}$, thus the interfacial formation cost can be compensated. Furthermore, the black dash line, ${\bar{\text{F}}}_{\mathrm{\text{e}}}$, and the purple dash line, ${\bar{\text{F}}}_{\mathrm{\text{c}}}$, stand for the average costs for the onion-like configuration of rods inside the chiral nematic tactoid and the tangential configuration in interface, respectively. As seen, the formation cost of the interfacial parallel anchoring, ${\bar{\text{F}}}_{\mathrm{\text{c}}}$, is ~2% of the interior cholesteric energy, ${\bar{\text{F}}}_{\mathrm{\text{e}}}$.

Conclusions

Building on our prior work [20], in this study, we have developed and validated a theoretical framework to study the spatio-temporal phase ordering of tropocollagen dispersed in acidic aqueous solutions into 2D drops. By use of the addition theorem for spherical harmonics (Equation 8), we first incorporated the biaxial order parameter P (Equation 3) into the orientational entropy (Equation 6), the second virial approximation Equations 7a–c), and the intermolecular interaction (Equation 10). We then obtained the LdG coefficients (Equations 21a–d), and formulated the net free energy of system, (Equations 21a–d). To capture the kinetic of the emerging 2D tactoids size, shape, and structure, we relied on the proposed net free energy and phase ordering/mass transfer process (Model C) to establish the governing equations, Equations (23a,b), which were numerically solved under the mentioned auxiliary conditions elaborated in subsection Computational Details.

Figures 3a–d reveal two findings. First, the physical origin for the non-singular escaped λ⁺¹ disclination. Basically, in the early evolution a τ⁺¹ defect emerges at center of nucleus. As time progresses, the central directors go through a defect shedding stage and the τ⁺¹ cholesteric defect evolves into the escaped λ⁺¹ disclination. Second, at the interface and defect core region, the biaxial order parameter takes appreciably large value in the early evolution. Furthermore, Figures 4a1–a3,b demonstrate that the resulting equilibrium state of collagen tactoid is an ~30 μm spherulite in which the rod-shaped macromolecules are aligned in concentric configuration, consistent with experimental observations [21]. Taken together, these results contribute to the development of optimized processing protocols for collagen-based materials and their material property characterization.

Data Availability

All datasets generated for this study are included in the manuscript and the Supplementary Files.

Author Contributions

SK developed the theoretical framework, carried out the simulations, and analyzed the results. AR supervised the study, analyzed and interpreted the results. All authors discussed the results, contributed to writing, and agree about the content.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

SK acknowledges financial support from the McGill Engineering Doctoral Awards (MEDA) program. This work is supported by a grant from Natural Sciences and Engineering Research Council of Canada (NSERC). AR is thankful to McGill University for financial support through the James McGill Professorship appointment.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2019.00088/full#supplementary-material

References

1. Voet D, Voet JG. Biochemistry. Hoboken, NJ: John Wiley & Sons (2011).

Google Scholar

2. Ashammakhi N, Hasan A, Kaarela O, Byambaa B, Sheikhi A, Gaharwar AK, et al. Advancing frontiers in bone bioprinting. Adv Healthc Mater. (2019) 8:1801048. doi: 10.1002/adhm.201801048

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Giraud Guille MM, Mosser G, Helary C, Eglin D. Bone matrix like assemblies of collagen: from liquid crystals to gels and biomimetic materials. Micron. (2005) 36:602–8. doi: 10.1016/j.micron.2005.07.005

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Kurfurst A, Henits P, Morin C, Abdalrahman T, Hellmich C. Bone ultrastructure as composite of aligned mineralized collagen fibrils embedded into a porous polycrystalline matrix: confirmation by computational electrodynamics. Front Phys. (2018) 6:18. doi: 10.3389/fphy.2018.00125

CrossRef Full Text | Google Scholar

5. Schwarcz HP, Abueidda D, Jasiuk I. The ultrastructure of bone and its relevance to mechanical properties. Front Phys. (2017) 5:13. doi: 10.3389/fphy.2017.00039

CrossRef Full Text | Google Scholar

6. Levis HJ, Kureshi AK, Massie I, Morgan L, Vernon AJ, Daniels JT. Tissue engineering the cornea: the evolution of RAFT. J Func Biomater. (2015) 6:50–65. doi: 10.3390/jfb6010050

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Torbet J, Malbouyres M, Builles N, Justin V, Roulet M, Damour O, et al. Orthogonal scaffold of magnetically aligned collagen lamellae for corneal stroma reconstruction. Biomaterials. (2007) 28:4268–76. doi: 10.1016/j.biomaterials.2007.05.024

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Rastian Z, Putz S, Wang YJ, Kumar S, Fleissner F, Weidner T, et al. Type I collagen from Jellyfish Catostylus mosaicus for biomaterial applications. ACS Biomater Sci Eng. (2018) 4:2115–25. doi: 10.1021/acsbiomaterials.7b00979

CrossRef Full Text | Google Scholar

9. Boraschi-Diaz I, Wang J, Mort JS, Komarova SV. Collagen type I as a ligand for receptor-mediated signaling. Front Phys. (2017) 5:11. doi: 10.3389/fphy.2017.00012

CrossRef Full Text | Google Scholar

10. Perez AG, Nieminen HJ, Finnila M, Salmi A, Pritzker KPH, Lampsijarvi E, et al. Delivery of agents into articular cartilage with electric spark-induced sound waves. Front Phys. (2018) 6:7. doi: 10.3389/fphy.2018.00116

CrossRef Full Text | Google Scholar

11. Poulon F, Chalumeau A, Jamme F, Pallud J, Varlet P, Mehidine H, et al. Multimodal analysis of central nervous system tumor tissue endogenous fluorescence with multiscale excitation. Front Phys. (2018) 6:10. doi: 10.3389/fphy.2018.00109

CrossRef Full Text | Google Scholar

12. Neville AC. Biology of Fibrous Composites: Development Beyond the Cell Membrane. New York, NY: Cambridge University Press (1993).

Google Scholar

13. Mitov M. Cholesteric liquid crystals in living matter. Soft Matter. (2017) 13:4176–209. doi: 10.1039/C7SM00384F

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Rey AD. Liquid crystal models of biological materials and processes. Soft Matter. (2010) 6:3402–29. doi: 10.1039/b921576j

CrossRef Full Text | Google Scholar

15. Rey AD, Herrera-Valencia EE. Liquid crystal models of biological materials and silk spinning. Biopolym Banner. (2012) 97:374–96. doi: 10.1002/bip.21723

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Gutierrez OFA, Rey AD. Theory and simulation of cholesteric film formation flows of dilute collagen solutions. Langmuir. (2016) 32:11799–812. doi: 10.1021/acs.langmuir.6b03443

CrossRef Full Text | Google Scholar

17. Aguilar Gutierrez OF, Rey AD. Biological plywood film formation from para-nematic liquid crystalline organization. Soft Matter. (2017) 13:8076–88. doi: 10.1039/C7SM01865G

PubMed Abstract | CrossRef Full Text | Google Scholar

18. De Sa Peixoto P, Deniset-Besseau A, Schmutz M, Anglo A, Illoul C, Schanne-Klein M-C, et al. Achievement of cornea-like organizations in dense collagen I solutions: clues to the physico-chemistry of cornea morphogenesis. Soft Matter. (2013) 9:11241–8. doi: 10.1039/c3sm52097h

CrossRef Full Text | Google Scholar

19. Dehsorkhi A, Castelletto V, Hamley IW, Adamcik J, Mezzenga R. The effect of pH on the self-assembly of a collagen derived peptide amphiphile. Soft Matter. (2013) 9:6033–6. doi: 10.1039/c3sm51029h

CrossRef Full Text | Google Scholar

20. Khadem SA, Rey AD. Thermodynamic modelling of acidic collagenous solutions: from free energy contributions to phase diagrams. Soft Matter. (2019) 15:1833–46. doi: 10.1039/C8SM02140F

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Gobeaux F, Belamie E, Mosser G, Davidson P, Panine P, Giraud-Guille MM. Cooperative ordering of collagen triple helices in the dense state. Langmuir. (2007) 23:6411–7. doi: 10.1021/la070093z

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Lovelady HH, Shashidhara S, Matthews WG. Solvent specific persistence length of molecular type I collagen. Biopolymers. (2014) 101:329–35. doi: 10.1002/bip.22365

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Echalier C, Jebors S, Laconde G, Brunel L, Verdie P, Causse L, et al. Sol-gel synthesis of collagen-inspired peptide hydrogel. Mater Today. (2017) 20:59–66. doi: 10.1016/j.mattod.2017.02.001

CrossRef Full Text | Google Scholar

24. Bernardino NR, Pereira MCF, Silvestre NM, da Gama MMT. Structure of the cholesteric-isotropic interface. Soft Matter. (2014) 10:9399–402. doi: 10.1039/C4SM01857E

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Zhou Y, Bukusoglu E, Martinez-Gonzalez JA, Rahimi M, Roberts TF, Zhang R, et al. Structural transitions in cholesteric liquid crystal droplets. ACS Nano. (2016) 10:6484–90. doi: 10.1021/acsnano.6b01088

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Almeida AP, Canejo JP, Fernandes SN, Echeverria C, Almeida PL, Godinho MH. Cellulose-based biomimetics and their applications. Adv Mater Banner. (2018) 30:1703655. doi: 10.1002/adma.201703655

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Wulf A. Biaxial order in cholesteric liquid crystals: phenomenological argument. J Chem Phys. (1973) 59:6596–8. doi: 10.1063/1.1680039

CrossRef Full Text | Google Scholar

28. Wright DC, Mermin ND. Crystalline liquids: the blue phases. Rev Mod Phys Rev Modern Phys. (1989) 61:385–432. doi: 10.1103/RevModPhys.61.385

CrossRef Full Text | Google Scholar

29. Kamil SM, Bhattacharjee AK, Adhikari R, Menon GI. The isotropic-nematic interface with an oblique anchoring condition. J Chem Phys. (2009) 131:9. doi: 10.1063/1.3253702

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Wincure B, Rey AD. Interfacial nematodynamics of heterogeneous curved isotropic-nematic moving fronts. J Chem Phys. (2006) 124:13. doi: 10.1063/1.2206768

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Wincure B, Rey AD. Growth and structure of nematic spherulites under shallow thermal quenches. Continuum Mech Thermodyn. (2007) 19:37–58. doi: 10.1007/s00161-007-0043-z

CrossRef Full Text | Google Scholar

32. Wincure B, Rey AD. Computational modelling of nematic phase ordering by film and droplet growth over heterogeneous substrates. Liquid Cryst. (2007) 34:1397–413. doi: 10.1080/02678290701614657

CrossRef Full Text | Google Scholar

33. Wincure BM, Rey AD. Nanoscale analysis of defect shedding from liquid crystal interfaces. Nano Lett. (2007) 7:1474–9. doi: 10.1021/nl0701408

PubMed Abstract | CrossRef Full Text | Google Scholar

34. PopaNita V, Sluckin TJ, Wheeler AA. Statics and kinetics at the nematic-isotropic interface: effects of biaxiality. J Phys II. (1997) 7:1225–43. doi: 10.1051/jp2:1997183

CrossRef Full Text | Google Scholar

35. Mirzaeifard S, Servio P, Rey AD. Molecular dynamics characterization of the water-methane, ethane, and propane gas mixture interfaces. Chem Eng Sci. (2019). doi: 10.1016/j.ces.2019.01.051. [Epub ahead of print].

CrossRef Full Text | Google Scholar

36. Mirzaeifard S, Servio P, Rey AD. Molecular dynamics characterization of temperature and pressure effects on the water-methane interface. Colloid Interface Sci Commun. (2018) 24:75–81. doi: 10.1016/j.colcom.2018.04.004

CrossRef Full Text | Google Scholar

37. Rey AD. Pitch contributions to the cholesteric– isotropic interfacial tension. Macromolecules. (2000) 33:9468–70. doi: 10.1021/ma0001685

CrossRef Full Text | Google Scholar

38. Wang XJ, Zhou QF. Liquid Crystalline Polymers. Singapore; London: World Scientific Publishing Company: (2004).

Google Scholar

39. Karttunen M, Vattulainen I, Lukkarinen A. Novel Methods in Soft Matter Simulations. Berlin: Heidelberg: Springer (2004).

Google Scholar

40. Halperin BI. Theory of dynamic critical phenomena. Phys Today. (2019) 72:42–3. doi: 10.1063/PT.3.4137

CrossRef Full Text | Google Scholar

41. Nyström G, Arcari M, Mezzenga R. Confinement-induced liquid crystalline transitions in amyloid fibril cholesteric tactoids. Nat Nanotechnol. (2018) 13:330–6. doi: 10.1038/s41565-018-0071-9

PubMed Abstract | CrossRef Full Text | Google Scholar

42. Nos RL, Roma AM, Garcia-Cervera CJ, Ceniceros HD. Three-dimensional coarsening dynamics of a conserved, nematic liquid crystal-isotropic fluid mixture. J Non-Newton Fluid Mech. (2017) 248:62–73. doi: 10.1016/j.jnnfm.2017.08.009

CrossRef Full Text | Google Scholar

43. Abukhdeir NM, Soulé ER, Rey AD. Non-isothermal model for nematic spherulite growth. Langmuir. (2008) 24:13605–13. doi: 10.1021/la8022216

PubMed Abstract | CrossRef Full Text | Google Scholar

44. Abukhdeir NM, Rey AD. Shape-dynamic growth, structure, and elasticity of homogeneously oriented spherulites in an isotropic/smectic-a mesophase transition. Liquid Cryst. (2009) 36:1125–37. doi: 10.1080/02678290902878754

CrossRef Full Text | Google Scholar

45. Soule ER, Abukhdeir NM, Rey AD. Thermodynamics, transition dynamics, and texturing in polymer-dispersed liquid crystals with mesogens exhibiting a direct isotropic/smectic-a transition. Macromolecules. (2009) 42:9486–97. doi: 10.1021/ma901569y

CrossRef Full Text | Google Scholar

46. Gennes PGd, Prost J. The Physics of Liquid Crystals. Oxford: Clarendon Press (1995).

Google Scholar

47. Doi M. Soft Matter Physics. Oxford: OUP (2013).

Google Scholar

48. Matsuyama A, Kato T. Theory of binary mixtures of a flexible polymer and a liquid crystal. J Chem Phys. (1996) 105:1654–60. doi: 10.1063/1.472024

CrossRef Full Text | Google Scholar

49. Odijk T. Theory of lyotropic polymer liquid crystals. Macromolecules. (1986) 19:2313–29. doi: 10.1021/ma00163a001

CrossRef Full Text | Google Scholar

50. Drwenski T, Dussi S, Hermes M, Dijkstra M, Roij RV. Phase diagrams of charged colloidal rods: can a uniaxial charge distribution break chiral symmetry? J Chem Phys. (2016) 144:094901. doi: 10.1063/1.4942772

PubMed Abstract | CrossRef Full Text | Google Scholar

51. Matsuyama A. Biaxiality of cholesteric phases in rod-like polymer solutions. Liquid Cryst. (2015) 42:423–9. doi: 10.1080/02678292.2015.1006148

CrossRef Full Text | Google Scholar

52. Matsuyama A. Biaxial nematic phases in rod/liquid crystal mixtures. Liquid Cryst. (2011) 38:729–36. doi: 10.1080/02678292.2011.570795

CrossRef Full Text | Google Scholar

53. Matsuyama A, Crystals L. Biaxial nematic phase in mixtures of a liquid crystal and a rodlike polymer. Liquid Cryst. (2011) 540:42–9. doi: 10.1080/15421406.2011.568325

CrossRef Full Text | Google Scholar

54. Stroobants A, Lekkerkerker HNW, Odijk T. Effect of electrostatic interaction on the liquid crystal phase transition in solutions of rodlike polyelectrolytes. Macromolecules. (1986) 19:2232–8. doi: 10.1021/ma00162a020

CrossRef Full Text | Google Scholar

55. Mirzaeifard S, Abel SM. Confined semiflexible polymers suppress fluctuations of soft membrane tubes. Soft Matter. (2016) 12:1783–90. doi: 10.1039/C5SM02556G

PubMed Abstract | CrossRef Full Text | Google Scholar

56. Matus Rivas OM, Rey AD. Effects of sodium and magnesium cations on the aggregation of chromonic solutions using molecular dynamics. J Phys Chem B. (2019) 123:1718–32. doi: 10.1021/acs.jpcb.8b12130

PubMed Abstract | CrossRef Full Text | Google Scholar

57. Rivas OMM, Rey AD. Molecular dynamics on the self-assembly of mesogenic graphene precursors. Carbon. (2016) 110:189–99. doi: 10.1016/j.carbon.2016.09.014

CrossRef Full Text | Google Scholar

58. Roohnikan M, Toader V, Rey A, Reven L. Hydrogen-bonded liquid crystal nanocomposites. Langmuir. (2016) 32:8442–50. doi: 10.1021/acs.langmuir.6b02256

PubMed Abstract | CrossRef Full Text | Google Scholar

59. Bagnani M, Nystrom G, De Michele C, Mezzenga R. Amyloid fibrils length controls shape and structure of nematic and cholesteric tactoids. ACS Nano. (2019) 13:591–600. doi: 10.1021/acsnano.8b07557

PubMed Abstract | CrossRef Full Text | Google Scholar

60. Soule ER, Rey AD. A good and computationally efficient polynomial approximation to the Maier-Saupe nematic free energy. Liquid Cryst. (2011) 38:201–5. doi: 10.1080/02678292.2010.539303

CrossRef Full Text | Google Scholar

61. De Luca G, Rey AD. Chiral front propagation in liquid-crystalline materials: formation of the planar monodomain twisted plywood architecture of biological fibrous composites. Phys Rev E Stat Nonlin Soft Matter Phys. (2004) 69(Pt 1):011706. doi: 10.1103/PhysRevE.69.011706

PubMed Abstract | CrossRef Full Text | Google Scholar

62. Gurevich S, Soule E, Rey A, Reven L, Provatas N. Self-assembly via branching morphologies in nematic liquid-crystal nanocomposites. Phys Rev E. (2014) 90:020501. doi: 10.1103/PhysRevE.90.020501

PubMed Abstract | CrossRef Full Text | Google Scholar

63. Das SK, Rey AD. Texture formation under phase ordering and phase separation in polymer-liquid crystal mixtures. J Chem Phys. (2004) 121:9733–43. doi: 10.1063/1.1804494

PubMed Abstract | CrossRef Full Text | Google Scholar

64. De Luca G, Rey AD. Monodomain and polydomain helicoids in chiral liquid-crystalline phases and their biological analogues. Eur Phys J E. (2003) 12:291–302. doi: 10.1140/epje/i2002-10164-3

PubMed Abstract | CrossRef Full Text | Google Scholar

65. De Luca G, Rey AD. Theory and simulation of texture transformations in chiral systems: applications to biological fibrous composites. In: Mather PT, Broer DJ, Bunning TJ, Walba DM, Zentel R, editors. Advances in Liquid Crystalline Materials and Technologies. Materials Research Society Symposium Proceedings. Phoenix, AZ. p. 141–6.

Google Scholar

66. Khabibullaev PK, Gevorkyan EV, Lagunov AS. Rheology of Liquid Crystals. New York, NY: Allerton Press (1994).

Google Scholar

67. Rey AD. Theory and simulation of gas diffusion in cholesteric liquid crystal films. Mol Cryst Liquid Cryst Sci Technol Section A. (1997) 293:87–109. doi: 10.1080/10587259708042767

CrossRef Full Text | Google Scholar

68. Fletcher NH. Size effect in heterogeneous nucleation. J Chem Phys. (1958) 29:572–6. doi: 10.1063/1.1744540

CrossRef Full Text | Google Scholar

69. Sear RP. Nucleation: theory and applications to protein solutions and colloidal suspensions. J Phys-Condens Matter. (2007) 19:28. doi: 10.1088/0953-8984/19/3/033101

CrossRef Full Text | Google Scholar

70. Rey AD, Servio P, Herrera-Valencia EE. Bioinspired model of mechanical energy harvesting based on flexoelectric membranes. Phys Rev E. (2013) 87:12. doi: 10.1103/PhysRevE.87.022505

PubMed Abstract | CrossRef Full Text | Google Scholar

71. Das SK, Rey AD. Computational thermodynamics of multiphase polymer-liquid crystal materials. Comput Mater Sci. (2006) 38:325–39. doi: 10.1016/j.commatsci.2005.10.009

CrossRef Full Text | Google Scholar

72. Das SK, Rey AD. Magnetic field-induced shape transitions in multiphase polymer-liquid crystal blends. Macromol Theory Simul. (2006) 15:469–86. doi: 10.1002/mats.200600024

CrossRef Full Text | Google Scholar

73. Dierking I. Textures of Liquid Crystals. Weinheim: Wiley-VCH (2003).

Google Scholar

74. Yang DK. Fundamentals of Liquid Crystal Devices. Wiley (2014).

Google Scholar

75. Ondriscrawford R, Boyko EP, Wagner BG, Erdmann JH, Zumer S, Doane JW. Microscope textures of nematic droplets in polymer dispersed liquid-crystals. J Appl Phys. (1991) 69:6380–6. doi: 10.1063/1.348840

CrossRef Full Text | Google Scholar

76. Das SK, Rey AD. Colloidal crystal formation via polymer-liquid-crystal demixing. Europhys Lett. (2005) 70:621–7. doi: 10.1209/epl/i2005-10034-2

CrossRef Full Text | Google Scholar

77. Sec D, Porenta T, Ravnik M, Zumer S. Geometrical frustration of chiral ordering in cholesteric droplets. Soft Matter. (2012) 8:11982–8. doi: 10.1039/c2sm27048j

CrossRef Full Text | Google Scholar

Nomenclature