Effective Rheology of Two-Phase Flow in a Capillary Fiber Bundle Model

We investigate the effective rheology of two-phase flow in a bundle of parallel capillary tubes carrying two immiscible fluids under an external pressure drop. The diameter of the tubes vary along the length which introduce capillary threshold pressures. We demonstrate through analytical calculations that a transition from a linear Darcy to a non-linear behavior occurs while decreasing the pressure drop ΔP, where the total flow rate 〈Q〉 varies with ΔP with an exponent 2 as 〈Q〉~ΔP² for uniform threshold distribution. The exponent changes when a lower cut-off P_m is introduced in the threshold distribution and in the limit where ΔP approaches P_m, the flow rate scales as $\langle Q\rangle ~{(|\Delta P|-P_m)}^{3/2}$. While considering threshold distribution with a power α, we find that the exponent γ for the non-linear regime vary as γ = α + 1 for P_m = 0 and γ = α + 1/2 for P_m > 0. We provide numerical results in support of our analytical findings.

Understanding the hydrodynamic properties of simultaneous flow of two or more immiscible fluids is essential due its relevance to a wide variety of different systems in industrial, geophysical and medical sectors [1, 2]. Different applications, such as bubble generation in microfluidics, blood flow in capillary vessels, catalyst supports used in the automotive industry, transport in fuel cells, oil recovery, ground water management and CO₂ sequestration, deal with the flow of bubble trains in different types of systems, ranging from single capillaries to more complex porous media. The underlying physical mechanisms in multiphase flow are controlled by a number of factors, such as the capillary forces at the interfaces, viscosity contrast between the fluids, wettability and geometry of the system, which make the flow properties different from single phase flow. When one immiscible fluid invades a porous medium filled with another fluid, different types of transient flow patterns, namely viscous fingering [3, 4], stable displacement [5], and capillary fingering [6] are observed while tuning the physical parameters [7]. These transient flow patterns were modeled by invasion percolation [8] and diffusion limited aggregation (DLA) models [9]. When steady state sets in after the initial instabilities, the flow properties in are characterized by relations between the global quantities, such as flow rate, pressure drop and fluid saturation [10, 11]. It has been observed theoretically and experimentally that, in the regime where capillary forces compete with the viscous forces, the two-phase flow rate of Newtonian fluids in the steady state no longer obeys the linear Darcy law [12, 13] but varies as a power law with the applied pressure drop [14–17]. Tallakstad et al.[14, 15] experimentally measured the exponent of the power law to be close to two (= 1/0.54) in a two-dimensional system and followed this observation up with arguments why the exponent should be two. Rassi et al.[16] found a value for the exponent varying between 2.2 (= 1/0.45) and 3.0 (= 1/0.33) in a three-dimensional system. Sinha et al.[17] considered a similar system to that which had been studied by Rassi et al. finding an exponent 2.17±0.24 (= 1/(0.46±0.05)). The reason behind the discrepancy between the results of Rassi et al. and those of Sinha et al. is the possibility of a non-zero threshold pressure that observed in the later study, under which there would be no flow, which was assumed to be zero in the former study. The reciprocals in the brackets are provided in order to compare the exponent values reported in the literature [14–17] with those we present here in this article, as we express our results as 〈Q〉 as a power law in ΔP, whereas in the cited papers ΔP was expressed as a power law in 〈Q〉.

This power law behavior is in contrast to the assumption of linearity in the relation between flow rate and pressure drop that is generally assumed in the relative permeability approach dominating reservoir simulations [18].

For a single capillary tube with varying diameter, Sinha et al.[19] showed that the average volumetric flow rate $\overline{q}$ in the steady state has a non-linear square-root type relationship with the pressure drop ΔP as $\overline{q}~\sqrt{\Delta P^2-P_c^2}$. This was shown analytically by integrating the instantaneous linear two-phase flow equation over the whole capillary tube. Here P_c is the threshold pressure difference below which there is no flow. It appears due to the capillary barriers at the interfaces at the narrow pore throats. Extending this non-linear relationship to a network of disordered pores, the relationship between the steady-state flow rate and an excess pressure drop leads to a quadratic relationship in the capillary dominated regime [20]. The quadratic relationship for the pore network, both in two and in three dimensions, was obtained analytically by mean-field calculations and numerically with pore network modeling [17, 20].

While increasing the pressure drop, the capillary forces become negligible compared to the viscous forces. This leads to a crossover from the non-linear regime to a linear Darcy regime for both the single capillary tube and for the pore network. Such non-linear quadratic relationship at low flow rate and a crossover to a linear regime at high flow rate was also observed in case of the single-phase flow of Bingham viscoplastic fluid in porous media [21, 22]. A Bingham fluid is a yield threshold fluid which behaves like a solid below the threshold and flows like a Newtonian fluid above it. The origin of the quadratic regime for the Bingham fluid flowing in a porous media can be understood intuitively in this way: the flow starts when one connected channel appears in the system just above a threshold pressure and the flow rate varies linearly with the excess pressure drop; while increasing the applied pressure drop further, more number of connected flow channels start to appear enhancing the overall flow rate more rapidly than the applied pressure drop leading to the quadratic relationship. Finally, when all possible flow paths become active, the flow become Newtonian following the linear Darcy law. Note that, in general, the rheology of the Bingham fluid is linear above the yield threshold. It is the disorder in the yield thresholds due to the porous medium that creates the quadratic regime.

The argument presented by Tallakstad et al.[14, 15] focused on the successive opening of fluid channels when the pressure drop across the system was increased. When |ΔP| is small, the flow will occur along isolated channels. The volumetric flow rate in such a channel will be proportional to |ΔP|/L. Between the channels there will be fluid clusters held in place by capillary forces, say of the order p_t. There is a pressure gradient |ΔP|/L in the flow direction. A given cluster of length l_∥ will be stuck if p_t > l_∥|ΔP|/L. The largest stuck cluster will then have a size l_{∥, max} = Lp_t/|ΔP|. If we now assume that this length, l_{∥, max} is same as the distance between the channels where there is flow, l_⊥, then the total flow rate must be equal to the number of channels, which is proportional to 1/l_⊥, multiplied by the flow rate in each channel. Hence, we have $Q\propto (1/l_{\perp })|\Delta P|\propto |\Delta P{|}^2$. Though this argument provides the same behavior as the one based on the mean field calculation [20] for two-dimensional networks, a difference appears in three dimensions. When following the same arguments, it leads the flow rate to vary with the pressure drop with third power as long as the isolated channels remain one-dimensional strings rather than two-dimensional sheets in three dimensions.

We present in this article a capillary fiber bundle model [23, 24], which is a system of N parallel capillary tubes, disconnected from each other, each carrying an independent bubble trail of two immiscible fluids under an external pressure drop. In a porous medium, a typical pore consists of two wide pore bodies at the ends and a narrow pore throat in the middle. When an interface moves along the pore, the capillary pressure associated with the interface becomes position dependent due to the change in the radius of curvature. This introduces an overall threshold pressure that depends on the position of all the interfaces [19]. One can simplify the shape of the pore by a sinusoidal type and a long capillary tube with varying radius can be seen as a series of many pores. In the capillary bundle model, the diameter of each tube varies along the axis identically and the disorder in the threshold appear due to the different interface positions in different tubes. This model is essentially the only model for immiscible two-phase flow which is analytically tractable. We calculate the total average flow rate as a function of the applied pressure drop and study the effect of disorder in the threshold distribution. We point out that, here we do not address the question of the relation between the fluid distributions in the capillaries and the respective threshold distributions. Our aim with this model is to investigate how the range of the disorder in the threshold distribution controls the effective flow properties. This provides an insight into the non-linearities in steady-state two-phase flow. We will see that the exponent for the non-linear regime depends on the lower cut-off of the threshold distribution as well as on the behavior of the distribution near the cut-off. The possibility to study analytically for this model how the competition between viscous and capillary forces renders the Darcy relation non-linear, is a new and useful discovery.

The capillary fiber bundle model is a hydrodynamic analog of the fiber bundle model used in fracture mechanics to study mechanical failure under stress [25]. The fiber bundle model is an ideal example of a disordered system in statistical mechanics that is driven by threshold activated dynamics. It is a simple, yet very rich model to understand failure events in mechanical systems. In its simplest form it is analytically tractable. In more complex versions of the model, analytical calculations go hand in hand with numerical simulations.

Figure 1 illustrates a bundle with N = 5 parallel capillaries. Each capillary tube has a length L and an average inner area a. For each capillary, the diameter varies along the long axis identically. Each capillary is filled with a bubble train of wetting and non-wetting fluids. Due to the varying diameter, the capillary forces at the interfaces vary as the bubble train moves along the tubes. We assume that the wetting fluid does not form films along the pore walls so that the fluids do not pass each other. The lengths of the wetting and non-wetting fluids in each tube is L_w and L_n, respectively such that the volume of the wetting fluid in each tube is L_wa and the volume of the non-wetting fluid is L_na, where a is the average cross-sectional area of the capillary tubes. Hence, the saturations are given by S_w = L_w/L and S_n = L_n/L for each capillary tube. The cross-sectional pore area of the capillary fiber bundle is

$\begin{array}{ll}{A}_p=Na.& (1)\end{array}$

Though each tube contains the same amount of each fluid, it has its own division of the fluids into bubbles. We average over the ensemble of capillary tubes in the bundle by averaging over the fluids in each tube that pass at a given instance through an imaginary cut as shown in the figure. We will obtain the same averages if we consider a single capillary tube, averaging over a time interval the fluid passing the imaginary cut [19, 26]. This shows that the model is ergodic.

FIGURE 1

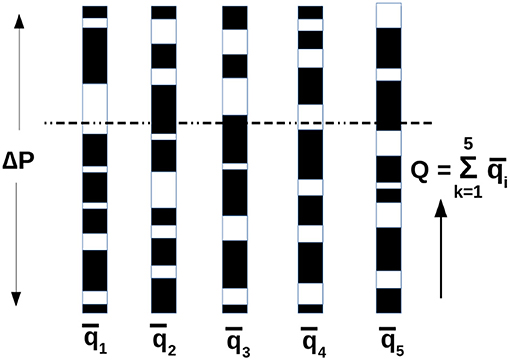
Figure 1. The capillary tube model. There are N = 5 capillaries, each filled with a bubble train of wetting (white) and non-wetting (black) fluids moving in the direction of the arrow. The diameter along each tube vary so that the capillary force from each interface vary with its position. The variation in the diameters are not illustrated in the figure. The average diameters are the same for all tubes. The broken line illustrates an imaginary cut through the capillary fiber bundle.

The volumetric flow rate in a capillary tube is given by [19]

$\begin{array}{ll}q=-\frac{a^2}{8\pi {\mu }_{\text{av}}L}\Theta (|\Delta P|-P_c)\left[\Delta P-P_c\right],& (2)\end{array}$

where ΔP is the pressure drop across the capillary tube, P_c the sum of all the capillary forces along the capillary tube due to the interfaces and

$\begin{array}{ll}{\mu }_{\text{av}}=S_w{\mu }_w+S_n{\mu }_n,& (3)\end{array}$

is the effective viscosity. Θ(|ΔP| − P_c) is the Heaviside function which is zero for negative arguments and one for positive arguments.

Sinha et al.[19] showed that the time average when the pressure difference across the tube is kept fixed is given by

$\begin{array}{l}\overline{q}(P_c)=\\ -\frac{a^2}{8\pi {\mu }_{\text{av}}L}\text{sgn}(\Delta P)\Theta (|\Delta P|-P_c)\sqrt{\Delta P^2-P_c^2},& (4)\end{array}$

where the function sgn(ΔP) is the sign of the argument. Suppose now that the thresholds P_c are distributed uniformly between zero and a maximum value P_M. The cumulative threshold probability is then

$\begin{array}{ll}\Pi (P_c)=\{\begin{array}{cc}0\hfill & ,P_c\le 0,\hfill \\ \frac{P_c}{P_M}& ,0<P_c\le P_M,\hfill \\ 1\hfill & ,P_c>P_M.\hfill \end{array}& (5)\end{array}$

We have N capillary tubes. Using order statistics, we may order the N averaged threshold values,

$\begin{array}{ll}\Pi (P_c(k))=\frac{k}{N+1},& (6)\end{array}$

where 1 ≤ k ≤ N. Hence,

$\begin{array}{ll}{P}_c(k)=P_M\frac{k}{N+1}.& (7)\end{array}$

The average volumetric flow rate through the capillary fiber bundle for |ΔP| > 0 is then

$\begin{array}{ll}\langle Q\rangle ={\displaystyle \sum _{k=1}^{(N+1)min\left(\frac{|\Delta P|}{P_M},1\right)}}\overline{q}(P_c(k))& (8)\end{array}$

We assume the limit N → ∞ turning the sum into an integral,

$\begin{array}{l}\frac{\langle Q\rangle }{N}=-\frac{a^2{P}_M\text{sgn}(\Delta P)}{8\pi {\mu }_{\text{av}}L}\\ {\displaystyle {\int }_0^{min\left(|\Delta P|/P_M,1\right)}}dx\sqrt{{\left(\frac{|\Delta P|}{P_M}\right)}^2-x^2}.& (9)\end{array}$

This integral is doable and we find

$\begin{array}{ll}\frac{\langle Q\rangle }{N}=-\frac{a^2}{32{\mu }_{\text{av}}L}{\displaystyle \left|\frac{\Delta P}{P_M}\right|}\Delta P& (10)\end{array}$

when |ΔP| ≤ P_M and

$\begin{array}{l}\frac{\langle Q\rangle }{N}=-\frac{a^2{P}_M\text{sgn}(\Delta P)}{16\pi {\mu }_{\text{av}}L}\\ [\sqrt{{\left(\frac{|\Delta P|}{P_M}\right)}^2-1}\\ +{\left(\frac{|\Delta P|}{P_M}\right)}^2\text{arcsin}\left(\frac{P_M}{|\Delta P|}\right)],& (11)\end{array}$

when |ΔP| > P_M. In the limit |ΔP| ≫ P_M, Equation (11) gives

$\begin{array}{ll}\frac{\langle Q\rangle }{N}=-\frac{a^2}{8\pi {\mu }_{\text{av}}L}\Delta P.& (12)\end{array}$

Hence, the Darcy relation for a tube is recovered.

We see that this picture is consistent with that central to the arguments of Tallakstad et al.[14, 15] leading to the quadratic dependence of Q on ΔP. From Equation (7) we deduce that a number k_c of the capillary tubes are active, where

$\begin{array}{ll}{k}_c=\frac{|\Delta P|}{P_M}(N+1).& (13)\end{array}$

The typical distance between active capillary tubes in units of the distance between the tubes is then given by

$\begin{array}{ll}{l}_{\perp }=\frac{N+1}{k_c}=\frac{P_M}{|\Delta P|},& (14)\end{array}$

in accordance with the argument of Tallakstad et al.

How stable is the square law Q ∝ |ΔP|²? That is, how much does it hinge on the choice of cumulative threshold probability Π(P_c). So far we have only considered the one given in Equation (5). Let us now generalize it to

$\begin{array}{ll}\Pi (P_c)=\{\begin{array}{cc}0\hfill & ,P_c\le 0,\hfill \\ {\left(\frac{P_c}{P_M}\right)}^{\alpha }\hfill & ,0<P_c\le P_M,\hfill \\ 1\hfill & ,P_c>P_M,\hfill \end{array}& (15)\end{array}$

where α > 0. The average ordered threshold are then given by

$\begin{array}{ll}{P}_c(k)=P_M{\left(\frac{k}{N+1}\right)}^{1/\alpha },& (16)\end{array}$

and when combined with the expression for 〈Q〉, Equation (8) in the limit N → ∞, we find

$\begin{array}{l}\frac{\langle Q\rangle }{N}=-\frac{a^2{P}_M\text{sgn}(\Delta P)}{8\pi {\mu }_{\text{av}}L}\\ {\displaystyle {\int }_0^{min({(|\Delta P|/P_M)}^{\alpha },1)}}dx\sqrt{{\left(\frac{|\Delta P|}{P_M}\right)}^2-x^{2/\alpha }}.& (17)\end{array}$

Since we are interested in the behavior for |ΔP| → 0, we do this integral under the assumption that |ΔP| < P_M finding

$\begin{array}{ll}\frac{\langle Q\rangle }{N}=-\frac{a^2\alpha }{32\sqrt{\pi }{\mu }_{\text{av}}L}\frac{\Gamma \left(\frac{\alpha }{2}\right)}{\Gamma \left(\frac{3+\alpha }{2}\right)}{\left(\frac{|\Delta P|}{P_M}\right)}^{\alpha }\Delta P,& (18)\end{array}$

where the Γ function for real positive z is defined as, $\Gamma (z)={\int }_{-\infty }^{\infty }{t}^{z-1}{e}^{-t}dt$. When α = 1, we recover Equation (10).

Equation (10) shows the behavior observed experimentally in References [14] and [15]. With Equation (18), we have just shown that 〈Q〉/N ~ |ΔP|^γ as |ΔP| → 0, where γ depends on the threshold distribution, i.e., on α in Equation (15). Does this imply that there is no universality; that the experimentally observed behavior is due to the presence of a very specific threshold distribution?

As we now argue, there is universality. We note that the threshold distribution p(P_c) = dΠ(P_c)/dP_c behaves as $p(P_c)\propto P_c^{\alpha -1}$. Hence, if α > 1, the distribution vanishes as P_c → 0, whereas it diverges for α < 1. Thus, the behavior of the distribution is vastly different for these two cases, and this causes γ to depend on α. However, for α = 1, the distribution reaches a constant, non-zero value for P_c → 0. Any threshold distribution with this behavior for small P_c, i.e., p(P_c) reaching a non-zero value and dp(P_c)/dP_c → 0 in the limit P_c → 0 will give rise to the square power law seen in Equation (10). Such distributions are ubiquitous, and γ = 2 is universal over this class of distributions.

We now consider α = 1 again, but introduce a minimum threshold P_m so that the cumulative threshold probability is given by

$\begin{array}{ll}\Pi (P_c)=\{\begin{array}{cc}0\hfill & ,P_c\le P_m,\hfill \\ \frac{P_c-P_m}{P_M-P_m}\hfill & ,P_m<P_c\le P_M,\hfill \\ 1\hfill & ,P_c>P_M.\hfill \end{array}& (19)\end{array}$

Equation (6) yields in this case the ordered threshold sequence

$\begin{array}{ll}{P}_c(k)=P_m+(P_M-P_m)\frac{k}{N+1}.& (20)\end{array}$

Equation (8) now becomes in the limit N → ∞

$\begin{array}{l}\frac{\langle Q\rangle }{N}=-\frac{a^2(P_M-P_m)\text{sgn}(\Delta P)}{8\pi {\mu }_{\text{av}}L}\\ {\displaystyle {\int }_{\frac{P_m}{P_M-P_m}}^{\frac{|\Delta P|}{P_M-P_m}}}dx\sqrt{{\left(\frac{|\Delta P|}{P_M-P_m}\right)}^2-x^2},& (21)\end{array}$

when we assume P_m ≤ |ΔP| ≤ P_M. We find

$\begin{array}{l}\frac{\langle Q\rangle }{N}=-\frac{a^2(P_M-P_m)\text{sgn}(\Delta P)}{32\pi {\mu }_{\text{av}}L}{\left(\frac{|\Delta P|}{P_M-P_m}\right)}^2\\ [\pi -4{\left(\frac{P_m}{|\Delta P|}\right)}^2\sqrt{{\left(\frac{|\Delta P|}{P_m}\right)}^2-1}\\ -2\text{arccot}\left(\frac{2\sqrt{{\left(\frac{|\Delta P|}{P_m}\right)}^2-1}}{2-{\left(\frac{|\Delta P|}{P_m}\right)}^2}\right)].& (22)\end{array}$

We find to lowest order in (|ΔP| − P_m), that this expression behaves as

$\begin{array}{ll}\frac{\langle Q\rangle }{N}=-\frac{a^2\text{sgn}(\Delta P)}{3\sqrt{2}\pi {\mu }_{\text{av}}L}\frac{\sqrt{P_m}}{(P_M-P_m)}{(|\Delta P|-P_m)}^{3/2},& (23)\end{array}$

as |ΔP| → P_m.

We now turn to numerical simulations and observe that the numerical results are in good a agreement with the analytical findings. The numerical simulations also allow us to explore the regions which are analytically challenging. Results are shown in Figure 2 for a bundle containing N = 10⁵ capillary tubes and averaged over 10⁴ configurations. In Figure 2A, we show the behavior of the volumetric flow rate 〈Q〉 as a function of increasing pressure drop ΔP for uniform threshold distributions with P_m = 0 and P_m > 0, given by Equations (5, 19), respectively. The results show that, for each threshold distribution, the relationship is linear for high ΔP obeying the Darcy law as predicted by Equation (12). For small pressure drops, 〈Q〉 follows a power law in ΔP with an exponent 2 when there is no lower cut-off in the threshold distribution, i.e., P_m = 0. This is predicted in Equation (10). When a lower cut-off is introduced in the threshold distribution (P_m > 0), this exponent shifts from 2 to 3/2 as predicted in Equation (23). These exponents in the non-linear regime are not sensitive to the span of the distribution as shown in Figure 2A. An insight to a more generalized picture is presented in Figures 2B,C for a threshold distribution given by a generalization of Equation (15) with an introduction of a lower cut-off P_m,

$\begin{array}{ll}\Pi (P_c)=\{\begin{array}{cc}0\hfill & ,P_c\le P_m,\hfill \\ {\left(\frac{P_c-P_m}{P_M-P_m}\right)}^{\alpha }& ,P_m<P_c\le P_M,\hfill \\ 1\hfill & ,P_c>P_M,\hfill \end{array}& (24)\end{array}$

With this distribution of thresholds, the exponent γ in the non-linear region shows a continuous variation with α as γ = α + 1 for P_m = 0. Such variation is given in Equation (18) and matches well with the numerical results as shown in Figure 2D. In presence of a lower cut-off P_m > 0, γ varies as (α + 1/2) instead of (α + 1) irrespective of the position of the lower cut-off. An analytical treatment for a general α value with P_m > 0 is rather challenging. Nevertheless, our numerical result matches with the analytical study (see Equation 23) in the limit α = 1.

FIGURE 2

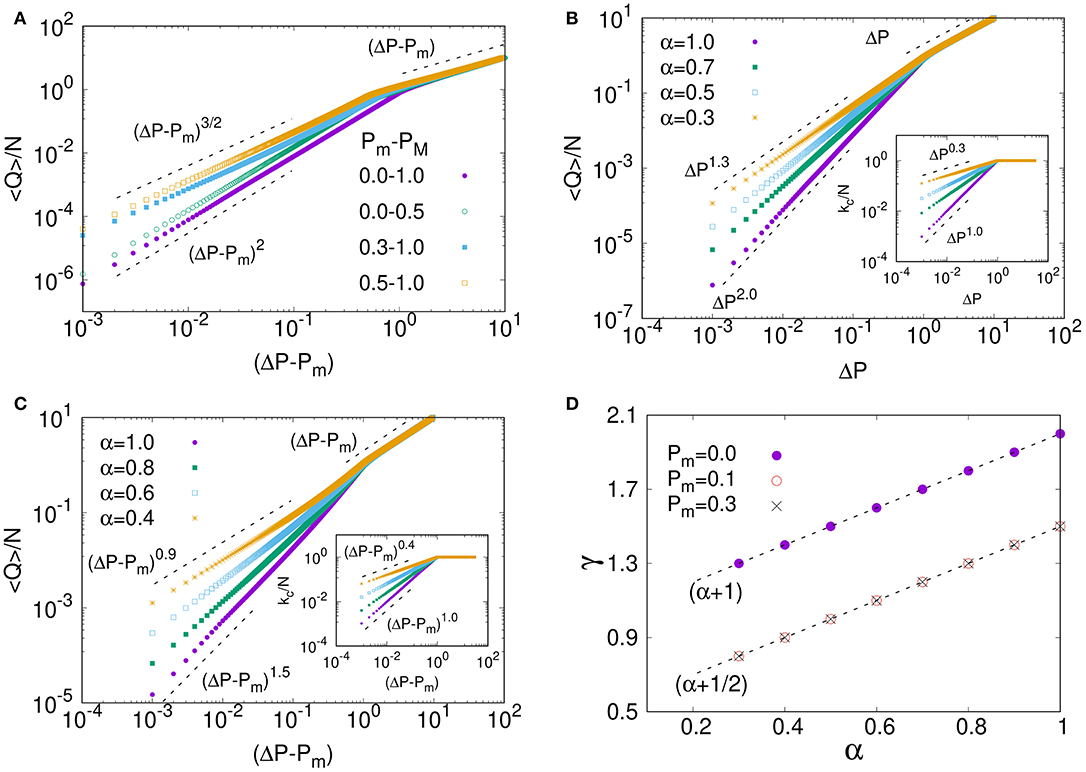
Figure 2. Results from numerical simulations performed with N = 10⁵ capillaries and averaged over 10⁴ configurations. Variation of 〈Q〉/N as a function of pressure drop ΔP for different threshold distributions are shown in (A–C) where non-linear to linear transitions are observed while increasing the pressure drop. (A) Corresponds to uniform threshold distribution (Equation 5) where the power-law exponent γ for the non-linear regime has a value 2 without a lower cut-off (P_m = 0). With any non-zero lower cut-off (P_m > 0), the exponent shifts to 3/2 (Equation 23). Results for the threshold distribution with a power α (Equation 24) are shown in (B,C) for P_m = 0 and P_m > 0, respectively, where γ varies with α as γ = α + 1 for P_m = 0 and as γ = α + 1/2 for P_m > 0. These two relations are shown in (D) for the range of α which show two distinct straight lines for P_m = 0 and for P_m > 0. Here, the number of active capillaries (k_c) vary with ΔP as $k_c/N~{(\Delta P-P_m)}^{\alpha }$ as shown in the insets of (B,C).

Equation (18) predicts an exponent γ = α + 1. A simple argument, related to that given by Roux and Herrmann [22], goes as follows: The number of active capillary tubes is proportional to ${(|\Delta P|-P_m)}^{\alpha }$. This behavior is observed in the insets in Figures 2B,C. The flow rate in an active capillary is proportional to ${(|\Delta P|-P_m)}^{1/2}$. Hence, the total flow rate should be $\langle Q\rangle \propto {(|\Delta P|-P_m)}^{\alpha +1/2}$. It is accidental that this argument works out for P_m > 0 (Figure 2C), as it does not when P_m = 0, where γ = α + 1. For the argument to function, the distribution of active capillaries and the flow rate in each capillary should be uncorrelated. It is not.

We find the same behavior with respect to the cut-off: An exponent 3/2 for the cumulative threshold probability

$\begin{array}{ll}\Pi (P_c)=\{\begin{array}{cc}0\hfill & ,P_c\le P_m,\hfill \\ \frac{\log \left(\frac{P_c}{P_m}\right)}{\log \left(\frac{P_c}{P_M}\right)}& ,P_m<P_c\le P_M,\hfill \\ 1\hfill & ,P_c>P_M,\hfill \end{array}& (25)\end{array}$

where $P_m=10^{-\beta }$ and $P_M=10^{\beta }$ and β ranging from 0.5 to 1.5. The same goes for the cumulative threshold probability

$\begin{array}{ll}\Pi (P_c)=\{\begin{array}{cc}0\hfill & ,P_c\le P_m,\\ 1-e^{-P_c-P_m/P_d}& ,P_m<P_c,\end{array}& (26)\end{array}$

where we have set P_m = 0.1 and P_d = 1. In both of these cases, the probability density at P_c = P_m is finite.

We have presented an analytical study supported by numerical simulations of steady-state two-phase flow in a system of parallel capillary tubes. Considering a uniform distribution for the threshold pressures for the capillaries, we have calculated the average flow rate as a function of the applied pressure drop. When the thresholds are distributed according to a uniform distribution between zero and a maximum value—or more generally, the threshold distribution approaches a non-zero value in the limit of zero thresholds—we obtain a quadratic relationship between the flow rate and the applied pressure drop when the applied pressure drop is below the maximum threshold pressure, and the linear Darcy relationship for higher pressure drops. This crossover between a quadratic non-linear and linear flow regimes is in agreement with many existing results of two-phase flow in porous media which shows that this simple model can capture effective two-phase flow properties of more complex porous media. When a lower cut-off is introduced in the threshold distribution, the quadratic relationship changes, and the flow rate varies with an excess pressure drop with an exponent 3/2 as the pressure drop approaches to the lowest threshold pressure.

The difference between the capillary fiber bundle model and a porous medium is that in the latter, the fluids meet and mix at the nodes of the pore network. This is an essential mechanism that leads to the non-linear Darcy law is a power law with an exponent two as seen in the experiments, the numerical simulations and the mean-field calculations. However, it remains a mystery how the mixing at the nodes leads to this universality.

Data Availability

The datasets for this manuscript are not publicly available because all data sets are included in manuscript. Requests to access the datasets should be directed to subhadeep.roy@ntnu.no.

Author Contributions

AH developed the theory and performed the analytical calculations of the manuscript. AH and SS wrote the first draft of the manuscript. SR did the numerical simulations. All the authors contributed in developing the theory and writing the manuscript to its final form.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

The authors thank Dick Bedeaux, Carl Fredrik Berg, Eirik G. Flekkøy, Signe Kjelstrup, Knut Jørgen Måløy, Per Arne Slotte, and Ole Torsæter for interesting discussions. This work was partly supported by the Research Council of Norway through its Centres of Excellence funding scheme, project number 262644. SS was supported by the National Natural Science Foundation of China under grant number 11750110430.

References

1. Bear J. Dynamics of Fluids in Porous Media. Mineola, NY: Dover (1988).

Google Scholar

2. Dullien FAL. Porous Media: Fluid, Transport and Pore Structure. San Diego, CA: Academic Press (1992).

Google Scholar

3. Chen JD, Wilkinson D. Pore-scale viscous fingering in porous media. Phys Rev Lett. (1985) 55:1892–5. doi: 10.1103/PhysRevLett.55.1892

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Måløy KJ, Feder J, Jøssang T. Viscous fingering fractals in porous media. Phys Rev Lett. (1985) 55:2688–91. doi: 10.1103/PhysRevLett.55.2688

CrossRef Full Text | Google Scholar

5. Lenormand R, Touboul E, Zarcone C. Numerical models and experiments on immiscible displacements in porous media. J Fluid Mech. (1988) 189:165–87. doi: 10.1017/S0022112088000953

CrossRef Full Text | Google Scholar

6. Lenormand R, Zarcone C. Invasion percolation in an etched network: measurement of a fractal dimension. Phys Rev Lett. (1985) 54:2226–9. doi: 10.1103/PhysRevLett.54.2226

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Løvoll G, Méheust Y, Toussaint R, Schmittbuhl J, Måløy KJ. Growth activity during fingering in a porous Hele-Shaw cell. Phys Rev E. (2004) 70:026301. doi: 10.1103/PhysRevE.70.026301

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Wilkinson D, Willemsen JF. Invasion percolation: a new form of percolation theory. J Phys A Math Gen. (1983) 16:3365–76. doi: 10.1088/0305-4470/16/14/028

CrossRef Full Text | Google Scholar

9. Witten TA Jr, Sander LM. Diffusion-limited aggregation, a kinetic critical phenomenon. Phys Rev E. (1981) 47:1400–3. doi: 10.1103/PhysRevLett.47.1400

CrossRef Full Text | Google Scholar

10. Valavanides M. Review of steady-state two-phase flow in porous media: independent variables, universal energy efficiency map, critical flow conditions, effective characterization of flow and pore network. Transp Porous Media. (2018) 123:45–99. doi: 10.1007/s11242-018-1026-1

CrossRef Full Text | Google Scholar

11. Hansen A, Sinha S, Bedeaux D, Kjelstrup S, Gjennestad MA, Vassvik M. Relations between seepage velocities in immiscible, incompressible two-phase flow in porous media. Transp Porous Media. (2018) 125:565–87. doi: 10.1007/s11242-018-1139-6

CrossRef Full Text | Google Scholar

12. Darcy H. Les Fontaines Publiques de la Ville de Dijon: Exposition et Application des Principes à Suivre et des Formules à Employer dans les Questions de Distribution d'eau. Paris: V. Dalamont (1856).

Google Scholar

13. Whitaker S. Flow in porous media I: a theoretical derivation of Darcy's law. Transp Porous Media. (1986) 1:3–25. doi: 10.1007/BF01036523

CrossRef Full Text | Google Scholar

14. Tallakstad KT, Knudsen HA, Ramstad T, Løvoll G, Måløy KJ, Toussaint R, et al. Steady-state two-phase flow in porous media: statistics and transport properties. Phys Rev Lett. (2009) 102:074502. doi: 10.1103/PhysRevLett.102.074502

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Tallakstad KT, Løvoll G, Knudsen HA, Ramstad T, Flekkøy EG, Måløy KJ. Steady-state, simultaneous two-phase flow in porous media: an experimental study. Phys Rev E. (2009) 80:036308. doi: 10.1103/PhysRevE.80.036308

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Rassi EM, Codd SL, Seymour JD. Nuclear magnetic resonance characterization of the stationary dynamics of partially saturated media during steady-state infiltration flow. New J Phys. (2011) 13:015007. doi: 10.1088/1367-2630/13/1/015007

CrossRef Full Text | Google Scholar

17. Sinha S, Bender AT, Danczyk M, Keepseagle K, Prather CA, Bray JM, et al. Effective rheology of two-phase flow in three-dimensional porous media: experiment and simulation. Transp Porous Media. (2017) 119:77–94. doi: 10.1007/s11242-017-0874-4

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Wyckoff RD, Botset HG. The flow of gas-liquid mixtures through unconsolidated sands. J Appl Phys. (1936) 7:325. doi: 10.1063/1.1745402

CrossRef Full Text | Google Scholar

19. Sinha S, Hansen A, Bedeaux D, Kjelstrup S. Effective rheology of bubbles moving in a capillary tube. Phys Rev E. (2013) 87:025001. doi: 10.1103/PhysRevE.87.025001

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Sinha S, Hansen A. Effective rheology of immiscible two-phase flow in porous media. Europhys Lett. (2012) 99:44004. doi: 10.1209/0295-5075/99/44004

CrossRef Full Text | Google Scholar

21. Chevalier T, Talon L. Generalization of Darcy's law for Bingham fluids in porous media: from flow-field statistics to the flow-rate regimes. Phys Rev E. (2015) 91:023011. doi: 10.1103/PhysRevE.91.023011

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Roux S, Herrmann HJ. Disorder-induced nonlinear conductivity. Europhys Lett. (1987) 4:1227. doi: 10.1209/0295-5075/4/11/003

CrossRef Full Text | Google Scholar

23. Scheidegger AE. Theoretical models of porous matter. Producers Monthly. (1953) 17:17.

Google Scholar

24. Scheidegger AE. The Physics of Flow Through Porous Media. Toronto, ON: University of Toronto Press (1974).

Google Scholar

25. Hansen A, Hemmer PC, Pradhan S. The Fiber Bundle Model: Modeling Failure in Materials. Berlin: Wiley (2015).

Google Scholar

26. Savani I, Sinha S, Hansen A, Bedeaux D, Kjelstrup S, Vassvik M. A Monte Carlo algorithm for immiscible two-phase flow in porous media. Transp Porous Media. (2016) 116:869–88. doi: 10.1007/s11242-016-0804-x

CrossRef Full Text | Google Scholar