The Birman-Schwinger Operator for a Parabolic Quantum Well in a Zero-Thickness Layer in the Presence of a Two-Dimensional Attractive Gaussian Impurity

1. Introduction

The study of point potentials in Quantum Physics has recently received a lot of attention for a wide range of interests. First of all, point potentials serve as solvable or quasi-solvable models that approximate the action of intense and very short range potentials [1–3]. They have been used to model several kinds of extra thin structures [4, 5], to mimic point defects in materials, or to study heterostructures [6–9]. In addition, point potentials play a role in modeling impurities in quantum field theory [10–13]. Furthermore, they play an important role after a recent interpretation of the Casimir effect [14, 15]. The unexpected relations between contact potentials and group theory should also be noted [16]. They also play a role in modeling Kronig-Penney crystals in condensed matter physics in various dimensions [1, 17–22].

More examples of physical applications of this kind of interactions are: Bose-Einstein condensation in a harmonic trap with a tight and deep “dimple” potential, modeled by a Dirac delta function [23]; non-perturbative study of the entanglement of two directed polymers subjected to repulsive interactions given by a Dirac δ-function potential [24]; a periodic array of Dirac delta interactions is useful to investigate the light propagation in a one-dimensional realistic dielectric superlattice, which has been investigated for the transverse electric and magnetic fields and for omnidirectional polarization modes [25–27].

One-dimensional quantum models with contact interactions are also useful to study a wide range of quantum properties, including scattering, since these models are quite often solvable. They also serve to acquire experience in order to analyse systems with contact potentials in higher dimensions. However, an important difference is to be pointed out: while one-dimensional contact potentials are usually defined through matching conditions at isolated points, their proper definition in higher dimensions requires a process of regularization.

Quantum two-dimensional systems are particularly interesting for their physical applications. In this particular context, the graphene deserves a special mention because of its importance, although this is not the only one two-dimensional quantum system of interest in physics. From a theoretical point of view, quantum theory in two dimensions has not yet been developed to the same extent of its one-dimensional and three-dimensional analogs, in spite of its enormous interest. Although two-dimensional quantum systems look rather simple, due to the presence of logarithmic singularities in the resolvent kernel of their free Hamiltonian, their level of complexity and, hence, their difficulty of study is far higher than the one-dimensional case (and, to a great extent, the three-dimensional case).

An important contribution to the understanding of two-dimensional quantum mechanics was provided by Duclos' article [28] on the two-dimensional hydrogen atom perturbed by a point interaction, a model that had not been dealt with in Albeverio et al. [1]. One of the main results of that paper is that the free Hamiltonian of that model, namely that of the 2D hydrogen atom, was rigorously shown to be the norm resolvent limit of the Hamiltonian of the 3D Hamiltonian of the hydrogen atom confined to an infinite planar slab of width a > 0 as a → 0₊.

A remarkable feature of two-dimensional models with contact interactions, manifesting itself even in the simple case of the negative Laplacian perturbed by a point interaction, is represented by their peculiar dependence of the bound state energies on the coupling constant. As is well known, the one-dimensional model exhibits a single bound state only when the point interaction is attractive and the eigenvalue is a quadratic function of the strength of the interaction. The three-dimensional case also exhibits a single bound state only in the attractive case but the eigenvalue depends quadratically on the reciprocal of the renormalized coupling constant. In two dimensions the bound state keeps existing even if the contact interaction is repulsive and the dependence becomes exponential (see [1]). The latter behavior is confirmed even when a confinement potential is present in addition to the contact potential, which physically mimics the presence of impurities or thin barriers in the material inside which the quantum particle is moving [29, 30].

In this note, partly motivated by Duclos' paper, we intend to study a different two-dimensional model with the free Hamiltonian given by:

$\begin{array}{ll}{H}_0=\left(-\frac{1}{2}\frac{d^2}{d{x}^2}+\frac{x^2}{2}\right)-\frac{1}{2}\frac{d^2}{d{y}^2},& (1.1)\end{array}$

to which we add an attractive impurity assumed to be modeled by the isotropic Gaussian potential

$\begin{array}{ll}W(x,y)=-\lambda V(x,y)=-\lambda e^{-(x^2+y^2)},\lambda >0,& (1.2)\end{array}$

so that the total Hamiltonian is

$\begin{array}{ll}{H}_{\lambda }=H_0+W(x,y)=H_0-\lambda V(x,y)=H_0-\lambda e^{-(x^2+y^2)},\lambda >0.& (1.3)\end{array}$

It is worth mentioning that the recent literature [31–34] has shown a renewed interest in the spectral analysis of the one-dimensional Hamiltonian with a Gaussian potential, namely

$\begin{array}{ll}H:=-\frac{1}{2}\frac{d^2}{d{x}^2}-\lambda e^{-x^2/2},\lambda >0.& (1.4)\end{array}$

Therefore, (1.3) could also be regarded as a possible two-dimensional generalization of (1.4).

At this point, it is interesting to recall that a three-dimensional material with confinement in only one dimension is said to be a quantum well [35], while a 3D material with two-dimensional confinement is called a quantum wire. Therefore, in the limiting case of a quantum well inside a layer with zero thickness, it makes sense to consider the model in which the confining potential is parabolic. Due to the mathematical subtleties required, in this note we have chosen to omit the proof of the resolvent convergence of the Hamiltonian of a three-dimensional parabolic quantum well inside a thin layer to the 2D Hamiltonian (1.3) as the thickness of the layer vanishes.

Instead we start directly by writing the Green function of the two-dimensional Hamiltonian with a one-dimensional harmonic potential. Once a perturbation given by an attractive two-dimensional Gaussian potential is added, we study the properties of the corresponding Birman-Schwinger operator, that is to say the crucial part in the interaction term of the resolvent of the perturbed Hamiltonian. We remind the reader that the resolvent is the key to obtain the energy eigenvalues. We later consider the model in which the 2D Gaussian impurity potential gets replaced by one having a Dirac delta for the coordinate subjected to the harmonic confinement maintaining the Gaussian character for the other coordinate.

It may be worth pointing out that the Hamiltonian (1.1) has been used by Dell'Antonio and collaborators [36] as the free Hamiltonian in the model of a quantum system consisting of two one-dimensional particles, one of which is harmonically bound to its equilibrium position, mutually interacting by means of the contact interaction δ(x − y). In other words, the interaction studied in [36] will be replaced by the one in (1.2).

Solving the eigenvalue problem for this kind of Hamiltonians is not, in general, an easy task and often requires rather sophisticated tools. One of the most widely used is the Birman-Schwinger operator, namely the integral operator

$\begin{array}{ll}{B}_E=(\text{sgn }W)|W{|}^{\frac{1}{2}}{(H_0-E)}^{-1}|W{|}^{\frac{1}{2}},& (1.5)\end{array}$

and the related technique: as in most applications B_E can be shown to be compact, the solutions of the eigenvalue problem for the Hamiltonian are given by those values of E for which B_E has an eigenvalue equal to -1 (see [22, 37, 38] and references therein as well as [39], p. 99). Therefore, the detailed study of the properties of the Birman-Schwinger operator arising from our model is quite relevant. In the present note, we show that the Birman-Schwinger operator is Hilbert-Schmidt. We also show that H_λ is self-adjoint and bounded from below.

In addition, H_λ has a special relation with a kind of two-dimensional contact operator that will be studied in section 2.1. This is given by the Hamiltonian described heuristically by

$\begin{array}{ll}{H}_{\lambda }^{\delta }=H_0-\lambda \sqrt{\pi }\delta (x)e^{-y^2},\lambda >0,& (1.6)\end{array}$

where δ(x) is the Dirac delta centered at the origin. We show that $H_{\lambda }^{\delta }$ is self-adjoint on a natural domain and can be obtained as the limit in the norm resolvent sense as n ↦ ∞ of the following sequence of Hamiltonians:

$\begin{array}{ll}{H}_{n,\lambda }:=H_0-\lambda n{e}^{-(n^2{x}^2+y^2)},\lambda >0,& (1.7)\end{array}$

thus with Gaussian type potentials (as was the case for H_λ) which become increasingly more attractive and anisotropic as n goes to infinity.

Finally, it will be shown that the Hamiltonian H_λ (resp. $H_{\lambda }^{\delta }$) is bounded from below and its lower bound can be obtained using a certain transcendental equation.

2. The Birman-Schwinger Operator for Our Model

Starting from the Hamiltonian H₀ in (1.1), it is rather straightforward to infer that the associated Green function, namely the integral kernel of the resolvent operator, reads for any $E<\frac{1}{2}$:

$\begin{array}{ll}{(H_0-E)}^{-1}(x,x^{\prime },y,y^{\prime })={\displaystyle \sum _{n=0}^{\infty }\frac{e^{-\sqrt{2\left(n+\frac{1}{2}-E\right)}\left|y-y^{\prime }\right|}}{\sqrt{2\left(n+\frac{1}{2}-E\right)}}}{\varphi }_n(x){\varphi }_n(x^{\prime }),& (2.1)\end{array}$

where ϕ_n(x) is the normalized n-th eigenfunction of the one-dimensional harmonic oscillator.

Once the above attractive Gaussian perturbation (1.2) is added, the total Hamiltonian is H_λ in (1.3). Therefore, its associated Birman-Schwinger integral kernel [22, 31, 32, 37, 38, 40, 41] given by (1.5) is:

$\begin{array}{l}{B}_E=-\lambda {\tilde{B}}_E\left(x,x_1,y,y_1\right)=-\lambda {\left|V\right|}^{\frac{1}{2}}\left(H_0-E^{-1}\right){\left|V\right|}^{\frac{1}{2}}(x,x_1,y,y_1)=\\ =-\lambda e^{-(x^2+y^2)/2}\left[{\displaystyle \sum _{n=0}^{\infty }\frac{e^{-\sqrt{2\left(n+\frac{1}{2}-E\right)}\left|y-y_1\right|}}{\sqrt{2\left(n+\frac{1}{2}-E\right)}}}{\varphi }_n(x){\varphi }_n(x_1)\right]e^{-(x_1^2+y_1^2)/2},& (2.2)\end{array}$

The main goal of this brief note is to rigorously prove that such an integral operator is Hilbert-Schmidt, that is to say $\mathrm{\text{tr}}({\tilde{B}}_E^2)<\infty$, given the evident positivity of the operator ${\tilde{B}}_E$ (and our choice λ > 0). As the kernel of the positive operator ${\tilde{B}}_E^2$ is clearly

$\begin{array}{l}{\tilde{B}}_E^2\left(x,x_2,y,y_2\right)=e^{-(x^2+y^2)/2}\{{\displaystyle {\int }_{-\infty }^{\infty }{\displaystyle {\int }_{-\infty }^{\infty }\left[{\displaystyle \sum _{m=0}^{\infty }\frac{e^{-\sqrt{2\left(m+\frac{1}{2}-E\right)}\left|y-y^{\prime }\right|}}{\sqrt{2\left(m+\frac{1}{2}-E\right)}}}{\varphi }_m(x){\varphi }_m(x^{\prime })\right]}}\\ \times e^{-({x^{\prime }}^2+{y^{\prime }}^2)}\left[{\displaystyle \sum _{n=0}^{\infty }\frac{e^{-\sqrt{2\left(n+\frac{1}{2}-E\right)}\left|y^{\prime }-y_2\right|}}{\sqrt{2\left(n+\frac{1}{2}-E\right)}}}{\varphi }_n(x^{\prime }){\varphi }_n(x_2)\right]d{x}^{\prime }d{y}^{\prime }\}{e}^{-(x_2^2+y_2^2)/2},& (2.3)\end{array}$

its trace reads

$\begin{array}{l}\text{tr}\left({\tilde{B}}_E^2\right)={\displaystyle {\int }_{-\infty }^{\infty }{\displaystyle {\int }_{-\infty }^{\infty }{\tilde{B}}_E^2}}\left(x,x,y,y\right)dxdy\\ ={\displaystyle {\int }_{-\infty }^{\infty }{\displaystyle {\int }_{-\infty }^{\infty }{\displaystyle {\int }_{-\infty }^{\infty }{\displaystyle {\int }_{-\infty }^{\infty }d}}}}xdyd{x}^{\prime }d{y}^{\prime }{e}^{-(x^2+y^2)}{e}^{-(x^{\prime 2}+y^{\prime 2})}\\ \times {\displaystyle \sum _{m=0}^{\infty }{\displaystyle \sum _{n=0}^{\infty }\frac{e^{-\left(\sqrt{2(m+\frac{1}{2}-E)}+\sqrt{2(n+\frac{1}{2}-E)}\right)\left|y-y^{\prime }\right|}}{2\sqrt{(m+\frac{1}{2}-E)(n+\frac{1}{2}-E)}}}}\\ {\varphi }_m(x){\varphi }_m(x^{\prime }){\varphi }_n(x){\varphi }_n(x^{\prime }).& (2.4)\end{array}$

The latter multiple integral can be rewritten as:

$\begin{array}{r}{\displaystyle \sum _{m=0}^{\infty }{\displaystyle \sum _{n=0}^{\infty }\left[{\displaystyle {\int }_{-\infty }^{\infty }{\displaystyle {\int }_{-\infty }^{\infty }{e}^{-y^2}}}\frac{e^{-\left(\sqrt{2(m+\frac{1}{2}-E)}+\sqrt{2(n+\frac{1}{2}-E)}\right)\left|y-y^{\prime }\right|}}{2\sqrt{(m+\frac{1}{2}-E)(n+\frac{1}{2}-E)}}{e}^{-{y^{\prime }}^2}dyd{y}^{\prime }\right]}}\\ {\langle {\varphi }_m,e^{-{(·)}^2}{\varphi }_n\rangle }^2& (2.5)\end{array}$

where 〈f, g〉 denotes the standard scalar product of the two functions.

Let us consider the double integral in (2.5). With the notation,

$\begin{array}{ll}f(y-y^{\prime }):=e^{-\left(\sqrt{2(m+\frac{1}{2}-E)}+\sqrt{2(n+\frac{1}{2}-E)}\right)\left|y-y^{\prime }\right|},g(y^{\prime })=e^{-{y^{\prime }}^2},& (2.6)\end{array}$

the second integral becomes the convolution (f * g)(y), so that the double integral may be written as

$\begin{array}{ll}\frac{1}{2\sqrt{(m+\frac{1}{2}-E)(n+\frac{1}{2}-E)}}{\displaystyle {\int }_{-\infty }^{\infty }{e}^{-y^2}}[(f*g)(y)]dy.& (2.7)\end{array}$

Using the Schwarz inequality (2.7) is smaller than or equal to

$\begin{array}{ll}\frac{1}{2\sqrt{(m+\frac{1}{2}-E)(n+\frac{1}{2}-E)}}\Vert e^{-{(·)}^2}{\Vert }_2\Vert f*g{\Vert }_2,& (2.8)\end{array}$

where ||·||_p denotes the norm in L^p(ℝ). Young's inequality [42] shows that

$\begin{array}{ll}\Vert f*g{\Vert }_r\le \Vert f{\Vert }_p\Vert g{\Vert }_q,\text{\hspace{1em}\hspace{1em}with\hspace{1em}\hspace{1em}}\frac{1}{p}+\frac{1}{q}=\frac{1}{r}+1.& (2.9)\end{array}$

Therefore, with p = r = 2 and q = 1, it follows that (2.8) is smaller than or equal to

$\begin{array}{ll}\frac{1}{2\sqrt{(m+\frac{1}{2}-E)(n+\frac{1}{2}-E)}}\Vert e^{-{(·)}^2}{\Vert }_2^2\Vert f{\Vert }_1.& (2.10)\end{array}$

The two norms in (2.9) yield two integrals which can be easily computed, so as to obtain

$\begin{array}{r}\frac{\sqrt{\pi }}{2^{\frac{3}{2}}\sqrt{(m+\frac{1}{2}-E)(n+\frac{1}{2}-E)}\left(\sqrt{2(m+\frac{1}{2}-E)}+\sqrt{2(n+\frac{1}{2}-E)}\right)}\\ \le \frac{\sqrt{\pi }}{4{(m+\frac{1}{2}-E)}^{\frac{3}{4}}{(n+\frac{1}{2}-E)}^{\frac{3}{4}}}.& (2.11)\end{array}$

Hence, the trace (2.4) is bounded by:

$\begin{array}{l}\text{tr}\left({\tilde{B}}_E^2\right)\le \frac{\sqrt{\pi }}{4}{\displaystyle \sum _{m=0}^{\infty }{\displaystyle \sum _{n=0}^{\infty }\frac{{\langle {\varphi }_m,e^{-{(·)}^2}{\varphi }_n\rangle }^2}{{(m+\frac{1}{2}-E)}^{\frac{3}{4}}{(n+\frac{1}{2}-E)}^{\frac{3}{4}}}}}\\ =\frac{{\pi }^{\frac{3}{2}}}{4}{\displaystyle \sum _{m=0}^{\infty }{\displaystyle \sum _{n=0}^{\infty }\frac{{\langle {\varphi }_m{\varphi }_0,{\varphi }_0{\varphi }_n\rangle }^2}{{(m+\frac{1}{2}-E)}^{\frac{3}{4}}{(n+\frac{1}{2}-E)}^{\frac{3}{4}}}}}.& (2.12)\end{array}$

The scalar products inside the double series can be estimated using Wang's results on integrals of products of eigenfunctions of the harmonic oscillator [43]. While the scalar product clearly vanishes if m + n = 2s + 1, when both indices are either even or odd we get:

$\begin{array}{l}{\langle {\varphi }_{2m}{\varphi }_0,{\varphi }_0{\varphi }_{2n}\rangle }^2=\frac{1}{2\pi }{\left[\frac{[2(m+n)]!}{(m+n)!}\right]}^2\frac{1}{2^{4(m+n)}(2m)!(2n)!}\\ \le \frac{1}{2\pi }{\left[\frac{[2(m+n)]!}{2^{2(m+n)}{[(m+n)!]}^2}\right]}^2\\ =\frac{{\varphi }_{2(m+n)}^4(0)}{2},& (2.13)\end{array}$

$\begin{array}{l}{\langle {\varphi }_{2m+1}{\varphi }_0,{\varphi }_0{\varphi }_{2n+1}\rangle }^2=\frac{1}{2\pi }{\left[\frac{[2(m+n+1)]!}{(m+n+1)!}\right]}^2\\ \frac{1}{2^{4(m+n+1)}(2m+1)!(2n+1)!}\\ \le \frac{1}{2\pi }{\left[\frac{[2(m+n+1)]!}{2^{2(m+n+1)}{[(m+n+1)!]}^2}\right]}^2\\ =\frac{{\varphi }_{2(m+n+1)}^4(0)}{2},& (2.14)\end{array}$

the final equalities in (2.13) and (2.14) resulting from Fassari and Inglese [44] and Mityagin and Siegl [45]. Therefore, the r.h.s. of (2.12) is bounded from above by:

$\begin{array}{l}\text{tr}\left({\tilde{B}}_E^2\right)\le \frac{{\pi }^{\frac{3}{2}}}{8}[{\displaystyle \sum _{m,n=0}^{\infty }\frac{{\varphi }_{2(m+n)}^4(0)}{{(2m+\frac{1}{2}-E)}^{\frac{3}{4}}{(2n+\frac{1}{2}-E)}^{\frac{3}{4}}}}\\ +{\displaystyle \sum _{m,n=0}^{\infty }\frac{{\varphi }_{2(m+n+1)}^4(0)}{{(2m+\frac{3}{2}-E)}^{\frac{3}{4}}{(2n+\frac{3}{2}-E)}^{\frac{3}{4}}}}].& (2.15)\end{array}$

As can be gathered from Mityagin and Siegl [45] using Stirling's formula,

$\begin{array}{l}{\varphi }_{2n}^4(0)\le \frac{1}{{\pi }^{2}n},n\ge 1,\\ {\varphi }_{2(m+n)}^4(0)\le \frac{1}{{\pi }^2(m+n)},m,n\ge 1,\\ {\varphi }_{2(m+n+1)}^4(0)\le \frac{1}{{\pi }^2(m+n+1)},m,n\ge 0,& (2.16)\end{array}$

which implies that (2.15) is bounded by

$\begin{array}{l}\text{tr}\left({\tilde{B}}_E^2\right)\le \frac{1}{8{\pi }^{\frac{1}{2}}}\left[\frac{1}{{(\frac{1}{2}-E)}^{\frac{3}{2}}}+\frac{2}{{(\frac{1}{2}-E)}^{\frac{3}{4}}}{\displaystyle \sum _{n=1}^{\infty }\frac{1}{n{(2n+\frac{1}{2}-E)}^{\frac{3}{4}}}}\right]\\ +\frac{1}{8{\pi }^{\frac{1}{2}}}{\displaystyle \sum _{m=1}^{\infty }{\displaystyle \sum _{n=1}^{\infty }\frac{1}{m^{\frac{1}{2}}{(2m+\frac{1}{2}-E)}^{\frac{3}{4}}{n}^{\frac{1}{2}}{(2n+\frac{1}{2}-E)}^{\frac{3}{4}}}}}\\ +\frac{1}{8{\pi }^{\frac{1}{2}}}{\displaystyle \sum _{m=0}^{\infty }{\displaystyle \sum _{n=0}^{\infty }\frac{1}{{(m+\frac{1}{2})}^{\frac{1}{2}}{(2m+\frac{3}{2}-E)}^{\frac{3}{4}}{(n+\frac{1}{2})}^{\frac{1}{2}}{(2n+\frac{3}{2}-E)}^{\frac{3}{4}}}}}\\ \le \frac{1}{8{\pi }^{\frac{1}{2}}}\left[\frac{1}{{(\frac{1}{2}-E)}^{\frac{3}{2}}}+\frac{2}{{(\frac{1}{2}-E)}^{\frac{3}{4}}}{\displaystyle \sum _{n=1}^{\infty }\frac{1}{n^{\frac{1}{2}}{(2n+\frac{1}{2}-E)}^{\frac{3}{4}}}}\right]\\ +\frac{1}{8{\pi }^{\frac{1}{2}}}{\left[{\displaystyle \sum _{n=1}^{\infty }\frac{1}{n^{\frac{1}{2}}{(2n+\frac{1}{2}-E)}^{\frac{3}{4}}}}\right]}^2\\ +\frac{1}{8{\pi }^{\frac{1}{2}}}{\left[{\displaystyle \sum _{n=0}^{\infty }\frac{1}{{(n+\frac{1}{2})}^{\frac{1}{2}}{(2n+\frac{3}{2}-E)}^{\frac{3}{4}}}}\right]}^2<\infty ,& (2.17)\end{array}$

since both series involved in the final expression are clearly absolutely convergent given that the summands are positive sequences decaying like $n^{-\frac{5}{4}}$. Hence, the trace of the square of the Birman-Schwinger operator, i.e., its Hilbert-Schmidt norm, is finite for any $E<\frac{1}{2}$.

Our result is not surprising at all since the norm could have been bounded by that of the Birman-Schwinger operator with the same impurity but with the resolvent of our H₀ replaced by that of $-\frac{\Delta }{2}$ in two dimensions, which is known to be finite [1]. However, it provides us with a far more accurate estimate of the norm, which in turn leads to a more precise determination of the spectral lower bound resulting from the use of the Hilbert-Schmidt norm of the Birman-Schwinger operator in the KLMN theorem [46]. In fact, the latter bound is what we wish to achieve by further estimating the bottom lines of (2.17).

The series in (2.17) can be bounded from above by their respective improper integrals as follows:

$\begin{array}{l}{S}_1={\displaystyle \sum _{n=1}^{\infty }\frac{1}{n^{\frac{1}{2}}{(2n+\frac{1}{2}-E)}^{\frac{3}{4}}}}={\displaystyle \sum _{n=1}^{\infty }\frac{\sqrt{2}}{{(2n)}^{\frac{1}{2}}{(2n+\frac{1}{2}-E)}^{\frac{3}{4}}}}\\ <{\displaystyle {\int }_0^{\infty }\frac{\sqrt{2}dx}{{(2x)}^{\frac{1}{2}}{(2x+\frac{1}{2}-E)}^{\frac{3}{4}}}}\\ =\frac{3\sqrt{2}}{4}{\displaystyle {\int }_0^{\infty }\frac{s^{\frac{1}{2}}ds}{{(s+\frac{1}{2}-E)}^{\frac{7}{4}}}}\le \frac{3\sqrt{2}}{4}{\displaystyle {\int }_0^{\infty }\frac{ds}{{(s+\frac{1}{2}-E)}^{\frac{5}{4}}}}\\ =\frac{3\sqrt{2}}{{(\frac{1}{2}-E)}^{\frac{1}{4}}}.& (2.18)\end{array}$

$\begin{array}{l}{S}_2={\displaystyle \sum _{n=0}^{\infty }\frac{1}{{(n+\frac{1}{2})}^{\frac{1}{2}}{(2n+\frac{3}{2}-E)}^{\frac{3}{4}}}}=\frac{\sqrt{2}}{{(\frac{1}{2}-E)}^{\frac{3}{4}}}\\ +{\displaystyle \sum _{n=1}^{\infty }\frac{\sqrt{2}}{{(2n+1)}^{\frac{1}{2}}{(2n+\frac{3}{2}-E)}^{\frac{3}{4}}}}\\ <\frac{\sqrt{2}}{{(\frac{1}{2}-E)}^{\frac{3}{4}}}+{\displaystyle {\int }_0^{\infty }\frac{\sqrt{2}dx}{{(2x+1)}^{\frac{1}{2}}{(2x+\frac{3}{2}-E)}^{\frac{3}{4}}}}\\ =\frac{\sqrt{2}}{{(\frac{1}{2}-E)}^{\frac{3}{4}}}-\frac{\sqrt{2}}{{(\frac{1}{2}-E)}^{\frac{3}{4}}}\\ +\frac{3\sqrt{2}}{4}{\displaystyle {\int }_0^{\infty }\frac{{(s+1)}^{\frac{1}{2}}ds}{{(s+\frac{3}{2}-E)}^{\frac{7}{4}}}}\le \frac{3\sqrt{2}}{4}{\displaystyle {\int }_0^{\infty }\frac{ds}{{(s+\frac{3}{2}-E)}^{\frac{5}{4}}}}\\ =\frac{3\sqrt{2}}{{(\frac{3}{2}-E)}^{\frac{1}{4}}}.& (2.19)\end{array}$

Therefore, the bottom lines of (2.17) are bounded by:

$\begin{array}{l}\text{tr}\left({\tilde{B}}_E^2\right)\le \frac{1}{8{\pi }^{\frac{1}{2}}}\left[\frac{1}{{(\frac{1}{2}-E)}^{\frac{3}{2}}}+\frac{6\sqrt{2}}{\frac{1}{2}-E}+\frac{18}{{(\frac{1}{2}-E)}^{\frac{1}{2}}}\right]\\ +\frac{1}{8{\pi }^{\frac{1}{2}}}\frac{18}{{(\frac{3}{2}-E)}^{\frac{1}{2}}}\\ =\frac{1}{8{\pi }^{\frac{1}{2}}{(\frac{1}{2}-E)}^{\frac{1}{2}}}{\left[3\sqrt{2}+\frac{1}{{(\frac{1}{2}-E)}^{\frac{1}{2}}}\right]}^2\\ +\frac{1}{4{\pi }^{\frac{1}{2}}}\frac{9}{{(\frac{3}{2}-E)}^{\frac{1}{2}}}.& (2.20)\end{array}$

Hence, our estimate of the Hilbert-Schmidt norm of the Birman-Schwinger operator is:

$\begin{array}{l}\text{tr}\left({\tilde{B}}_E^2\right)={\left|\left|e^{-\frac{x^2+y^2}{2}}{(H_0-E)}^{-1}{e}^{-\frac{x^2+y^2}{2}}\right|\right|}_2^2\\ \le \frac{1}{8{\pi }^{\frac{1}{2}}{(\frac{1}{2}-E)}^{\frac{1}{2}}}{\left[3\sqrt{2}+\frac{1}{{(\frac{1}{2}-E)}^{\frac{1}{2}}}\right]}^2+\frac{1}{4{\pi }^{\frac{1}{2}}}\frac{9}{{(\frac{3}{2}-E)}^{\frac{1}{2}}}.\end{array}$

As is well known [22, 31, 32, 37, 38, 40, 41], the operator

${\left(H_0-E\right)}^{-1/2}{e}^{-(x^2+y^2)}{\left(H_0-E\right)}^{-1/2}$

is isospectral to the Birman-Schwinger operator so that their Hilbert-Schmidt norms are identical. Hence, what has been achieved so far can be summarized by means of the following claim.

Theorem 2.1 The integral operators

$\begin{array}{r}{\left(H_0-E\right)}^{-1/2}{e}^{-(x^2+y^2)}{\left(H_0-E\right)}^{-1/2}and\\ e^{-\frac{x^2+y^2}{2}}{\left(H_0-E\right)}^{-1}{e}^{-\frac{x^2+y^2}{2}}\end{array}$

are Hilbert-Schmidt and their Hilbert-Schmidt norms satisfy

$\begin{array}{l}{\left|\left|{(H_0-E)}^{-1/2}{e}^{-(x^2+y^2)}{(H_0-E)}^{-1/2}\right|\right|}_2^2\\ ={\left|\left|e^{-\frac{x^2+y^2}{2}}{(H_0-E)}^{-1}{e}^{-\frac{x^2+y^2}{2}}\right|\right|}_2^2\\ \le \frac{1}{8{\pi }^{\frac{1}{2}}{(\frac{1}{2}-E)}^{\frac{1}{2}}}{\left[3\sqrt{2}+\frac{1}{{(\frac{1}{2}-E)}^{\frac{1}{2}}}\right]}^2\\ +\frac{1}{4{\pi }^{\frac{1}{2}}}\frac{9}{{(\frac{3}{2}-E)}^{\frac{1}{2}}}.& (2.21)\end{array}$

As an immediate consequence of the above theorem we get:

Corollary 1 The Hamiltonian

$H_{\lambda }=H_0-\lambda e^{-(x^2+y^2)},$

defined in the sense of quadratic forms, is self-adjoint and bounded from below by E(λ), the solution of the equation:

$\begin{array}{ll}\frac{1}{2{(\frac{1}{2}-E)}^{\frac{1}{2}}}{\left[3\sqrt{2}+\frac{1}{{(\frac{1}{2}-E)}^{\frac{1}{2}}}\right]}^2+\frac{9}{{(\frac{3}{2}-E)}^{\frac{1}{2}}}=\frac{4{\pi }^{\frac{1}{2}}}{{\lambda }^2}.& (2.22)\end{array}$

Proof. For any E < 0 and $\psi \in Q(H_0)=D(H_0^{\frac{1}{2}})$ (the form domain of H₀):

$\begin{array}{l}\lambda \langle \psi ,e^{-(x^2+y^2)}\psi \rangle \\ =\lambda \langle {(H_0-E)}^{1/2}\psi ,\left[{(H_0-E)}^{-1/2}{e}^{-(x^2+y^2)}{(H_0-E)}^{-1/2}\right]{(H_0-E)}^{1/2}\psi \rangle \\ \le \lambda {\left|\left|{(H_0-E)}^{-1/2}{e}^{-(x^2+y^2)}{(H_0-E)}^{-1/2}\right|\right|}_2{\left|\left|{(H_0-E)}^{1/2}\psi \right|\right|}_2^2\\ \le \lambda {\left[\frac{1}{8{\pi }^{\frac{1}{2}}{(\frac{1}{2}-E)}^{\frac{1}{2}}}{\left[3\sqrt{2}+\frac{1}{{(\frac{1}{2}-E)}^{\frac{1}{2}}}\right]}^2+\frac{1}{4{\pi }^{\frac{1}{2}}}\frac{9}{{(\frac{3}{2}-E)}^{\frac{1}{2}}}\right]}^{\frac{1}{2}}\\ \left[\left(\psi ,H_0\psi \right)-E{\left|\left|\psi \right|\right|}_2^2\right].& (2.23)\end{array}$

By taking E sufficiently negative, the first factor in the bottom line of (2.23) can be made arbitrarily small, which ensures that the Gaussian perturbation is infinitesimally small with respect to H₀ in the sense of quadratic forms. Hence, we need only invoke the KLMN theorem (see [42]) to infer that H_λ is self-adjoint and bounded from below by the quantity

$\begin{array}{ll}\frac{\lambda }{2{\pi }^{\frac{1}{4}}}{\left[\frac{1}{2{(\frac{1}{2}-E)}^{\frac{1}{2}}}{\left[3\sqrt{2}+\frac{1}{{(\frac{1}{2}-E)}^{\frac{1}{2}}}\right]}^2+\frac{9}{{(\frac{3}{2}-E)}^{\frac{1}{2}}}\right]}^{\frac{1}{2}}E,E<0,& (2.24)\end{array}$

so that the supremum of such lower bounds is attained for that particular value of E solving (2.22).

In the following subsections we first consider a Hamiltonian with a point interaction all along the x-direction in place of the Gaussian potential and then we investigate in detail the solution of (2.22), that is to say the lower bound of the spectrum of H_λ.

2.1. Hamiltonian With a Point Interaction Along the x-Direction

Let us consider now the Hamiltonian

$H_{\lambda }^{\delta }=H_0-\lambda \sqrt{\pi }\delta (x)e^{-y^2},$

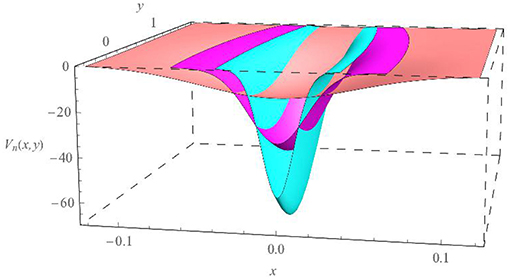
that is to say the energy operator given by the same H₀ as before but with the interaction term having a point interaction in place of the Gaussian along the x-direction. Our goal is to prove that such an operator is self-adjoint and that it is the limit in the norm resolvent sense of the sequence H₀ − λV_n(x, y) as n → ∞, with $V_n(x,y)=n{e}^{-(n^2{x}^2+y^2)}$. As is to be expected, our approximating sequence is quite different from the one used in Albeverio et al. [1] to get the Laplacian perturbed by a point interaction in two dimensions. Before stating and proving the main result of this section, we wish to provide the reader with the visualization of the approximating potentials in Figure 1.

FIGURE 1

Figure 1. Approximating potentials $V_n(x,y)=n{e}^{-(n^2{x}^2+y^2)}$ for n = 15 (pink), 30 (magenta), and 70 (cyan).

Corollary 2 The Hamiltonian $H_{\lambda }^{\delta }=H_0-\lambda \sqrt{\pi }\delta (x)e^{-y^2}$, defined in the sense of quadratic forms, is self-adjoint and is the norm resolvent limit of the sequence of Hamiltonians

$H_{n,\lambda }=H_0-\lambda n{e}^{-(n^2{x}^2+y^2)}.$

Furthermore, $H_{\lambda }^{\delta }$ is bounded from below by E_δ(λ), the solution of the equation:

$\begin{array}{ll}\frac{1}{{(\frac{1}{2}-E)}^{\frac{1}{2}}}{\left[\frac{1}{{(\frac{1}{2}-E)}^{\frac{1}{2}}}+3\sqrt{2}\right]}^2=\frac{4{\pi }^{\frac{1}{2}}}{{\lambda }^2}.& (2.25)\end{array}$

Proof. First of all, it is quite straightforward to show that the integral operator

${(H_0-E)}^{-1/2}\sqrt{\pi }\delta (x)e^{-y^2}{(H_0-E)}^{-1/2},E<0,$

is Hilbert-Schmidt with the square of the Hilbert-Schmidt norm given by:

$\begin{array}{l}\pi {\left|\left|{(H_0-E)}^{-1/2}\delta (x)e^{-y^2}{(H_0-E)}^{-1/2}\right|\right|}_2^2\\ =\pi {\left|\left|{(\delta (x)e^{-y^2})}^{\frac{1}{2}}{(H_0-E)}^{-1}{(\delta (x)e^{-y^2})}^{\frac{1}{2}}\right|\right|}_2^2\\ =\pi {\displaystyle {\int }_{-\infty }^{\infty }{\displaystyle {\int }_{-\infty }^{\infty }{e}^{-y^2}}}{e}^{-{y^{\prime }}^2}{\left[{(H_0-E)}^{-1}(0,0,y,y^{\prime })\right]}^{2}dyd{y}^{\prime }\\ =\pi {\displaystyle {\int }_{-\infty }^{\infty }{\displaystyle {\int }_{-\infty }^{\infty }{e}^{-y^2}}}{e}^{-{y^{\prime }}^2}{\left[{\displaystyle \sum _{n=0}^{\infty }\frac{e^{-\sqrt{2\left(2n+\frac{1}{2}-E\right)}\left|y^{\prime }-y^{″}\right|}}{\sqrt{2\left(2n+\frac{1}{2}-E\right)}}}{\varphi }_{2n}^2(0)\right]}^{2}dyd{y}^{\prime }\\ =\frac{\pi }{2}{\displaystyle \sum _{m=0}^{\infty }{\displaystyle \sum _{n=0}^{\infty }{\varphi }_{2m}^2}}(0){\varphi }_{2n}^2(0)\\ {\displaystyle {\int }_{-\infty }^{\infty }{\displaystyle {\int }_{-\infty }^{\infty }{e}^{-y^2}}}\frac{e^{-\sqrt{2\left(2m+\frac{1}{2}-E\right)}\left|y-y^{\prime }\right|}{e}^{-\sqrt{2\left(2n+\frac{1}{2}-E\right)}\left|y-y^{\prime }\right|}}{\sqrt{\left(2m+\frac{1}{2}-E\right)\left(2n+\frac{1}{2}-E\right)}}{e}^{-{y^{\prime }}^2}dyd{y}^{\prime }.\end{array}$

As the double integral involving the convolution has already been estimated in (2.11), the latter expression is bounded by:

$\begin{array}{r}\frac{{\pi }^{3/2}}{4}{\displaystyle \sum _{m=0}^{\infty }{\displaystyle \sum _{n=0}^{\infty }\frac{{\varphi }_{2m}^2(0){\varphi }_{2n}^2(0)}{{(2m+\frac{1}{2}-E)}^{\frac{3}{4}}{(2n+\frac{1}{2}-E)}^{\frac{3}{4}}}}}\\ =\frac{{\pi }^{3/2}}{4}{\left[{\displaystyle \sum _{n=0}^{\infty }\frac{{\varphi }_{2n}^2(0)}{{(2n+\frac{1}{2}-E)}^{\frac{3}{4}}}}\right]}^2,& (2.26)\end{array}$

which, using (2.17), is bounded by:

$\begin{array}{l}\frac{1}{4{\pi }^{1/2}}{\left[\frac{1}{{(\frac{1}{2}-E)}^{\frac{3}{4}}}+{\displaystyle \sum _{n=1}^{\infty }\frac{1}{n^{\frac{1}{2}}{(2n+\frac{1}{2}-E)}^{\frac{3}{4}}}}\right]}^2\\ \le \frac{1}{4{\pi }^{1/2}}{\left[\frac{1}{{(\frac{1}{2}-E)}^{\frac{3}{4}}}+\frac{3\sqrt{2}}{{(\frac{1}{2}-E)}^{\frac{1}{4}}}\right]}^2\\ =\frac{1}{4{\pi }^{\frac{1}{2}}{(\frac{1}{2}-E)}^{\frac{1}{2}}}{\left[\frac{1}{{(\frac{1}{2}-E)}^{\frac{1}{2}}}+3\sqrt{2}\right]}^2,& (2.27)\end{array}$

having taken advantage of (2.18). As the right hand side of (2.27) can be made arbitrarily small by taking E < 0 large in absolute value, the KLMN theorem ensures, as was done previously in the case of H_λ, the self-adjointness of $H_{\lambda }^{\delta }$ as well as the existence of the spectral lower bound E_δ(λ) given by the solution of (2.25).

As to the convergence of H_{n, λ} to $H_{\lambda }^{\delta }$, we start by noting that, for any E < 0, the operator ${(H_0-E)}^{-1/2}n{e}^{-(n^2{x}^2+y^2)}{(H_0-E)}^{-1/2}$ converges weakly to ${(H_0-E)}^{-1/2}\sqrt{\pi }\delta (x)e^{-y^2}{(H_0-E)}^{-1/2}$ as n → ∞. Furthermore,

$\begin{array}{l}{\left|\left|{(H_0-E)}^{-1/2}n{e}^{-(n^2{x}^2+y^2)}{(H_0-E)}^{-1/2}\right|\right|}_2^2\\ ={\left|\left|n{e}^{-\frac{n^2{x}^2+y^2}{2}}{(H_0-E)}^{-1}{e}^{-\frac{n^2{x}^2+y^2}{2}}\right|\right|}_2^2\\ ={\displaystyle \sum _{l,m=0}^{\infty }\left[{\displaystyle {\int }_{-\infty }^{\infty }{\displaystyle {\int }_{-\infty }^{\infty }{e}^{-y^2}}}\frac{e^{-\left(\sqrt{2(l+\frac{1}{2}-E)}+\sqrt{2(m+\frac{1}{2}-E)}\right)\left|y-y^{\prime }\right|}}{2\sqrt{(l+\frac{1}{2}-E)(m+\frac{1}{2}-E)}}{e}^{-{y^{\prime }}^2}dyd{y}^{\prime }\right]}\\ {\langle {\varphi }_l,n{e}^{-n^2{(·)}^2}{\varphi }_m\rangle }^2\text{}.& (2.28)\end{array}$

Since

$\begin{array}{l}\langle {\varphi }_l,n{e}^{-n^2{(·)}^2}\text{}{\varphi }_m\rangle =n{\displaystyle {\int }_{-\infty }^{\infty }\text{}}{e}^{-n^2{x}^2}\text{}{\varphi }_l(x){\varphi }_m(x)dx\\ ={\displaystyle {\int }_{-\infty }^{\infty }\text{}}{e}^{-x^2}\text{}{\varphi }_l(x/n){\varphi }_m(x/n)dx\to \sqrt{\pi }{\varphi }_l(0){\varphi }_m(0),\end{array}$

as n → ∞, the right hand side of (2.28) converges to

$\begin{array}{l}\frac{\pi }{2}{\displaystyle \sum _{l=0}^{\infty }{\displaystyle \sum _{m=0}^{\infty }{\varphi }_{2l}^2}}(0){\varphi }_{2m}^2(0)\\ \left[{\displaystyle {\int }_{-\infty }^{\infty }{\displaystyle {\int }_{-\infty }^{\infty }{e}^{-y^2}}}\frac{e^{-\left(\sqrt{2(2l+\frac{1}{2}-E)}+\sqrt{2(2m+\frac{1}{2}-E)}\right)\left|y-y^{\prime }\right|}}{\sqrt{(2l+\frac{1}{2}-E)(2m+\frac{1}{2}-E)}}{e}^{-{y^{\prime }}^2}dyd{y}^{\prime }\right]\\ =\pi {\left|\left|{(\delta (x)e^{-y^2})}^{\frac{1}{2}}{(H_0-E)}^{-1}{(\delta (x)e^{-y^2})}^{\frac{1}{2}}\right|\right|}_2^2\\ =\pi {\left|\left|{(H_0-E)}^{-1/2}\delta (x)e^{-y^2}{(H_0-E)}^{-1/2}\right|\right|}_2^2.\end{array}$

Hence, the Hilbert-Schmidt norm of ${(H_0-E)}^{-1/2}n{e}^{-(n^2{x}^2+y^2)}{(H_0-E)}^{-1/2}$ converges to the Hilbert-Schmidt norm of ${(H_0-E)}^{-1/2}\sqrt{\pi }\delta (x)e^{-y^2}{(H_0-E)}^{-1/2}$ as n → ∞. Due to Theorem 2.21 in Simon [47], this fact and the previous weak convergence imply that the convergence actually takes place in the Hilbert-Schmidt norm. Then, the norm convergence of these integral operators ensures the norm resolvent convergence of H_{n, λ} to $H_{\lambda }^{\delta }$, as guaranteed by Theorem VIII.25 in Reed and Simon [46], which completes our proof of Corollary 2.

2.2. The Lower Bound of $\sigma (H_0-\lambda e^{-(x^2+y^2)})$

As anticipated earlier, the lower bound of the spectrum of H_λ in (1.3) is the function E(λ) given implicitly by the equation (2.22). From this expression, some approximate results can be easily obtained in two different regimes. For example, it is possible to prove that the asymptotic behavior of (2.22) for large values of both variables E(_λ), λ is

$\begin{array}{ll}E{(}_{\lambda })=-\frac{81}{4{\pi }^2}{\lambda }^4.& (2.29)\end{array}$

On the other hand, for small values of λ we can prove that (2.22) behaves approximately as follows

$\begin{array}{ll}E{(}_{\lambda })=\frac{1}{2}-\frac{1}{4{\pi }^{2/3}}{\lambda }^{4/3}.& (2.30)\end{array}$

A plot of the λ-dependence (λ being the strength of the potential of H_λ) of the lower bound of the energy E(_λ), resulting from the solution of (2.22), as well as those of the two approximations given by (2.29) and (2.30), are given in Figure 2.

FIGURE 2

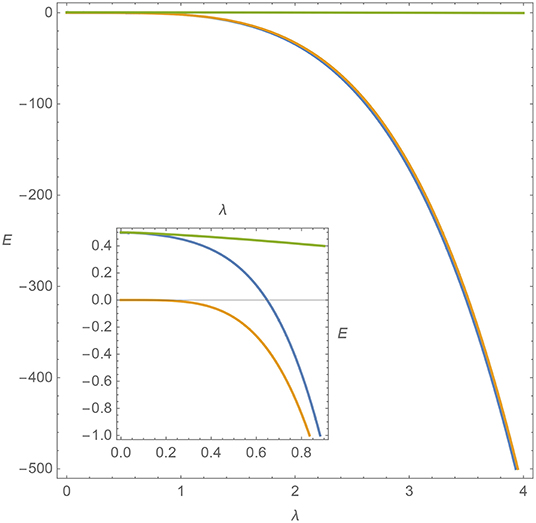
Figure 2. A plot of the lower bound of the energy E as a function of λ resulting from the solution of Equation (2.22) (blue curve), the approximate expression valid for large values of E and λ obtained in (2.29) (yellow curve) and the approximation for small values of λ as in (2.30) (green curve). In the inset we have enlarged the region where λ and E are small. While the similarity between the solution of (2.22) and the funtion (2.29) is quite acceptable for a wide range of the parameters, the solution of (2.22) is satisfactorily approximated by (2.30) only for very small values of λ.

3. Final Remarks

In this note we have analyzed in detail the Birman-Schwinger operator of the two-dimensional Hamiltonian $H_{\lambda }=H_0-\lambda e^{-(x^2+y^2)}$, namely the integral operator $-\lambda e^{-\frac{x^2+y^2}{2}}{(H_0-E)}^{-1}{e}^{-\frac{x^2+y^2}{2}}$ where $H_0=(-\frac{1}{2}\frac{d^2}{d{x}^2}+\frac{x^2}{2})-\frac{1}{2}\frac{d^2}{d{y}^2}$. In particular, we have rigorously shown that the operator is Hilbert-Schmidt and have estimated its Hilbert-Schmidt norm. This fact has enabled us to use the KLMN theorem to determine a lower bound for the spectrum of H_λ, that is to say E(λ), the implicit function representing the solution of an equation involving the energy parameter and the coupling constant. Furthermore, we have investigated the Hamiltonian $H_{\lambda }^{\delta }=H_0-\lambda \sqrt{\pi }\delta (x)e^{-y^2}$, having the Gaussian impurity in the direction subjected to the harmonic confinement replaced by a point impurity.

As anticipated in the introduction, the proof of the resolvent convergence, as the thickness of the layer vanishes, of the Hamiltonian of a three-dimensional parabolic quantum well inside a thin layer to the 2D Hamiltonian (1.3) has been put off as it may deserve a separate paper.

The results of this article will enable us to study the lowest bound states created by the Gaussian impurity potential of the aforementioned Hamiltonian by means of the modified Fredholm determinant ${\mathrm{\text{det}}}_2\left[1-\lambda e^{\frac{x^2+y^2}{2}}{(H_0-E)}^{-1}{e}^{-\frac{x^2+y^2}{2}}\right]$, the regularized determinant used to handle Hilbert-Schmidt operators. Work in this direction is in progress.

Data Availability

All datasets generated for this study are included in the manuscript and/or the supplementary material.

Author Contributions

All authors listed have made a substantial, direct and intellectual contribution to the work, and approved it for publication.

Funding

This work was partially supported by the Spanish MINECO (MTM2014-57129-C2-1-P), Junta de Castilla y León and FEDER projects (BU229P18, VA057U16, and VA137G18).

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

The authors are indebted to both referees for their suggestions and corrections resulting in the significant improvement of the paper.

References

1. Albeverio S, Gesztesy F, Høegh-Krohn R, Holden H. Solvable Models in Quantum Mechanics, 2nd ed. Providence, RI: AMS Chelsea Publishing (2004). doi: 10.1090/chel/350

CrossRef Full Text | Google Scholar

2. Seba P. Some remarks on the δ-interaction in one dimension Czech. J Phys. (1986) 36:667–73. doi: 10.1007/BF01597402

CrossRef Full Text | Google Scholar

3. Bräunlich G, Hainzl C, Seiringer R. On contact interactions as limits of short-range potentials Met. Funct Anal Top. (2013) 19:364–75.

Google Scholar

4. Zolotaryuk AV, Zolotaryuk Y A zero-thickness limit of multilayer structures: a resonant-tunnelling δ′-potential. J Phys A. (2015) 48:035302. doi: 10.1088/1751-8113/48/3/035302

CrossRef Full Text | Google Scholar

5. Zolotaryuk AV, Zolotaryuk Y. Controllable resonant tunnelling through single-point potentials: a point triode. Phys Lett A. (2015) 379:511–7. doi: 10.1016/j.physleta.2014.12.016

CrossRef Full Text | Google Scholar

6. Gadella M, Heras FJH, Negro J, Nieto LM. A delta well with a mass jump. J Phys A. (2009) 42:465207. doi: 10.1088/1751-8113/42/46/465207

CrossRef Full Text | Google Scholar

7. Kulinskii VL, Panchenko DY. Physical structure of point-like interactions for one-dimensional Schrödinger and the gauge symmetry. Phys B Cond Matt. (2015) 472:78–83. doi: 10.1016/j.physb.2015.05.011

CrossRef Full Text | Google Scholar

8. Kulinskii VL, Panchenko DY. Mass-jump and mass-bump boundary conditions for singular self-adjoint extensions of the Schrödinger operator in one dimension. Ann Phys. (2019) 404:47–56. doi: 10.1016/j.aop.2019.03.001

CrossRef Full Text | Google Scholar

9. Kulinskii VL, Panchenko DY. Point-like rashba interactions as singular self-adjoint extensions of the Schrödinger operator in one dimension. Front Phys. (2019) 7:44. doi: 10.3389/fphy.2019.00044

CrossRef Full Text | Google Scholar

10. Muñoz-Castañeda JM, Mateos-Guilarte J, Mosquera AM. Quantum vacuum energies and Casimir forces between partially transparent δ-function plates. Phys Rev D (2013) 87:105020. doi: 10.1103/PhysRevD.87.105020

CrossRef Full Text | Google Scholar

11. Asorey M, García-Alvarez D, Muñoz-Castañeda JM. Casimir effect and global theory of boundary conditions. J Phys A Math Gen. (2006) 39:6127–36. doi: 10.1088/0305-4470/39/21/S03

CrossRef Full Text | Google Scholar

12. Muñoz-Castañeda JM, Kirsten K, Bordag M. QFT over the finite line. Heat kernel coefficients, spectral zeta functions and selfadjoint extensions. Lett Math Phys. (2015) 105:523–49. doi: 10.1007/s11005-015-0750-5

CrossRef Full Text | Google Scholar

13. Muñoz-Castañeda JM, Mateos-Guilarte J. δ − δ′ generalized Robin boundary conditions and quantum vacuum fluctuations. J Phys Rev D. (2015) 91:025028. doi: 10.1103/PhysRevD.91.025028

CrossRef Full Text | Google Scholar

14. Bordag M. Monoatomically thin polarizable sheets. Phys Rev D. (2014) 89:125015. doi: 10.1103/PhysRevD.89.125015

CrossRef Full Text | Google Scholar

15. Asorey M, Muñoz-Castañeda JM. Attractive and repulsive Casimir vacuum energy with general boundary conditions. Nucl Phys B. (2013) 874:852–76. doi: 10.1016/j.nuclphysb.2013.06.014

CrossRef Full Text | Google Scholar

16. Gadella M, Mateos-Guilarte J, Muñoz-Castañeda JM, Nieto LM. Two-point one-dimensional δ − δ′ interactions: non-abelian addition law and decoupling limit. J Phys A Math. Theor. (2016) 49:015204. doi: 10.1088/1751-8113/49/1/015204

CrossRef Full Text | Google Scholar

17. Fairbairn WM, Glasser ML, Steslicka M. Relativistic theory of surface states. Surf Sci. (1973) 36:462–71. doi: 10.1016/0039-6028(73)90394-4

CrossRef Full Text | Google Scholar

18. Fassari S. On the Schrödinger operator with periodic point interactions in the three-dimensional case. J Math Phys. (1984) 25:2910–7. doi: 10.1063/1.526038

CrossRef Full Text | Google Scholar

19. Fassari S. Spectral properties of the Kronig-Penney Hamiltonian with a localized impurity. J Math Phys. (1989) 30:1385–92. doi: 10.1063/1.528320

CrossRef Full Text | Google Scholar

20. Fassari S. On the bound states of non-relativistic Kronig-Penney Hamiltonians with short range impurities. Helv Phys Acta. (1990) 63:849–83.

Google Scholar

21. Fassari S. On the bound states of relativistic Kronig-Penney Hamiltonians with short range impurities. Helv Phys Acta. (1990) 63:884–907.

Google Scholar

22. Fassari S, Klaus M. Coupling constant thresholds of perturbed periodic Hamiltonians. J Math Phys. (1998) 39:4369–16. doi: 10.1063/1.532516

CrossRef Full Text | Google Scholar

23. Uncu H, Tarhan D, Demiralp E, Müstecaplıoğlu ÖE. Bose-Einstein condensate in a harmonic trap decorated with Dirac δ-functions. Phys Rev A. (2007) 76:013618. doi: 10.1103/PhysRevA.76.013618

CrossRef Full Text | Google Scholar

24. Ferrari F, Rostiashvilii VG, Vilgis TA. Directed polymers with constrained winding angle. Phys Rev E. (2005) 71:061802. doi: 10.1103/PhysRevE.71.061802

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Alvarado-Rodríguez I, Halevi P, Sánchez-Mondragón JJ. Density of states for a dielectric superlattice: TE polarization. Phys Rev E (1999) 59:3624–30. doi: 10.1103/PhysRevE.59.3624

CrossRef Full Text | Google Scholar

26. Zurita-Sánchez JR, Halevi P. Density of states for a dielectric superlattice. II. TM polarization. Phys Rev E. (2000) 61:5802–7. doi: 10.1103/PhysRevE.61.5802

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Lin MC, Jao RF. Quantitative analysis of photon density of states for a realistic superlattice with omnidirectional light propagation. Phys Rev E. (2006) 74:046613. doi: 10.1103/PhysRevE.74.046613

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Duclos P, Štovícek P, Tušek M. On the two-dimensional Coulomb-like potential with a central point interaction. J Phys A Math Theor. (2010) 43:474020. doi: 10.1088/1751-8113/43/47/474020

CrossRef Full Text | Google Scholar

29. Fassari S, Gadella M, Glasser ML, Nieto LM, Rinaldi F. Level crossings of eigenvalues of the Schrödinger Hamiltonian of the isotropic harmonic oscillator perturbed by a central point interaction in different dimensions. Nanosyst Phys Chem Math. (2018) 9:179–86. doi: 10.17586/2220-8054-2018-9-2-179-186

CrossRef Full Text | Google Scholar

30. Fassari S, Gadella M, Glasser ML, Nieto LM, Rinaldi F. Spectral properties of the 2D Schrödinger Hamiltonian with various solvable confinements in the presence of a central point perturbation. Phys Scr. (2019) 94:055202. doi: 10.1088/1402-4896/ab0589

CrossRef Full Text | Google Scholar

31. Muchatibaya G, Fassari S, Rinaldi, F, Mushanyu J. A note on the discrete spectrum of Gaussian wells (I): the ground state energy in one dimension. Adv Math Phys. (2016) 2016:2125769. doi: 10.1155/2016/2125769

CrossRef Full Text | Google Scholar

32. Fassari S, Gadella M, Nieto L M, Rinaldi F. On the spectrum of the 1D Schrödinger Hamiltonian perturbed by an attractive Gaussian potential. Acta Polytech. (2017) 57:385–90. doi: 10.14311/AP.2017.57.0385

CrossRef Full Text | Google Scholar

33. Fernández FM. Quantum Gaussian wells and barriers. Am J Phys. (2011) 79:752–4. doi: 10.1119/1.3574505

CrossRef Full Text | Google Scholar

34. Nandi S. The quantum Gaussian well. Am J Phys. (2010) 78:1341–5. doi: 10.1119/1.3474665

CrossRef Full Text | Google Scholar

35. Harrison P. Quantum wells, wires, dots. In: Theoretical and Computational Physics of Semiconductor Nanostructures. 3rd ed. Chichester: Wiley (2009).

Google Scholar

36. Correggi M, Dell'Antonio G, Finco D. Spectral analysis of a two-body problem with zero-range perturbation. J Funct Anal. (2008) 255:502–531. doi: 10.1016/j.jfa.2008.04.005

CrossRef Full Text | Google Scholar

37. Klaus M. A remark about weakly coupled one-dimensional Schrödinger operators. Helv Phys Acta. (1979) 52:223.

Google Scholar

38. Klaus M. Some applications of the Birman-Schwinger principle. Helv Phys Acta. 55, 49–68.

Google Scholar

39. Reed M, Simon B. Analysis of Operators. Methods in modern mathematical physics. New York, NY: Academic Press (1978).

Google Scholar

40. Fassari S. An estimate regarding one-dimensional point interactions. Helv Phys Acta. (1995) 68:121–5.

Google Scholar

41. Fassari S, Rinaldi F. On the spectrum of the Schrödinger Hamiltonian with a particular configuration of three point interactions. Rep Math Phys. (2009) 64:367–93. doi: 10.1016/S0034-4877(10)00004-2

CrossRef Full Text | Google Scholar

42. Reed M, Simon B. Fourier Analysis, Self-adjointness. Methods in modern mathematical physics. New York, NY: Academic Press (1975).

Google Scholar

43. Wang WM. Pure point spectrum of the floquet Hamiltonian for the quantum harmonic oscillator under time quasi-periodic perturbations commun. Math Phys. (2008) 277:459–96. doi: 10.1007/s00220-007-0379-z

CrossRef Full Text | Google Scholar

44. Fassari S, Inglese G. On the spectrum of the harmonic oscillator with a δ-type perturbation. Helv Phys Acta. (1994) 67:650–9.

Google Scholar

45. Mityagin BS, Siegl P. Root system of singular perturbations of the harmonic oscillator type operators. Lett Math Phys. (2016) 106:147–67. doi: 10.1007/s11005-015-0805-7

CrossRef Full Text | Google Scholar

46. Reed M, Simon B. Functional Analysis. Methods in Modern Mathematical Physics. New York, NY: Academic Press (1972).

Google Scholar

47. Simon B. Trace Ideals and Their Applications. Cambridge: Cambridge University Press (1979).

Google Scholar