Transient Anomalous Diffusion in a Heterogeneous Environment

This work provides an analytical model for the diffusive motion of particles in a heterogeneous environment where the diffusivity varies with position. The model for diffusivity describes the environment as being homogeneous with randomly positioned pockets of larger diffusivity. This general framework for heterogeneity is amenable to a systematic expansion of the Green's function, and we employ a diagrammatic approach to identify common terms in this expansion. Upon collecting a common family of these diagrams, we arrive at an analytical expression for the particle Green's function that captures the spatially varying diffusivity. The resulting Green's function is used to analyze anomalous diffusion and kurtosis for varying levels of heterogeneity, and we compare these results with numerical simulations to confirm their validity. These results act as a basis for analysis of a range of diffusive phenomena in heterogeneous materials and living cells.

Introduction

Brownian motion of microscopic objects [1–3] is a ubiquitous phenomenon that plays a significant role in virtually all molecular processes. Predictive understanding of the statistical behavior of objects undergoing Brownian motion is essential to our ability to determine and control the outcome of processes that fundamentally rely on stochastic motion at the molecular level. Given the general nature of Brownian motion, it is essential to establish a mathematical framework that is transferable to a diverse range of materials with varying microscopic structural characteristics.

Foundational studies of Brownian motion [1, 2, 4] establish a mathematical approach for predicting trajectory statistics in a homogeneous environment, thus capturing diffusive random-walk processes described by Gaussian statistics. However, all materials exhibit microscopic heterogeneity at length scales approaching that of individual chemical units (i.e., approaching atomic scales), and a broad range of materials, including glasses, gels, and other amorphous solids, exhibit heterogeneity across a broad range of length scales [5–11]. Furthermore, experimental measurements of particle motion in living cells reveal anomalous diffusive transport [12–25] that is tied to a range of physical effects, including heterogeneity and cell-to-cell variability [26] as well as viscoelasticity [26–29], dynamic arrest due to glassy disorder [11, 19], and active biological processes [9, 17, 25, 30]. Heterogeneity in soft materials and living cells results in non-Gaussian statistics for the step distribution over a range of time scales [8, 9, 26, 31–33], which acts as a signature for heterogeneous diffusion.

Theoretical modeling of heterogeneous diffusion provides fundamental insight into the impact of spatially varying diffusivity. Homogenization [34–38] and effective medium theory [39–47] are powerful analytical approaches to modeling spatially varying diffusivity. Such approaches leverage a systematic averaging of the microscopic heterogeneity as an effective large-scale medium, resulting in predictions for the effective diffusion at large length scales. However, the initial diffusive transport is distinct from the behavior in this effective medium. Thus, the behavior across broad time scales exhibits both the initial sampling of the local environment and the long-time sampling of the surrounding effective medium.

To capture this temporal evolution of the effective diffusivity, theoretical approaches employ frameworks that allow the diffusivity to stochastically change with time, dubbed a “diffusing diffusivity” [48–51]. This approach has been valuable in interpreting particle dynamics in living cells across a broad range of time scales, where the particles generally transition from complex heavy-tailed statistics to effective Gaussian behavior [8, 9, 26, 31–33]. However, the microscopic interpretation of the diffusing diffusivity picture is not straightforward. Thus, an analytical treatment that directly relates the specific microscopic structural heterogeneity to particle diffusion across all time scales would be valuable in establishing a fundamental understanding of heterogeneous transport. Such a development would impact a broad range of soft-materials and biological phenomena with varying microscopic structural characteristics.

Our work provides an analytical approach to determining the Green's function for diffusion in a spatially varying environment. We present an exact solution for the Green's function for an arbitrary spatial diffusivity function. We then define a heterogeneous diffusivity model with randomly positioned pockets of large diffusivity in an otherwise homogeneous background. Based on this model, we develop a systematic approach to determining the diffusivity-averaged Green's function over a range of degrees of heterogeneity. This approach applies a diagrammatic representation of the terms in the exact solution. We exploit this diagrammatic representation to collect like-powered terms in the strength of heterogeneity, resulting in an analytical expression for the Green's function.

Our solution is then used to analyze the transient anomalous diffusion of particles in a heterogeneous environment. We also analyze the temporal evolution of the kurtosis as a signature of the underlying non-Gaussian nature of the step distribution. These results demonstrate the signature feature of heterogeneous diffusion, where a particle transitions from sampling its local environment before transitioning to exploring the surrounding effective medium. These results provide a new framework for interpreting the temporal evolution of diffusive transport in complex heterogeneous materials and living cells.

Theory

We consider the diffusion of a particle in a heterogeneous environment (in d dimensions) with a spatially varying diffusivity $D(\overrightarrow{r})$. The transport of the particle is defined by the Green's function $G(\overrightarrow{r}|{\overrightarrow{r}}_0;t)$, which gives the probability that a particle that begins at position ${\overrightarrow{r}}_0$ and time t = 0 is located at $\overrightarrow{r}$ at time t. The Green's function G is governed by the Smoluchowski equation

$\begin{array}{ll}\frac{\partial G(\overrightarrow{r}|{\overrightarrow{r}}_0;t)}{\partial t}=\overrightarrow{\nabla }·\left[D(\overrightarrow{r})\overrightarrow{\nabla }G(\overrightarrow{r}|{\overrightarrow{r}}_0;t)\right]& (1)\end{array}$

with the initial condition

$\begin{array}{ll}G(\overrightarrow{r}|{\overrightarrow{r}}_0;t=0)=\delta (\overrightarrow{r}-{\overrightarrow{r}}_0).& (2)\end{array}$

We perform a Laplace transform from time t to the Laplace variable s and a Fourier transform from position $\overrightarrow{r}$ to Fourier variable $\overrightarrow{k}$. We then arrive at the expression

$\begin{array}{ll}\widehat{\tilde{G}}(\overrightarrow{k};s)=\frac{exp(i\overrightarrow{k}·{\overrightarrow{r}}_0)}{s}-\frac{1}{{(2\pi )}^d}\frac{1}{s}{\displaystyle \int }d{\overrightarrow{k}}_1(\overrightarrow{k}·{\overrightarrow{k}}_1)\tilde{D}(\overrightarrow{k}-{\overrightarrow{k}}_1)\widehat{\tilde{G}}({\overrightarrow{k}}_1;s),& (3)\end{array}$

where the tilde indicates a Fourier-transformed function and the hat indicates a Laplace-transformed function.

The current form of $\widehat{\tilde{G}}$ is transcendental (i.e., $\widehat{\tilde{G}}$ is a function of $\widehat{\tilde{G}}$), and an explicit expression for $\widehat{\tilde{G}}(\overrightarrow{k};s)$ requires recursive insertion of Equation (3) into itself. This leads to a general form

$\begin{array}{ll}\widehat{\tilde{G}}(\overrightarrow{k};s)=exp(i\overrightarrow{k}·{\overrightarrow{r}}_0){\displaystyle \sum _{n=0}^{\infty }}\frac{{(-1)}^n}{s^{n+1}}{D}_n(\overrightarrow{k}).& (4)\end{array}$

The k-dependent terms D_n represent the contributions from spatially varying diffusivity at various powers of $\tilde{D}$. The expressions for D_n up to n = 3 are given by

$\begin{array}{ll}{D}_0=1,& (5)\end{array}$

$\begin{array}{ll}{D}_1=\frac{1}{{(2\pi )}^d}{\displaystyle \int }d{\overrightarrow{k}}_1(\overrightarrow{k}·{\overrightarrow{k}}_1)\tilde{D}(\overrightarrow{k}-{\overrightarrow{k}}_1),& (6)\end{array}$

$\begin{array}{ll}{D}_2=\frac{1}{{(2\pi )}^{2d}}{\displaystyle \int }d{\overrightarrow{k}}_{1}d{\overrightarrow{k}}_2(\overrightarrow{k}·{\overrightarrow{k}}_1)({\overrightarrow{k}}_1·{\overrightarrow{k}}_2)\tilde{D}(\overrightarrow{k}-{\overrightarrow{k}}_1)\tilde{D}({\overrightarrow{k}}_1-{\overrightarrow{k}}_2)& (7)\end{array}$

$\begin{array}{l}{D}_3=\frac{1}{{(2\pi )}^{3d}}{\displaystyle \int }d{\overrightarrow{k}}_{1}d{\overrightarrow{k}}_{2}d{\overrightarrow{k}}_3(\overrightarrow{k}·{\overrightarrow{k}}_1)({\overrightarrow{k}}_1·{\overrightarrow{k}}_2)({\overrightarrow{k}}_2·{\overrightarrow{k}}_3)\tilde{D}(\overrightarrow{k}-{\overrightarrow{k}}_1)\\ \tilde{D}({\overrightarrow{k}}_1-{\overrightarrow{k}}_2)\tilde{D}({\overrightarrow{k}}_2-{\overrightarrow{k}}_3),\hfill & (8)\end{array}$

and the general expression for D_n is given by

$\begin{array}{l}{D}_n=\frac{1}{{(2\pi )}^{nd}}{\displaystyle \int }{\displaystyle \prod _{i=1}^n}d{\overrightarrow{k}}_i(\overrightarrow{k}·{\overrightarrow{k}}_1)({\overrightarrow{k}}_1·{\overrightarrow{k}}_2)\dots ({\overrightarrow{k}}_{n-1}·{\overrightarrow{k}}_n)\tilde{D}(\overrightarrow{k}-{\overrightarrow{k}}_1)\\ \tilde{D}({\overrightarrow{k}}_1-{\overrightarrow{k}}_2)\dots \tilde{D}({\overrightarrow{k}}_{n-1}-{\overrightarrow{k}}_n).\hfill & (9)\end{array}$

Thus, the nth term D_n contains n factors of $\tilde{D}$ and n integrals over the Fourier variables ${\overrightarrow{k}}_i$.

This result is valid for any spatially varying diffusivity $D(\overrightarrow{r})$. We now specialize our discussion to a model for heterogeneity where the diffusivity $D(\overrightarrow{r})$ has a homogeneous component with M localized pockets of larger diffusivity. We focus our analysis on the diffusivity

$\begin{array}{ll}D(\overrightarrow{r})=1+{\displaystyle \sum _{i=1}^M}\delta exp\left(-\frac{1}{2{\sigma }^2}|\overrightarrow{r}-{\overrightarrow{c}}_i{|}^2\right),& (10)\end{array}$

where the ith pocket is centered at ${\overrightarrow{c}}_i$. Each pocket contributes magnitude δ to the diffusivity, and the spread σ defines the radial size of the pocket. In this model, we assume each pocket has the same contribution δ and spread σ. However, variability in these parameters are easily inserted into the model. The Fourier-transformed diffusivity $\tilde{D}(\overrightarrow{k})$ is given by

$\begin{array}{ll}\tilde{D}(\overrightarrow{k})={(2\pi )}^d\delta (\overrightarrow{k})+{(2\pi )}^{d/2}\delta {\sigma }^d{\displaystyle \sum _{i=1}^M}exp\left(-\frac{1}{2}{\sigma }^2{k}^2+i\overrightarrow{k}·{\overrightarrow{c}}_i\right),& (11)\end{array}$

and we define the rescaled magnitude ${\delta }_{\sigma }={(2\pi )}^{d/2}\delta {\sigma }^d$ to simplify our notation, and we define $k=\left|\overrightarrow{k}\right|$. We note that our definition of diffusivity is dimensionless, which implies that time t and position $\overrightarrow{r}$ are also dimensionless.

This framework provides a basis for determining the Green's function for a fixed system configuration, defined by ${\overrightarrow{c}}_i$. We now consider the case where we average the Green's function over an ensemble of system realizations, i.e., average over diffusivity configurations ${\overrightarrow{c}}_i$. In this work, we assume the configuration is randomly distributed with no spatial correlations between pockets. We define a diffusivity average of the quantity A to be

$\begin{array}{ll}{\langle A\rangle }_D=\frac{1}{V^M}{\displaystyle \int }{\displaystyle \prod _{i=1}^M}d{\overrightarrow{c}}_{i}A(D),& (12)\end{array}$

where V is the system volume, which is assumed to be very large relative to the displacements that are considered. This average is akin to determining the step distributions from individual realizations of the heterogeneity and then averaging these together. In this regard, the diffusivity average still captures heterogeneity as experienced by individual trajectories. Thus, the treatment does not assume the step distribution captures a homogenized environment at all time scales.

The ensemble average Green's function is written as

$\begin{array}{ll}{\langle \widehat{\tilde{G}}(\overrightarrow{k};s)\rangle }_D={\displaystyle \sum _{n=0}^{\infty }}\frac{{(-1)}^n}{s^{n+1}}{\langle D_n(\overrightarrow{k})\rangle }_D,& (13)\end{array}$

where we set the initial position ${\overrightarrow{r}}_0$ to the origin without loss of generality (since the ensemble average exhibits translational invariance). Within the nth term ${\langle D_n(\overrightarrow{k})\rangle }_D$, we shift the $\overrightarrow{k}$ integrals by defining ${\overrightarrow{k}}_i^{\prime }$ through the expression ${\overrightarrow{k}}_i=\overrightarrow{k}+\sum _{j=1}^i{\overrightarrow{k}}_j^{\prime }$, which gives ${\overrightarrow{k}}_i-{\overrightarrow{k}}_{i-1}={\overrightarrow{k}}_i^{\prime }$. Thus, we now reset the arguments of the spatially varying diffusivity $\tilde{D}({\overrightarrow{k}}_{i-1}-{\overrightarrow{k}}_i)$ to $\tilde{D}({\overrightarrow{k}}_i^{\prime })$.

The ensemble average of the nth term now requires us to evaluate ${\langle \tilde{D}({\overrightarrow{k}}_1^{\prime })\tilde{D}({\overrightarrow{k}}_2^{\prime })\dots \tilde{D}({\overrightarrow{k}}_n^{\prime })\rangle }_D$. This average involves integrals over ${\overrightarrow{c}}_i$, leading to delta functions in the ${\overrightarrow{k}}_i^{\prime }$. Each factor of $\tilde{D}$ contains a summation over the M pockets. For example, the n = 2 term contains the factor

$\begin{array}{lll}{\langle \tilde{D}({\overrightarrow{k}}_1^{\prime })\tilde{D}({\overrightarrow{k}}_2^{\prime })\rangle }_D\hfill & =\hfill & \frac{1}{V^M}{\displaystyle \int {\displaystyle \prod _{i=1}^{M}d}}{c}_i[{(2\pi )}^d\delta ({\overrightarrow{k}}_1^{\prime })\hfill \\ \hfill & \hfill & +{\delta }_{\sigma }{\displaystyle \sum _{j=1}^M\exp }\left(-\frac{1}{2}{\sigma }^2{k^{\prime }}_1^2+i{\overrightarrow{k}}_1^{\prime }·{\overrightarrow{c}}_j\right)]\hfill \\ \hfill & \hfill & \times [{(2\pi )}^d\delta ({\overrightarrow{k}}_2^{\prime })+{\delta }_{\sigma }{\displaystyle \sum _{k=1}^M\exp }\hfill \\ \hfill & \hfill & \left(-\frac{1}{2}{\sigma }^2{k^{\prime }}_2^2+i{\overrightarrow{k}}_2^{\prime }·{\overrightarrow{c}}_k\right)]\hfill \\ \hfill & =\hfill & {(1+\rho {\delta }_{\sigma })}^2{(2\pi )}^{2d}\delta ({\overrightarrow{k}}_1^{\prime })\delta ({\overrightarrow{k}}_2^{\prime })\hfill \\ \hfill & \hfill & +\rho {\delta }_{\sigma }^2{(2\pi )}^d\delta ({\overrightarrow{k}}_2^{\prime }+{\overrightarrow{k}}_2^{\prime })\exp \left(-{\sigma }^2{k^{\prime }}_1^2\right),\hfill & (14)\end{array}$

where $k=\left|\overrightarrow{k}\right|$. In Equation (14), we define the pocket density ρ = M/V as the number of pockets per unit volume. Details of this derivation are found in the Appendix. This leads to selection rules for the k-vectors in the integrals that simplify the evaluation of 〈D_n〉_D.

We visualize the selection rules by adopting a diagrammatic representation. For 〈D_n〉_D, the ${\overrightarrow{k}}_i^{\prime }$ are sequentially listed as dots on a line, and an arc is drawn between each ${\overrightarrow{k}}_i^{\prime }$ that appear together in a delta function. Figure 1A shows a selection diagram of the two ${\overrightarrow{k}}_i^{\prime }$ that appear within 〈D₂〉_D, explicitly derived in Equation (14). The first diagram shows two self loops that each contribute a factor $(1+\rho {\delta }_{\sigma }){(2\pi )}^d\delta ({\overrightarrow{k}}_i^{\prime })$. The second diagram shows a single arc between ${\overrightarrow{k}}_1^{\prime }$ and ${\overrightarrow{k}}_2^{\prime }$ that contributes a factor of $\rho {\delta }_{\sigma }^2{(2\pi )}^d\delta ({\overrightarrow{k}}_1^{\prime }+{\overrightarrow{k}}_2^{\prime })exp(-{\sigma }^2{k^{\prime }}_1^2)$.

FIGURE 1

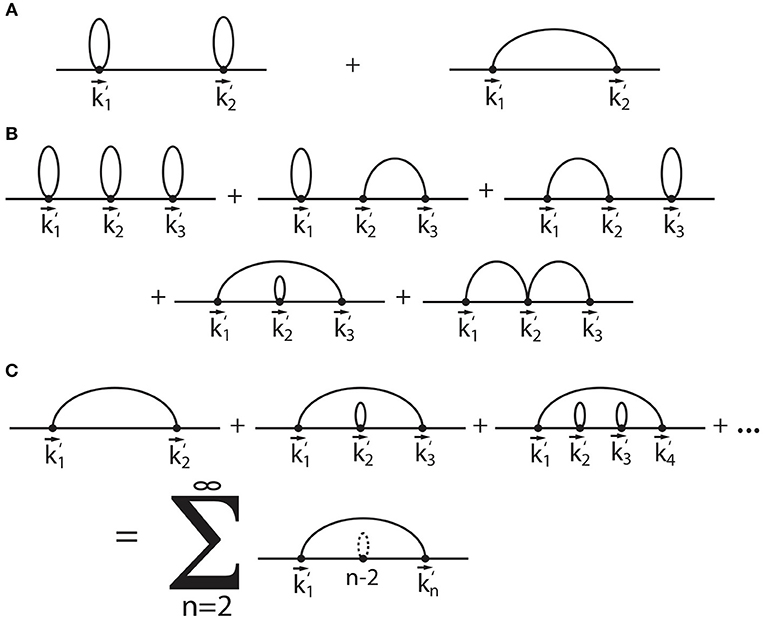
Figure 1. Diagrammatic representation of the expansion terms ${\langle D_n(\overrightarrow{k})\rangle }_D$ within the Fourier-Laplace transformed Green's function ${\langle \widehat{\tilde{G}}(\overrightarrow{k};s)\rangle }_D$ (Equation 13). The diagrams in (A) represent the selection rules for 〈D₂〉_D, and the diagrams in (B) identify the selection rules for 〈D₃〉_D. The infinite sum of diagrams found in (C) represent the set of irreducible diagrams Δg₁ (Equation 16) that form the basis for the lowest-order correction due to heterogeneity.

Our diagrammatic representation provides a visual framework for identifying all contributions that have common factors. Figure 1B shows all of the selection diagrams that appear in 〈D₃〉_D. These diagrams can be sorted according to powers of (1 + ρδ_σ), ρ, and δ_σ. The first diagram is order ${(1+\rho {\delta }_{\sigma })}^3$, since there are three self loops and no arcs. The second, third, and fourth diagrams scale as $(1+\rho {\delta }_{\sigma })\rho {\delta }_{\sigma }^2$, and the fifth diagram scales as $\rho {\delta }_{\sigma }^3$.

We identify the irreducible diagrams as those that cannot be decomposed into a subset of other diagrams. Within Figure 1B, the diagrams of order $(1+\rho {\delta }_{\sigma })\rho {\delta }_{\sigma }^2$ can be categorized into whether the diagram can be split into two distinct contributions. The second and third diagrams are both composed of a separate arc and self loop. When represented mathematically, both of these diagrams result in a product of terms that are separate from each other, i.e., they are reducible. However, the fourth diagram results in a single term that cannot be reduced into a product.

We determine the sum of all of the irreducible diagrams that up to order $\rho {\delta }_{\sigma }^2$, which is the lowest order contribution beyond order (1 + ρδ_σ). First, we identify the sum of all self loops g₀ to be given by

$\begin{array}{ll}{g}_0={\displaystyle \sum _{n=0}^{\infty }}\frac{{(-1)}^n}{s^{n+1}}{(1+\rho {\delta }_{\sigma })}^n{k}^{2n}=\frac{1}{s+(1+\rho {\delta }_{\sigma })k^2}=\frac{1}{s+D_0{k}^2},& (15)\end{array}$

where we have identified D₀ = 1 + ρδ_σ as the zero-time diffusivity (explained further below), and $k=\left|\overrightarrow{k}\right|$. Figure 1C shows the sum of all diagrams at the order $\rho {\delta }_{\sigma }^2$ that are irreducible. The summation of these diagrams results in the mathematical expression for the correction term

$\begin{array}{lll}\Delta g_1\hfill & =\hfill & {\displaystyle \sum _{n=2}^{\infty }\frac{{(-1)}^n}{s^{n+1}}}{D}_0^{n-2}\rho {\delta }_{\sigma }^2\frac{1}{{(2\pi )}^d}\hfill \\ \hfill & \hfill & {\displaystyle \int d}{\overrightarrow{k}}_1^{\prime }{[\overrightarrow{k}·(\overrightarrow{k}+{\overrightarrow{k}}_1^{\prime }\left)\right]}^2{\left|\overrightarrow{k}+{\overrightarrow{k}}_1^{\prime }\right|}^{2(n-2)}\exp \left(-{\sigma }^2{k^{\prime }}_1^2\right)\hfill \\ \hfill & =\hfill & \frac{\rho {\delta }_{\sigma }^2}{s^2}\frac{1}{{(2\pi )}^d}{\displaystyle \int \text{}}\text{}d{\overrightarrow{k}}_1^{\prime }\frac{{[\overrightarrow{k}·(\overrightarrow{k}+{\overrightarrow{k}}_1^{\prime }\left)\right]}^2}{s+D_0{\left|\overrightarrow{k}+{\overrightarrow{k}}_1^{\prime }\right|}^2}\exp \left(-{\sigma }^2{k^{\prime }}_1^2\right).\hfill & (16)\end{array}$

The two irreducible sets of diagrams g₀ and Δg₁ form the basis for the lowest-order correction to the Green's function due to heterogeneity. The combination of all possible diagrams that include both self loops and single arcs results in the approximate expression for the Green's function

$\begin{array}{lll}{\langle \widehat{\tilde{G}}\rangle }_D\hfill & \approx \hfill & {\displaystyle \sum _{n=0}^{\infty }{g}_0}{\left(s^2{g}_0\Delta g_1\right)}^n=\frac{1}{s+D_0{k}^2-s^2\Delta g_1}\hfill \\ \hfill & =\hfill & \frac{1}{s+D_0{k}^2-\frac{\rho {\delta }_{\sigma }^2}{{(2\pi )}^d}{\displaystyle \int \text{}}d{\overrightarrow{k}}_1^{\prime }\frac{{[\overrightarrow{k}·(\overrightarrow{k}+{\overrightarrow{k}}_1^{\prime })]}^2}{s+D_0{(\overrightarrow{k}+{\overrightarrow{k}}_1^{\prime })}^2}\exp \left(-{\sigma }^2{k^{\prime }}_1^2\right)}.\hfill & (17)\end{array}$

This result forms the basis for our subsequent analyses. For this discussion, we focus our attention on 3-dimensional diffusion. Though, our results are amenable to analysis in arbitrary dimensions.

The Green's function ${\langle \widehat{\tilde{G}}\rangle }_D$ adopts a form that reflects a mathematical structure that is notably non-Gaussian. The expansion of the Green's function in Equation (13) is reminiscent of a straight-forward moment-based expansion, particularly if the expansion terms scale as ${\langle D_n\rangle }_D~k^{2n}$. This is precisely the outcome if only the self-loop diagrams are included (i.e., Δg₁ = 0). The resulting expression for ${\langle \widehat{\tilde{G}}\rangle }_D$ is the Fourier-Laplace transform of the Gaussian distribution. Inclusion of the correction Δg₁ results in non-Gaussian contributions to the Green's function that reveal the underlying role of heterogeneity in the diffusive transport.

The Green's function ${\langle \widehat{\tilde{G}}\rangle }_D$ can be used to determine various statistical averages of the diffusivity-averaged motion of the particles. In other words, the statistical behavior of the particle motion after averaging over an ensemble of heterogeneous diffusivities. Here, we consider the 2n-th moment of the distribution projected onto the z-axis in our 3-dimensional space, given by

$\begin{array}{ll}{\langle \langle z^{2n}\rangle \rangle }_D={(-1)}^n{{L}}_{s\to t}^{-1}\left[{\displaystyle \underset{k\to 0}{lim}}\frac{{\partial }^{2n}{\langle \widehat{\tilde{G}}\rangle }_D}{\partial k^{2n}}\right],& (18)\end{array}$

where the two sets of angle brackets (${\langle \langle z^{2n}\rangle \rangle }_D$) indicates a statistical average over both an ensemble of trajectories and an ensemble of diffusivities D. In Equation (18), the operator ${{L}}_{s\to t}^{-1}$ indicates a Laplace inversion from the Laplace variable s to time t. From our results in Equation (17), we find the expressions for the second and fourth moments to be

$\begin{array}{ll}{\langle \langle z^2\rangle \rangle }_D=2D_{0}t-\frac{1}{6{\pi }^{3/2}}\frac{\rho {\delta }_{\sigma }^2}{\sigma D_0^2}\left(\tau -1+\frac{1}{\sqrt{2\tau +1}}\right),& (19)\end{array}$

$\begin{array}{lll}\hfill {\langle \langle z^4\rangle \rangle }_D& =\hfill & 12D_0^2{t}^2-\frac{4}{{\pi }^{3/2}}\frac{\sigma \rho {\delta }_{\sigma }^2}{D_0^2}[{\tau }^2-\frac{12}{5}\tau -\frac{11}{5}+2\sqrt{2\tau +1}\hfill \\ \hfill & & +\frac{1}{2}\frac{1}{\sqrt{2\tau +1}}-\frac{3}{10}\frac{1}{{(2\tau +1)}^{3/2}}]\\ \hfill & & +\frac{1}{12{\pi }^3}{\left(\frac{\rho {\delta }_{\sigma }^2}{\sigma D_0^2}\right)}^2[{\tau }^2-4\tau -2+2\sqrt{2\tau +1}\\ \hfill & & -\frac{2}{\sqrt{2\tau +1}}\\ \hfill & & +\frac{2}{{(2\tau +1)}^{3/2}}+\frac{2\tau (4{\tau }^2+6\tau +3)}{(\tau +1){(2\tau +1)}^{3/2}}].& (20)\end{array}$

We define the diffusive time τ = t/t_σ, where $t_{\sigma }=2{\sigma }^2/D_0$ gives the time scale for diffusion to a distance of order σ (i.e., the scale of heterogeneity). Notably, corrections to normal diffusion due to heterogeneity naturally depend on the time scale for diffusion to a distance comparable to the length scale of the heterogeneity. These results form the basis of our subsequent analyses of diffusive transport in a heterogeneous environment.

Results and Discussion

In this work, we explore the statistical behavior of particle motion in a heterogeneous environment, as defined by our random diffusivity model (Equation 10). We first consider the mean-square displacement (MSD) of particle diffusion ${\langle \langle r^2\rangle \rangle }_D=3{\langle \langle z^2\rangle \rangle }_D$. Figure 2 shows the mean-square displacement for diffusion in a heterogeneous environment with δ = 5, D₀ = 2 (i.e., ρ = 1/δ_σ), and σ = 1/2. For this set of parameters, the heterogeneity time scale $t_{\sigma }=2{\sigma }^2/D_0=1/4$ results in the relationship τ = 4t.

FIGURE 2

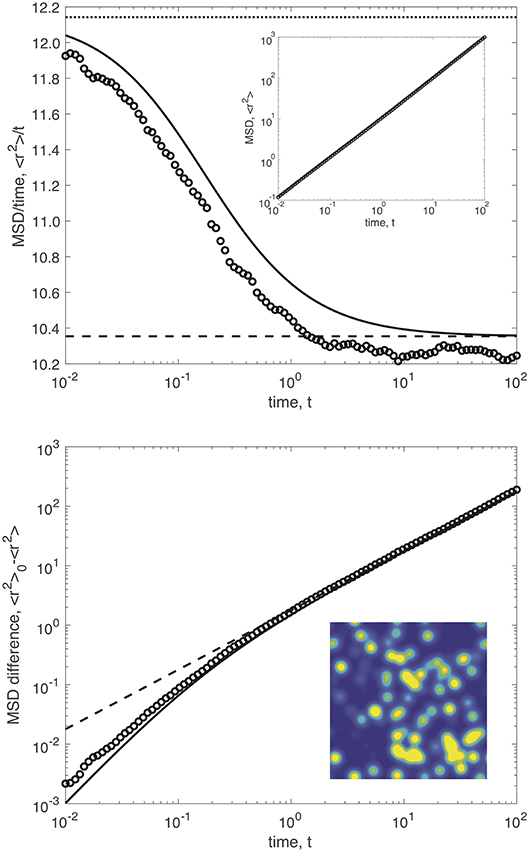
Figure 2. The mean-square displacement (MSD) for particle diffusion in a heterogeneous environment. The top plot shows the ratio MSD/t ${\langle \langle r^2\rangle \rangle }_D$ (solid curve) vs. time for heterogeneous diffusivity with δ = 5, D₀ = 2 (i.e., ρ = 1/δ_σ), and σ = 1/2. The dotted curved indicates the short-time MSD ${\langle \langle r^2\rangle \rangle }_D^{(0)}$, and the dashed curve shows the long-time MSD ${\langle \langle r^2\rangle \rangle }_D^{(\infty )}$. Results from numerical simulations are shown as dots. The inset plot shows the MSD before dividing by time. The bottom plot shows the MSD difference ${\langle \langle r^2\rangle \rangle }_D^{(0)}-{\langle \langle r^2\rangle \rangle }_D$. The inset image shows a realization of the diffusivity with color scaling from blue (D = 1) to yellow (D = 5).

To validate our analytical theory, we perform numerical simulations of particle diffusion in a heterogeneous environment based on our model for microscopic heterogeneity. We define the position-dependent diffusivity $D(\overrightarrow{r})$ in a square box of length Δ by randomly selecting the positions ${\overrightarrow{c}}_i$ (for i = 1, …, M) for a given pocket density ρ = M/Δ³, and the position-dependent diffusivity $D(\overrightarrow{r})$ is defined by Equation (10). The simulations are performed with periodic boundary conditions to capture an effectively infinite medium, and we set Δ = 10 for our simulations, which is determined to be adequate to capture the long-time dynamics (i.e., all results shown are insensitive to this choice of Δ). We perform Brownian dynamics simulations using the discrete-time algorithm for particle displacement with time-step Δt, given by

$\begin{array}{ll}\overrightarrow{r}(t+\Delta t)=\overrightarrow{r}(t)+\left[\sqrt{2D(\overrightarrow{r}(t))\Delta t}\right]\overrightarrow{u}+\left[\frac{1}{2}\overrightarrow{u}·\overrightarrow{\nabla }D(\overrightarrow{r}(t))\Delta t\right]\overrightarrow{u},& (21)\end{array}$

where $\overrightarrow{u}$ is a 3-dimensional vector with components selected from a Gaussian distribution with unit variance.

The top plot of Figure 2 shows ${\langle \langle r^2\rangle \rangle }_D$ with an inset that shows a realization of the heterogeneous diffusivity (blue indicating D = 1 to yellow indicating D = 5). The solid curve shows our analytical result, given by Equation (19). Figure 2 also contains results from numerical simulations (dots). The short-time MSD ${\langle \langle r^2\rangle \rangle }_D^{(0)}=6D_{0}t$ is indicated by the dotted line, where D₀ = 1 + ρδ_σ. The long-time MSD ${\langle \langle r^2\rangle \rangle }_D^{(\infty )}=6D_{\infty }t$ is shown as a dashed line, where $D_{\infty }=D_0-\rho {\delta }_{\sigma }^2/(24{\pi }^{3/2}{\sigma }^3{D}_0)$. The influence of heterogeneity on the mean-square displacement is relatively modest over the broad range of timescales in Figure 2. The bottom plot shows the MSD difference ${\langle \langle r^2\rangle \rangle }_D^{(0)}-{\langle \langle r^2\rangle \rangle }_D$ to clearly show the comparison between our analytical theory and the numerical simulations over the entire range of times.

The short-time diffusivity D₀ is governed by the motion of the particle within a local environment. Thus, the particle is not yet able to sample the surrounding heterogeneity. In this regard, the diffusivity difference D₀ − D_∞ is a measure of the impact of heterogeneity on the particle motion. Figure 3 shows a plot of the long-time diffusivity D_∞ (top plot) and the diffusivity difference D₀ − D_∞ (bottom plot) over of range of the strength of heterogeneity δ. The right images in Figure 3 show realizations of the diffusivity over the range of values of δ within the plots. The results in Figure 3 have a fixed short-time diffusivity D₀ = 1 + ρδ_σ = 2. Thus, the density ρ decreases with increasing δ to maintain an equivalent D₀. In Figure 3, the length scale of heterogeneity is σ = 1/2, and the dots indicate results from our numerical simulations as a check of our analytical theory.

FIGURE 3

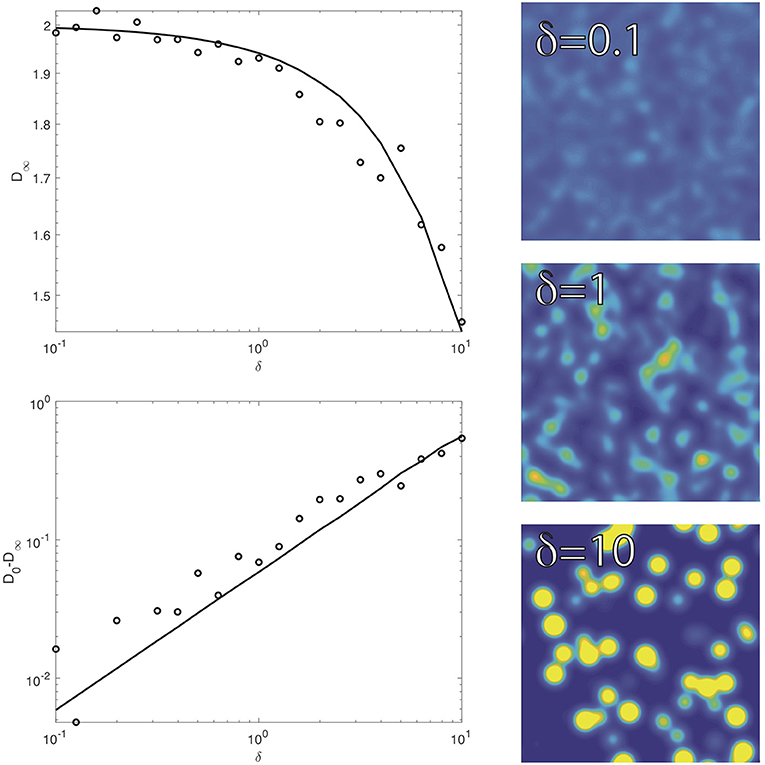
Figure 3. The long-time diffusivity D_∞ and the diffusivity difference D₀ − D_∞ over a range of the strength of heterogeneity δ (with fixed D₀ = 2 and σ = 1/2). The solid curves show our analytical theory, and the dots give results from numerical simulations. The right images show realizations of the heterogeneous diffusivity over the range of δ in the plots (same color scaling as Figure 2).

Our results thus far suggest that our analytical results are valid within the range of the heterogeneity parameters explored in Figures 2, 3. However, the impact of heterogeneity on the mean-square displacement is somewhat modest (see Figure 2). Experimental measurements of MSD may exhibit considerable noise due to measurement precision and insufficient sampling over both an ensemble of trajectories and an ensemble of diffusivity samples. In this regard, MSD may be insufficient to characterize the heterogeneity. Furthermore, many physical or biological processes are dependent on statistical metrics that are not weighted heavily in the MSD. In this regard, a statistical quantity that represents higher moments of the distribution would better represent the impact of heterogeneity.

We turn to the kurtosis as a metric that reveals the impact of heterogeneity on diffusive transport. The kurtosis represents the lowest-order metric that determines to what extent the step distribution deviates from a Gaussian distribution, which is the expectation for diffusion in a homogeneous environment. We define the excess kurtosis κ as

$\begin{array}{ll}\kappa =\frac{{\langle \langle z^4\rangle \rangle }_D}{{\langle \langle z^2\rangle \rangle }_D^2}-3,& (22)\end{array}$

where ${\langle \langle z^2\rangle \rangle }_D$ and ${\langle \langle z^4\rangle \rangle }_D$ are given by Equations (19) and (20), respectively. The excess kurtosis is zero for a Gaussian distribution. Positive values of κ indicate a heavy-tailed distribution that implies trajectories that are significantly more mobile than a random walk with an averaged diffusivity.

Figure 4 shows the excess kurtosis vs. time for δ = 10, D₀ = 2, and σ = 2 (note, t_σ = 1/4). Our results demonstrate two regimes. At short time, the excess kurtosis κ exhibits a short-time plateau that represents the excess kurtosis that arises from averaging over an ensemble of quenched diffusivities that are selected from the statistical distribution of our model (discussed further below). At long times, the excess kurtosis κ relaxes to zero as κ ~ τ⁻¹. This asymptotic behavior suggests that individual trajectories within a fixed diffusivity realization have sufficiently sampled their surrounding microenvironments and now experience an effective diffusivity D_∞. As a result, the individual trajectories are random walk at long time scales, and the D-averaged step distribution tends to a Gaussian.

FIGURE 4

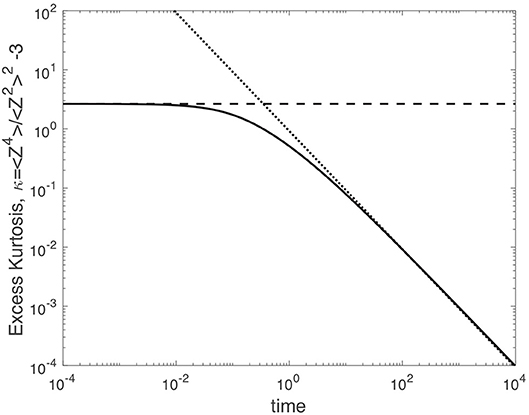
Figure 4. The excess kurtosis κ vs. time for δ = 10, D₀ = 2, and σ = 2. The dashed curve indicates the short-time behavior of the excess kurtosis based on our model for heterogeneity. The dotted curve gives the long-time relaxation of the excess kurtosis to zero.

At short times, the particles are unable to sufficiently explore their surrounding environment. Thus, the diffusivity of each particle is dictated by the random-selected diffusivity of its initial position. The statistical distribution for the diffusivity at a fixed point (here given by the origin) is given by

$\begin{array}{ll}{P}_D(D)=\frac{1}{V^M}{\displaystyle \int }{\displaystyle \prod _{i=1}^M}d{\overrightarrow{c}}_i\delta \left[D-1-\delta {\displaystyle \sum _{k=1}^M}exp\left(-\frac{1}{2{\sigma }^2}{c}_k^2\right)\right],& (23)\end{array}$

which captures the contributions of the pockets as a superposition of Dirac delta distributions. We perform a Laplace transform from D to u, and upon taking the limit M, V → ∞ such that M/V = ρ, we arrive at the Laplace-transformed D-distribution

$\begin{array}{ll}{\widehat{P}}_D=exp\left[-u+{(2\pi )}^{3/2}\rho {\sigma }^3{\displaystyle \sum _{n=1}^{\infty }}\frac{{(-1)}^n}{n!n^{3/2}}{\delta }^n{u}^n\right].& (24)\end{array}$

From this distribution, we determine the first two moments of the local diffusivity, given by

$\begin{array}{ll}{\langle D\rangle }_D=-{\displaystyle \underset{u\to 0}{lim}}\left(\frac{d{\widehat{P}}_D}{du}\right)=1+\rho {\delta }_{\sigma }=D_0,& (25)\end{array}$

$\begin{array}{lll}{\langle D^2\rangle }_D& =& {\displaystyle \underset{u\to 0}{lim}}\left(\frac{d^2{\widehat{P}}_D}{d{u}^2}\right)={(1+\rho {\delta }_{\sigma })}^2+{\pi }^{3/2}\rho {\delta }^2{\sigma }^3\\ & =& D_0^2+\frac{\rho {\delta }_{\sigma }^2}{2{\pi }^{3/2}{\sigma }^3}.& (26)\end{array}$

These statistical quantities capture the instantaneous environment that a particle experiences prior to diffusion into a surrounding microenvironment.

The short-time behavior of the excess kurtosis is given by

$\begin{array}{ll}{\kappa }^{(0)}=\frac{12{\langle D^2\rangle }_D{t}^2}{{(2{\langle D\rangle }_{D}t)}^2}-3=3\left(\frac{{\langle D^2\rangle }_D}{{\langle D\rangle }_D^2}-1\right)=\frac{3\rho {\delta }_{\sigma }^2}{2{\pi }^{3/2}{\sigma }^3{D}_0^2}.& (27)\end{array}$

This short-time behavior coincides with the dashed curve in Figure 4. For the parameters in Figure 4, the short-time excess kurtosis is given by κ⁽⁰⁾ = 2.652. For reference, the value of the excess kurtosis for a Laplace distribution [52, 53] is κ = 9. The Laplace distribution is of particular interest for cellular transport [26, 31, 32, 54], since the step distribution in both yeast cells and bacterial cells trends from a Laplace distribution to a Gaussian distribution with increasing time [26].

Conclusions

Our solutions for the Green's function provide insight into the impact of microscopic heterogeneity of diffusive transport across a broad range of time scales. At short time scales, the particles explore the local environment around their initial position. The local diffusivity is randomly determined from the distribution of diffusivities from the specific model of heterogeneity. With increasing time, the stochastic trajectories of the particles lead to a transition to the exploration of a spatially averaged environment. The time scale of this transition is naturally linked to the time scale of diffusion to a distance defined by the correlation length of the heterogeneity. The excess kurtosis exhibits a short-time, non-zero value that implies a heavy-tailed step distribution associated with the distribution of initial diffusivities, and the excess kurtosis decays to zero as the diffusive transport leads to exploration of the surrounding effective medium, implying a Gaussian step distribution at long times.

Further refinement of the model can be developed by including higher order loop diagrams in the expansion. The structure of our diagrammatic representation is akin to Feynman diagrams commonly employed in quantum field theory and condensed matter physics [55, 56]. Notably, one can extend our approach to include higher-order diagrams, or alternatively, one can employ renormalization group methods to determine a renormalized one-loop contribution [55] based on the structure of the solutions presented in this manuscript. These developments would improve the level of accuracy of our solutions, particular in the limit of large heterogeneity (δ ≫ 1). However, the agreement between numerical simulations and our results presented in this manuscript suggest the solutions are not limited to conditions where δ ≪ 1, and the results presented here are not strictly limited to conditions of weak heterogeneity.

Heterogeneity is prevalent in a range of soft materials, particularly in living cells. We specifically note the observed heterogeneity of the organization of chromosomal DNA within eukaryotic nuclei [57–61]. Underlying the observed heterogeneity is the physical segregation of chromosomes into compartments due to epigenetic modifications to the proteins that packaged the DNA, which is captured by models that incorporate incompatibility between segments in a chromosome polymer [62–68]. The connection between spatial segregation of chromosomes and the dynamics and accessibility of regulatory proteins [69–71] remains a challenging problem that would shed light on the structure-function relationships in chromosome biology. This work provides a valuable analytical approach to analyzing heterogeneous transport in the complex environment of the nucleus that may be valuable in establishing these connections.

Data Availability

The datasets generated for this study are available on request to the corresponding author.

Author Contributions

AS performed the research and wrote the manuscript.

Funding

Financial support for this work was provided by the National Science Foundation, Physics of Living Systems Program (PHY-1707751).

Conflict of Interest Statement

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2019.00119/full#supplementary-material

References

1. Von Smoluchowski M. Drei vortrage uber diffusion. Brownsche bewegung und koagulation von kolloidteilchen. Z Phys. (1916) 17:557–585.

Google Scholar

2. Fick A. Eber diffusion. Ann Phys. (1855) 170:59–86.

Google Scholar

3. Einstein A. Investigations on the theory of the Brownian movement.Ann. D. Phys. (1905) 17:549.

Google Scholar

4. Perrin J. Mouvement brownien et realite moleculaire. Ann. de Chim. Phys. (1909) 18:5–114.

5. Munder MC, Midtvedt D, Franzmann T, Nulske E, Otto O, Herbig M, et al. A pH-driven transition of the cytoplasm from a fluid-to a solid-like state promotes entry into dormancy. eLife. (2016) 5:e09347. doi: 10.7554/eLife.09347

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Valentine MT, Kaplan PD, Thota D, Crocker JC, Gisler T, Prudâhomme RK, et al. Investigating the microenvironments of inhomogeneous soft materials with multiple particle tracking. Phys Rev E. (2001) 64:061506. doi: 10.1103/PhysRevE.64.061506

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Kegel WK, van Blaaderen A. Direct observation of dynamical heterogeneities in colloidal hard-sphere suspensions. Science. (2000) 287:290–3. doi: 10.1126/science.287.5451.290

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Burov S, Jeon J-H, Metzler R, Barkai E. Single particle tracking in systems showing anomalous diffusion: the role of weak ergodicity breaking. Phys Chem Chem Phys. (2011) 13:1800–12. doi: 10.1039/c0cp01879a

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Toyota T, Head DA, Schmidt CF, Mizuno D. Non-Gaussian athermal fluctuations in active gels. Soft Matter. (2011) 7:3234–9. doi: 10.1039/C0SM00925C

CrossRef Full Text | Google Scholar

10. Cao J. Single molecule tracking of heterogeneous diffusion. Phys Rev E. (2001) 63:041101. doi: 10.1103/PhysRevE.63.041101

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Weeks ER, Crocker JC, Levitt AC, Schofield A, Weitz DA. Three-dimensional direct imaging of structural relaxation near the colloidal glass transition. Science. (2000) 287:627–31. doi: 10.1126/science.287.5453.627

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Joyner RP, Tang JH, Helenius J, Dultz E, Brune C, Holt LJ, et al. A glucose-starvation response regulates the diffusion of macromolecules. eLife. (2016) 5:e09376. doi: 10.7554/eLife.09376

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Duits MH, Li Y, Vanapalli SA, Mugele F. Mapping of spatiotemporal heterogeneous particle dynamics in living cells. Phys Rev E. (2009) 79:051910. doi: 10.1103/PhysRevE.79.051910

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Guo M, Ehrlicher AJ, Jensen MH, Renz M, Moore JR, Goldman RD, et al. Probing the stochastic, motor-driven properties of the cytoplasm using force spectrum microscopy. Cell. (2014) 158:822–32. doi: 10.1016/j.cell.2014.06.051

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Fodor É, Guo M, Gov N, Visco P, Weitz D, van Wijland F. Activity driven fluctuations in living cells. arXiv preprint (2015) arXiv:1505.06489. doi: 10.1209/0295-5075/110/48005

CrossRef Full Text | Google Scholar

16. Knight SC, Xie L, Deng W, Guglielmi B, Witkowsky LB, Bosanac L, et al. Dynamics of CRISPR-Cas9 genome interrogation in living cells. Science. (2015) 350:823–6. doi: 10.1126/science.aac6572

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Bursac P, Fabry B, Trepat X, Lenormand G, Butler JP, Wang N, et al. Cytoskeleton dynamics: fluctuations within the network. Biochem Biophys Res Commun. (2007) 355:324–30. doi: 10.1016/j.bbrc.2007.01.191

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Wirtz D. Particle-tracking microrheology of living cells: principles and applications. Ann Rev Biophys. (2009) 38:301–26. doi: 10.1146/annurev.biophys.050708.133724

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Parry BR, Surovtsev IV, Cabeen MT, O'Hern CS, Dufresne ER, Jacobs-Wagner C. The bacterial cytoplasm has glass-like properties and is fluidized by metabolic activity. Cell. (2014) 156:183–94. doi: 10.1016/j.cell.2013.11.028

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Stylianidou S, Kuwada NJ, Wiggins PA. Cytoplasmic dynamics reveals two modes of nucleoid-dependent mobility. Biophys J. (2014) 107:2684–92. doi: 10.1016/j.bpj.2014.10.030

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Hajjoul H, Mathon J, Ranchon H, Goiffon I, Mozziconacci J, Albert B, et al. High-throughput chromatin motion tracking in living yeast reveals the flexibility of the fiber throughout the genome. Genome Res. (2013) 23:1829–38. doi: 10.1101/gr.157008.113

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Backlund MP, Joyner R, Weis K, Moerner W. Correlations of three-dimensional motion of chromosomal loci in yeast revealed by the double-helix point spread function microscope. Mol Biol Cell. (2014) 25:3619–29. doi: 10.1091/mbc.E14-06-1127

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Backlund MP, Joyner R, Moerner W. Chromosomal locus tracking with proper accounting of static and dynamic errors. Phys Rev E. (2015) 91:062716. doi: 10.1103/PhysRevE.91.062716

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Golding I, Cox EC. RNA dynamics in live Escherichia coli cells. Proc Natl Acad Sci USA. (2004) 101:11310–5. doi: 10.1073/pnas.0404443101

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Silva MS, Stuhrmann B, Betz T, Koenderink GH. Time-resolved microrheology of actively remodeling actomyosin networks. New J Phys. (2014) 16:075010. doi: 10.1088/1367-2630/16/7/075010

CrossRef Full Text | Google Scholar

26. Lampo TJ, Stylianidou S, Backlund MP, Wiggins PA, Spakowitz AJ. Cytoplasmic RNA-protein particles exhibit non-Gaussian subdiffusive behavior. Biophys J. (2017) 112:532–42. doi: 10.1016/j.bpj.2016.11.3208

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Weber S, Theriot J, Spakowitz A. Subdiffusive motion of a polymer composed of subdiffusive monomers. Phys Rev E. (2010) 82:011913. doi: 10.1103/PhysRevE.82.011913

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Weber S, Spakowitz A, Theriot J. Bacterial chromosomal loci move subdiffusively through a viscoelastic cytoplasm. Phys Rev Lett. (2010) 104:238102. doi: 10.1103/PhysRevLett.104.238102

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Weber SC, Thompson MA, Moerner WE, Spakowitz AJ, Theriot JA. Analytical tools to distinguish the effects of localization error, confinement, and medium elasticity on the velocity autocorrelation function. Biophys J. (2012) 102:2443–50. doi: 10.1016/j.bpj.2012.03.062

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Weber SC, Spakowitz AJ, Theriot JA. Nonthermal ATP-dependent fluctuations contribute to the in vivo motion of chromosomal loci. Proc Natl Acad Sci USA. (2012) 109:7338–43. doi: 10.1073/pnas.1119505109

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Wang B, Anthony SM, Bae SC, Granick S. Anomalous yet Brownian. Proc Natl Acad Sci USA. (2009) 106:15160–4. doi: 10.1073/pnas.0903554106

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Wang B, Kuo J, Bae SC, Granick S. When Brownian diffusion is not Gaussian. Nat Mater. (2012) 11:481–5. doi: 10.1038/nmat3308

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Ghosh SK, Cherstvy AG, Grebenkov DS, Metzler R. Anomalous, non-Gaussian tracer diffusion in crowded two-dimensional environments. New J Phys. (2016) 18:013027. doi: 10.1088/1367-2630/18/1/013027

CrossRef Full Text | Google Scholar

34. Papanicolaou GC. Surveys in Applied Mathematics. New York, NY: Springer (1995), 205–53.

35. Stevens A, Papanicolaou G, Heinze S. Variational principles for propagation speeds in inhomogeneous media. SIAM J Appl Math. (2001) 62:129–48. doi: 10.1137/S0036139999361148

CrossRef Full Text | Google Scholar

36. Lewandowska J, Laurent J-P. Homogenization modeling and parametric study of moisture transfer in an unsaturated heterogeneous porous medium. Transport Porous Med. (2001) 45:319–43. doi: 10.1023/A:1012450327408

CrossRef Full Text | Google Scholar

37. Auriault J-L, Lewandowska J. Effective diffusion coefficient: from homogenization to experiment. Transport Porous Med. (1997) 27:205–23.

Google Scholar

38. Avellaneda M. Homogenization and renormalization: the mathematics of multi-scale random media and turbulent diffusion. Dyn Syst Probab Methods Partial Differ Equat. (1996) 31:251–68.

Google Scholar

39. Novikov DS, Kiselev VG. Effective medium theory of a diffusion-weighted signal. NMR Biomed. (2010) 23:682–97. doi: 10.1002/nbm.1584

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Alonso S, Kapral R, Bär M. Effective medium theory for reaction rates and diffusion coefficients of heterogeneous systems. Phys Rev Lett. (2009) 102:238302. doi: 10.1103/PhysRevLett.102.238302

PubMed Abstract | CrossRef Full Text | Google Scholar

41. Kröner E. Micromechanics and Inhomogeneity. New York, NY: Springer (1990), 197–211.

42. Alonso S, Baer M, Kapral R. Effective medium approach for heterogeneous reaction-diffusion media. J Chem Phys. (2009) 131:214102. doi: 10.1063/1.3265987

PubMed Abstract | CrossRef Full Text | Google Scholar

43. Duan H, Karihaloo B, Wang J, Yi X. Effective conductivities of heterogeneous media containing multiple inclusions with various spatial distributions. Phys Rev B. (2006) 73:174203. doi: 10.1103/PhysRevB.73.174203

CrossRef Full Text | Google Scholar

44. Sahimi M, Tsotsis TT. Transient diffusion and conduction in heterogeneous media: beyond the classical effective-medium approximation. Ind Eng Chem Res. (1997) 36:3043–52.

Google Scholar

45. Chang H-C. Multi-scale analysis of effective transport in periodic heterogeneous media. Chem Eng Commun. (1982) 15:83–91.

Google Scholar

46. Akanni K, Evans J, Abramson I. Effective transport coefficients in heterogeneous media. Chem Eng Sci. (1987) 42:1945–54.

Google Scholar

47. Saez AE, Otero CJ, Rusinek I. The effective homogeneous behavior of heterogeneous porous media. Transport Porous Med. (1989) 4:213–38.

Google Scholar

48. Chubynsky MV, Slater GW. Diffusing diffusivity: a model for anomalous, yet Brownian, diffusion. Phys Rev Lett. (2014) 113:098302. doi: 10.1103/PhysRevLett.113.098302

PubMed Abstract | CrossRef Full Text | Google Scholar

49. Metzler R, Jeon J-H, Cherstvy AG, Barkai E. Anomalous diffusion models and their properties: non-stationarity, non-ergodicity, and ageing at the centenary of single particle tracking. Phys Chem Chem Phys. (2014) 16:24128–64. doi: 10.1039/C4CP03465A

PubMed Abstract | CrossRef Full Text | Google Scholar

50. Cherstvy AG, Metzler R. Anomalous diffusion in time-fluctuating non-stationary diffusivity landscapes. Phys Chem Chem Phys. (2016) 18:23840–52. doi: 10.1039/C6CP03101C

PubMed Abstract | CrossRef Full Text | Google Scholar

51. Chechkin AV, Seno F, Metzler R, Sokolov IM. Brownian yet non-Gaussian diffusion: from superstatistics to subordination of diffusing diffusivities. Phys Rev X. (2017) 7:021002. doi: 10.1103/PhysRevX.7.021002

CrossRef Full Text | Google Scholar

52. Kozubowski TJ, Meerschaert MM, Podgorski K. Fractional Laplace motion. Adv Appl Probab. (2006) 38:451–64. doi: 10.1017/S000186780000104X

CrossRef Full Text | Google Scholar

53. Kotz S, Kozubowski T, Podgorski K. The Laplace Distribution and Generalizations: A Revisit With Applications to Communications, Exonomics, Engineering, and Finance. New York, NY: Springer (2001).

Google Scholar

54. Phillies GDJ. In complex fluids the Gaussian diffusion approximation is generally invalid. Soft matter. (2015) 11:580–6. doi: 10.1039/C4SM02506G

PubMed Abstract | CrossRef Full Text | Google Scholar

55. Amit DJ, Martin-Mayor V. Field Theory, The Renormalization Group, and Critical Phenomena: Graphs to Computers 3rd Edn. Singapore: World Scientific Publishing Company (2005).

Google Scholar

56. Peskin ME. An Introduction to Quantum Field Theory. Boca Raton, FL: CRC Press (2018).

Google Scholar

57. Grewal SI, Moazed D. Heterochromatin and epigenetic control of gene expression. Science. (2003) 301:798–802. doi: 10.1126/science.1086887

PubMed Abstract | CrossRef Full Text | Google Scholar

58. Lieberman-Aiden E, Van Berkum NL, Williams L, Imakaev M, Ragoczy T, Telling A, et al. Comprehensive mapping of long-range interactions reveals folding principles of the human genome. Science. (2009) 326:289–93. doi: 10.1126/science.1181369

PubMed Abstract | CrossRef Full Text | Google Scholar

59. Zidovska A, Weitz DA, Mitchison TJ. Micron-scale coherence in interphase chromatin dynamics. Proc Natl Acad Sci USA. (2013) 110:15555–60. doi: 10.1073/pnas.1220313110

PubMed Abstract | CrossRef Full Text | Google Scholar

60. Rao SS, Huntley MH, Durand NC, Stamenova EK, Bochkov ID, Robinson JT, et al. A 3D map of the human genome at kilobase resolution reveals principles of chromatin looping. Cell. (2014) 159:1665–80. doi: 10.1016/j.cell.2014.11.021

PubMed Abstract | CrossRef Full Text | Google Scholar

61. Ou HD, Phan S, Deerinck TJ, Thor A, Ellisman MH, O'shea CC. ChromEMT: visualizing 3D chromatin structure and compaction in interphase and mitotic cells. Science. (2017) 357:eaag0025. doi: 10.1126/science.aag0025

PubMed Abstract | CrossRef Full Text | Google Scholar

62. Jost D, Carrivain P, Cavalli G, Vaillant C. Modeling epigenome folding: formation and dynamics of topologically associated chromatin domains. Nucleic Acids Res. (2014) 42:9553–61. doi: 10.1093/nar/gku698

PubMed Abstract | CrossRef Full Text | Google Scholar

63. Chiariello AM, Annunziatella C, Bianco S, Esposito A, Nicodemi M. Polymer physics of chromosome large-scale 3D organisation. Sci Rep. (2016) 6:29775. doi: 10.1038/srep29775

PubMed Abstract | CrossRef Full Text | Google Scholar

64. Michieletto D, Orlandini E, Marenduzzo D. Polymer model with epigenetic recoloring reveals a pathway for the de novo establishment and 3D organization of chromatin domains. Phys Rev X. (2016) 6:041047. doi: 10.1103/PhysRevX.6.041047

CrossRef Full Text | Google Scholar

65. Di Pierro M, Zhang B, Aiden EL, Wolynes PG, Onuchic JN. Transferable model for chromosome architecture. Proc Natl Acad Sci USA. (2016) 113:12168–73. doi: 10.1073/pnas.1613607113

PubMed Abstract | CrossRef Full Text | Google Scholar

66. Di Pierro M, Cheng RR, Aiden EL, Wolynes PG, Onuchic JN. De novo prediction of human chromosome structures: Epigenetic marking patterns encode genome architecture. Proc Natl Acad Sci USA. (2017) 114:12126–31. doi: 10.1073/pnas.1714980114

PubMed Abstract | CrossRef Full Text | Google Scholar

67. MacPherson Q, Beltran B, Spakowitz AJ. Bottom-up modeling of chromatin segregation due to epigenetic modifications. Proc Natl Acad Sci USA. (2018) 115:12739–44. doi: 10.1073/pnas.1812268115

PubMed Abstract | CrossRef Full Text | Google Scholar

68. Nuebler J, Fudenberg G, Imakaev M, Abdennur N, Mirny LA. Chromatin organization by an interplay of loop extrusion and compartmental segregation. Proc Natl Acad Sci USA. (2018) 115:E6697–706. doi: 10.1073/pnas.1717730115

PubMed Abstract | CrossRef Full Text | Google Scholar

69. de la Rosa MAD, Koslover EF, Mulligan PJ, Spakowitz AJ. Dynamic strategies for target-site search by DNA-binding proteins. Biophys J. (2010) 98:2943–53. doi: 10.1016/j.bpj.2010.02.055

PubMed Abstract | CrossRef Full Text | Google Scholar

70. Koslover EF, de la Rosa MAD, Spakowitz AJ. Theoretical and computational modeling of target-site search kinetics in vitro and in vivo. Biophys J. (2011) 101:856–65. doi: 10.1016/j.bpj.2011.06.066

PubMed Abstract | CrossRef Full Text | Google Scholar

71. Koslover EF, de la Rosa MD, Spakowitz AJ. Crowding and hopping in a protein's diffusive transport on DNA. J Phys A Math Theor. (2017) 50:074005. doi: 10.1088/1751-8121/aa53ee

CrossRef Full Text | Google Scholar