Drag Force for Asymmetrically Grafted Colloids in Polymer Solutions

We consider the situation in which a colloidal particle modifies locally the solvent leading to a spatially dependent viscosity. This situation is typical for colloidal particles in crowded environment, for example DNA-grafted particles in a polymer solution, or a hot particle which implies a temperature gradient to a viscous liquid. By means of suitable approximations we calculate the dependence of the friction force on the profile of the local viscosity. Our results show that in the case of axially symmetric viscosity profile the friction force is sensitive to the anisotropy of the viscous profile whereas it is not sensitive to for-ahead asymmetries. Our results are crucial for active microrheology measurements where tracer particles are pulled through complex fluids.

1. Introduction

Particles in the nanometer size range coated with polymers are of growing importance for rather diverse applications [1]. In hybrid materials such as nanocomposites, the use of polymers grafted to nanoparticles is widely exploit to suppress aggregation of particles and to enhance their dispersion and mixing into solvent or matrix. The nanoparticles coated with DNA are used for building highly sensitive probes or drug carriers in biological systems [2, 3] and to assemble crystals and other structures of numerous morphologies [4].

In the absence of external driving, the transport of nanobjects in the fluid environment is dominated by diffusion, a process due to random molecular motion excited by thermal fluctuations [5–7]. Diffusion of isolated spherical nanoparticle in the simple molecular liquids is well-described by the Fick's law, which says that the mean-square displacement changes linearly in time. The rate of this change, the translational diffusion coefficient D_t, is related to the macroscopic viscosity of the solvent η_m (as measured rheometer) via Stokes-Sutherland-Einstein (SSE) relation [6, 8]; D_t = k_BT/ζ_m where ζ_m is the hydrodynamic drag coefficient given by the Stokes equation ζ_m = 6πη_mR. In this equation R is the hydrodynamic radius of diffusing particle, k_B is the Boltzmann constant and T is the temperature.

However, various experiments [9–20] and simulation studies [21–23] show that diffusion of nano-sized particles in complex fluids is not accurately described by Fick's law and that the SSE relation is violated in certain regimes of parameters. For polymer solutions, these parameters involve the size of the particle and the polymer length scales [24, 25]. For example, if the particle size is comparable to or smaller than the characteristic length scale in a polymer solution, its diffusion is significantly faster than the one predicted based on the macroscopic viscosity [13, 17, 18]. This is because on such length scales the nanoparticle does not experience the homogeneous continuum medium with high viscosity, rather, the individual polymer chains or blobs and their fluctuations as well as entanglements influence its dynamics.

Grafting nanoparticles with macromolecules, such as polymers or DNA, complicates their interactions with the complex medium and, therefore, stronger deviations from the SSE relation are expected. These deviations can be tested in rheological experiments [26] by measuring the drag force. The experiments for a bare (non-grafted) colloid in DNA solutions demonstrated that by using optical tweezers it is possible to move a particle through a highly monodispersed polymer solution at a given velocity as well as to measure the drag force on the colloid with piconewton resolution at the same time [26].

Here we provide a theoretical prediction for a drag force based on the assumption that interactions between grafted particle and the complex medium result in an effective spatially dependent viscosity. A similar idea was used by Tuinier et al. [27], Fan et al. [28, 29], and Feng et al. [30] to calculate the hydrodynamic resistance force for a bare spherical particle in a non-adsorbing polymer solution, where polymer depletion results in a reduced polymer concentration near the particle surface. Using the concept of local viscosity [31], the polymer concentration profile was related to the viscosity profile near a spherical particle. Hydrodynamics was formulated by the modified Stokes equation with non-uniform spherically symmetric viscosity, which was solved by a regular perturbation approximation using the Green function method.

In the present paper, we extend this analysis to account for anisotropic viscosity profile around a spherical particle, which may result from anisotropically grafted nanoparticles in a non-adsorbing polymer solution (see Figure 1). Such anisotropically grafted nanoparticles, e.g., DNA-grafted Janus particles can be manufactured [33–35]. They provide a basic structural element that can be used to produce useful nanoparticle clusters of different topologies through DNA-based self-assembly [33–35]. The concept of anisotropic viscosity might also be applicable for describing the transport of protein through the nuclear pore complex, where the transporting protein encounters heterogeneous polymer brush or gel like environment [36–38].

FIGURE 1

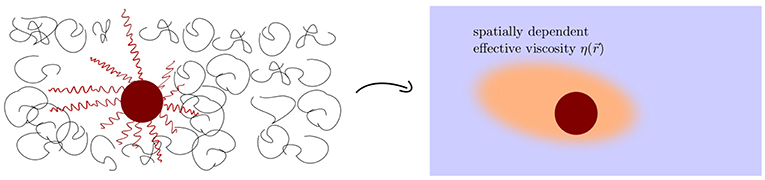
Figure 1. Sketch of an anisotropic polymer concentration profile around a DNA-grafted colloid in a non-adsorbing polymer solution. The concentration profile of the free polymers depends on the grafting density and length of the DNA strings [32]. The anisotropic concentration profile leads to a non-uniform viscosity variation. We want to stress that the system is in equilibrium and there is no netforce.

Because the concentration profile of free polymers in the solution depends on the length of grafted macromolecules and on the grafting density [32], an anisotropic grafting changes the depletion zone around the particle, which leads to anisotropic polymer concentration and thus to anisotropic effective viscosity. We assume that the particle is dragged slow enough such that the polymer solution can adiabatically follow the motion of the colloid. This means that the advective transport rate must be smaller than the diffusive transport rate of the polymers, which can be expressed via the Peclét number Pe = l_pu/D_p ≪ 1, where l_p is the characteristic length scale of the polymer, u the characteristic velocity of the solvent u, and D_p diffusivity of the polymers. Further, we assume that the characteristic length scale of the variation of polymer concentration is bigger than the length of an effective statistical chain element. This assures a sufficiently large number of chain elements in small volume element to apply the concept of local viscosity [31]. Solving the modified Stokes equations with a spatial-dependent viscosity of a general form is not easy—even within a regular perturbation approximation. However, for the axisymmetric systems some simplifications occur. For axisymmetric Stokes equations with constant viscosity, translational and rotational motion are decoupled. For translational motion a scalar stream function, which transforms vectorial equations to the scalar ones is well-established. We demonstrate that these properties also hold for the modified Stokes equations with axisymmetric viscosity profile and provide a formalism to calculate the drag force experienced by a translating particle.

Our paper is structured as follows. In section 2, we present the extended Stokes equations with the spatially dependent viscosity and introduce the perturbation calculation scheme. In section 3 the drag force for the axisymmetric systems is calculated and analyzed for various grafting geometries. We conclude in section 5.

2. Model

2.1. Extended Stokes Equation

The Stokes equations are valid for small Reynolds numbers Re = ρul/η ≪ 1, where ρ is the density of the fluid, u is the characteristic velocity of the flow, and l is the characteristic length scale of the particle. This assures that viscous forces dominate the inertial forces. The stationary incompressible Stokes equations with spatially dependent viscosity η(r) are given by

$\begin{array}{llllll}\nabla ·\tau =0,& & & & \nabla ·v=0,& (1)\end{array}$

where τ = −pI + 2η(r)Δ the stress tensor, p is a pressure and Δ = [∇v + (∇v)^T]/2 is the strain rate. The superscript T denotes the transposed of a tensor, I is the identity matrix. Expanding the divergence in the momentum equation one obtains an additional term, which is proportional to the gradient of the viscosity

$\begin{array}{ll}0=-\nabla p+\eta ({\nabla }^{2}v)+(\nabla \eta )·\left[\nabla v+{(\nabla v)}^T\right].& (2)\end{array}$

We consider a quiescent, unbounded fluid which is dragged by a particle with no-slip and vanishing far-field boundary conditions:

$\begin{array}{lll}v=U+\Omega \times (r_p-r_c),& r\in {\Sigma }_p& (\mathrm{3a})\end{array}$

$\begin{array}{lll}v\to 0,p\to 0,& \left|r\right|\to \infty .& (\mathrm{3b})\end{array}$

where Σ_p is the particle surface and r_p is a point on the particle surface Σ_p. The particle is translating with velocity U and rotating with angular velocity Ω, which requires a force F and a torque T acting on the particle. The angular motion of the particle is described in a coordinate system fixed to the particle at r_c.

The drag force on the particle is determined by the force acting on the particle surface Σ_p, which corresponds to the momentum flux through the surface

$\begin{array}{ll}F={\displaystyle {\int }_{{\Sigma }_p}}\text{dS }\tau ·n,& (4)\end{array}$

where n is the surface normal vector. In the following all quantities are represented in dimensionless units: v ∝ U, Ω ∝ U/a, $\tau \propto \stackrel{-}{\eta }U/a$ and $p\propto \stackrel{-}{\eta }U/a$, where a is the particle radius and $\stackrel{-}{\eta }$ is the bulk viscosity. Accordingly, the drag force and viscosity are also dimensionless.

2.2. Small Viscosity Variations

We consider an expansion of the system in small viscosity perturbations of order ${O}(ϵ)$

$\begin{array}{ll}\eta =1+ϵ{\eta }_1+{ϵ}^2{\eta }_2+{O}({ϵ}^3)& (\mathrm{5a})\end{array}$

$\begin{array}{ll}v=v_0+ϵv_1+{ϵ}^2{v}_2+{O}({ϵ}^3)& (\mathrm{5b})\end{array}$

$\begin{array}{ll}p=p_0+ϵp_1+{ϵ}^2{p}_2+{O}({ϵ}^3).& (\mathrm{5c})\end{array}$

The fluid velocity at the surface of the particle is determined by the leading order velocity field v₀. Thus, the higher order fluid velocity fields at the surface must vanish. The far-field condition of the quiescent fluid requires that both the pressure and the velocity fields have to vanish at infinity.

We expand the stationary Stokes equations in small viscosity variations of order ϵ. The leading order system ${O}({ϵ}^0)$ is given by

$\begin{array}{lll}-\nabla p_0+{\nabla }^2{v}_0=0,& 0=\nabla ·v_0& (\mathrm{6a})\end{array}$

$\begin{array}{lll}{v}_0=U+\Omega \times (r_p-r_c),& r\in {\Sigma }_p& (\mathrm{6b})\end{array}$

$\begin{array}{lll}{v}_0,p_0\to 0,& \left|r\right|\to \infty & (\mathrm{6c})\end{array}$

and the first order system ${O}({ϵ}^1)$

$\begin{array}{ll}-\nabla p_1+{\nabla }^2{v}_1=-{\eta }_1{\nabla }^2{v}_0+\nabla {\eta }_1·\left[\nabla v_0+{(\nabla v_0)}^T\right]& (\mathrm{7a})\end{array}$

$\begin{array}{ll}0=\nabla ·v_1& (\mathrm{7b})\end{array}$

$\begin{array}{ll}{v}_1=0,r\in {\Sigma }_p& (\mathrm{7c})\end{array}$

$\begin{array}{ll}{v}_1,p_1\to 0,\left|r\right|\to \infty & (\mathrm{7d})\end{array}$

The leading order solutions fulfill common Stokes equations with constant viscosity.

3. Axisymmetric Systems

Axisymmetric systems possess at least one axis of rotational symmetry, which we choose to be parallel to e_z. We use spherical coordinates {r, θ, ϕ} with the corresponding orthonormal basis $\left\{\widehat{r},e_{\theta },e_{\varphi }\right\}$ and the origin located at the center of the particle. Due to the rotational symmetry the system is independent of the azimuthal angle ϕ. Thus, the viscosity η(r, θ) is a function of radial distance r and the polar angle θ. Accordingly, the $\widehat{r}$- and e_θ-components of the extended Stokes equations Equation (1) depend on the components v_r and v_θ of the fluid velocity, whereas the e_ϕ-component of Equation (1) depends only on v_ϕ. The velocity field of the fluid for translational motion of the particle U ∥ e_z is determined by {v_r, v_θ} and for rotational motion Ω ∥ e_z is determined by v_ϕ. These properties are summarized in Figure 2.

FIGURE 2

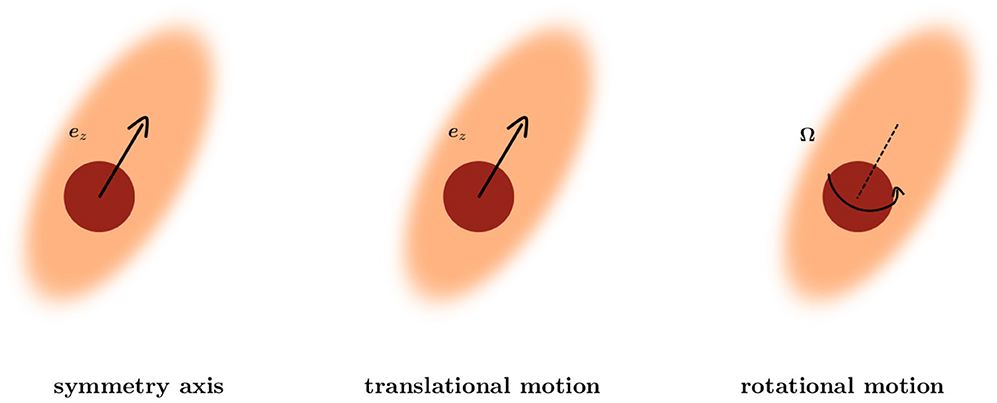
Figure 2. Short summary of the decoupling of translational and rotational motion of the extended Stokes equations for an axisymmetric system. The velocity field of the fluid for translational motion of the particle U ∥ e_z is determined by {v_r, v_θ} and for rotational motion Ω ∥ e_z is determined by v_ϕ.

For axisymmetric Stokes equations translational and rotational motion are decoupled. For translational motion a scalar stream function formalism is well-established to simplify the vectorial equation to a scalar one (see, e.g., Happel and Brenner [39]). This formalism can be extended to a non-uniform viscosity as long as it is axisymmetric (see Appendix A). In the following we focus on translational motion of a particle in an axisymmetric system which is characterized by the particle velocity U.

3.1. Leading Order Solution

The leading order axisymmetric momentum equation [see (A5) in the Appendix A] is the same as for the homogeneous system. So the stream function (see Equation A1) for the leading order system is [39]

$\begin{array}{ll}{\psi }_0(r,\theta )=\frac{1}{4}{r}^2{\text{sin}}^2\theta \left[{\left(\frac{1}{r}\right)}^3-\frac{3}{r}\right].& (8)\end{array}$

The corresponding velocity field is given by

$\begin{array}{ll}{v}_{r0}=\text{cos }\theta \left[\frac{3}{2r}-\frac{1}{2}{\left(\frac{1}{r}\right)}^3\right]& (\mathrm{9a})\end{array}$

$\begin{array}{ll}{v}_{\theta 0}=-\text{sin }\theta \left[\frac{3}{4r}+\frac{1}{4}{\left(\frac{1}{r}\right)}^3\right].& (\mathrm{9b})\end{array}$

As expected, the leading order decay of the velocity is ∝ 1/r. The pressure is determined by integration

$\begin{array}{l}\nabla p_0={\nabla }^2{v}_0,\Rightarrow p_0(r,\theta )=\frac{3}{2}\frac{\text{cos }\theta }{r^2}.\end{array}$

3.2. First Order Solution

For the first order velocity field we use Equations (B3) (see Appendix B), which correspond to the stream function ansatz (B2). In order to determine the first order pressure contribution p₁(r = 1, θ) at the particle surface, we exploit the e_θ-component of the stationary Stokes equation

$\begin{array}{ll}\nabla ·{\tau }_{|e_{\theta }}=0\Rightarrow \frac{1}{r}\frac{\partial p}{\partial \theta }=\nabla ·{(\eta (r=1,\theta )[\nabla v+{(\nabla v)}^T])}_{|e_{\theta }}.& (10)\end{array}$

Using the stream function relations for v₀ (9) and v₁ (B3) we integrate over θ to obtain the pressure at the surface r = 1

$\begin{array}{lll}\hfill p_1(r=1,\theta )& =& {\displaystyle \sum _{n\ge 3}}{f}_n^{(3)}(r=1){\displaystyle \int }\frac{{ℐ}_n}{\text{sin }\theta }\text{d}\theta -\frac{1}{2}{f}_2^{(3)}(r=1)\text{cos }\theta \\ \hfill & -& \frac{3}{2}{\displaystyle \int }{\left({\eta }_1(r=1,\theta )-\frac{\partial {\eta }_1(r,\theta )}{\partial r}\right)}_{r=1}\text{sin }\theta \text{d}\theta +c(r).& (11)\end{array}$

The integration constant c(r) does not contribute to the drag force. Here, superscript (i) defines the ith derivative.

3.3. Drag Force

The drag force on the particle is calculated by integrating the stress tensor over the particle surface (see Equation 4). First, we derive an expression for the forces f_s(r, θ) at the particle surface r = 1

$\begin{array}{ll}{f}_s(r=1,\theta )=\tau ·\widehat{r}=-p\widehat{r}+2\eta (r=1,\theta )\Delta ·\widehat{r}& (12)\end{array}$

($\widehat{r}$ is a vector normal to the surface denoted in Equation 4 by n). Up to the first order, the surface force can be expressed as f_s = f_s0 + ϵf_s1. Using solutions for zero and first order velocities and pressures derived above, we find

$\begin{array}{lll}{f}_s{\mid }_{\widehat{r}}& =& f_{0s}{\mid }_{\widehat{r}}-ϵ\{\stackrel{\text{vanish under surface integration}}{\overbrace{{\displaystyle \sum _{n\ge 3}}{f}_n^{(3)}(r=1){\displaystyle \int }\frac{{ℐ}_n}{\text{ sin }\theta }\text{d}\theta }}+\frac{1}{2}{f}_2^{(3)}(r=1)\text{cos }\theta \\ & +& \frac{3}{2}{\displaystyle \int }\left({\eta }_1(r=1,\theta )-\frac{\partial {\eta }_1(r,\theta )}{\partial r}{\mid }_{r=1}\right)\text{ sin }\theta \text{d}\theta \}& (\mathrm{13a})\end{array}$

$\begin{array}{lll}{f}_s{\mid }_{e_{\theta }}& =& f_{0s}{\mid }_{e_{\theta }}+ϵ\{\stackrel{\text{vanish under surface integration}}{\overbrace{{\displaystyle \sum _{n\ge 3}}{f}_n^{(2)}(r=1)\frac{{ℐ}_n}{\text{ sin }\theta }}}\\ & +& \frac{1}{2}{f}_2^{(2)}(r=1)\text{ sin }\theta +\frac{3}{2}{\eta }_1(r=1,\theta )\text{ sin }\theta \}.& (\mathrm{13b})\end{array}$

In the leading order, $f_{s0}{\mid }_{\widehat{r}}=-3/2\text{ cos }\theta$ and f_0s∣_eθ = 3/2 sin θ. It turns out that the orthogonal component $f_s·\widehat{r}$ of the surface force is determined by the pressure whereas the tangential component f_s·e_θ is determined by the shear force contribution.

The last step to calculate the drag force F is to integrate the surface forces over the whole surface of the particle $F={\int }_{{\Sigma }_p}\text{dS}{f}_s$. Due to the symmetry of the system the drag force is aligned parallel to the symmetry axis e_z. The resolved part of the surface force f_s in e_z direction is obtained by using $e_z=\widehat{r}\text{ cos }\theta$ and e_z = −e_θ sin θ. Performing partial integration and applying the orthogonality of Gegenbauer functions (C2) as well as relation (C3) (see Appendix C) the drag force can be expressed as

$\begin{array}{ll}\Rightarrow F_z=-6\pi +ϵ2\pi \{\frac{f_2^{(3)}(r=1)}{3}& (\mathrm{14a})\end{array}$

$\begin{array}{ll}-\frac{3}{4}{\displaystyle \underset{0}{\overset{\theta }{\int }}}({\eta }_1(r=1,\theta )-\frac{\partial {\eta }_1(r,\theta )}{\partial r}{|}_{r=1}){\text{ sin}}^3\theta \text{d}\theta & (\mathrm{14b})\end{array}$

$\begin{array}{ll}+ϵ2\pi \{-\frac{2f_2^{(2)}(r=1)}{3}-\frac{3}{2}{\displaystyle \underset{0}{\overset{\pi }{\int }}}{\eta }_1(r=1,\theta ){\text{ sin}}^3\theta \text{d}\theta \}& (\mathrm{14c})\end{array}$

The first line (14a) is the leading order drag force corresponding to a sphere and a homogeneous viscosity. The negative sign shows that the force is opposite to the particle moving direction. It turns out that in the leading order, the pressure contributes 1/3 and the shear force 2/3 of the total drag force. The last two lines (14b) and (14c), give the first order correction to the drag force. The contribution of the first order pressure at the surface is shown in line (14b) and the first order shear force contribution is shown in line (14c). Equation (13) implies that only the second Gegenbauer coefficient f₂ is needed to calculate the first order drag force. A general solution for f₂ can be provided by the Green function of the ODE (14) with n = 2, which has a form

$\begin{array}{ll}\left(\frac{{\partial }^4}{\partial r^4}-\frac{4}{r^2}\frac{{\partial }^2}{\partial r^2}+\frac{8}{r^3}\frac{\partial }{\partial r}-\frac{12}{r^4}+\frac{4}{r^4}\right)f_2(r)=R_2(r).& (15)\end{array}$

For a sphere in an unbounded quiescent fluid with vanishing velocity at the sphere surface, this Green function has been calculated by Tuinier et al. [28]:

$\begin{array}{ll}\hfill G_1(r,r^{\prime })& =(\frac{-r^{\prime 4}}{30r}+\frac{r}{6}{r\prime }^2+\frac{1}{12}\left(\frac{r^{\prime }}{r}+\frac{r}{r^{\prime }}\right)\hfill \\ \hfill & -\frac{r{r}^{\prime }}{4}-\frac{1}{20r{r}^{\prime }}),1<r^{\prime }<r\hfill \\ \hfill G_2(r,r^{\prime })& =(\frac{-r^4}{30r^{\prime }}+\frac{r^{\prime }}{6}{r}^2+\frac{1}{12}(\frac{r}{r^{\prime }}+\frac{r^{\prime }}{r})\hfill \\ \hfill & -\frac{r^{\prime }r}{4}-\frac{1}{20r^{\prime }r}),r<r^{\prime }<\infty .\hfill & (16)\end{array}$

The coefficient f₂ is obtained via integration of the Green function and the second Gegenbauer mode of the inhomogeneity R₂(r)

$\begin{array}{ll}{f}_2(r)={\displaystyle {\int }_1^r}{G}_1(r,r^{\prime })R_2(r^{\prime })\text{d}{r}^{\prime }+{\displaystyle {\int }_r^{\infty }}{G}_2(r,r^{\prime })R_2(r^{\prime })\text{d}{r}^{\prime }.& (17)\end{array}$

It satisfies the following boundary conditions: at the sphere surface $f_2(r=1)=0,f_2^{(1)}(r=1)=0,$ and in far-field ${\displaystyle \underset{r\to \infty }{lim}}:f_2(r)/r^2=0,f_2^{(1)}(r)/r=0$. All integrands in (17) are smooth functions, therefore, even if for a given r-dependence of the viscosity an analytical solution does not exist, the integrals can be easily calculated using the standard quadrature method. For the first order drag force, also the derivatives f⁽²⁾(r = 1) and f⁽³⁾(r = 1) at the surface of the sphere are needed. Considering the Leibnitz rule and the continuity of the given Green function up to the second derivative, the derivatives of f₂ at the surface are

$\begin{array}{lll}\hfill {\displaystyle \underset{r\to 1}{lim}}{f}_2^{(k)}(r)& =& {\displaystyle {\int }_1^{\infty }}{G}_2^{(k)}(r=1,r^{\prime })R_2(r^{\prime })\text{d}{r}^{\prime }\\ \hfill G_2^{(3)}(r=1,r^{\prime })& =& -\frac{1}{2r^{\prime }}-\frac{r^{\prime }}{2},G_2^{(2)}(r=1,r^{\prime })=-\frac{1}{2r^{\prime }}+\frac{r^{\prime }}{2}& (18)\end{array}$

3.3.1. Multipol Representation

In order to proceed, we represent the first order viscosity variation in Equation (5a) as a multipole expansion with r-dependent coefficients

$\begin{array}{ll}{\eta }_1(r)=m(r)+d(r)·\widehat{r}+Q(r):\frac{3\widehat{r}\widehat{r}-I}{2}+\dots .& (19)\end{array}$

In the above, the symbol “:” denotes the double dot product. The projections of the viscosity variation are: the monopole $m(r)=\frac{1}{4\pi }\int \text{ sin }\theta \text{d}\theta \text{d}\varphi {\eta }_1(r)$, the dipole $d(r)=\frac{3}{4\pi }\int \text{ sin }\theta \text{d}\theta \text{d}\varphi \widehat{r}{\eta }_1(r)$ and the quadrupole $Q(r)=\frac{5}{8\pi }\int \text{ sin }\theta \text{d}\theta \text{d}\varphi {\eta }_1(r)(3\widehat{r}\widehat{r}-I)$. The quadrupole matrix Q is traceless and symmetric by definition. It follows that the second Gegenbauer coefficient R₂(r) of the inhomogeneity h₁(r, θ) in Equation (B4) depends on the monopole and quadrupole contributions to the axisymmetric viscosity but does not depend on the dipole contribution. Thus, for the total drag force F one has

$\begin{array}{l}{F}_z=-6\pi \{1+ϵ\left[\frac{1}{2}m(r=1)-\frac{1}{6}{m}^{(1)}(r=1)\right]\hfill \\ -\frac{ϵ}{6}\left[Q_{33}(r=1)-Q_{33}^{(1)}(r=1)\right]\hfill \\ +\frac{ϵ}{12}{\displaystyle {\int }_1^{\infty }}\text{d}{r}^{\prime }𝒢(r^{\prime })[-r^{\prime }\left(1+3{r\prime }^2\right)m^{(1)}(r^{\prime })+{r\prime }^2{Q}_{33}^{(2)}(r^{\prime })]\hfill \\ +\frac{ϵ}{12}{\displaystyle {\int }_1^{\infty }}\text{d}{r}^{\prime }𝒢(r^{\prime })[r^{\prime }\left(1+3{r\prime }^2\right)Q_{33}^{(1)}(r^{\prime })-{r\prime }^2{Q}_{33}^{(2)}(r^{\prime })\hfill \\ -18Q_{33}(r^{\prime })+9r^{\prime }(1-{r\prime }^2)Q_{33}^{(1)}(r^{\prime })\left]\right\}.\hfill & (20)\end{array}$

In the above

$𝒢(r^{\prime })\equiv \left(\frac{1}{{r\prime }^6}-\frac{3}{{r\prime }^4}\right),{\displaystyle {\int }_1^{\infty }}\text{d}{r}^{\prime }𝒢(r^{\prime })=-\frac{4}{5}.$

This result includes the solution of Tuinier et al. [28] for isotropic viscosity variations η₁(r).

4. Analysis

We start the analysis of our result for the drag force with the general case of viscosity variations that decay beyond a certain length scale. The decay of viscosity variations is expected because the overall polymer concentration profile approaches its bulk value sufficiently far away from the grafted particle. Specifically, we assume that each multipole mode n of η₁ decays beyond the (possibly different) length scale d_n. Since merely the first three multipoles are relevant, we have

$\begin{array}{ll}m(r)=Z_0(r;d_0)·m& (21)\end{array}$

$\begin{array}{ll}d(r)=Z_1(r;d_1)·d& (22)\end{array}$

$\begin{array}{ll}Q(r)=Z_2(r;d_2)·Q.& (23)\end{array}$

In order to grasp the basics of the role of the viscosity profile on the drag force on the colloid, we follow Tuinier and Taniguchi [31] and consider the decay profile of the following functional form:

$\begin{array}{ll}{Z}_n(r;d_n)=1-{tanh}^2\left(\frac{r-1}{d_n}\right),& (24)\end{array}$

with the properties Z_n(r = 1; d_n) = 1, $Z_n^{(1)}(r=1;d_n)=0$, and ${\displaystyle \underset{r\to \infty }{lim}}{Z}_n(r;d_n)=0$. An example of the decay profile is shown in Figure 3 for different values of d.

FIGURE 3

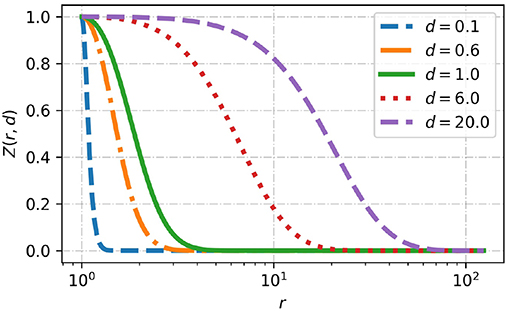
Figure 3. The decay profile Z(r; d) next to the particle surface r = 1 is plotted for different d ∈ {0.1, 0.6, 1, 8, 20}. d < 1 corresponds to a fast decay compared to the particle size and d > 1 corresponds to a slow decay.

The drag force can be represented in terms of an isotropic viscosity contribution ϵm α_i(d) and the anisotropic viscosity contributions ϵQ₃₃ α_a(d) as follows:

$\begin{array}{ll}\frac{F_z}{-6\pi }=1+ϵ[m{\alpha }_i(d_0)+Q_{33}{\alpha }_a(d_2)]& (25)\end{array}$

with

$\begin{array}{lll}{\alpha }_i(d)& =& \frac{1}{2}+\frac{1}{12}{\displaystyle {\int }_1^{\infty }}\text{d}{r}^{\prime }𝒢(r^{\prime })[-r^{\prime }\left(1+3{r\prime }^2\right)Z_0^{(1)}(r^{\prime },d)\\ & +& {r\prime }^2{Z}_0^{(2)}(r^{\prime },d)]& (26)\end{array}$

$\begin{array}{l}{\alpha }_a(d)=-\frac{1}{6}+\frac{1}{12}{\displaystyle {\int }_1^{\infty }}\text{d}{r}^{\prime }𝒢(r^{\prime })[r^{\prime }\left(10-6{r\prime }^2\right)Z_2^{(1)}(r^{\prime },d)\\ -{r\prime }^2{Z}_2^{(1)}(r^{\prime },d)-18Z_2(r^{\prime },d)].& (27)\end{array}$

In Figure 4 we plot the forces α_i and α_a as function of the decay length d ∈ [10⁻³, 10³]. As expected, for variations very quickly decaying with the distance from the sphere, i.e., for (d ≪ 1), both functions vanish and the drag force is similar to a particle in a homogeneous solution. Thus, in this limit the viscosity variation is negligible. On the other hand, in the limit of very slow decays (d ≫ 1)

$\begin{array}{ll}{\displaystyle \underset{d\to \infty }{lim}}{\alpha }_i=1,{\displaystyle \underset{d\to \infty }{lim}}{\alpha }_a=\frac{7}{25}& (28)\end{array}$

the solution correspond to the case of viscosity variations that depend only on the angle θ.

FIGURE 4

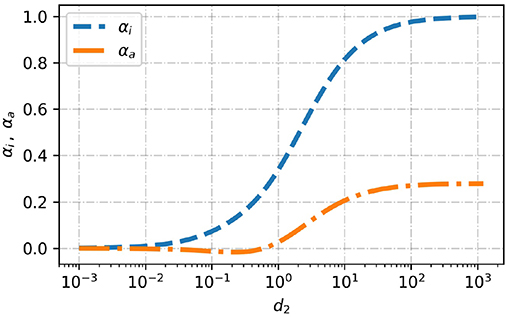
Figure 4. Dimensionless drag force due to a solely monopole contribution, α_i (see Equation 27), and solely due to quadrupole contribution, α_a (see Equation 29), as a function of the dimensionless decay length, d₂.

In between there is a transition region from short length scales to long length scales. The isotropic viscosity variation is the main contribution to the drag force. The contribution from the anisotropic viscosity variation is weaker. At d ≈ 1 the anisotropic contribution becomes negligibly small because α_a shows a zero crossing in that region. Thus, up to the first order the drag force is independent of anisotropic viscosity variations that decay on the length scale of the particle. In order to get a better understanding of the zero crossing we look at the specific quadrupole like viscosity variation Q = [(−1, 0, 0), (0, −1, 0), (0, 0, 2)]/2, which is shown in Figure 5 for d₂ ∈ {0.3, 7}. This specific viscosity variation does not change the net viscosity. The viscosity in front and at the back of the particle is increased whereas at the waist it is decreased. The corresponding drag force is increased for d₂ > 1 and decreased for d₂ < 1. In a more general context this indicates that higher viscosity at the back and front of a particle leads to larger drag force if the viscosity variation decays on a longer length scale compared to the length scale of the particle and to a weaker drag force if the variation decays on a shorter length scale compared to the length scale of the particle.

FIGURE 5

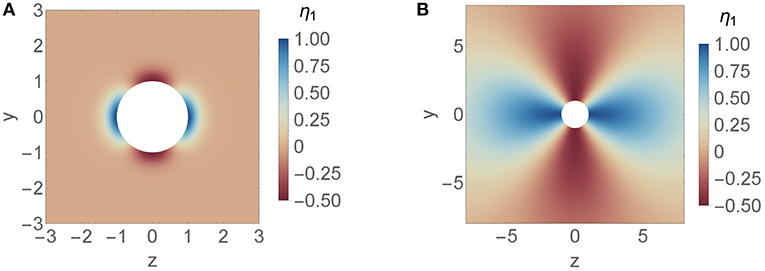
Figure 5. Axisymmetric, quadrupolar viscosity variation Q = [(−1, 0, 0), (0, −1, 0), (0, 0, 2)]/2 around a spherical particle with length scale decay (A) d₂ = 0.3 and (B) d₂ = 7.

4.1. Analysis of the Velocity Mode v_d

Our formalism allows us to analyze how the velocity field adapts to modulations in the local viscosity. In the following we focus on the dependence of the local velocity field on the local viscosity for anisotropic viscosity profiles (isotropic profiles have been analyzed in Fan et al. [28]). In this case only the quadrupolar component of the viscosity profile (with magnitude given by Q₃₃ = l₂, where l₂ is the coefficient of the projection of η₁ on the second Legendre mode¹) affects the translational friction, thus we study the velocity field variations which are related to those viscosity variations and call them v_d ∝ ϵl₂.

In Figure 7 we show the velocity field variation v_d (calculated using Equation 16) for different decay length of the quadrupolar contribution d₂ ∈ {0.1, 1, 8, 20} (in units of ϵl₂). For each decay d₂ two figures are shown. The semi-logarithmic plot gives information about the long ranged velocity field v_dz along the lines θ = 0 and θ = π/2 whereas the vector-density-plot indicates the absolute value of the velocity component |v_d| and the arrows give additional information about the direction of the velocity variation. For comparison the leading order velocity field is shown in Figure 6.

FIGURE 6

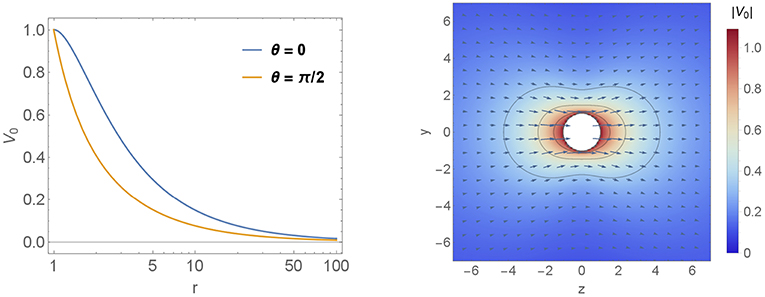
Figure 6. Velocity profiles. The leading order velocity field is shown in two plots. The first one is a semi-logarithmic plot which gives information about the long ranged velocity field v₀ decay parallel to the symmetry axis. Therefore we calculated v₀ along the lines θ = 0 and θ = π/2. The second one is a vector-density-plot which indicates the absolute value of |v₀| and the arrows give additional information about the direction of the velocity field. The particle is denoted by the white sphere in the middle of the plot and it is moving to the right parallel to e_z.

In the semi-logarithmic plot we see the algebraic decay of the velocity field and at the surface r = 1 the dimensionless velocity of the particle v ∝ 1. Thus, a positive sign in the semi-logarithmic plot as well as arrows with positive z-component corresponds to an increase of the velocity field. On the other hand, a negative sign in the semi-logarithmic plot as well as arrows with negative z-component corresponds to a decrease of the velocity field. For short ranged viscosity variations d₂ ≲ 1 the semi-logarithmic plot is negative as shown in the top right panel of Figure 7. Thus, the velocity variation decreases the velocity field. For viscosity variations of the particle length scale d₂ ≈ 1 (middle left panel of Figure 7) the semi-logarithmic plot is mainly positive except close to the particle surface. Hence, the velocity variation increases the velocity field. This property is maintained in the far-field for long ranged viscosity variations. Finally, in the bottom right panel of Figure 7 the vector-density-plot shows two velocity regions which are separated by a crossover area (blue area) with very small velocity variations. The first region is close to the particle surface. Here the fluid velocity is reduced compared to the homogeneous case. The second region is outside the crossover area and increases the velocity field. With increasing length scale of the viscosity variation d the layers get stretched.

FIGURE 7

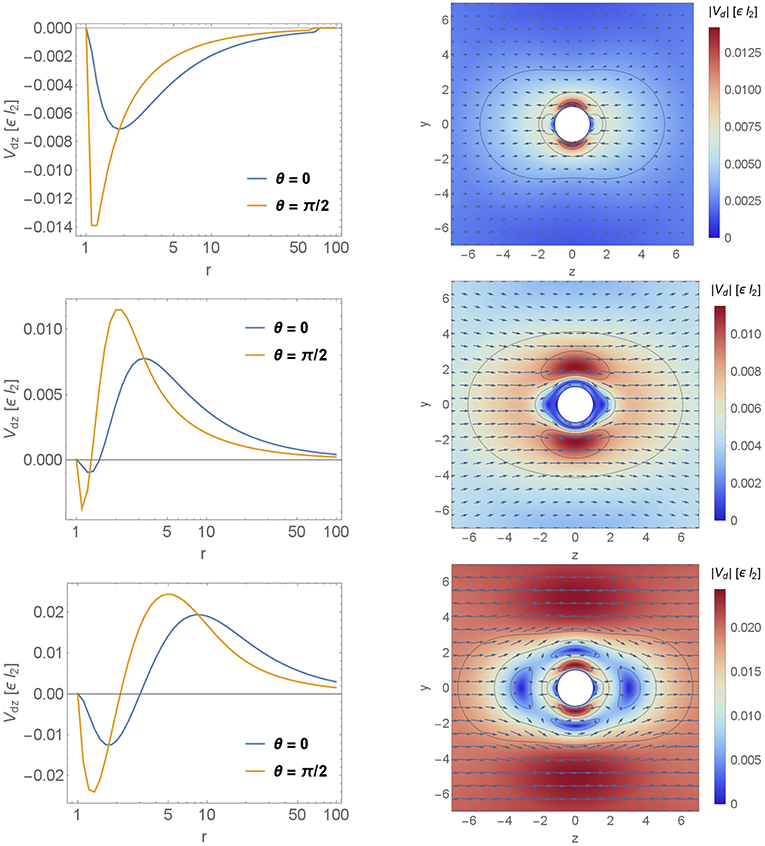
Figure 7. Velocity profiles. The velocity field variation v_d is shown for different decays of the viscosity variation d₂ ∈ {0.1, 1, 8} top to bottom, respectively. Each velocity field is shown in two plots. The first one is a semi-logarithmic plot which gives information about the long ranged velocity field v_dz decay parallel to the symmetry axis. Therefore we calculated v_dz along the lines θ = 0 and θ = π/2. The second one is a vector-density-plot which indicates the absolute value of |v_d| and the arrows give additional information about the direction of the velocity variation. The particle is denoted by the white sphere in the middle of the plot and it is moving to the right parallel to e_z.

4.2. Janus and Quadrupole Particles

We consider a spherical particle that is anisotropically grafted with polymer chains in a polymer suspension. The grafted polymers induce an anisotropic depletion zone of suspended polymers whose width is controlled by the mutual interaction between the grafted and suspended polymers. In the following we assume that the motion of the particle occurs on time scales τ_particle that are much larger than the relaxation time of the polymers (τ_particle ≫ τ_polymer), i.e., the Peclét number Pe = l_pu/D_p ≪ 1.

Under these conditions the semi empirical Martin Equation [40] can be used to relate the local polymer concentration to a local viscosity:

$\begin{array}{ll}{\eta }_p/{\eta }_s=1+\left[\eta \right]c_b\rho (r){\text{e}}^{k_H\left[\eta \right]c_b\rho (r)}.& (29)\end{array}$

where ρ is the dimensionless, normalized total polymer (i.e., grafted plus suspended polymers) concentration profile, η_s is the viscosity of the solvent, k_H is the Huggins coefficient, which is specific for a given polymer-solvent combination. The intrinsic viscosity [η] is approximately the inverse of the polymer overlap concentration $1/c_b^{*}$ in the bulk, which corresponds to the hydrodynamic volume of a polymer chain in solution per unit mass. We expand the Martin equation for small variations of the polymer concentration profile c_bρ(r), which is in the dilute regime ϵ = c_b[η] ≪ 1

$\begin{array}{ll}{\eta }_p/{\eta }_s=1+ϵ\rho (r)+{ϵ}^2{k}_H\rho {(r)}^2.& (30)\end{array}$

We identify η₁ = ρ.

Now, we discuss the following (physically realizable) grafting geometries [33–35]:

• isotropic: bare particle – index ′i′;

• dipolar grafting: a Janus like particle – index ′j′;

• quadrupolar grafting two cases

– dominant length scale at back and front – index ′q′;

– dominant length scale at the waist – index $\prime q_2^{\prime }$;

which are defined by the following concentration profiles

$\begin{array}{ll}{\rho }_i=R(r,d)& (31)\end{array}$

$\begin{array}{ll}{\rho }_j=\frac{\left(R(r,d_1)+R(r,d)\right)}{2}+\frac{\left(R(r,d)-R(r,d_1)\right)}{2}\text{cos }\theta & (32)\end{array}$

$\begin{array}{ll}{\rho }_q=\frac{\left(R(r,d_1)+R(r,d)\right)}{2}+\frac{R(r,d)-R(r,d_1)}{2}(3{\text{ cos}}^2\theta -1)/2& (33)\end{array}$

$\begin{array}{ll}{\rho }_{q2}=\frac{\left(R(r,d_1)+R(r,d)\right)}{2}+\frac{R(r,d_1)-R(r,d)}{2}(3{\text{ cos}}^2\theta -1)/2.& (34)\end{array}$

The lowest monopoles of the viscosity corresponding to these concentration profiles are:

$\begin{array}{ll}{m}_i(r)=R(r,d)& (35)\end{array}$

$\begin{array}{ll}{m}_{j,q}(r)=\frac{\left(R(r,d_1)+R(r,d)\right)}{2}& (36)\end{array}$

$\begin{array}{ll}{d}_j(r)=\frac{R(r,d)-R(r,d_1)}{2}·d& (37)\end{array}$

$\begin{array}{ll}{Q}_q(r)=\frac{R(r,d)-R(r,d_1)}{2}·Q& (38)\end{array}$

$\begin{array}{ll}{Q}_{q2}(r)=\frac{R(r,d_1)-R(r,d)}{2}·Q.& (39)\end{array}$

We assume that near a surface of the bare particle polymers are depleted, which corresponds to the polymer concentration profile [41]

$\begin{array}{ll}R(r,d)={tanh}^2\left(\frac{r-1}{d}\right).& (40)\end{array}$

The polymer concentration profile ρ_j next to a Janus like colloidal particle is shown in Figure 8A. The polymer concentration profile for the two cases ρ_q, ρ_q2 of quadrupolar grafting are shown in Figures 8A,C.

FIGURE 8

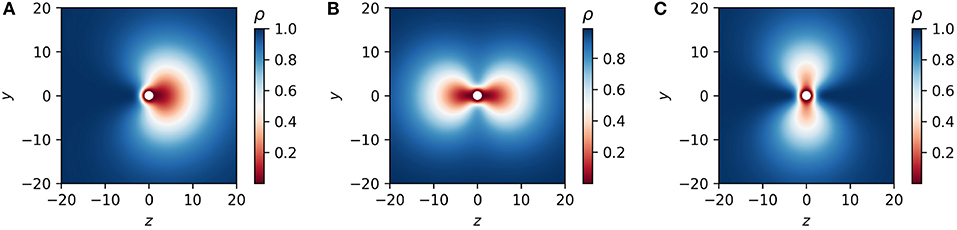
Figure 8. Concentration profile ρ (see Equation 32) next to a dipolar grafted (Janus-like) colloidal particle (A), next to a quadrupolar back-front grafted colloidal particle (B), and a quadrupolar waist grafted particle (C). The length scale of the depletion zone at one hemisphere of the dipolar grafted particle and at the waist (back front) of the quadrupolar grafted particle is fixed at (d₁ = 1) whereas at the other parts of the particle it is fixed at d = 10.

We calculate the drag force for different length scales d ∈ [0.01, 50] of the depletion zone at the grafted sides and compare it to the isotropic case. The length scale of the depletion zone at one hemisphere of the dipolar grafted particle, the waist of the quadrupolar back-front grafted particle ′q′ as well as the back and front of the waist grafted particle ($\prime q_2^{\prime }$) are fixed at d₁ = 1 or at d₁ = 0.01.

The results for the first order correction to the drag force F_z,1 = (F_z − 1)/(−6π) (in units of ϵ) are shown in Figure 9 for two cases: (1) d₁ = 1 and (2) d₁ = 0.01. One can see that for all cases F_z,1 is positive, i.e., the total drag force always increase, and that the first order correction decays monotonically upon increasing the decay length d. Because the dipolar part of the axisymmetric viscosity variations does not contribute to the first order correction to the drag force, for the Janus like grafting F_z,1 is determined by the monopol part (36). For the quadrupolar grafting both monopol and quadrupole viscosity variations contribute to F_z,1. By the choice of the polymer concentration profiles, at d₁ = d the drag force F_z,1 for all cases of grafted particles equals the one for the bare particle. If d₁ < d, i.e., when the grafting induce a larger depletion zone, the first order correction to the drag force is smaller than that for a bare particle. If d₁ or d are < 1, F_z,1 is almost the same for all three cases of grafting. For d > d₁, the back-front grafting leads to a weaker F_z,1 than the waist grafting.

FIGURE 9

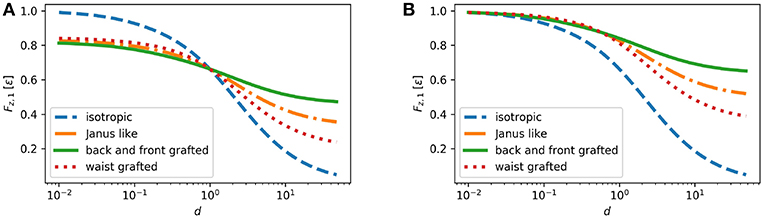
Figure 9. The first order correction to the drag force F_z,1 = (F_z−1)/(−6π) (see Equation 25) for three cases of the grafting geometry as defined by Equations (32–34) compared to the case of isotropic (bare) particle Equation (31). Polymer concentration profiles corresponding to the drag force for the Janus and back-front quadrupolar grafting in (A) are shown, respectively, in panels (A,B) in Figure 8.

5. Conclusions

We have characterized the friction force of colloidal particles dragged across a fluid that show an inhomogeneous and anisotropic viscosity profile. We have derived closed formulas for both the drag force as well as for the velocity profile. In order to rationalize our results we have expressed the local viscosity profile in terms of its multipole expansion. As expected, we found that the drag force is sensitive to the amplitude of the monopole, i.e., the drag force increases upon increasing the average viscosity. Interestingly, higher order multipoles have quite different roles. In fact, our results show that the drag force is insensitive to the amplitude of the dipole, i.e., for a fore-and-aft asymmetric particle pulling it back and forwards leads to the same drag force. In contrast, the drag force is sensitive to the amplitude of the quadrupole. In particular, we found that a proper choice of the quadrupole orientation (i.e., with higher viscosity on the waist and lower on the axis of motion) with a long decay, d ≫ 1 leads to a net reduction of the drag force. We emphasize that such a reduction occurs with “fixed” average viscosity, i.e., at fixed monopole contribution. Hence this is a genuine effect of the anisotropic viscosity distribution and cannot be reduced to a simple reduction of the average drag. Moreover, the sign of this contribution can be switched by changing either the sign of the quadrupole, i.e., moving the higher viscosity from the waist of the particle to the axis of motion, or by reducing the decay length, d ≪ 1.

We have analyzed the cases of physically plausible grafting shown in Figure 7 in more detail. Interestingly, we found that the net drag force can be controlled by tuning the relative magnitude of the monopole and quadrupole contribution to the density of the grafted polymers (see Figure 8). In particular, our results show that for the Janus grafting the anisotropic grafting can both reduce and enhance the drag force as compared to the isotropic case. In contrast, for the case of back-front grafting the net effect of the anisotropic contribution is to enhance the drag force as compared to the isotropic case.

Concerning the velocity profile, we have shown that the inhomogeneous and anisotropic viscosity profile induces quite involved modulations in the velocity field. Interestingly, the modulations of the velocity profile can oppose t the main flow. Due to our perturbation approach, the magnitude of these modulations are tiny. In this perspective, our results are pinpointing the relevance of the modulations in the viscosity that, possibly, may persist also for stronger variations of the viscosity. We have truncated our expansion at first order since, typically, this is also the leading order when the perturbation parameter is small. Indeed this is the case for monopole and quadrupole contributions to the density of grafted polymers. Interestingly, dipole contributions to the density distribution, at linear order, do not affect the effective friction. Therefore, for the dipolar contribution a higher order expansion is required. Since this quadratic contribution is relevant only when the monopole and quadrupole are vanishing small, we have decided to disregard this contribution in the present manuscript and to focus on the leading contributions, namely monopole and quadrupole. We plan to investigate higher order contribution (and hence also dipole ones) in forthcoming works. Results of Fan et al. [28] suggest that they may be relevant for variations at short length scales.

Data Availability

The datasets generated for this study are available on request to the corresponding author.

Author Contributions

MW, PM, and AM contributed conception and design of the study. MW wrote the first draft. AM rewrote several sections. All authors contributed to manuscript revision.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

The work of AM was partially supported by Polish National Science Center (Harmonia Grant No. 2015/18/M/ST3/0403).

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2019.00122/full#supplementary-material

Footnotes

1. ^A function f defined on the interval [−1, 1] can be represented in Legendre's polynomials $f(x)=\sum _{n\ge 0}{l}_n{P}_n(x)$. The coefficients l_n are the projections onto the corresponding Legendre's mode $\frac{2n+1}{2}{\langle f\mid P_n\rangle }_P=l_n$.

References

1. Mezzenga R, Ruokolainen J. Nanocomposites: nanoparticles in the right place. Nat Mater. (2009) 8:926–8. doi: 10.1038/nmat2576

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Rosi NL, Mirkin CA. Nanostructures in biodiagnostics. Chem Rev. (2009) 105:1547. doi: 10.1021/cr030067f

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Tiwari PM, Vig K, Dennis VA, Singh SR. Functionalized gold nanoparticles and their biomedical applications. Nanomaterials. (2011) 1:31–62. doi: 10.3390/nano1010031

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Nykypanchuk D, Maye MM, van der Lelie D, Gang O. DNA-guided crystallization of colloidal nanoparticles. Nature. (2008) 451:549–52. doi: 10.1038/nature06560

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Brown R. In: Bennett JJ, Hardwicke R, editors. The Miscellaneous Botanical Works of Robert Brown. Vol. 1. London (1866). p. 463–86.

Google Scholar

6. Einstein A. Investigations on the Theory of the Brownian Movement. New York, NY: Dover (1956).

Google Scholar

7. Smoluchowski M. Zur kinetischen theorie der brownschen molekularbewegung und der suspensionen. Ann Phys. (1906) 21:756–80.

Google Scholar

8. Sutherland W. A dynamical theory of diffusion for non-electrolytes and the molecular mass of albumin. Philos Mag. (1905) 9:781–85.

Google Scholar

9. Odijk T. Depletion theory of protein transport in semi-dilute polymer solutions. Biophys J. (2000).79:2314–21. doi: 10.1016/S0006-3495(00)76477-0

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Kalwarczyk T, Sozanski K, Ochab-Marcinek A, Szymanski J, Tabaka M, Hou S, et al. Motion of nanoprobes in complex liquids within the framework of the length-scale dependent viscosity model. Adv Colloid Interface Sci. (2015) 223:55–63. doi: 10.1016/j.cis.2015.06.007

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Wong IY, Gardel ML, Reichman DR, Weeks ER, Valentine MT, Bausch AR, et al. Anomalous diffusion probes microstructure dynamics of entangled F-actin networks. Phys Rev Lett. (2004) 92:178101. doi: 10.1103/PhysRevLett.92.178101

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Banks DS, Fradin C. Anomalous diffusion of proteins due to molecular crowding. Biophys J. (2005) 89:2960–71. doi: 10.1529/biophysj.104.051078

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Tuteja A, Mackay ME, Narayan S, Asokan S, Wong MS. Hydroxylated quantum dots as luminescent probes for in situ hybridization. Nano Lett. (2006) 7:1276–81. doi: 10.1021/nl070192x

CrossRef Full Text

14. Saxton MJ. A biological interpretation of transient anomalous. Biophys J. (2007) 92:1178–91. doi: 10.1529/biophysj.106.092619

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Grabowski CA, Adhikary B, Mukhopadhyay A. Dynamics of gold nanoparticles in a polymer melt. Appl Phys Lett. (2009) 94:021903. doi: 10.1063/1.3070533

CrossRef Full Text | Google Scholar

16. Ziȩbacz N, Wieczorek SA, Kalwarczyk T, Fiałkowski M, Hołyst R. Crossover regime for the diffusion of nanoparticles in polyethylene glycol solutions: influence of the depletion layer. Soft Matter. (2011) 7:7181–6. doi: 10.1039/C0SM01357A

CrossRef Full Text | Google Scholar

17. Kohli I, Mukhopadhyay A. Diffusion of nanoparticles in semidilute polymer solutions: effect of different length scales. Macromolecules. (2012) 45:6143–9. doi: 10.1021/ma301237r

CrossRef Full Text | Google Scholar

18. Guo H, Bourret G, Lennox RB, Sutton M, Harden JL, Leheny RL. Entanglement-controlled subdiffusion of nanoparticles within concentrated polymer solutions. Phys Rev Lett. (2012) 109:055901. doi: 10.1103/PhysRevLett.109.055901

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Chapman CD, Lee K, Henze D, Smith DE, Robertson-Anderson RM. Onset of non-continuum effects in microrheology of entangled polymer solutions. Macromolecules. (2014) 47:1181–6. doi: 10.1021/ma401615m

CrossRef Full Text | Google Scholar

20. Grabowski CA, Mukhopadhyay A. Size effect of nanoparticle diffusion in a polymer melt. Macromolecules. (2014) 47:7238–42. doi: 10.1021/ma501670u

CrossRef Full Text | Google Scholar

21. Ganesa V, Pryamitsyn V, Surve M, Narayanan B. Noncontinuum effects in nanoparticle dynamics in polymers. J Chem Phys. (2006) 124:221102. doi: 10.1063/1.2209241

CrossRef Full Text | Google Scholar

22. Liu J, Cao D, Zhang L. Molecular dynamics study on nanoparticle diffusion in polymer melts: a test of the stokes Einstein law. J Phys Chem C. (2008) 112:6653–661. doi: 10.1021/jp800474t

CrossRef Full Text | Google Scholar

23. Kalathi JT, Yamamoto U, Grest GS, Schweizer KS, Kumar SK. Nanoparticle diffusion in polymer nanocomposites. Phys Rev Lett. (2014) 112:108301. doi: 10.1103/PhysRevLett.112.108301

PubMed Abstract | CrossRef Full Text | Google Scholar

24. de Gennes PG. Scaling Concepts in Polymer Physics. Ithaca, NY: Cornel University Press (1979).

Google Scholar

25. Rubinstein M, Colby RH. Polymer Physics. New York, NY: Oxford University Press (2003).

Google Scholar

26. Gutsche C, Elmahdy MM, Kegler K, Semenov I, Stangner T, Otto O, et al. Micro-rheology on (polymer-grafted) colloids using optical tweezers. J Phys. (2011) 23:184114. doi: 10.1088/0953-8984/23/18/184114

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Tuinier R, Dhont JKG, Fan TH. How depletion affects sphere motion through solutions containing macromolecules. Europhys Lett. (2006) 75:929–35. doi: 10.1209/epl/i2006-10200-0

CrossRef Full Text | Google Scholar

28. Fan TH, Xie B, Tuinier R. Asymptotic analysis of tracer diffusivity in nonadsorbing polymer solutions. Phys Rev E. (2007) 76:051405. doi: 10.1103/PhysRevE.76.051405

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Fan TH, Dhont JKG, Tuinier R. Motion of a sphere through a polymer solution. Phys Rev E. (2007) 75:011803. doi: 10.1103/PhysRevE.75.011803

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Feng X, Chen A, Wang J, Zhao N, Hou Z. Understanding protein diffusion in polymer solutions: a hydration with depletion model. J Phys Chem B. (2016) 120:10114–23. doi: 10.1021/acs.jpcb.6b06248

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Tuinier R, Taniguchi T. Polymer depletion-induced slip near an interface. J Phys. (2005) 17:L9–14. doi: 10.1088/0953-8984/17/2/l01

CrossRef Full Text | Google Scholar

32. Wijmans CM, Zhulina EB, Fleer GJ. Effect of free polymer on the structure of a polymer brush and interaction between two polymer brushes. Macromolecules. (1994) 27:3238–48. doi: 10.1021/ma00090a017

CrossRef Full Text | Google Scholar

33. Maye M, Nykypanchuk D, Cuisinier M, van der Lelie D, Gang O. Stepwise surface encoding for high-throughput assembly of nanoclusters. Nat Mater. (2009) 8:388–91. doi: 10.1038/nmat2421

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Vivek MP, Steven DH. Nanoparticle assembly: DNA provides control. Nat Mater. (2009) 8:346–6. doi: 10.1038/nmat2436

CrossRef Full Text | Google Scholar

35. Lattuada M, Hatton TA. Synthesis, properties and applications of Janus nanoparticles. Nano Today. (2011) 6:286–308. doi: 10.1016/j.nantod.2011.04.008

CrossRef Full Text | Google Scholar

36. Chakrabarti R, Debnath A, Sebastian KL. Diffusion in an elastic medium: a model for macromolecule transport across the nuclear pore complex. Phys A. (2014) 404:65–78. doi: 10.1016/j.physa.2014.02.059

CrossRef Full Text | Google Scholar

37. Mair A, Tung C, Cacciuto A, Coluzza I. Translocation of a globular polymer through a hairy pore. J Mol Liquids. (2018) 265:603–10. doi: 10.1016/j.molliq.2018.06.009

CrossRef Full Text | Google Scholar

38. Chakrabarti R, Kesselheim S, Košovan P, Holm C. Tracer diffusion in a crowded cylindrical channel. Phys Rev E. (2013) 87: 062709. doi: 10.1103/PhysRevE.87.062709

PubMed Abstract | CrossRef Full Text | Google Scholar

39. Happel J, Brenner H. Low Reynolds Number Hydrodynamics. The Hague: Martinus Nijhoff (1983).

Google Scholar

40. Weissberg SG, Simha R, Rothman S. Viscosities of very dilute polymer solutions. J Res Natl Bur Stand. (1951) 47:2257.

Google Scholar

41. Fleer GJ, Skvortsov AM, Tuinier R. Mean-field equation for the depletion thickness. Macromolecules. (2003) 36:7857–72. doi: 10.1021/ma0345145

CrossRef Full Text | Google Scholar