- 1Key Laboratory of Low-Dimensional Quantum Structures and Quantum Control of Ministry of Education, Department of Physics and Synergetic Innovation Center of Quantum Effects and Applications, Hunan Normal University, Changsha, China
- 2College of Physics and Optoelectronic Engineering, Shenzhen University, Shenzhen, China
We investigated the quantum phase transitions in a cross-cavity quantum Rabi model which possesses the parity-time symmetric structure. Both the dissipative quantum Rabi phase transition and the spontaneous parity-time symmetry breaking exist simultaneously in such system. The competition between these two phase transitions produces the plentiful phase diagram. We also propose the detection of the dissipative cross-cavity quantum Rabi phase transition through the measurement of the parity-time symmetric or asymmetric states, which shed light on the precise detection of the few-body phase transition.
1. Introduction
Quantum Rabi model (QRM) describing the coupling between one two-level atom and one quantized cavity's electromagnetic mode provides the simplest paradigm of the quantum light-matter interaction [1, 2], which plays crucial role in many areas of the modern physics such as quantum optics [3–5], quantum information processing [6–9], and condensed matter science [10–14]. Under the rotating wave approximation to neglect the counter-rotating terms [15], quantum Rabi model (a.k.a. Jaynes-Cummings model) can be readily solved for the near resonance or the weak coupling parameter regions in many experiments. Thanks to the development of the experimental techniques, the ultra-strong and deep-strong coupling regime can be accessed in recent experiments [16–23]. In these regimes, the counter-rotating terms can not be neglected any more which results in several intriguing phenomenon. One of them is the finite-component system phase transition, where the ground state experiences a non-analytic change in the ultrastrong atom-cavity-mode coupling together with large detuning [24–31]. The quantum phase transition in an dissipative quantum Rabi model has also been studied for a realistic purpose, where the cavity emits photons at a certain decay rate. The quantum Rabi model just provides a promising platform to investigate the physics of the phase transition in quantum optical systems, which has already attracted a lot of interest. If another kind of the phase transition is introduced in such system, the competition between different phase transition mechanisms is supposed to lead to plentiful phase diagram.
On the other hand, parity-time (PT) symmetric structure is also an intriguing topic in quantum optical system [32–34]. A system with PT symmetry can undergo a phase transition at the exceptional point, where the eigenvalues of the non-Hermitian Hamiltonian varies from real values to complex values when crossing the exceptional point [35–37]. The PT symmetry breaking actually results in various interesting phenomenon studied both theoretically and experimentally such as non-reciprocal photonic transmission [38], enhancement of nonlinear interaction [39, 40], loss-induced or gain-induced transparency [41, 42], efficient photon or phonon lasing [43–47], ultralow-threshold optical chaos [48, 49], quantum metrology [50], and so on. If PT symmetric structure can be introduced in the QRM, two phase transition mechanisms actually compete with each other and provide plentiful phase diagram. Such system can be experimentally implemented by the whispering-gallery modes in the ring cavities or the superconducting transmission lines coupling to one Cooper pair box.
In this paper, we investigate the plentiful phase transitions and phase diagram of the cross-cavity quantum Rabi model together with PT symmetric structure. Since the PT symmetric structure requires a balanced loss and gain on different cavities, the two cavities coupling to the same atom as the simplest model has been taken into consideration. We find that the competition between the quantum Rabi phase transition and the PT symmetry breaking results in plentiful phase transitions and phase diagram. The normal phase and superradiant phase emerging in the previous dissipative quantum Rabi model still exist in our system. The effective coupling is inversely proportional to g2 in the superradiant phase instead of being proportional to g2 in the normal phase. In contrast, the PT asymmetric phase and symmetric phase can also affect the dissipative quantum Rabi model. For the PT asymmetric phase, the total system has steady state when the time tends to infinite because the energy will eventually dissipate into the surrounding environment. When the PT asymmetric phase changes to a symmetric one, the gain and loss of the system can be rebalanced and the original dissipative quantum Rabi model behaves like a decay free Rabi model. It means that except the normal phase and superradiant phase existing in the previous dissipative quantum Rabi model, an oscillating phase emerges in the current system, which exactly is attributed from the PT symmetric structure. It also changes the PT symmetry breaking from a second-order phase transition to a first order one.
The paper is organized as follows. In section The Dissipative QRM Together With PT Symmetric Structure, we introduce the cross-cavity QRM together with PT symmetric structure. We perform a semiclassical analysis of the model to show the steady state and the oscillating state. In section Dissipative Phase Transition, we present a full quantum mechanical solution for the PT symmetry breaking. The competition between the two phase transition mechanisms results in a plentiful phase diagram, which is shown and discussed in section Dissipative Phase Transition. We also propose a self-consistent equation. Finally, we conclude our paper in section Conclusion.
2. The Dissipative QRM Together With PT Symmetric Structure
In this article, we consider the dissipative cross-cavity quantum Rabi model (QRM) together with parity-time (PT) symmetric structure (shown in Figure 1), which is described by a master equation as
where Hamiltonian(ℏ = 1)
governs the coherent dynamics of the cross-cavity QRM with the annihilation (creation) operator of the two cavity modes a(a†) and b(b†), σx and σz are Pauli matrices for a two-level system. Here, Ω is the qubit transition frequency and λa(b) is the coupling strength between the first (second) cavity and the atom. The dissipative nature of the cross-cavity including the loss of the first cavity and the gain of the second cavity is described by Lindblad operators as with and . The oscillator frequencies of the cavity modes and the coupling strengths are tuned to the same one as ωa = ωb = ω0 and λa = λb = λ, and the loss of the first cavity and the gain of the second cavity are symmetric as κa = κb = κ in order to introduce the PT symmetry into the dissipative cross-cavity QRM. Although the PT symmetric and asymmetric phases can also exist when the frequencies, the coupling strengths and the loss (gain) of cavities are not identical, in the sake of the simplicity we consider the identical parameters of the cavities in the following discussion.
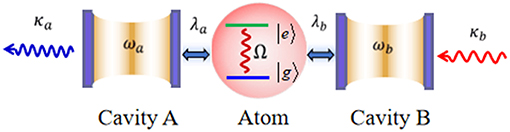
Figure 1. The schematics of the dissipative QRM together with PT symmetric structure when ωa = ωb = ω0, λa = λb = λ, and κa = κb = κ.
By applying the same semi-classical analysis in Hwang et al. [30], in the limit of extremely large detuning Ω/ω0 ≫ 1 and ultra-strong coupling λ/ω0 ≫ 1, the quantum fluctuations are neglected and the mean-field properties are captured. From the standard Heisenberg-Langevin equation of motion acquired from the master equation in Equation (1) where the quantum fluctuations and the correlations between the operators are neglected, a set of semiclassical equation of motion of the dissipative cross-cavity QRM together with the PT symmetry as
If there is only pure dissipation in the system, the solution of the above semiclassical equation eventually tends to a steady one when the evolution time is much larger than the dissipative time κ−1. However, this is not always true in a system with PT symmetric structure because both loss and gain simultaneously exist. It depends on whether the spontaneous symmetry breaking of the PT symmetry occurs or not. If the system stays at the PT asymmetric state, the total energy still dissipate into the surrounding environment of the first cavity even the second cavity gains energy from its surrounding environment and the above semiclassical equation has steady solution. While at the PT symmetric state, the energy loss in the first cavity and the energy gain in the second cavity achieve delicate balance and an oscillating solution possibly exist in our cross-cavity QRM. In this sense, the phase transitions could be more plentiful in our model.
Firstly, the steady-state solution should satisfy
where and are renormalized steady-state mean amplitude of the cavity modes, and S+ ≡ 〈σ+〉s and Sz ≡ 〈σz〉s are the steady-state qubit expectation values. Here, we introduce a dimensionless coupling constant and a frequency ratio η ≡ Ω/ω0 for computational convenience.
The following constrain is introduced due to the conservation of the classical pseudo-spin. Interestingly, the steady solution of the dissipative cross-cavity QRM still exhibits a bifurcation at g = gc with
Below the critical point(g < gc), we get the trivial solution
as the normal phase solution with zero mean field amplitude of cavity modes and the ground state of the pseudo-spin. Above the critical point (g > gc), we get the superradiant phase solution as
where cavity modes have nonzero mean field amplitude and the pseudo-spin stays at an excited state as well. Such phase transition of the dissipative cross-cavity QRM exactly inherit from the dissipative QRM. Additionally, α = β* still implies the PT symmetric structure here.
Now the oscillating solution is taken into consideration. Where the cavity modes oscillate at frequency ω, the x and y component of the qubit should eventually oscillate at the same frequency ω along the z-axis because the coupling in Equation (2) effectively provide an oscillating driven magnetic field in the x−direction. Therefore the oscillating solution should satisfy For a conserved classical pseudo-spin rotating along z-axis, the z−component of the pseudo-spin can be steady as . However, the oscillating frequency can not be simply determined. The oscillating solution exists due to the unbroken PT symmetry, while the PT symmetry breaking is not clear under the current semi-classical treatment. In the next section, we will try to find a self-consistent equation to obtain the oscillating frequency. The Heisenberg-Langevin equation can be rewritten as
If the oscillator frequencies of the cavity modes and the qubit transition frequency are shifted by ω as and Ω′ = Ω + ω, the above set of equations have the same form of the Equations (3a–3d). It means even for the oscillating solution there exhibits a bifurcation at with
Below the new critical point , the oscillating solution will degenerate to a normal phase as
Above the new critical point, the oscillating solution also bifurcates into two stable solutions as
which actually corresponds to a new phase where both the cavity modes and the pseudo-spin eventually oscillates all the time when the energy loss and the gain are delicate balanced. We will call it oscillating phase and determine the oscillating frequency in the next section.
3. Dissipative Phase Transition
In this section, we derive an effective master equation for the cross-cavity modes when tracing out the qubit degree of freedom in the limit of extremely large detuning Ω/ω0 ≫ 1. Based on the Heisenberger–Langevin approach, the quantum dynamics of the system can be investigated in details together with the quantum fluctuations. Both the QRM phase transition and the PT symmetry breaking are demonstrated in united method. The part of QRM phase transition agrees with the semiclassical solution derived in the previous section. The oscillating frequency of the oscillating phase is also illustrated by a self-consistent equation.
3.1. Normal Phases and Oscillating in the Regime g < gc
After applying a unitary transformation
to the Hamiltonian in Equation (2), the coherent part of the Hamiltonian can be transformed to
Because of the extremely large detuning limit η ≫ 1, the last term in the transformed Hamiltonian can be omitted. Additionally, the unitary transformation actually is a infinitesimal one due to η ≫ 1, which would not affect the form of the loss and gain shown as Lindblad operator in Equation (1). It has been proven in Hwang et al. [30].
In order to demonstrate the property of the normal phase where the qubit eventually stays at the ground state |↓〉, the qubit degree of freedom can be traced out by averaging the transformed master equation on the ground state of the qubit as
with
and Obviously, two cross-cavity couples to each other with the coupling constant up to the second order of g and the PT symmetric structure is still preserved. For the mean amplitude u = (〈a〉, 〈a†〉, 〈b〉, 〈b†〉)T, a set of linear equations can be derived from the Equation (15) as with
δω = ω0 − γn and The eigenvalues of the Lnp are with
Both the PT symmetry breaking and the dissipative cross-cavity QRM phase transition can be illustrated by the eigenvalues If the real part of is smaller than 0, the total system eventually decay to the trivial solution u = (0, 0, 0, 0)T which is the exact normal phase of the QRM. This critical point is determined by which can be rewritten as agreeing with the semiclassical solution in the Equation (5). However, the Bnp could varies from a positive value to a negative one when crossing another critical point at Bnp = 0 which corresponds to
As shown in the Figure 2, the regime g < gc can be divided into three regions as: Bnp < 0 for normal phase I; for normal phase II; for oscillating phase. Here the oscillating phase emerges due to the competition between the PT symmetry breaking and the QRM phase transition. It is supposed to emerge when g > gc due to the same mechanism which will be discussed in the next subsection.
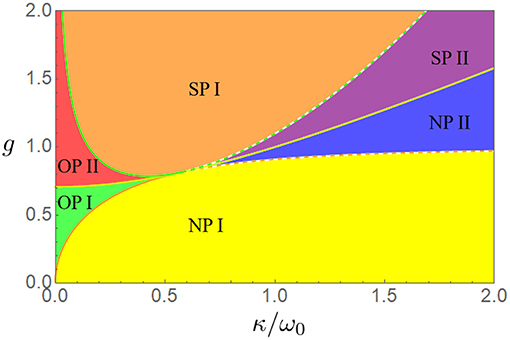
Figure 2. The phase diagram of the dissipative QRM together with PT symmetric structure. The normal phase, the superradiant phase and the oscillating phase are denoted by the letters “NP,” “SP,” and “OP,” respectively. To illustrate more details of the phase diagram, the phases NP I, NP II, SP I, SP II, OP I, and OP II are plotted with yellow, blue, orange, purple, green, and red blocks, respectively.
3.2. Superradiant Phase and Oscillating Phase in the Regime g > gc
To take into the consideration of the oscillating phase when g > gc, a displacement unitary transformation D[α] = Da[α]Db[β] with and is applied to the Hamiltonian in Equation (2) to displace the cavity modes. The natural choice of the displacements are and in Equation (7) in order to consistent with the semiclassical solution. Here, the fact that the displacement for the first and the second cavity are complex conjugate as α = β* reflects the PT symmetric structure.
With the help of the following relations derived from the Equations (4a–4d)
the Hamiltonian can be transformed as
Clearly, the ± sign corresponds to the bifurcation of the steady solutions. We only consider the + case in the following discussion. The displacement unitary transformation not only displace the mean field amplitude of the cavity modes out of zero, but also change the magnetic field on the qubit from the z−axis to a new direction determined by . When the mean-field amplitude of 〈σx〉 is a nonzero value at superradiant phase, the unitary transformation applied previously should along the new direction as
with τz = cos θσz − sin θσx, τx = sin θσz + cos θσx, and After neglecting the constant term, the effective transformed master equation is obtained as
with
In the same method with the one applied for normal phase for the mean amplitude u = (〈a〉, 〈a†〉, 〈b〉, 〈b†〉)T, a set of linear equations can be derived from the Equation (15) as . If we replace the γn with in Equation (17), the eigenvalues of the Lsp can be obtained immediately as with
As we can see in the regime g > gc, the effective coupling is inversely proportional to g2 instead of being proportional to g2 when g < gc, which results in quite different phase transitions in comparison with the ones in the regime g < gc. As shown in the Figure 2, the regime g > gc can be also divided into three regions as: Bsp < 0 for superradiant phase I; for superradiant phase II; for oscillating phase.
3.3. Determine the Oscillating Frequency at the Oscillating Phase
In the last two subsections, the existence of the oscillating phase are verified by the effective master equation. However, the oscillating frequency is not yet determined. Actually the oscillating solution only introduce an additional frequency shift ω into the Hamiltonian H0 as . Such shift would not change the form of effective master equation as Equation (15) in the regimes g < gc and Equation (24) in the regimes g > gc. In those oscillating phases, the imaginary parts of the pure imaginary eigenvalues of the Lnp or Lsp actually are the oscillating frequency, which indicates that the oscillating frequency is actually determined by a self-consistent equation. In this sense, the self-consistent equation is in the regimes g < gc and in the regimes g > gc with
and
The oscillating frequency solved by the above self-consistent equations are shown in Figure 3. As we can see, the behaviors of the oscillating frequencies in the oscillating phase I (OP I) and oscillating phase II (OP II) are quite different. When the decay rate κ is fixed and the coupling strength g increases, it increases in the OP I while decreases in the OP II. The oscillating frequencies is almost independent of the decay rate. Another important feature of the oscillating frequencies is discontinuity at the transition edge from the oscillating phases to the normal phase I (NP I) or superradiant phase I (SP I) shown in the phase diagram. It results in the discontinuity of the order parameters in Equations (11–12) which corresponds to the first order quantum phase transition.
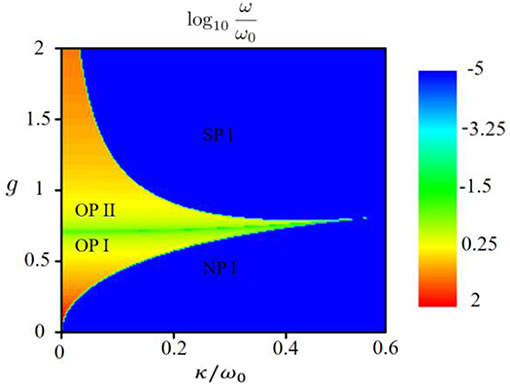
Figure 3. The oscillating frequencies in the oscillating phases I and II. Obviously, the oscillating frequencies is zero in the normal phase I and superradiant phase I. When the decay rate κ is fixed and the coupling strength g increases, it increases in the OP I while decreases in the OP II. It is discontinuous at the transition edge from the oscillating phases to the normal phase I or superradiant phase I.
4. Conclusion
In this paper, we investigate the plentiful phase transitions and phase diagram of the cross-cavity quantum Rabi model together with PT symmetric structure. We find that the competition between the quantum Rabi phase transition and the PT symmetry breaking results in plentiful phase transitions and phase diagram. The normal phase and superradiant phase emerging in the previous dissipative quantum Rabi model still exist in our system. The effective coupling is inversely proportional to g2 in the superradiant phase instead of being proportional to g2 in the normal phase. In contrast, the PT asymmetric phase and symmetric phase can also affect the dissipative quantum Rabi model. For the PT asymmetric phase, the total system has steady state when the time tends to infinite because the energy will eventually dissipate into the surrounding environment. When the PT asymmetric phase changes to a symmetric one, the gain and loss of the system can be rebalanced and the original dissipative quantum Rabi model behaves like a decay free Rabi model. It means that except the normal phase and superradiant phase existing in the previous dissipative quantum Rabi model, an oscillating phase emerges in the current system, which exactly attributed from the PT symmetric structure. Since the oscillating frequencies is no longer continuous at the transition edge from the oscillating phases to the normal phases or the superradiant phases, a first order phase transition emerges due to the discontinuity of the order parameters inherited from the oscillating frequencies. It may shed light on the research of the first order quantum phase transition.
Data Availability
All datasets generated for this study are included in the manuscript/supplementary files.
Author Contributions
Z-RG tutored and participated in the writing of some of the papers. LZ tutored the revised paper. JL tutored the calculation and urged the revision of the thesis. NW conducts deductive calculations, plots, and participates in thesis writing.
Funding
This work was supported by National Natural Science Foundation of China (Grants Nos. 11575058, 11434011, 11935006, and 11975095).
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
We also thank Dr. Zhihai Wang for helpful discussion.
References
1. Rabi II. On the process of space quantization. J Phys Rev. (1936) 49:324–8. doi: 10.1103/PhysRev.49.324
2. Rabi II. Space quantization in a gyrating magnetic field. Phys Rev. (1937) 51:652–4. doi: 10.1103/PhysRev.51.652
3. Todorov Y, Andrews AM, Sagnes I, Colombelli R, Klang P, Strasser G, et al. Strong light-matter coupling in subwavelength metal-dielectric microcavities at terahertz frequencies. Phys Rev Lett. (2019) 102:186402. doi: 10.1103/PhysRevLett.102.186402
4. Ballester D, Romero G, García-Ripoll JJ, Depp F, Solano E. Quantum Simulation of the Ultrastrong-Coupling Dynamics in Circuit Quantum Electrodynamics. Phys Rev X. (2012) 2:1421. doi: 10.1103/PhysRevX.2.021007
5. Pedernales JS, Lizuain I, Felicetti S, Romero G, Lamata L, Solano E. Quantum Rabi model with trapped ions. Sci Rep. (2015) 5:15472. doi: 10.1038/srep15472
6. Muravev VM, Andreev IV, Kukushkin IV, Schmult S, Dietsche W. Observation of hybrid plasmon-photon modes in microwave transmission of coplanar microresonators. Phys Rev B. (2011) 83:1-5. doi: 10.1103/PhysRevB.83.075309
7. Scalari G, Maissen C, Turcinkova D, Hagenmüller D, De Liberato S, Ciuti C, et al. Ultrastrong coupling of the cyclotron transition of a 2D electron gas to a THz metamaterial. Science. (2012) 335:1323–6. doi: 10.1126/science.1216022
8. Kéna-Cohen S, Maier SA, Bradley DDC. Ultrastrongly coupled exciton-polaritons in metal-clad organic semiconductor microcavities. Adv Opt Mater. (2013) 1:827–33. doi: 10.1002/adom.201300256
9. Askenazi B, Vasanelli A, Delteil A, Todorov Y, Andreani LC, Beaudoin G, et al. Ultra-strong light-Cmatter coupling for designer Reststrahlen band. N J Phys. (2014) 16:043029. doi: 10.1088/1367-2630/16/4/043029
10. Crespi A, Longhi S, Osellame R. Photonic realization of the quantum Rabi model. Phys Rev Lett. (2012) 108:163601. doi: 10.1103/PhysRevLett.108.163601
11. Rodríguez-Lara BM, Soto-Eguibar F, Cárdenas AZ, Moya-Cessa HM. A classical simulation of nonlinear Jaynes-Cummings and Rabi models in photonic lattices. Opt Express. (2013) 21:12888. doi: 10.1364/OE.21.012888
12. Wolf FA, Kollar M, Braak D. Exact real-time dynamics of the quantum Rabi model. Phys Rev A. (2012) 85:1956–61. doi: 10.1103/PhysRevA.85.053817
13. Zhong H, Xie Q, Batchelor M, Lee C. Analytical eigenstates for the quantum Rabi model. Physics. (2013) 46:295–8. doi: 10.1088/1751-8113/46/41/415302
14. Gardas B, Dajka J. New symmetry in the Rabi model. J Phys A Math Theor. (2013) 46:493–4. doi: 10.1088/1751-8113/46/26/265302
15. Jaynes ET, Cummings FW. Comparison of quantum and semiclassical radiation theories with application to the beam maser. Proc IEEE. (1963) 51:89–109.
16. Niemczyk T, Deppe F, Huebl H, Menzel EP, Schwarz MJ, Garcia-Ripoll JJ, et al. Circuit quantum electrodynamics in the ultrastrong-coupling regime. Nat Phys. (2010) 6:772–6. doi: 10.1038/nphys1730
17. Todorov Y, Andrews AM, Colombelli R, De Liberato S, Ciuti C, Klang P, et al. Ultrastrong light-matter coupling regime with polariton dots. Phys Rev Lett. (2010) 105:196402. doi: 10.1103/PhysRevLett.105.196402
18. Geiser M, Castellano F, Scalari G, Beck M, Nevou L, Faist J. Ultrastrong coupling regime and plasmon polaritons in parabolic semiconductor quantum wells. Phys Rev Lett. (2012) 108:106402. doi: 10.1103/PhysRevLett.108.106402
19. Cacciola A, Di SO, Stassi R, Saija R, Savasta S. Ultrastrong coupling of plasmons and excitons in a nanoshell. ACS Nano. (2012) 8:11483–92. doi: 10.1021/nn504652w
20. Baust A, Hoffmann E, Haeberlein M, Schwarz MJ, Eder P, Goetz J, et al. Ultrastrong coupling in two-resonator circuit QED. Phys Rev B. (2016) 93:214501. doi: 10.1103/PhysRevB.93.214501
21. Dlaz PF, Garcla-Ripoll JJ, Peropadre B, Orgiazzi JL, Yurtalan MA, Belyansky R, et al. Ultrastrong coupling of a single artificial atom to an electromagnetic continuum in the nonperturbative regime. Nat Phys. (2017) 13:39–43. doi: 10.1038/nphys3905
22. Yoshihara F, Fuse T, Ashhab S, Kakuyanagi K, Saito S, Semba K. Superconducting qubit-oscillator circuit beyond the ultrastrong-coupling regime. Nat Phys. (2017) 13:44–7. doi: 10.1038/nphys3906
23. Gu X, Kockum AF, Miranowicz A, Liu Y-X, Nori F. Microwave photonics with superconducting quantum circuits. Phys Rep. (2017) 718-9:1–102. doi: 10.1016/j.physrep.2017.10.002
24. Hwang MJ, Puebla R, Plenio MB. Quantum phase transition and universal dynamics in the Rabi model. Phys Rev Lett. (2015) 115:180404. doi: 10.1103/PhysRevLett.115.180404
25. Hwang MJ, Plenio MB. Quantum phase transition in the finite jaynes-cummings lattice systems. Phys Rev Lett. (2016) 117:123602. doi: 10.1103/PhysRevLett.117.123602
26. Puebla R, Hwang MJ, Plenio MB. Excited-state quantum phase transition in the Rabi model. Phys Rev A. (2016) 94:023835. doi: 10.1103/PhysRevA.94.023835
27. Bakemeier L, Alvermann A, Fehske H. Quantum phase transition in the Dicke model with critical and noncritical entanglement. Phys Rev A. (2012) 85:043821. doi: 10.1103/PhysRevA.85.043821
28. Ashhab S. Superradiance transition in a system with a single qubit and a single oscillator. Phys Rev A. (2013) 87:679–85. doi: 10.1103/PhysRevA.87.013826
29. Larson J, Irish EK. Some remarks on ‘superradiant’ phase transitions in light-matter systems. J Phys A Math Theor. (2017) 50:174002. doi: 10.1088/1751-8121/aa65dc
30. Hwang MJ, Rabl P, Plenio MB. Dissipative phase transition in the open quantum Rabi model. Phys Rev A. (2018) 97:013825. doi: 10.1103/PhysRevA.97.013825
31. Ai Q, Li Y, Zheng H, Sun CP. Quantum anti-Zeno effect without rotating wave approximation. Phys Rev A. (2010) 81:82. doi: 10.1103/PhysRevA.81.042116
32. Bender CM, Boettcher S. Real spectra in non-Hermitian Hamiltonians having PT symmetry. Phys Rev Lett. (1998) 80:5243.
33. Bender CM, Weir DJ. scrPT phase transition in multidimensional quantum systems. J Phys A Math Theor. (2007) 45:425303. doi: 10.1088/1751-8113/45/42/425303
34. Mostafazadeh A. Pseudo-hermiticity versus PT symmetry: the necessary condition for the reality of the spectrum of a non-Hermitian Hamiltonian. J Math Phys. (2002) 43:205–14. doi: 10.1063/1.1418246
35. Peng B, Odemir SK, Lei F, Monifi F, Gianfreda M, Long GL, et al. Parity-time-symmetric whispering-gallery microcavities. Nat Phys. (2014) 10:394–8. doi: 10.1038/nphys2927
36. Chang L, Jiang X, Hua S, Yang C, Wen J, Jiang L, et al. Parity-time symmetry and variable optical isolation in active-passive-coupled microresonators. Nat Photon. (2014) 8:524–9. doi: 10.1038/nphoton.2014.133
37. Wu JH, Artoni M, Rocca GCL. Non-Hermitian degeneracies and unidirectional reflectionless atomic lattices. Phys Rev Lett. (2014) 113:123004. doi: 10.1103/PhysRevLett.113.123004
38. Li C, Jin L, Song Z. Non-Hermitian interferometer: unidirectional amplification without distortion. Phys Rev A. (2017) 95:022125. doi: 10.1103/PhysRevA.95.022125
39. Ramezani H, Kottos T, Elganainy R, Christodoulides DN. Unidirectional nonlinear PT-symmetric optical structures. Phys Rev A. (2010) 82:1015–8. doi: 10.1103/PhysRevA.82.043803
40. Lin Z, Ramezani H, Eichelkraut T, Kottos T, Cao H, Christodoulides DN, et al. Unidirectional invisibility induced by PT-symmetric periodic structures. Phys Rev Lett. (2011) 106:213901. doi: 10.1103/PhysRevLett.106.213901
41. Guo A, Salamo GJ, Duchesne D, Morandotti R, Volatier-Ravat M, Aimez V, et al. Observation of PT-symmetry breaking in complex optical potentials. Phys Rev Lett. (2009) 103:093902. doi: 10.1103/PhysRevLett.103.093902
42. Jing H, Odemir SK, Geng Z, Zhang J, Lu XY, Peng B, et al. Optomechanically-induced transparency in parity-time-symmetric microresonators. Sci Rep. (2015) 5:9663. doi: 10.1038/srep09663
43. Peng B, Odemir SK, Rotter S, Yilmaz H, Liertzer M, Monifi F, et al. Loss-induced suppression and revival of lasing. Science. (2014) 346:328–32. doi: 10.1126/science.1258004
44. Feng L, Wong ZJ, Ma RM, Wang Y, Zhang X. Single-mode laser by parity-time symmetry breaking. Science. (2014) 346:972–5. doi: 10.1126/science.1258479
45. Hodaei H, Miri MA, Heinrich M, Christodoulides DN, Khajavikhan M. Parity-time-symmetric microring lasers. Science. (2014) 346:975–8. doi: 10.1126/science.1258480
46. Jing H, Odemir SK, Lu XY, Zhang J, Yang L, Nori F. PT-symmetric phonon laser. Phys Rev Lett. (2014) 113:053604. doi: 10.1103/PhysRevLett.113.053604
47. He B, Yang L, Xiao M. Dynamical phonon laser in coupled active-passive microresonators. Phys Rev A. (2016) 94:031802. doi: 10.1103/PhysRevA.94.031802
48. West CT, Kottos T, Prosen T. PT-symmetric wave Chaos. Phys Rev Lett. (2010) 104:054102. doi: 10.1103/PhysRevLett.104.054102
49. LV XY, Jing H, Ma JY, Wu Y. PT-symmetry-breaking Chaos in optomechanics. Phys Rev Lett. (2015) 114:253601. doi: 10.1103/PhysRevLett.114.253601
Keywords: phases transitions, cross-cavity, quantum Rabi model, PT symmetric, PT symmetry breaking PACS numbers: 42.50.-p, 03.67.Lx
Citation: Wang N, Gong Z-R, Lu J and Zhou L (2019) Phases Transitions in a Cross-Cavity Quantum Rabi Model Possessing PT Symmetric Structure. Front. Phys. 7:127. doi: 10.3389/fphy.2019.00127
Received: 04 July 2019; Accepted: 22 August 2019;
Published: 10 September 2019.
Edited by:
Yanpeng Zhang, Xi'an Jiaotong University, ChinaReviewed by:
Qing Ai, Beijing Normal University, ChinaYoubin Yu, Zhejiang Sci-Tech University, China
Copyright © 2019 Wang, Gong, Lu and Zhou. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Jing Lu, bHVqaW5nQGh1bm51LmVkdS5jbg==
 Ning Wang
Ning Wang Zhi-Rui Gong
Zhi-Rui Gong Jing Lu1*
Jing Lu1*