Ideas From Bounded Confidence Theory Applied to Dynamical Networks of Interacting Free-Bodies

1. Introduction

Network-science has long been used as a theoretical framework to model many physical phenomena [1]. See for example: Fatt [2] who proposed a network of tubes as a model for porous media in 1956; Cusatis et al. [3] who used a network structure to model fracture propagation in concrete in 2016.

In Dassios et al. [4, 5] use networks to model plastic and elastic deformation. In general lattice models for deformation and fracture of solid materials were developed firstly for quasi-brittle materials, such as concretes and rocks [3, 6], and extended recently for elastic-plastic materials, such as structural steels [5]. The benefit of modeling materials, treated as continua in classical mechanics, with discrete lattices is that the nucleation, growth and coalescence of discontinuities (cracks) become natural processes. As these are non-topological changes in the system, the classical solid mechanics, being a thermodynamic bulk theory, does not work. Additional benefit of the discrete approach is the possibility for introducing heterogeneities and local anisotropies in the modeled structure by appropriate spatial and directional variation of lattice properties, as well as natural and/or essential boundary conditions in what would be considered an interior in the continuum approach (since each lattice vertex is a boundary).

A lattice, in the language of algebraic topology, is a 1 complex embedded in ℝ², or ℝ³, i.e., a graph with nodes (sites) equipped with Cartesian coordinates and edges (bonds) between some nodes. The first challenge is to ensure the elastic response of a graph is equivalent to the continuum response measured experimentally, ie, to derive a link between properties of lattice elements, e.g., bond stiffness coefficients, and macroscopic properties. Isotropic materials, described by macroscopic constants, can be represented exactly by 2D graphs based on hexagonal structure, see Dassios et al. [4], Esqueda et al. [7], Karihaloo et al. [8], and by 3D graphs based on truncated octahedral structure, see Jivkov and Yates [9] and Zhang et al. [10].

A mathematically rigourous analysis of graphs is based on discrete exterior calculus, see Grady and Polimeni [11]. However, the analysis on graphs developed in this reference is applicable to physical problems, where the nodal unknown (a 0 cochain) is a scalar, ie, temperature, pressure, and concentration, and its gradient is also a scalar over the edges (1 cochain). In mechanical problems, the nodal unknown is a vector, e.g., nodal displacements in linearized kinematics or nodal coordinates in exact kinematics, which makes the problem critically different.

Mathematics of networks have been also used in the modeling of gas networks, see Ekhtiari et al. [12] and in the modeling of electrical power systems, see Dassios et al. [13, 14], Dassios [15], and Cuffe et al. [16], were a key motivation is to begin to link power flow analysis with the mature literature, see Chung and Graham [17], on spectral graph theory.

Finally, the study of the geometric evolution problem of networks of curves in planar domains is another example and has always been very important in modeling of many phenomena in various fields of science, physics and engineering, see Bellettini and Chermisi [18], Fried and Morton [19], Gurtin and Anand [20], Xiaofeng and Wei [21], Boutarfa and Dassios [22], and Dassios [23, 24].

Suppose a system of free-bodies exists in space wherein each free-body imparts a force on all of the other free-bodies. This type of system is regularly simulated in many real-world scenarios including: tracking the motion of extraterrestrial objects, video-game development, and modeling the motion of electrically charged particles. In this study, we combine ideas from bounded confidence theory (BCT)—a concept which is usually used to model social dynamics—with asymptotic analysis, to demonstrate a framework for modeling the motion of interacting free-bodies.

BCT was first introduced by Deffuant et al. [25] in 2000, and it posits that if two people's current opinions (where an opinion exists as a point in some n-dimensional belief-space) are too far apart when they interact (i.e., if the euclidean distance between their two opinions differs by more than some pre-defined threshold), then their opinions—and thus the belief-state of the overall system—will remain unaffected by this interaction. In Physics, asymptotic analysis has some parallels to BCT; using asymptotic analysis, if two particles exert negligible forces on each other, these forces can be ignored to approximate a system [26]. Asymptotic analysis can be used to vastly reduce the complexity (and thus computational intensity) required to model physical phenomena. The asymptotic analysis presented in this study demonstrates how ideas from a BCT network-science framework can be applied to model the physical motion of free-bodies.

In section 2 we introduce a continuous-time model for a system free-bodies interacting with each other under the action of gravity. We then asymptotically approximate this system before converting it into a discrete-time model. In section 3 we present a case-study with arbitrary parameter values which are used to present, analyze, and discuss the approximated model's performance under various conditions. In section 4 we discuss the model presented in this paper, potential future applications, and future research opportunities.

2. Model

2.1. Introduction

We consider the dynamics of a system of N free-bodies wherein each free-body imparts some physical force on every other free-body in accordance to some physical law. As an example, we suppose that the forces of interaction are determined by Newton's law of universal gravitation, however, we note that the general modeling framework presented here can be applied more broadly. This system can be represented by a dynamical network of n = N free-bodies (which are the network's nodes) in some three-dimensional (ℝ³) space, wherein each node is used to represent a free body, and each free body, i, has a mass, $m_i\in {ℝ}^{+}$, position, $p_i=\left[p_{i,1},p_{i,2},p_{i,3}\right]\in {ℝ}^3$, and velocity, $v_i=\left[v_{i,1},v_{i,2},v_{i,3}\right]\in {ℝ}^3$.

In order to model this system, we let

$\begin{array}{lll}P& =& \left[\begin{array}{c}{p}_1\\ p_2\\ ⋮\\ p_N\end{array}\right]\in {ℝ}^{N\times 3},M=\left[\begin{array}{c}{m}_1\\ m_2\\ ⋮\\ m_N\end{array}\right]\in {ℝ}^{N\times 1},\text{and}\\ V& =& \left[\begin{array}{c}{v}_1\\ v_2\\ ⋮\\ v_N\end{array}\right]\in {ℝ}^{N\times 3},\end{array}$

be sets containing all positions, masses, and velocities of the free bodies, respectively. Each free-body, i imparts a force of F_i,j on each other free-body, j, in accordance to Newton's law of universal gravitation, and so

$F_{i,j}=\{\begin{array}{c}G\frac{m_i{m}_j(p_i-p_j)}{\Vert p_i-p_j{\Vert }^3},\text{ if }i\ne j,\\ 0,\text{ if }i=j\end{array}$

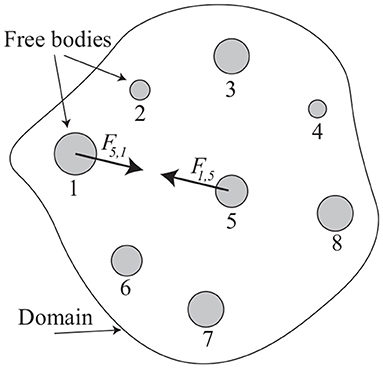
where i, j = [1, 2, …, N], G is the universal gravitational constant, and ||·|| is the L2-norm. Figure 1 provides an illustrative example of this type of network (without the edges shown) where N = 8. This figure also depicts two of the forces, F_1,5, the force imparted by the first free-body on the fifth-free body, and F_5,1, the force imparted by the fifth free-body on the first-free body.

FIGURE 1

Figure 1. System with eight free bodies.

In this study, the network of free-bodies is defined such that a free-body is connected (by an edge) to any other free-body which imparts a force on it. More specifically, we introduce the matrix $\widehat{A}={\left[{\widehat{a}}_{ij}\right]}_{i=1,2,\dots ,n}^{j=1,2,\dots ,n}\in {ℝ}^{n\times n}$, where

${\widehat{a}}_{ij}=\{\begin{array}{cc}0,& \text{if free-body }i\text{ does not impart a force on free-body }j,\\ 1,& \text{if free-body }i\text{ imparts a force on free-body }j,\end{array}$

which is a standard un-directed incidence matrix and describes the connectivity of the network. Since the network of free-bodies is fully connected, $\widehat{A}$ is a dense matrix. Specifically, $\widehat{A}$ = J_N − I_N where J_N is an N × N matrix of ones, and I_N is an N × N identity matrix; later, in section 2.3, we will introduce an approximation method (informed by asymptotic analysis) which will approximate $\widehat{A}$ with a much sparser matrix.

The motion of the free-bodies is governed by the coupled ordinary differential equations:

$\begin{array}{ll}{m}_i\frac{\text{d}{v}_i}{\text{d}t}=-{\displaystyle \sum _{j=1}^N}{F}_{i,j},& (1)\end{array}$

$\begin{array}{ll}\frac{\text{d}{p}_i}{\text{d}t}=v_i.& (2)\end{array}$

2.2. An Approximate Closed Formula of Solutions for the Non-linear System

This non-linear system has an approximate closed formula of solutions which we demonstrate as follows: By combining (1) and (2) the overall system can be written as

$\begin{array}{ll}\frac{{\text{d}}^2{p}_i}{\text{d}{t}^2}=-\frac{1}{m_i}{\displaystyle \sum _{j=1}^N}{F}_{i,j}.& (3)\end{array}$

Next we let

$G_{i,j}:=G_{i,j}(p_i,p_j)=\{\begin{array}{c}\frac{G}{\Vert p_i-p_j{\Vert }^3},\text{ if }i\ne j,\\ 0,\text{ if }i=j\end{array}$

then (3) can be written in the form:

$\begin{array}{l}\frac{{\text{d}}^2{p}_i}{\text{d}{t}^2}=-{\displaystyle \sum _{j=1}^N}{G}_{i,j}{m}_j(p_i-p_j),\end{array}$

or, equivalently,

$\begin{array}{l}\frac{{\text{d}}^2{p}_i}{\text{d}{t}^2}=-p_i{\displaystyle \sum _{j=1}^N}{G}_{i,j}{m}_j+{\displaystyle \sum _{j=1}^N}{G}_{i,j}{m}_j{p}_j,\end{array}$

or, equivalently,

$\begin{array}{l}\frac{{\text{d}}^2{p}_i}{\text{d}{t}^2}=-p_i{\displaystyle \sum _{j=1}^N}{G}_{i,j}{m}_j+\left[\begin{array}{cccc}{m}_1{G}_{1,j}& m_2{G}_{2,j}& \dots & m_N{G}_{i,N}\end{array}\right]\left[\begin{array}{c}{p}_1\\ p_2\\ ⋮\\ p_N\end{array}\right].\end{array}$

Now, by taking i = 1, 2, …, N we have:

$\begin{array}{l}\begin{array}{c}\frac{{\text{d}}^2{p}_1}{\text{d}{t}^2}=-p_1{\displaystyle {\sum }_{j=1}^N}{G}_{1,j}{m}_j+\left[\begin{array}{cccc}{m}_1{G}_{1,1}& m_2{G}_{1,2}& \dots & m_N{G}_{1,N}\end{array}\right]\left[\begin{array}{c}{p}_1\\ p_2\\ ⋮\\ p_N\end{array}\right];\\ \frac{{\text{d}}^2{p}_2}{\text{d}{t}^2}=-p_2{\displaystyle {\sum }_{j=1}^N}{G}_{2,j}{m}_j+\left[\begin{array}{cccc}{m}_1{G}_{2,1}& m_2{G}_{2,2}& \dots & m_N{G}_{2,N}\end{array}\right]\left[\begin{array}{c}{p}_1\\ p_2\\ ⋮\\ p_N\end{array}\right];\\ ⋮\\ \frac{{\text{d}}^2{p}_N}{\text{d}{t}^2}=-p_N{\displaystyle {\sum }_{j=1}^N}{G}_{N,j}{m}_j+\left[\begin{array}{cccc}{m}_1{G}_{N,1}& m_2{G}_{N,2}& \dots & m_N{G}_{N,N}\end{array}\right]\left[\begin{array}{c}{p}_1\\ p_2\\ ⋮\\ p_N\end{array}\right],\end{array}\end{array}$

and the above equations can be written in matrix form:

$\begin{array}{l}\frac{{\text{d}}^2}{\text{d}{t}^2}\left[\begin{array}{c}{p}_1\\ p_2\\ ⋮\\ p_N\end{array}\right]=-diag({\displaystyle \sum _{j=1}^N}{G}_{i,j}{m}_j)\left[\begin{array}{c}{p}_1\\ p_2\\ ⋮\\ p_N\end{array}\right]\\ +\left[\begin{array}{cccc}{m}_1{G}_{1,1}& m_2{G}_{1,2}& \dots & m_N{G}_{1,N}\\ m_1{G}_{2,1}& m_2{G}_{2,2}& \dots & m_N{G}_{2,N}\\ ⋮& ⋮& \ddots & ⋮\\ m_1{G}_{N,1}& m_2{G}_{N,2}& \dots & m_N{G}_{N,N}\end{array}\right]\left[\begin{array}{c}{p}_1\\ p_2\\ ⋮\\ p_N\end{array}\right],\end{array}$

or, equivalently,

$\begin{array}{l}{\text{P}}^{″}=\text{A}\text{P}.\end{array}$

Where

$\begin{array}{l}P=\left[\begin{array}{c}{p}_1\\ p_2\\ ⋮\\ p_N\end{array}\right],A=\left[\begin{array}{cccc}-{\displaystyle {\sum }_{j=1}^N}{G}_{1,j}{m}_j+m_1{G}_{1,1}& m_2{G}_{1,2}& \dots & m_N{G}_{1,N}\\ m_1{G}_{2,1}& -{\displaystyle {\sum }_{j=1}^N}{G}_{2,j}{m}_j+m_2{G}_{2,2}& \dots & m_N{G}_{2,N}\\ ⋮& ⋮& \ddots & ⋮\\ m_1{G}_{N,1}& m_2{G}_{N,2}& \dots & -{\displaystyle {\sum }_{j=1}^N}{G}_{N,j}{m}_j+m_N{G}_{N,N}\end{array}\right].\end{array}$

2.3. Approximation of System

We define K to be some predefined lower bound on “meaningful” acceleration; below this threshold, any acceleration effects are considered negligible to the overall system's dynamics. This acceleration threshold, K, is analogous to the belief-space threshold from BCT which determines which people can interact with each other in order to change the belief-state of the overall system. First we let

${\overline{G}}_{i,j}:={\overline{G}}_{i,j}(p_i,p_j,m_j)=\{\begin{array}{c}{G}_{i,j},\text{ if }|G_{i,j}{m}_j(p_i-p_j)|\ge K,\\ 0,\text{ if }|G_{i,j}{m}_j(p_i-p_j)|<K,\end{array}$

and this matrix, ${\overline{G}}_{i,j}$, is sparser than G_i,j. Using sparse matrices rather than dense matrices can save a significant amount of memory and speed up the processing times for simulating models computationally. As discussed earlier, since each of the free-bodies imparts a force on each of the other free-bodies, the matrix describing the connectivity of the network, $\widehat{A}$, is dense; however, similarly to G_i,j, $\widehat{A}$ may be approximated by the sparser matrix $\widehat{A}$^*, where ${\widehat{A}}^{*}={\left[{\widehat{a}}_{ij}^{*}\right]}_{i=1,2,\dots ,n}^{j=1,2,\dots ,n}\in {ℝ}^{n\times n}$, is defined such that

${\widehat{a}}_{ij}^{*}=\{\begin{array}{cc}0,& \text{ if }{\overline{G}}_{i,j}=0,\\ 1,& \text{ if }{\overline{G}}_{i,j}\ne 0\end{array}$

thus, (3) can be approximated by:

$\begin{array}{ll}\frac{{\text{d}}^2{p}_i}{\text{d}{t}^2}\approx -{\displaystyle \sum _{j=1}^N}{\overline{G}}_{i,j}{m}_j(p_i-p_j),& (4)\end{array}$

and the closed form of solutions can be approximated by:

$\begin{array}{l}{\text{P}}^{″}=\overline{\text{A}}\text{P}.\end{array}$

Where

$\begin{array}{l}\overline{A}=\left[\begin{array}{cccc}-{\displaystyle {\sum }_{j=1}^N}{\overline{G}}_{1,j}{m}_j+m_1{\overline{G}}_{1,1}& m_2{\overline{G}}_{1,2}& \dots & m_N{\overline{G}}_{1,N}\\ m_1{\overline{G}}_{2,1}& -{\displaystyle {\sum }_{j=1}^N}{\overline{G}}_{2,j}{m}_j+m_2{\overline{G}}_{2,2}& \dots & m_N{\overline{G}}_{2,N}\\ ⋮& ⋮& \ddots & ⋮\\ m_1{\overline{G}}_{N,1}& m_2{\overline{G}}_{N,2}& \dots & -{\displaystyle {\sum }_{j=1}^N}{\overline{G}}_{N,j}{m}_j+m_N{\overline{G}}_{N,N}\end{array}\right].\end{array}$

2.4. Discretizing the System

We discretize the governing system, (4), via the Störmer-Verlet scheme (sometimes denoted leapfrog Euler method), and thus, the coupled time-dependent difference equations describing the discrete motion of the free-bodies are

$\begin{array}{ll}{v}_i^{n+1}=v_i^n-\Delta t{\displaystyle \sum _{j=1}^N}{\tilde{G}}_{i,j}{m}_j(p_i^n-p_j^n),& (5)\end{array}$

$\begin{array}{ll}{p}_i^{n+1}=p_i^n+\Delta t{v}_i^{n+1},& (6)\end{array}$

where t is discretized into Ñ time-steps, the super-script n ∈ [1, 2, ..Ñ], and for each time-step * there exist p_*,i, p_*,j which satisfy the solution of (4), such that: ${\tilde{G}}_{i,j}:={\overline{G}}_{i,j}$.

Thus, we have proved the following Theorem:

Theorem 4.1. Consider the non-linear system of differential Equations (1) and (2). If t is discretized into Ñ time-steps, and the super-script n ∈ [1, 2, ..Ñ], then in the area of a time-step * an effective approximate linearization of system (1) and (2) is:

$\begin{array}{l}{\text{P}}^{″}=\tilde{\text{A}}\text{P}.\end{array}$

Where

$\begin{array}{l}P=\left[\begin{array}{c}{p}_1\\ p_2\\ ⋮\\ p_N\end{array}\right],Ã=\left[\begin{array}{cccc}{\displaystyle {\sum }_{j=1}^N}{\tilde{G}}_{1,j}{m}_j-m_1{\tilde{G}}_{1,1}& m_2{\tilde{G}}_{1,2}& \dots & m_N{\tilde{G}}_{1,N}\\ m_1{\tilde{G}}_{2,1}& {\displaystyle {\sum }_{j=1}^N}{\tilde{G}}_{2,j}{m}_j-m_2{\tilde{G}}_{2,2}& \dots & m_N{\tilde{G}}_{2,N}\\ ⋮& ⋮& \ddots & ⋮\\ m_1{\tilde{G}}_{N,1}& m_2{\tilde{G}}_{N,2}& \dots & {\displaystyle {\sum }_{j=1}^N}{\tilde{G}}_{N,j}{m}_j-m_N{\tilde{G}}_{N,N}\end{array}\right].\end{array}$

2.5. Error Analysis

Since $\overline{A}$ is an asymptotic approximation of the much denser matrix A, some error, E, is introduced to the system's dynamics by only considering accelerations above a certain threshold. We define this error such that it is the average distance a free-body is from where it would have been if K = 0. More specifically,

$\begin{array}{ll}{E}^n=\frac{1}{N}{\displaystyle \sum _{i=1}^N}\parallel P_i^n-{\tilde{P}}_i^n\parallel ,& (7)\end{array}$

where P is the position as calculated by the discretized fully connected network model (i.e., when K = 0), and $\tilde{P}$ is the position as calculated by the approximation of the system (i.e., when K > 0).

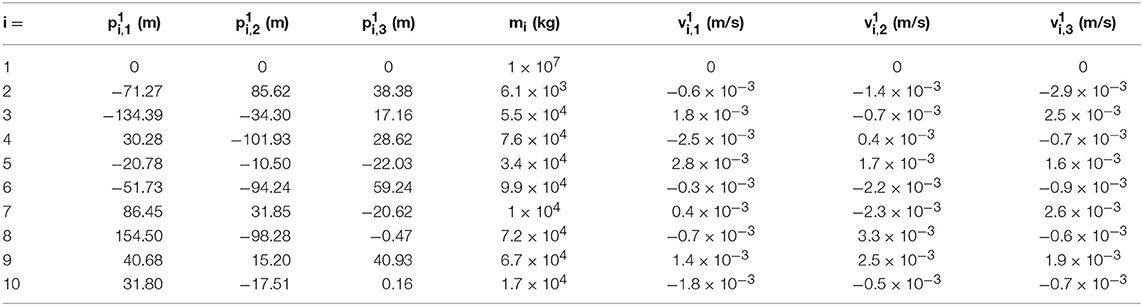
One potential down-side to this definition of error is that it does not distinguish between global drift and local drift. We define global drift to be drift/error wherein all of the free-bodies conserve their relative positions to each other in the system (i.e., global rotation, global translation, global reflection), meanwhile, we define local drift to be when free-bodies drift independently (i.e., in such a way that distorts their relative positions to each other). Depending on the application, global drift may be acceptable, however factoring this into the error measurement is beyond the scope of this research and so we leave it for future work. Figure 2 illustrates the difference between these two forms of drift. In this figure, a global translation is used as an example for global drift; in this example, each free-body drifts by the same magnitude and the same direction. Meanwhile, in the local drift example each free-body drifts by the same magnitude but in different directions. Since drift direction is not considered in the error measurement defined in (7) (only drift magnitude), both of these scenarios would have the same error score.

FIGURE 2

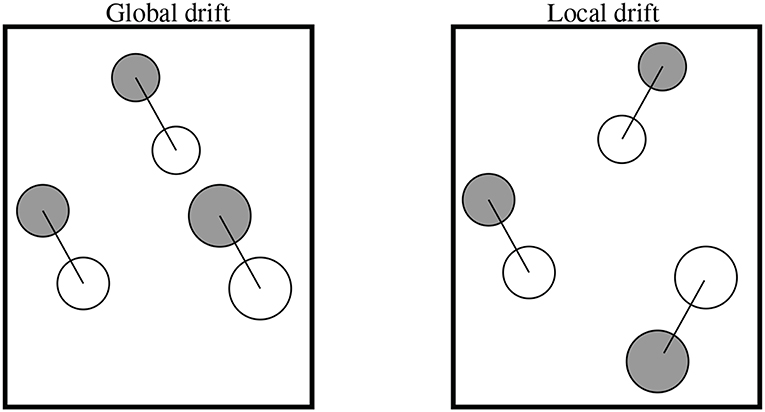
Figure 2. Global and local drift. Here the white bodies are the exact locations of the free-bodies, and the gray bodies are the approximated locations (which have drifted from their exact locations).

3. Case-Study

In this section we consider a specific case-study for studying the model's dynamics. Parameter values were selected on an arbitrary basis with K = 1 × 10⁻⁸ m/s², Δt = 60 s and (unless otherwise stated) the initial conditions and masses of the free-bodies are given by Table 1.

TABLE 1

Table 1. Parameter values used for the case study in this study.

Since $\tilde{G}$, and thus Ã, $\widehat{A}$, and $\widehat{A}$^*, are time-dependent (i.e., the network topology is constantly evolving as the free-bodies are displaced), these matrices must be recalculated in each time step. We refer to this calculation as the “network connectivity calculation” (NCC) hereafter. The computational load required to simulate the motion of free-bodies can be reduced by reducing the frequency of the NCC; however, this approach can introduce further errors. Therefore, in this case-study, we also examine the effect of reducing the frequency of the NCC by exploring cases where it is performed every 10 timesteps and every 100 timesteps, respectively.

3.1. Results

Figure 3 shows the error when the NCC is performed: every timestep (solid lines), every 10 timesteps (dashed lines), and every 100 timesteps (dashed-dotted lines) vs. (i) 1,000 timesteps, and (ii) 10,000 timesteps for: (a) K = 1 × 10⁻⁹ m/s², (b) K = 1 × 10⁻⁸ m/s², and (c) K = 1 × 10⁻⁷ m/s². We note from these examples that in general, the error increases with time. We note from Figures 3Aii,Bii,Cii how the error seems to be growing at an approximately linear rate over time, in these examples this linear rate of growth is caused by scenarios where the overall error term is dominated by one of the approximated free-bodies (${\tilde{P}}_i$ for some i) which is drifting away from its exactly calculated paired particle (P_i for the same i) at a much faster (linear) rate than any of the other free-bodies. We also note that the error is generally larger when the NCC is performed less frequently or when the threshold, K, is larger. Both of these behaviors are to be expected. When the NCC is performed in each timestep, acceleration effects can be erroneously ignored from free-bodies which were below the connectivity threshold at the time of the previous NCC but may have increased above the threshold since. Furthermore, when any acceleration affects are neglected in any timestep, more error is introduced into the system—larger values of K result in more acceleration effects being neglected in each timestep.

FIGURE 3

Figure 3. Error when the NCC is performed: every timestep (solid lines), every 10 timesteps (dashed lines), and every 100 timesteps (dashed-dotted lines) vs. (i) 1000 timesteps, and (ii) 10,000 timesteps for: (A) K = 1 × 10⁻⁹ m/s², (B) K = 1 × 10⁻⁸ m/s², and (C) K = 1 × 10⁻⁷ m/s².

However, sometimes the error can decrease (or remain static) with time. See for example Figures 3Ai,ii where the error trends upwards while oscillating. One of the potential causes for this oscillation is when an approximated particle takes the same trajectory as its exact paired-particle, however, it does so with some lag. Figure 4 illustrates how the error can oscillate across three different timesteps when particle drift is out of phase, i.e., $P_i^n={\tilde{P}}_i^{n+\tau }$ for some constant τ and free-body i. In this figure, the particle trajectory is denoted by dashed arc, the approximated free-body is denoted by the gray circle, and the exact free-body is denoted by the white circle. Even though the particles are taking the same trajectory, in timesteps 1 and 3 the error is much smaller than in timestep 2, due to the fact that the approximated free-body's motion lags behind the exact free-body's motion.

FIGURE 4

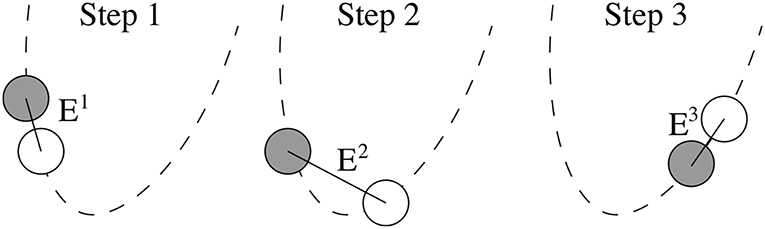
Figure 4. Error (magnitude of black line) across three different timesteps when particle drift is out of phase. Particle trajectory is denoted by the dashed arc, the approximated free-body is denoted by the gray circle, and the exact free body is denoted by white circle.

In this system, a free-body's dynamics are highly sensitive to changes in the initial conditions. Figure 5 demonstrates the inter-quartile range of the error when the NCC is performed: every timestep (red), every 10 timesteps (black), and every 100 timesteps (blue). Data for this figure was obtained via Monte-Carlo simulations (with 500 realizations) wherein each free-body's mass, initial position, and initial velocity, was multiplied by a random factor drawn from a uniform distribution in the range (a) [0.9, 1.1], and (b) [0.5, 1.5]. In both Figures 5A,B the inter-quartile range of the error grows at an approximately linear rate over time. Further to this, the inter-quartile range grows faster in Figure 5B than it does in Figure 5A, this further highlights the dependence of this system's dynamics on the boundary conditions—the system's dynamics variance increase as the variance of the boundary conditions increase. As one might expect, this figure demonstrates that when the NCC is performed more frequently, the error is generally lower. However, due to the underlying chaotic nature of systems of N interacting free-bodies, this is not always the case—see for example Figure 3Bii, where the model wherein the NCC is performed every 100 timesteps outperforms the model where this calculation is performed every timestep.

FIGURE 5

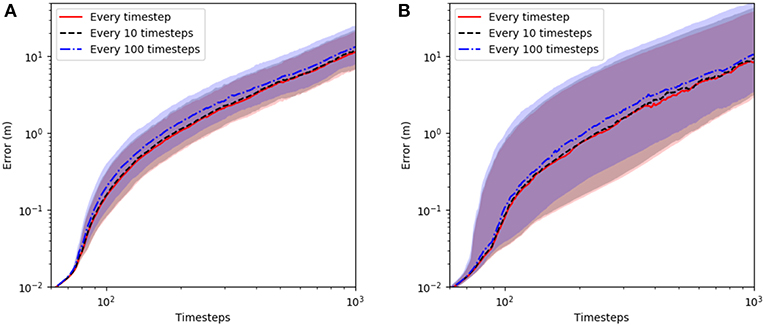
Figure 5. Inter-quartile range of error vs. time when the NCC is performed: every timestep (red), every 10 timesteps (black), and every 100 timesteps (blue). Data for this figure was obtained via two Monte-Carlo simulations which both had 500 realizations wherein the initial conditions: P¹, M¹, and V¹ were multiplied (element-wise) by a vector of random elements drawn from uniform distributions between (A) [0.9,1.1], and (B) [0.5,1.5].

4. Discussion

Ideas from bounded confidence theory can be applied to approximate the motion of free-bodies in a system of interacting free-bodies. While this modeling approach can reduce the computational load required to simulate the system of free-bodies, it also introduces error, and furthermore, this error generally increases with time. This study uses Newton's theory of universal gravitation as an example for demonstration purposes, however, the general framework presented here easily extends to other physical laws (such as Coulomb's law); one may replace the F_i,j term with an appropriate alternative force law to study the dynamics in such instances.

There is much scope for future research in this area of science. As mentioned in section 2.5, the error measurement in this study does not distinguish between global and local drift effects. Depending on the application, global drift may be an acceptable form of drift, in the future, we plan to explore alternative definitions of error and explore their effects. Further to this, there is much scope for additional mathematical analysis. In this study we provided arbitrary parameter values to demonstrate the model, further analysis may be used to explore better understand why and under which circumstances some parameter-value combinations lead to lower error values than other parameter-value combinations. Finally, we strongly believe that is it possible to develop the same approach to multibody systems where some particles form aggregates (up to a limited number of elementary particle) while the other do not aggregate. For all these there is already some research on development.

Data Availability

The datasets generated for this study can be found in the library available at reference [27].

Author Contributions

All authors listed have made a substantial, direct and intellectual contribution to the work, and approved it for publication.

Funding

This material is supported by the Science Foundation Ireland (SFI), by funding ID under Investigator Programme Grant No. SFI/15/IA/3074.

Conflict of Interest Statement

GO'K was employed by calculate.xyz Ltd.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

1. Sahini M, Sahimi M. Applications of Percolation Theory. CRC Press (2014).

Google Scholar

2. Fatt I. The Network Model of Porous Media. Society of Petroleum Engineers (1956).

PubMed Abstract | Google Scholar

3. Cusatis G, Bazant ZP, Cedolin L. Confinement-shear lattice CSL model for fracture propagation in concrete. Comput Methods Appl Mech Eng. (2006) 195:7154–71. doi: 10.1016/j.cma.2005.04.019

CrossRef Full Text | Google Scholar

4. Dassios I, Jivkov AP, Abu-Muharib A, James P. A mathematical model for plasticity and damage: a discrete calculus formulation. J Comput Appl Math. (2017) 312:27–38. doi: 10.1016/j.cam.2015.08.017

CrossRef Full Text | Google Scholar

5. Dassios I, O'Keeffe G, Jivkov AP. A mathematical model for elasticity using calculus on discrete manifolds. Math Methods Appl Sci. (2018) 41:9057–70. doi: 10.1002/mma.4892

CrossRef Full Text | Google Scholar

6. Griffiths DV, Mustoe GGW. Modelling of elastic continua using a grillage of structural elements based on discrete element concepts. Int J Numer Methods Eng. (2001) 50:1759–75. doi: 10.1002/nme.99

CrossRef Full Text | Google Scholar

7. Esqueda H, Herrera R, Botello S, Moreles MA. A geometric description of Discrete Exterior Calculus for general triangulations. arXiv:1802.01158. (2018). doi: 10.23967/j.rimni.2018.11.003

CrossRef Full Text | Google Scholar

8. Karihaloo BL, Shao PF, Xiao QZ. Lattice modelling of the failure of particle composites. Eng Fract Mech. (2003) 70:2385–406. doi: 10.1016/S0013-7944(03)00004-3

CrossRef Full Text | Google Scholar

9. Jivkov AP, Yates JR. Elastic behaviour of a regular lattice for meso-scale modelling of solids. Int J Solids Struct. (2012) 49:3089–99. doi: 10.1016/j.ijsolstr.2012.06.010

CrossRef Full Text | Google Scholar

10. Zhang M, Morrison CN, Jivkov AP. A meso-scale site-bond model for elasticity: theory and calibration. Mater Res Innovat. (2014) 18:982–6. doi: 10.1179/1432891714Z.000000000537

CrossRef Full Text | Google Scholar

11. Grady LJ, Polimeni JR. Discrete Calculus: Applied Analysis on Graphs for Computational Science. London: Springer (2010).

Google Scholar

12. Ekhtiari A, Dassios I, Liu M, Syron E. A novel approach to model a gas network. Appl Sci. (2019) 9:1024. doi: 10.3390/app9061047

CrossRef Full Text | Google Scholar

13. Dassios IK, Cuffe P, Keane A. Visualizing voltage relationships using the unity row summation and real valued properties of the FLG matrix. Electr Power Syst Res. (2016) 140:611–8. doi: 10.1016/j.epsr.2016.05.013

CrossRef Full Text | Google Scholar

14. Dassios I, Cuffe P, Keane A. Calculating nodal voltages using the admittance matrix spectrum of an electrical network. Mathematics. (2019) 7:106. doi: 10.3390/math7010106

CrossRef Full Text | Google Scholar

15. Dassios I. Analytic loss minimization: theoretical framework of a second order optimization method. Symmetry. (2019) 11:136.

Google Scholar

16. Cuffe P, Dassios I, Keane A. Analytic loss minimization: a proof. IEEE Trans Power Syst. (2016) 31:3322–23. doi: 10.1109/TPWRS.2015.2479408

CrossRef Full Text | Google Scholar

17. Chung FR, Graham FC. Spectral Graph Theory. Providence, RI: American Mathematical Society (1997).

Google Scholar

18. Bellettini G, Chermisi M. Novaga crystalline curvature flow of planar networks. Interfaces Free Bound. (2006) 8:481–521. doi: 10.4171/IFB/152

CrossRef Full Text | Google Scholar

19. Fried E, Morton E. Gurtin Gradient nano-scale polycrystalline elasticity: inter grain interactions and triple-junction conditions. J Mech Phys Solids. (2009) 57:1749–79. doi: 10.1016/j.jmps.2009.06.004

CrossRef Full Text | Google Scholar

20. Gurtin ME, Anand L. Nano-crystalline grain boundaries that slip and separate: a gradient theory that accounts for grain-boundary stress and conditions at a triple-junction. J Mech Phys Solids. (2008) 56:184–99. doi: 10.1016/j.jmps.2007.09.001

CrossRef Full Text | Google Scholar

21. Xiaofeng R, Wei J. A double bubble in a ternary system with inhibitory long range interaction. Arch Ration Mech Anal. (2013) 208:201–53. doi: 10.1007/s00205-012-0593-5

CrossRef Full Text | Google Scholar

22. Boutarfa B, Dassios I. A stability result for a network of two triple junctions on the plane. Math Methods Appl Sci. (2017) 40:6076–84. doi: 10.1002/mma.3767

CrossRef Full Text | Google Scholar

23. Dassios I. Stability of basic steady states of networks in bounded domains. Comput Math Appl. (2015) 70:2177–96. doi: 10.1016/j.camwa.2015.08.011

CrossRef Full Text | Google Scholar

24. Dassios I. Stability of bounded dynamical networks with symmetry. Symmetry. 10:121. doi: 10.3390/sym10040121

CrossRef Full Text | Google Scholar

25. Deffuant G, Neau D, Amblard F, Weisbuch G. Mixing beliefs among interacting agents. Adv Comp Syst. (2000) 3:87–98. doi: 10.1142/S0219525900000078

CrossRef Full Text | Google Scholar

26. Hunter JK. Asymptotic Analysis and Singular Perturbation Theory. Department of Mathematics, University of California at Davis (2004).

Google Scholar

27. O'Keeffe G, Dassios I. Software written for the publication: ideas from bounded confidence theory applied to dynamical networks of interacting free-bodies. (Version 1.0). Zenodo (2019). Available online at: http://doi.org/10.5281/zenodo.3359686

Google Scholar