Significant Instances in Motor Gestures of Different Songbird Species

The nervous system representation of a motor program is an open problem for most behaviors. In birdsong production, it has been proposed that some special temporal instances, linked to significant aspects of the motor gestures used to generate the song, are preferentially represented in the cortex. In this work, we compute these temporal instances for two species, and report which of them is better suited to test the proposed coding (as well as alternative models) against data.

Introduction

Behavior emerges from the interaction between a nervous system and a biomechanical body whose dynamics are complex and ruled by non-linear phenomena. For this reason, it is not trivial to unveil how the nervous system represents the motor program behind a given behavior. A particularly complex behavior is vocal communication, which in several species requires the coordination of many muscles in order to generate the rich variety of acoustic signals necessary to convey a message. Even in phylogenetically distant species such as humans and birds, it has been recognized that a wide variety of sounds can be achieved through the temporal coordination of simple motor instructions, or motor gestures. In the case of human speech, those are the object of study of articulatory phonology [1]. The coordination of very simple motor gestures controlling the tongue, lips, and jaw [2] is capable of accounting for the acoustic features that allow a message to be shared between humans. Recent work reports that reasonably simple somatotopic representations of these gestures can be found in cortical regions of the human brain [3]. In the case of the sounds generated by songbirds, it has also been reported that a variety of different acoustic signals can be generated by changing only the phase difference between simple gestures controlling the respiration and the configuration of the avian vocal organ [4]. Moreover, some subtle features of a sound's timbre have been directly associated with the dynamics exhibited by the biomechanics involved in its generation [5], relieving the nervous system from controlling a myriad of subtle instructions in order to produce a complex sound. This suggests that a complex and rich behavior can be decomposed into simpler motor instructions, whose simplicity might help to understand its representation coding at the level of the nervous system.

Songbirds are an optimal neuroethological model to study motor control. Singing behavior is easy to record, stereotyped, and stable throughout a bird's adult life. It emerges from a subtle interaction between a dedicated brain circuit and a biomechanical device. The outcome of the nervous system is a set of electrical signals that activate the muscles responsible for the time dependent configurations of the avian vocal organ and the respiratory system. A complex song typically consists of a sequence of sounds whose acoustic features evolve continuously in time. The time dependent physiological instructions necessary for the generation of those continuous segments are the motor gestures. The question then naturally arises: how are these motor gestures represented in the nervous system?

Unveiling how different parts of the nervous system code this rich behavior has proven to be a difficult task. Fee and collaborators proposed a model in a seminal work published in 2004 [6]. The analysis of the neural activity in a cortical nucleus of zebra finches (Taenopygia guttata) [7] led the authors to claim that a sequence of projecting neurons was activated continuously during the execution of the song. Each projecting neuron was active during approximately 10 ms, and the set of consecutively activated projecting neurons continuously spanned the duration of the song.

Amador and collaborators proposed an alternative view [8]. In that work, they recorded the neural activity of singing birds of the same species analyzed by Fee et al. The work was originally designed to study the neural response of sleeping birds to synthetic songs generated by a dynamical model. Therefore, the authors had a motor template in terms of which to interpret the temporal instances of the recorded neural activity for each syllable (defined as a segment of continuous sound flanked by silence). Moreover, they preferentially used birds with long syllables of constant pitch to enable a more accurate song synthesis. The neural recordings, in light of the motor gestures obtained by the biomechanical model, led to the claim that there was preferential neural activity at significant motor instances of the song, which they called gesture trajectory extrema (GTEs). A sound requiring complex motor instructions would be characterized by a large number of GTEs.

That work originated a series of replies [9–12]. A suggestive argument for the continuous representation hypothesis was that many neurons were measured in a large set of birds, which led the authors to claim that the neural activity was distributed continuously during the songs. None of those studies reported a bias toward birds with simple songs, although the somewhat simpler songs of juveniles were investigated in one of them [9].

In this work, we show that the GTE distribution in zebra finch song seems to continuously cover the duration of the song, and therefore, these two models cannot be easily disambiguated using this species. Another songbird species might be more suitable for this task. For this reason, we studied the song structure of a different songbird species, the domestic canary (Serinus canaria), which has longer and simpler syllables than the zebra finch. Here, we quantify these features and relate them to the GTEs. In this way, we suggest a way to distinguish between the two alternative models of neural coding by studying birds that produce syllables with specific acoustic features. One of the two models predicts a continuous neural representation of the motor patterns, regardless of the acoustic features of the songs. The second model predicts a sparser neural representation for simpler syllables (i.e., syllables with sparser GTEs).

Materials and Methods

Zebra Finch and Canary Song Structure

We randomly selected 20 zebra finch songs and 20 canary songs from our historical records. The birds were obtained from commercial breeders as adults within the last 10 years, with no familial relationship between them. They were recorded with a directional microphone from adult male birds (zebra finches and canaries) individually housed in a sound-isolation chamber. Food and water were provided ad libitum, in accordance with a protocol approved by the University of Buenos Aires (FCEN-UBA) Institutional Animal Care and Use Committee (CICUAL). The recordings were obtained using the software Avisoft—RECORDER (https://www.avisoft.com/recorder.htm). All sound files were filtered using Praat 6.0.04 software (http://www.fon.hum.uva.nl/praat/) to eliminate environment noise (pass Hann band from 200 Hz to half the sampling rate). This is the standard recording protocol in our laboratory.

Zebra finch song has a different structure than canary song (see examples in Figures 1A,B, respectively). A zebra finch song is composed of a repetition of motifs: M1, M2, M3 in Figure 1A. A motif is a sequence of syllables sung once in a stereotyped order, as shown in Figure 1C where each different letter indicates a syllable [13, 14]. Canary songs show a different organization. A phrase is formed by the repetition of a given syllable, and the song is composed of a sequence of different phrases. A representative example is shown in Figure 1B, indicating different phrases with different numbers: Ph1, Ph2, …, Ph6 [15, 16].

FIGURE 1

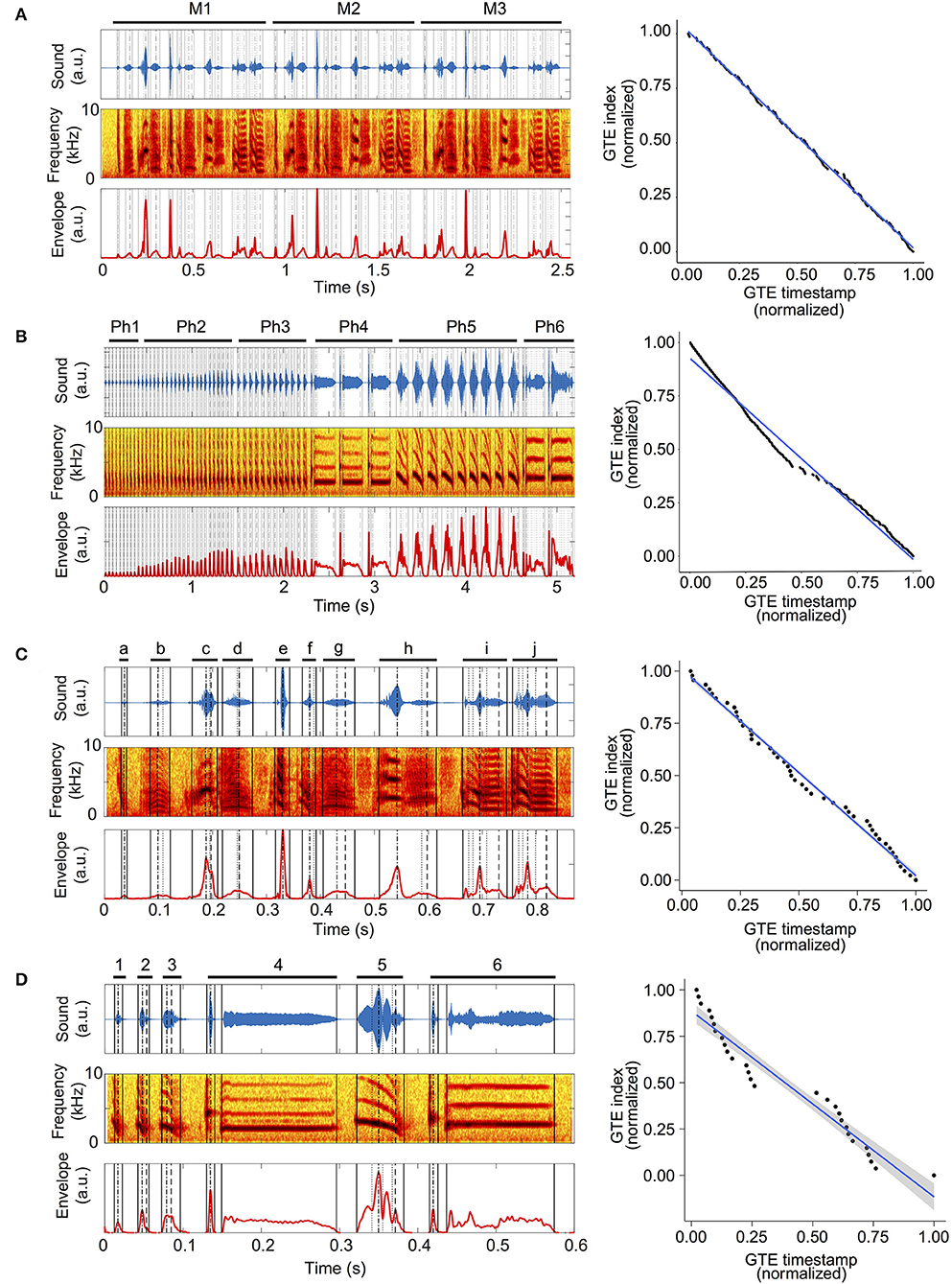
Figure 1. GTEs in zebra finch and canary songs. (A) Left top: sound of a zebra finch song. Labels M1–M3 and bars indicate a motif that is repeated three times during the song. Left middle: spectrogram of the song. Left bottom: envelope trace calculated from the sound in the left top panel. Vertical lines indicate the timestamps of the Gesture Trajectory Extrema (GTEs) calculated from the envelope trace: solid lines indicate onset and offset GTEs; dotted lines, minima; dashed-and-dotted lines, absolute maximum and dashed lines indicate last maximum. Right: normalized GTE position plots of the zebra finch song. The GTE timestamps in the song and the GTE indices are normalized. The blue line shows the best fit using ordinary least squares. The gray area corresponds to the 95% confidence interval (see Methods). (B) Left top: sound of a canary song. Labels Ph1–Ph6 and bars indicate repetitions of one syllable, also called phrases. Left middle, left bottom, and right panel as in (A). (C) Left top: sound of zebra finch motif M1 from (A). Letters a–j and bars indicate individual syllables. Left middle, left bottom, and right panel as in (A). (D) Left top: sound of a canary pseudo-motif. Letters a–f and bars indicate unique instances of the syllables in each phrase showed in (C). Left middle, left bottom, and right panel as in (A).

We compared the motifs in the songs of zebra finches to a construction of what we called pseudo-motifs of the songs of canaries. The pseudo-motifs have the same syllables in the same order as in the original canary song, but each syllable is repeated only once (Figure 1D). In other words, in the pseudo-motifs, the original phrases in the song are shortened to one repetition of each syllable. In this way, syllable “k” in Figure 1D (k = 1, …, 6) is a representative example of the syllables that compose the phrase Phk in Figure 1B. The silent gap between two syllables in a pseudo-motif corresponds to the gap between the original phrases.

Automatic Calculation of Gesture Trajectory Extrema (GTEs)

An automatic procedure for detecting GTEs was proposed by Boari et al. [17]. The key observation behind this procedure is that the transitions between the song segments with qualitatively different acoustic features are reflected as minima in the envelope of the songs. In this work, we used a similar approach to the one used in [17] to obtain the GTEs of the songs in two species and study them comparatively.

The envelope of the song was obtained as follows. First, we computed the Hilbert transform of the sound, obtaining a time trace s(t). Then, we smoothed s(t) by integration of the linear system:

$\begin{array}{l}\frac{dz}{dt}=-\frac{1}{\tau }z+s(t),\end{array}$

with τ = 1 ms. After this, we applied a Savitzky-Golay filter [18] (window size = 513 samples, 4th order of the smoothing polynomial). Finally, the obtained time trace was normalized with respect to the absolute maximum of the envelope, obtaining n(t). A five-point stencil derivation of the signal was computed and further filtered with a Savitzky-Golay filter (same parameters as before) to obtain d(t), representing a smoothed derivative function of the original sound.

Additionally, we obtained a time trace without artifacts in syllable beginnings and ends, by filtering s(t) using a moving window average (window size = 250 samples, that at 40 kHz correspond to 6.25 ms), both in the forward and reverse directions to avoid introducing spurious phase delays. We normalized the resulting time trace with respect to the absolute maximum of the envelope, obtaining a(t).

We used a(t) to compute syllable beginnings and ends. We set a threshold of 3% of the maximum value of a(t). A syllable onset was defined when the signal a(t) went over the threshold, and its offset when the signal went back under the threshold.

The intra-syllabic maxima and minima were computed analyzing sign changes in the smoothed derivative d(t). After calculating all the timestamps of the minima in d(t), we considered minima to be significant if their values in n(t) were at least 5% smaller than the maxima before and after. The absolute maximum and the last maximum in signal n(t) were considered significant regardless of their relative value.

For canaries, even though syllables of the same phrase are expected to have the same GTEs, occasionally, due to variations in song production, syllables of the same phrase have different GTEs. In those cases, we only considered the GTEs that were systematic for all the uttered syllables.

Using these definitions, we extracted GTEs from the sound which corresponded to beginnings and ends of syllables, significant minima (indicating the instances when gesture transitions within a syllable take place), and significant maxima (taken as proxies of maxima of the air sac pressure). The codes for implementing this procedure can be downloaded from http://www.lsd.df.uba.ar.

Normalized GTE Position Plots for a Song

To visualize the distribution of GTEs in a song, we plotted the GTE index normalized to the total number of GTEs in the song against the GTE timestamp normalized to the song duration. Then, the data was fitted using lm function from R (Version 3.5.3—https://www.r-project.org). Figure 1 shows examples of sound waves of different songs, their spectrogram and sound envelope, together with the associated GTEs (vertical lines). The corresponding normalized GTE position plot for each song is shown in the right panels of Figure 1.

Chi² Parameter

The Chi² parameter defined in this work was calculated from the normalized GTE position plots (right panels of Figures 1, 2A,B) using the following formula

$\begin{array}{l}Chi={\displaystyle \sum _{i=1}^n}\frac{(Ob{s}_i-Ex{p}_i)}{|Ex{p}_i|}.\frac{1}{n}\end{array}$

where n is the number of data points; Obs_i is the observed value of the normalized timestamp (x-axis value) of the GTE whose index value is i; Exp_i is the value of the normalized GTE timestamp (x-axis value in the normalized GTE position plots) that the line of best fit takes when the GTE index value is i. The Chi² parameter increases as the data points fall further away from the line of best fit.

FIGURE 2

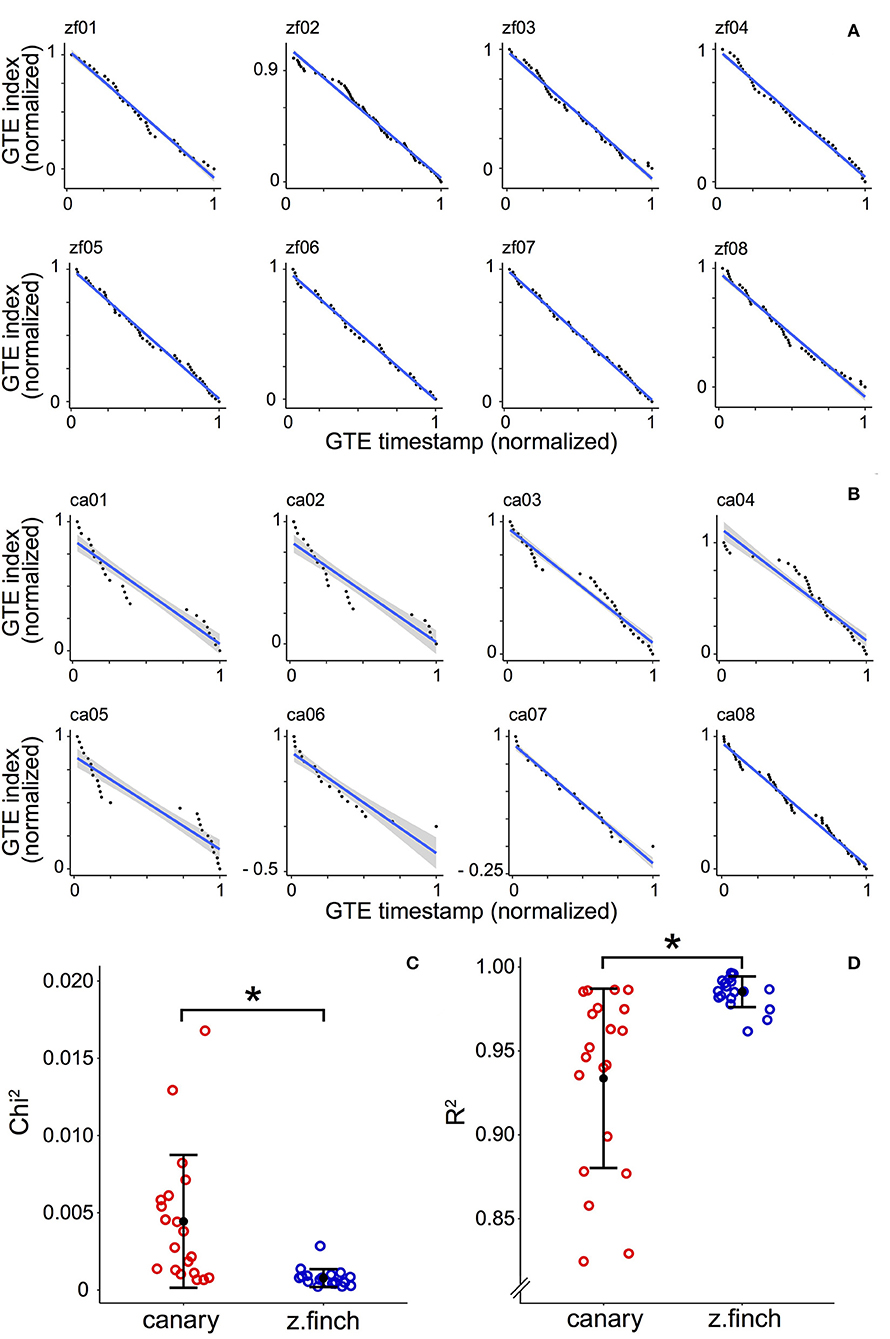
Figure 2. Normalized Gesture Trajectory Extrema (GTE) position plots for zebra finches and canaries. (A) Normalized GTE position plots for eight zebra finch motifs selected at random. The GTE timestamps in the motif and the GTE indices are normalized. The blue line shows the best fit using ordinary least squares. The gray area corresponds to the 95% confidence interval (see Methods). (B) Normalized GTE position plots for eight canary pseudo-motifs selected at random. Same analysis as in (A) of the 20 analyzed (the remaining 12 plots are shown in Supplementary Figure 2). (C) Each circle shows the Chi² value of the linear fit for one individual. Black dots represent the mean Chi² while error bars represent ± SD of the data. The average Chi² is 0.0044 ± 0.0043 (mean ± SD) for canaries (n = 20) and 0.0008 ± 0.0006 (mean ± SD) for zebra finches (n = 20). (D) Each circle shows the R² value of the linear fit for one individual. Black dots represent the mean R² while error bars represent ± SD of the data. The average R² is 0.93 ± 0.05 (mean ± SD, n = 20) for canaries and 0.99 ± 0.01 (mean ± SD, n = 20) for zebra finches. In (C,D) asterisks indicate that both distributions are statistically different (Kolmogorov-Smirnov test, p < 0.01).

Spectrogram Metrics of Syllables

Each song was segmented using Avisoft Bioacoustics SAS Lab Pro (Version 5.2.13—www.avisoft.com/) using automatic detection of waveform events with a threshold and hold time such that we obtained the same syllables as the automatic procedure for detecting GTEs. We sought to identify one salient syllable type that was long and simple in each species. The clearest to categorize were tonal whistles in the case of canaries (constant frequency, low energy in the harmonics) and harmonic stacks (constant frequency with high energy in distinct harmonics) for zebra finches. Two trained independent observers inspected all syllables and labeled harmonic stacks and whistles.

SAS Lab Pro was used to automatically calculate syllable duration, duration of a constant frequency segment within the syllable, and mean entropy of the syllable from the song spectrograms (shown in Figure 3). The spectrograms were computed with FFT length 512, frame size 100%, gauss window and a temporal overlap of 87.5% for all songs. To calculate the constant frequency segment duration, the tolerance was set to 300 Hz. For zebra finches, we found that the software sporadically detected peak frequencies in the high energy harmonics instead of at the fundamental frequency, and thus underestimated the constant frequency segment durations. In order to limit the detection of segments to low frequencies that included the fundamental frequency of harmonics stacks, we filtered the syllables in which the peak frequency during the whole syllable was <3.5 kHz in SAS Lab using the lowpass Frequency Domain Transformation with a cutoff at 3.5 kHz and re-ran the calculation of this metric.

FIGURE 3

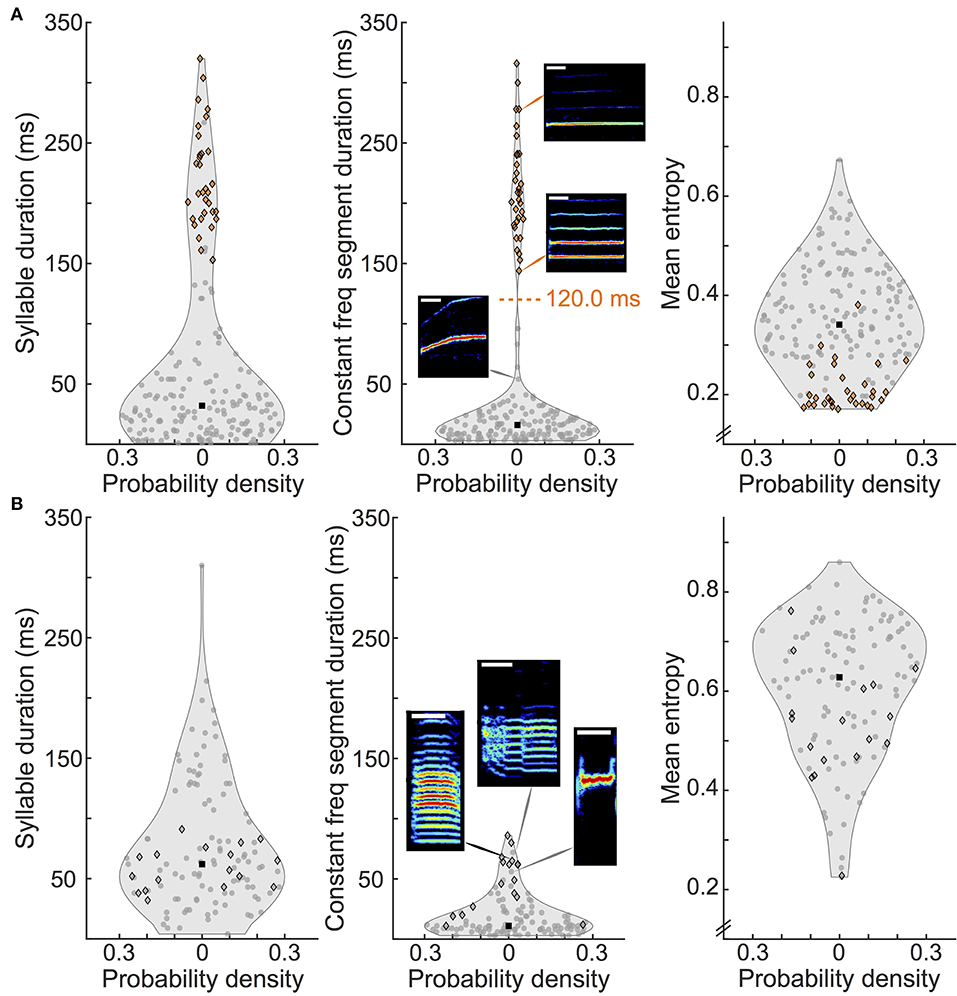
Figure 3. Distribution of spectrogram metrics of canary and zebra finch syllables. (A) Violin plots showing the distributions of syllable duration (left panel), duration of constant frequency segment (middle panel) and mean entropy (right panel) for canary syllables. The gray area represents the distribution density (symmetrically plotted on the x-axis) and its median is shown with a black square. One hundred and eighty seven canary syllables total, bin sizes are 30, 10, and 50 ms for each metric respectively. A scatter graph with the y-value of each individual syllable is overlaid on each distribution plot. Scatter points are orange if the syllable contains a constant frequency segment duration larger than the threshold value (120 ms) indicated with a dashed line in the middle panel, and gray otherwise. Syllables of a categorized type are outlined with a black diamond (whistles in canaries and harmonic stacks in zebra finches). Note that all syllables that surpass the threshold are whistles. Constant segment duration ranges from 3 to 96 ms and 144 to 316 ms. Spectrogram insets show example syllables (see text). Height of spectrograms is 10 kHz. White bar indicates 50 ms. (B) Same as in (A), for zebra finches, 119 syllables total and same bin sizes per metric. Constant segment duration range: 3–86 ms. Harmonic stacks are not isolated in any of the metrics analyzed.

The mean entropy ranges from close to zero for tonal signals and one for random noisy signals. We calculated the sample density probability estimates using the default probability density estimation in the ksdensity function from MathWorks Matlab (Version 2018a—www.mathworks.com) with appropriate bin size. For each metric, the bin size was determined as 10% of the metric's value range, and the minimum bin size of the two species was used for both species. This strategy allowed us to use the same bin size for each metric for both species.

Example and non-example bird syllable subgroups shown in Supplementary Figure 3 were tested for differences in the probability densities of each metric using the Kolmogorov-Smirnov test (kstest2 function in Matlab). Bin sizes for each metric were the same as those used for the complete sample in Figure 3.

Results

Motor Gesture Extrema in Birdsong

Motor gestures have previously been identified as the time dependent parameters of a dynamical system capable of synthesizing a realistic replica of the birdsong [4, 8, 19]. GTEs were defined in [8] as a measure of a song's complexity and consist of a set of temporal instances that include syllable beginnings, syllable endings, maxima of the parameter representing the air sac pressure used in the vocalization, and the discontinuities of the fundamental frequency during continuous vocalization (see Methods). The rationale behind defining GTEs is that many continuous acoustic features of a song occur between discrete (impulse-like) instructions, constituting significant temporal instances in the song. For example, the characteristic down-sweep syllables of a zebra finch (i.e., syllables with fundamental frequencies that decay as time evolves) are generated with a pulse like contraction of the syringealis ventralis muscle at the beginning of the vocalization. This pulse is passively transduced into a smooth stretching of the oscillating labia responsible for the sound [20]. In complex syllables that require using both sound sources, a discontinuity of the fundamental frequency can arise when the sound ceases to be generated by one of the two sound sources and starts to be generated by the other sound source. This requires the rapid alternating activation of gating muscles (e.g., [21, 22]).

In this work, we analyzed 40 songs from adult male birds: 20 from zebra finches and 20 from canaries (see Methods). We show an example of a zebra finch song in Figure 1A and one of a canary song in Figure 1B. The average duration of the canary songs was 14.65 ± 4.60 s (mean ± SD) while for zebra finches the song duration was 2.2 ± 1.4 s (mean ± SD), and their motifs lasted on average 0.67 ± 0.21 s (mean ± SD). An example of a zebra finch motif is shown in Figure 1C.

The songs of canaries and zebra finches both consist of sequences of continuous sounds called syllables, separated by brief silences. Yet they differ in two important ways. First, acoustic features within a syllable vary smoothly in canary song, while there can be abrupt changes in acoustic features within a zebra finch syllable. Second, the syntax is different. A canary will repeat a syllable several times, before switching to sing several copies of a different one. A canary song is built as a sequence of repeated syllables. A zebra finch song, however, consists of a succession of different syllables (a motif), which is sung repeatedly. We are interested in the first difference, at syllabic level, between zebra finch and canary song, since it suggests that syllable generation by each species might require a different degree of motor sophistication. For this reason, we constructed what we called pseudo-motifs for the canary songs. This allowed us to generate a song with structure similar to the zebra finch motif and compare syllable complexity. Briefly, the syllable repetitions present in canary songs were removed in the pseudo-motifs (example shown in Figure 1D). See Methods for a detailed description of the procedure. The average duration of canary pseudo-motifs was 0.99 ± 0.40 s (mean ± SD), which is comparable to zebra finch motif duration.

Using an adaptation of previously developed software [17], we extracted GTEs automatically from the song recordings. The left panels of Figure 1 show the resulting GTEs as vertical lines overlaid on the sound, spectrogram, and sound envelope of the zebra finch and canary songs. Note that in the syllables of the canary pseudo-motif in Figure 1D, only the GTEs that are systematic throughout the phrase remain. For example, the reported GTEs in syllable 6 are only those present in all syllables of Phrase 6 in Figure 1B. Our next step was to investigate the differences in the distribution of the GTEs of both species. In the rest of this article, we will refer to analyses performed on canary pseudo-motifs and true zebra finch motifs, unless stated otherwise.

GTE Distribution in Canaries Is More Heterogeneous Than in Zebra Finches

To visualize the distribution of GTEs in a song, we created the normalized GTE position plots (right panels in Figure 1). These show the normalized index of each GTE against its normalized timestamp, fitted to a linear model (see Methods). The right panel of Figure 1A shows that the zebra finch complete song closely follows the linear fit. However, the patterning of points around the line are repeated, because the stereotyped motif is repeated three times in the song. In the case of the complete canary song (Figure 1B), there is a large deviation from the linear fit, which makes the song seem more heterogeneous, but is exaggerated because it considers all the repeated syllables in each phrase. The corresponding analysis for one motif of the zebra finch song and one syllable per phrase of the canary song (pseudo-motif) are shown in the right panels of Figures 1C,D. To study differences between species at the syllabic level, we compared the distribution of GTEs in zebra finch motifs with the distribution of GTEs in canary pseudo-motifs.

In Figures 2A,B, we show eight examples of the GTE index distribution from each species (selected randomly, see Methods). The plots for the remaining 12 songs are shown in Supplementary Figures 1, 2. We calculated the Chi² parameter (see Methods) and the R² (coefficient of determination) from the normalized GTE position plots. The Chi² parameter takes larger values as data points fall further away from the line of best fit. We calculated the mean Chi² for every bird (Figure 2C) and obtained 0.0044 ± 0.0043 (mean ± SD) for canaries (n = 20) and 0.0008 ± 0.0006 (mean ± SD) for zebra finches (n = 20). A Kolmogorov-Smirnov test (KS test) showed that the distributions are statistically different (p < 0.01). A similar result was obtained for R² (KS test, p < 0.01). The average R² value for canaries was 0.93 ± 0.05 (mean ± SD) and for zebra finches it was 0.99 ± 0.01 (mean ± SD, see Figure 2D). All these results suggest that the GTE distribution in canary songs is more heterogeneous than in zebra finch songs. To further investigate the origin of this heterogeneity, we studied the acoustical properties of syllables and further analyzed the distribution of GTEs.

Spectrogram Metrics of Canary and Zebra Finch Syllables

To further quantify song characteristics and compare both species, we analyzed the distribution of three syllable metrics, including a temporal and a spectrum-based parameter. These metrics were syllable duration, duration of a constant frequency segment within the syllable, and mean entropy (Figure 3). We looked with particular attention at one salient type of syllables in each species: whistles in canaries and harmonic stacks in zebra finches (see Methods, black diamond outlined points in Figure 3). Song segmentation produced 187 syllables for canaries (from 20 pseudo-motifs) and 119 for zebra finches (from 20 motifs).

Canary syllable duration (Figure 3A, left panel) fell into two defined groups: syllables that ranged up to 100 ms (max 96 ms), including very short syllables (note the amount of points indicating syllables with duration below 10 ms), and long syllables that lasted from 121 to 320 ms. Within the group of longer syllables, whistles had durations from 153 to 320 ms and made up 74% of this group.

To investigate in further detail syllables that contained long and simple sounds, we calculated the duration of a constant frequency segment within the syllable (see Methods). The distribution of this metric in canaries (Figure 3A, middle panel) has a defined minimum at 120 ms, separating two groups. We treated this value as a threshold. All the syllables that contain a constant frequency segment above threshold (orange points) were whistles (black diamond outline) and correspond to percentile 82.9. This shows that this metric is suitable for separating long simple syllables such as whistles. The constant frequency segment duration of the syllables above threshold ranged from 144 to 316 ms, whereas the rest of the syllables were in the range of 3–96 ms.

Examples of simple syllable spectrograms are shown as insets in the middle panel of Figure 3A. The supra-threshold, more tonal syllables are characterized in the top two insets: long whistle of a single fundamental frequency (other examples in Figure 1D, syllables 4 and 6). Other syllables that contained a mid-range constant frequency segment duration were made up of an upward or downward sweep as well as a tone and are usually shorter in length (bottom inset example of subthreshold syllable).

In the right panel of Figure 3A, we show the distribution of the entropy of canary syllables. The black dot indicates the median value of 0.34. Note that the canary whistle syllables take the lowest of the entropy values. Even though they ranged from 0.17 to 0.38, we found that the median of only the whistles was 0.19 (not shown in plot).

In the case of zebra finches, syllable duration was less widespread (see Figure 3B, left panel). Syllables lasted from 4 to 310 ms (note that the largest value is an outlier and that the second largest is 214 ms), with a median of 62 ms. Harmonic stacks are outlined with a black diamond. Their durations ranged from 32 to 91 ms, which is around the median value.

The middle panel of Figure 3B shows that constant frequency segments do occur in zebra finches (in the tail of the distribution), but they are shorter than those in canaries: their maximum value was 86 ms. This distribution did not present a well-defined feature that would allow us to naturally set a threshold. Harmonic stacks tend to have longer constant frequency segments but do not dominate the tail. However, almost all harmonic stacks surpassed the median value of the syllables which is 11 ms. They range from 11 to 86 ms and the median of only the harmonic stacks is 49 ms (not shown in plot). Examples of syllables from the tail of the distribution are shown in the insets of Figure 3B, middle panel. These include canonical harmonic stacks such as the one shown in the left inset, and syllables not classified as harmonic stacks: in the middle inset we show a syllable with two abrupt transitions containing two segments with harmonic stacks and in the right inset, one which is a short high frequency tone.

In terms of entropy, zebra finches tend to produce syllables of higher entropy than canaries (median 0.63 and ranging from 0.23 to 0.86, see right panel of Figure 3B). This agrees with the fact that their song is characteristically “noisier” than canary song. Harmonic stacks do not cluster in this metric as canary whistles do, since they have a wider entropy range and more variation in values (from 0.23 to 0.76). All but three of the harmonic stacks had an entropy value less than the median, which points out that they are not typically noisy syllables nor completely flat.

In summary, there is no equivalent long and simple syllable for the canary whistle in the zebra finch songs we analyzed. The syllable type we considered as a candidate were harmonic stacks, but not only do they fall short of the length of the canary whistles, they also do not emerge as an isolated group within this set of metrics.

Time Differences Between Consecutive GTEs

To further analyze the GTEs distribution, we analyzed the time difference between consecutive GTEs (20 canary pseudo-motifs, 505 GTE time intervals and 20 zebra finch motifs, 637 GTE time intervals). The silent gaps between syllables were not considered. The time difference between consecutive GTEs for each bird is shown in Figure 4A, using red markers for canaries and blue markers for zebra finches. In the canary distribution, all birds have at least one large time difference. We identified the largest time differences (belonging to the 95th percentile, larger than 173 ms) in canaries (red filled markers) and found all these are from whistle syllables (diamond markers). Note that the largest GTE time difference in zebra finches was 76 ms, while in canaries it was 330 ms.

FIGURE 4

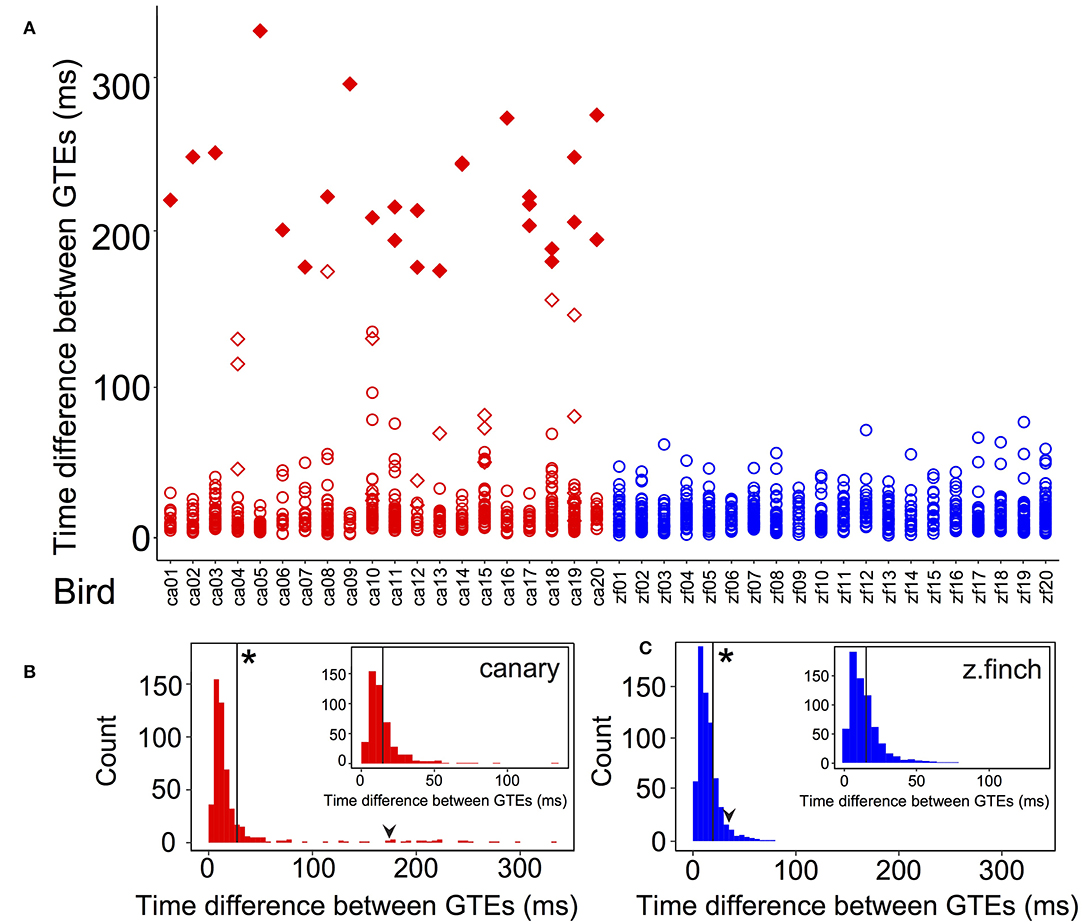
Figure 4. Time differences between GTEs of each bird and grouped by species. (A) Time differences between GTEs for canaries (red markers) and zebra finches (blue markers). In canaries, diamonds indicate that the time difference belongs to a whistle syllable. Note that every canary has at least one diamond. The largest time differences of the canary distribution (in the 95th percentile, larger than 173 ms) are indicated with filled markers. Every time difference included in this group was from a whistle. (B) Histogram (5 ms bins) of time differences between consecutive GTEs in canaries and (C) in zebra finches. The black arrowheads show the value of the 95th percentile of each distribution (173 ms for canaries and 35 ms for zebra finches). The vertical black lines show the value of the mean of each distribution: 28.0 ± 2.2 ms (mean ± SEM) for canaries (n = 505) and 15.1 ± 0.4 ms (mean ± SEM) for zebra finches (n = 637). Asterisks in (B,C) indicate that these means were significantly different (t-test, p < 0.01). In canaries, the longest GTE time interval was 330 ms while in finches it was 76 ms. The standard deviation was 50.2 ms (n = 505) in canaries and 10.5 ms (n = 637) in zebra finches. These were significantly different (Levene test centering with the median, p < 0.05). (Inset B) Histogram (5 ms bins) of time differences between consecutive GTEs in canaries discarding those from whistle syllables. (Inset C) Zebra finch distribution of time differences as in (C), at the same scale as (Inset B) for comparison. The vertical black lines in the insets show the mean of each distribution. For the new canary distribution, the value was 14.7 ± 0.6 ms (mean ± SEM, n = 472). The value for zebra finches is unchanged from (C). In the new canary distribution, the standard deviation was 12.4 ms and the longest GTE time interval was 134 ms. The new canary mean and standard deviation were not significantly different from those of zebra finches (t-test, p > 0.5 and Levene test, p > 0.5).

The distribution of time differences between consecutive GTEs is shown in Figure 4B for canaries and in Figure 4C for zebra finches. For both species, the mean time difference between consecutive GTEs is marked by solid vertical lines. For canaries, the mean was 28.0 ± 2.2 ms (mean ± SEM) and for zebra finches, it was 15.1 ± 0.4 ms (mean ± SEM). The values of the means are significantly different (t-test, p < 0.01). The larger value for canaries is due to the long tail in the distribution of time differences between GTEs. The 95th percentile is indicated in both distributions with black arrowheads (173 ms for canaries and 35 ms for zebra finches). It is worth mentioning that the median values were similar for both species: 12.2 ms for zebra finches and 12.6 ms for canaries. The standard deviation was 50.2 ms (n = 505) for canaries and for zebra finches it was 10.5 ms (n = 637). The standard deviations of the time difference distribution of the two species were significantly different (Levene test centering with the median, p < 0.05). These significant differences between the means and the standard deviations of the two species indicate that the distributions of GTE time intervals are more heterogeneous in canaries than in zebra finches.

We hypothesized that the difference between distributions was driven by the time differences from whistle notes in canaries. To test this hypothesis, we discarded all intervals that belonged to whistle syllables in canaries, i.e., we removed the values shown as diamonds in Figure 4A from the distribution of canary time differences. The mean of this new distribution was 14.7 ± 0.6 ms (mean ± SEM, n = 472), and the standard deviation was 12.4 ms (n = 472). The histogram of the new distribution is shown in the inset of Figure 4B. We did not modify the distribution of zebra finch time differences, but it is plotted with the same range in the inset of Figure 4C for comparison. In contrast with the previous comparison, the mean and the standard deviation of the modified canary distribution were not significantly different to the zebra finch unmodified distribution (t-test, p > 0.5 and Levene test centering with median, p > 0.5). This result shows that the difference between distributions were mainly driven by the canary whistle syllables.

Discussion

The study of animal behavior requires contributions from many disciplines. An animal's nervous system acts upon its environment through a biomechanical device. Therefore, neural coding is best understood in the context of the specific motor instructions needed to control this device. In the case of birdsong, the control of the avian vocal organ and the respiratory system can be described in terms of continuous time dependent parameters called motor gestures. Complex songs imply a succession of different motor gestures, and the distribution of the instances known as GTEs is an indication of the complexity of the song. In this work, we studied the distribution of these significant temporal instances in the song of two species.

In this work, we show that the distribution of time differences between GTEs was significantly different between the compared species: canaries have long intervals between GTEs that occur mostly during their characteristic whistle syllables. We analyzed the acoustical properties of all syllables and found that canary whistles can be easily discriminated from other syllables by their long segments of constant frequency. In contrast, the distribution constant frequency segments in zebra finch syllables reaches a smaller value and does not contain two separate groups.

Birdsong requires the control of the respiration and of the syringeal configuration, which both affect acoustic features such as the song's fundamental frequency. The acoustic features of some simple syllables emerge from the interaction of a biomechanical process with brief interventions of the nervous system. As previously noted for zebra finches, it has been recently shown that some syllables only require impulsive activity in a syringeal muscle right before the onset of the sound and that the passive posterior relaxation of the labia is wholly responsible for the slow decay of the syllable's fundamental frequency [20]. Therefore, it is sensible to ask whether this simplicity in the muscle control of the biomechanical device requires simple instructions from the nervous system.

In the field of birdsong, it is debated whether telencephalic regions display a continuous code for the song, or a sparser code that reflects the song's structure. The original claim by Amador and collaborators that projecting neurons in the cortical nucleus HVC spike mostly at specific temporal instances (GTEs) falls into the latter alternative [8]. In 2015, this claim was refuted by Okubo and collaborators, since they found that neuronal bursts in HVC spanned almost the complete duration of the song [9]. However, their description of the ontogenesis of the song reveals that the heterogeneity of gestures does leave a fingerprint in the mature cortical activity. Studying the songs of juvenile zebra finches, the authors found that close to 50% of the recorded neurons were active only at the beginning of the simple syllables that the juveniles uttered. As the birds developed, they started to sing complex syllables that were different simple proto-syllables joined together. For those syllables, the projecting neurons in HVC kept their relative timing with respect to the song and, therefore, the temporal instances at which there were changes in the acoustics remained coded in the timing of the HVC-projecting neurons. As the birds continued to develop more complex songs, neuronal activity covered the duration of the song almost continuously. Given that developmental processes leave their fingerprint as a temporal heterogeneity in the cortical coding, our comparative study of the complexity of the motor gestures between two species allows us to identify a more suitable species to disambiguate between a heterogeneous, motor related, coding and a continuous one.

Recently, a neural model of the song system capable of reproducing the pressure and syringeal gestures of canaries during song production, incorporated a sparse activity pattern in HVC mounted on a continuous component [23]. Having a model is useful because it not only integrates anatomical and functional data, but also helps to understand plausible dynamical mechanisms behind the observed behavior. A puzzling aspect of observing cortical activity simultaneous with a temporally significant instance of the song (like a GTE) is that, intuitively, a delay between causally connected parts of the nervous system is expected. Yet, in the mentioned study of juvenile songs [9], neurons in HVC were found bursting simultaneously with the beginning of syllables. In recent work [24], a model with continuous and sparse HVC coding describes the way in which causally connected regions of the song system can display activity simultaneous with the output of the nervous system, after a brief introductory transient. This makes it possible to predict, for example, an important increase of neural activity in the population of projection neurons at the beginning of the whistle syllables in canary song [23, 25]. Given the existence of large time differences between GTEs in the whistle syllables quantified in this work, we provide a specific and testable prediction.

We generated a visual representation of GTEs as a function of time similar to the way in which the neural activity in the HVC nucleus of zebra finches has been presented in the literature. We showed that, for the case of zebra finches, it is very difficult to distinguish between the representation that would be obtained if the coding were continuous from one produced by sparse coding. On the contrary, the whistle syllables of domestic canaries make it a suitable animal model to discriminate between a continuous and mostly uniform coding, and one where the fingerprints of the motor gestures are present. In the spirit of neuroethology, which studies behavior in the species that better displays it, we compared the distribution of GTEs in zebra finches and canaries and identified canaries as the species in which is it possible to discriminate between alternative models of cortical coding.

Data Availability Statement

Datasets are available on request. The raw data supporting the conclusions of this manuscript will be made available by the authors, without undue reservation, to any qualified researcher.

Ethics Statement

Experimentation was conducted following protocols approved by the Institutional Animal Care and Use Committee (IACUC) of the University of Buenos Aires (FCEN, UBA).

Author Contributions

GM and AA conceived and designed the experiments. JL and AA performed the experiments. JL, CH, AA, and GM analyzed the data and wrote the manuscript.

Funding

This work describes research partially funded by Consejo Nacional de Investigaciones Científicas y Técnicas (CONICET, Argentina), Agencia Nacional de Promoción Científica y Tecnológica (ANCyT, Argentina), Universidad de Buenos Aires (UBA, Argentina).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

We also wish to thank all the members of the Laboratorio de Sistemas Dinámicos (DF, FCEN, UBA, Argentina) for comments and discussions.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2019.00142/full#supplementary-material

References

1. Goldstein L. Temporal patterning in speech and birdsong. In: Bowern C, Horn L, Zanuttini R, editors. On Looking Into Words (and Beyond): Structures, Relations, Analyses. Berlin: Language Science Press (2017). p. 457–70.

Google Scholar

2. Assaneo MF, Ramirez Butavand D, Trevisan MA, Mindlin GB. Discrete anatomical coordinates for speech production and synthesis. Front Commun. (2019) 4:13. doi: 10.3389/fcomm.2019.00013

CrossRef Full Text | Google Scholar

3. Bouchard KE, Mesgarani N, Johnson K, Chang EF. Functional organization of human sensorimotor cortex for speech articulation. Nature. (2013) 495:327–32. doi: 10.1038/nature11911

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Gardner T, Cecchi G, Magnasco M, Laje R, Mindlin GB. Simple motor gestures for birdsongs. Phys Rev Lett. (2001) 87:208101. doi: 10.1103/PhysRevLett.87.208101

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Amador A, Mindlin GB. Beyond harmonic sounds in a simple model for birdsong production. Chaos. (2008) 18:043123. doi: 10.1063/1.3041023

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Fee MS, Kozhevnikov AA, Hahnloser RHR. Neural mechanisms of vocal sequence generation in the songbird. Ann N Y Acad Sci. (2004) 1016:153–170. doi: 10.1196/annals.1298.022

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Hahnloser RHR, Kozhevnikov AA, Fee MS. An ultra-sparse code underlies the generation of neural sequences in a songbird. Nature. (2002) 419:65–70. doi: 10.1038/nature00974

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Amador A, Perl YS, Mindlin GB, Margoliash D. Elemental gesture dynamics are encoded by song premotor cortical neurons. Nature. (2013) 495:59–64. doi: 10.1038/nature11967

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Okubo TS, Mackevicius EL, Payne HL, Lynch GF, Fee MS. Growth and splitting of neural sequences in songbird vocal development. Nature. (2015) 528:352–7. doi: 10.1038/nature15741

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Picardo MA, Merel J, Katlowitz KA, Vallentin D, Okobi DE, Benezra SE, et al. Population-level representation of a temporal sequence underlying song production in the zebra finch. Neuron. (2016) 90:866–76. doi: 10.1016/j.neuron.2016.02.016

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Lynch GF, Okubo TS, Hanuschkin A, Hahnloser RHR, Fee MS. Rhythmic continuous-time coding in the songbird analog of vocal motor cortex. Neuron. (2016) 90:877–92. doi: 10.1016/j.neuron.2016.04.021

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Katlowitz KA, Picardo MA, Long MA. Stable sequential activity underlying the maintenance of a precisely executed skilled behavior. Neuron. (2018) 98:1133–40.e3. doi: 10.1016/j.neuron.2018.05.017

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Sossinka R, Böhner J. Song types in the zebra finch Poephila guttata castanotis. Z Tierpsychol. (1980) 53:123–32. doi: 10.1111/j.1439-0310.1980.tb01044.x

CrossRef Full Text | Google Scholar

14. Konishi M. Birdsong: from behavior to neuron. Annu Rev Neurosci. (1985) 8:125–70. doi: 10.1146/annurev.ne.08.030185.001013

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Nottebohm F, Stokes TM, Leonard CM. Central control of song in the canary, Serinus canarius. J Comp Neurol. (1976) 165:457–86. doi: 10.1002/cne.901650405

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Hartley RS, Suthers RA. Airflow and pressure during canary song: direct evidence for mini-breaths. J Comp Physiol. (1989) 165:15–26. doi: 10.1007/BF00613795

CrossRef Full Text | Google Scholar

17. Boari S, Sanz Perl Y, Amador A, Margoliash D, Mindlin GB. Automatic reconstruction of physiological gestures used in a model of birdsong production. J Neurophysiol. (2015) 114:2912–22. doi: 10.1152/jn.00385.2015

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Ziegel E, Press W, Flannery B, Teukolsky S, Vetterling W. Numerical Recipes: The Art of Scientific Computing. 3rd ed. Cambridge: Cambridge University Press (2007).

Google Scholar

19. Perl YS, Arneodo EM, Amador A, Goller F, Mindlin GB. Reconstruction of physiological instructions from zebra finch song. Phys Rev E Stat Nonlin Soft Matter Phys. (2011) 84:051909. doi: 10.1103/PhysRevE.84.051909

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Döppler JF, Bush A, Amador A, Goller F, Mindlin GB. Gating related activity in a syringeal muscle allows the reconstruction of zebra finches songs. Chaos. (2018) 28:75517. doi: 10.1063/1.5024377

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Goller F, Suthers RA. Role of syringeal muscles in gating airflow and sound production in singing brown thrashers. J Neurophysiol. (1996) 75:867–76. doi: 10.1152/jn.1996.75.2.867

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Suthers RA, Vallet E, Tanvez A, Kreutzer M. Bilateral song production in domestic canaries. J Neurobiol. (2004) 60:381–93. doi: 10.1002/neu.20040

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Alonso RG, Amador A, Mindlin GB. An integrated model for motor control of song in Serinus canaria. J Physiol. (2016) 110:127–39. doi: 10.1016/j.jphysparis.2016.12.003

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Dima GC, Copelli M, Mindlin GB. Anticipated synchronization and zero-lag phases in population neural models. Int J Bifurc Chaos. (2018) 28:1830025. doi: 10.1142/S0218127418300252

CrossRef Full Text | Google Scholar

25. Alonso RG, Trevisan MA, Amador A, Goller F, Mindlin GB. A circular model for song motor control in Serinus canaria. Front Comput Neurosci. (2015) 9:41. doi: 10.3389/fncom.2015.00041

PubMed Abstract | CrossRef Full Text | Google Scholar