Single Electron Memory Effect Using Random Telegraph Signals at Room Temperature

We show a manipulation of a single electron at room temperature by controlling Random Telegraph Signals (RTSs) by voltage pulses. Our silicon nanowire triple-gate transistor exhibited RTSs when potential barriers were electrically created by two of the three gates. From the statistics of the signals, we optimized the voltage pulse such that a single electron was intentionally captured in the potential well, and the retention time of approximately 10 ms was observed in this memory operation. This study indicates that a single electron effect can be controllable in a form of RTSs at room temperature by electrically defining a potential well.

1. Introduction

As the size of complementary-metal-oxide-semiconductor (CMOS) field-effect-transistor (FET) approaches to an atomic scale, various quantum mechanical effects become more apparent [1–8]. One example is the gate-leakage current due to quantum mechanical tunneling through gate oxide in a MOSFET, which increases the stand-by power of the system [6, 9]. The effect of inversion layer capacitance due to quantum confinement is also prominent, which decreases the total capacitance of a MOSFET, leading to the reduction of the device's transconductance [4, 5, 7]. Another example is random telegraph signals (RTSs). RTSs are considered to be caused by a trapping and detrapping of a single electron in a defect state, inducing undesired current fluctuation [10–13]. Noise introduced by RTSs, random telegraph noise (RTN), is one of the most extensively investigated reliability issues in state-of-art CMOS devices [8]. First observed in 1984 [8, 10], RTSs have been observed in MOSFETs [11, 12, 14, 15], static random access memory (SRAM) [16, 17], resistive random access memory (ReRAM) [18–25], and flash memory devices [26–33]. Overall, quantum mechanical effects were considered to be an obstacle for the silicon (Si) industry due to their negative impacts on the operation of CMOS circuits.

However, as the merit of quantum computations started to be recognized [34–37], a possibility of employing such quantum effects in Si device for a quantum bit (qubit) application is being actively sought by research groups [38, 39]. In order to implement a qubit in a solid state device, an isolated energy level that can contain a single electron must be embedded in a host material. Si is, in fact, an ideal material to host a spin qubit, since the spin-orbit coupling in Si is weak and thus a long coherence time is expected [40]. The presence of RTSs also indicates that there is an isolated energy level in a device that can accommodate a single electron [8]. Indeed, an electron spin resonance (ESR) signal was detected in a Si MOSFET that exhibited a RTS [41, 42]. From the observed g-factor, a single electron in a trap state was identified to cause the resonance. This indicates that an electron in a trap state responsible for a RTS can behave quantum mechanically, and thus such a trap state could potentially be used as a qubit [41, 42]. Nowadays, the importance of RTSs is highly recognized in the context of the reliability of CMOS circuits [8] as well as the future quantum computation [41–44].

In order to study RTSs, finding a device that exhibits RTSs is necessary. However, because such trap states are usually undesired and engineered away in device fabrication processes, identifying a device with RTSs requires a significant amount of measurement time [8]. Statistically large number of devices (around 10⁴) needed to be investigated in order to find a device with RTSs [8, 11]. A systematic method to find RTSs in a single CMOS transistor at low temperature (2K) was proposed, though it still requires a highly accurate current-voltage (I–V) measurement with a long integration time [45].

2. Device Fabrication

A 2D schematic of our device and a scanning electron microscope (SEM) image are shown in Figures 1A,B, respectively [46]. Our Si nanowire transistor was fabricated at the Southampton Nanofabrication Facility on a Si-on-insulator (SOI) wafer with 145 nm-thick buried oxide (BOX). A 3D schematic of the device is shown in Figure 1A. Firstly, the nanowire (NW) was defined by electron-beam (e-beam) lithography and anisotropic wet etching, allowing the sidewalls of the nanowire to be flattened at an atomic level [(111) surface]. The thickness of SOI was 10 nm after the patterning of NW. 17.6 nm oxide was grown on top of Si NW by dry oxidation at 1,000°C, resulting in the nanowire width of 30 nm. polycrystalline Si (poly-Si) was deposited by low-pressure-chemical-vapor-deposition (LPCVD). Phosphorous dopants were heavily doped on poly-Si by spin-on-dopant (SOD) technique, followed by the rapid-thermal-annealing activation at 950°C. Two FGs (FG1 and FG2) were then defined by e-beam lithography and inductively-coupled-plasma (ICP) etching. The lengths of FG1 and FG2 (L_FG) are both 75 nm. Interlayer dielectric of 9 nm was thermally grown on FGs before defining TG, where the same patterning technique was used in the definition of FG. TG covers the entire nanowire and the two FGs. The length of TG (L_TG) is 125 nm. Standard aluminum (Al) process was used for metal interconnect. Finally, annealing in forming gas in 450°C was performed in an effort to terminate interface traps.

FIGURE 1

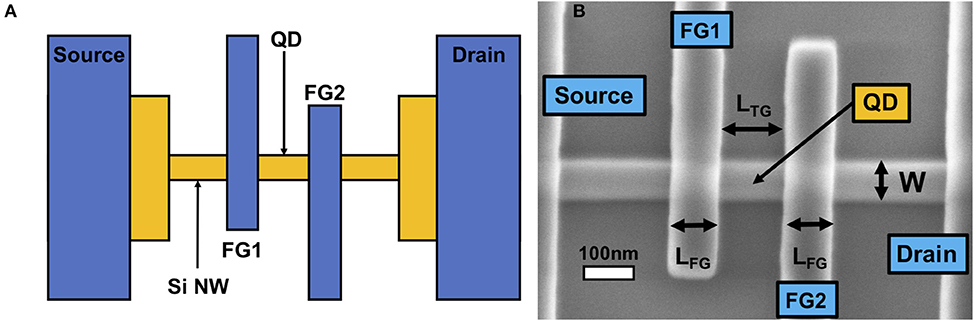
Figure 1. Device schematics of the silicon nanowire transistor. (A) A 2D graphic of the nanowire transistor. TG is not shown to clarify the structure [46]. (B) A SEM image of the device before poly-Si deposition for TG. A quantum dot (QD) is electrically defined by inverting the entire channel by TG with V_FG being 0 V.

3. Results

3.1. RTS Characterization for the Pulse Design

All the experiments at room temperature were performed with a Cascade M150 probe station and a Keysight B1500A Semiconductor Device Analyser. Figure 2A and its inset show the transfer characteristics of the device, in linear scale and log scale, respectively [46]. The length of the NW of our transistor is 2 μm, and it should be operational as a simple NW transistor when FGs are fully turned on. When V_FG was set to 1.4 V, our NW transistor presented an ideal transfer characteristic, exhibiting a linear increase after threshold voltage (V_th) (Figure 2A) as well as a steep subthreshold slope of 68 mV/decade (Figure 2A inset), approaching the theoretical limit of 60 mV/decade [9]. Then, V_FG was decreased from 1.4 to −1.4 V in 200 mV decrements. Degradation of SS and positive shift of threshold voltage are seen in Figure 2A inset. This can be attributed to the short channel effect of FG transistors. The output characteristics were evaluated with different V_TG values, from 0.5 to 1 V, and the saturation was observed in all V_TG values (Figure 2B). We also observed current fluctuations and its dependence on V_TG. The impact of noise became more prominent as V_TG increased, and its behavior was not systematically controlled by V_D.

FIGURE 2

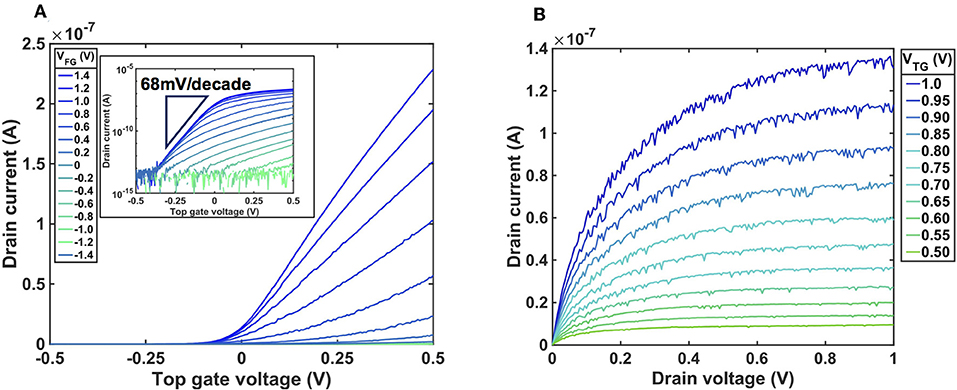
Figure 2. Transistor characteristics of the silicon nanowire transistor. (A) The transfer characteristics of the device when V_TG was swept from −0.5 to 0.5 V, shown in linear scale. V_FG was varied from 1.4 to −1.4 V in 200 mV decrements. The inset shows the same characteristic in log scale. V_D was 50 mV. (B) The output characteristics of the device when V_D was swept from 0 to 1.0 V, while V_FG was 0 V and V_TG was varied from 0.5 to 1.0 V in 50 mV increments.

Then, time domain measurements were carried out in order to investigate this current fluctuation [45, 46]. V_FG was fixed to 0 V, while V_TG was varied from 0.5 to 2 V in 100 mV increments. V_D was set to 200 mV to observe the fluctuation, while maintaining thermal equilibrium [9]. I_D was monitored with a sampling rate of 20 kHz for 1 s. In Figures 3A–D, the examples of time domain characteristics are shown. Two discrete current levels are seen in Figures 3A–D, noted as high and low, which are typical RTSs. When V_TG was set to 0.7 V, the high state was the favored current state (Figure 3D). As V_TG increased up to 1.1 V (Figure 3C), the low current state was observed more often. Further increase of V_TG led to fewer observations of the high current state, and the low current state was predominantly observed (Figures 3A,B). This reveals that the current fluctuation seen in Figure 2B was RTSs and V_TG controlled its dependence.

FIGURE 3

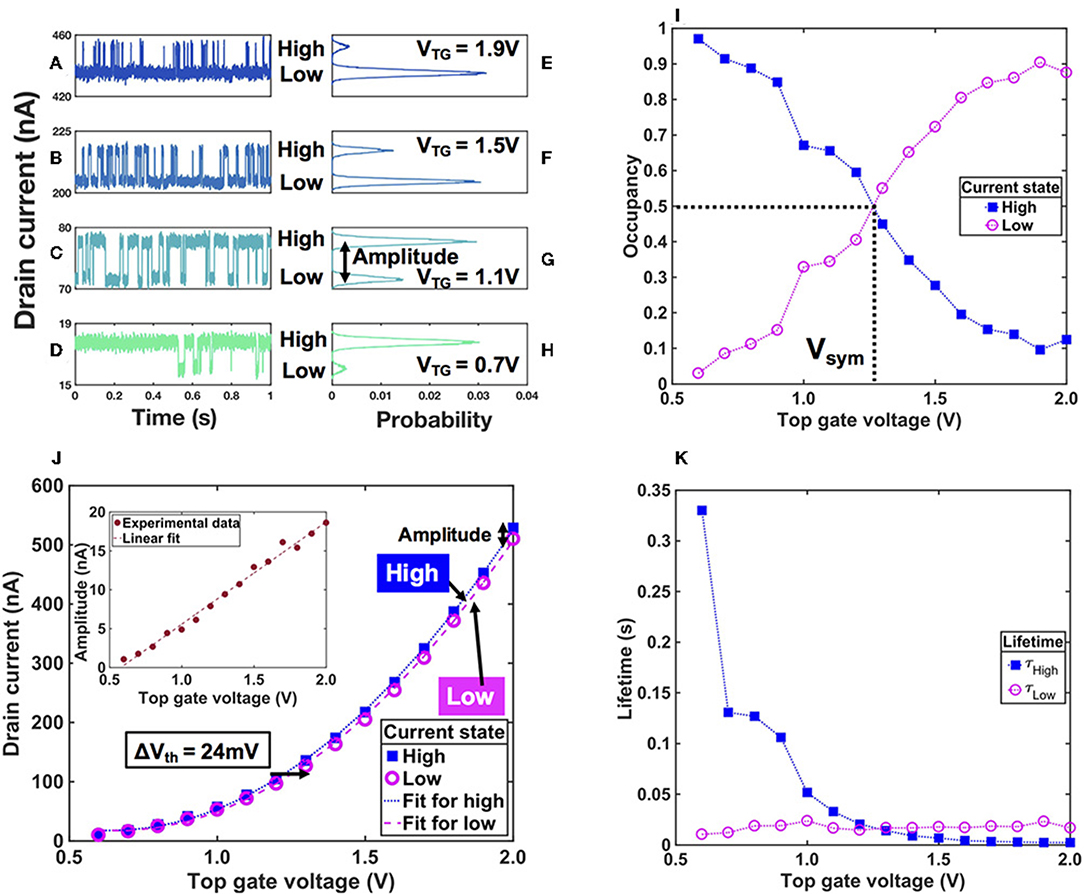
Figure 3. Time domain characteristics of the silicon nanowire transistor and properties of the observed random telegraph signals. (A–D) Examples of the time domain characteristics of the device. I_D was monitored for one second at different voltage conditions. V_FG and V_D were 0 V and 200 mV, respectively, while V_TG was 1.9 V in (A), 1.5 V in (B), 1.1 V in (C), and 0.7 V in (D). Two discrete current states are clearly seen in all measurements and are labeled as high and low. (E–H) The histograms of the corresponding time domain characteristics (E) for (A), (F) for (B), (G) for (C), and (H) for (D). (I) The occupancy of the QD against V_TG, calculated by the Equations (1) and (2). The dotted lines are visual guides. (J) The transfer characteristic of the device reproduced from time domain measurements with the presence of RTS. I_High and I_Low were plotted against V_TG as squares and circles, respectively. The dotted lines are parabolic functions for fitting. The inset shows the difference between I_High and I_Low, which is linearly increasing as a function of V_TG. (K) The lifetimes of the current states. The blue filled circles are lifetimes of high state (τ_High) in different bias conditions, while the magenta filled circles are the ones of low states (τ_Low). The dotted lines are visual guides.

We quantitatively analyzed this trend by calculating histograms of each current trace against time [46], and found the nature of the RTS to be stochastic shifts in the V_th of the transistor. A histogram gives the probability of observing a certain current value [P(I_D)] in a certain time domain measurement. Figures 3E–H show the histograms of time domain measurements displayed in Figures 3A–D, respectively. Two current peaks were observed in all four plots, indicating that the two discrete current states were clearly distinguishable. Therefore, the probabilities of observing the high current state (n_High) and low current state (n_Low) can be defined as follows

$\begin{array}{ll}{n}_{\text{High}}=\frac{1}{I_{\text{T}}}{\displaystyle {\int }_{I_{\text{D,mid}}}^{\infty }}P(I_{\text{D}})d{I}_{\text{D}}& (1)\end{array}$

$\begin{array}{ll}{n}_{\text{Low}}=\frac{1}{I_{\text{T}}}{\displaystyle {\int }_{-\infty }^{I_{\text{D,mid}}}}P(I_{\text{D}})d{I}_{\text{D}},& (2)\end{array}$

where I_D,High (I_D,Low) is the I_D value that gives the maximum of the peak for the high (low) current state, I_D,mid = (I_D,High + I_D,Low)/2 separates the two current states and $I_{\mathrm{\text{T}}}={\int }_{-\infty }^{\infty }P(I_{\mathrm{\text{D}}})d{I}_{\mathrm{\text{D}}}$ is a normalizing factor. The probabilities of observing the high and low current state are plotted against V_TG in Figure 3I. As V_TG increased, the probability to observe low current state increased, while the probability to observe high current state decreased. The V_TG that gave a symmetric probability distribution is around 1.3 V, noted as V_sym in Figure 3I. In Figure 3J, I_D,High was plotted against V_TG as squares, while I_D,Low was plotted against V_TG as circles. These two plots (I_D,High vs. V_TG and I_D,Low vs. V_TG) can be considered as two transfer characteristics with different V_th values (low V_th and high V_th) in the same device. The difference in V_th between the two V_th states can be precisely evaluated by finding a fitting function for I_D,High [f(V_TG)] and shift f(V_TG) by ΔV_th. The fitting function f(V_TG) was determined phenomenologically as a parabolic function with regards to the linear trend of the amplitude of RTS (ΔI = I_D,High – I_D,Low) against V_TG (Figure 3J and its inset). f(V_TG) was plotted as a dotted line in Figure 3J. f(V_TG − ΔV_th) was plotted with a ΔV_th of 24 mV, shown in Figure 3J as a broken line, which reproduced the original data trends with sufficiently small deviations. Here, ΔV_th of 24 mV was determined by the least square fitting. Therefore, the high current state can be attributed to the low V_th state, while the low current state can be assigned to the high V_th state. This indicates that the V_th of our transistor was randomly switching between two states, exhibiting itself as RTSs, and as V_TG increased it eventually ended up predominantly in the high V_th state. Although the amplitudes of RTS in I_D were increasing as V_TG increased, this can be understood as a result of a constant, parallel shift of the transfer characteristic that is not a linear function of gate voltage. This analysis provides an objective method to uniquely identify the shift of threshold voltage caused by RTS, from static RTS measurements.

We attribute this positive threshold voltage shift to a charging of an electron in the QD [46]. Once an electron was trapped in the QD, it was fixed in the QD and therefore reduced the number of mobile carriers that contributed I_D. The coupling of an electron and the resulting shift in V_th can be evaluated by the coupling capacitance;

$\begin{array}{ll}{C}_{\text{RTS}}=\frac{e}{\Delta V_{\text{th}}}.& (3)\end{array}$

By substituting ΔV_th = 24 mV, C_RTS of 6.67 aF was obtained. This is in good agreement from the capacitance of the TG, C_QD = ϵ₀κ_oxS/t_ox = 6.65 aF, where ϵ₀ is the permittivity of vacuum, κ_ox = 3.9 is the relative permittivity of Silicon dioxide, S is the size of the QD (30 nm in width and 125 nm in length) and t_ox is the thickness of the gate dielectric.

Finally, the average lifetimes of each current state (τ_High for the high state and τ_Low for the low state) were calculated at each V_TG values. τ_High and τ_Low can be efficiently calculated using time derivative of I_D for each time domain measurement [46]. Figure 3K shows τ_High and τ_Low against V_TG. τ_High rapidly decreased as V_TG increased, while such a steep trend was not observed in τ_Low's dependence on V_TG, which stayed almost constant around 20 ms. At V_TG = 0.6 V, the lifetime of the high state was more than 150 ms, meaning that the observation of the low state in shorter time scales was not expected. At V_TG = 2.0 V, the lifetime of the low state (20 ms) is much longer than that of the high state, meaning that the high state would not last long even if it is observed.

3.2. Single Electron Memory Effect

To demonstrate the single electron memory effect based on RTS, an arbitrary waveform generator module of the B1500 was used to output a single pulse with a sufficiently short ramp-up/down time (around 10 μs). The pulse was designed based on the RTS statistics. I_D was monitored before, during and after the pulse to capture the dynamics of an electron with V_D = 200 mV. The first step was to confirm that the QD was empty by applying 0.5 V to TG, where the high current state of the RTS dominated. Then, V_TG was ramped up to 2.0 V such that the low current state was preferred while the QD was still empty [47]. The transition from the high state to the low state, equivalent to the trapping of an electron, was observed as a discretized current drop [47]. V_TG was then ramped down to the initial value, 0.5 V, such that the favored current state is now the high state while the trapped electron remained in the QD. An electron stayed in the QD until it was emitted, leading to a discretized current increase in I_D [47].

Examples of successful demonstrations of the single electron memory effect are shown in Figure 4. In Figure 4H, for example, a sudden, sharp drop of I_D (about 5 nA) was observed at 52 ms, as expected. Similar current drops were seen in Figures 4I,K–M. This suggests that an electron was certainly injected into the QD, and at the time of ramp down (60 ms) it was still inside the QD. After the voltage ramp down, clearly the value of I_D after the pulse is lower than before (about 0.5 nA, Figures 4A–G) [47–49], even in the presence of the unwanted noise in I_D with the frequency of 50 Hz. In the case of Figure 4A, for example, I_D stayed in the low level (5.0 nA) for about 40 ms before returning to the original current value, 6 nA. The current jump is highlighted by black arrows for Figures 4A–G. To our best knowledge, this is the first demonstration of dynamic manipulation of an electron based on RTSs at room temperature.

FIGURE 4

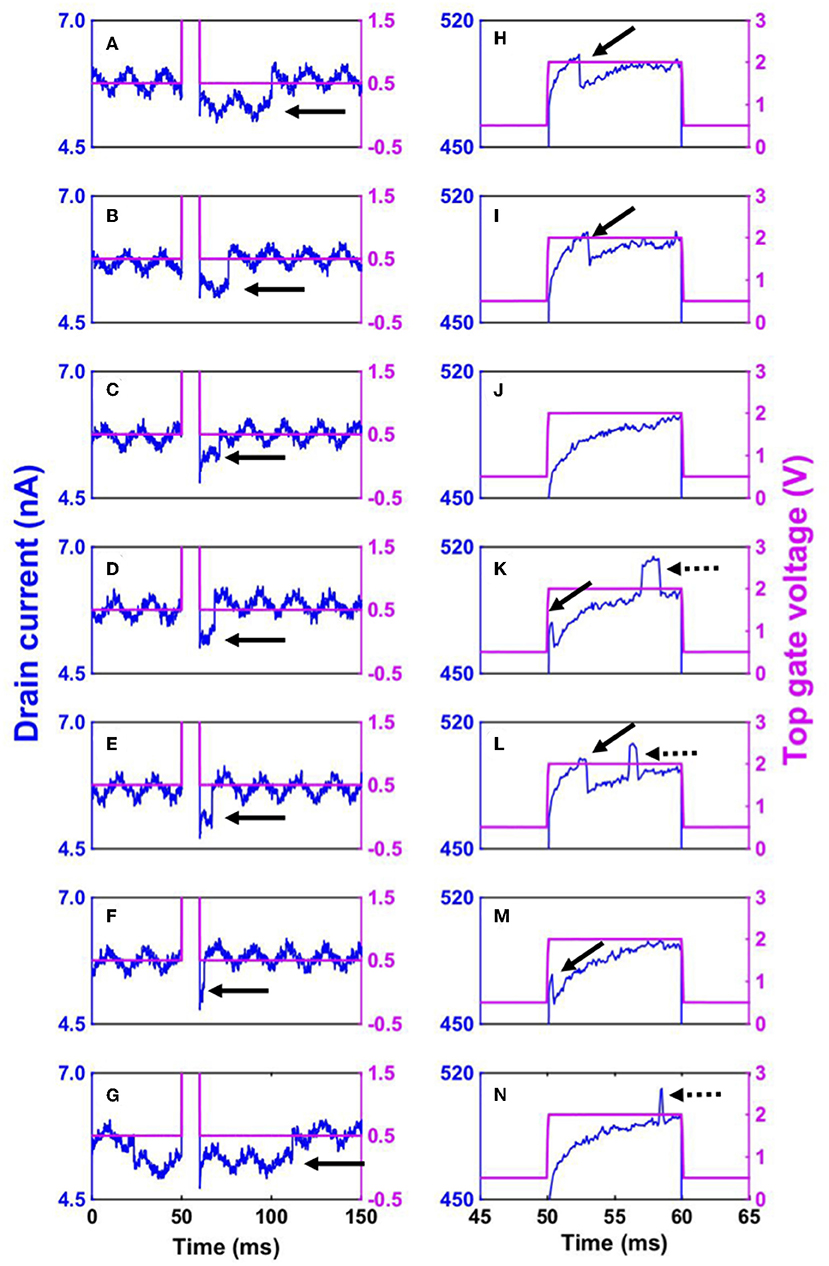
Figure 4. Single electron memory effect utilizing Random Telegraph Signals. (A–G) I_D monitored from 0 s to 150 ms in the range of 4.5 to 7.0 nA. (H–N) I_D monitored from 45 to 65 ms in the range of 450 to 520 nA. V_D was set to 0.2 V. In the first 50 ms, V_TG = 0.5 V was applied to empty the QD (A–G). After the initialization, V_TG was ramped up to 2 V over 30 μs (H–N). Until 60 ms, V_TG was kept 2 V to capture an electron in the QD (H–N). V_TG was then decreased to 0.5 V over 30 μs, and I_D was monitored for a further 90 ms (A–G).

A sharp current drop was not always observed during the pulse, as can be seen in Figures 4J,N. For Figure 4N, this is expected as before the pulse the electronic state was already filled by an accidental RTS event. For Figure 4J, as the initial electronic state was empty, the only possibility is that the RTS event happened during 30 μs of ramp up. Also, as in Figures 4K,L,N, accidental RTS events were observed during the pulse, changing the electronic state from desired filled state to the empty state. However, as the bias condition was properly optimized, after 10 ms of the pulsing time the electronic state returned to the filled state. This means that this memory operation is robust against such a bit error. We also observed the delay in I_D, where the response of I_D did not follow the exact waveform of the pulse. This transient effect can be attributed to the capacitive coupling of the wafer stage of the probe station and the substrate, which is insulated by back oxide masked by undoped poly-Si. The effect of floating body effect (FBE) can be eliminated in this context, as FBE usually involves holes injected by impact ionization, where drain is pulsed with an amplitude of around 1 V [50]. In our single electron memory experiment, the drain voltage was fixed to 200 mV and only the gate voltage was pulsed in a ramp up/down time of 30 μs, and it is unlikely that impact ionization could have occurred in this situation. With regards to the relation between the transient effect and the capture of an electron in the QD, we can conclude these two phenomena are not correlated because of the presence of the accidental RTSs, observed in Figures 4K,L,N (highlighted by dashed arrows). If the transient effect plays the central role in the trapping process of an electron in the QD, that mechanism cannot explain as to why an electron could be detrapped from the QD. On the other hand, if the capture and emission process is thought to be governed by the RTS statistics, which is a function of TG voltage (Figures 3I,K), the accidental detrap and recapture of an electron (seen in Figures 4K,L,N) can naturally occur, as such RTS event cannot be completely avoided even though the probability to occur is <10% (Figure 3).

4. Discussion

4.1. Physical Origin of the RTSs

The nature of the RTS was identified as a stochastic switching between two threshold voltage states, which ended up in the high V_th state due to the occupation of the QD by an electron. That is, the drain current of our transistor can only be determined probabilistically, which is a clear manifestation of quantum/single electron effect in our Si transistor. We already attributed this quantum effect to the electrically defined QD; a single electron gets trapped and detrapped in the QD region defined by two FGs in section 3.1 [46]. Standard CMOS devices with a smaller device size do not exhibit such a trapping and detrapping of an electron as there is no electrically defined potential well in the channel. Built-in potential between the doped region and the body of the transistor can be overcome by the diffusion mechanism [9]. The electrically defined potential barriers cannot simply be surmounted by the difference in doping concentration, such that electrons with sufficiently high energy can thermally surpass the energy barrier, obeying Boltzmann distribution [51]. While the majority of electrons can travel to drain after overcoming the barrier, a single electron can lose significant kinetic energy by scattering, and becomes trapped in the potential well defined by FGs. For an electron to be detrapped from the QD, it needs to be thermally activated again. The presence of a trapped, fixed electron leads to lower drain current output under the same voltage condition, as V_TG induces the same number of electrons under the TG regardless of whether they can be mobile or fixed. This is equivalent to the positive shift in V_th.

To confirm our hypothesis, we first characterized our device at 4.2 K to confirm the presence of a QD defined by potential barriers [52]. We identified the presence of Coulomb blockade features, shown in Figure 5. V_FG1 and V_FG2 were set to 0.5 and 0 V, respectively. Coulomb diamonds around V_TG = 0.8 V (labeled as 2 in Figure 5) and 0.95 V (labeled as 3 in Figure 5) share the similar size, which are smaller than that around V_TG = 0.6 V (labeled as 1 in Figure 5), indicating the presence of a single QD when V_TG was more than about 0.7 V, where the RTSs were observed. Conductance peaks that surround the Coulomb blockade features were also observed, highlighted by arrows in Figure 5 [45]. With respect to the asymmetry observed in the charge stability diagram, we attributed it to the physical asymmetry of the device, particularly the position of the QD located between source and drain. Such an asymmetry could have been caused during the fabrication process, such as e-beam misalignment and poor patterning [46]. A quantum dot can couple differently with two leads, which appears as different coupling capacitances (C_S and C_D) and therefore asymmetric Coulomb blockade features [52]. This asymmetry can be corrected by adjusting voltage applied on source, drain, gate, and substrate [53]. However, the reason why we performed this low temperature measurement is to confirm the presence of the QD in our device, and for this purpose observing a Coulomb blockade was sufficient.

FIGURE 5

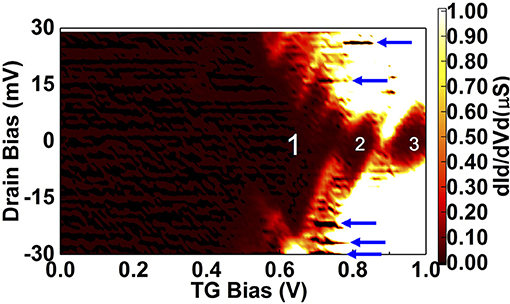
Figure 5. Coulomb blockade observed in our device at 4.2 K. V_FG1 = 0.5 V and V_FG1 = 0 V. Conductance peaks are observed outside of the blockade region.

To extract the size of the QD, we used the diamond observed when V_TG was swept from 0.9 to 1 V, as the RTS and single electron memory effects were observed in the similar voltage condition. Also, the size of the QD could be underestimated due to the inversion layer capacitance [54]. The capacitance of the QD (C_QD) and its couplings to the TG, source and drain (C_TG, C_S, C_D) are 21, 1.58, 6.32, and 13.1 aF, respectively. The charging energy ($E_{\mathrm{\text{C}}}=e^2/2C_{\mathrm{\text{QD}}}$) and the size of the QD in this voltage condition can be estimated from these capacitances, which are 3.75 meV and 28 × 28 nm, respectively. The estimated size of the dot was smaller than the designed QD, implying that the broadening of the field effect decreased the effective size of the QD. This means that a QD was realized in our nanowire transistor at low temperature with well-defined electrostatic potential barrier formed by FGs. This also means that the effective length of the gate in the QD region should also be around 30 nm. At room temperature, a Coulomb blockade effect is masked by the thermal fluctuation energy, 26 meV [52]. However, the potential barriers formed by FGs are not altered much upon the change in temperature. Therefore, we understand an isolated energy level is still present inside the QD, causing RTSs on drain current characteristics. This energy level cannot be observed as Coulomb blockades, due to its low charging energy.

Certainly, the possibility that the RTS occurred due to unintentional electron traps or defect states cannot be excluded without directly observing the absence of such traps in our device. However, based on the fabrication process and the result of characterization of our device, we still believe that the proposed RTS mechanism of an electron trapped and de-trapped in the QD can explain the observed phenomena more comprehensively than that based on interface traps or dopants. The best possible care has been taken in order to eliminate any electron traps generated during the fabrication process. The formation of the gate oxide on top of nanowire was performed by dry thermal oxidation at 1,000°C, avoiding introducing electron traps in the gate oxide during the oxidation process. The final stage of the fabrication process was forming gas anneal at 450°C, in an attempt to terminate any surface states [9]. Phosphorous dopants were activated by rapid thermal annealing, such that dopant profile was well controlled while maintaining the conductivity between the body and source/drain of the transistor. The transistor characteristics implied that the device was successfully fabricated with a high quality, exhibiting the subthreshold slope of 68 mV/decade and no hysteresis. Three kinds of electron traps can be identified to cause RTSs, which are (1) trap levels in the oxide (2) surface states (3) dopant atoms in the channel. The possibility of RTS caused by a trap level in the oxide can be excluded from the time domain analysis. The average lifetime of RTSs and the trap depth can be correlated with each other by the following formula [8, 55]

$\begin{array}{ll}\frac{X_{\text{T}}}{t_{\text{OX}}}=-\frac{kT}{e}\frac{\text{d}ln({\tau }_{\text{c}}/{\tau }_{\text{e}})}{\text{d}{V}_{\text{TG}}},& (4)\end{array}$

where X_T is the depth of the trap, t_OX is thickness of the oxide, k is the Boltzmann constant, T is the temperature, e is elementary charge, τ_c is the average lifetime of high state and τ_e is the average lifetime of low state. Using the Equation (4), the depth of the trap level is about 1.76 nm (X_T/t_OX = 0.1). It is unlikely that the RTS with an average lifetime of 10 ms caused by this rather deep trap, based on the report studying transistors in 40 nm generation, where such a fast RTS should occur from trap levels around 0.2 nm in depth [55]. Regarding surface states, this possibility can also be removed as the transistor was operating at strong inversion and Fermi energy should be much higher than the conduction band bottom. Surface states are located in the bandgap of silicon, and thus they are located below the bottom of the conduction band [9]. When Fermi energy is above the trap level, the level is occupied and cannot influence the transport. RTS caused by a discrete dopant level at room temperature is rather rare, and majority of such RTSs are reported at low temperature [48, 56], which is not the main scope in this paper. The number of intrinsic dopant traps in the QD area is <1, considering the trap density in Si devices (10¹⁰cm⁻³) and the designed size of the device, 30 × 125 nm.

4.2. Potential Energy Diagram

Then, we calculated the energy level in the QD as well as the height of the energy barriers, from the time domain measurements (Figures 6A,B) [8, 46]. Here, we assumed that capture and emission events of an electron are the result of the thermal activation process [8, 46, 51, 57]. Figures 6C–E describes the schematic of the energy landscape assumed in this paper. Fermi energy of source is noted as E_S on the left of FG1, and the solid, curved line represents the energy potential along the nanowire. The peak of the potential barrier is named ΔE + E_S, meaning that the summit of the potential is higher than Fermi energy of source by ΔE. The discrete energy level in the QD is called ϵ + E_S, meaning that the energy level is higher than E_S by ϵ. These parameters that underpin the energy diagram of the system can be then correlated with the average lifetimes of RTS

$\begin{array}{ll}{P}_{\text{capture}}=\frac{1}{{\tau }_{\text{High}}}=n_{\text{inv}}{v}_{\text{thn}}{\sigma }_{0}exp\left(-\frac{\Delta E}{kT}\right)& (5)\end{array}$

$\begin{array}{ll}{P}_{\text{emission}}=\frac{1}{{\tau }_{\text{Low}}}=n_{\text{inv}}{v}_{\text{thn}}{\sigma }_{0}exp\left(-\frac{\Delta E-ϵ}{kT}\right),& (6)\end{array}$

where P_capture and P_emission is the probability of observing a capture event (a transition from the high state to the low state) and an emission event (a transition from the low state to the high state) in one second, n_inv is the electron density in the inversion layer, v_thn is the thermal velocity of electrons in the channel, σ₀ is the temperature independent capture cross section coefficient, k is the Boltzmann constant and T is temperature [8]. This formula can be understood conceptually as follows; a cloud of electrons with an average velocity of v_thn and an average density of n_inv are moving toward a capturing target with a capture cross section of σ_c = σ₀ exp(−E_b/kT), where E_b is an energy barrier to be overcome for an electron to be captured [8]. Therefore, this gives the probability of an electron in the cloud being captured by the capturing target in a unit time [8, 57]. For an electron to be captured from the source to the QD, it must overcome the energy barrier of ΔE, while for an electron to be emitted from the QD to source, it must surpass the energy barrier of δE = ΔE − ϵ (Figures 6C–E), justifying the exponential term in the Equations (5) and (6), respectively.

FIGURE 6

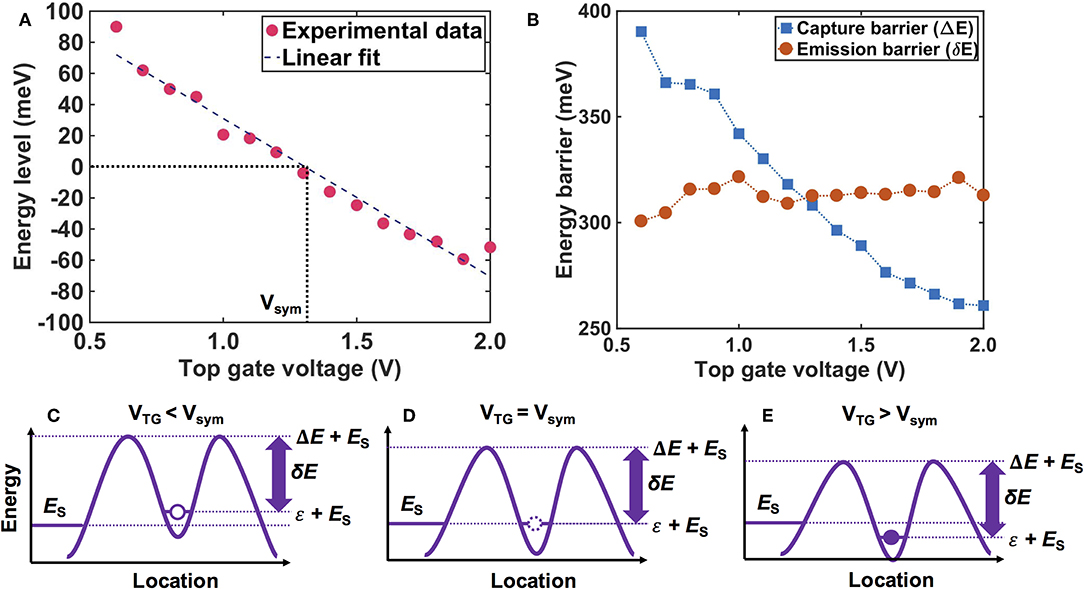
Figure 6. Capture and emission mechanism of an electron from estimated energy barriers. (A) The energy level in the QD against V_TG calculated using Equation (7). The filled circles are extracted from the ratio of the lifetimes, while the broken line is the linear fit of the data. V_sym is the voltage value when the energy level is completely aligned to the conduction band bottom of source, which is around 1.3 V. (B) The energy barriers for an electron to be captured and to be emitted from the quantum dot. The capture barrier ΔE and the emission barrier δE = ΔE − ϵ are plotted against V_TG as squares and filled circles, respectively. The dotted lines are visual guides. (C–E) The energy diagram inferred from the estimated energy barriers, depending on V_TG with respect to V_sym.

The energy level in the QD with respect to E_S can be calculated from Equations (5) and (6) by canceling ΔE out, without assuming numerical values of n_inv, v_thn and σ₀ [46];

$\begin{array}{ll}ϵ=kTln\left(\frac{{\tau }_{\text{High}}}{{\tau }_{\text{Low}}}\right)& (7)\end{array}$

Figure 6A shows ϵ against V_TG, revealing the linear dependence of ϵ on V_TG. This means that the energy level in the QD is controlled linearly by changing the voltage applied on TG.

To calculate ΔE from τ_High, n_inv, v_thn, and σ₀ must be assumed. n_inv was assumed to be 10¹⁶cm⁻³. The typical value for inversion layer, 10¹⁸cm⁻³, should be valid when our transistor operates with two FGs completely turned on [9]. Since we limit the net current by applying 0 V to FGs, the on current is two orders of magnitude less than the one when V_TG = 1.4 V (Figure 2A inset). We attributed this degradation of on current to the decrease in the electron density in the channel. v_thn was assumed to be 10⁷m/s [9]. σ₀ was set to 10 × 10nm = 10⁻¹²cm², reflecting the order of magnitude of the nanowire width and the thickness of SOI.

Assuming those numerical values, ΔE and δE were calculated and plotted against V_TG as squares and filled circles (Figure 6A), by solving the Equations (5) and (6), respectively. As V_TG increased, the capture barrier ΔE decreased, while the emission barrier δE stayed around 310 meV (Figure 6B). The energy barriers calculated were much higher than the thermal energy of kT = 26 meV at room temperature, which is reasonable as this explains the long lifetime of RTS states compared to the kinetics of electrons (around pico second). The asymmetric behavior of capture and emission barriers can be attributed to TG's capacitive coupling to FGs, reducing the capture barrier height as a second order effect (Figures 6C–E).

A similar potential diagram was proposed to explain Coulomb blockades at relatively higher temperature [58]. However, absence of Coulomb blockade in our device at room temperature is clear from the transfer characteristics (Figure 2), and therefore it is difficult to explain the observed RTS and resulting threshold voltage shift within the regime of Coulomb-blockade transport. At room temperature, our device operated as a FET and the channel is assumed to be uniform. Several studies report that a FET becomes a single-electron-transistor at low temperature [54] or even at room temperature [59, 60], due to inhomogeneity of the channel, leading to a pseudo one-dimensional conduction path accompanied with a QD. In such a situation, electrons must transport via the QD, either by quantum-mechanical tunneling [52] or by thermal activation [58]. Therefore, when an electron occupies the dot, the conduction must be blocked. However, in our case, as the channel is uniform, electrons do not necessarily transport from source to drain via the QD, and therefore a trapped electron would not stop electric current going through. Instead, we understand a trapped electron shift the threshold voltage of the transistor.

5. Conclusion

In this work, we demonstrated a dynamic manipulation of a single electron based on RTSs in a triple-gate Si NW transistor at room temperature, namely single electron memory effect. Our device exhibited a RTS when two FGs formed potential barriers to create an electrically-defined QD, while voltage on TG was varied to control the probability to observe two current states, the high and low states. The nature of the RTS was revealed to be a parallel shift of the threshold voltage, and a systematic method to extract the shift from time-domain measurements was also explained. Based on the characteristic of the RTS, the capture and emission of an electron were dynamically controlled by a voltage pulse at room temperature. We also confirmed that our device manifested Coulomb blockades at low temperature in a similar voltage condition, meaning that our device operates as a conventional single electron transistor.

A systematic method with a reasonably short characterization time is required to find a RTS for future application of RTSs for quantum technology. We approach this demand by fabricating a device that can simulate a physical situation causing RTSs, and we successfully controlled the RTSs both statically and dynamically. Our work should pave the way to a new way of manipulating carriers at a single electron level for quantum application.

Data Availability Statement

The data from the paper can be obtained from the University of Southampton ePrint research repository: https://doi.org/10.5258/SOTON/D0843.

Author Contributions

SS, MH, and ZL designed the mask layout and fabricated the device. KI, JH, FL, YT, and HR set up the measurement system. IT made a theoretical model. KI, ZL, IT, and SS characterized the device. KI drafted the manuscript. All authors participated in the analysis of the data.

Funding

This work was supported by EPSRC Manufacturing Fellowship (EP/M008975/1), Lloyds Register Foundation International Consortium of Nanotechnology, and the Joint Research Project [e-SI-Amp (15SIB08)]. This work was also supported by the European Metrology Programme for Innovation and Research (EMPIR) co-financed by the Participating States and from the European Union's Horizon 2020 research and innovation programme.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

We would like to thank Dr. S. Giblin, Dr. J. Fletcher, and Dr. M. Kataoka for their help in characterizing our device at low temperature.

References

1. Feynman RP. There's plenty of room at the bottom [data storage]. J Microelectromech Syst. (1992) 1:60–6. doi: 10.1109/84.128057

CrossRef Full Text | Google Scholar

2. Moore GE. Cramming more components onto integrated circuits. Electronics. (1965) 38:114–7.

Google Scholar

3. Dennard RH, Gaensslen FH, Rideout VL, Bassous E, LeBlanc AR. Design of ion-implanted MOSFET's with very small physical dimensions. IEEE J Solid-State Circuits. (1974) 9:256–68. doi: 10.1109/JSSC.1974.1050511

CrossRef Full Text | Google Scholar

4. Ando T, Fowler AB, Stern F. Electronic properties of two-dimensional systems. Rev Mod Phys. (1982) 54:437. doi: 10.1103/RevModPhys.54.437

CrossRef Full Text | Google Scholar

5. Takagi S, Toriumi A. Quantitative understanding of inversion-layer capacitance in Si MOSFET's. IEEE Trans Elec Dev. (1995) 42:2125–30. doi: 10.1109/16.477770

CrossRef Full Text | Google Scholar

6. Wilk GD, Wallace RM, Anthony J. High-κ gate dielectrics: current status and materials properties considerations. J Appl Phys. (2001) 89:5243–75. doi: 10.1063/1.1361065

CrossRef Full Text | Google Scholar

7. Saito S, Torii K, Hiratani M, Onai T. Analytical quantum mechanical model for accumulation capacitance of MOS structures. IEEE Elec Dev Lett. (2002) 23:348–50. doi: 10.1109/LED.2002.1004231

CrossRef Full Text | Google Scholar

8. Simoen E, Claeys CL. Random Telegraph Signals in Semiconductor Devices. Bristol: IOP Publishing Limited (2016).

Google Scholar

9. Taur Y, Ning TH. Fundamentals of Modern VLSI Devices. Cambridge: Cambridge University Press (2013)

Google Scholar

10. Ralls K, Skocpol W, Jackel L, Howard R, Fetter L, Epworth R, et al. Discrete resistance switching in submicrometer silicon inversion layers: individual interface traps and low-frequency (1/f) noise. Phys Rev Lett. (1984) 52:228. doi: 10.1103/PhysRevLett.52.228

CrossRef Full Text | Google Scholar

11. Tega N, Miki H, Pagette F, Frank D, Ray A, Rooks M, et al. Increasing threshold voltage variation due to random telegraph noise in FETs as gate lengths scale to 20 nm. In: Symposium on VLSI Technology Dig. Tech. Papers. Piscataway, NJ: IEEE (2009). p. 50–1.

Google Scholar

12. Tega N, Miki H, Ren Z, Christoper P, Zhu Y, Frank DJ, et al. Impact of HK/MG stacks and future device scaling on RTN. In: Proceedings of 49th Ann. International Reliability Physics Symposium - IRPS11. Piscataway, NJ: IEEE (2011). p. 6A–5. doi: 10.1109/IRPS.2011.5784546

CrossRef Full Text | Google Scholar

13. Toledano-Luque M, Degraeve R, Roussel PJ, Ragnarsson LÅ, Chiarella T, Horiguchi N, et al. Fast ramped voltage characterization of single trap bias and temperature impact on time-dependent Vth variability. IEEE Trans Elec Dev. (2014) 61:3139–44. doi: 10.1109/TED.2014.2340699

CrossRef Full Text | Google Scholar

14. Yonezawa A, Kuroda R, Teramoto A, Obara T, Sugawa S. A statistical evaluation of effective time constants of random telegraph noise with various operation timings of in-pixel source follower transistors. In: Image Sensors and Imaging Systems 2014. Vol. 9022. International Society for Optics and Photonics. San Francisco, CA (2014). p. 90220F. doi: 10.1117/12.2041090

CrossRef Full Text | Google Scholar

15. Obara T, Yonezawa A, Teramoto A, Kuroda R, Sugawa S, Ohmi T. Extraction of time constants ratio over nine orders of magnitude for understanding random telegraph noise in metal–oxide–semiconductor field-effect transistors. Jpn J Appl Phys. (2014) 53:04EC19. doi: 10.7567/JJAP.53.04EC19

CrossRef Full Text | Google Scholar

16. Tega N, Miki H, Yamaoka M, Kume H, Mine T, Ishida T, et al. Impact of threshold voltage fluctuation due to random telegraph noise on scaled-down SRAM. In: Proceedings of 46th Ann. International Reliability Physics Symposium - IRPS08. Piscataway, NJ: IEEE (2008). p. 541–6.

Google Scholar

17. Yamaoka M, Miki H, Bansal A, Wu S, Frank D, Leobandung E, et al. Evaluation methodology for random telegraph noise effects in SRAM arrays. In: 2011 International Electron Devices Meeting. Piscataway, NJ (2011). p. 745–8. doi: 10.1109/IEDM.2011.6131656

CrossRef Full Text | Google Scholar

18. Terai M, Sakotsubo Y, Saito Y, Kotsuji S, Hada H. Effect of bottom electrode of ReRAM with Ta2O5/TiO2 stack on RTN and retention. In: Electron Devices Meeting, 1988. IEDM '88. Technical Digest. Piscataway, NJ: IEEE (2009). p. 1–4.

Google Scholar

19. Terai M, Sakotsubo Y, Saito Y, Kotsuji S, Hada H. Memory-state dependence of random telegraph noise of Ta2O5/TiO2 stack ReRAM. IEEE Elec Dev Lett. (2010) 31:1302–4. doi: 10.1109/LED.2010.2068033

CrossRef Full Text | Google Scholar

20. Ielmini D, Nardi F, Cagli C. Resistance-dependent amplitude of random telegraph-signal noise in resistive switching memories. Appl Phys Lett. (2010) 96:053503. doi: 10.1063/1.3304167

CrossRef Full Text | Google Scholar

21. Tseng YH, Shen WC, Huang CE, Lin CJ, King YC. Electron trapping effect on the switching behavior of contact RRAM devices through random telegraph noise analysis. In: 2010 International Electron Devices Meeting. Piscataway, NJ (2010). p. 28–5. doi: 10.1109/IEDM.2010.5703439

CrossRef Full Text | Google Scholar

22. Raghavan N, Degraeve R, Fantini A, Goux L, Strangio S, Govoreanu B, et al. Microscopic origin of random telegraph noise fluctuations in aggressively scaled RRAM and its impact on read disturb variability. In: 2013 IEEE International Reliability Physics Symposium (IRPS). Piscataway, NJ: IEEE (2013). p. 5E–3. doi: 10.1109/IRPS.2013.6532042

CrossRef Full Text | Google Scholar

23. Veksler D, Bersuker G, Vandelli L, Padovani A, Larcher L, Muraviev A, et al. Random telegraph noise (RTN) in scaled RRAM devices. In: 2013 IEEE International Reliability Physics Symposium (IRPS)- IRPS13. Piscataway, NJ: IEEE (2013). p. MY–10. doi: 10.1109/IRPS.2013.6532101

CrossRef Full Text | Google Scholar

24. Ambrogio S, Balatti S, Cubeta A, Calderoni A, Ramaswamy N, Ielmini D. Statistical fluctuations in HfOx resistive-switching memory: part II Random telegraph noise. IEEE Trans Elec Dev. (2014) 61:2920–7. doi: 10.1109/TED.2014.2330202

CrossRef Full Text | Google Scholar

25. Lin Y, Lin Y, Lee F, Ho Y, Hsu K, Lee M, et al. Device instability of ReRaM and a novel reference cell design for wide temperature range operation. IEEE Elec Dev Lett. (2017) 38:1224–7. doi: 10.1109/LED.2017.2732025

CrossRef Full Text | Google Scholar

26. Tega N, Miki H, Osabe T, Kotabe A, Otsuga K, Kurata H, et al. Anomalously large threshold voltage fluctuation by complex random telegraph signal in floating gate flash memory. In: International Electron Devices Meeting. Piscataway, NJ: IEEE (2006). p. 218–21. doi: 10.1109/IEDM.2006.346821

CrossRef Full Text | Google Scholar

27. Fukuda K, Shimizu Y, Amemiya K, Kamoshida M, Hu C. Random telegraph noise in flash memories-model and technology scaling. In: Electron Devices Meeting, 1988. IEDM '88. Technical Digest. Piscataway, NJ: IEEE (2007). p. 169–72. doi: 10.1109/IEDM.2007.4418893

CrossRef Full Text | Google Scholar

28. Kurata H, Otsuga K, Kotabe A, Kajiyama S, Osabe T, Sasago Y, et al. Random telegraph signal in flash memory: its impact on scaling of multilevel flash memory beyond the 90-nm node. IEEE J Solid-State Circuits. (2007) 42:1362–9. doi: 10.1109/JSSC.2007.897158

CrossRef Full Text | Google Scholar

29. Li SR, Lu YLR, McMahon W, Lee YH, Mielke N. RTS and 1/f noise in flash memory. In: International Symposium on VLSI Technology, Systems and Applications (VLSI-TSA). Piscataway, NJ: IEEE (2007). p. 56–7. doi: 10.1109/VTSA.2007.378918

CrossRef Full Text | Google Scholar

30. Ghetti A, Compagnoni CM, Biancardi F, Lacaita A, Beltrami S, Chiavarone L, et al. Scaling trends for random telegraph noise in deca-nanometer Flash memories. In: 2008 IEEE International Electron Devices Meeting. Piscataway, NJ: IEEE (2008). p. 835–8. doi: 10.1109/IEDM.2008.4796827

CrossRef Full Text | Google Scholar

31. Ghetti A, Compagnoni CM, Spinelli AS, Visconti A. Comprehensive analysis of random telegraph noise instability and its scaling in deca–nanometer flash memories. IEEE Trans Elec Dev. (2009) 56:1746–52. doi: 10.1109/TED.2009.2024031

CrossRef Full Text | Google Scholar

32. Ielmini D. Reliability issues and modeling of flash and post-flash memory. Microelectron Eng. (2009) 86:1870–5. doi: 10.1016/j.mee.2009.03.054

CrossRef Full Text | Google Scholar

33. Lin T, Ku S, Cheng C, Lee C, Tsai WJ, Lu T, et al. Chip-level characterization and RTN-induced error mitigation beyond 20nm floating gate flash memory. In: 2018 IEEE International Reliability Physics Symposium (IRPS)–IRPS18. Piscataway, NJ: IEEE (2018). doi: 10.1109/IRPS.2018.8353679

CrossRef Full Text | Google Scholar

34. Shor PW. Algorithms for quantum computation: Discrete logarithms and factoring. In: Proceedings 35th Annual Symposium on Foundations of Computer Science. Piscataway, NJ: IEEE (1994). p. 124–34.

Google Scholar

35. Kadowaki T, Nishimori H. Quantum annealing in the transverse Ising model. Phys Rev E. (1998) 58:5355. doi: 10.1103/PhysRevE.58.5355

CrossRef Full Text | Google Scholar

36. Ladd TD, Jelezko F, Laflamme R, Nakamura Y, Monroe C, O'Brien JL. Quantum computers. Nature. (2010) 464:45–53. doi: 10.1038/nature08812

PubMed Abstract | CrossRef Full Text | Google Scholar

37. Johnson MW, Amin MH, Gildert S, Lanting T, Hamze F, Dickson N, et al. Quantum annealing with manufactured spins. Nature. (2011) 473:194–8. doi: 10.1038/nature10012

PubMed Abstract | CrossRef Full Text | Google Scholar

38. Maurand R, Jehl X, Kotekar-Patil D, Corna A, Bohuslavskyi H, Laviéville R, et al. A CMOS silicon spin qubit. Nat Commun. (2016) 7:13575. doi: 10.1038/ncomms13575

PubMed Abstract | CrossRef Full Text | Google Scholar

39. Yoneda J, Takeda K, Otsuka T, Nakajima T, Delbecq MR, Allison G, et al. A quantum-dot spin qubit with coherence limited by charge noise and fidelity higher than 99.9%. Nat Nanotechnol. (2018) 13:102–6. doi: 10.1038/s41565-017-0014-x

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Itoh KM, Watanabe H. Isotope engineering of silicon and diamond for quantum computing and sensing applications. MRS Commun. (2014) 4:143–57. doi: 10.1557/mrc.2014.32

CrossRef Full Text | Google Scholar

41. Xiao M, Martin I, Jiang H. Probing the spin state of a single electron trap by random telegraph signal. Phys Rev Lett. (2003) 91:078301. doi: 10.1103/PhysRevLett.91.078301

PubMed Abstract | CrossRef Full Text | Google Scholar

42. Xiao M, Martin I, Yablonovitch E, Jiang H. Electrical detection of the spin resonance of a single electron in a silicon field-effect transistor. Nature. (2004) 430:435–9. doi: 10.1038/nature02727

PubMed Abstract | CrossRef Full Text | Google Scholar

43. Maurer PC, Kucsko G, Latta C, Jiang L, Yao NY, Bennett SD, et al. Room-temperature quantum bit memory exceeding one second. Science. (2012) 336:1283–6. doi: 10.1126/science.1220513

PubMed Abstract | CrossRef Full Text | Google Scholar

44. Schleser R, Ruh E, Ihn T, Ensslin K, Driscoll D, Gossard A. Time-resolved detection of individual electrons in a quantum dot. Appl Phys Lett. (2004) 85:2005–7. doi: 10.1063/1.1784875

CrossRef Full Text | Google Scholar

45. Li Z, Sotto M, Liu F, Husain MK, Yoshimoto H, Sasago Y, et al. Random telegraph noise from resonant tunnelling at low temperatures. Sci Rep. (2018) 8:250. doi: 10.1038/s41598-017-18579-1

PubMed Abstract | CrossRef Full Text | Google Scholar

46. Liu F, Ibukuro K, Husain MK, Li Z, Hillier J, Tomita I, et al. Manipulation of random telegraph signals in a silicon nanowire transistor with a triple gate. Nanotechnology. (2018) 29:475201. doi: 10.1088/1361-6528/aadfa6

PubMed Abstract | CrossRef Full Text | Google Scholar

47. Vandersypen L, Elzerman J, Schouten R, van Beveren WL, Hanson R, Kouwenhoven L. Real-time detection of single-electron tunneling using a quantum point contact. Appl Phys Lett. (2004) 85:4394–6. doi: 10.1063/1.1815041

CrossRef Full Text | Google Scholar

48. Morello A, Pla JJ, Zwanenburg FA, Chan KW, Tan KY, Huebl H, et al. Single-shot readout of an electron spin in silicon. Nature. (2010) 467:687–91. doi: 10.1038/nature09392

PubMed Abstract | CrossRef Full Text | Google Scholar

49. Elzerman J, Hanson R, Van Beveren LW, Witkamp B, Vandersypen L, Kouwenhoven LP. Single-shot read-out of an individual electron spin in a quantum dot. Nature. (2004) 430:431–5. doi: 10.1038/nature02693

PubMed Abstract | CrossRef Full Text | Google Scholar

50. Ohsawa T, Hamamoto T. Floating Body Cell: A Novel Capacitor-Less DRAM Cell. Boca Raton, FL: CRC Press (2011).

Google Scholar

51. Nishiguchi K, Ono Y, Fujiwara A. Single-electron thermal noise. Nanotechnology. (2014) 25:275201. doi: 10.1088/0957-4484/25/27/275201

PubMed Abstract | CrossRef Full Text | Google Scholar

52. Grabert H, Devoret MH. Single Charge Tunneling: Coulomb Blockade Phenomena in Nanostructures. Vol. 294. New York, NY: Springer US (1992).

Google Scholar

53. Ono K, Tanamoto T, Ohguro T. Pseudosymmetric bias and correct estimation of Coulomb/confinement energy for unintentional quantum dot in channel of metal-oxide-semiconductor field-effect transistor. Appl Phys Lett. (2013) 103:183107. doi: 10.1063/1.4827817

CrossRef Full Text | Google Scholar

54. Li Z, Husain MK, Yoshimoto H, Tani K, Sasago Y, Hisamoto D, et al. Single carrier trapping and de-trapping in scaled silicon complementary metal-oxide-semiconductor field-effect transistors at low temperatures. Semicond Sci Technol. (2017) 32:075001. doi: 10.1088/1361-6641/aa6910

CrossRef Full Text | Google Scholar

55. Nagumo T, Takeuchi K, Hase T, Hayashi Y. Statistical characterization of trap position, energy, amplitude and time constants by RTN measurement of multiple individual traps. In: International Electron Devices Meeting. Piscataway, NJ: IEEE (2010). p. 28–3.

Google Scholar

56. Jehl X, Niquet YM, Sanquer M. Single donor electronics and quantum functionalities with advanced CMOS technology. J Phys Condens Matter. (2016) 28:103001. doi: 10.1088/0953-8984/28/10/103001

PubMed Abstract | CrossRef Full Text | Google Scholar

57. Kirton M, Uren M. Capture and emission kinetics of individual Si:SiO2 interface states. Appl Phys Lett. (1986) 48:1270–2. doi: 10.1063/1.97000

CrossRef Full Text | Google Scholar

58. Matveev K, Glazman L. Coulomb blockade of activated conduction. Phys Rev B. (1996) 54:10339. doi: 10.1103/PhysRevB.54.10339

PubMed Abstract | CrossRef Full Text | Google Scholar

59. Lavieville R, Triozon F, Barraud S, Corna A, Jehl X, Sanquer M, et al. Quantum dot made in metal oxide silicon-nanowire field effect transistor working at room temperature. Nano Lett. (2015) 15:2958–64. doi: 10.1021/nl504806s

PubMed Abstract | CrossRef Full Text | Google Scholar

60. Durrani Z, Jones M, Abualnaja F, Wang C, Kaestner M, Lenk S, et al. Room-temperature single dopant atom quantum dot transistors in silicon, formed by field-emission scanning probe lithography. J Appl Phys. (2018) 124:144502. doi: 10.1063/1.5050773

CrossRef Full Text | Google Scholar