- Department of Mathematics, School of Natural Sciences, National University of Sciences and Technology, Islamabad, Pakistan
This article deals with the nanofluid flow and heat transfer of the MHD free stream over an exponentially radiating stretching sheet accompanied by constant and variable fluid characteristics together. The underlying governing partial differential equations (PDEs) have been translated into nonlinear ordinary differential equations (ODEs) by incorporating adequate similarity transformations. By using the shooting method and the MATLAB built-in solver bvp4c, the corresponding ODEs are effectively solved. The impact on the skin friction coefficient (quantifying resistance), the local Nusselt number (heat transfer rate) and the local Sherwood number (mass transfer rate) on the surface due to the flow field variables has been computed against various parameters i.e., magnetic parameter M, Prandtl number Pro, Lewis number Le, thermophoresis parameter Nt, Brownian motion parameter Nb, velocity parameter λ, radiation parameter Rd and thermal conductivity parameter ϵ. Graphs are also plotted to study the impact of distinct parameters on velocity, temperature and concentration profiles. It has been noted by raising the values of ϵ, the heat transfer rate reduces for variable fluid properties. On the other hand, raising Pro increases the heat transfer rate.
1. Introduction
Because of a stretching surface, studying fluid dynamics is essential as it has many practical and industrial applications. In a number of industrial and manufacturing processes, material production occurs and involves sheets of metal, and polymer. For instance, cooling an infinite metal plate in a cooling bath, the boundary layer along material handling conveyors, plastic sheet aerodynamic extrusion, the boundary layer along a liquid film in condensation procedures, paper manufacturing, glass blowing, steel spinning and plastic film drawing.
Boundary layer for incompressible flow on a moving flat plate was studied by Sakiadis [1]. The study focused on the flow through a moving flat plate while considered static fluid contrary to the work by Blasius [2] who considered flow over a fixed plate. The study carried out by Crane [3] diverted to the study of boundary layer flow of a fluid with high viscosity and uniform density on a plate being stretched linearly. Magyari and Keller [4] conducted the research on an exponentially stretching steady surface to explore heat and mass transfer in the boundary layers but without variable fluid properties and MHD consideration. Elbashbeshy [5], who researched the features of flow and heat transfer over an exponentially stretching permeable sheet, adds a different dimension to this inquiry. The considered research is without the characteristics of MHD and varying fluid properties. Many researchers have extended the work for different flow model. But most of those studies have been focusing on constant fluid properties. The analysis of boundary layer flow with variable fluid properties on a moving flat plate in a parallel free stream was studied by Bachok et al. [6]. They computed solution numerically. Andersson and Aarseth [7] investigated the properties of fluid under the influence of temperature.
Magnetohydrodynamics (MHD) is the study of the flow of electrically conducting fluids in an electro-magnetic-fields. MHD flow research is of significant concern in contemporary processes of metallurgy and metalworking. Makinde et al. [8] examined the MHD flow of variable viscosity of nanofluid over a radially stretching sheet. They indicated that Brownian motion enhances the rate of mass transfer. Mukhopadhyay et al. [9] carried out the study of investigation of magnetic field effects on a fluid flow with variable viscosity on heated surface. They reported that the fluid velocity reduces as the viscosity declines. The influence of temperature on viscosity during heating surface was investigated by Elbashbeshay and Bazid [10] and evaluated solution with the help of a shooting method. The effect of variable fluid properties on the hydro-magnetic flow and heat transfer over a nonlinearly stretching sheet was discussed by Popley et al. [11]. They have numerically addressed their problem. Similarly, the influence of a study of temperature-dependent fluid properties on MHD free stream flow and heat transfer over a nonlinearly stretching sheet was studied by Prasad et al. [12].
Some important applications for radiative heat transfer are the MHD accelerator, high temperature plasmas, power generation devices and cooling of nuclear reactors. Many procedures occur in engineering areas at higher temperatures and understanding the transfer of radiative heat becomes very crucial for the design of appropriate equipment. Heat transfer assessment of boundary layer flow with radiation is also vital in electrical power generation, astrophysical flows, solar power technology, and other industrial areas. Raptis et al. [13] recorded the impact of thermal radiation over a semi-infinite stationary plate on the MHD flow of a viscous fluid. Devi and Reddy [14] presented analysis of the radiation and mass transfer effects on MHD boundary layer flow due to an exponentially stretching sheet with heat source. Mukhopadhyay [15] discussed the slip effects on MHD flow over an radiating exponentially stretching sheet with suction/blowing. The influence of radiation effect over an exponentially stretching sheet was studied by Ishak [16] and Mabood et al. [17]. Bidin and Nazar [18] carried out a numerical study to investigate the effect of thermal radiation on boundary layer flow over an exponentially stretching sheet. Poornima and Reddy [19] presented an analysis of the radiation effects on MHD free convective boundary layer flow of nanofluids over a nonlinear stretching sheet. Most of the above studies have not discussed variable fluid properties and radiation simultaneously.
Because of the unique physical and chemical properties of nanometer-sized products, nanofluids have many applications in the industrial sector. Nanofluids are composites of solid-liquid materials, typically 1–100 nm, consisting of powerful nanoparticles or liquid-suspended nanofibers. The term nanofluid was suggested by Choi [20]. He revealed that supplying a tiny quantity of nanoparticles to conventional fluids (<1 percent by volume fraction) improved the heat conductivity of the fluid by ~2 times. Nield and Kuznestov [21] studied convected boundary layer flow of nanofluid in a porous medium. They considered natural convection past a vertical flat plate. Khan et al. [22] presented non-aligned MHD stagnation point flow of nanofluid with variable viscosity over a stretching sheet with radiation effect. They found that non-alignment of the reattachment point decreases with an increase in magnetic parameter M. Bachok et al. [23] discussed stagnation-point and heat transfer flow over an exponentially stretching/shrinking sheet in a nanofluid. They discovered that the solution obtained for shrinking sheet is not unique. Nada et al. [24] examined the effect of nanofluid while variable properties are taken into account. They considered enclosures for the studies. Malik et al. [25] studied Casson nanofluid's boundary layer flow over a cylinder that stretches exponentially and found solution numerically. Eid [26] addressed the impact of chemical reaction over an exponentially stretching sheet on the MHD boundary layer flow of two-phase nanofluid. They found that thermal boundary layer is dependent on the reaction and source parameter. Gangaiah et al. [27] examined the MHD flow of nanofluid in the presence of viscous dissipation and chemical reaction over an exponentially stretching sheet. They showed that thermal boundary layer depends on viscous dissipation parameter. The effect of different variables like variable viscosity, buoyancy and variable thermal conductivity on mixed convection heat transfer due to an exponentially stretching sheet was discussed by Abel et al. [28]. They obtained solution numerically. In Yousif et al. [29] and Ellahi et al. [30], they have discussed MHD Carreau and non-Newtonian nanofluid flow over an exponentially and slippery walls, respectively. Unsteady flow with CNT-based MHD nanofluid, variable viscosity and a permeable shrinking surface have been discussed in Ahmed et al. [31]. See also Thoi et al. [32] for a different fluid flow aspect in a Y-shaped fin. Previous studies mostly concern with nanofluid with variable viscosity but these are devoid of variable thermal conductivity.
There exists a very extensive literature with and without nanofluid on the topic of a constant fluid properties. But not many studies were dedicated to explore the effects of variable fluid properties on nanofluid flow. To bridge that gap, the present research focuses on the effects of variable viscosity and variable thermal conductivity on the boundary layer nanofluid flow. The structure of the paper is as follows. In section 2, we formulate the fundamental physical problem's mathematical model. The constant and variable fluid characteristics are discussed in section 3. The numerical methods are outlined in section 4. Results and analysis are presented in section 5. Conclusion of the current work is drawn at the end in section 6.
2. Problem Formulation
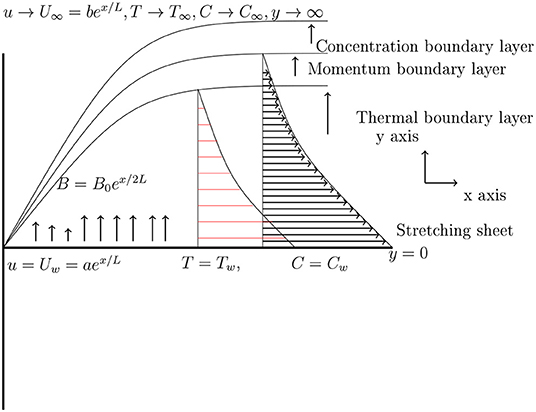
We consider a laminar, MHD nanofluid flow over an exponentially stretching sheet with thermal radiation. The sheet is situated at y = 0. A variable magnetic field has been applied normal to the sheet. Figure 1 is the geometry of the flow, in which x-axis is along and y-axis is taken as normal to the sheet.
Let is the wall velocity, whereas is a free stream velocity, in which stretching parameters a, b > 0. The sheet has been kept at constant wall temperature Tw and T∞ refers to the ambient temperature. Under the hypothesis of a low magnetic Reynolds number, the induced magnetic field is ignored. The boundary layer equations with Buongiorno model [33] which regulate the above flow are:
where the coordinates of velocities (u, v) are along x− and y− axes, respectively. μ is a fluid viscosity coefficient, B(x) is a variable magnetic field along the y− axis. Here T is the temperature, C is the nanoparticles concentration, cp is the specific heat constant, DB is the Brownian motion coefficient, DT is the thermophoretic diffusion coefficient, is the ratio of the effective heat capacity of the nanoparticle material to the heat capacity of the fluid and qr is the radiative heat flux. Appropriate boundary conditions complete the above system by:
Using the following similarity transformation on above equations which are defined as:
Equation (1) is identically satisfied. Moreover, when above similarity variables used in Equations (2), (3), and (4) which yields:
The boundary conditions transformed into:
where is a magnetic parameter, is a ratio of the free stream velocity to the velocity of the stretching sheet, is the Prandtl number, is the Brownian motion parameter, is the thermophoresis parameter, denotes the radiation parameter and is the Lewis number.
3. Analysis on Fluid Properties
This section comprises of two subsections. Firstly, an overview of the constant fluid properties will be presented followed by the discussion on variable fluid properties.
3.1. Case A: Constant Fluid Properties
For this case, Equations (7), (8), and (9) can be adjusted as follows to incorporate constant fluid properties:
3.2. Case B: Variable Fluid Properties
For this case, viscosity and thermal conductivity in Equations (7), (8), and (9) is considered variable and taken as a function of a temperature. For viscosity we write:
where we follow Andersson and Aarseth [7] and reference within to write above expression (14). In above γ is a fluid property. If To ≈ Tref then above formula (14) becomes:
here . If the above viscosity relation is incorporated in the Equation (7), then it can be rewritten as:
The variable thermal conductivity is expressed in terms of temperature by following Prasad et al. [12] as:
Under this above relation the mathematical form of Equation (8) can be described as:
To measure the roughness, heat transfer rate and mass transfer rate onto the surface, we calculate the skin friction coefficient Cf the local Nusselt number Nux and the local Sherwood number Shx, respectively, i.e.,
4. Numerical Procedure
4.1. Shooting Method
To apply the shooting technique to Cases A and B together with the boundary conditions, we transformed boundary value problem (BVP) into an initial value problem (IVP) and convert higher order ODEs into a system of first order ODEs. The Newton-Raphson technique was used to locate the root. After that, the order five Runge-Kutta method was implemented to determine the IVP solution. The shooting method is implemented in MATLAB. For Cases A and B, the system of first order ODEs are written as,
(a) Case A:
(b) Case B:
4.2. bvp4c
Using MATLAB bvp4c algorithm, BVP can even be solved. bvp4c solver employs the collocation technique in the background. It manages to find a solution after supplying initial guess, domain size and the number of points. Please see reference [34] for more detail and examples.
5. Results and Discussion
In Table 1, we compute the local Nusselt number and compared its values with published results for distinct parameters Prandtl number Pr0, radiation parameter Rd and magnetic parameter M.
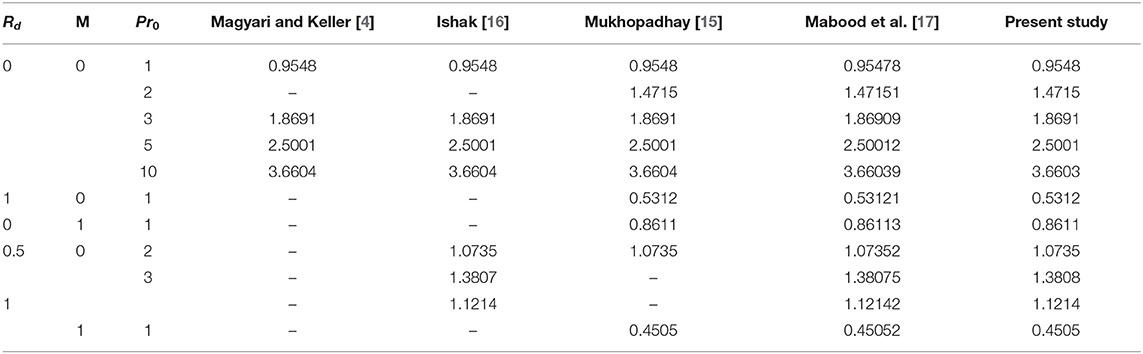
Table 1. (For Case A) Comparison of −θ′(0) for different values of M, Rd and Pr0, when λ = Nb = Nt = Le = 0.
Table 2 illustrates that the skin friction coefficient is not significantly changed whereas the local Nusselt number drops for ϵ and increases for the values of λ. The local Sherwood number grows with the rise of λ and ϵ. It is observed in Table 3 that the local Nusselt and the Sherwood numbers rises with a rise of λ but the skin friction coefficient held opposite behavior. For fixed values of λ = 0, 0.5 and an increase in viscosity parameter θr brings the increasing change in the skin friction coefficient but the local Nusselt and Sherwood numbers has shown decreasing behavior. Table 4 demonstrates that as Pro and Rd rises, there is a negligible change in the skin friction coefficient. But the local Nusselt numbers decreases and local Sherwood number increases by increasing the values of radiation parameter Rd. Moreover, the local Nusselt number increases by increasing Prandtl number but the local Sherwood number decreases.
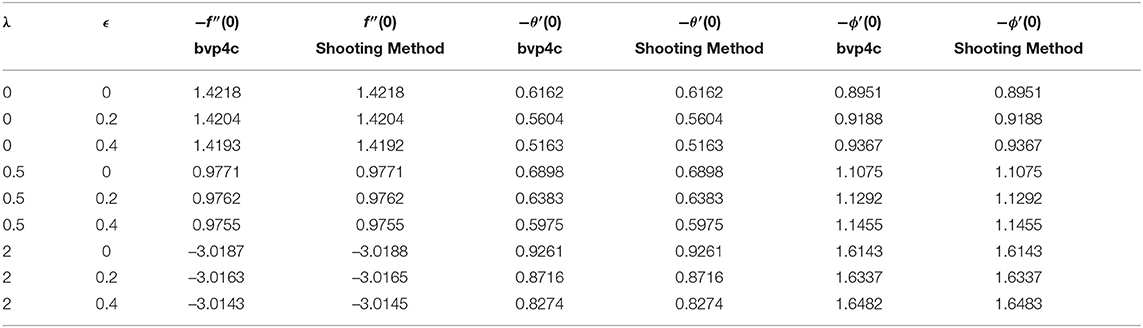
Table 2. (For Case B) Comparison of the values of f″(0), θ′(0) and ϕ′(0) for different values of ϵ and λ when M = λ = Rd = 0, Pr0 = 1, θr = −5, Le = 1.3.
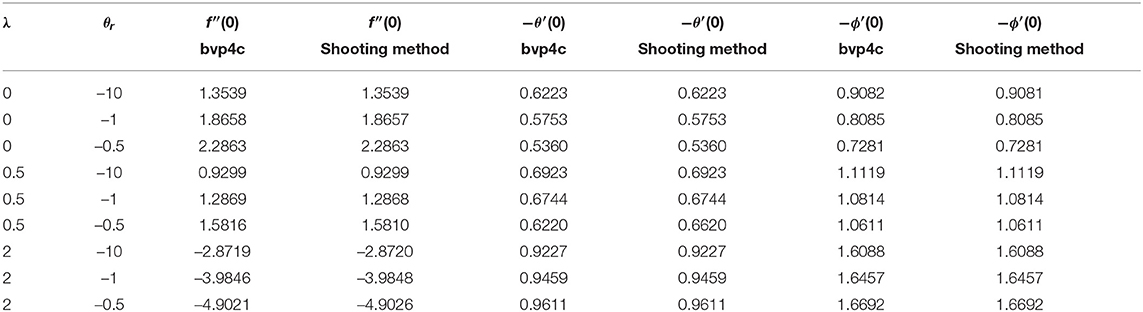
Table 3. (For Case B) Comparison of the values of f″(0) and θ′(0) for different values of θr and λ when M = 0, Pr0 = 10, ϵ = 0.
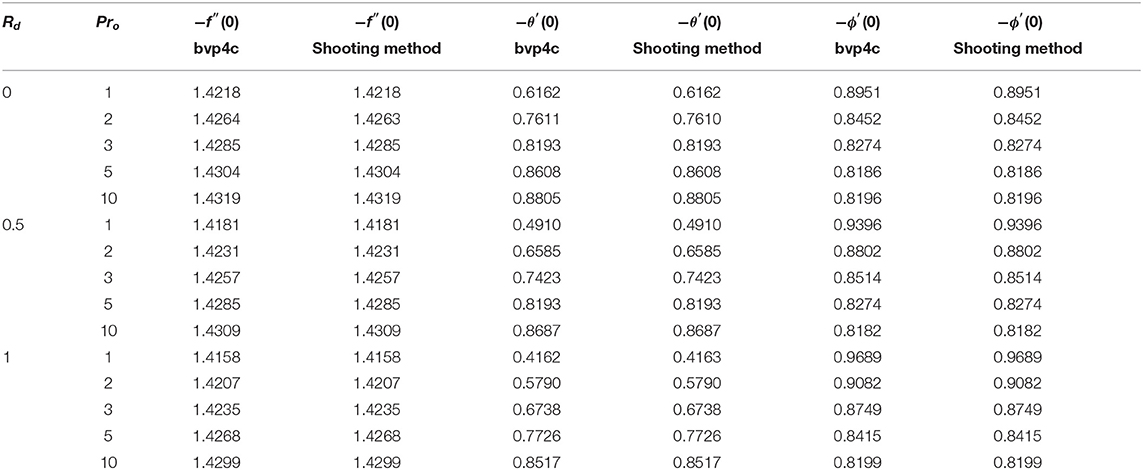
Table 4. (For Case B) Comparison of the values of f″(0) and θ′(0) for different values of Rd and Pr0 when M = λ = ϵ = 0, θr = −5, Nb = 0.8, Nt = 0.5, Le = 1.3.
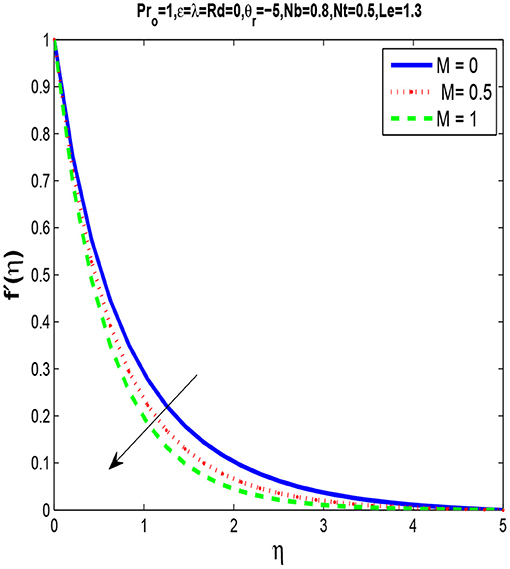
Figure 2 shows that the momentum boundary layer thickness is reduced with the increase in M. It happens because of a transverse magnetic field as it opposes the phenomenon of transport. The Lorentz force generates resistance to the fluid flow with a rise of M and slows down the velocity.
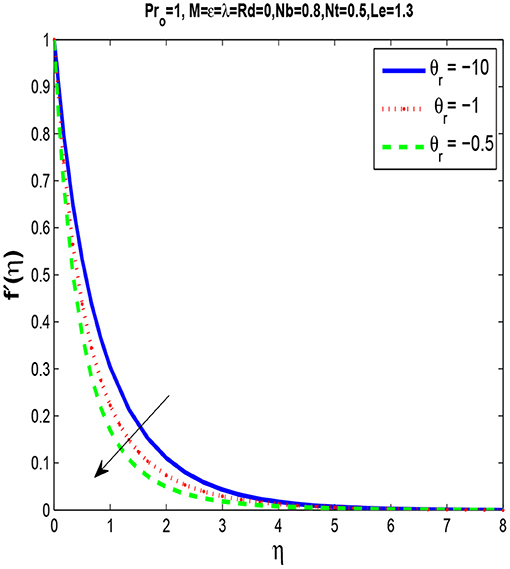
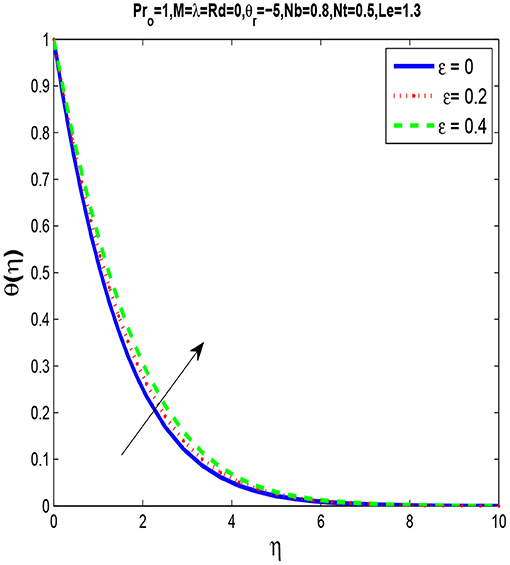
In Figure 3, we observe that by rising the viscosity parameter θr, a momentum boundary layer thins. Figure 4 shows that there is a rise in temperature profile with an increase in thermal conductivity parameter ϵ.
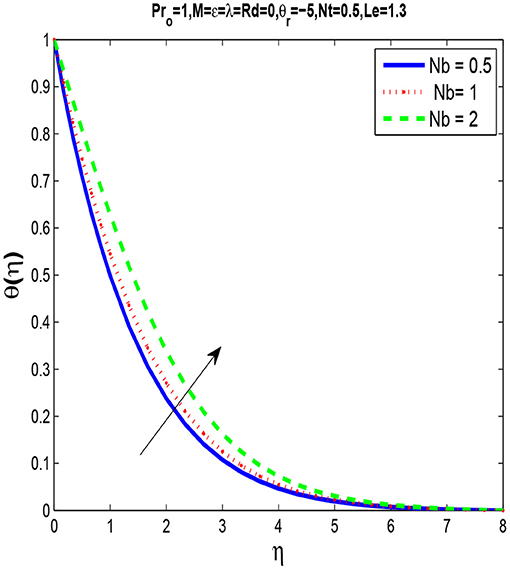
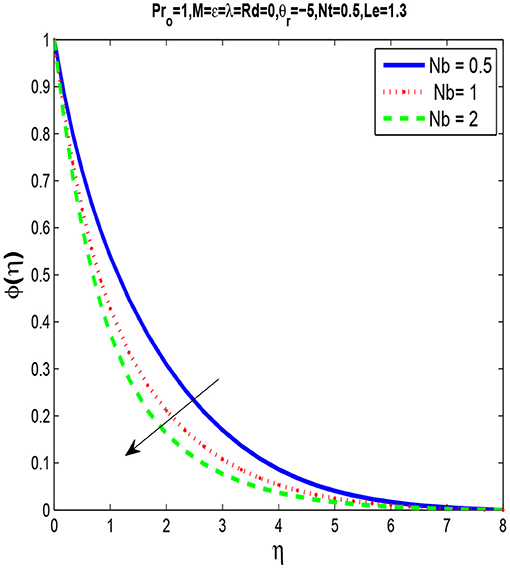
Figures 5, 6 are plotted for different values of Brownian motion parameter Nb and we observe that by increasing Nb thermal boundary layer thickness increases while concentration boundary layer decrease by increasing Nb.
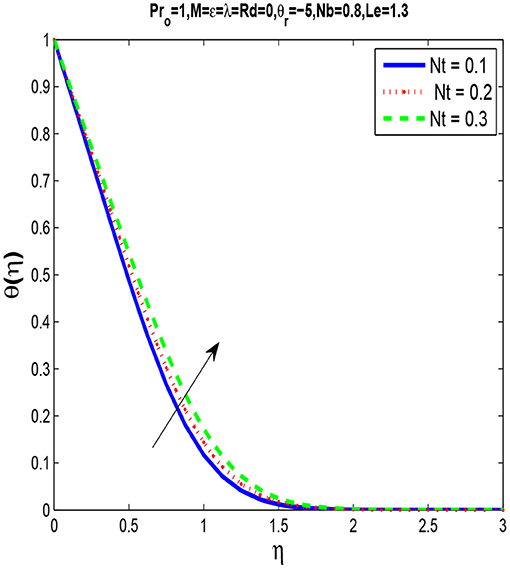
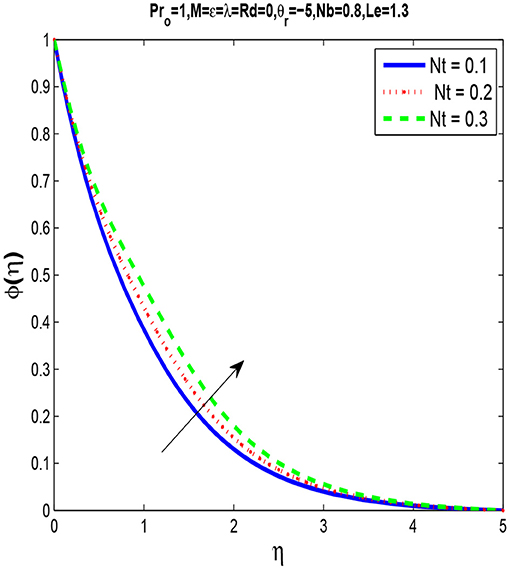
As seen in Figures 7, 8 that by increasing thermophoresis parameter Nt, temperature and concentration profiles increases.
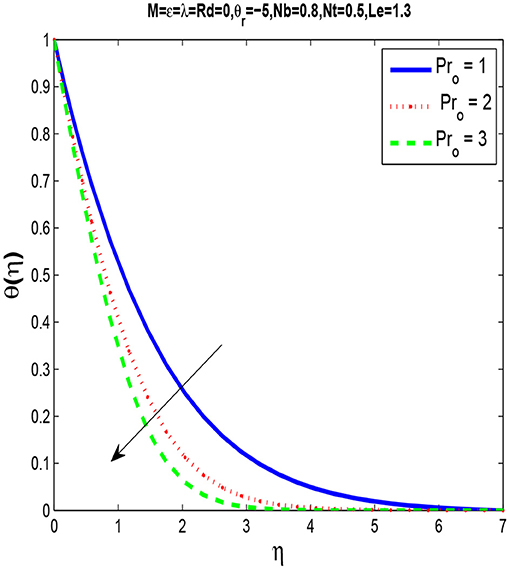
Figure 9 indicates that by increasing Pro the thermal boundary layer thickness decreases. This is because, when Pro increases, the thermal diffusivity decreases and thus the heat is diffused away from the heated surface more slowly and in consequence increase the temperature gradient at surface.
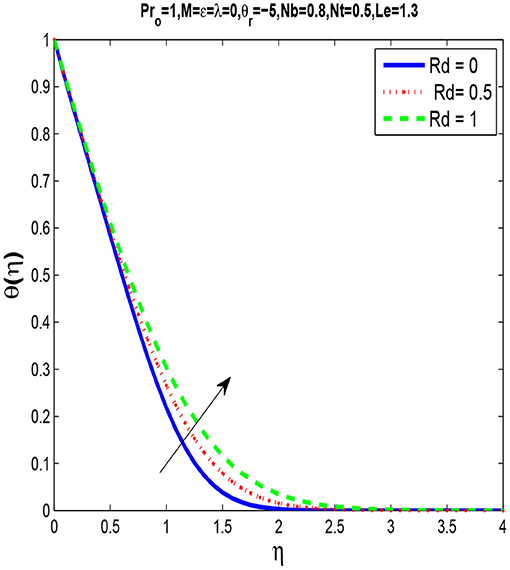
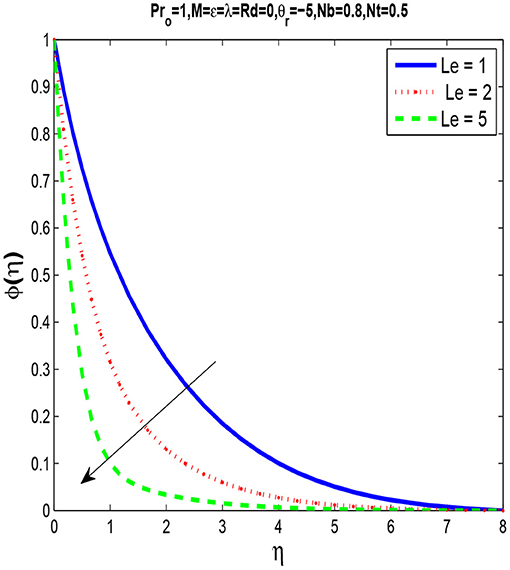
Figure 10 shows that temperature and thermal boundary layer thickness increases when the radiation parameter intensifies. Figure 11 describe the influence of the Lewis number Le on concentration profile. We observe that by increasing Le there is decrease in concentration profile. Lewis number is the ratio of Prandtl number and Schmidt number, so with the increase in Lewis number Le, molecular diffusivity decreases. As a result, increase in Le the nanoparticle fraction is lowered.
6. Conclusions
The current study offers the findings of a two-dimensional MHD flow of an incompressible fluid through an exponentially stretched sheet whereas treating viscosity and thermal conductivity constant in Case A and variable for Case B. The significance of various parameters on velocity, temperature and concentration is examined. The study's main results for Case B are as follows:
• Momentum boundary layer thickness decrease by increasing fluid viscosity parameter θr and magnetic parameter M.
• Thermal boundary layer thickness increases by increasing the thermal conductivity parameters ϵ, Brownian motion parameter Nb and thermophoretic parameter Nt.
• Thermal boundary layer thickness decreases by increasing the Prandtl number Pr0 whereas increases for radiation parameter Rd.
• Concentration boundary layer thickness increases by increasing thermophoretic parameter Nt whereas decreases by increasing Brownian motion parameter Nb and Lewis number Le.
Data Availability Statement
All datasets generated for this study are included in the article/supplementary material.
Author Contributions
MI collected the data and wrote the paper. MF made the analysis of the paper. TI made the geometry of problem and arrange the setting of the paper.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
1. Sakiadis BC. Boundary layer behavior on continuous solid surfaces: I. Boundary layer equations for two-dimensional and axisymmetric flow. AIChE J. (1961) 7:26–8. doi: 10.1002/aic.690070108
2. Blasius H. Grenzschichten in Flussigkeiten mit Kleiner Reibung. Z Angew Math Phys. (1908) 56:1–37.
4. Magyari E, Keller B. Heat and mass transfer in the boundary layers on an exponentially stretching continuous surface. J Phys D Appl Phys. (1999) 32:577.
5. Elbashbeshy EMA. Heat transfer over an exponentially stretching continuous surface with suction. Arch Mechan. (2001) 53:643–51.
6. Norfifah B, Ishak A, Pop I. Boundary layer flow and heat transfer with variable fluid properties on a moving flat plate in a parallel free stream. J Appl Math. (2012) 2012:372623. doi: 10.1155/2012/372623
7. Andersson HI, Jan B. Aarseth. Sakiadis flow with variable fluid properties revisited. Int J Eng Sci. (2007) 45:554–61. doi: 10.1016/j.ijengsci.2007.04.012
8. Makinde OD, Mabood F, Khan WA, Tshehla MS. MHD flow of a variable viscosity nanofluid over a radially stretching convective surface with radiative heat. J Mol Liquids. (2016) 219:624–30. doi: 10.1016/j.molliq.2016.03.078
9. Mukhopadhyay S, Layek GC, Samad SkA. Study of MHD boundary layer flow over a heated stretching sheet with variable viscosity. Int J Heat Mass Transfer. (2005) 48:4460–6. doi: 10.1016/j.ijheatmasstransfer.2005.05.027
10. Elbashbeshy EMA, Bazid MAA. The effect of temperature-dependent viscosity on heat transfer over a continuous moving surface. J Phys D Appl Phys. (2000) 33:2716. doi: 10.1088/0022-3727/33/21/309
11. Poply V, Singh P, Yadav AK. A study of Temperature-dependent fluid properties on MHD free stream flow and heat transfer over a non-linearly stretching sheet. Proc Eng. (2015) 127:391–7. doi: 10.1016/j.proeng.2015.11.386
12. Prasad KV, Vajravelu K, Datti PS. The effects of variable fluid properties on the hydro-magnetic flow and heat transfer over a non-linearly stretching sheet. Int J Thermal Sci. (2010) 49:603–10. doi: 10.1016/j.ijthermalsci.2009.08.005
13. Raptis A, Christos P, Takhar HS. Effect of thermal radiation on MHD flow. Appl Math Comput. (2004) 153:645–9. doi: 10.1016/S0096-3003(03)00657-X
14. RLV Renuka D, Poornima T, Bhaskar Reddy N, Venkataramana S. Radiation and mass transfer effects on MHD boundary layer flow due to an exponentially stretching sheet with heat source. Int J Eng Innovative Technol. (2014) 3:33–9.
15. Mukhopadhyay S. Slip effects on MHD boundary layer flow over an exponentially stretching sheet with suction/blowing and thermal radiation. Ain Shams Eng J. (2013) 4:485–91. doi: 10.1016/j.asej.2012.10.007
16. Ishak A. MHD boundary layer flow due to an exponentially stretching sheet with radiation effect. Sains Malaysiana. (2011) 40:391–5.
17. Mabood F, Khan WA, Md Ismail AI. MHD flow over exponential radiating stretching sheet using homotopy analysis method. J King Saud Univ Eng Sci. (2017) 29:68–74. doi: 10.1016/j.jksues.2014.06.001
18. Bidin B, Nazar R. Numerical solution of the boundary layer flow over an exponentially stretching sheet with thermal radiation. Eur J Sci Res. (2009) 33:710–7.
19. Poornima T, Bhaskar Reddy N. Radiation effects on MHD free convective boundary layer flow of nanofluids over a nonlinear stretching sheet. Adv Appl Sci Res. (2013) 4:190–202.
20. Choi SUS, Eastman JA. Enhancing Thermal Conductivity of Fluids With Nanoparticles. Argonne National Lab. (1995).
21. Nield DA, Kuznetsov AV. The Cheng-Minkowycz problem for natural convective boundary-layer flow in a porous medium saturated by a nanofluid. Int J Heat Mass Transf. (2009) 52:5792–5. doi: 10.1016/j.ijheatmasstransfer.2009.07.024
22. Khan WA, Makinde OD, Khan ZH. Non-aligned MHD stagnation point flow of variable viscosity nanofluids past a stretching sheet with radiative heat. Int J Heat Mass Transf. (2016) 96:525–34. doi: 10.1016/j.ijheatmasstransfer.2016.01.052
23. Bachok N, Ishak A, Pop I. Boundary layer stagnation-point flow and heat transfer over an exponentially stretching/shrinking sheet in a nanofluid. Int J Heat Mass Transf. (2012) 55:8122–8. doi: 10.1016/j.ijheatmasstransfer.2012.08.051
24. Abu-Nada E, Masoud Z, Oztop HF, Campo A. Effect of nanofluid variable properties on natural convection in enclosures. Int J Therm Sci. (2010) 49:479–91. doi: 10.1016/j.ijthermalsci.2009.09.002
25. Malik MY, Naseer M, Nadeem S, Rehman A. The boundary layer flow of Casson nanofluid over a vertical exponentially stretching cylinder. Appl Nanosci. (2014) 4:869–73. doi: 10.1007/s13204-013-0267-0
26. Eid MR. Chemical reaction effect on MHD boundary-layer flow of two-phase nanofluid model over an exponentially stretching sheet with a heat generation. J Mol Liquids. (2016) 220:718–25. doi: 10.1016/j.molliq.2016.05.005
27. Gangaiah T, Saidulu N, Venkata Lakshmi A. Magnetohydrodynamic flow of nanofluid over an exponentially stretching sheet in presence of viscous dissipation and chemical reaction. J Nanofluids. (2018) 7:439–48. doi: 10.1166/jon.2018.1465
28. Abel M. Mahantesh S, Nandeppanavar M, Basanagouda V. Effects of variable viscosity, buoyancy and variable thermal conductivity on mixed convection heat transfer due to an exponentially stretching surface with magnetic field. Proc Natl Acad Sci India Sec A Phys Sci. (2017) 87:247–56. doi: 10.1007/s40010-016-0338-1
29. Yousif MA, Farhan Ismael H, Abbas T, Ellahi R. Numerical study of momentum and heat transfer of MHD Carreau nanofluid over an exponentially stretched plate with internal heat source/sink and radiation. Heat Transf Res. (2019) 50:649–58. doi: 10.1615/HeatTransRes.2018025568
30. Ellahi R, Zeeshan A, Hussain F, Abbas T. Thermally charged MHD Bi-phase flow coatings with non-Newtonian nanofluid and Hafnium particles along slippery walls. Coatings. (2019) 9:300. doi: 10.3390/coatings9050300
31. Ahmed Z, Nadeem S, Saleem S, Ellahi R. Numerical study of unsteady flow and heat transfer CNT-based MHD nanofluid with variable viscosity over a permeable shrinking surface. Int J Numer Methods Heat Fluid Flow. (2019). doi: 10.1108/HFF-04-2019-0346. [Epub ahead of print].
32. Nguyen-Thoi T, Bhatti MM, Ali JA, Mustafa Hamad S, Sheikholeslami M, Shafee A, Haq R. Analysis on the heat storage unit through a Y-shaped fin for solidification of NEPCM. J Mol Liquids. (2019) 292:111378. doi: 10.1016/j.molliq.2019.111378
34. Shampine LF, Kierzenka J, Reichelt MW. Solving boundary value problems for ordinary differential equations in MATLAB with bvp4c. Tutor Notes. (2000) 2000:1–27.
Nomenclature
Keywords: magnetohydrodynamics (MHD), exponentially stretching sheet, nanofluid, shooting method, constant and variable fluid properties
Citation: Irfan M, Farooq MA and Iqra T (2019) Magnetohydrodynamic Free Stream and Heat Transfer of Nanofluid Flow Over an Exponentially Radiating Stretching Sheet With Variable Fluid Properties. Front. Phys. 7:186. doi: 10.3389/fphy.2019.00186
Received: 11 September 2019; Accepted: 29 October 2019;
Published: 15 November 2019.
Edited by:
Muhammad Mubashir Bhatti, Shanghai University, ChinaReviewed by:
Tehseen Abbas, University of Education Lahore, PakistanAnwar Shahid, International Islamic University, Islamabad, Pakistan
Copyright © 2019 Irfan, Farooq and Iqra. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Muhammad Irfan, aXJmYW4uYWtiYXIzMEBnbWFpbC5jb20=
 Muhammad Irfan
Muhammad Irfan Muhammad Asif Farooq
Muhammad Asif Farooq Tousif Iqra
Tousif Iqra