Fractional Approach for Equation Describing the Water Transport in Unsaturated Porous Media With Mittag-Leffler Kernel

In this paper, we find the solution for a fractional Richards equation describing the water transport in unsaturated porous media using the q-homotopy analysis transform method (q-HATM). The proposed technique is to use graceful amalgamations of the Laplace transform technique with the q-homotopy analysis scheme as well as the fractional derivative that is defined with the Atangana-Baleanu (AB) operator. The fixed point hypothesis is considered in order to demonstrate the existence and uniqueness of the obtained solution for the proposed fractional order model. In order to validate and illustrate the efficiency of the future technique, we analyze the projected model in terms of fractional order. Meanwhile, the physical behavior of the q-HATM solutions are captured in terms of plots for diverse fractional order and the numerical simulation is also demonstrated. The achieved results illuminate that the future algorithm is easy to implement, highly methodical, effective, and very accurate in its analysis of the behavior of non-linear differential equations of fractional order that arise in the connected areas of science and engineering.

Introduction

Fractional calculus (FC) was originated in Newton's time, but, lately, it has fascinated and captured the attention of many scholars. For the last 30 years, the most intriguing leaps in scientific and engineering applications have been found within the framework of FC. The concept of the fractional derivative has been industrialized due to the complexities associated with a heterogeneous phenomenon. The fractional differential operators are capable of capturing the behavior of multifaceted media as they have diffusion processes. It has been a very essential tool, and many problems can be illustrated more conveniently and more accurately with differential equations having an arbitrary order. Due to the swift development of mathematical techniques that use computer software, many researchers started to work on generalized calculus to present their viewpoints while analyzing many complex phenomena.

Numerous pioneering directions are prescribed for the diverse definitions of fractional calculus by many senior researchers, and these have prearranged the foundation [1–6]. Calculus with fractional order is associated with practical ventures and is extensively employed within nanotechnology [7], optics [8], human diseases [9], chaos theory [10], and other areas [11–39]. The numerical as well as analytical solutions for these equations illustrate that these models have an important role in portraying the nature of non-linear problems within connected areas of science.

In order to illustrate the importance of the novel fractional order derivative and future scheme, we, in the present framework, consider the Richards equation, which plays a vital role in describing the nature of the porous medium as well as the penetration of unsaturated regions in the soil. In 1931, Lorenzo A. Richards was the first person to pioneer work on the unsaturated porous material in order to model water movement. Later, he derived an equation based on continuum mechanics, which govern the water flow in the soil [40]. In the proposed model for the momentum equation, the continuity equation is an amalgam with Darcy's law, and is defined in a one-dimensional form as follows, with soil water diffusivity symbolized by ρ and hydraulic conductivity by σ for unsaturated soil moisture content u

$\begin{array}{ll}\frac{\partial u}{\partial t}=\frac{\partial }{\partial z}\left(\rho \frac{\partial u}{\partial z}-\sigma \right),& (1)\end{array}$

where z designates the elevation above a vertical datum. Recently, many authors employed numerical as well as analytical techniques in order to analyze and predict the suitable models for parameters in the equation and solve the governing equation of unsaturated flow in soils. Meanwhile, three models are generally applied, namely (i) the exponential model, (ii) the van Genuchten model, and (iii) the Brook-Coreysmodel (BCM). Among these models, BCM is extensively applied due to its well-defined configuration and because it is associated with the largest pore size. The following equations describe the complete wet ability of the BC model [41, 42]:

$\begin{array}{l}\sigma \left(u\right)={\sigma }_0{u}^k,\\ \rho \left(u\right)={\rho }_0\left(n+1\right)u^n,& (2)\end{array}$

where σ₀, k, ρ₀, and n are constants denoting particle shape, pore-size distribution and many other soil properties. For n = 0 and k = 2, Equation (2) simplified it to the classic Burgers equation [43, 44], and some particular values signify the generalized Burgers equation, which is essential to describing the important physical phenomena. In the present study, we consider that BCM employed the RC equation. In this case, for the (n, 1) order, the RC equation coincides with the Burgers equation, and this is presented here [45, 46]:

$\begin{array}{ll}{u}_t+a{\left(u^n\right)}_x+b{u}_{xx}=0,a,b\ne 1,n\ge 1.& (3)\end{array}$

The analytical solution for the above equation is presented:

$\begin{array}{ll}u\left(x,t\right)={\left(\frac{c}{2a}\left(1+\tanh \left(\frac{c\left(n-1\right)}{2b}\left(x-ct\right)\right)\right)\right)}^{\frac{1}{n-1}}.& (4)\end{array}$

In the present scenario, many important and non-linear models are methodically and effectively analyzed with the help of fractional calculus. There have been diverse definitions that have been suggested by many senior research scholars like, Riemann, Liouville, Caputo, and Fabrizio. However, these definitions have their own limitations. The Riemann-Liouville derivative is unable to explain the importance of the initial conditions; the Caputo derivative has overcome this shortcoming but cannot explain the singular kernel of the phenomena. In 2015, Caputo and Fabrizio solved the above issues [47], and many researchers consult this derivative in order to analyze and find the solution for diverse classes of non-linear complex problems. Some issues, however, were pointed out in the CF derivative; non-singular kernel and non-local properties are very essential in describing the physical behavior and nature of the non-linear problems. In 2016, Atangana and Baleanu introduced and natured a novel fractional derivative, namely the AB derivative. This novel derivative was defined with the aid of Mittag-Leffler functions [48]. This fractional derivative buried all the above-cited issues and helps us to understand the natural phenomena in the systematic and effective way.

In this framework, we consider the fractional RC equation of the form

$\begin{array}{ll}{}_a^{ABC}{D}_t^{\alpha }u\left(x,t\right)+a{\left(u^n\right)}_x+b{u}_{xx}=0,& (5)\end{array}$

where α is fractional order of the system and defined with AB fractional operator, u is the water content with depth x. The fractional order is introduced in order to incorporate the memory effects and hereditary consequence in the system, and these properties aid us in capturing the essential physical properties of the complex problems.

Recently, many mathematicians and physicists have developed very effective and more accurate methods in order to find and analyze solutions for complex and non-linear problems that have arisen in science and technology. In connection with this is the homotopy analysis method (HAM) proposed by Chinese Mathematician Liao Shijun [49, 50]. HAM has been profitably and effectively applied to study the behavior of non-linear problems without perturbation or linearization. But, for computational work, HAM requires significant time and computer memory. To overcome this, there is a possibility of using an amalgamation of the considered method and well-known transformation techniques.

In the present investigation, we analyzed the nature of the q-homotopy analysis transform method (q-HATM) solution for the FCDG equation by applying q-HATM. The future algorithm is the combination of q-HAM with LT [51]. The method of the considered scheme is merging two strong methods to solve linear and non-linear fractional differential equations both analytically as well as numerically. The future technique has many sturdy properties, including a non-local effect, straight forward solution procedure, and a promising large convergence region; moreover, it is free from any assumptions, discretization, and perturbation. Recently, due to its reliability and efficacy, the considered method has been exceptionally applied by many researchers to understand physical behavior in diverse classes of complex problems [52–60]. The novelty of the future method is that it aids a modest algorithm to evaluate the solution, and it is natured by the homotopy and axillary parameters, which provide the rapid convergence of the obtained solution for a non-linear portion of the given problem. Meanwhile, it has prodigious generality because it plausibly contains the results obtained by many algorithms like q-HAM, HPM, ADM and some other traditional techniques. The considered method can preserve great accuracy while decreasing the computational time and work in comparison with other methods.

The considered non-linear model recently caught the attention of researchers from different areas of science. Since RC equation plays a significant role in portraying several complex phenomena, many authors have found and analyzed the solution using analytical as well as numerical schemes; for instance, authors in [61] considered analytical techniques and found solutions for the considered model with arbitrary surface boundary conditions, and authors in [62] presented the compression approximation and infiltration of the RC equation with an analytical solution, authors in [45] applied the Adomian decomposition scheme, and authors in [46] applied HAM in order to find the approximated analytical solution. In this paper, we made an attempt to find the solution for the FRC equation using q-HATM.

Preliminaries

Recently, many authors considered these derivatives to analyze a diverse class of models in comparison with classical order as well as other fractional derivatives, and they prove that the AB derivative is more effective while analyzing the nature and physical behavior of the models [63, 64]. Here, we define the basic notion of Atangana-Baleanu derivatives and integrals [48].

Definition 1. The fractional Atangana-Baleanu-Caputo derivative for a function f ∈ H¹ (a, b) (b > a, α ∈ [0, 1]) is presented:

$\begin{array}{ll}{}_a^{ABC}{D}_t^{\alpha }\left(f(t)\right)=\frac{ℬ\left[\alpha \right]}{1-\alpha }{\displaystyle {\int }_a^t{f}^{\prime }}\left(\vartheta \right)E_{\alpha }\left[\alpha \frac{{\left(t-\vartheta \right)}^{\alpha }}{\alpha -1}\right]d\vartheta .& (6)\end{array}$

Definition 2. The AB derivative of fractional order for a function f ∈ H¹ (a, b), b > a, α ∈ [0, 1] in the Riemann-Liouville sense is presented:

$\begin{array}{ll}{}_a^{ABR}{D}_t^{\alpha }\left(f(t)\right)=\frac{ℬ\left[\alpha \right]}{1-\alpha }\frac{d}{dt}{\displaystyle {\int }_a^{t}f\left(\vartheta \right)E_{\alpha }\left[\alpha \frac{{\left(t-\vartheta \right)}^{\alpha }}{\alpha -1}\right]d\vartheta }.& (7)\end{array}$

Definition 3. The fractional AB integral related to the non-local kernel is defined by

$\begin{array}{ll}{}_a^{AB}{I}_t^{\alpha }\left(f(t)\right)=\frac{1-\alpha }{ℬ\left[\alpha \right]}f\left(t\right)+\frac{\alpha }{ℬ\left[\alpha \right]\Gamma \left(\alpha \right)}{\displaystyle {\int }_a^{t}f\left(\vartheta \right){\left(t-\vartheta \right)}^{\alpha -1}d\vartheta }.& (8)\end{array}$

Definition 4. The Laplace transform (LT) of AB derivative is defined by

$\begin{array}{ll}L\left[{}_0^{ABR}{D}_t^{\alpha }(f(t))\right]=\frac{ℬ\left[\alpha \right]}{1-\alpha }\frac{s^{\alpha }L\left[f\left(t\right)\right]-s^{\alpha -1}f\left(0\right)}{s^{\alpha }+\left(\alpha /(1-\alpha )\right)}.& (9)\end{array}$

Theorem 1. The following Lipschitz conditions, respectively, hold true for both Riemann-Liouville and AB derivatives defined in Equations (6) and (7) [48],

$\begin{array}{ll}\Vert {}_a^{ABC}{D}_t^{\alpha }{f}_1\left(t\right){-}_a^{ABC}{D}_t^{\alpha }{f}_2\left(t\right)\Vert <K_1\Vert f_2\left(x\right)-f_2\left(x\right)\Vert ,& (10)\end{array}$

and

$\begin{array}{ll}\Vert {}_a^{ABC}{D}_t^{\alpha }{f}_1\left(t\right){-}_a^{ABC}{D}_t^{\alpha }{f}_2\left(t\right)\Vert <K_2\Vert f_1\left(x\right)-f_2\left(x\right)\Vert .& (11)\end{array}$

Theorem 2. The time-fractional differential equation ${}_a^{ABC}{D}_t^{\alpha }{f}_1\left(t\right)=s\left(t\right)$ has a unique solution, which is defined as [48]

$\begin{array}{ll}f\left(t\right)=1-\frac{\alpha }{ℬ\left[\alpha \right]}s\left(t\right)+\frac{\mu }{ℬ\left[\alpha \right]\Gamma \left(\alpha \right)}{\displaystyle {\int }_a^{t}s\left(\varsigma \right){\left(t-\varsigma \right)}^{\alpha -1}d\varsigma }.& (12)\end{array}$

Fundamental Idea of the Proposed Scheme

Here, we consider the arbitrary order differential equation in order to demonstrate the basic solution procedure [65, 66]

$\begin{array}{l}{}_a^{ABC}{D}_t^{\alpha }v\left(x,t\right)+ℛv\left(x,t\right)+{N}v\left(x,t\right)\\ =f\left(x,t\right),n-1<\alpha \le n,& (13)\end{array}$

with the initial condition

$\begin{array}{ll}v\left(x,0\right)=g\left(x\right),& (14)\end{array}$

where ${}_a^{ABC}{D}_t^{\alpha }v(x,t)$ symbolize the AB derivative of v(x, t). On using the LT on Equation (13), we have after simplification

$\begin{array}{l}ℒ\left[v\left(x,t\right)\right]-\frac{g\left(x\right)}{s}+\frac{1}{ℬ\left[\alpha \right]}\left(1-\alpha +\frac{\alpha }{s^{\alpha }}\right)\{ℒ\left[ℛv\left(x,t\right)\right]\\ +ℒ\left[{N}v\left(x,t\right)\right]-ℒ\left[f\left(x,t\right)\right]\}=0.& (15)\end{array}$

The non-linear operator is presented as

$\begin{array}{l}{N}\left[\phi \left(x,t;q\right)\right]=ℒ\left[\phi \left(x,t;q\right)\right]-\frac{g\left(x\right)}{s}\\ +\frac{1}{ℬ\left[\alpha \right]}\left(1-\alpha +\frac{\alpha }{s^{\alpha }}\right)\{ℒ\left[ℛ\phi \left(x,t;q\right)\right]\\ +L\left[{N}\phi \left(x,t;q\right)\right]-L\left[f\left(x,t\right)\right]\}.& (16)\end{array}$

Here, φ(x, t; q) is the real valued function with respect to x, t and $\left(q\in \left[0,\frac{1}{n}\right]\right)$. Now, we define a homotopy as follows

$\begin{array}{ll}\left(1-nq\right)ℒ\left[\phi \left(x,t;q\right)-v_0\left(x,t\right)\right]=\hslash q{N}\left[\phi \left(x,t;q\right)\right],& (17)\end{array}$

where L is signifies LT, $q\in \left[0,\frac{1}{n}\right](n\ge 1)$ is the embedding parameter and ℏ ≠ 0 is an auxiliary parameter. For q = 0 and $q=\frac{1}{n}$, the results given below are hold true

$\begin{array}{ll}\phi \left(x,t;0\right)=v_0\left(x,t\right),\phi \left(x,t;\frac{1}{n}\right)=v\left(x,t\right).& (18)\end{array}$

Now, by intensifying q from 0 to $\frac{1}{n}$, then φ(x, t; q) varies from v₀(x, t) to v(x, t). By using the Taylor theorem near to q, we define φ(x, t; q) in series form and then we get

$\begin{array}{ll}\phi \left(x,t;q\right)=v_0\left(x,t\right)+{\displaystyle {\sum }_{m=1}^{\infty }{v}_m\left(x,t\right)q^m},& (19)\end{array}$

where

$\begin{array}{ll}{v}_m\left(x,t\right)=\frac{1}{m!}\frac{{\partial }^m\phi (x,t;q)}{\partial q^m}{|}_{q=0}.& (20)\end{array}$

The series (16) converges at $q=\frac{1}{n}$ for the proper chaise of v₀ (x, t), n and ℏ. Then

$\begin{array}{ll}v\left(x,t\right)=v_0\left(x,t\right)+{\displaystyle {\sum }_{m=1}^{\infty }{v}_m\left(x,t\right){\left(\frac{1}{n}\right)}^m}.& (21)\end{array}$

On m-times differentiating Equation (17) with q and lately dividing by m! and then substituting q = 0, we get

$\begin{array}{ll}ℒ[v_m\left(x,t\right)-k_m{v}_{m-1}\left(x,t\right)]=\hslash {\Re }_m\left({\overrightarrow{v}}_{m-1}\right),& (22)\end{array}$

where the vectors are defined as

$\begin{array}{ll}{\overrightarrow{v}}_m=\left\{v_0\left(x,t\right),v_1\left(x,t\right),\dots ,v_m\left(x,t\right)\right\}.& (23)\end{array}$

On employing the inverse LT on Equation (22), we have

$\begin{array}{ll}{v}_m\left(x,t\right)={\text{k}}_m{v}_{m-1}\left(x,t\right)+\hslash {ℒ}^{-1}[{\Re }_m\left({\overrightarrow{v}}_{m-1}\right),& (24)\end{array}$

where

$\begin{array}{l}{\Re }_m\left({\overrightarrow{v}}_{m-1}\right)=L\left[v_{m-1}\left(x,t\right)\right]-\left(1-\frac{{\text{k}}_m}{n}\right)\\ \left(\frac{g\left(x\right)}{s}+\frac{1}{ℬ\left[\alpha \right]}\left(1-\alpha +\frac{\alpha }{s^{\alpha }}\right)L\left[f\left(x,t\right)\right]\right)\\ +\frac{1}{ℬ\left[\alpha \right]}\left(1-\alpha +\frac{\alpha }{s^{\alpha }}\right)L\left[R{v}_{m-1}+{\mathscr{H}}_{m-1}\right],& (25)\end{array}$

and

$\begin{array}{ll}{\text{k}}_m=\{\begin{array}{c}0,m\le 1,\\ n,m>1.\end{array}& (26)\end{array}$

In Equation (25), ${\mathscr{H}}_m$ signifies a homotopy polynomial and presented as follows

$\begin{array}{l}{\mathscr{H}}_m=\frac{1}{m!}{\left[\frac{{\partial }^m\phi \left(x,t;q\right)}{\partial q^m}\right]}_{q=0}\text{ and }\phi \left(x,t;q\right)\\ ={\phi }_0+q{\phi }_1+q^2{\phi }_2+\dots .& (27)\end{array}$

By the aid of Equations (24) and (25), one can get

$\begin{array}{l}{v}_m\left(x,t\right)=\left({\text{k}}_m+\hslash \right)v_{m-1}\left(x,t\right)-\left(1-\frac{{\text{k}}_m}{n}\right){ℒ}^{-1}\\ \left(\frac{g\left(x\right)}{s}+\frac{1}{ℬ\left[\alpha \right]}\left(1-\alpha +\frac{\alpha }{s^{\alpha }}\right)L\left[f\left(x,t\right)\right]\right)\\ +\hslash {ℒ}^{-1}\left\{\frac{1}{ℬ\left[\alpha \right]}\left(1-\alpha +\frac{\alpha }{s^{\alpha }}\right)L\left[R{v}_{m-1}+{\mathscr{H}}_{m-1}\right]\right\}.& (28)\end{array}$

Then, the terms of v_m(x, t) we can obtain using the Equation (28). The q-HATM series solution is presented as

$\begin{array}{ll}v\left(x,t\right)={\displaystyle \sum _{m=0}^{\infty }{v}_m\left(x,t\right)}.& (29)\end{array}$

Solution for FRC Equation

In order to present the solution procedure and efficiency of the future scheme, in this segment we consider the DSW equation of fractional order with two distinct cases. Further, by the help of obtained results we made an attempt to capture the behavior of q-HATM solution for different fractional order. By the help of Equation (5) for the function of cubic water content and constant, we have

$\begin{array}{ll}{}_a^{ABC}{D}_t^{\alpha }u\left(x,t\right)+u^2{u}_x-u_{xx}=0,0<\alpha \le 1,& (30)\end{array}$

with initial conditions

$\begin{array}{ll}u\left(x,0\right)=u_0\left(x,t\right).& (31)\end{array}$

Taking LT on Equation (29) and then using Equation (30), we get

$\begin{array}{l}L\left[u\left(x,t\right)\right]=\frac{1}{s}\left(u_0\left(x,t\right)\right)\\ +\frac{1}{ℬ\left[\alpha \right]}\left(1-\alpha +\frac{\alpha }{s^{\alpha }}\right)L\left\{u^2{u}_x-u_{xx}\right\}.& (32)\end{array}$

The non-linear operator N is presented with the help of future algorithm as below

$\begin{array}{l}N\left[\phi \left(x,t;q\right)\right]=L\left[\phi \left(x,t;q\right)\right]-\frac{1}{s}\left(u_0\left(x,t\right)\right)\\ +\frac{1}{ℬ\left[\alpha \right]}\left(1-\alpha +\frac{\alpha }{s^{\alpha }}\right)\\ L\left\{\phi \left(x,t;q\right)\frac{\partial \phi }{\partial x}\left(x,t;q\right)-\phi \left(x,t;q\right)\right\}.& (33)\end{array}$

The deformation equation of m-th order by the help of q-HATM at ℋ(x, t) = 1, is given as follows

$\begin{array}{ll}L\left[u_m\left(x,t\right)-{\text{k}}_m{u}_{m-1}\left(x,t\right)\right]=\hslash {\Re }_m\left[{\overrightarrow{u}}_{m-1}\right],& (34)\end{array}$

where

$\begin{array}{l}{\Re }_m\left[{\overrightarrow{u}}_{m-1}\right]=L\left[u_{m-1}\left(x,t\right)\right]-\left(1-\frac{{\text{k}}_m}{n}\right)\left\{\frac{1}{s}\left(u_0\left(x,t\right)\right)\right\}\\ +\frac{1}{ℬ\left[\alpha \right]}\left(1-\alpha +\frac{\alpha }{s^{\alpha }}\right)\\ L\{{\displaystyle {\sum }_{j=0}^i{\displaystyle {\sum }_{i=0}^{m-1}{u}_j{u}_{i-j}\frac{\partial u_{m-1-i}}{\partial x}}}-\frac{{\partial }^2{u}_{m-1}}{\partial x^2}\}.& (35)\end{array}$

On applying inverse LT on Equation (34), it reduces to

$\begin{array}{ll}{u}_m\left(x,t\right)={\text{k}}_m{u}_{m-1}\left(x,t\right)+\hslash L^{-1}\left\{{\Re }_m\left[{\overrightarrow{u}}_{m-1}\right]\right\}.& (36)\end{array}$

On simplifying the above equation systematically by using u₀ (x, t), we can evaluate the terms of the series solution

$\begin{array}{ll}u\left(x,t\right)=u_0\left(x,t\right)+{\displaystyle \sum _{m=1}^{\infty }{u}_m\left(x,t\right){\left(\frac{1}{n}\right)}^m}.& (37)\end{array}$

Existence of Solutions for the Future Model

Here, we considered the fixed-point theorem in order to demonstrate the existence of the solution for the proposed model. Since the considered model cited in Equation (30) is non-local as well as complex, there are no particular algorithms or methods that exist to evaluate the exact solutions. However, under some particular conditions, the existence of the solution is assured. Now, Equation (30) is considered:

$\begin{array}{ll}{}_0^{ABC}{D}_t^{\alpha }\left[u\left(x,t\right)\right]={G}\left(x,t,u\right).& (38)\end{array}$

The foregoing system is transformed to the Volterra integral equation using the Theorem 2 as follows

$\begin{array}{l}u\left(x,t\right)-u\left(x,0\right)=\frac{\left(1-\alpha \right)}{ℬ\left(\alpha \right)}g\left(x,t,u\right)\\ +\frac{\alpha }{ℬ\left(\alpha \right)\Gamma \left(\alpha \right)}{\displaystyle {\int }_0^{t}g\left(x,\zeta ,u\right){\left(t-\zeta \right)}^{\alpha -1}d\zeta }.& (39)\end{array}$

Theorem 3. The kernel g satisfies the Lipschitz condition and contraction if the condition 0 ≤ (δ (a² + b² + ab)− δ²) < 1 holds.

Proof. In order to prove the required result, we consider the two functions u and u₁, then

$\begin{array}{l}\Vert g\left(x,t,u\right)-g\left(x,t,u_1\right)\Vert =\Vert \left[u^2\left(x,t\right)\frac{\partial u\left(x,t\right)}{\partial x}-u^2\left(x,t_1\right)\frac{\partial u\left(x,t_1\right)}{\partial x}\right]-\left[\frac{{\partial }^{2}u\left(x,t\right)}{\partial x^2}-\frac{{\partial }^{2}u\left(x,t_1\right)}{\partial x^2}\right]\Vert \\ =\Vert \left[\frac{1}{3}\frac{\partial }{\partial x}\left(u^3\left(x,t\right)-u^3\left(x,t_1\right)\right)\right]-\left[\frac{{\partial }^{2}u\left(x,t\right)}{\partial x^2}-\frac{{\partial }^{2}u\left(x,t_1\right)}{\partial x^2}\right]\Vert \\ \le \Vert \delta \left(a^2+b^2+ab\right)-{\delta }^2\Vert \Vert u\left(x,t\right)-u(x,t_1)\\ \le \left(\delta \left(a^2+b^2+ab\right)-{\delta }^2\right)\Vert u\left(x,t\right)-u\left(x,t_1\right)\Vert ,\end{array}$

where a = ||u|| and b = ||u₁|| (since u and u₁ are the bounded functions). Putting η = δ (a² + b² + ab) − δ² in the above inequality, then we have

$\begin{array}{ll}\Vert g\left(x,t,u\right)-g\left(x,t,u_1\right)\Vert \le \eta \Vert u\left(x,t\right)-u(x,t_1)\Vert .& (40)\end{array}$

The Lipschitz condition is thus obtained for ${g}$. Further, we can see that if 0 ≤ (δ (a² + b² + ab)− δ²) < 1, then it implies the contraction. The recursive form of Equation (36) is defined as

$\begin{array}{l}{u}_n\left(x,t\right)=\frac{\left(1-\alpha \right)}{ℬ\left(\alpha \right)}g\left(x,t,u_{n-1}\right)\\ +\frac{\alpha }{ℬ\left(\alpha \right)\Gamma \left(\alpha \right)}{\displaystyle {\int }_0^{t}g\left(x,\zeta ,u_{n-1}\right){\left(t-\zeta \right)}^{\alpha -1}d\zeta }.& (41)\end{array}$

The associated initial condition is

$\begin{array}{ll}u\left(x,0\right)=u_0\left(x,t\right).& (42)\end{array}$

The successive difference between the terms is presented as

$\begin{array}{l}{\varphi }_n\left(x,t\right)=u_n\left(x,t\right)-u_{n-1}\left(x,t\right)\\ =\frac{\left(1-\alpha \right)}{ℬ\left(\alpha \right)}\left(g_1\left(x,t,u_{n-1}\right)-g\left(x,t,u_{n-2}\right)\right)\\ +\frac{\alpha }{ℬ\left(\alpha \right)\Gamma \left(\alpha \right)}{\displaystyle {\int }_0^{t}g\left(x,\zeta ,u_{n-1}\right){\left(t-\zeta \right)}^{\alpha -1}d\zeta }& (43)\end{array}$

Notice that

$\begin{array}{ll}{u}_n\left(x,t\right)={\displaystyle \sum _{i=1}^n{\varphi }_i\left(x,t\right)}.& (44)\end{array}$

By using Equation (39) after applying the norm on the Equation (43), one can get

$\begin{array}{l}\Vert {\varphi }_n(x,t)\Vert \le \frac{(1-\alpha )}{ℬ(\alpha )}\eta \Vert {\varphi }_{(n-1)}(x,t)\Vert \\ +\frac{\alpha }{ℬ(\alpha )\Gamma (\alpha )}\eta {\displaystyle {\int }_0^t\Vert {\varphi }_{(n-1)}(x,\zeta )\Vert d\zeta }.& (45)\end{array}$

We prove the following theorem by using the above result.

Theorem 4. The solution for the Equation (30) will exist, and if we have specific t₀, then

$\frac{\left(1-\alpha \right)}{ℬ\left(\alpha \right)}\eta +\frac{\alpha }{ℬ\left(\alpha \right)\Gamma \left(\alpha \right)}\eta <1.$

Proof. Let us consider the bounded function u(x, t) satisfying the Lipschitz condition. Then, by Equation (43), we have

$\begin{array}{ll}\Vert {\varphi }_i\left(x,t\right)\Vert \le \Vert u_n\left(x,0\right)\Vert {\left[\frac{\left(1-\alpha \right)}{ℬ\left(\alpha \right)}\eta +\frac{\alpha }{ℬ\left(\alpha \right)\Gamma \left(\alpha \right)}\eta \right]}^n.& (46)\end{array}$

Therefore, the continuity as well as existence of the obtained solution is proved. Subsequently, in order to show the Equation (46) is a solution for the Equation (29), we consider

$\begin{array}{ll}u\left(x,t\right)-u\left(x,0\right)=u_n\left(x,t\right)-{{K}}_n\left(x,t\right).& (47)\end{array}$

In order to obtain require a result, we consider

$\begin{array}{l}\Vert {{K}}_n\left(x,t\right)\Vert =\Vert \frac{\left(1-\alpha \right)}{ℬ\left(\alpha \right)}\left(g\left(x,t,u\right)-{G}\Leftarrow x,t,u_{n-1})\right)\\ +\frac{\alpha }{ℬ\left(\alpha \right)\Gamma \left(\alpha \right)}{\displaystyle {\int }_0^t{\left(t-\zeta \right)}^{\mu -1}\left(g\left(x,\zeta ,u\right)-g\left(x,\zeta ,u_{n-1}\right)\right)d\zeta }\Vert \\ \le \frac{\left(1-\alpha \right)}{ℬ\left(\alpha \right)}\Vert g\left(x,\zeta ,u\right)-g\left(x,\zeta ,u_{n-1}\right)\Vert \\ +\frac{\alpha }{ℬ\left(\alpha \right)\Gamma \left(\alpha \right)}{\displaystyle {\int }_0^t\Vert g\left(x,\zeta ,u\right)-g\left(x,\zeta ,u_{n-1}\right)\Vert d}\zeta \\ \le \frac{\left(1-\alpha \right)}{ℬ\left(\alpha \right)}{\eta }_1\Vert u-u_{n-1}\Vert +\frac{\alpha }{ℬ\left(\alpha \right)\Gamma \left(\alpha \right)}{\eta }_1\Vert u-u_{n-1}\Vert t.& (48)\end{array}$

Similarly, at t₀ we can obtain

$\begin{array}{ll}\Vert {{K}}_n\left(x,t\right)\Vert \le {\left(\frac{\left(1-\alpha \right)}{ℬ\left(\alpha \right)}+\frac{\alpha t_0}{ℬ\left(\alpha \right)\Gamma \left(\alpha \right)}\right)}^{n+1}{\eta }^{n+1}M.& (49)\end{array}$

As n approaches to ∞, we can see that form Equation (49), ||${K}$_n (x, t)|| tends to 0.

Next, it is a necessity to demonstrate uniqueness for the solution of the considered model. Suppose u^*(x, t) is the other solution, then we have

$\begin{array}{l}u\left(x,t\right)-u^{\ast }\left(x,t\right)=\frac{\left(1-\alpha \right)}{ℬ\left(\alpha \right)}\left(g\left(x,t,u\right)-g\left(x,t,u^{\ast }\right)\right)\\ +\frac{\alpha }{ℬ\left(\alpha \right)\Gamma \left(\alpha \right)}{\displaystyle {\int }_0^t\left(g\left(x,\zeta ,u\right)-g\left(x,\zeta ,u^{\ast }\right)\right)d\zeta }.& (50)\end{array}$

On applying norm, the Equation (50) simplifies to

$\begin{array}{l}\Vert u\left(x,t\right)-u^{\ast }\left(x,t\right)\Vert =\Vert \frac{\left(1-\alpha \right)}{ℬ\left(\alpha \right)}\left(g\left(x,t,u\right)-g\left(x,,t,u^{\ast }\right)\right)\\ +\frac{\alpha }{ℬ\left(\alpha \right)\Gamma \left(\alpha \right)}{\displaystyle {\int }_0^t\left(g\left(x,\zeta ,u\right)-g\left(x,\zeta ,u^{\ast }\right)\right)d\zeta }\Vert \\ \le \frac{\left(1-\alpha \right)}{ℬ\left(\alpha \right)}\eta \Vert u\left(x,t\right)-u^{\ast }\left(x,t\right)\Vert \\ +\frac{\alpha }{ℬ\left(\alpha \right)\Gamma \left(\alpha \right)}\eta t\Vert u\left(x,t\right)-u^{\ast }\left(x,t\right)\Vert .& (51)\end{array}$

On simplification

$\begin{array}{ll}\Vert u\left(x,t\right)-u^{\ast }\left(x,t\right)\Vert \left(1-\frac{\left(1-\alpha \right)}{ℬ\left(\alpha \right)}\eta -\frac{\alpha }{ℬ\left(\alpha \right)\Gamma \left(\alpha \right)}\eta t\right)\le 0.& (52)\end{array}$

From the above condition, it is clear that u(x, t) = u^*(x, t), if

$\begin{array}{ll}\left(1-\frac{\left(1-\alpha \right)}{ℬ\left(\alpha \right)}\eta -\frac{\alpha }{ℬ\left(\alpha \right)\Gamma \left(\alpha \right)}\eta t\right)\ge 0.& (53)\end{array}$

Hence, Equation (53) proves our essential result.

Theorem 5. Suppose u_n (x, t) and u (x, t) are defined in the Banach space (𝔅[0, T], ||·||). The series solution defined in Equation (29) converges to the solution of the Equation (13), if 0 < λ < 1.

Proof: Consider the sequence {${S}$_n}, which is the partial sum of the Equation (29), and we have to prove {${S}$_n} is the Cauchy sequence in (𝔅[0, T], ||·||). Now consider

$\begin{array}{l}\Vert {{S}}_{n+1}\left(x,t\right)-{{S}}_n\left(x,t\right)\Vert =\Vert u_{n+1}\left(x,t\right)\Vert \\ \le \lambda \Vert u_n\left(x,t\right)\Vert \\ \le {\lambda }^2\Vert u_{n-1}\left(x,t\right)\Vert \le \dots \le {\lambda }^{n+1}\Vert u_0\left(x,t\right)\Vert .\end{array}$

Now, we have for every n, m ∈ N (m ≤ n)

$\begin{array}{l}\Vert {{S}}_n-{{S}}_m\Vert =\Vert \left({{S}}_n-{{S}}_{n-1}\right)+\left({{S}}_{n-1}-{{S}}_{n-2}\right)+\dots +\left({{S}}_{m+1}-{{S}}_m\right)\Vert \\ \le \Vert {{S}}_n-{{S}}_{n-1}\Vert +\Vert {{S}}_{n-1}-{{S}}_{n-2}\Vert +\dots +\Vert {{S}}_{m+1}-{{S}}_m\Vert \\ \le \left({\lambda }^n+{\lambda }^{n-1}+\dots +{\lambda }^{m+1}\right)\Vert u_0\Vert \\ \le {\lambda }^{m+1}\left({\lambda }^{n-m-1}+{\lambda }^{n-m-2}+\dots +\lambda +1\right)\Vert u_0\Vert \\ \le {\lambda }^{m+1}\left(\frac{1-{\lambda }^{n-m}}{1-\lambda }\right)\Vert u_0\Vert .& (54)\end{array}$

But 0 < λ < 1, therefore ||${S}$_n − ${S}$_m|| = 0. Hence, {${S}$_n} is the Cauchy sequence. This proves the required result.

Numerical Results and Discussion

In the present investigation, we have found the solution for equation describing the water transport in unsaturated porous media using q-HATM with the help of Mittag-Leffler law. Here, we consider two distinct cases to present the effectiveness of the proposed method.

Case 1: In this case, we consider the conductivity term as a function of cubic water content and constant $\sigma =\frac{u^3}{3}cm/h$ and ρ = 1 cm^2/h. At $a=c=\frac{1}{3},n=3$and b = −1, Equation (4) becomes

$\begin{array}{ll}{}_a^{ABC}{D}_t^{a}u(x,t)+u^2{u}_x-u_{xx}=0,0<\alpha \le 1,& (55)\end{array}$

with initial condition

$\begin{array}{ll}u\left(x,0\right)=\sqrt{\frac{1}{2}\left(1+\tanh \left(-\frac{x}{3}\right)\right)}.& (56)\end{array}$

Case 2: In this segment, we consider the conductivity term as a function of quadric water content and constant $\sigma =\frac{u^4}{4}cm/h$ and ρ = 1 cm^2/h. At $a=c=\frac{1}{1},n=1$and b = −1, the Equation (4) becomes

$\begin{array}{ll}{}_a^{ABC}{D}_t^{\alpha }u\left(x,t\right)+u^3{u}_x-u_{xx}=0,0<\alpha \le 1,& (57)\end{array}$

with initial condition

$\begin{array}{ll}u\left(x,0\right)=\sqrt[3]{\frac{1}{2}\left(1+\tanh \left(-\frac{3x}{8}\right)\right)}.& (58)\end{array}$

Here, we demonstrate the numerical simulation for the considered non-linear. In Tables 1 and 2, the error analysis has been validated. From the tables we can see that the proposed scheme is more accurate, and we confirm that the iterations increase the q-HATM solutions so that they get closer to the analytical solution.

TABLE 1

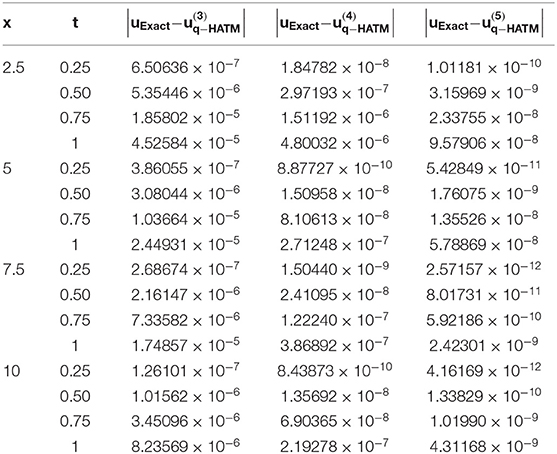
Table 1. Numerical simulation presented for u(x, t) of FR equation consider in Case 1 at n = 1, ℏ = −1 and α = 1.

TABLE 2

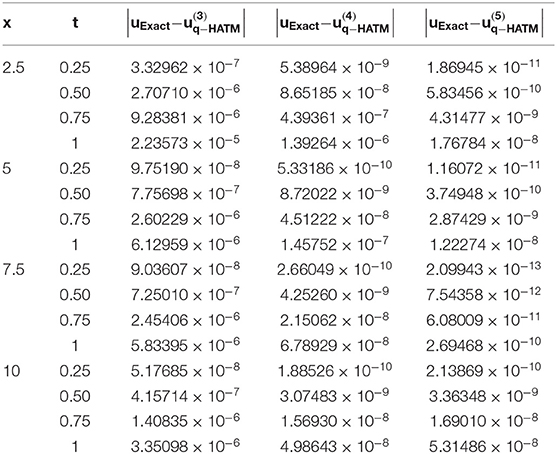
Table 2. Numerical simulation presented for u(x, t) of FR equation consider in Case 2 at n = 1, ℏ = −1 and α = 1.

The surfaces of the obtained solution and the exact solution in comparison with absolute error have been captured, respectively, in Figures 1 and 2 for Case 1 and Case 2. The behavior of the obtained solution for different orders is presented in Figure 3 for both the cases in terms of 2D plots. In order to analyze the variations of the obtained solution for the FRC equation cited in Case 1 and Case 2 with respect to the homotopy parameter (ℏ), and the (ℏ) curves are drawn for diverse μ and presented in Figure 4 with distinct n. In the plots, the horizontal line signifies the convergence region of the q-HATM solution and these curves aid us to adjust and handle the convergence province of the solution. For an appropriate value of ℏ, the achieved solution quickly tends to the exact solution. The small deviation in the physical behavior of the complex models stimulates the enormous new results to analyze and understand the nature in a better and systematic manner. Moreover, from all the plots we can see that the proposed method is more accurate and very effective in its analysis of the considered non-linear fractional order equations.

FIGURE 1

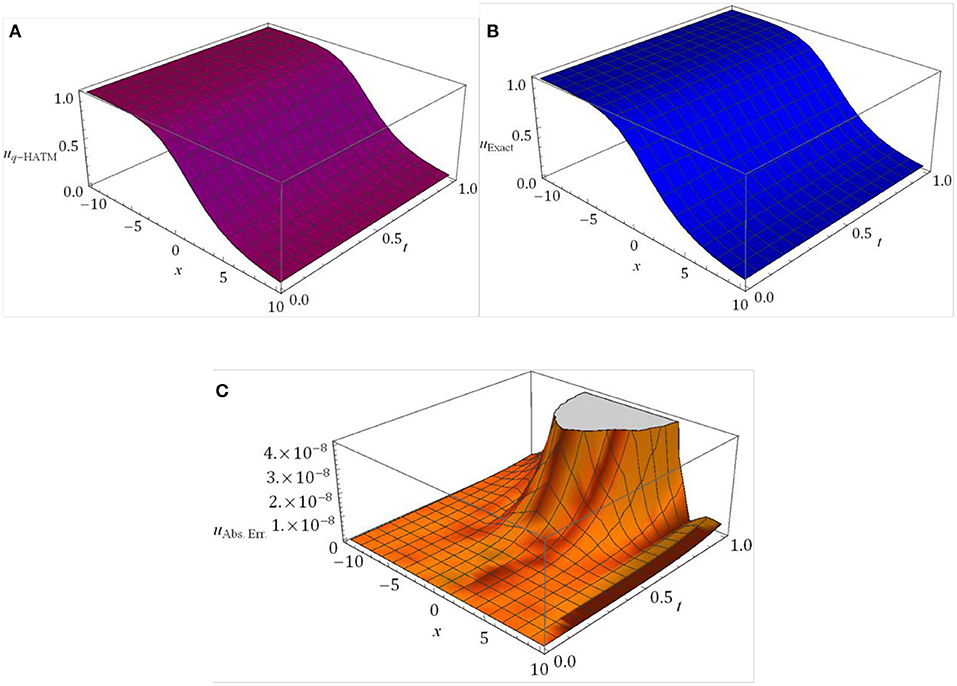
Figure 1. Surfaces of (A) u_q−HATM, (B) u_Exact (C) u_{Abs. Err.} = |u_Exact − u_q−HATM| for FR equation considered in Case 1 at ℏ = −1, n = 1 and α = 1.

FIGURE 2

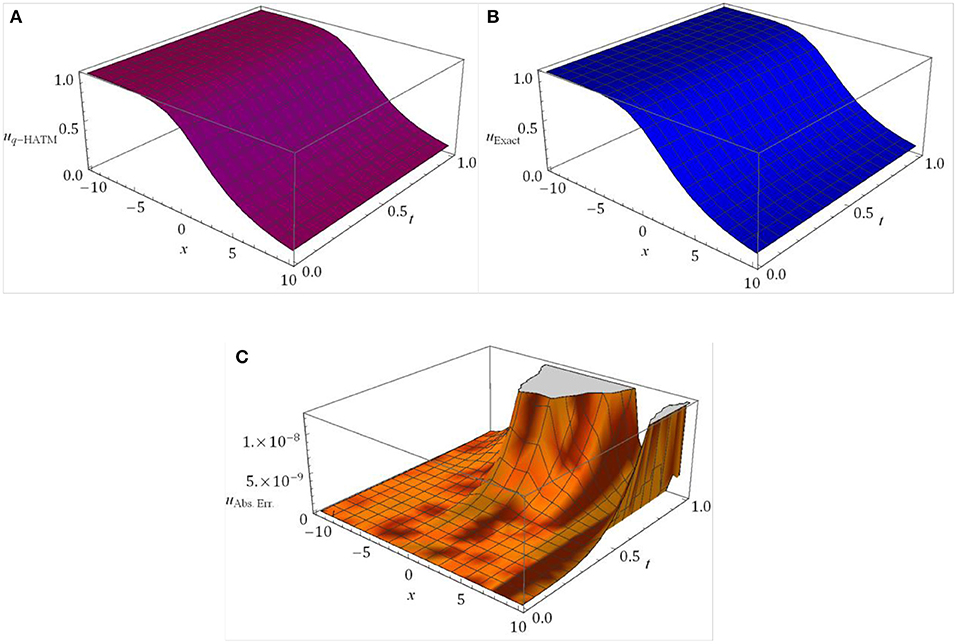
Figure 2. Surfaces of (A) u_q−HATM, (B) u_Exact (C) u_{Abs. Err.} = |u_Exact − u_q−HATM| for FR equation considered in Case 2 at ℏ = −1, n = 1 and α = 1.

FIGURE 3

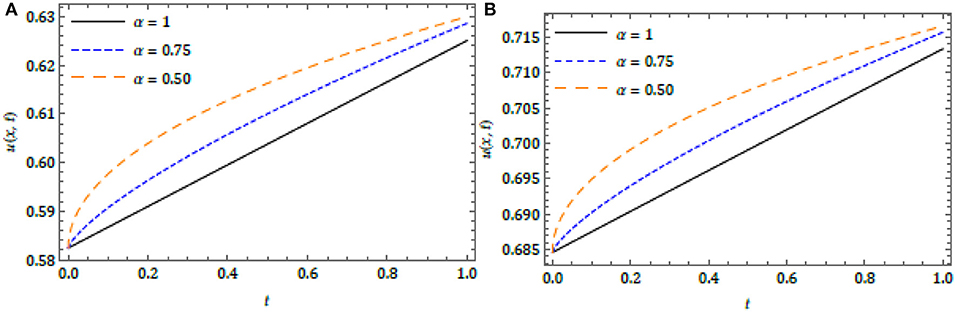
Figure 3. Nature of theq-HATM solution for (A) Case 1 and (B) Case 2 with distinct α at ℏ = −1, n = 1 and x = 1.

FIGURE 4

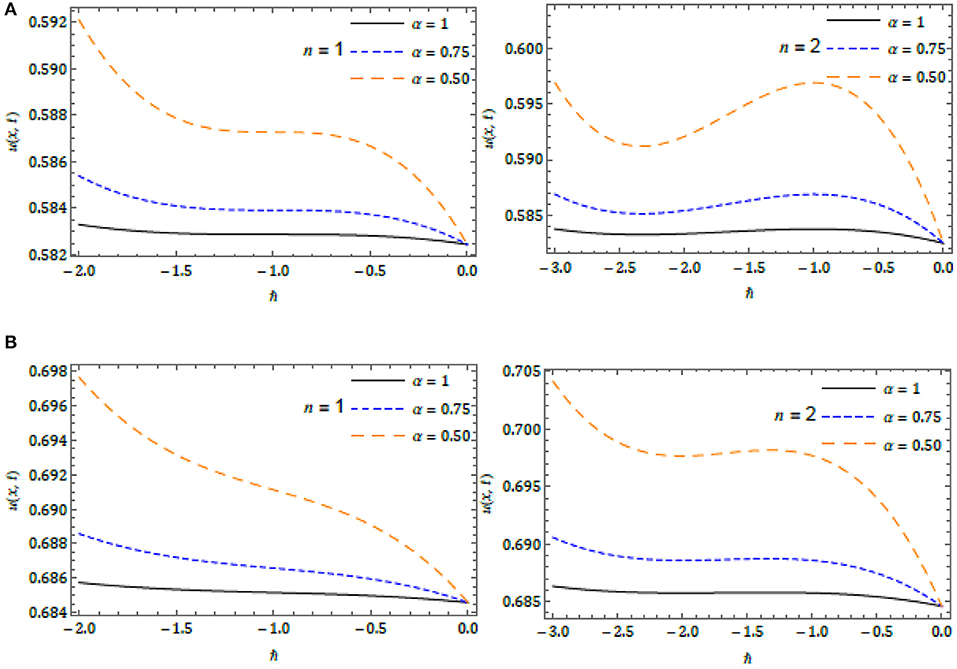
Figure 4. ℏ-curves for (A) Case 1 (B) Case 2 with distinct α at x = 1 and t = 0.01 with n = 1 and 2.

Since every non-linear differential equation does not have an exact solution we look for an approximated analytical solution thorugh which we can prove the exactness or accuracy of the proposed scheme, as opposed to an exact solution. As we mentioned earlier, the q-HATM is a modified algorithm of HAM, and it thus does not require perturbation, dissertation, linearization, or any assumptions. More importantly, the future method generalizes many traditional techniques, such as HAM, HPM, FRDTM, and others, because these are a special case of q-HATM (n = 1, ℏ = 1). In connection with this, we capture the physical behavior of q-HATM solution to illustrate the accuracy. Further, we noticed that the considered non-linear phenomenon is highly dependent on a fractional operator. In order to illustrate the computational level and computational cost, the numerical simulation has been presented. From the table, it shows that as a number of series terms increases the solution converges to an analytical solution.

Conclusion

In this paper, the q-HATM is applied profitably to find the solution for an arbitrary order RC equation describing the water transport in the unsaturated porous media. Since AB derivatives and integrals having fractional order are defined with the help of generalized Mittag-Leffler function as the non-local kernel and non-singular, the present investigation illuminates the effectiveness of the considered derivative. The existence and uniqueness of the obtained solution is demonstrated by the fixed point hypothesis. The results obtained by the future scheme are more stimulating as compared to results available in the literature. Further, the proposed algorithm finds the solution of the non-linear problem without considering any discretization, perturbation or transformations.

The behavior of the obtained series solution has been captured in terms of 2D and 3D plots for distinct fractional order. These plots show that the q-HATM solution is more accurate and also conformed with the help of numerical simulation, and this is cited in the tables. Further, we confirm that, as the order of the solution increases, the obtained solutions converge to the exact solution. The present investigation illuminates how the considered complex non-linear phenomena noticeably depend on the time history and the time instant, which can be proficiently analyzed by applying the concept of calculus to fractional order. The present investigation helps the researchers to study the behavior of non-linear problems, and this gives very interesting and useful consequences. The proposed derivative provides non-singular kernel and non-local properties; these properties are very essential in describing the physical behavior and nature of the non-linear problems, and hence researchers can consider the AB derivative to solve many non-linear complex problems. Lastly, we can conclude the projected method is extremely methodical, effective and very accurate, and that it can be applied to the analysis of the diverse classes of non-linear problems that exist in science and technology.

Data Availability Statement

All datasets generated for this study are included in the article/supplementary material.

Author Contributions

All the authors have worked equally in this manuscript. All the authors have read and approved the final manuscript.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

1. Liouville J. Memoire surquelques questions de geometrieet de mecanique, etsur un nouveau genre de calcul pour resoudreces questions. JEcolePolytech. (1832) 13:1–69.

2. Riemann GFB. Versuch Einer Allgemeinen Auffassung der Integration und Differentiation. Leipzig: Gesammelte Mathematische Werke (1896).

3. Caputo M. Elasticita e Dissipazione. Bologna: Zanichelli (1969).

4. Miller KS, Ross B. An Introduction to Fractional Calculus and Fractional Differential Equations. New York, NY: Wiley (1993).

5. Podlubny I. Fractional Differential Equations. New York, NY: Academic Press (1999).

Google Scholar

6. Kilbas AA, Srivastava HM, Trujillo JJ. Theory and Applications of Fractional Differential Equations. Amsterdam: Elsevier (2006).

Google Scholar

7. Baleanu D, Guvenc ZB, Tenreiro Machado JA. New Trends in Nanotechnology and Fractional Calculus Applications. London; New York, NY: Springer Dordrecht Heidelberg (2010). doi: 10.1007/978-90-481-3293-5

CrossRef Full Text | Google Scholar

8. Esen S, Sulaiman TA, Bulut H, Baskonus HM. Optical solitons and other solutions to the conformable space-time fractional Fokas-Lenells equation. Optik. (2018) 167:150–6. doi: 10.1016/j.ijleo.2018.04.015

CrossRef Full Text

9. Veeresha P, Prakasha DG, Baskonus HM. Solving smoking epidemic model of fractional order using a modified homotopy analysis transform method. Math Sci. (2019) 13:115–28. doi: 10.1007/s40096-019-0284-6

CrossRef Full Text | Google Scholar

10. Baleanu D, Wu GC, Zeng SD. Chaos analysis and asymptotic stability of generalized Caputo fractional differential equations. Chaos Solitons Fractals. (2017) 102:99–105. doi: 10.1016/j.chaos.2017.02.007

CrossRef Full Text | Google Scholar

11. Veeresha P, Prakasha DG, Baskonus HM. New numerical surfaces to the mathematical model of cancer chemotherapy effect in Caputo fractional derivatives Chaos. (2019) 29:013119. doi: 10.1063/1.5074099

CrossRef Full Text | Google Scholar

12. Baskonus HM, Sulaiman TA, Bulut H. On the new wave behavior to the Klein-Gordon-Zakharov equations in plasma physics. Indian J Phys. (2019) 93:393–9. doi: 10.1007/s12648-018-1262-9

CrossRef Full Text | Google Scholar

13. Prakasha DG, Veeresha P, Baskonus HM. Analysis of the dynamics of hepatitis E virus using the Atangana-Baleanu fractional derivative, Eur Phys J Plus. (2019) 134:1–11. doi: 10.1140/epjp/i2019-12590-5

CrossRef Full Text | Google Scholar

14. Veeresha P, Prakasha DG, Baleanu D. An efficient numerical technique for the nonlinear fractional Kolmogorov-Petrovskii-Piskunov equation. Mathematics. (2019) 7:1–18. doi: 10.3390/math7030265

CrossRef Full Text | Google Scholar

15. Yokuş A, Gülbahar S. Numerical solutions with linearization techniques of the fractional Harry Dym equation. Appl Math Nonlinear Sci. (2019) 4:35–42. doi: 10.2478/AMNS.2019.1.00004

CrossRef Full Text | Google Scholar

16. Cattani C. Haar wavelet-based technique for sharp jumps classification. Math Comp Model. (2004) 39:255–78. doi: 10.1016/S0895-7177(04)90010-6

CrossRef Full Text | Google Scholar

17. Yang A-M, Zhang Y-Z, Cattani C, Xie G-N, Rashidi MM, Zhou Y-J, et al. Application of local fractional series expansion method to solve Klein-Gordon equations on Cantor sets. Abstr Appl Anal. (2014) 2014:372741. doi: 10.1155/2014/372741

CrossRef Full Text | Google Scholar

18. Zhang Y, Cattani C, Yang X-J. Local fractional homotopy perturbation method for solving non-homogeneous heat conduction equations in fractal domains. Entropy. (2015) 17:6753–64. doi: 10.3390/e17106753

CrossRef Full Text | Google Scholar

19. Prakasha DG, Veeresha P, Baskonus HM. Residual power series method for fractional Swift–Hohenberg equation. Fractal Fract. (2019) 3:1–9. doi: 10.3390/fractalfract3010009

CrossRef Full Text | Google Scholar

20. Singh J, Kumar D, Hammouch Z, Atangana A. A fractional epidemiological model for computer viruses pertaining to a new fractional derivative. Appl Math Comput. (2018) 316:504–15. doi: 10.1016/j.amc.2017.08.048

CrossRef Full Text | Google Scholar

21. Asif NA, Hammouch Z, Riaz MB, Bulut H. Analytical solution of a Maxwell fluid with slip effects in view of the Caputo-Fabrizio derivative. Eur Phys J Plus. (2018) 133:272. doi: 10.1140/epjp/i2018-12098-6

CrossRef Full Text | Google Scholar

22. Veeresha P, Prakasha DG, Magesh N, Nandeppanavar MM, Christopher AJ. Numerical simulation for fractional Jaulent–Miodek equation associated with energy-dependent Schrödinger potential using two novel techniques. Waves Random Complex Media. (2019). doi: 10.1080/17455030.2019.1651461. [Epub ahead of print].

CrossRef Full Text | Google Scholar

23. Baskonus HM, Mekkaoui T, Hammouch Z, Bulut H. Active control of a chaotic fractional order economic system. Entropy. (2015) 17:5771–83. doi: 10.3390/e17085771

CrossRef Full Text | Google Scholar

24. Ravichandran C, Jothimani K, Baskonus HM, Valliammal N. New results on nondensely characterized integrodifferential equations with fractional order, EurPhys J Plus. (2018) 133:1–10. doi: 10.1140/epjp/i2018-11966-3

CrossRef Full Text | Google Scholar

25. Gao W, Ghanbari B, Baskonus HM. New numerical simulations for some real world problems with Atangana-Baleanu fractional derivative. Chaos Solitons Fractals. (2019) 128:34–43. doi: 10.1016/j.chaos.2019.07.037

CrossRef Full Text | Google Scholar

26. Atangana A, Koca I. Chaos in a simple nonlinear system with Atangana–Baleanu derivatives with fractional order. Chaos Solitons Fractals. (2016) 89:447–54. doi: 10.1016/j.chaos.2016.02.012

CrossRef Full Text | Google Scholar

27. Abro KA, Mirbhar MN, Gómez-Aguilar JF. Functional application of Fourier sine transform in radiating gas flow with non-singular and non-local kernel. J Braz Soc Mech Sci Eng. (2019) 41:400. doi: 10.1007/s40430-019-1899-0

CrossRef Full Text | Google Scholar

28. Abro KA, Khan I, Gómez-Aguilar JF. Thermal effects of magnetohydrodynamic micropolar fluid embedded in porous medium with Fourier sine transform technique. J Braz Soc Mech Sci Eng. (2019) 41:174. doi: 10.1007/s40430-019-1671-5

CrossRef Full Text | Google Scholar

29. Abro KA, Gómez-Aguilar JF. A comparison of heat and mass transfer on a Walter's B fluid via Caputo-Fabrizio versus Atangana-Baleanu fractional derivatives using the Fox-H function. Eur Phys J Plus. (2019) 134:101. doi: 10.1140/epjp/i2019-12507-4

CrossRef Full Text | Google Scholar

30. Gómez-Aguilar1 JF, Yépez-Martínez H, Torres-Jiménez J, Córdova-Fraga T, Escobar-Jiméne RF, Olivares-Peregrino VH. Homotopy perturbation transform method for nonlinear differential equations involving to fractional operator with exponential kernel. Adv Diff Equ. (2017) 2017:68. doi: 10.1186/s13662-017-1120-7

CrossRef Full Text | Google Scholar

31. Yepez-Martineza H, Gomez-Aguilar JF, Sosaa IO, Reyesa JM, Torres-Jimenez J. The Feng's first integral method applied to the nonlinear mKdV space-time fractional partial differential equation. Rev Mex Fís. (2016) 62:310–6. doi: 10.1155/2016/7047126

CrossRef Full Text | Google Scholar

32. Gómez-Aguilar JF, Torres L, Yépez-Martínez H, Baleanu D, Reyes JM, Sosa IO. Fractional Liénard type model of a pipeline within the fractional derivative without singular kernel. Adv Diff Equ. (2016) 2016:173. doi: 10.1186/s13662-016-0908-1

CrossRef Full Text | Google Scholar

33. Morales-Delgado VF, Taneco-Hernández MA, Gómez-Aguilar JF. On the solutions of fractional order of evolution equations. Eur Phys J Plus. (2017) 132:47. doi: 10.1140/epjp/i2017-11341-0

CrossRef Full Text | Google Scholar

34. Singh J, Kumar D, Baleanu D. New aspects of fractional Biswas-Milovic model with Mittag-Leffler law. Math Model Nat Phenom. (2019) 14:1–23. doi: 10.1051/mmnp/2018068

CrossRef Full Text | Google Scholar

35. Bhatter S, Mathur A, Kumar D, Singh J. A new analysis of fractional Drinfeld–Sokolov–Wilson model with exponential memory. Phys A. (2020) 537:122578. doi: 10.1016/j.physa.2019.122578

CrossRef Full Text | Google Scholar

36. Kumar D, Singh J, Baleanu D. On the analysis of vibration equation involving a fractional derivative with Mittag-Leffler law. Math Methods Appl Sci. (2019). doi: 10.1002/mma.5903. [Epub ahead of print].

CrossRef Full Text | Google Scholar

37. Goswami A, Singh J, Kumar D, Sushila. An efficient analytical approach for fractional equal width equations describing hydro-magnetic waves in cold plasma. Phys A. (2020) 524:563–75. doi: 10.1016/j.physa.2019.04.058

CrossRef Full Text | Google Scholar

38. Kumar D, Singh J, Qurashi MA, Baleanu D. A new fractional SIRS-SI malaria disease model with application of vaccines, anti-malarial drugs, and spraying. Adv Diff Equ. (2019) 2019:278. doi: 10.1186/s13662-019-2199-9

CrossRef Full Text | Google Scholar

39. Veeresha P, Prakasha DG, Kumar D. An efficient technique for nonlinear time-fractional Klein–Fock–Gordon equation. Appl Math Comput. (2020) 364:124637. doi: 10.1016/j.amc.2019.124637

CrossRef Full Text | Google Scholar

40. Richards LA. Capillary conduction of liquids through porous medium. Physics. (1931) 1:318–33. doi: 10.1063/1.1745010

CrossRef Full Text | Google Scholar

41. Brooks RH, Corey AT. Hydraulic Properties of Porous Media. Hydrol Paper 3. Fort Collins, CO: Colorado State University (1964).

Google Scholar

42. Corey AT. Mechanics of Immiscible Fluids in Porous Media. Highlands Ranch, CO: Water Resource Publications (1994).

Google Scholar

43. Whitam GB. Linear and Nonlinear Waves. New York, NY: Wiley. (1974).

Google Scholar

44. Basha HA. Burgers' equation: a general nonlinear solution of infiltration and redistribution. Water Resour Res. (2002) 38:1–9. doi: 10.1029/2001WR000954

CrossRef Full Text | Google Scholar

45. Nasseri M, Shaghaghian MR, Daneshbod Y, Seyyedian H. An analytic solution of water transport in unsaturated porous media. J Porous Media. (2008) 11:591–601. doi: 10.1615/JPorMedia.v11.i6.60

CrossRef Full Text | Google Scholar

46. Jafari H, Firoozjaee MA. Application of homotopy analysis method for water transport in unsaturated porous media. Stud Nonlinear Sci. (2010) 1:8–13.

Google Scholar

47. Caputo M. Fabrizio M. A new definition of fractional derivative without singular kernel. Prog Fract Diff Appl. (2015) 1:73–85. doi: 10.12785/pfda/010201

CrossRef Full Text | Google Scholar

48. Atangana A, Baleanu D. New fractional derivatives with non-local and non-singular kernel theory and application to heat transfer model. Therm Sci. (2016) 20:763–9. doi: 10.2298/TSCI160111018A

CrossRef Full Text | Google Scholar

49. Liao SJ. Homotopy analysis method and its applications in mathematics. J Basic Sci Eng. (1997) 5:111–25.

Google Scholar

50. Liao SJ. Homotopy analysis method: a new analytic method for nonlinear problems. Appl Math Mech. (1998) 19:957–62. doi: 10.1007/BF02457955

CrossRef Full Text | Google Scholar

51. Singh J, Kumar D, Swroop R. Numerical solution of time- and space-fractional coupled Burgers' equations via homotopy algorithm. Alexandria Eng J. (2016) 55:1753–63. doi: 10.1016/j.aej.2016.03.028

CrossRef Full Text | Google Scholar

52. Srivastava HM, Kumar D, Singh J. An efficient analytical technique for fractional model of vibration equation. Appl Math Model. (2017) 45:192–204. doi: 10.1016/j.apm.2016.12.008

CrossRef Full Text | Google Scholar

53. Prakasha DG, Veeresha P, Baskonus HM. Two novel computational techniques for fractional Gardner and Cahn-Hilliard equations, Comp Math Methods. (2019) 1:1–19. doi: 10.1002/cmm4.1021

CrossRef Full Text | Google Scholar

54. Bulut H, Kumar D, Singh J, Swroop R, Baskonus HM. Analytic study for a fractional model of HIV infection of CD4+T lymphocyte cells. Math Nat Sci. (2018) 2:33–43. doi: 10.22436/mns.02.01.04

CrossRef Full Text

55. Veeresha P, Prakasha DG. Solution for fractional Zakharov-Kuznetsov equations by using two reliable techniques. Chinese J Phys. (2019) 60:313–30. doi: 10.1016/j.cjph.2019.05.009

CrossRef Full Text | Google Scholar

56. Kumar D, Agarwal RP, Singh J. A modified numerical scheme and convergence analysis for fractional model of Lienard's equation. J Comput Appl Math. (2018) 399:405–13. doi: 10.1016/j.cam.2017.03.011

CrossRef Full Text | Google Scholar

57. Prakash A, Prakasha DG, Veeresha P. A reliable algorithm for time-fractional Navier-Stokes equations via Laplace transform. Nonlinear Eng. (2019). 8:695–701. doi: 10.1515/nleng-2018-0080

CrossRef Full Text | Google Scholar

58. Veeresha P, Prakasha DG, Baskonus HM. Novel simulations to the time-fractional Fisher's equation. Math Sci. (2019) 13:33–42. doi: 10.1007/s40096-019-0276-6

CrossRef Full Text | Google Scholar

59. Prakash A, Veeresha P, Prakasha DG, Goyal M. A homotopy technique for fractional order multi-dimensional telegraph equation via Laplace transform. Eur Phys J Plus. (2019) 134:19. doi: 10.1140/epjp/i2019-12411-y

CrossRef Full Text | Google Scholar

60. Singh J, Kumar D, Baleanu D, Rathore S. An efficient numerical algorithm for the fractional Drinfeld–Sokolov–Wilson equation. Appl Math Comput. (2018) 335:12–24. doi: 10.1016/j.amc.2018.04.025

CrossRef Full Text | Google Scholar

61. Parlang J-Y, Barry DA, Parlange MB, Hogarth WL, Haverkamp R, Ross PJ, et al. New approximate analytical technique to solve Richards equation for arbitrary surface boundary conditions. Water Resour Res. (1997) 33:903–6. doi: 10.1029/96WR03846

CrossRef Full Text | Google Scholar

62. Parlang J-Y, Hogarth WL, Barry DA, Parlange MB, Haverkamp R, Ross PJ, et al. Analytical approximation to the solutions of Richards' equation with applications to infiltration, ponding, and time compression approximation. Adv Water Resour. (1999) 23:189–94. doi: 10.1016/S0309-1708(99)00022-6

CrossRef Full Text | Google Scholar

63. Atangana A, Alkahtani BT. Analysis of the Keller-Segel model with a fractional derivative without singular kernel. Entropy. (2015) 17:4439–53. doi: 10.3390/e17064439

CrossRef Full Text | Google Scholar

64. Alkahtani BT, Atangana A. Analysis of non-homogenous heat model with new trend of derivative with fractional order. Chaos Solitons Fractals. (2016) 89:566–71. doi: 10.1016/j.chaos.2016.03.027

CrossRef Full Text | Google Scholar

65. Singh J, Kumar D, Swroop R, Kumar S. An Efficient computational approach for time-fractional Rosenau-Hyman equation. Neural Comput Appl. (2018) 30:3063–70. doi: 10.1007/s00521-017-2909-8

CrossRef Full Text | Google Scholar

66. Veeresha P, Prakasha DG. A novel technique for (2+1)-dimensional time-fractional coupled Burgers equations. Math Comput Simulation. (2019) 166:324–45. doi: 10.1016/j.matcom.2019.06.005

CrossRef Full Text | Google Scholar