- 1Unidad Cientifica de Innovación empresarial, Instituto de Neurociencias, CSIC-UMH, Sant Joan d'Alacant, Spain
- 2Departamento de Estructura de la Materia, Instituto de Física de Cantabria, CSIC-UC, Santander, Spain
We study the role of the system response time in the computational capacity of delay-based reservoir computers. Photonic hardware implementation of these systems offers high processing speed. However, delay-based reservoir computers have a trade-off between computational capacity and processing speed due to the non-zero response time of the non-linear node. The reservoir state is obtained from the sampled output of the non-linear node. We show that the computational capacity is degraded when the sampling output rate is higher than the inverse of the system response time. We find that the computational capacity depends not only on the sampling output rate but also on the misalignment between the delay time of the non-linear node and the data injection time. We show that the capacity degradation due to the high sampling output rate can be reduced when the delay time is greater than the data injection time. We find that this mismatch gives an improvement of the performance of delay-based reservoir computers for several benchmarking tasks. Our results show that the processing speed of delay-based reservoir computers can be increased while keeping a good computational capacity by using a mismatch between delay and data injection times. It is also shown that computational capacity for high sampling output rates can be further increased by using an extra feedback line and delay times greater than the data injection time.
1. Introduction
Reservoir computing (RC) is a successful brain-inspired concept to process information with temporal dependencies [1, 2]. RC conceptually belongs to the field of recurrent neural networks (RNN) [3]. In these systems, the input signal is non-linearly projected onto a high-dimensional state space where the task can be solved much more easily than in the original input space. The high-dimensional space is typically a network of interconnected non-linear nodes (called neurons). The ensemble of neurons is called the reservoir. RC implementations are generally composed of three layers: input, reservoir, and output (see Figure 1). The input layer feeds the input signal to the reservoir via fixed weighted connections. The input weights are often chosen randomly. These weights determine how strongly each of the inputs couples to each of the neurons. In traditional RNN the connections among the neurons are optimized to solve the task. Nevertheless, in RC, the coupling weights in the reservoir are not trained and can be chosen at random. The reservoir state is given by the combined states of all the individual nodes. Under the influence of input signals, the nodes of the reservoir remain in a transient state such that each input is injected in the presence of the response to the previous input. As a result the reservoir can retain input data for a finite amount of time (short-term memory [4]), and it can compute linear and non-linear functions of the retained information. The reservoir output is constructed through a linear combination of neural responses, with readout weights that are trained for the specific task. These weights are typically obtained by a simple linear regression. The strength of the reservoir computing scheme lies in the simplicity of its training method, where only the connections with the output are optimized.
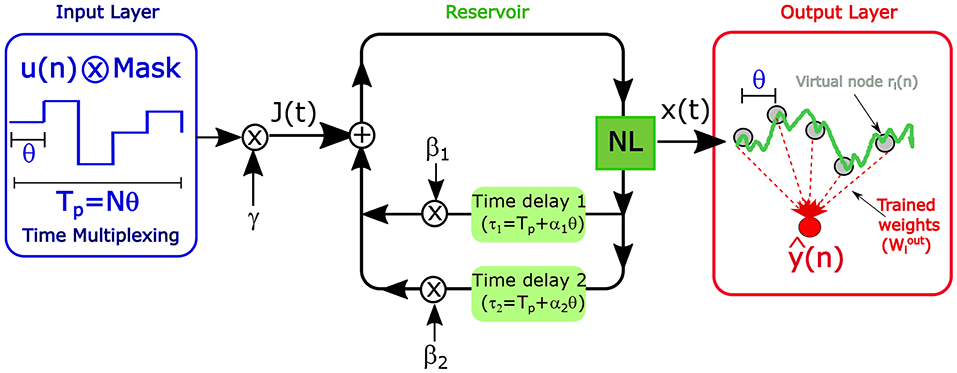
Figure 1. Schematic illustration of delay-based RC. NL stands for Non-linear Node. The NL can have one (β2 = 0) or two delay lines. The points ri(n) represent the virtual nodes separated by time intervals θ. The masked input u(n+1) ⊗ Mask is injected directly following u(n) ⊗Mask.
Hardware implementations of RC are sought because they offer high processing speed [5], parallelism, and low power consumption [6] compared to digital implementations. However, traditional RC involves a large number of interconnected non-linear neurons, so the hardware implementation is very challenging. Recently, it has been shown that RC can be efficiently implemented using a single non-linear dynamical system (neuron) subject to delayed feedback (delay-based RC) [7]. This architecture emulates the dynamic complexity traditionally achieved by a network of neurons. In delay-based RC, the spatial multiplexing of the input in standard RC systems with N neurons is replaced by time-multiplexing (see Figure 1). The reservoir is composed of N sampled outputs of the non-linear node distributed along the delay line, called virtual nodes. Connections between these N virtual nodes are established through the delayed feedback when a mismatch between the delay and data injection times is introduced [8]. Delay-based RC has facilitated hardware implementation in photonic systems that have the potential to develop high-speed information processing. An overview of recent advances is given in Van der Sande et al. [9]. However, the information processing rate is limited by the non-zero response time of the system. The reservoir state is obtained from the sampled output of the non-linear node. The information processing (or data injection) time is given by Tp = Nθ, where θ is the inverse of the output sampling rate, i.e., the time interval between two virtual nodes (see Figure 1). The information processing rate can be increased by decreasing the node distance (higher sampling output rate). However, when θ is less than the response time of the system T, virtual nodes are connected through the non-linear node dynamics. Network connections due to inertia lead to virtual node-states with similar dependence on inputs. Then the number of independent virtual nodes decreases and the diversity of the reservoir states is reduced. As a consequence computational capacity is degraded. Then there is a trade-off between information processing capacity and rate in delay-based reservoir computers.
In this work we show, using numerical simulations, that the computational capacity is degraded when the sampling output rate is higher than the inverse of the system response time. We obtain the memory capacities for different values of θ/T and the mismatch between the delay and data injection times. Until now only two different delay-based reservoir architectures have been considered: θ < T without mismatch [7] and θ ≫ T with mismatch time θ [8]. We find that the computational capacity depends not only on the sampling output rate but also on the misalignment between the delay time of the non-linear node and the data injection time. We show that the capacity degradation due to high sampling output rate can be reduced when the delay time is greater than the data injection time. We also find that this mismatch gives an improvement of the performance of delay-based reservoir computers for several benchmarking tasks. Then, delay-based reservoir computers can achieve a high processing speed and good computational capacity using a mismatch between delay and data injection times.
We first consider a simple architecture of a single non-linear node with one feedback delay line. The linear and non-linear information processing capacities are obtained for different values of θ/T. It is found that information processing capacity is boosted for small values of θ/T if the delay of the non-linear node τ is greater than Tp. A similar performance is obtained for small and large values of θ/T for channel equalization and also for NARMA-10 task if values of the delay time greater than Tp are used. Then the information processing rate is increased without causing system performance degradation. This is due to the increase in reservoir diversity. Another strategy to increase reservoir diversity is to use an extra feedback line. We show that memory capacity can be further increased with this architecture for small values of θ/T when the delay time is greater than the information processing time.
2. Materials and Methods
2.1. Delay-Based Reservoir Computers
Traditional RC implementations consist of a large number N of randomly interconnected non-linear nodes [3]. The state of the reservoir at time step n, r(n), is determined by:
where u(n) is sequentially injected input data and f is the reservoir activation function. The matrices W and Win contain the (generally random) reservoir and input connection weights, respectively. The matrix W (Win) is rescaled with a connection (input) scaling factor β (γ). The exact internal connectivity is not crucial. In fact, it has been shown that simple non-random connection topologies (e.g., a simple chain or ring) gives a good performance [10].
Delay-based RC is a minimal approach to information processing based on the emulation of a recurrent network via a single non-linear dynamical node subject to delayed feedback. The reservoir nodes (called virtual nodes) are the sampled outputs of the non-linear node distributed along the delay line (see Figure 1). In the time delay-based approach there is only one real non-linear node. Thus, the spatial multiplexing of the input in standard RC is replaced here by time multiplexing. The advantage of delay-based RC lies in the minimal hardware requirements. There is a price to pay for this hardware simplification: compared to an N-node standard spatially-distributed reservoir, the dynamical behaviour in the system has to run at an N-times higher speed in order to have equal input-throughput.
The dynamics of a delay-based reservoir has been described as [7, 11–16]:
where T is the response time of the system, τ the delay time, β > 0 the feedback strength and γ the input scaling. The masked input J(t) is the continuous version of the discrete random mapping of the original input Winu(n). In our approach, every time interval of the data injection/processing time Tp represents another discrete time step. This time is given by Tp = Nθ, where θ is the temporal separation between virtual nodes. Individual virtual nodes are addressed by time-multiplexing the input signal. An input mask is used to emulate the input weights of traditional RC. This mask function is a piecewise constant function, constant over an interval of θ, and periodic with period Tp. The N mask values mi are drawn from a random uniform distribution in the interval [–1,1] The procedure to construct the continuous data J(t) is the following. First, the input stream u(n) undergoes a sample and hold operation to define a stream which is constant during one Tp, before it is updated. Every segment of length Tp is multiplied by the mask (see Figure 1). The masked input u(n+1)⊗ Mask is injected directly following u(n)⊗Mask. After a time Tp, each virtual node is updated.
The reservoir state that corresponds to the input u(n), r(n) = [r1(n)…rN(n)], is the collection of N outputs of the dynamical system, ri(n) = x(nTp − (N − i)θ), where i = 1, …, N (see Figure 1). These N points are called virtual nodes because they correspond to taps in the delay line and play the same role as the neurons in standard RC. The node responses ri(n) are used to train the reservoir to perform a specific task. As in the standard RC [1, 17], only the output weights Wout are computed to obtain the output ŷ = Wout r. A linear regression method is used to minimize the error between the output ŷ and the desired target y in the training phase. The testing is then performed using previously unseen input data of the same kind as those used for training.
2.1.1. Interconnection Structure of Delay-Based Reservoir Computers
In delay-based reservoir computers virtual nodes are connected through the feedback loop with nodes affected by previous inputs. Virtual node states also depend on close (in time) nodes through the inherent dynamics of the non-linear node. We can identify four time scales in the delayed feedback system with external input described by Equation (2): the response time T of the non-linear node, the delay time τ, the separation of the virtual nodes θ, and the data injection/processing time Tp. Setting the values of the different time scales creates a fixed interconnection structure. The virtual nodes can set up a network structure via the feedback loop by introducing a mismatch between Tp and τ. Interconnection between virtual nodes due to the inherent dynamics of the non-linear node is obtained if the node separation θ is smaller than the response time of the system T. Due to inertia the response of the system is not instantaneous. Therefore, the state of a virtual node depends on the states of nodes that correspond to previous taps in the delay line. However, if θ is too short, the non-linear node will not be able to follow the changes in the input signal and the response signal will be too small to measure. Typically, a number of θ = 0.2T is quoted [7, 11–16, 18].
When θ ≫ T the state of a given virtual node is independent of the states of the neighboring virtual nodes. Then virtual nodes are not coupled through the non-linear node dynamics. The reservoir state is only determined by the instantaneous value of the input J(t) and the delayed reservoir state. The system given by Equation (2) can then be described with a map:
A network structure can be obtained via the feedback loop by introducing a mismatch between Tp and τ. This mismatch can be quantified in terms of the number of virtual nodes by α = (τ − Nθ)/θ. In the case of 0 ≤ α < N and θ ≫ T, the virtual node states are given by:
The network topology depends on the value of α. When α = 1 (i.e., τ = Tp+θ) the topology is equivalent to the ring topology in standard RC systems [10]. When α < 0, a number |α| of virtual nodes are not connected through the feedback line with nodes at a previous time. When α and N have no common divisors, all virtual nodes are connected through feedback in a single ring. However, when N and α are not coprimes, subnetworks are formed with a similar dependence on inputs and the reservoir diversity is reduced.
Although the two types of virtual node connections are not exclusive, only two cases have been considered until now: delay-based reservoirs connected through system dynamics (α = 0 and θ < T) [7, 12–18], or by the feedback line (θ ≫ T) [8, 15, 19].
It is clear that the information processing rate of delay-based reservoir computers depends on the node separation. Then reservoir computers with nodes connected only through the feedback line (θ ≫ T) are slower than a counterpart exploiting the virtual connections through the system dynamics (θ < T). However, as we will show in 3.1, information processing capacity is degraded when θ < T. In this case, the computational capacity increases with the mismatch between the delay and data injection times (see section 3.1).
2.2. Computational Capacity
Delay-based reservoir computers can reconstruct functions of h previous inputs yk(n) = y(u(n − k1), …, u(n − kh)) from the state of a dynamical system using a linear estimator . Here k denotes the vector (k1, …, kh). The estimator is obtained from N internal variables (node states) of the system. The suitability of a reservoir to reconstruct yk can be quantified by using the capacity [20]:
The capacity is C[yk] = 1 when the reconstruction error for yk is zero. The capacity for reconstructing a function of the inputs y, C[y], is given by the sum of C[yk] over all sequences of past inputs [20]:
The total computational capacity CT is the sum of C[yk] over all sequences of past inputs and a complete orthonormal set of functions. When yk is a linear function of one of the past inputs, yk(n) = u(n − k), the capacity C[y] corresponds to the linear memory capacity introduced in Jaeger [4]. The capacity of the system to compute non-linear functions of the retained information is given by the non-linear memory capacity [20]. The computational capacity is given by the sum of the linear and non-linear memory capacities. The total capacity is limited by the dimension of the reservoir. As a consequence, there is a trade-off between linear and non-linear memory capacities [20].
The total computational capacity of delay-based reservoirs is given by the number of linearly independent virtual nodes. The computational power of delay-based reservoir computers is therefore hidden in the diversity of the reservoir states. In the presence of inertia (θ < T) non-linear node dynamics couples close (in time) virtual nodes. This coupling reduces reservoir diversity, and then computational capacity is degraded. The computational capacity of delay-based reservoir depends not only on the separation between the virtual nodes but also on the misalignment between Tp and τ, given by α. When α < 0, the state of a virtual node of index i > (N − |α|), ri(n), is a function of the virtual node state ri−N+|α|(n) at the same time. Then the reservoir diversity and computational capacity are reduced. Computational capacity is also reduced if |α| and N are not coprimes. In this case, the N virtual nodes form gcd(|α|, N) ring subnetworks, where gcd is the greatest common divisor. Each subnetwork has p = N/gcd(|α|, N) virtual nodes. Virtual node-states belonging to different subnetworks have a similar dependence on inputs and reservoir diversity is reduced.
2.3. Reservoir Computers With Two Delay Lines
An architecture with several delay lines has been proposed [21, 22] to increase the memory capacity of delay-based reservoir computers with virtual nodes connected only through non-linear system dynamics (θ < T and α = 0). Several delay lines are added to preserve older information. The longer the delay, the older the response that is being fed back. Even without explicitly reading the older states from the delay line, the information is re-injected into the system and its memory can be extended. We apply this approach to delay-based reservoir computers with virtual nodes that are connected through non-linear node dynamics and by the feedback line.
The dynamics of reservoir computers with two delay lines is described by:
where βi ≥ 0 is the feedback strength of the delay line i. The total feedback strength is β = β1 + β2. The corresponding delays are given by τ1 = Nθ + α1 and τ2 = 2Nθ + α2, where 0 ≤ αi < Nθ. The reservoir state is the same as in one delay-based RC, i.e., the virtual nodes correspond to taps only in the shorter (τ1) delay line. In the case of α1 = 0, it has been shown [23] that the best performance for NARMA-10 task is obtained when τ1 and τ2 are coprimes. In this case, the number of virtual nodes that are mixed together within the history of each virtual node is maximized.
If the mismatches αi (i = 1, 2) are zero, the virtual node states at time n depend on the reservoir state at time (n − 1) and (n − 2) via the delay line 1 and 2, respectively. In one-delay reservoirs (β2 = 0), the number of virtual nodes whose state at time n depends on the reservoir state at time (n − 2) increases with the mismatch (see Equation 2.1.1 for the case without inertia). When a second delay is added with a mismatch α2 > 0, some virtual nodes at time n are connected with nodes at time (n − 3). The number of virtual nodes with states at time n that depend on the reservoir state at time (n − 3) increases with α2. These connections with older states can extend the memory of the two-delay reservoir computer.
3. Results
In this section, we show the numerical results obtained for the memory capacities and performance of a non-linear delay-based RC system. We study a delay-based reservoir computer with a single non-linear node for the one and two delay lines architectures. The one-delay system is governed by Equation (2) and the two-delay reservoir by Equation (6). In both cases the reservoir activation function f is given by:
where a = 2 and λ = 1. The value of fs = 2.5 is chosen to have, when β < 1, a stable fixed point for the system defined by Equation (2) in absence of input (γ = 0). This non-linear function is asymmetric to allow that the reservoir computer reconstructs even functions of the input. Similar results are obtained for different reservoir activation functions, in particular for a sin2 function, that corresponds to an optoelectronic implementation [8, 11, 13–15].
The number of virtual nodes used in the numerical simulations is a prime number, N = 97, to avoid the capacity degradation due to the formation of subnetworks. The rest of fixed parameters are: T = 1 and β = β1 = 0.8 for the one-delay reservoir computer and β1 + β2 = β = 0.8 for the two-delay reservoir computer. The effective non-linearity of the delay-based reservoir computer can be changed with the scaling input parameter γ. In this work, we consider γ = 0.1 and γ = 1 that correspond to low-to-moderate and strong non-linearity, respectively. The total capacity of a linear reservoir computer with f(z) = z will also be analyzed.
All the results presented in this paper are the average over 5 simulation runs with different training/test sets and different masks. A total of 8,000 inputs (6,000 for training and 2,000 for testing) are used for computational capacities and the NARMA-10 task. The dataset for the channel equalization task has 10,000 points for training and 6,000 for testing.
3.1. Computational Capacity
To analyze the computational capacity of the non-linear delay-based reservoir computer, we calculate by using (Equations 4 and 5) four capacities as in Duport et al. [19], namely linear (LMC), quadratic (QMC), cubic (CMC) and cross (XMC) memory capacities, which correspond to functions y given by the first, second and third order Legendre polynomials, respectively. In order to obtain these capacities a series of i.i.d. input samples drawn uniformly from the interval [–1, 1] is injected into the reservoir. The LMC is obtained by summing over k the capacity C[yk] for reconstructing yk(n) = u(n − k). It corresponds to the linear memory capacity introduced in Jaeger [4]. The QMC and CMC are obtained by summing over k the capacity for and , respectively. The XMC is obtained by summing over k, k′ for k < k′ the capacities for the product of two inputs, . In non-linear systems, the sum Cs = LMC+QMC+CMC+XMC does not include all possible contributions to CT, so Cs ≤ CT, whereas for linear systems Cs = LMC = CT. Finally, note that in some cases the main contribution to the LMC is due to the sum of C[yk] over a large range of values of k greater than a certain value kc with large normalized-root-mean-square reconstruction errors NRMSRE(k) = . This corresponds to a memory function m(k) = C[yk] with a long tail. In these cases a high LMC can be obtained but the reconstruction error for yk when k > kc is large. This low quality memory capacity leads to poor performance for tasks requiring long memory, such as NARMA-10 task [10]. A memory capacity with good quality (quality memory capacity) can be calculated by summing only the capacities for yk over k until they drop below a certain value q. If we consider that the error is small when NRMSRE(k) < 0.3, this corresponds to C[yk] > 0.91. Then we consider a value q = 0.9 to obtain the quality memory capacity C[y ]q = 0.9.
3.1.1. Memory Capacities of One-Delay Reservoir Computers
First, we simulate a delay-based reservoir computer with a single delay line. We focus on the influence of the system response time on the computational capacity for different values of the mismatch α between the data injection and delay times. Until now two values of the mismatch have been used: α = 0 with θ = 0.2T [7, 12–18], and α = 1 with θ ≫ T [8, 15, 19].
We first consider a linear system with f(z) = z in Equation (2). As stated before, the total computational capacity of this system can be obtained from the linear memory capacity, e.g., . Figure 2 shows the total computational capacity of the linear reservoir computer as a function of the node separation for two different values of the detuning between Tp and τ: α = 0 and α = 1. For α = 1 (Figure 2B), increases with θ/T and the upper bound CT = N = 97 is almost reached for θ/T = 10. Similar behaviour is obtained for detuning values 1 < α < N. Then almost all the nodes are linearly independent for θ/T = 10 and non-zero α. The quality memory of the linear delay-based reservoir computer also increases with θ/T following the same behavior than for α = 1. However, when θ < T a total capacity is obtained. Then a clear degradation of the capacity is observed with respect to its upper bound, given by N = 97, when the node separation is smaller than the response time of the non-linear node dynamics. In this case virtual nodes with an index difference smaller than T have similar states. Then reservoir diversity is reduced and the information processing capacity is degraded. When θ/T increases the coupling between close (in time) virtual nodes decreases, and the capacity increases.
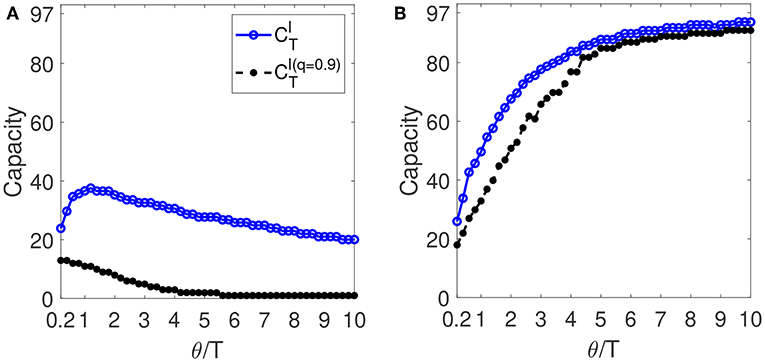
Figure 2. Computational capacity of the linear delay-based RC with one delay line as a function of θ/T for (A) α = 0 and (B) α = 1. The solid line with blue circles is the total computational capacity () and the dashed line with black points is the total quality computational capacity calculated for q = 0.9.
In the special case of zero detuning (α = 0), the only coupling between the virtual nodes is through the system dynamics with non-zero response time. For α = 0, the total capacity of the linear delay-based reservoir computer has a maximum value at θ/T ~ 1.2 (see Figure 2A). In this case a clear degradation of the capacity is observed for any value of θ/T. The maximum is due to the trade-off between the fading of the coupling through the system dynamics for low sampling output rates and the very similar responses to different inputs for small θ. Furthermore, for α = 0, the quality memory capacity decreases with θ/T and the maximum is obtained at θ/T = 0.2. For low inertia, θ/T = 4, we obtain a normalized-root-mean-square reconstruction error NRMSRE(k) > 0.6 when k > 2. For θ/T = 1 a NRMSRE(k) > 0.3 when k > 12 is obtained.
We consider now a non-linear delay-based reservoir computer with an activation function given by Equation (7) and a low-to-moderate non-linearity (γ = 0.1). In this case, the capacity Cs has a behaviour as a function of θ similar to that of the total capacity of the linear case (see Figure 3). For α = 1, Cs increases with θ/T, and a value of Cs = 93 is obtained at θ/T = 4. If all the capacities would be considered for α = 1, CT ~ N. The increase in Cs with θ/T is mainly due to the XMC and to the LMC. When θ/T < 1 a capacity Cs < 75 is obtained. However, this degradation in Cs is smaller than in the linear case. It is worth mentioning that for α = 1, Cs is greater than the total capacity of the linear case . Then we have , where is the total capacity of the non-linear system. This is due to the fact that non-linearity increases the number of linearly independent virtual node states, since correlations between virtual nodes are smaller for non-linear delay-based reservoir computer. In the case without mismatch (α = 0) the capacity Cs of the non-linear reservoir computer (see Figure 3A) has a maximum as in the linear case at θ/T ~ 1.2. The degradation of Cs is smaller than that of in the linear case.
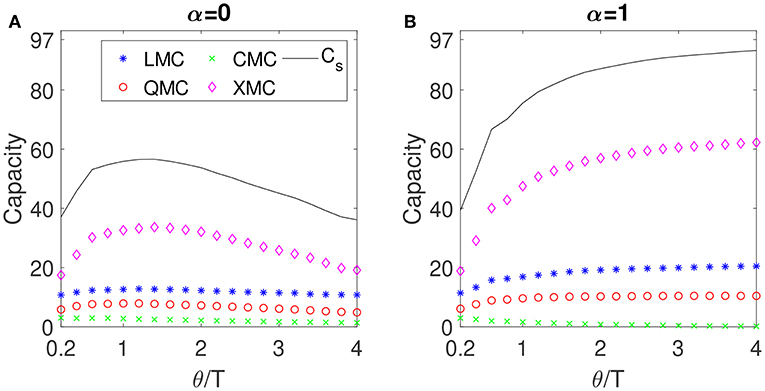
Figure 3. Memory capacities of the non-linear delay-based RC with one delay line as a function of θ/T for (A) α = 0 and (B) α = 1 when γ = 0.1. The blue stars, red circles, green crosses, pink diamonds correspond to the LMC, QMC, CMC, and XMC. The black solid line is the Cs.
We have shown that the computational capacity is degraded when the sampling output rate is higher than the inverse of the system response time. However, the information processing capacity of delay-based reservoir computers depends not only on output sampling rate (i.e., the separation between the virtual nodes) but also on the detuning between Tp and τ, i.e., α. To study this dependency, we calculate the memory capacities as a function of α for a non-linear delay-based reservoir computer with two different response times: an instantaneous response to the input T = 0 (Figures 4C,D) and T = θ/0.2 (Figures 4A,B). This node separation θ = 0.2T is the one used in most of the reservoirs with connections through system dynamics [7, 12–18]. The capacities for T = 0 correspond to a node separation much larger than T. When θ/T ≫ 1 the nodes response to an input reach the steady state after a time θ. Then the reservoir state is given by Equation (2) for T = 0. As a consequence, when θ/T ≫ 1 the computational capacity tends to the value obtained for T = 0. For a mismatch α = 1 this limit is reached for θ/T > 4 (see Figure 3B). Two values of γ = 0.1 and γ = 1 that correspond to low-to-moderate and strong non-linearity, respectively are considered. We also calculate the total capacity as a function of α for a linear reservoir computer with θ = 0.2T (Figure 4B).
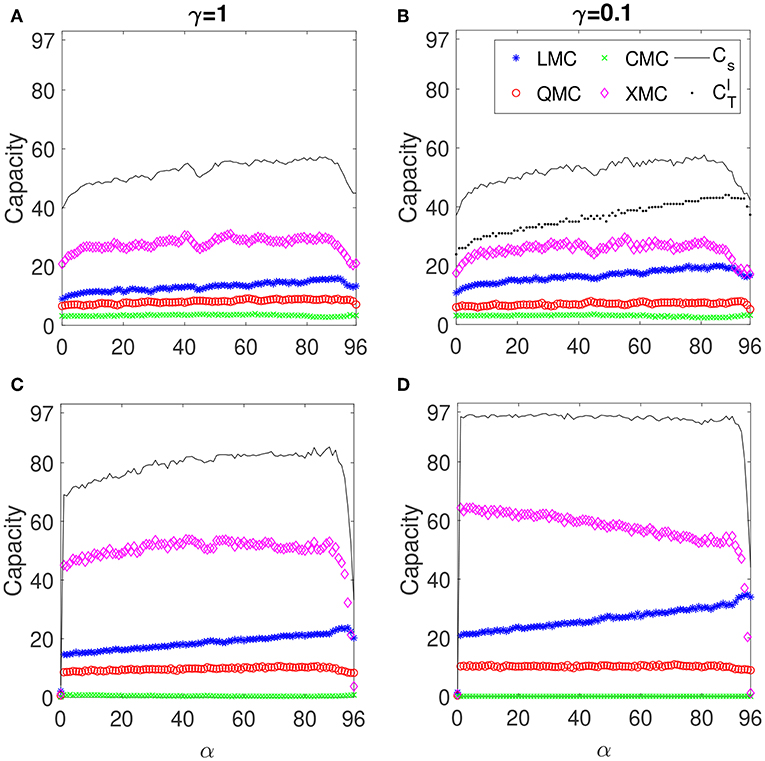
Figure 4. Memory capacities of the one delay-based RC as a function of α. Left panels (A,C): γ = 1. Right panels (B,D): γ = 0.1. Top panels (A,B): T = θ/0.2. Bottom panels (C,D) T = 0. The blue stars, red circles, green crosses, pink diamonds correspond to the LMC, QMC, CMC, XMC, respectively. The solid black line is the Cs. The dotted black line in (B) is the .
The virtual states of delay-based systems with an instantaneous response to the input are given by the map of Equation (3). When N and α are coprimes, we have for 0 < α < N a total capacity CT ≈ N. Thus, increasing α in the case of T = 0 does not increase the total capacity; it only changes the relative contribution of the different capacities to . This is clearly shown in Figure 4D where a low-to-moderate non-linearity (γ = 0.1) is considered. Here, the non-linear memory capacities of degree greater than two are zero (i.e., CMC), and Cs ~ 95 for 0 < α < 90. This value is very close to the upper bound for the capacity CT = N = 97. Since CT is limited by N, there is a trade-off between the linear and non-linear capacities. Then the increase in the LMC with α is compensated by a decrease of the XMC in Figure 4D. In the case of strong non-linearity (γ = 1), Figure 4C shows that Cs is not close to the upper bound for the capacity CT = N = 97. Then there is a significant contribution to of capacities with a non-linear degree greater than the ones considered in Cs. An increase in Cs with α is obtained. This increase is mainly due to LMC and XMC. It only indicates that the contribution to of the capacities with a lower non-linear degree considered in Cs increases.
Now we analyze the capacity dependence on α when θ/T = 0.2. We consider integer values of α. Similar results are obtained when α is not an exact integer. We first consider the linear system. In this case the total capacity is given by the LMC. As seen in Figure 2A the capacity is degraded when θ < T due to the similar evolution in time of close (in time) virtual nodes connected through non-linear node dynamics. Figure 4B shows that increases with α. A significant increase of nearly 50% is obtained for the capacity when the mismatch is large. This is due to an increase in reservoir diversity. When the mismatch α is increased, virtual nodes are connected through feedback to nodes that are not connected through system dynamics. This improves reservoir diversity, and a larger capacity can be achieved.
In the non-linear case with θ/T = 0.2, Figures 4A,B show that regardless of the non-linearity, Cs increases with α. This increase can not be attributed only to a change in the contribution of linear and non-linear capacities to the total capacity . As seen for the linear case, when θ/T = 0.2 the total capacity increases with α due to an increase in reservoir diversity. This should also lead in the non-linear case to an increase in the total capacity with α. It is worth mentioning that in the case of T = θ/0.2 we obtain a similar Cs for low-to-moderate (see Figure 4B) and strong (Figure 4A) non-linearity. However, the relative contribution of the linear memory capacity is higher for low non-linearity. Finally, note that regardless of the non-linearity and T, higher order capacities such as QMC and CMC remain almost constant with α and the change of Cs is due to LMC and XMC.
3.1.2. Memory Capacities of Two-Delay Reservoir Computers
We have shown that the computational capacity is boosted for small values of θ/T when the delay time of the non-linear node is greater than the data injection time. This mismatch between τ and Tp allows higher processing speeds of delay-based reservoir computers without performance degradation. This is due to the increase in reservoir diversity. To further increase reservoir diversity in the case of T = θ/0.2, we explore the effect of adding a extra feedback line to the non-linear node. Figure 5 shows the Cs of the two-delay reservoir computer vs. the misalignment of the second delay when γ = 0.1. The mismatch of the first delay is fixed at α1 = 73 (Figure 5, left) and α = 1 (Figure 5, right). In both cases the maximum of Cs reached for the two-delay system is Cs ~ 61. This value is obtained in the two cases, α1 = 1 and α1 = 73, for α2 ~ 70 when β2 = 0.75 and just in the case of α1 = 73 also for α2 ~ 82 and β2 = β1 = 0.4. The maximum Cs obtained for the two-delay system is slightly higher than the one reached for its one-delay counterpart. In the one-delay system the maximum capacity is Cs ~ 57 that is obtained for α ~ 80 (see Figure 4B). Therefore, the calculated information processing capacity for high sampling output rates can be further increased by using an extra feedback line and delay times greater than the information processing time. However, the second delay does not significantly improve the computational capacity of the one-delay system. Moreover, when the first delay mismatch is fixed near its optimal value for the one-delay system (α ~ 80), the effect of the second delay feedback strength or misalignment is small [see Figure 5 (right)]. However, when the first delay mismatch is not close to its optimal value for the one-delay system, the maximum Cs reached for the one-delay system is outperformed by adding a second delay with a high strength (β2 = 0.75) and a mismatch 10 < α2 < 90 [see Figure 5 (left)].
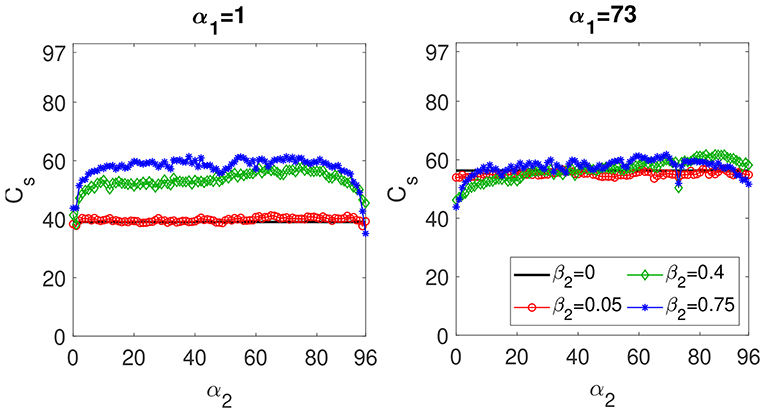
Figure 5. Cs of the two-delay-based RC as function of α2. Left: α1 = 1. Right: α1 = 73. The solid black line is the value of Cs for the one-delay case with α = α1. Red circles, green diamonds and blue starts correspond to the Cs with two delays and a β2 of 0.05, 0.4, and 0.75, respectively. These results are obtained for T = θ/0.2 and γ = 0.1.
The contributions of the individual memory capacities to Cs for the two-delay system are depicted in Figures 6, 7 for α1 = 1 and α1 = 73, respectively. Figure 6 shows that the increase in Cs obtained for α1 = 1 is mainly due to the increase in LMC and QMC. It is interesting that in the case of α2 = 73, the same Cs ~ 61 can be obtained with different relative contributions of the memory capacities to Cs. The case of α2 ~ 70 and β2 = 0.75 yields to a higher LMC and a lower XMC than in the one-delay system. The case of α2 ~ 82 and β2 = 0.4 gives the Cs ~ 61 thanks mainly to the increase in the XMC.
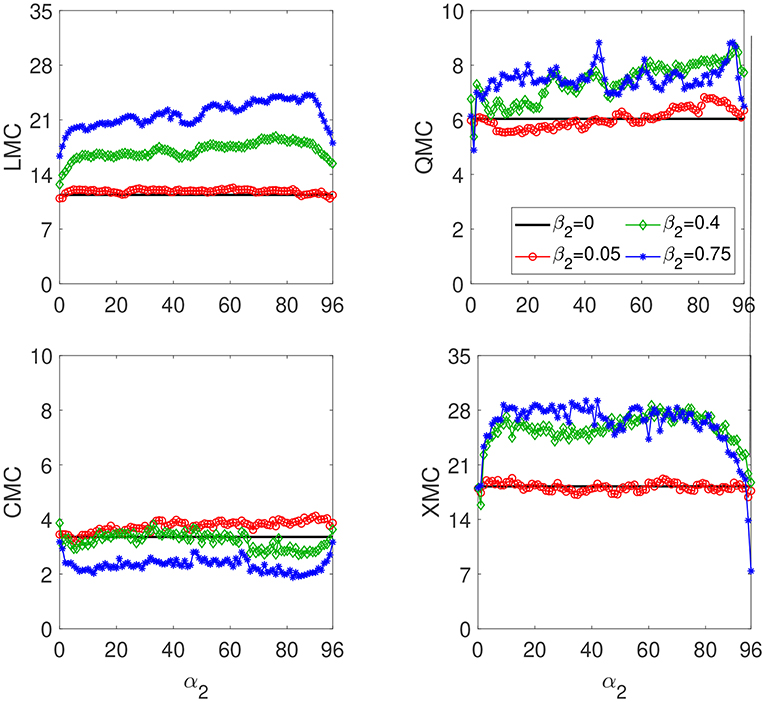
Figure 6. Memory capacities for the two-delay RC as function of α2 for a fixed α1 = 1, T = θ/0.2 and γ = 0.1. The red circles, green diamonds and blue stars correspond to β2 equal to 0.05, 0.4, and 0.75, respectively. The solid black line is for β2 = 0 and corresponds to the one-delay system with α = 1 and β = 0.8.
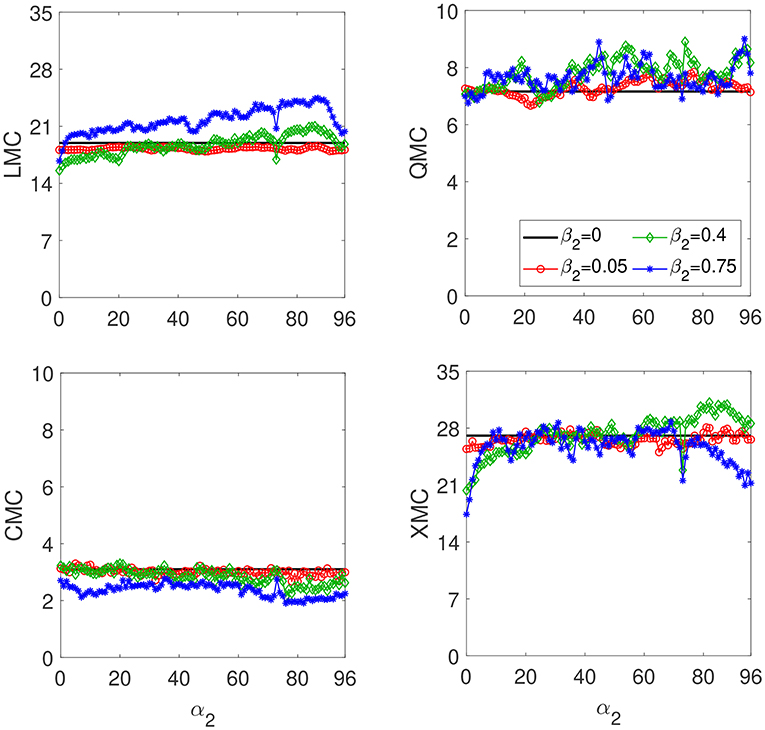
Figure 7. Memory capacities for the two-delay-based RC as function of α2 for a fixed α1 = 73, T = θ/0.2 and γ = 0.1. The red circles, green diamonds and blue stars correspond to β2 equal to 0.05, 0.4, and 0.75, respectively. The solid black line is for β2 = 0 and corresponds to the one-delay case with α = 1 and β = 0.8.
3.2. Delay-Based Reservoir Computer Performance
Finally we study the effect of increasing the mismatch α on the performance of a delay-based reservoir computer for two different response times of the non-linear node dynamics: T = 0 and T = 0.2θ. Two tasks are considered: the NARMA-10 task and the equalization of a wireless communication channel. These two tasks are benchmarking tasks used to assess the performance of RC [1, 10].
The NARMA-10 task consists in predicting the output of an auto-regressive moving average from the input u(t). The output y(t+1) is given by:
The input u(t) is independently and identically drawn from the uniform distribution in [0, 0.5]. Solving the NARMA-10 task requires both memory and non-linearity. Figure 8 (left) shows the normalized-root-mean-square error (NRMSE) of the NARMA-10 task as a function of α for γ = 0.1. We consider a small value of γ = 0.1 because a long memory is required to obtain a good performance for NARMA-10 task. Regardless the response time (T = 0 or T = θ/0.2), the NRMSE decreases when the processing and delay times are mismatched (α > 0). However, for T = 0 the NRMSE is almost the same for a wide variety of values of α, and a mismatch α = 1 is enough to obtain a NRMSE = 0.31 close to the absolute minimum (NRMSE = 0.28 for α = 78). When the response time of the non-linear node is larger than node separation (T = θ/0.2), the NRMSE decreases from a NRMSE ≈ 0.46 at α = (0, 1) to a NRMSE = 0.34 at α ~ 72. This is due to the long memory required to obtain a good performance for NARMA-10 task. In the case of T = θ/0.2, the required LMC is not reached until α ~ 72 (see Figure 4B). Our results show that a similar performance can be obtained for small and large values of T/θ thanks to the mismatch α. Therefore, increasing α allows a faster processing information (higher sampling output rate) without causing system performance degradation.
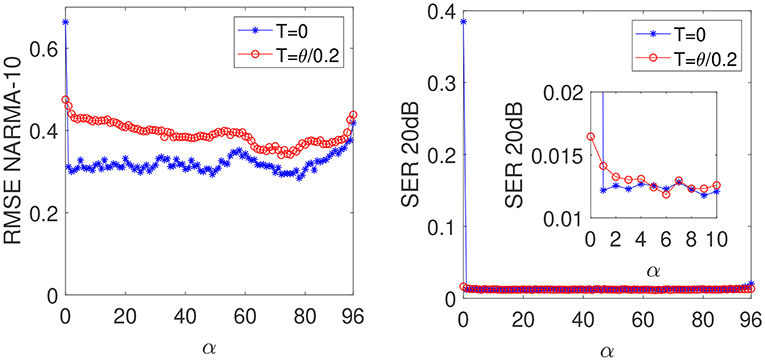
Figure 8. Performance of the non-linear one delay-based RC for two tasks as function of α. Left: NARMA-10 for γ = 0.1. Right: Equalization with SNR = 20 dB and γ = 1. The blue stars correspond to the case of T = 0 and the red circles to the case of T = θ/0.2.
The equalization of a wireless communication channel consists in reconstructing the input signal s(i) from the output sequence of the channel u(i) [1]. The input to the channel is a random sequence of values s(i) taken in {−3, −1, 1, 3}. The input s(i) first goes through a linear channel yielding:
It then goes through a noisy non-linear channel:
where v(i) is a Gaussian noise with zero mean adjusted in power to give a signal-to-noise ratio (SNR) of 20 dB. The performance is measured using the Symbol Error Rate (SER), that is the fraction of inputs s that are misclassified. The SER for the equalization with a SNR of 20dB is depicted as a function of α for γ = 1 in Figure 8 (right). In the case of T = 0, there is a clear improvement of the performance from α = 0 to α = 1 but the errors are almost constant when α is further increased. When T = θ/0.2 performance improves with α until a minimum SER = 0.012 is reached when α ~ 4. This SER is similar to that obtained when T = 0. Then, regardless the value of T/θ, a similar performance is obtained by using the mismatch α. A SER of 0.01 for the channel equalization task has been obtained using an optoelectronic reservoir computer [15].
It is not straightforward how the processing capacity will translate into the performance for specific tasks. Different tasks require to compute functions with different degrees of non-linearity and memory. Information processing capacity should be complemented with those requirements to identify optimized operating conditions for the reservoir. For the channel equalization task, when T = 0 the capacities LMC and XMC increase with α showing a very large increase from α = 0 to α = 1 (see Figure 4C). The SER shows also a clear decrease from α = 0 to α = 1 but it is almost constant when α > 1 [see Figure 8 (right)]. The capacities LMC and XMC achieved for α = 1 when T = 0 are enough to solve the channel equalization task. However, the quadratic capacity QMC is almost constant when α > 1. As a consequence the SER is almost constant for α > 1. When taking a small node separation (θ = 0.2T) the capacities LMC and XMC increase with α (see Figure 4A). This increase in processing capacity leads to a better performance with α and the SER decreases from 0.017 for α = 0 to a minimum error of 0.012 for α = 4. This is an improvement in performance of around 30%. However, the increase in the total capacity for α > 4 (mainly due to the LMC) does not translate into the performance. The reason is the same as for the case of T = 0. The capacities LMC and XMC achieved for α = 4 are enough to solve the channel equalization task while the capacities QMC and CMC do not increase with α.
The addition of the second delay line to the non-linear node does not improve the performance for the equalization task. In the case of T = 0, the extra delay line slightly improves the performance for the NARMA-10 task. The minimum error is NRMSE ~ 0.25 when α1 = 77, α2 = 20 and β1 = β2 = 0.4. When T = θ/0.2 a NRMSE = 0.27 is obtained for α1 = 77, α2 = 86, β1 = 0.05, and β2 = 0.75, while a minimum NRMSE=0.34 was obtained with one delay line for α ~ 72. This performance improvement for the NARMA-10 task when T = θ/0.2 is at the cost of adding second delay line and optimizing more parameters to minimize the error. A NRMSE of 0.22 for the NARMA-10 task has been obtained using a photonic reservoir computer based on a coherently driven passive cavity with a greater number of virtual nodes N = 300 [24] than the one we used, N = 97.
4. Discussion
We have investigated the role of the system response time in the computational capacity of delay-based reservoir computers with a single non-linear neuron. These reservoir computers can be easily implemented in hardware, potentially allowing for high-speed information processing. The information processing rate, given by , can be increased by using a high sampling output rate (small node separation θ). However, we have shown that the computational capacity is reduced when node separation is smaller than system response time. We can thus conclude that there is a trade-off between information capacity and rate in delay-based reservoir computers. In this context, parallel-based architectures with k non-linear nodes reduce the information processing time by a factor of k for the same total number of virtual nodes. It has been shown [16, 25] that for (θ/T) < 1 and without mismatch between Tp and τ, performance is improved when different activation functions are used for the non-linear nodes. However, the hardware implementation becomes more involved than the one of a delay-based reservoir computer with a single non-linear node.
We have considered a different strategy still based on the simple architecture of a single non-linear node to tackle the trade-off between information capacity and rate. In this strategy, the mismatch between delay and data injection times α is used to increase reservoir diversity when θ < T. For small values of (θ/T) and α, the states of virtual nodes that are separated by less than T (i.e., with an index difference smaller than T/θ) are similar. When the mismatch is increased, virtual nodes are connected through feedback to nodes that are not connected through non-linear node dynamics. Reservoir diversity is then increased. Our results show that the linear memory capacity increases the mismatch α. In this way the capacity degradation due to high sampling output rate is reduced by increasing α.
Another strategy to increase reservoir diversity when θ < T is to use an extra feedback line. We show that the linear memory capacity can be further increased with this architecture by using long delay times (large mismatch α). However, only a slight increase in the calculated capacity is obtained.
We have also obtained the performance of delay-based reservoir computers for two benchmarking tasks: channel equalization and NARMA-10. Our results show that for fast reservoirs with θ < T performance improves when the mismatch α increases. A similar performance is obtained for small and large values of (θ/T) for channel equalization and also for NARMA-10 tasks if delay and injection times are mismatched.
We can thus conclude that the processing speed of delay-based reservoir computers can be increased while keeping a good computational capacity by using a mismatch between delay and data injection times.
Data Availability Statement
The datasets generated for this study are available on request to the corresponding author.
Author Contributions
SO implemented the program and performed the numerical calculations. All authors contributed to the conception, design of the study, contributed to the discussion of the results, and to the writing of the manuscript.
Funding
This work has been funded by the Spanish Ministerio de Ciencia, Innovación y Universidades and Fondo Europeo de Desarrollo Regional (FEDER) through project RTI2018-094118-B-C22.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
1. Jaeger H, Haas H. Harnessing nonlinearity: predicting chaotic systems and saving energy in wireless communication. Science. (2004) 304:78–80. doi: 10.1126/science.1091277
2. Maass W, Natschläger T, Markram H. Real-time computing without stable states: a new framework for neural computation based on perturbations. Neural Comput. (2002) 14:2531–60. doi: 10.1162/089976602760407955
3. Lukoševicius M, Jaeger H. Reservoir computing approaches to recurrent neural network training. Comput Sci Rev. (2009) 3:127–49. doi: 10.1016/j.cosrev.2009.03.005
4. Jaeger H. Short Term Memory in Echo State Networks. GMD Forschungszentrum Informationstechnik GmbH. GMD Report 152, Sankt Augustin (2002).
5. Larger L, Baylón-Fuentes A, Martinenghi R, Udaltsov VS, Chembo YK, Jacquot M. High-speed photonic reservoir computing using a time-delay-based architecture: million words per second classification. Phys Rev X. (2017) 7:11015. doi: 10.1103/PhysRevX.7.011015
6. Moon J, Ma W, Shin JH, Cai F, Du C, Lee SH, et al. Temporal data classification and forecasting using a memristor-based reservoir computing system. Nat Electr. (2019) 2:480–7. doi: 10.1038/s41928-019-0313-3
7. Appeltant L, Soriano MC, Van Der Sande G, Danckaert J, Massar S, Dambre J, et al. Information processing using a single dynamical node as complex system. Nat Communicat. (2011) 2:468. doi: 10.1038/ncomms1476
8. Paquot Y, Duport F, Smerieri A, Dambre J, Schrauwen B, Haelterman M, et al. Optoelectronic reservoir computing. Sci Rep. (2012) 2:287. doi: 10.1038/srep00287
9. Van der Sande G, Brunner D, Soriano MC. Advances in photonic reservoir computing. Nanophotonics. (2017) 6:561–76. doi: 10.1515/nanoph-2016-0132
10. Rodan A, Tino P. Minimum complexity echo state network. IEEE T Neural Netw. (2011) 22:131–44. doi: 10.1109/TNN.2010.2089641
11. Martinenghi R, Rybalko S, Jacquot M, Chembo YK, Larger L. Photonic nonlinear transient computing with multiple-delay wavelength dynamics. Phys Rev Let. (2012) 108:244101. doi: 10.1103/PhysRevLett.108.244101
12. Soriano MC, Ortín S, Keuninckx L, Appeltant L, Danckaert J, Pesquera L, et al. Delay-based reservoir computing: noise effects in a combined analog and digital implementation. IEEE Trans Neural Netw Learn Syst. (2015) 26:388–93. doi: 10.1109/TNNLS.2014.2311855
13. Larger L, Soriano MC, Brunner D, Appeltant L, Gutierrez JM, Pesquera L, et al. Photonic information processing beyond Turing: an optoelectronic implementation of reservoir computing. Opt Express. (2012) 20:3241–49. doi: 10.1364/OE.20.003241
14. Soriano MC, Ortín S, Brunner D, Larger L, Mirasso CR, Fischer I, et al. Optoelectronic reservoir computing: tackling noise-induced performance degradation. Opt Express. (2013) 21:12–20. doi: 10.1364/OE.21.000012
15. Ortín S, Soriano MC, Pesquera L, Brunner D, San-Martín D, Fischer I, et al. A unified framework for reservoir computing and extreme learning machines based on a single time-delayed neuron. Sci Rep. (2015) 5:14945. doi: 10.1038/srep14945
16. Ortín S, Pesquera L. Reservoir computing with an ensemble of time-delay reservoirs. Cogn Comput. (2017) 9:327–36. doi: 10.1007/s12559-017-9463-7
17. Jaeger H. Tutorial on training recurrent neural networks, covering BPTT, RTRL, EKF and the ‘echo state network' approach. Technical Report GMD Report 159, German National Research Center for Information Technology, Sankt Augustin (2002).
18. Brunner D, Soriano MC, Mirasso CR, Fischer I. Parallel photonic information processing at gigabyte per second data rates using transient states. Nat Commun. (2013) 4:1364. doi: 10.1038/ncomms2368
19. Duport F, Schneider B, Smerieri A, Haelterman M, Massar S. All-optical reservoir computing. Opt Express. (2012) 20:22783–95. doi: 10.1364/OE.20.022783
20. Dambre J, Verstraeten D, Schrauwen B, Massar S. Information processing capacity of dynamical systems. Sci Rep. (2012) 2:514. doi: 10.1038/srep00514
21. Appeltant L. Reservoir Computing Based on Delay-Dynamical Systems. Vrije Universiteit Brussel/Universitat de les Illes Balears, Brussels (2012).
22. Ortín S, Appeltant L, Pesquera L, der Sande G, Danckaert J, Gutierrez JM. Information processing using an electro-optic oscillator subject to multiple delay lines. In: International Quantum Electronics Conference. Piscataway, NJ: Optical Society of America (2013).
23. Nieters P, Leugering J, Pipa G. Neuromorphic computation in multi-delay coupled models. IBM J Res Dev. (2017) 61:8:1–8:9. doi: 10.1147/JRD.2017.2664698
24. Vinckier Q, Duport F, Smerieri A, Vandoorne K, Bienstman P, Haelterman M, et al. High-performance photonic reservoir computer based on a coherently driven passive cavity. Optica. (2015) 2:438–46. doi: 10.1364/OPTICA.2.000438
Keywords: reservoir computing, delayed-feedback systems, memory capacity, system response time, information processing rate
Citation: Ortín S and Pesquera L (2019) Tackling the Trade-Off Between Information Processing Capacity and Rate in Delay-Based Reservoir Computers. Front. Phys. 7:210. doi: 10.3389/fphy.2019.00210
Received: 20 August 2019; Accepted: 21 November 2019;
Published: 12 December 2019.
Edited by:
Víctor M. Eguíluz, Institute of Interdisciplinary Physics and Complex Systems (IFISC), SpainReviewed by:
Alexander Vladimirovich Bogdanov, Saint Petersburg State University, RussiaIgnazio Licata, Institute for Scientific Methodology (ISEM), Italy
Guy Verschaffelt, Vrije University Brussel, Belgium
Apostolos Argyris, Institute of Interdisciplinary Physics and Complex Systems (IFISC), Spain
Copyright © 2019 Ortín and Pesquera. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Silvia Ortín, c2lsb3J0aW5AZ21haWwuY29t
 Silvia Ortín
Silvia Ortín Luis Pesquera
Luis Pesquera