- Physics Department, University of Idaho, Moscow, ID, United States
In this review, we concentrate on recent efforts of our group aimed at investigating the nuclear equation of state of symmetric nuclear matter (equal concentrations of protons and neutrons) and the one of pure neutron matter. Although idealized, these systems are suitable “laboratories" to probe nuclear forces in the many-body system. The energy per particle as a function of density can reveal rich information about the nature of nuclear forces in the medium and how they impact observable properties. For instance, the pressure in neutron-rich matter has been found to have profound impact on very diverse systems, ranging from the thickness of the neutron skin in a heavy nucleus to the properties of compact stars. The current trend in nuclear physics is to build few-nucleon forces according to the prescription of chiral effective field theory. We open by reviewing in depth how we develop equations of state based on state-of-the-art chiral interactions. We then highlight some applications in neutron-rich nuclei and neutron stars.
1. Introduction
Understanding the interaction of hadrons in nuclei is a most fundamental problem in nuclear physics. Our present knowledge of the nuclear force in vacuum is still incomplete, although decades of efforts have been devoted to this problem. The study of nuclear forces in many-body systems is, of course, much more challenging because additional aspects are involved beyond those which can be constrained by free-space nucleon-nucleon (NN) scattering. Predictive power with respect to the properties of nuclei is the true test for a successful microscopic theory.
The system known as “nuclear matter" is a suitable, although idealized, theoretical “test bench” for many-body theories. Nuclear matter is defined as an infinite system of nucleons interacting via strong forces in the absence of electromagnetic interactions. Nuclear matter's “signature” is its energy per particle as a function of density and potentially additional “variables” (for instance, isospin polarization or temperature). The nuclear matter equation of state (EoS) is precisely the energy per particle as a function of density and other appropriate quantities. Naturally, the idealized nature of this system, which implies translational invariance, simplifies theoretical calculations. Furthermore, within the “local density approximation” (LDA), one can utilize the EoS directly in calculations of actual nuclei. (We recall that LDA amounts to the assumption that the properties at a point with density ρ in a nucleus are the same as they would be in infinite nuclear matter at the same density).
When the densities of protons and neutrons are equal, we speak of isospin-symmetric nuclear matter. The latter has been studied since the earlier works by Brueckner and others [1–4], who introduced what became known as the Brueckner-Hartree-Fock (BHF) theory. The BHF theory seeks to find the ground state energy of a many-body system [1–6] as a linked-cluster perturbation expansion. The main point was the realization that regrouping the linked-cluster diagrams by the number of hole lines allowed the series to converge.
Other approaches to the development of the EoS were also pursued, one of them being the variational method [7, 8]. The latter yielded predictions in close agreement with those from Brueckner theory if realistic NN potentials were adopted [9].
The BHF theory, or “conventional approach,” was followed by the Dirac-Brueckner-Hartree-Fock (DBHF) approach [10–13], developed during the 1980's. The novel, and most striking feature of the DBHF theory was its ability to describe the saturation properties (both energy and density) of nuclear matter, a fundamental aspect which reflects the saturating nature of the nuclear force. The DBHF method contains important relativistic features through the description of the nuclear mean field in terms of a scalar and a vector components, strong and of opposite sign. In their combination, they provide an explanation for the binding of nucleons and the spin-orbit splitting in nuclear states. The reader is referred to Muether et al. [14] for a relatively recent review of the DBHF method and a variety of applications to both nuclear matter and nuclei.
Irrespective of the many-body framework, a quantitative NN potential must be part of its input. Presently, forces based on nuclear chiral effective field theory (χEFT) [15–18] are the most popular. Chiral effective field theory respects the symmetries of quantum chromodynamics (QCD) but, at the same time, makes use of the degrees of freedom typical of low-energy nuclear physics, nucleons, and pions. Furthermore, it provides a clear systematics to determine the few- and many-body diagrams which must be present at each order of the perturbation.
Deriving nuclear forces directly from QCD is problematic. For starters, each nucleon is, itself, a complicated many-body system consisting of quarks, quark-antiquark pairs, and gluons, thus rendering the two-nucleon problem an even more complex many-body problem. Second, the interaction among quarks, which is due to the exchange of gluons, is very strong at the low energies involved in nuclear physics processes. For this reason, it is difficult to find converging perturbative solutions. Therefore, the first attempts to incorporate QCD in nuclear physics consisted mostly of QCD-inspired quark models. On the positive side, these models sought to explain nucleon structure (which consists of three quarks) and nucleon-nucleon processes (involving six-quarks) in an internally consistent manner. Some global features of the two-nucleon force, like the “hard core,” could be explained by these quark models. On the other hand, quark-based approaches are, in fact, models rather than a theory. From an entirely different point of view, one may confront the six-quark problem by putting this system on a four dimensional discrete lattice representing three dimensions in space and one in time. This method is known as lattice QCD. Although progress in lattice QCD goes on, such calculations are computationally very demanding and thus the approach is not (currently) feasible as a standard tool to make predictions of nuclear properties.
A new era for the theory of nuclear forces started when Steven Weinberg worked out an effective field theory (EFT) for low-energy QCD [16, 19]. He argued that all one needs to do is to write the most general Lagrangian consistent with all the properties of low-energy QCD, as this action would render the theory equivalent to low-energy QCD. A crucially important property for this discussion is SU(2)R × SU(2)L symmetry, or chiral symmetry, which is “spontaneously” broken, as briefly reviewed next. Massless spin- fermions have their spin and momentum either parallel to each other (“right-handed”) or anti-parallel (“left-handed”), a property which is referred to as having definite chirality. Since nucleons are made of “up” and “down” quarks, which have nearly zero mass, chiral symmetry holds approximately. As a consequence of this symmetry, one might expect to find in nature mesons of the same mass but opposite parity. However, such parity “doublets” are not observed, which amounts to a “spontaneous” breaking of the symmetry. According to a theorem first proven by Goldstone, the spontaneous symmetry breaking implies the existence of a pseudoscalar meson, the pion. Thus, the pion plays an outstanding role in generating the nuclear force. Pions and nucleons interact weakly at low energies as compared to the gluons and quarks. Therefore, calculations of pion-nucleon processes pose no problems. Moreover, in EFT one makes use of expansions in powers of momentum over an appropriate “scale,” which is the “chiral symmetry breaking scale,” close to 1 GeV. In short, this is the essence chiral perturbation theory or ChPT, and the reason why it allows to calculate the various contributions to the potential systematically order by order, where each order refers to a particular power of the momentum. Furthermore, χEFT can generate not only the force between two nucleons, but also many-nucleon forces in a consistent manner [17]. The χEFT approach continues to gain popularity and is applied with great success in contemporary theoretical nuclear physics [18, 20–22].
However, it is important to keep in mind that a low-momentum expansion has a limited range of applicability. For that reason, interactions derived from chiral perturbation theory are not meant for applications to high energy processes or in dense matter, where high Fermi momenta are involved, as is the case in the interior of compact stars. In such situations, strategies to extend chiral predictions must be adopted, and we will discuss some instances where extensions become necessary.
Mean-field models, both relativistic and non-relativistic (see, for instance [23, 24]) are still a popular, although non-microscopic alternative to methods based on the in-medium reaction matrix. They continue to be utilized frequently in the development of the EoS and related predictions.
Describing the properties of (dense) systems from elementary forces and including all required contributions is an extremely challenging program, whose completion is not in sight. However, χEFT provides a path on which to proceed systematically toward that goal. We share the point of view that χEFT is currently the most fundamental approach due to its strong link with QCD. At the same time, the degrees of freedom of the theory make calculations of low-energy observables a manageable task.
Our main objective in this article is to provide a self-contained review of the recent work with isospin symmetric and asymmetric matter done systematically by our group and based mainly on chiral interactions, comparing with empirical constraints when available. We will place particular emphasis on neutron-rich matter, which is currently the focus of numerous empirical investigations both in terrestrial laboratories (especially through experiments aimed at constraining the thickness of neutron skins), or through astrophysical observations of neutron stars and related phenomena.
This article is organized as follows. After these opening remarks, in section 2 we describe in detail the calculations of the EoS, starting with the two-nucleon forces (2NF) and the three-nucleon forces (3NF) which we apply (see sections 2.2.1 and 2.2.2, respectively). In section 2.3, we review and discuss some of our results of the energy per particle in both symmetric and neutron matter [25]. In section 3, we focus specifically on the symmetry energy and the chief role its density dependence plays for neutron-rich systems. We then develop a discussion on the EoS in neutron stars (see section 4). We conclude with a summary and an outlook in section 5.
2. Nuclear Matter and the Equation of State
2.1. The G-Matrix and the Energy per Particle
In the previous section, we mentioned the linked-cluster perturbation series for the energy of a many-body system [1–6]. To facilitate convergence (otherwise problematic in view of the strong repulsive core of the NN force), the linked-cluster expansion for the energy per particle in nuclear matter [3] is written in terms of the reaction matrix or “G-matrix,” which itself is solution of the Bethe-Goldstone equation. Schematically, the Bethe-Goldstone equation can be written as
where V is the NN potential, Q is the Pauli operator, and E0 the starting energy of the two nucleons. The second term on the RHS of Equation (1) represents the infinite ladder sum which builds short-range correlations (SRC) into the wave function. The correlated (ψ) and the uncorrelated (ϕ) wave functions satisfy
from which one can write
At large distances, the correlated wave function is expected to approach the uncorrelated one (a behavior known as the “healing” property), whereas the two can be very different at short range. Hence, the difference between the correlated and the uncorrelated wave functions, or “defect function” f = ψ − ϕ, can be associated to the degree of SRC.
Usually, its momentum-dependent Bessel transform is considered instead, so as to bring out the dependence on specific partial waves. For each angular momentum state [5], we then have
where the angle-averaging has been applied to the Pauli operator, . Equation (4) is related to the probability of exciting two nucleons having relative momentum k0 and relative orbital angular momentum L to a state with relative momentum k and relative orbital angular momentum L′. The integral of the probability amplitude squared is known as the “wound integral” and defined, for each partial wave at some density ρ, as
Thus, both f and κ contain information on correlations present in the wave function and the G-matrix. The degree of SRC has been traditionally associated with the “strength” of a given potential, as indicated, for instance, by the deuteron D-state probability [26].
The topic of SRC deserves a review by itself and will not be covered here. However, we have taken the opportunity to recall how one may obtain, through Equations (4–5), some information about SRC in nuclear matter. The latter is complementary to studies of SRC in nuclei, which are currently the object of intense experimental investigations through high momentum-transfer (inclusive or exclusive) electron scattering measurements. (For a review on this topic, see [27] and references therein). Two-nucleon dynamics at short distances is mostly determined by the presence of short-range repulsion in the two-nucleon force, which is one of the reasons why a mean-field picture of the nucleus has strong limitations. Short-range correlations, particularly two-nucleon correlations, are therefore fundamentally important and open intriguing questions concerning momentum distributions in nuclei as a tool to probe the off-shell nature of the NN potential. For a recent work of our group on SRC in A=2,3 nuclei see [28].
Back to Equation (1), we solve it self-consistently to obtain the G-matrix together with the single-particle potential, which we define for (anti-symmetrized) states below and above the Fermi level according to the so-called “continuous choice”:
The starting energy is written as
in terms of on-shell single-particle energies
where T is the kinetic energy. The average energy per particle in nuclear matter is then obtained from
Equation (9) as a function of density is the nuclear EoS. Next, we will address how the NN potential V in Equation (1) is constructed.
2.2. The Equation of State From Chiral Forces
It is our philosophy that constructing the EoS microscopically from state-of-the-art few-body interactions is the right way to gain insight into effective nuclear forces in the medium. High-precision meson-theoretic interactions [29–31] are often utilized in contemporary calculations of nuclear matter, structure, and reactions. However, in the meson-theoretic approach it is difficult, if not impossible, to maintain a strong connection between the 3NF, or more generally the A-nucleon forces with A > 2, and the associated 2NF [32]. On the other hand, χEFT [18, 20, 22] provides a systematic way to construct nuclear many-body forces consistently [17] with two-body forces, as well as to assess theoretical uncertainties through a systematic expansion controlled by a counting scheme [15]. Furthermore, and perhaps most importantly, χEFT maintains consistency with the symmetries and symmetry breaking pattern of the fundamental theory of strong interactions, QCD.
Because of the strengths described above, χEFT has become the authoritative approach for developing nuclear forces. Applications include few-nucleon reactions [33–38], nuclear structure, especially of light- and medium-mass nuclei [39–55], cold infinite matter [22, 53, 56–64], infinite matter at finite temperature [65, 66], and various aspects of nuclear dynamics [67–73].
In regard to the connection between nuclear matter properties and finite nuclei, it is interesting to point out a persistent problem encountered in structure calculations and related to the bulk properties of medium-mass nuclei. Typically charge radii are underpredicted [74] while the opposite is true for binding energies [75]. Including the desired properties of medium-mass nuclei directly into the fitting protocol for the low-energy constants (LECs) which parametrize short-distance physics in chiral nuclear forces has resulted in improved predictions [76]. However, for a truly microscopic approach the 2NF should be constrained by two-nucleon data and the 3NF by three-nucleon data, without additional adjustments. Applications to A > 3 systems would then be actual predictions, although they may carry substantial uncertainties.
Two recent studies [54, 55] provide indications for how the overbinding problem may be overcome. In these studies, a rather soft nucleon-nucleon (NN) potential (due to renormalization group evolution) along with 3NFs fitted to the binding energy of 3H and the charge radius of 4He were employed to calculate the ground-state properties of closed shell nuclei from 4He to the light Tin isotopes [54, 55]. Predictions of the ground-state energies were accurate, whereas the radii were somewhat underpredicted, although still in fairly good agreement with experiment. These features can be linked to the good nuclear matter saturation properties of the employed 2NF + 3NF combination [57]. In the above example, the 2NF was soft and alone would lead to substantial overbinding in nuclear matter, whereas the addition of a repulsive 3NF contribution leads to a much better description of the nuclear matter saturation point [57]. As we mentioned earlier, the first quantitative explanation of nuclear matter saturation was achieved in this way within the framework of Dirac-Brueckner-Hartree-Fock theory [12, 14, 77–79]. As an alternative, one could begin with a relatively repulsive 2NF and then add an attractive, density-dependent 3NF contribution. An example of such combination is provided by the Argonne v18 (AV18) 2NF [31] together with the Urbana IX 3NF [80]. However, in this way satisfactory predictions for both the nuclear matter saturation energy and density cannot be obtained [81] and the binding energies of medium-mass nuclei are seriously underpredicted [82]. A similar scenario presents itself when the AV18 2NF is used in combination with the Illinois-7 3NF [82, 83]. Efforts to treat the 3NF microscopically were reported in Zuo et al. [84] and Li et al. [85]. In Li et al. [85], in particular, a 3NF including the Δ, Roper, and nucleon-antinucleon excitations was proposed, based on the Bonn [86] and the Nijmegen [30] one-boson-exchange potentials.
The predictions reviewed in this work are based on the high-quality soft chiral NN potentials from leading order to fifth order of the chiral expansion constructed in Entem et al. [87]. More details are provided below.
2.2.1. Two-Nucleon Forces
The NN potentials used in this review go over five orders in the χEFT series, from leading order (LO) to fifth order (N4LO). This set of interactions is more internally consistent as compared to earlier ones [88, 89], in that the same power counting and regularization schemes are used for each order.
Furthermore, the long-range contributions are fixed by the πN LECs provided by the recent analysis of Hoferichter et al. [90, 91], which provided very accurate determinations. The errors in those πN LECs are small enough to be safely ignored in the process of uncertainty quantification. We also recall that, at the fifth (and highest) order, the NN data below pion production threshold are reproduced with the precision of a χ2/datum equal to 1.15.
Prior to iterating the potential in the Lippmann-Schwinger equation, one must remove high-momentum components, in line with the low-momentum expansion concept of chiral perturbation theory. For the interactions we use, this step is carried out through the application of a non-local regulator function:
where and are the final and initial nucleon momenta in their center-of-mass system, respectively. We will consider only values of the cutoff parameter Λ smaller than or equal to 500 MeV, which have been found to have good perturbative properties. The soft nature of the potentials has been confirmed by the Weinberg eigenvalue analysis of Hoppe et al. [92] and in the context of the perturbative calculations of infinite matter of Drischler et al. [93].
2.2.2. Three-Nucleon Forces
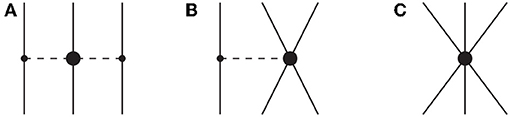
Three-nucleon forces contribute for the first time at the third order of the chiral expansion (N2LO), where they contain three parts [33]: the two-pion-exchange (2PE) term, which is of long-range nature, the medium-range one-pion exchange (1PE) contribution, and a short-range contact term. These diagrams are shown in Figure 1. We apply these 3NFs in the form of the density-dependent effective two-nucleon interactions [94, 95], which can be expressed in terms of the well-known non-relativistic two-body nuclear force operators and thus easily incorporated in the usual NN partial wave formalism and subsequently in the computation of the EoS via the particle-particle ladder approximation. We recall that the strategy of including the 3NF as an effective density dependent 2NF was first proposed in Baldo et al. [96] within the BHF theory.
The effective density-dependent two-nucleon interactions can be regrouped into six topologies involving one loop. Three of them originate from the 2PE graph of the chiral 3NF (Figure 1A), and depend on the LECs c1, 3, 4, which already appear in the 2PE part of the NN force. Two one-loop topologies are derived from the 1PE diagram (Figure 1B), and contain the LEC cD. Last, we have the one-loop topology related to the 3NF contact diagram (Figure 1C), associated with the LECs cE. Note that, in pure neutron matter, the contributions proportional to the LECs c4, cD, and cE vanish [56]. In recent nuclear matter calculations [63, 93], progress has been made toward including N3LO three-body interactions in the two-body normal-ordering approximation as well as including the residual three-body normal-ordered force. Our group is in the process of including effective density-dependent 3NF at N3LO as from Kaiser et al. [97, 98]. We have preliminary evidence that the contributions from the short-range terms [97] may be negligibly small.
The LECs cD and cE which we use are determined via the three-nucleon system. They are constrained to reproduce the A = 3 binding energies and the Gamow-Teller matrix element of tritium β-decay through the procedure described in Gardestig and Phillips [99], Gazit et al. [100], and Marcucci et al. [101]. The regulator function applied to the 3NF is
as in Navrátil [102], with the momentum transfer. Note that this choice makes the 3NF local in coordinate space, which, in turn, facilitates the construction of the A = 3 wave functions [103].
The complete 3NF at orders higher than the third (N2LO) is very challenging, both in its development and applications, and, therefore, it is frequently excluded from nuclear structure studies. Note, though, that good progress is being made toward the inclusion of the subleading 3NF at N3LO [63, 93, 97, 98, 104, 105]. However, in Krebs et al. [106] it was shown that the 2PE 3NF has nearly the same analytical structure at the third (N2LO), fourth (N3LO), and fifth (N4LO) orders. Thus, one can parametrize the sum of all the three orders of 3NF contributions in terms of a set of effective LECs. Therefore, at least for this very important component of the 3NF, complete calculations up to N4LO are possible.
In the N4LO rows of Table 2 we give the effective LECs c1, 3, 4 obtained in Krebs et al. [106]. Concerning the 2PE 3NF at N3LO, Equation (2.8) of Bernard et al. [107] provides the corrections to the ci. (Note, though, that there is an error in the values given below that equation. The correct values for δc3 and δc4 are δc3 = −δc4 = 0.89 GeV−1.) With these corrections, we obtain the values given in the N3LO rows of Table 2. Then, inserting the ci of Table 2 in the expression for the N2LO 3NF, we are able to include the 2PE parts of the 3NF up to N3LO and up to N4LO in a straightforward way, with the LECs cD and cE refitted. Their values, also listed in Table 2, are different from those listed in Table 1 but of the same order and with the same sign.
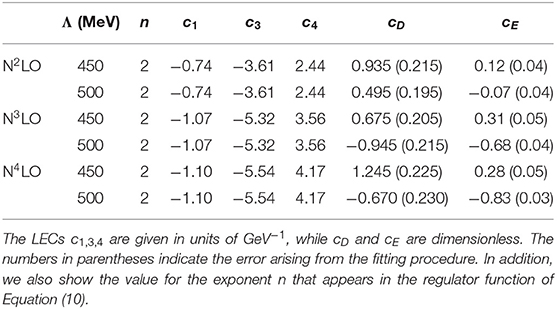
Table 1. Values of the LECs c1, 3, 4, cD, and cE for different orders of the 2NF in the χEFT expansion, and the 3NF at N2LO, and different values of the momentum-space cutoff Λ.
We close this section by highlighting that, of all possible 3NF contributions, the 2PE 3NF is the first to have been calculated [108]. The prescriptions outlined above allow to include this very important 3NF up to the highest order we consider at this time.
2.3. Predictions for the Equation of State
2.3.1. Symmetric Matter Predictions
We begin with the symmetric nuclear matter (SNM) EoS. This is displayed in Figure 2, where, on the left, the momentum-space cutoff is fixed at 450 MeV but the chiral order of the two-body force is varied from leading to fifth order. The 3NFs are chosen with LECs in Table 2, which at N3LO and N4LO include the 2PE 3NF at fourth and fifth order, respectively. (We note that, in all that follows, when we refer to predictions obtained with 3NF at N3LO or at N4LO, we mean to say that the 2PE 3NF is included up to those orders). The dashed lines indicate results at N2LO and above with no three-body forces present, while the solid lines include the 3NF when appropriate, that is, at N2LO and up. Formally, we observe a good convergence pattern at the two-body level with this family of NN potentials, but naturally we do not expect realistic saturation behavior when soft two-body forces alone are included in the calculation of the EoS. We see that the inclusion of 3NFs is necessary beyond about half nuclear matter saturation density and that for this set of nuclear potentials the total 3NF contribution to the EoS decreases with the chiral order from N2LO to N4LO.
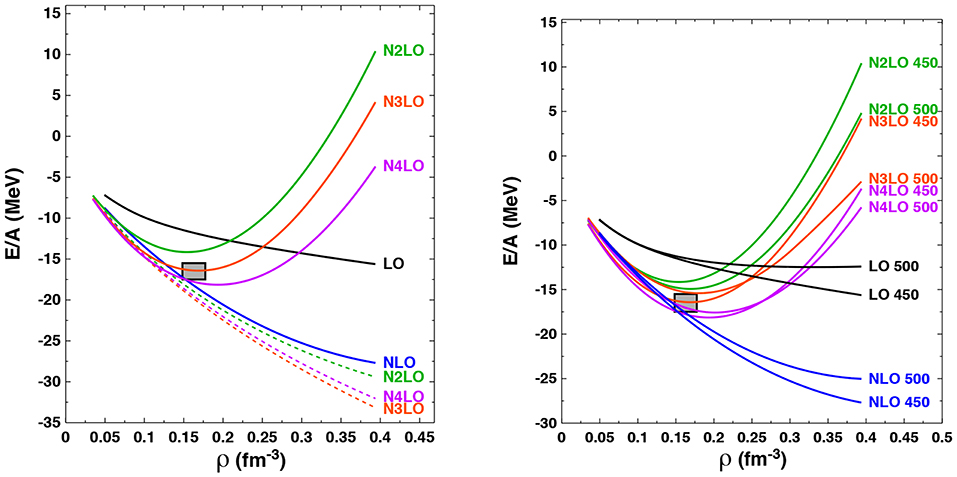
Figure 2. (Left) Ground state energy per particle of SNM as a function of density from the chiral two- and three-body forces with cutoff Λ = 450 MeV. The three dotted curves show predictions which include only two-body forces. For the 3NF contributions at N2LO and above, the LECs of Table 2 are used. The shaded box locates the approximate empirical saturation energy and density. (Right) Ground state energy per particle of SNM as a function of density at the indicated orders and with varying cutoff parameters. Other details as on the left.
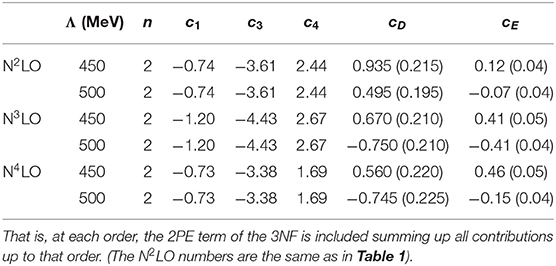
Table 2. Same as Table 1, but including the 2PE 3NF at N3LO and N4LO.
We note that the uncertainty band obtained by varying the chiral order from N2LO to N4LO while keeping Λ fixed to 450 MeV encloses the empirical saturation point. The saturation energy varies in the range −14MeV ≲ E0 ≲ −18MeV while the saturation density varies between . We stress that, once the two- and three-nucleon forces are fixed by the NN data and the properties of the three-nucleon system, no parameters are readjusted, making the many-body calculation parameter-free. Since the predicted binding energies and charge radii of intermediate-mass nuclei are closely related to the corresponding saturation point in SNM, we see the possibility that the new class of chiral potentials constructed in Entem et al. [87] and used in this work may lead to more reliable predictions in ab initio calculations of finite nuclei. For densities larger than ρ ≳ 0.20fm−3, the predictions shown on the LHS of Figure 2 display a trend that does not suggest satisfactory convergence, since the three (saturating) solid curves are about equally spaced. This is most likely due to the incompleteness of the 3NF at orders above N2LO. It is natural to expect that such trend will be a recurrent theme in later results. As discussed in section 2.2.2, we believe that including the important 2PE contribution consistently across all orders is important and insightful. For instance, our results suggest that the missing 3NF contributions at orders higher than N3LO can be expected to play a substantial role toward a successful convergence.
On the RHS of Figure 2 we show the dependence of the SNM EoS on the choice of momentum-space cutoff Λ in the two- and three-body forces as well as the order in the chiral expansion. In the present work we consider only the two cases Λ = 450, 500 MeV, see comments in section 2.2.1. At orders N2LO, N3LO, and N4LO, the cutoff dependence appears to be comparable but generally smaller than the truncation errors.
In Figure 2, we show the impact of choosing at fourth (N3LO) and fifth (N4LO) order in the chiral expansion either the N2LO 3NF coupling strengths shown in Table 1 (labeled “I” in the figure) or those obtained by including the 2PE 3NF contributions at higher order shown in Table 2 (labeled “II” in the figure). We only show results for potentials with momentum-space cutoff Λ = 450 MeV, but we expect similar results for the Λ = 500 MeV cutoff potentials due to the identical change in the important ci LECs (i = 1, 3, 4). We see that at N4LO the impact is rather large and roughly of the same size as variations in the chiral order from N2LO to N4LO. However, the additional theoretical uncertainty resulting from the choice of LECs entering into the 2PE 3NF would extend the overall error band inferred from the RHS of Figure 2 only moderately and only at the largest densities considered. In other words, Figure 3 shows that the truncation error (compare N3LO II and N4LO II) can be much smaller than the uncertainty arising from using different sets of LECs (compare N4LO I and N4LO II), indicating the importance of completeness in the 3NF at all orders.
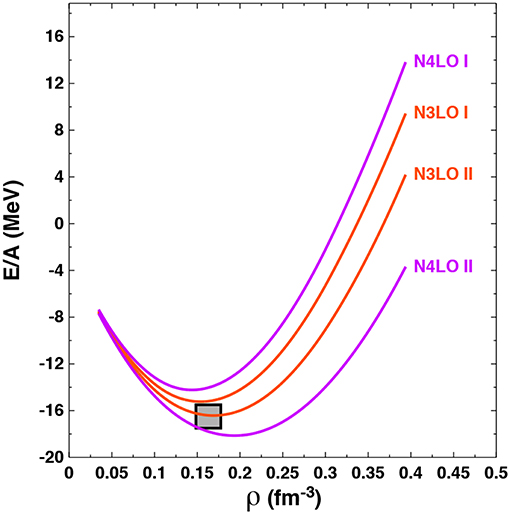
Figure 3. Energy per particle in SNM as a function of density at N3LO and N4LO with a cutoff of Λ = 450 MeV. For the 3NF contributions, the LECs of either Table 1 or Table 2 are applied as indicated by labels “I” or “II”, respectively. Case “II” is characterized by including the 2PE 3NF up to the given order. The approximate empirical saturation energy and density are indicated by the gray box.
Before closing this section, we summarize the saturation properties of SNM at the various orders and cutoff values. In Table 3, we show saturation density, saturation energy, and the isoscalar incompressibility. For the latter, constraints can be obtained from giant monopole resonance energies. In De et al. [109], the authors obtain a range of 211.9 ± 24.5 MeV. Our predictions at N3LO are consistent with this range, whereas the larger values at N4LO reflect the larger saturation density at that order.
Parameters which involve isospin asymmetry will be discussed later.
2.3.2. Neutron Matter Predictions
We next consider the ground state energy of neutron matter (NM) as a function of density, employing the same set of chiral potentials and many-body methods discussed previously in the case of symmetric nuclear matter. The EoS for both SNM and NM are crucial to determine the density-dependent nuclear symmetry energy and to better understand the properties of neutron-rich nuclei and neutron stars, aspects which will be addressed in later sections.
In Figure 4, on the LHS, we show the energy per particle of NM as a function of density starting from chiral two- and three-body forces with the same value of the momentum-space cutoff Λ = 450 MeV but at different orders in the chiral expansion. As in the case of symmetric nuclear matter, we observe good convergence at the level of 2NF alone. When 3NFs are included, we find somewhat smaller truncation errors compared to the case of SNM. This may be due in part to the absence of large, central isospin-0 partial waves in NM, which appear to be more sensitive to differences among interactions. Clearly, the 3NF plays an outstanding role in very neutron-rich systems at and beyond nuclear saturation density, where its contribution to the EoS grows more strongly with the density than the 2NF contributions.
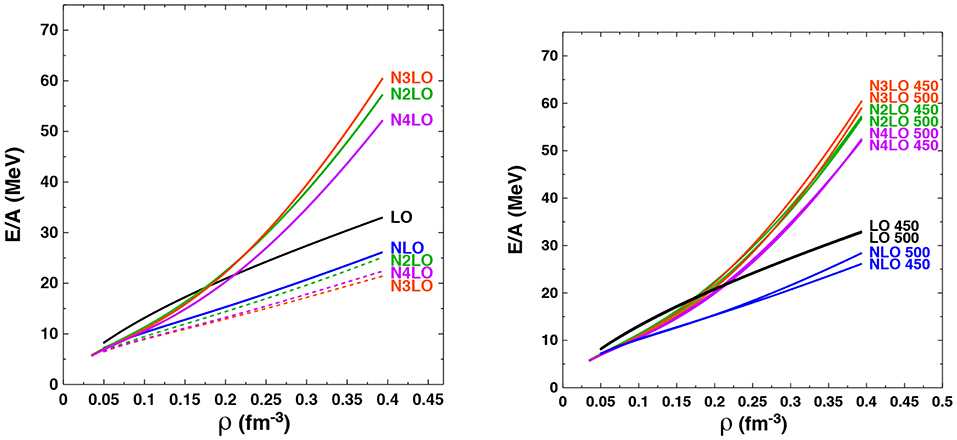
Figure 4. (Left) Ground state energy per particle of NM as a function of density at the indicated orders in the chiral expansion. The three dotted curves show predictions including only the 2NF. The cutoff parameter is fixed at Λ = 450 MeV and the 3NF LECs from Table 2 are used. (Right) Ground state energy per particle of NM as a function of density at the indicated chiral orders and with varying cutoff. The LECs of Table 2 are used.
On the RHS of Figure 4 we display the energy per particle of pure neutron matter as a function of density when varying both the order in the chiral expansion and the momentum-space cutoff Λ from 450 to 500 MeV. We see that, in comparison to the analogous study in symmetric nuclear matter, the pure neutron matter results display a much weaker cutoff dependence, which may again be due to the absence of strong isospin-0 partial waves. Interestingly, even in the case of the relatively large density ρ = 0.4 fm−3, corresponding to a Fermi momentum of kF = 450 MeV which lies at the effective breakdown scale of the expansion, there is relatively little cutoff dependence.
Once again, we observe that the order-by-order pattern is not satisfactory when moving from N3LO to N4LO. The impact of including the 2PE 3NF up to fourth (N3LO) and fifth (N4LO) order (consistent with the order of the 2NF), compared to including only the third-order (N2LO) contributions, through the adoption of the LECs given in Table 2, is demonstrated in Figure 5. As in the case of symmetric nuclear matter, the effect at N4LO is much larger than at N3LO due to the larger change Δc3 = 2.16 GeV−1 vs. Δc3 = 0.89 GeV−1, respectively, in the c3 LEC at these two orders in the chiral expansion. Moreover, the choice of LECs entering into the 2PE 3NF contributions again results in a moderate systematic increase in the pure neutron matter energy per particle at the highest densities considered. As we mentioned earlier, the investigation of higher-order 3NF contributions is in progress.
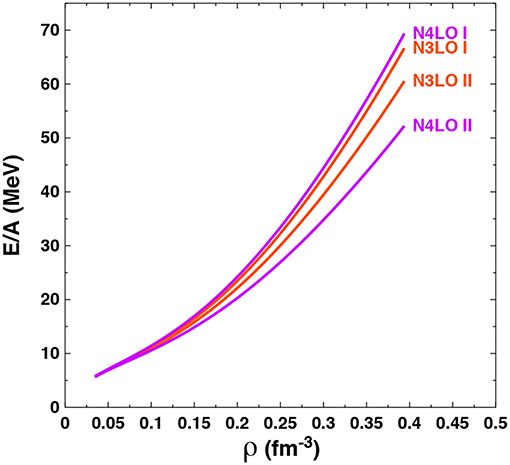
Figure 5. Ground state energy per particle of NM as a function of density at N3LO and N4LO with cutoff equal to 450 MeV. Similar to Figure 3, for the 3NF contributions the LECs of either Table 1 or Table 2 are applied as indicated by labels “I” or “II,” respectively.
Before closing this section, we take the opportunity to comment on how our SNM and NM EoS compare with those from Drischler et al. [93]. There, chiral interactions including full 3NF and 4NF at N3LO are applied to investigate nuclear saturation. Judging from the RHS of Figure 4 in Drischler et al. [93], where the EoS for both SNM and NM [63] are displayed, we conclude that our EoS at N3LO are qualitatively comparable with them within the density range covered in Figure 4 in Drischler et al. [93], namely up to ρ=0.20 fm−3, with ours revealing more attraction. We also point out that, in Drischler et al. [93], the 3NF couplings are fit to triton and to saturation properties, whereas we do not impose any constraints other than those from the two- and the three-nucleon systems. Even so, we find (confirming the conclusion from [93]) that realistic saturation properties are possible at N3LO.
3. The Symmetry Energy and Related Aspects
3.1. Review of Some Basic Concepts and Definitions
The properties of isospin-polarized matter have relevance for a number of open questions in nuclear physics and nuclear astrophysics. For instance, the existance of the neutron drip lines, the thickness of neutron skins, and the properties of neutron stars all have in common a strong sensitivity to the EoS of neutron-rich matter. The symmetry energy determines to a good approximation the energy per particle in homogeneous nuclear matter with any degree of isospin asymmetry (cf. Equation 14 below). The symmetry energy and its density dependence are therefore a key focus of contemporary theoretical and experimental investigations, and much effort has been devoted to identifying nuclear observables which correlate with this important property of infinite matter [25, 45, 53, 56–64, 110–120].
The isospin asymmetry parameter is a measure of the relative densities of neutrons and protons and is defined as
where ρn and ρp are the neutron and proton densities. It is useful to write the energy per particle in isospin asymmetric matter at some density as an expansion with respect to α:
Frequently, the expansion above is truncated at the term quadratic in α, resulting in the popular parabolic approximation:
where e0(ρ) = e(ρ, α = 0). [Equation (14) has been verified to be valid up to fairly high densities [119].] Within the assumption of Equation (14), the symmetry energy, esym, is the difference between the energy per particle in neutron matter and the one in symmetric matter. We can expand the symmetry energy about the saturation density, ρ0,
The slope parameter, L, is defined as
and therefore is a measure of the density dependence of the symmetry energy around saturation density. We recall that L is an important quantity because of its significance for the skin thickness in neutron-rich nuclei. Experiments which plan to measure the neutron radius of 208Pb and 48Ca using electroweak probes, such as PREX II [121] and CREX [122], respectively, are expected to provide accurate measurements of the neutron skin. As a consequence, one hopes for reliable constraints on the symmetry pressure, clearly related to the slope parameter (see section 3.3.1 below). Also, the radius of the average-mass neutron star is known to be sensitive to the pressure in neutron matter at normal density, , which is simply related to L (for fixed ρ0) due to the vanishing of the density derivative of e(ρ, α = 0) at saturation. That is:
The reader is referred, for instance, to Sammarruca and Millerson [123] and the comprehensive list of citations therein.
The isovector incompressibility, Ksym, is associated with the next higher-order derivative, that is, it measures the curvature of the symmetry energy at saturation density. It is defined as:
Correlations between L and both Ksym and the symmetry energy at saturation, esym(ρ0) [124–126] have been examined. Predictions for the isovector incompressibility carry large uncertainty, as is the case for the isoscalar one. Attempts to constrain the second derivative of the symmetry energy (that is, its curvature) are discussed in Vidaña et al. [127], Ducoin et al. [128], and Santos et al. [129].
3.2. Predictions of Symmetry Energy and Related Properties
Figure 6 displays the energy per particle in isospin asymmetric matter as a function of density and for increasing degree of asymmetry, cf. Equation (14), for one selected order and cutoff [130].
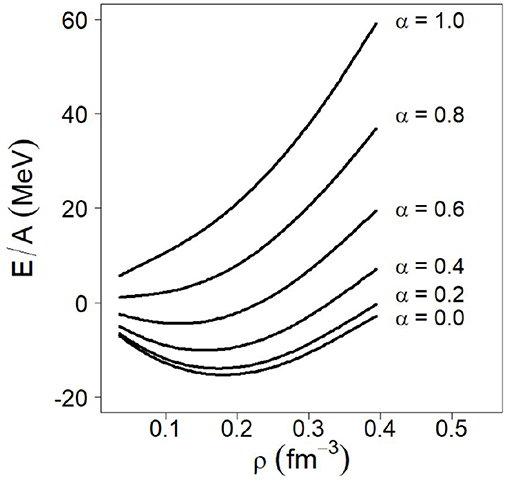
Figure 6. Energy per particle in isospin-asymmetric nuclear matter. In each case, the isospin asymmetry parameter is given. Calculations conducted at N3LO of the 2NF (and the 2PE 3NF included up to N3LO) with cutoff equal to 500 MeV.
As we already noted in conjunction with Figure 2, the saturation properties of the chiral interactions we are considering are different from one another, with the saturation density varying between about 0.16 and 0.20 fm−3. Clearly, this will impact the expansion parameters contained in Equation (15), see definitions in Equations (16–18), differently than if the derivative were evaluated, in all cases, at some common, nominal saturation density ρ0. On the other hand, analyses of correlations between the symmetry energy, its density slope, and the neutron skin thickness are typically done utilizing families of phenomenological models, such as large sets of Skyrme interactions or relativistic mean-field (RMF) models [131]. These models are constructed so as to have in common good saturation properties (usually by adjusting parameters to empirical properties of nuclei) while differing in the slope of the symmetry energy which, at saturation, is essentially a measure for the pressure in pure neutron matter (see Equation 17). Already almost two decades ago, Brown [132] considered a set of Skyrme interactions whose predictions of the density slope of the NM EoS around normal density differed dramatically and found a linear relation between such derivative and the neutron skin thickness in 208Pb. Similar investigations have been and continue to be done with RMF models, with families of interactions constructed so as to span a large range of L values. For instance, RMF models such as NL3 [133] and IU-FSU [134] give values of L equal to 118.2 and 47.2 MeV, respectively. (Not surprisingly, these models span a large range of both neutron skin values and stellar radii). In Roca-Maza et al. [24], the authors utilize a large set of RMF models all of which describe accurately the nuclear binding energies and charge radii across the periodic table (which should constrain tightly the binding energy and saturation density of SNM). On the other hand, the same models predict very different neutron root-mean-squared (r.m.s.) radii, since the isovector channel is poorly constrained [24].
Our EoS are microscopic and parameter-free and we are not in the practice of constructing families of parameterized EoS models to establish phenomenological correlations. Nevertheless, for the purpose of demonstration, next we wish to perform a study meant to highlight the role of neutron matter pressure for the neutron skin thickness once the uncertainty associated with the saturation point in SNM, cf. Figure 2, is removed. To that end, we will construct “semi-microscopic” models of asymmetric matter as follows: for the symmetric part, we will use an established phenomenological EoS, such as the one from Alam et al. [135]. For the neutron matter part, currently our focal point, we will continue to use the chiral EoS presented in section 2.3.2. We then proceed treating these six cases (three chiral orders and two cutoffs) as six EoS models differing in their NM components. Figure 7 shows the phenomenological EoS of SNM in comparison with our chiral predictions with cutoff equal to 450 MeV. Figure 8 displays the symmetry energy obtained with our microscopic NM EoS combined with SNM EoS represented by the black curve in Figure 7. We also include in the figures the results of several analyses and constraints [136–139]. The predictions based on our microscopic NM EoS are considerably softer than those constraints above normal density. Table 4 contains values for the parameters defined previosly through Equation (15), for the six EoS models which we have constructed as described.
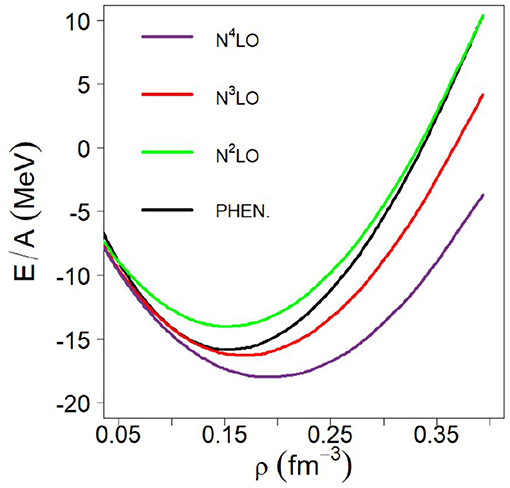
Figure 7. The EoS of SNM at the three chiral orders considered here (cutoff fixed at 450 MeV) compared with the phenomenological EoS of Alam et al. [135].
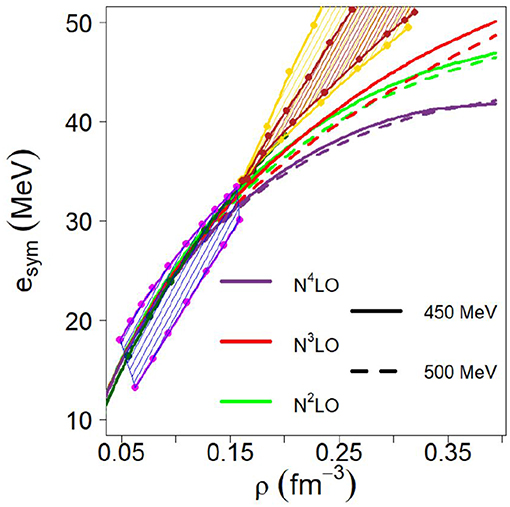
Figure 8. The symmetry energy vs. density. The curves are obtained from the various microscopic EoS for NM at the indicated chiral orders and cutoff values, combined with the phenomenological EoS for SNM [135] as explained in the text. The additional predictions and various constraints are from: Danielewicz and Lee [136], dark green; Tsang et al. [137], magenta contour; Russotto et al. [138, 139], yellow and brown shaded areas. (The data points were extracted from the graphs assuming ρ0 = 0.16 fm−3 and using WebPlotDigitizer opensource software, https://automeris.io/WebPlotDigitizer).
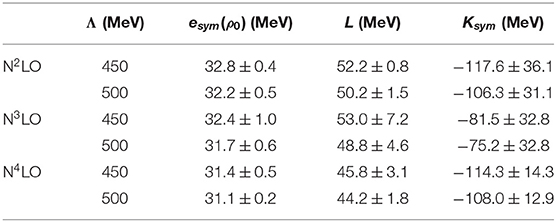
Table 4. Predicted values of symmetry energy and related properties at three orders of chiral perturbation theory and two values of the cutoff parameter obtained as explained in the text.
We now proceed to discuss the spread of our values for the symmetry energy, the L parameter, and the isovector incompressibility in the framework of chiral uncertainties of the NM EoS. We recall that one of the strengths of χEFT is the opportunity of order-by-order improvement of the predictions. Naturally, the truncation error at a given order should be a reasonable measure of the uncertainty which arises from omitting the next order contributions. If the value of the observable X has been calculated at order n+1, than the truncation error at order n can be estimated as the difference between the values at order n+1 and n:
which is a reasonable way to estimate what one is missing by retaining only terms up to order n. On the other hand, if Xn+1 is not known, then some alternative prescription must be used. We use the definition [87]
where Q is a momentum characteristic for the observable under consideration and Λ is the cutoff. For the fifth (and highest) order, we use Equation (20) and we find it reasonable to define Q as the r.m.s. value of the relative momentum of two neutrons in neutron matter at the given density [see [123] and references therein].
We wish to express our final results for the symmetry energy, the slope parameter, and the isovector incompressibility at N3LO. To that end, we average the predictions for the quantity X obtained with the two values of the cutoff separately at N3LO and N4LO, yielding and , respectively. The truncation uncertainty at N3LO can then be estimated as . As an alternative, we choose to take the largest of the errors at the two cutoff values.
Applying that prescription, we obtain for the symmetry energy, the slope parameter, and the isovector incompressibility at N3LO (all numbers in MeV):
We see that Ksym shows large variations, which reflect the extreme sensitivity of the second derivative to the details of the interactions for each of the curves in Figure 8. We emphasize that variations among those curves are due entirely to the NM predictions.
A phenomenological study of the EoS based on Skyrme density functionals [135] reports the slope parameter to be L = 65.4±13.5 MeV, whereas the isovector incompressibility is found to be within the range Ksym = −22.9±73.2 MeV. Lattimer and Lim [140] determined L to be between 40.5 and 61.9 MeV. For the isovector incompressibility, they suggest a linear relation between Ksym and L, that is, Ksym ≈ aL − b, with a, b equal to 3.33 and 281 MeV, respecively [128], or 2.867 and 260 MeV [127]. More recent constraints obtained from tidal deformabilitie inferred from GW170817, report 30 < L < 86 MeV and −140 < Ksym < 16 MeV or 40 < L < 62 MeV and −112 < Ksym < −52 MeV [141].
Before closing this section, we take the opportunity to address the pressure in neutron matter at saturation density, which, for the EoS of SNM which we have chosen is equal to 0.155 fm−3. Using Equation (17) and the uncertainty on L, we find (in MeV/fm3):
3.3. Symmetry Energy Slope and Neutron Skins
The neutron skin is defined as the difference between the r.m.s. radii of the neutron and proton density distributions:
where
i = n, p and Tn, Tp = N, Z respectively.
As mentioned before, the neutron skin thickness, particularly for 208Pb, is of great contemporary interest due to the possibility of constraining the slope of the symmetry energy through skin measurements [24, 142–147].
3.3.1. The Experimental State-of-the-Art
While electron scattering has been very successful in providing accurate information on the proton distributions within the nucleus, mapping neutron densities is a much more challenging task. In particular, measurements which make use of hadronic probes carry large uncertainties due to the model dependence of the nuclear interactions used in the analyses.
On the other hand, parity-violating electron scattering is in principle capable of providing accurate information on the weak charge distribution in the nucleus through the coupling of the neutron to the Z-boson. The typical parity-violating electron scattering experiment measures the difference between the cross sections for scattering of right-handed and left-handed electrons, that is
which is proportional to the ratio of the weak to the charge form factor of the nucleus [110] and thus can be related to coordinate space densities by Fourier transform. The challenging aspects of measuring observables related to parity violation is that they can be etremely small, in the case of APV between 10−4 to 10−7 [110].
The first PREX experiment [148, 149] provided a value of 0.33(+0.16, −0.18) fm for the skin of 208Pb, which carries a large experimental error due to technical problems which resulted into poor statistics. However, the planned PREX-II and CREX experiments have a target uncertainty of ±0.06 fm and ±0.02 fm for the neutron skin of 208Pb and 48Ca, respectively [121, 122].
Furthermore, additional constraints are expected from the forthcoming MESA accelerator in Mainz [150], which promises to constraint the neutron skin of 208Pb within ±0.03 fm and the one of 48Ca within ±0.02 fm, same as the target uncertainty of CREX. Note that these two nuclei are both stable, doubly-magic, and with a relatively large neutron to proton asymmetry, which is part of the reasons why investigations have concentrated on them.
For an extensive review of correlation analyses based on a large set of relativistic and non-relativistic nuclear density functionals see [110].
3.3.2. Predictions
We now move to neutron skins, specifically for the 208Pb and 48Ca nuclei, as predicted by the EoS models based on the six chiral interactions in NM as described previously. Using the energy per particle in infinite isospin-asymmetric matter as given in Equation (14), we can establish a simple but direct connection with the energy per nucleon in a spherically symmetric nucleus through the semi-empirical mass formula:
where the Coulomb contribution is written as:
The parameter f0 is a fitted constant for which we used a value of 65 MeV fm5, consistent with the range determined in Oyamatsu et al. [151].
We use the two-parameter Thomas-Fermi distribution function to describe the nucleon density:
The “radius” rb and the “diffuseness” c are themselves evaluated through minimization of the energy per nucleon, while ρa is easily obtained from normalization.
Table 5 shows the values of the neutron skin thickness predictions along with the truncation error for 208Pb and 48Ca. Proceeding as described previously, and taking the largest of the errors at the two cutoff values, we state our final estimates for the neutron skins of 208Pb and 48Ca as
Note that the skin depends considerably on the constant f0 appearing in Equation (28). We have not included that uncertainty in Equations (31–32) as we are focusing on chiral truncation errors. We report, however, that varying f0 between 60 and 70 MeV fm5 introduces an uncertainty of 0.01 fm, essentially independent of chiral order or cutoff.
We close this section by showing in Figure 9 a typical correlation between L and the thickness of the neutron skin in 208Pb obtained with a large set of successful RMF models. As we discussed previously, the ranges we give in Equations (22) and (31) are relatively small, which is, of course, desirable, since they originate from chiral uncertainties in the NM rather than variations of phenomenological parameterizations. We note that our range of values seem to be located on the low end of the correlation in Figure 9, with L approximately between 44 and 58 MeV and the skin between approximately 0.14 and 0.16 fm.
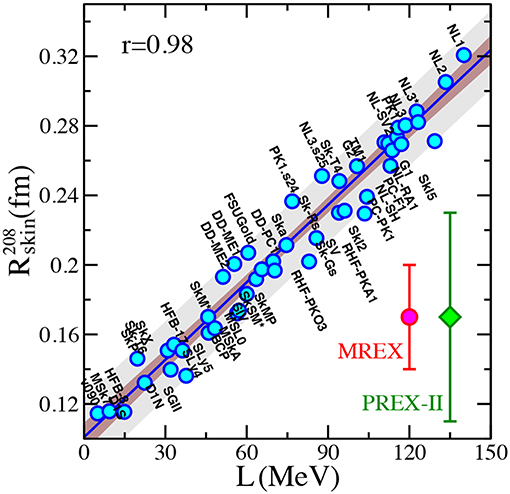
Figure 9. Correlation between the slope parameter (L) and the neutron skin thickness of 208Pb obtained with RMF models. The error bars represent the target precision for the future PREX-II [121] and MREX [150] experiments. Reproduced from Physics Today 72, 7, 30 (2019) (https://doi.org/10.1063/PT.3.4247) with the permission of the American Institute of Physics.
4. The Equation of State and Neutron Stars
4.1. Some General Aspects
It is remarkable that the relation between the mass and the radius of neutron stars is uniquely determined by the EoS together with the star's self-gravity through the Tolman-Oppenheimer-Volkoff (TOV) equations of General Relativity [152]. In fact, although the detailed structure of a neutron star is complex and varies as a function of density, the part of its core mostly composed of a uniform liquid of neutrons, protons, and leptons in β-equilibrium accounts for almost all the mass and the volume. Therefore, these compact systems are intriguing testing grounds for both nuclear physics [153–156] and General Relativity. Extensive effort has been and continue to be devoted to constraining properties of compact stars from astrophysical observations see, for instance [156–160].
The largest possible value for the mass of a neutron star was estimated by Rhoades and Ruffini [161] based on the following assumptions: (1) General Relativity is the appropriate theory of gravitation; (2) the EoS obeys the Le Chatelier's principle (∂P/∂ϵ ≥ 0) and is consistent with causality, ∂P/∂ϵ ≤ c2; and (3) the EoS is reliably known below some density. Subject to these conditions, it was determined that the maximum mass of a neutron star cannot exceed 3.2 solar masses. Note that, releasing the causality constraint, the limit can be as high as 5 solar masses [162, 163] due to the increased stiffness of the EoS at supernuclear densities.
While the maximum mass is mostly determined by the stiffness of the EoS at densities greater than a few times saturation density, the star radius is impacted mainly by the slope of the symmetry energy. More precisely, it is closely connected to the internal pressure (that is, the energy gradient) of matter at densities between about 1.5ρ0 and 2-3ρ0 [157]. The mass and the radius of the neutron star are predicted by the TOV equation as we review next.
The equations for a perfect fluid in hydrostatic equilibrium allow to determine the pressure and the total mass-energy density as a function of the radial distance from the center of the star. These coupled equations are
with
where ϵ is the total mass-energy density. The star gravitational mass is
with R the value of r where the pressure vanishes. It's worth recalling that no mass limit exists in Newtonian gravitation.
Recently, the LIGO/Virgo [164] detection of gravitational waves originating from two neutron stars spiraling inward and merging, the neutron star merger GW170817, has generated even more interest and excitement around these highly exotic systems.
The dimensionless tidal deformability is related to the neutron star response to the tidal field induced by the companion star and is defined as
where the Love number k2 reflects the quadrupole component of the gravitational potential induced by the companion star at the surface [165]. It depends on the neutron star compactness, M/R, and the energy density and pressure profile of the star. The tidal deformability can be obtained by solving the appropriate equations together with the TOV equations which yield the M(R) relation [166]. Hence, the merger detection can provide constraints on the star radius based on the tidal deformabilities of the colliding system [167]. In fact, the August 2017 first direct detection of a binary neutron star merger helped establish new limits on the radius of a 1.4 M⊙ neutron star. Additional references addressing the radius of a 1.4 M⊙ neutron star include [166, 168–172].
The correlation between the neutron skin thickness (discussed in section 3.3) and the radius of a neutron star originates from the sensitivity of the star radius to the pressure at normal density. Note that such correlation weakens as the mass increases see, for instance [110], which is why the radii of lighter stars are good candidate to help constrain the neutron skin of 208Pb and, in turn, the slope of the symmetry energy around saturation density. Based on these considerations, an upper limit of 0.25 fm was found for the neutron skin thickness of 208Pb. Additional observations from the LIGO-Virgo collaboration scheduled for 2019 are likely to provide stronger constraints.
In the remainder of this section, after reviewing how the EoS of β-stable matter is obtained from conditions of charge neutrality and energy minimization (section 4.2), we will address (spherical) neutron star properties, with emphasis on the radius of a “typical” neutron star, namely one with a mass approximately equal to 1.4 M⊙. The reasons for this choice have been given in the previous paragraph.
4.2. The EoS of β-Stable Matter
In this section, we review the basic equations which we use to obtain the EoS for stellar matter in β-equilibrium.
The total energy per particle, etot, related to the total energy density, ϵtot, by etot = ϵtot/ρ, for neutrons and protons in β equilibrium with leptons (electrons and muons) is given by:
where Yi, i = n(p), stands for the neutron(proton) fraction. On the right-hand side are the baryon contributions including their rest energies (first three terms), and the relativistic electron and the muon energies per baryon (last two terms). Note that, in the equation above, e0 and esym are the EoS of symmetric nuclear matter and the symmetry energy, respectively. All terms are functions of density.
The relativistic energy density for particle species “i” having Fermi momentum (kF)i is given by
where γ is an appropriate degeneracy factor. The partial densities are related to the respective Fermi momenta as
which gives, for spin- fermions (γ = 2),
with the corresponding particle fractions given by
The chemical potential for species “i” is defined as
where we have used Equations (38–39) to perform the derivatives with respect to the upper integration limit.
The standard procedure is to minimize the total energy per particle with the constraints of fixed baryon density and global charge neutrality:
and
The resulting set of equations allow to solve for the various lepton fractions from which one can easily obtain the corresponding energy densities.
For the purpose of applying the Lagrange multipliers method, we define the functional
where
and
and set
Equations (45–48) then yield
Thus,
and
The equations above allow to solve for the various lepton fractions and, through Equation (38), the corresponding energies are easily obtained. For electrons, we find the ultra-relativistic approximation to be appropriate and set their rest energy to zero in Equation (38).
In Figure 10, we show the predicted fractions for the various species (neutrons, protons, and leptons) at the three highest orders of χEFT which we consider. We note that the proton fraction goes up to just above 10% at the highest densities being considered. This is a rather low value, most likely related to the relatively soft nature of the symmetry energy displayed in Figure 8. It implies that neutron stars (with central densities up to those included in the figure) will not cool down via direct Urca processes.
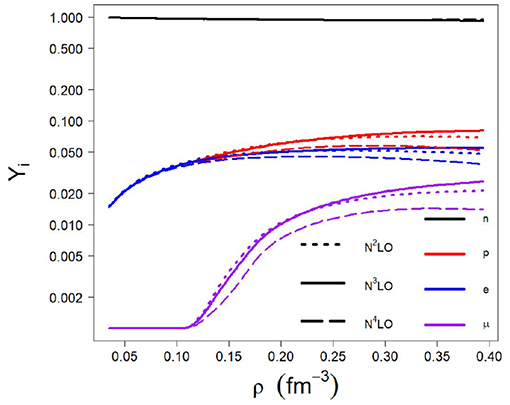
Figure 10. Fractions of neutrons, protons, electrons, and muons as a function of density at the indicated orders for Λ = 450 MeV.
One is now in the position to calculate the pressure in β-stable matter. The pressure is related to the energy density through
In order to continue the discussion started in section 3.2 and extend it to neutron star radii in a consistent manner, in this section we will use the same interactions constructed in section 3 in terms of an empirical SNM EoS and the microscopic NM chiral EoS. Note, from section 4.2, that the symmetry energy, and thus the EoS of both SNM and NM are needed to obtain the various particle fractions. As mentioned earlier, those fractions tend to be rather small (see Figure 10), and thus the results shown in this and the next sections are to a large extent determined by our chiral predictions in NM.
We close this section by showing in Figure 11 the calculated pressure in β-stable matter at the third, fourth, and fifth orders of the 2NF together with the 3NF constructed as described in section 2.2.2. Of course we are referring to the chiral 3NF appropriate for NM, where the LECs c4, cD, and cE vanish [56].
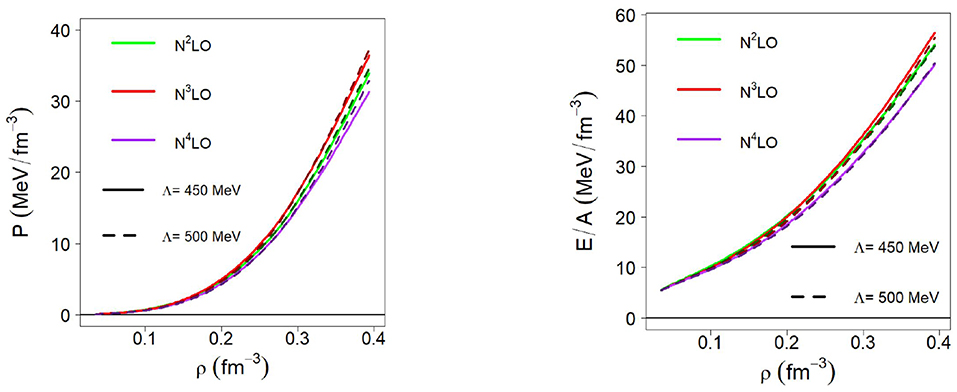
Figure 11. (Left) pressure in β-equilibrated matter vs. density at the given chiral orders (of the NM chiral EoS). Predictions with both cutoffs are shown, revealing that the two sets of curves are very similar. (Right) the corresponding energy per particle. These are the predictions which we retain up to 2ρ0.
The BHF approach to nuclear matter is appropriate for the description of homogeneous matter, such as a homogeneous fluid of nucleons. Below nuclear densities, the chiral EoS are joined with the crustal equations of state from Harrison and Wheeler [173] and Negele and Vautherin [174], performing a smooth interpolation between the two EoS. The crust has crystal-like composition, and contains light [173] or heavy [174] metals together with a gas of electrons.
4.3. Predicting Neutron Star Masses and Radii
We now proceed to discuss specifically neutron star predictions. As mentioned above, we will focus on the radius of a star with mass equal to 1.4 M⊙. We note, in passing, that the increased population of neutron stars observed around the mass range of 1.4 M⊙ may be related to the physics of white dwarfs, atomic stars supported by electron (rather than neutron) degeneracy pressure. Since the Chandrasekhar limit of white dwarfs is approximately 1.4 M⊙ [175], their collapse is likely to generate neutron stars in that mass range.
As stated in section 1, χEFT is a low-energy theory and thus limitations to its domain of applicability must be carefully considered. To begin with, the chiral symmetry breaking scale, Λχ ≈ 1 GeV, imposes clear limitations on the momentum or energy ranges where pions and nucleons can be taken as suitable degrees of freedom [15, 17]. Furthermore, the cutoff parameter Λ appearing in the regulator function (cf. Equation 10), has the purpose to remove high momentum components. Naturally, the strength of the cutoff determines to which degree such high-momentum components are suppressed. On the other hand, central densities of compact astrophysical systems can reach as high as several times the density of normal saturated matter, resulting, of course, in the presence of Fermi momenta which are beyond the reach of χEFT. Therefore, if one wishes to make predictions based, to some extent, on χEFT, methods to extend those predictions must be devised.
It has been observed that the pressure as a function of baryon density (or mass density) for a very large number of existing EoS can be fitted by piecewise polytropes, namely functions of the form P(ρ) = αρΓ [176]. (Note that, in our definitions, ρ denotes the baryon density). Guided by this observation, we find it reasonable to extrapolate the pressure predictions obtained from the EoS shown in Figure 11 using polytropes, as we have done in Sammarruca and Millerson [123]. More precisely, we employ our semi-microscopic predictions up to about 2ρ0, where ρ0 is defined to be 0.16 fm−3, approximately the density of saturated matter. The reason for choosing 2ρ0 as a matching density is as follows: since we are dealing with a perturbative expansion in the parameter Q/Λ, we base our arguments on the size of the expansion parameter for typical momenta of the system under consideration. The highest momentum for pure neutron matter around twice normal density is approximately 420 MeV, as obtained from the usual relation , with kF, n the neutron Fermi momentum. And of course, the highest momentum in β-stable matter is slightly lower due to the presence of a small proton fraction. In conclusion, we are still below (although getting close to) Λ ~ 450 − 500 MeV. Furthermore, the r.m.s. value of the relative momentum for two nucleons in infinite matter is lower than their maximum momentum, and in fact it can be estimated to be about 60% of the Fermi momentum [177]. Thus, on statistical grounds, we should be safe from “cutoff artifacts,” even in the presence of smooth regulators.
We then proceed to match polytropes with diverse adiabatic indices, preserving continuity of the pressure. The range of the polytropic index was taken to be between 1.5 and 4.5 [123] (based on guidelines from the literature [176]), and these extensions are calculated up to about 3ρ0. At this density, every polytrope is again joined continuously with another set of polytropes spanning the same range in values of Γ. In this way, we are able to cover a large set of possible EoS continuations, simulating scenarios where the EoS displays different degrees of “softness” or “stiffness” in different density regions, and thus we can estimate a realistic uncertainty. We stress again that this procedure is a way to simulate the uncertainty arising from reasonable parameterizations of the EoS as determined by phenomenological studies in the literature, and is not to be understood as a replacement for a theoretical model. A demonstration of this procedure is shown in Figure 12 (top row) for the case of N3LO with Λ = 450 MeV. (Note that cgs units are adopted in Figure 12 as those are popular in astronomy and may facilitate comparison by other authors).
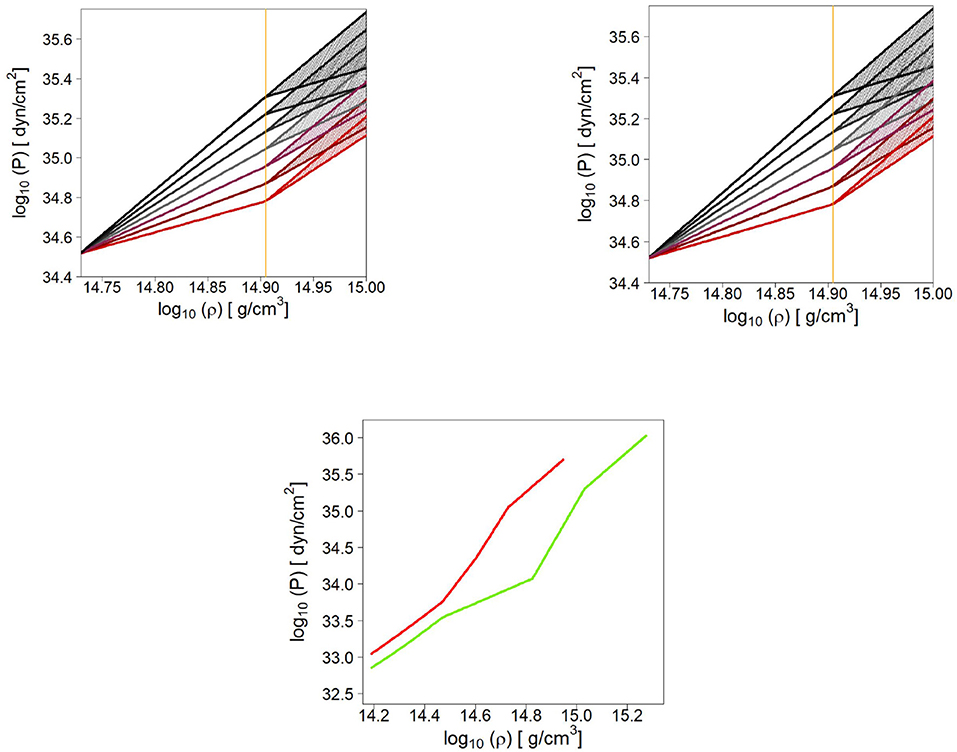
Figure 12. (Top) Pressure in β-equilibrated matter vs. density at N3LO for Λ=450 MeV (left) and Λ=500 MeV (right) extended with polytropes as explained in the text. The vertical axis and the vertical yellow line mark the two matching densities (see text for details). (Bottom) Vaues of the pressure as a function of density taken from Table 5 of Hebeler et al. [178]. The lower (higher) values correspond to the “soft” (“stiff”) predictions shown in that table.
In Hebeler et al. [178], the β-equilibrated EoS based on microscopic chiral interactions in neutron matter, is extended to high densities employing a general piecewise polytropic extrapolation, which leads to a very large number of EoS. Applying causality and the requirement that the EoS must be able to support a mass of 1.97 M⊙, the author select a range of possible EoS, ranging from “soft” to “stiff.” We show the resulting uncertainty band in the bottom row of Figure 12, noting that our uncertainty band from Figure 12 is consistent with it.
Having built up the EoS at all needed densities, we are now in the position to solve the TOV [152] star structure equations and obtain the mass as a function of the radius for a sequence of stars differing in their central densities, up to several times normal density. The M(R) relations we obtain are shown on the bottom row of Figure 13. Note that only combinations of polytropic indices which can support a maximum mass of at least 1.97 M⊙ have been retained for the purpose of Figure 13, to account for the observation of a pulsar with a mass of 2.01 ± 0.04 M⊙ [179]. It is appropriate to point out here that most recent observations [180] are consistent with the even higher value of 2.14 M⊙. In future work, we will apply this new constraint, which will result in a more limited set of acceptable EoS.
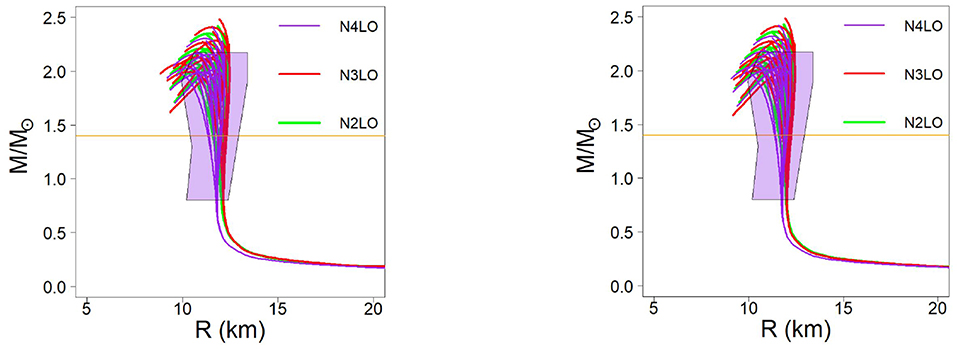
Figure 13. The mass vs. radius relation at the given chiral order. (Left) Λ=450 MeV; (Right) Λ=500 MeV. The purple curves are the result of extending the predictions at N4LO, while the red and the green curves are obtained extrapolating the predictions at N3LO and at N2LO, respectively. The horizontal yellow lines marks the value of 1.4 M⊙. The shaded area in the background is the constraint taken from Steiner et al. [159].
The causality constraint imposes limitations and those are applied in Figure 13. That is, one must require that the speed of sound in stellar matter is less than the speed of light, a condition which can be expressed as 1, where ϵ is the total energy density.
Table 6 shows the the radius and the central density of the 1.4 M⊙ neutron star when the pressure curves at the fourth and fifth orders from Figure 11 are extrapolated via piecewise polytropes with adiabatic indices Γ1 and Γ2 as shown. The speed of sound at central density is also included. Confirming what we found in Sammarruca and Millerson [123], Table 6 demonstrates quite clearly that the radius is practically insensitive to how the continuation is done. In particular, no changes are observed due to variations of the polytrope attached at 3ρ0, and changes by less that one kilometer occurr in response to varying the first polytropic index. Note that the central densities we predict for the canonical-mass star are typically in the order of, and can exceed 3ρ0. These densities are at or above those where the spreading of the pressure can be quite large (see Figure 12). Evidently, the radius of a star with this kind of mass responds to pressures at much lower than central densities, in line with earlier observations (see, for instance [178, 181]), where the insensitivity of the radius to the higher densities was pointed out. Tables similar to Table 6 with Λ=500 MeV and at N4LO with changing value of Λ are not included but do lead to very similar observations.
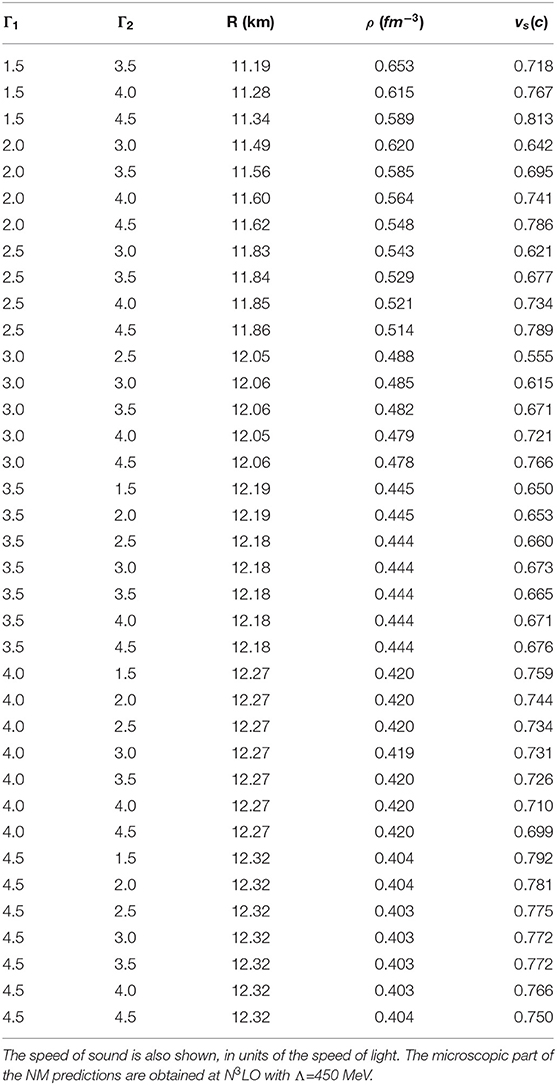
Table 6. Adiabatic indices, Γ1 and Γ2, of the polytropes attached at the two matching densities, followed by the radius and the central density of the 1.4 M⊙ neutron star.
At the same time, the very small spreading of the pressure at normal to moderately high densities (see Figure 11), would suggest similarity of the radius in all cases (differing in chiral order and/or cutoff). This is in fact the case. Taking into consideration both the truncation error and the uncertainty from the polytropes, one may state, estimating the error pessimistically, that 11.8 ± 1 km for M=1.4M⊙.
For completeness, in Figure 13 the full M(R) relation is also displayed. However, we stress that, at the high central densities probed by the heaviest stars, it is not possible to make reliable statements at this time. Predictions are no longer constrained by the chiral theory and are mostly phenomenology.
To broaden the scopes of this discussion, we will include next a set of predictions obtained in a more “traditional” way rather than with χEFT. In particular, we will use a meson-exchange potential (the Bonn B potential [86]) and the DBHF approach mentioned in the Introduction and used extensively in the past by one of the authors of this review [14]. We recall that the characteristic feature of the DBHF method is its ability to effectively take into account an important class of 3NF generated by the so-called “nucleon-antinucleon Z-diagrams” (see [14] and references therein).
However, one of the problems with the traditional approaches based either on meson-theoretic potentials (such as Bonn B or CD-Bonn [29]) or entirely phenomenological ones (such as AV18 [31]), is the absence of guidelines to select the 3NF contributions to be included (among the infinitely many possibilities). Typically, a particular diagram or set of 3NF diagrams are chosen to accompany the 2NF, but no well-defined link exists between the 2NF and the associated 3NF. On the other hand, the chiral approach, through the order-by-order scheme, prescribes exactly which 2NF, 3NF, and higher-body force must be retained at each order.
In Figure 14, we show the pressure in β-stable matter from the DBHF EoS. Comparison between the blue and the red curves demonstrate that choosing a phenomenological SNM EoS (red curve) as compared to the microscopic one (blue curve) has only a minor impact on the EoS for β-stable matter (which is comprised mostly of neutrons), particularly from low to medium densities.
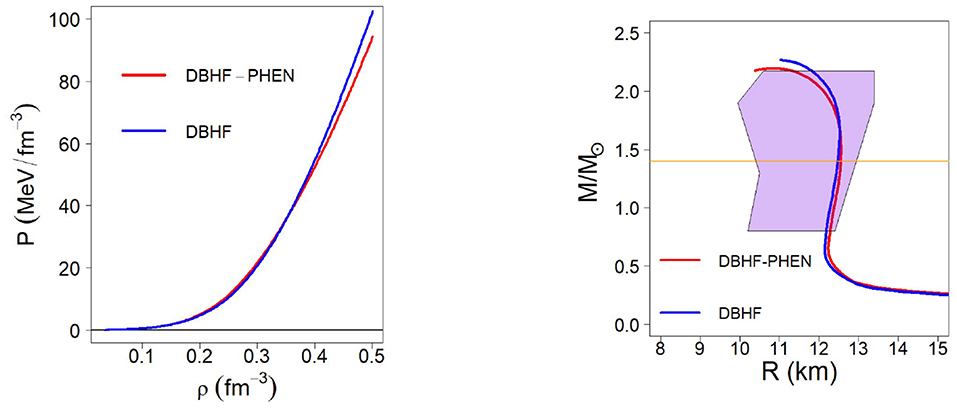
Figure 14. (Left) Pressure in β-stable matter as a function of density obtained with the Bonn B meson-exchange potential and the DBHF approach to nuclear and neutron matter. The blue and the red curves are obtained using the phenomenological EoS for SNM or the microscopic one, respectively. (Right) The mass vs. radius relation for a neutron star obtained with the DBHF calculations as explained in the text. As before, the lavender shaded area is the constraint from Steiner et al. [159].
We then proceed to compare the pressure predictions based on the meson-exchange model with the predictions from Figure 11. As to be expected, differences become larger with increasing density, with the chiral EoS being substantially softer at the higher densities.
Once again, we place our focus on the radius of the average-mass star, which we find to be approximately equal to 12.5 km for the DBHF calculations. This value is reasonably close to our previous, chirally based predictions, which makes sense based on our earlier discussions and the fact that the DBHF pressure around normal density is not very different from the one in the chirally-based models (see Figure 15).
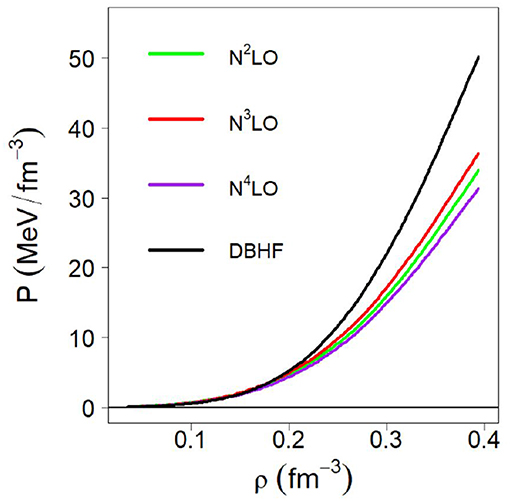
Figure 15. Pressure in β-stable matter from the red curve on the LHS of Figure 14 compared with the predictions from the LHS of Figure 11.
Finally, we employ the DBHF EoS in the TOV equations and calculate the M(R) relation, which is shown on the RHS of Figure 14. The blue and red curves correspond to the blue and red curves in Figure 14. Differences become noticible for the heavier stars and are consistent with those seen in Figure 14. In other words, the model with the larger pressure at the higher densities generates the larger maximum mass.
We end this exercise with an important comment: even if a theory (of nucleons and mesons) can be formally taken to high densities, as we have done with the DBHF predictions, the composition and thus the EoS of stellar matter in the inner core is simply unknown. At densities as high as those typical of compact stars, hyperons are expected to exist on simple energetic grounds. Similarly, other non-nucleonic degrees of freedom, such as quark degrees of freedom, can exist as the result of phase transitions. These possibilities have been explored by several groups (see, for instance [182–185]). Such investigations are not within the scope or the reach of χEFT. The polytropic extrapolations we have performed do indeed simulate a broad set of possible EoS consistent with current constraints but whose specific composition remains unknown.
Of course, we also take note of some other works aimed at incorporating aspects of chiral dynamics in the development of EoS suitable for astrophysical phenomena, such as Rapaj et al. [186]. In the latter reference, the authors calculate neutron star masses and radii with mean-field models whose parameters are made consistent with a chiral EoS at low to moderate densities. Constraints from χEFT on neutron star tidal deformabilities were investigated in Lim and Holt [166]. General relativistic simulations of neutron star mergers based on the EoS of Bombaci and Logoteta [111] have been reported in Endrizzi et al. [187].
We close this section with a few final remarks addressing predictions vs. constraints. Masses of neutron stars can be and have been measured with high precision. However, simultaneous measurements of radii are much more problematic. Some techniques do exist, such as those based on photospheric radius expansion [188]. Current observations have begun to determine the M(R) relation. In Steiner et al. [159], the authors determine the radius of a 1.4 M⊙ neutron star to be between 10.4 and 12.9 km. Furthermore, from their Bayesian analysis of several EoS parameterized so as to be consistent with a baseline data set (see [159] and references therein), they are able to determine the M(R) relation within a range of masses. Our predictions fall within those constraints, shown in Figure 13 as the shaded purple area. Recent LIGO/Virgo measurements have constrained the radius of a 1.4 M⊙ neutron star to be between 11.1 and 13.4 km [164, 167]. The predictions from our group are well within these new constraints.
5. Summary and Conclusions
In this review, we have stressed the importance of the nuclear EoS toward understanding of nuclear interactions in the medium. First, we presented a detailed review of our most recent EoS based on state-of-the-art chiral NN potentials. We operate within the framework of chiral effective field theory. Our approach is microscopic in that chiral two-nucleon forces are fitted to two-nucleon data and never readjusted in the medium. To render the nuclear matter calculations manageable, the leading chiral 3NF is included as an effectively two-body density-dependent potential. The relevant LECs, cD and cE, are obtained from accurate fittings within the three-nucleon sector. Actually, we go beyond the leading 3NF by effectively including the 2PE 3NF up to the highest order we consider at this time. This is possible because the 2PE 3NF has essentially the same analytical structure at N2LO, N3LO, and N4LO. Thus, one can add the three orders of 3NF contributions and parameterize the result in terms of effective LECs.
The contribution from the 3NF is remarkable, although somewhat weaker in NM, due to the fact that some of the leading 3NF contributions vanish in a system of only neutrons. Therefore, the lack of full order consistency between the 2NF and the 3NF sectors is likely to impact the EoS of NM to a lesser degree as compared to the the case of SNM. In fact, we find that the NM EoS is under better control with regard to the order-by-order pattern.
In view of the considerations above, in discussions of some observables sensitive to the EoS of neutron-rich matter, we have chosen to emphasize the role of the NM EoS by constraining the SNM EoS to be an empirical one. This allowed us to better scrutinize the role of neutron matter pressure on the neutron skin thickness.
A contemporary discussion of neutron-rich matter must include some of the most exotic and intriguing (neutron-rich) systems in the universe—neutron stars. We reviewed the outstanding role of the EoS in calculations of neutron star structure.
We discussed the limitations of χEFT as a low-energy theory. The high Fermi momenta involved in the core of neutron stars cannot be probed with χEFT. This is also the case for average-mass stars, where typical central densities can be as high as three times normal nuclear density. Therefore, we extend our EoS to high densities via polytropes with a broad range of adiabatic indices.
Although extrapolation with polytropes, or any other continuation method one may choose, should in no way be seen as a replacement for true predictions, it gave us the opportunity to explore the sensitivity of specific predictions to the behavior of the EoS at the high densities unreachable to χEFT. In fact, we were able to confirm what has been observed previously with other methods. Namely, the radius of the typical-mass neutron star is essentially insensitive to the pressure in the high-density regime. Instead, it is mostly controlled by the pressure in NM at normal densities. Therefore, we feel confident that our χEFT-based predictions of neutron-rich matter are on solid ground for lighter stars, including those with the “canonical” mass of 1.4 M⊙.
At this point, to broaden the scopes of the discussion, we included a set of predictions based on a very different, and more traditional philosophy. We calculated the NM EoS from the Bonn B meson-theoretic potential and the DBHF approach to neutron matter. The purpose of this comparison was, mostly, to highlight the different philosophy of the “single-shot” calculation as compared to the chiral approach, where order-by-order and other uncertainty considerations play a major role in the extraction and interpretation of the result.
In line with the observed sensitivity of the radius to, mainly, the pressure in NM at normal density, and the fact that the meson-theoretic and the chiral EoS are similar up to moderate densities, the value we obtained for the radius of the M = 1.4M⊙ neutron star was close to those from the chirally-based calculations.
Of course, the complete chiral 3NF at N3LO must be included, as done in Drischler et al. [93]. Our approach to fitting the cD and cE LECs is different, as the authors of Drischler et al. [93] include nuclear matter saturation properties in their fitting protocol, whereas we fit those constants within the three-nucleon sector. We are presently calculating the various contributions of the 3NF at N3LO in the form of density-dependent effective interactions [97, 98] and noticed that the short-range terms [97] tend to be very small. It will be interesting to see how the full contribution impacts our calculations of the NM EoS and related observables.
Author Contributions
As the senior member of the team, FS coordinated the conceptual design and development of the paper. Both authors contributed to the production of the results being shown.
Funding
This work was supported by the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences, under Award Number DE-FG02-03ER41270.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
FS wishes to acknowledge L. E. Marcucci, L. Coraggio, J. W. Holt, N. Itaco, and R. Machleidt, for their contributions to the development of the equations of state reviewed in this article.
References
1. Brueckner KA, Levinson CA, Mahmoud HM. Two-body forces and nuclear saturation. I. Central forces. Phys Rev. (1954) 95:217–28. doi: 10.1103/PhysRev.95.217
3. Goldstone J. Derivation of the Brueckner many-body theory. Proc R Soc. (1957) A239:267–79. doi: 10.1098/rspa.1957.0037
4. Bethe HA. Theory of nuclear matter. Annu Rev Nucl Sci. (1971) 21:93–214. doi: 10.1146/annurev.ns.21.120171.000521
5. Haftel MI, Tabakin F. Nuclear saturation and the smoothness of nucleon-nucleon potentials. Nucl Phys. (1970) A158:1–42. doi: 10.1016/0375-9474(70)90047-3
6. Sprung DWL. Nuclear matter calculations. Adv Nucl Phys. (1972) 5:225–343. doi: 10.1007/978-1-4615-8231-1_2
7. Pandharipande VR, Wiringa RB. Variations on a theme of nuclear matter. Rev Mod Phys. (1979) 51:821–59. doi: 10.1103/RevModPhys.51.821
8. Lagaris IE, Pandharipande VR. Variational calculations of realistic models of nuclear matter. Nucl Phys. (1981) A359:349–64. doi: 10.1016/0375-9474(81)90241-4
9. Day BD, Wiringa RB. Brueckner-Bethe and variational calculations of nuclear matter. Phys Rev C. (1985) 32:1057–62. doi: 10.1103/PhysRevC.32.1057
10. Anastasio MR, Celenza LS, Pong WS, Shakin CM. Relativistic nuclear structure physics. Phys Rep. (1983) 100:327–92. doi: 10.1016/0370-1573(83)90060-1
11. Horowitz CJ, Serot BD. Two-nucleon correlations in a relativistic theory of nuclear matter. Phys Lett. (1984) 137B:287–93. The relativistic two-nucleon problem in nuclear matter, Nucl. Phys. A464, 613-699 (1987).
12. Brockmann R, Machleidt R. Nuclear saturation in a relativistic Bruckner-hartree-fock Approach. Phys Lett. (1984) 149B:283–7.
13. Brockmann R, Machleidt R. Relativistic nuclear structure. I: Nuclear matter. Phys Rev C. (1990) 42:1965.
14. Muether H, Sammarruca F, Ma Z. Relativistic effects and three-nucleon forces in nuclear matter and nuclei. Int J Mod Phys E. (2017) 26:1730001. doi: 10.1142/S0218301317300016
15. Weinberg S. Nuclear forces from chiral Lagrangians. Phys Lett B. (1990) 251:288–92. doi: 10.1016/0370-2693(90)90938-3
16. Weinberg S. Effective chiral lagrangians for nucleon-pion interactions and nuclear forces. Nucl Phys B. (1991) 363:3–18. doi: 10.1016/0550-3213(91)90231-L
17. Weinberg S. Three-body interactions among nucleons and pions. Phys Lett B. (1992) 295:114–21. doi: 10.1016/0370-2693(92)90099-P
18. Machleidt R, Entem DR. Chiral effective field theory and nuclear force. Phys Rep. (2011) 503:1–75. doi: 10.1016/j.physrep.2011.02.001
20. Epelbaum E. Hammer HW, Meissner UG. Modern theory of nuclear forces. Rev Mod Phys. (2009) 81:1773–825. doi: 10.1103/RevModPhys.81.1773
21. Meißner UG. The long and winding road from chiral effective Lagrangians to nuclear structure. Phys Scr. (2016) 91:033005. doi: 10.1088/0031-8949/91/3/033005
22. Machleidt R, Sammarruca F. Chiral EFT based nuclear forces: achievements and challenges. Phys Scr. (2016) 91:083007. doi: 10.1088/0031-8949/91/8/083007
23. Fattoyev FJ, Piekarewicz J. Accurate calibration of relativistic mean-field models: correlating observables and providing meaningful theoretical uncertainties. Phys Rev C. (2011) 84:064302. doi: 10.1103/PhysRevC.84.064302
24. Roca-Maza X, Centelles M, Viñas X, Warda M. Neutron skin of 208Pb, nuclear symmetry energy, and the parity radius experiment. Phys Rev Lett. (2011) 106:252501. doi: 10.1103/PhysRevLett.106.252501
25. Sammarruca F, Marcucci LE, Coraggio L, Holt JW, Itaco N, Machleidt R. Nuclear and neutron matter equations of state from high-quality potentials up to fifth order of the chiral expansion. arXiv:1807.06640 (2018).
26. Sammarruca F. Short-range correlations in the deuteron: chiral effective field theory, meson-exchange, and phenomenology. Phys Rev C. (2015) 92:044003. doi: 10.1103/PhysRevC.92.044003
27. Hen O, Miller GA, Piasetzky E, Weinstein LB. Nucleon-nucleon correlations, short-lived excitations, and the quarks within. Rev Mod Phys. (2017) 89:045002. doi: 10.1103/RevModPhys.89.045002
28. Marcucci LE, Sammarruca F, Viviani M, Machleidt R. Momentum distributions and short-range correlations in the deuteron and 3He with modern chiral potentials. Phys Rev C. (2019) 99:034003. doi: 10.1103/PhysRevC.99.034003
29. Machleidt R. High-precision, charge-dependent Bonn nucleon-nucleon potential. Phys Rev C. (2001) 63:024001. doi: 10.1103/PhysRevC.63.024001
30. Stoks VGJ, Klomp RAM, Terheggen CPF, de Swart JJ. Construction of high-quality NN potential models. Phys Rev C. (1994) 49:2950–63. doi: 10.1103/PhysRevC.49.2950
31. Wiringa RB, Stoks VGJ, Schiavilla R. Accurate nucleon-nucleon potential with charge-independence breaking. Phys Rev C. (1995) 51:38–51. doi: 10.1103/PhysRevC.51.38
32. Machleidt R. Historical perspective and future prospects for nuclear interactions. Int J Mod Phys E. (2017) 26:1730005. doi: 10.1142/S0218301317300053
33. Epelbaum E, Nogga A, Gl'́ockle W, Kamada H, Meißner UG, Witala H. Three nucleon forces from chiral effective field theory. Phys Rev C. (2002) 66:064001. doi: 10.1103/PhysRevC.66.064001
34. Navratil P, Roth R, Quaglioni S. Ab initio many-body calculations of nucleon scattering on 4He, 7Li, 7Be, 12C and 16O. Phys Rev C. (2010) 82:034609. doi: 10.1103/PhysRevC.82.034609
35. Viviani M, Girlanda L, Kievsky A, Marcucci LE. Effect of three-nucleon interaction in p-3He elastic scattering. Phys Rev Lett. (2013) 111:172302. doi: 10.1103/PhysRevLett.111.172302
36. Golak J, Skibiński R, Topolnicki K, Witala H, Epelbaum E, Krebs H, et al. Low-energy neutron-deuteron reactions with N3LO chiral forces. Eur Phys J A. (2014) 50:177–89. doi: 10.1140/epja/i2014-14177-7
37. Kalantar-Nayestanaki N, Epelbaum E, Messchendorp JG, Nogga A. Signatures of three-nucleon interactions in few-nucleon systems. Rept Prog Phys. (2012) 75:016301. doi: 10.1088/0034-4885/75/1/016301
38. Navratil P, Quaglioni S, Hupin G, Romero-Redondo C, Calci A. Unified ab initio approaches to nuclear structure and reactions. Phys Scr. (2016) 91:053002. doi: 10.1088/0031-8949/91/5/053002
39. Coraggio L, Covello A, Gargano A, Itaco N, Kuo TTS, Entem DR, et al. Low-momentum nucleon-nucleon interactions and shell-model calculations. Phys Rev C. (2007) 75:024311. doi: 10.1103/PhysRevC.75.024311
40. Coraggio L, Covello A, Gargano A, Itaco N. Shell-model calculations for neutron-rich carbon isotopes with a chiral nucleon-nucleon potential. Phys Rev C. (2010) 81:064303. doi: 10.1103/PhysRevC.81.064303
41. Coraggio L, Covello A, Gargano A, Itaco N, Kuo TTS. Effective shell-model hamiltonians from realistic nucleon-nucleon potentials within a perturbative approach. Ann Phys. (2012) 327:2125–51. doi: 10.1016/j.aop.2012.04.013
42. Hagen H, Hjorth-Jensen M, Jansen GR, Machleidt R, Papenbrock T. Continuum effects and three-nucleon forces in neutron-rich oxygen isotopes. Phys Rev Lett. (2012) 108:242501. doi: 10.1103/PhysRevLett.108.242501
43. Hagen H, Hjorth-Jensen M, Jansen GR, Machleidt R, Papenbrock T. Evolution of shell structure in neutron-rich calcium isotopes. Phys Rev Lett. (2012) 109:032502. doi: 10.1103/PhysRevLett.109.032502
44. Barrett BR, Navratil P, Vary JP. Ab initio no core shell model. Prog Part Nucl Phys. (2013) 69:131–81. doi: 10.1016/j.ppnp.2012.10.003
45. Gezerlis A, Tews I, Epelbaum E, Gandolfi S, Hebeler K, Nogga A, et al. Quantum Monte Carlo calculations with chiral effective field theory interactions. Phys Rev Lett. (2013) 111:032501. doi: 10.1103/PhysRevLett.111.032501
46. Hergert H, Bogner SK, Binder S, Calci A, Langhammer J, Roth R, Schwenk A. In-medium similarity renormalization group with chiral two- plus three-nucleon interactions. Phys Rev C. (2013) 87:034307. doi: 10.1103/PhysRevC.87.034307
47. Hagen G, Papenbrock T, Hjorth-Jensen M, Dean DJ. Coupled-cluster computations of atomic nuclei. Rept Prog Phys. (2014) 77:096302. doi: 10.1088/0034-4885/77/9/096302
48. Somà V, Cipollone A, Barbieri C, Navratil P, Duget T. Chiral two- and three-nucleon forces along medium-mass isotope chains. Phys Rev C. (2014) 89:061301(R). doi: 10.1103/PhysRevC.89.061301
49. Hebeler K, Holt JD, Menéndez J, Schwenk A. Nuclear forces and their impact on neutron-rich nuclei and neutron-rich matter. Annu Rev Nucl Part Sci. (2015) 65:457–84. doi: 10.1146/annurev-nucl-102313-025446
50. Hagen G, Ekström A, Forssén C, Jansen GR, Nazarewicz W, Papenbrock T, et al. Neutron and weak-charge distributions of the 48Ca nucleus. Nat Phys. (2015) 12:186–90. doi: 10.1038/nphys3529
51. Carlson J, Gandolfi S, Pederiva F, Pieper SC, Schiavilla R, Schmidt KE, Wiringa RB. Quantum Monte Carlo methods for nuclear physics. Rev Mod Phys. (2015) 87:1067–118. doi: 10.1103/RevModPhys.87.1067
52. Hergert H, Bogner SK, Morris TD, Schwenk A, Tsukiyama K. The in-medium similarity renormalization group: a novel ab initio method for nuclei. Phys Rep. (2016) 621:165–222. doi: 10.1016/j.physrep.2015.12.007
53. Holt J W, Kaiser N. Equation of state of nuclear and neutron matter at third-order in perturbation theory from chiral effective field theory. Phys Rev C. (2017) 95:034326. doi: 10.1103/PhysRevC.95.034326
54. Simonis J, Stroberg SR, Hebeler K, Holt JD, Schwenk A. Saturation with chiral interactions and consequences for finite nuclei. Phys Rev C. (2017) 96:014303. doi: 10.1103/PhysRevC.96.014303
55. Morris TD, Simonis J, Stroberg SR, Stumpf C, Hagen G, Holt JD, et al. Structure of the lightest Tin isotopes. arXiv:1709.02786 [nucl-th] (2017). doi: 10.1103/PhysRevLett.120.152503
56. Hebeler K, Schwenk A. Chiral three-nucleon forces and neutron matter. Phys Rev C. (2010) 82:014314. doi: 10.1103/PhysRevC.82.014314
57. Hebeler K, Bogner SK, Furnstahl RJ, Nogga A, Schwenk A. Improved nuclear matter calculations from chiral low-momentum interactions. Phys Rev C. (2011) 83:031301(R). doi: 10.1103/PhysRevC.83.031301
58. Baardsen G, Ekström A, Hagen G, Hjorth-Jensen M. Coupled-cluster studies of infinite nuclear matter. Phys Rev C. (2013) 88:054312. doi: 10.1103/PhysRevC.88.054312
59. Hagen G, Papenbrock T, Ekström A, Wendt KA, Baardsen G, Gandolfi S, et al. Coupled-cluster calculations of nucleonic matter. Phys Rev C. (2014) 89:014319. doi: 10.1103/PhysRevC.89.014319
60. Coraggio L, Holt JW, Itaco N, Machleidt R, Sammarruca F. Reduced regulator dependence of neutron-matter predictions with perturbative chiral interactions. Phys Rev C. (2013) 87:014322. doi: 10.1103/PhysRevC.87.014322
61. Coraggio L, Holt JW, Itaco N, Machleidt R, Marcucci LE, Sammarruca F. Nuclear-matter equation of state with consistent two- and three-body perturbative chiral interactions. Phys Rev C. (2014) 89:044321. doi: 10.1103/PhysRevC.89.044321
62. Sammarruca F, Coraggio L, Holt JW, Itaco N, Machleidt R, Marcucci LE. Toward order-by-order calculations of the nuclear and neutron matter equations of state in chiral effective field theory. Phys Rev C. (2015) 91:054311. doi: 10.1103/PhysRevC.91.054311
63. Drischler C, Carbone A, Hebeler K, Schwenk A. Neutron matter from chiral two- and three-nucleon calculations up to N3LO. Phys Rev C. (2016) 94:054307. doi: 10.1103/PhysRevC.94.054307
64. Tews I, Gandolfi S, Gezerlis A, Schwenk A. Quantum Monte Carlo calculations of neutron matter with chiral three-body forces. Phys Rev C. (2016) 93:024305. doi: 10.1103/PhysRevC.93.024305
65. Wellenhofer C, Holt JW, Kaiser N, Weise W. Nuclear thermodynamics from chiral low-momentum interactions. Phys Rev C. (2014) 89:064009. doi: 10.1103/PhysRevC.89.064009
66. Wellenhofer C, Holt JW, Kaiser N. Thermodynamics of isospin-asymmetric nuclear matter from chiral effective field theory. Phys Rev C. (2015) 92:015801. doi: 10.1103/PhysRevC.92.015801
67. Bacca S, Hally K, Pethick CJ, Schwenk A. Chiral effective field theory calculations of neutrino processes in dense matter. Phys Rev C. (2009) 80:032802. doi: 10.1103/PhysRevC.80.032802
68. Bartl A, Pethick CJ, Schwenk A. Supernova matter at subnuclear densities as a resonant fermi gas: enhancement of neutrino rates. Phys Rev Lett. (2014) 113:081101. doi: 10.1103/PhysRevLett.113.081101
69. Rapaj E, Holt JW, Bartl A, Reddy S, Schwenk A. Charged-current reactions in the supernova neutrino-sphere. Phys Rev C. (2015) 91:035806. doi: 10.1103/PhysRevC.91.035806
70. Buraczynski M, Gezerlis A. Static response of neutron matter. Phys Rev Lett. (2016) 116:152501. doi: 10.1103/PhysRevLett.116.152501
71. Holt JW, Kaiser N, Miller GA. Microscopic optical potential for exotic isotopes from chiral effective field theory. Phys Rev C. (2016) 93:064603. doi: 10.1103/PhysRevC.93.064603
72. Birkhan J, Miorelli M, Bacca S, Bassauer S, Bertulani CA, Hagen C, et al. Electric dipole polarizability of 48Ca and implications for the neutron skin. Phys Rev Lett. (2017) 118:252501. doi: 10.1103/PhysRevLett.118.252501
73. Rotureau J, Danielewicz P, Hagen G, Nunes F, Papenbrock T. Optical potential from first principles. Phys Rev C. (2017) 95:024315. doi: 10.1103/PhysRevC.95.024315
74. Lapoux V, Somà V, Barbieri C, Hergert H, Holt JD, Stroberg SR. Radii and binding energies in oxygen isotopes: a challenge for nuclear forces. Phys Rev Lett. (2016) 117:052501. doi: 10.1103/PhysRevLett.117.052501
75. Binder S, Langhammer J, Calci A, Roth R. Ab initio path to heavy nuclei. Phys Lett B. (2014) 736:119–23. doi: 10.1016/j.physletb.2014.07.010
76. Ekström A, Jansen GR, Wendt KA, Hagen G, Papenbrock T, Carlsson BD, et al. Accurate nuclear radii and binding energies from a chiral interaction. Phys Rev C. (2015) 91:051301. doi: 10.1103/PhysRevC.91.051301
77. Alonso D, Sammarruca F. A Microscopic calculation of asymmetric nuclear matter properties. Phys Rev C. (2003) 67:054301. doi: 10.1103/PhysRevC.67.054301
78. Sammarruca F. The 'Ab initio' approach to the nuclear equation of state: review and discussion. arXiv:0807.0263 [nucl-th] (2008).
79. Sammarruca F, Chen B, Coraggio L, Itaco N, Machleidt R. Dirac-Brueckner-Hartree-Fock versus chiral effective field theory. Phys Rev C. (2012) 86:054317. doi: 10.1103/PhysRevC.86.054317
80. Pudliner BS, Pandharipande VR, Carlson J, Wiringa RB. Quantum Monte Carlo calculations of A ≤ 6 nuclei. Phys Rev Lett. (1995) 74:4396–9. doi: 10.1103/PhysRevLett.74.4396
81. Akmal A, Pandharipande VR, Ravenhall DG. The Equation of state of nucleon matter and neutron star structure. Phys Rev C. (1998) 58:1804–28. doi: 10.1103/PhysRevC.58.1804
82. Lonardoni D, Lovato A, Pieper SC, Wiringa RB. Variational calculation of the ground state of closed-shell nuclei up to A = 40. Phys Rev C. (2017) 96:024326. doi: 10.1103/PhysRevC.96.024326
83. Pieper SC. The Illinois extension to the Fujita-Miyazawa three-nucleon force. AIP Conf Proc. (2008) 1011:143–52. doi: 10.1063/1.2932280
84. Zuo W, Lejeune A, Lombardo U, Mathiot JF. Microscopic three-body force for asymmetric nuclear matter. Eur Phys J A. (2002) 14:469–75. doi: 10.1140/epja/i2002-10031-y
85. Li ZH, Lombardo U, Schulze HJ, Zuo W. Consistent nucleon-nucleon potentials and three-body forces. Phys Rev C. (2008) 77:034316. doi: 10.1103/PhysRevC.77.034316
86. Machleidt R. The meson theory of nuclear forces and nuclear structure. Adv Nucl Phys. (1989) 19:189–376. doi: 10.1007/978-1-4613-9907-0_2
87. Entem DR, Machleidt R, Nosyk Y. High-quality two-nucleon potentials up to fifth order of the chiral expansion. Phys Rev C. (2017) 96:024004. doi: 10.1103/PhysRevC.96.024004
88. Entem DR, Machleidt R. Accurate charge-dependent nucleon-nucleon potential at fourth order of chiral perturbation theory. Phys Rev C. (2003) 68:041001. doi: 10.1103/PhysRevC.68.041001
89. Marji E, Canul A, MacPherson Q, Winzer R, Zeoli C, Entem DR, et al. Nonperturbative renormalization of the chiral nucleon-nucleon interaction up to next-to-next-to-leading order. Phys Rev C. (2013) 88:054002. doi: 10.1103/PhysRevC.88.054002
90. Hoferichter M, de Elvira RJ, Kubis B, Meissner UG. Matching pion-nucleon roy-steiner equations to chiral perturbation theory. Phys Rev Lett. (2015) 115:192301. doi: 10.1103/PhysRevLett.115.192301
91. Hoferichter M, de Elvira RJ, Kubis B, Meissner UG. Roy-Steiner-equation analysis of pion-nucleon scattering. Phys Rep. (2016) 625:1–88. doi: 10.1016/j.physrep.2016.02.002
92. Hoppe J, Drischler C, Furnstahl RJ, Hebeler K, Schwenk A. Weinberg eigenvalues for chiral nucleon-nucleon interactions. Phys Rev C. (2017) 96:054002. doi: 10.1103/PhysRevC.96.054002
93. Drischler C, Hebeler K, Schwenk A. Chiral interactions up to N3LO and nuclear saturation. Phys Rev Lett. (2019) 122:042501. doi: 10.1103/PhysRevLett.122.042501
94. Holt JW, Kaiser N, Weise W. Chiral three-nucleon interaction and the 14C-dating β decay. Phys Rev C. (2009) 79:054331. doi: 10.1103/PhysRevC.79.054331
95. Holt JW, Kaiser N, Weise W. Density-dependent effective nucleon-nucleon interaction from chiral three-nucleon forces. Phys Rev C. (2010) 81:024002. doi: 10.1103/PhysRevC.81.024002
96. Baldo M, Bombaci I, Burgio GF. Microscopic nuclear equation of state with three-body forces and neutron star structure. Astron Astrophys. (1997) 328:274–84.
97. Kaiser N, Niessner V. Density-dependent NN interaction from subleading chiral 3N forces: short-range terms and relativistic corrections. Phys Rev C. (2018) 98:054002. doi: 10.1103/PhysRevC.98.054002
98. Kaiser N, Singh B. Density-dependent NN interaction from subleading chiral three-nucleon forces: long-range terms. Phys Rev C. (2019) 100:014002. doi: 10.1103/PhysRevC.100.014002
99. Gardestig A, Phillips DR. How low-energy weak reactions can constrain three-nucleon forces and the neutron-neutron scattering length. Phys Rev Lett. (2006) 96:232301. doi: 10.1103/PhysRevLett.96.232301
100. Gazit D, Quaglioni S, Navrátil P. Three-nucleon low-energy constants from the consistency of interactions and currents in chiral effective field theory. Phys Rev Lett. (2009) 103:102502. doi: 10.1103/PhysRevLett.103.102502
101. Marcucci LE, Kievsky A, Rosati S, Schiavilla R, Viviani M. Chiral effective field theory predictions for muon Capture on Deuteron and 3He, Phys Rev Lett. (2012) 108:052502; Erratum: Chiral effective field theory predictions for muon capture on deuteron and 3He. (2018) 121:049901(E). doi: 10.1103/PhysRevLett.108.052502
102. Navrátil P. Local three-nucleon interaction from chiral effective field theory. Few-Body Syst. (2007) 41:117–40. doi: 10.1007/s00601-007-0193-3
103. Kievsky A, Rosati S, Marcucci LE, Girlanda L. A high-precision variational approach to three- and four-nucleon bound and zero-energy scattering states. J Phys G. (2008) 35:063101. doi: 10.1088/0954-3899/35/6/063101
104. Tews I, Krüger T, Hebeler K, Schwenk A. Neutron matter at next-to-next-to-next-to-leading order in chiral effective field theory. Phys Rev Lett. (2013) 110:032504. doi: 10.1103/PhysRevLett.110.032504
105. Hebeler K, Krebs H, Epelbaum E, Golak J, Skibinski R. Efficient calculation of chiral three-nucleon forces up to N3LO for ab initio studies. Phys Rev C. (2015) 91:044001. doi: 10.1103/PhysRevC.91.044001
106. Krebs H, Gasparyan A, Epelbaum E. Chiral three-nucleon force at N4LO: longest-range contributions. Phys Rev C. (2012) 85:054006. doi: 10.1103/PhysRevC.85.054006
107. Bernard V, Epelbaum E, Krebs H, Meißner UG. Subleading contributions to the chiral three-nucleon force: long-range terms. Phys Rev C. (2008) 77:064004. doi: 10.1103/PhysRevC.77.064004
108. Fujita JI, Miyazawa H. Pion theory of three-body forces. Prog Theor Phys. (1957) 17:360–5. doi: 10.1143/PTP.17.360
109. De JN, Samadar SK, Agrawal BK. Reassessing nuclear matter incompressibility and its density dependence. Phys Rev C. (2015) 92:014304. doi: 10.1103/PhysRevC.92.014304
110. Thiel M, Sfienti C, Piekarewicz J, Horowitz CJ, Vanderhaeghen M. Neutron skins of atomic nuclei: per aspera ad astra. arXiv:1904.12269 (2019). doi: 10.1088/1361-6471/ab2c6d
111. Bombaci I, Logoteta D. Equation of state of dense nuclear matter and neutron star structure from nuclear chiral interactions. Astron Astrophys. (2018) 609:A128. doi: 10.1051/0004-6361/201731604
112. Oertel M, Hempel M, Klahn T, Typel S. Equations of state for supernovae and compact stars. Rev Mod Phys. (2017) 89:015007. doi: 10.1103/RevModPhys.89.015007
113. Baldo M, Burgio GF. The nuclear symmetry energy. Prog Part Nucl Phys. (2016) 91:101016. doi: 10.1016/j.ppnp.2016.06.006
114. Le Fevre A, Leifels Y, Reisdorf W, Aichelin J, Hartnack Ch. Constraining the nuclear matter equation of state around twice saturation density. Nucl Phys A. (2016) 945:112–3. doi: 10.1016/j.nuclphysa.2015.09.015
115. Horowitz CJ, Brown EF, Kim Y, Lynch WG, Michaels R, Ono A, et al. A way forward in the study of the symmetry energy: experiment, theory, and observation. J Phys G. (2014) 41:093001. doi: 10.1088/0954-3899/41/9/093001
116. Verde G. Probing the nuclear equation-of-state and the symmetry energy with heavy-ion collisions. EPJ Web Conf. (2014) 66:01018. doi: 10.1051/epjconf/20146601018
117. Trautmann W, Wolter HH. Elliptic flow and the symmetry energy at supra-saturation density. Int J Mod Phys E. (2012) 21:1230003. doi: 10.1142/S0218301312300032
118. Steiner AW, Prakash M, Lattimer JM, Ellis PJ. Isospin asymmetry in nuclei and neutron stars. Phys Rep. (2005) 411:325–75. doi: 10.1016/j.physrep.2005.02.004
119. Bombaci I, Lombardo U. Asymmetric nuclear matter equation of state. Phys Rev C. (1991) 44:1892–900. doi: 10.1103/PhysRevC.44.1892
120. Sammarruca F. Recent advances in microscopic approaches to nuclear matter and symmetry energy. Symmetry. (2014) 6:851–79. doi: 10.3390/sym6040851
121. Paschke K, Kumar K, Michael R, Souder PA, Urciuoli GM. PREX-II: Precision Parity-Violating Measurement of the Neutron Skin of Lead. Available online at: http://hallaweb.jlab.org/parity/prex/prexII.pdf
122. Mammei J, McNulty D, Michaels R, Paschke K, Riordan S, Souder P. C-REX: parity-violating measurement of the weak charge of 48Ca to an accuracy of 0.02 fm. Available online at: http://hallaweb.jlab.org/parity/prex/c-rex2013_v7.pdf
123. Sammarruca F, Millerson R. The radius of the canonical-mass neutron star and chiral effective field theory. J Phys G. (2019) 46:024001. doi: 10.1088/1361-6471/aafbcd
124. Santos BM, Dutra M, Lourenco O, Delfino A. Correlations between bulk parameters in relativistic and nonrelativistic hadronic mean-field models. Phys Rev C. (2015) 92:015210. doi: 10.1103/PhysRevC.92.0152
125. Tong H, Ren XL, Ring P, Shen SH, Wang SB, Meng J. Relativistic Brueckner-Hartree-Fock theory in nuclear matter without the average momentum approximation. Phys Rev C. (2018) 98:054302. doi: 10.1103/PhysRevC.98.054302
126. Holt JW, Lim Y. Universal correlations in the nuclear symmetry energy, slope parameter, and curvature. Phys Lett. (2018) B784:77–81. doi: 10.1016/j.physletb.2018.07.038
127. Vidaña I, Providencia C, Polls A, Rios A. Density dependence of the nuclear symmetry energy: a microscopic perspective. Phys Rev C. (2009) 80:045806. doi: 10.1103/PhysRevC.80.045806
128. Ducoin C, Margueron J, Providencia CMC, Vidaña I. Core-crust transition in neutron stars: predictivity of density developments. Phys Rev C. (2011) 83:045810. doi: 10.1103/PhysRevC.83.045810
129. Santos BM, Dutra M, Lourenco O, Delfino A. Correlations between the nuclear matter symmetry energy, its slope, and curvature from a nonrelativistic solvable approach and beyond. Phys Rev C. (2014) 90:035203. doi: 10.1103/PhysRevC.90.035203
130. Millerson R, Sammarruca F. Properties of isospin asymmetric matter derived from chiral effective field theory. arXiv:1906.02905 [nucl-th] (2019).
131. Piekarewicz J, Fattoyev FJ. Neutron rich matter in heaven and on Earth. arXiv:1907.02561 [nucl-th].
132. Brown BA. Neutron radii in nuclei and the neutron equation of state. Phys Rev Lett. (2000) 85:5296–9. doi: 10.1103/PhysRevLett.85.5296
133. Lalazissis GA, Konig J, Ring P. New parametrization for the Lagrangian density of relativistic mean field theory. Phys Rev C. (1997) 55:540–3. doi: 10.1103/PhysRevC.55.540
134. Fattoyev FJ, Horowitz CJ, Piekarewicz J, Shen G. Relativistic effective interaction for nuclei, giant resonances, and neutron stars. Phys Rev C. (2010) 82:055803. doi: 10.1103/PhysRevC.82.055803
135. Alam N, Agrawal BK, De JN, Samaddar SK, Colo G. Equation of state of nuclear matter from empirical constraints. Phys Rev C. (2014) 90:054317. doi: 10.1103/PhysRevC.90.054317
136. Danielewicz P, Lee J. Symmetry energy II: isobaric analog states. Nucl Phys A. (2014) 922:1–70. doi: 10.1016/j.nuclphysa.2013.11.005
137. Tsang MB, Zhang Y, Danielewicz P, Famiano M, Li Z, Lynch WG, et al. Constraints on the density dependence of the symmetry energy. Phys Rev Lett. (2009) 102:122701. doi: 10.1103/PhysRevLett.102.122701
138. Russotto P, Gannon S, Kupny S, Lasko P, Acosta L, Adamczyk M, et al. Results of the ASY-EOS experiment at GSI: the symmetry energy at suprasaturation density. Phys Rev C. (2016) 94:034608. doi: 10.1103/PhysRevC.94.034608
139. Russotto P, Wu PZ, Zoric M, Chartier M, Leifels Y, Lemmon RC, et al. Symmetry energy from elliptic flow in 197Au + 197Au. Phys Lett B. (2011) 697:471–6. doi: 10.1016/j.physletb.2011.02.033
140. Lattimer JM, Lim Y. Constraining the symmetry parameters of the nuclear interaction. Astrophys J. (2013) 771:51–65. doi: 10.1088/0004-637X/771/1/51
141. Malik T, Alam N, Fortin M, Providencia C, Agrawal BK, Jha TK, et al. GW170817: constraining the nuclear matter equation of state from the neutron star tidal deformability. Phys Rev C. (2018) 98:035804. doi: 10.1103/PhysRevC.98.035804
142. Sammarruca F. Proton skins, neutron skins, and proton radii of mirror nuclei. Front Phys. (2018) 6:90–8. doi: 10.3389/fphy.2018.00090
143. Sammarruca F. Investigation of constraints on few-neutron forces in neutron matter by empirical information on the neutron skin of 48Ca and 208Pb. Phys Rev C. (2016) 94:054317. doi: 10.1103/PhysRevC.94.054317
144. Inakura T, Nakada N. Constraining the slope parameter of the symmetry energy from nuclear structure. Phys Rev C. (2015) 92:064302. doi: 10.1103/PhysRevC.92.064302
145. Warda M., Viñas X, Roca-Maza X, Centelles M. Neutron skin thickness in the droplet model with surface width dependence: indications of softness of the nuclear symmetry energy. Phys Rev C. (2009) 80:024316. doi: 10.1103/PhysRevC.80.024316
146. Xu C, Li B, Chen L, Ko CM. Analytical relations between nuclear symmetry energy and single-nucleon potentials in isospin asymmetric nuclear matter. Nucl Phys A. (2011) 865:1–16. doi: 10.1016/j.nuclphysa.2011.06.027
147. Roca-Maza X, Brenna M, Agrawal BK, Bortignon PF, Colo G, Cao LG, et al. Giant quadrupole resonances in 208Pb, the nuclear symmetry energy, and the neutron skin thickness. Phys Rev C. (2013) 87:034301. doi: 10.1103/PhysRevC.87.034301
148. Abrahamyan S, Ahmed Z, Albataineh H, Aniol K, Armstrong DS, Armstrong W, et al. Measurement of the neutron radius of 208Pb through parity violation in electron scattering. Phys Rev Lett. (2012) 108:112502. doi: 10.1103/PhysRevLett.108.112502
149. Mammei J, (for the PREX Collaboration). The Pb radius experiment (PREX). AIP Conf Proc. (2013) 1560:620–3. doi: 10.1063/1.4826855
150. Becker D, Bucoveanu R, Grzesik C, Imai K, Kempf R, Molitor M, et al. The P2 experiment. Eur Phys J. (2018) A54:208–69. doi: 10.1140/epja/i2018-12611-6
151. Oyamatsu K, Iida K, Koura H. Neutron drip line and the equation of state of nuclear matter. Phys Rev C. (2010) 82:027301. doi: 10.1103/PhysRevC.82.027301
152. Oppenheimer JR, Volkoff GM. On massive neutron cores. Phys Rev C. (1939) 55:374–80. doi: 10.1103/PhysRev.55.374
153. Weber F. Pulsar as Astrophysical Laboratories for Nuclear and Particle Physics. Bristol; Philadelphia, PA: IOP (1999).
155. Özel F, Freire P. Masses, radii, and the equation of state of neutron stars. Annu Rev Astron Astrophys. (2016) 54:401–40. doi: 10.1146/annurev-astro-081915-023322
156. Lattimer JM, Prakash M. The physics of neutron stars. Science. (2004) 304:536–42. doi: 10.1126/science.1090720
157. Lattimer JM, Prakash M. Neutron star observations: prognosis for equation of state constraints. Phys Rep. (2007) 442:109–65. doi: 10.1016/j.physrep.2007.02.003
158. Lattimer JM, Prakash M. The equation of state of hot, dense matter and neutron stars. Phys Rep. (2016) 621:127–64. doi: 10.1016/j.physrep.2015.12.005
159. Steiner AW, Lattimer JM, Brown E.F. The neutron star mass-radius relation and the equation of state of dense matter. Astrophys J. (2013) 765:L5. doi: 10.1088/2041-8205/765/1/L5
160. Özel F. Surface emission from neutron stars and implications for the physics of their interiors. Rep Prog Phys. (2013) 76:016901. doi: 10.1088/0034-4885/76/1/016901
161. Rhoades CD, Ruffini R. Maximum mass of a neutron star. Phys Rev Lett. (1974) 32:324–7. doi: 10.1103/PhysRevLett.32.324
162. Sabbadini AG, Hartle JB. Bounds on the moment of inertia of nonrotating neutron stars. Ann Phys NY. (1977) 104:95–113. doi: 10.1016/0003-4916(77)90047-1
163. Hartle JB. Bounds on the mass and moment of inertia of non-rotating neutron stars. Phys Rep. (1978) 46:201–47. doi: 10.1016/0370-1573(78)90140-0
164. Abbott BP, [LIGO Scientific and Virgo Collaborations]. GW170817: Observation of gravitational waves from a binary neutron star inspiral. Phys Rev Lett. (2017) 119:161101. doi: 10.1103/PhysRevLett.119.161101
165. Hinderer T, Lackey BD, Lang RN, Read JS. Tidal deformability of neutron stars with realistic equations of state and their gravitational wave signatures in binary inspiral. Phys Rev D. (2010) 81:123016. doi: 10.1103/PhysRevD.81.123016
166. Lim Y, Holt JW. Neutron star tidal deformabilities constrained by nuclear theory and experiment. Phys Rev Lett. (2018) 121:062701. doi: 10.1103/PhysRevLett.121.062701
167. Annala E, Gorda T, Kurkela A, Vuorinen A. Gravitational-wave constraints on the neutron-star-matter equation of state. Phys Rev Lett. (2018) 120:172703. doi: 10.1103/PhysRevLett.120.172703
168. Fattoyev FJ, Piekarewicz J, Horowitz CJ. Neutron skins and neutron stars in the multimessenger era. Phys Rev Lett. (2018) 120:172702. doi: 10.1103/PhysRevLett.120.172702
169. Most ER, Weih LR, Rezzolla L, Schffner-Bielich J. New constraints on radii and tidal deformabilities of neutron stars from GW170817. Phys Rev Lett. (2018) 120:261103. doi: 10.1103/PhysRevLett.120.261103
170. Raithel CA, Ozel F, Psaltis D. Tidal Deformability from GW170817 as a direct probe of the neutron star radius. Astrophys J. (2018) 857:L23. doi: 10.3847/2041-8213/aabcbf
171. Nandi R, Char P, Pal S. Constraining the relativistic mean-field model equations of state with gravitational wave observations. Phys Rev C. (2019) 99:052802. doi: 10.1103/PhysRevC.99.052802
172. Burgio GF, Drago A, Pagliara G, Schulze HJ, Wei JB. Are small radii of compact stars ruled out by GW170817/AT2017gfo?. Astrophys J. (2018) 860:139-144. doi: 10.3847/1538-4357/aac6ee
173. Harrison BK, Wheeler JA. Gravitation Theory and Gravitational Collapse. Chicago, IL: University of Chicago Press (1965).
174. Negele JW, Vautherin D. Neutron star matter at sub-nuclear densities. Nucl Phys. (1973) A207:298–320. doi: 10.1016/0375-9474(73)90349-7
175. Liebert J. White dwarf stars. Annu Rev Astron Astrophys. (1980) 18:363–98. doi: 10.1146/annurev.aa.18.090180.002051
176. Read JS, Lackey BD, Owen BJ, Friedman JL. Constraints on a phenomenologically parametrized neutron-star equation of state. Phys Rev D. (2009) 79:124032. doi: 10.1103/PhysRevD.79.124032
177. Sammarruca F. Short-range correlations in isospin symmetric and asymmetric nuclear matter: a microscopic perspective. Phys Rev C. (2014) 90:064312. doi: 10.1103/PhysRevC.90.064312
178. Hebeler K, Lattimer JM, Pethick CJ, Schwenk A. Equation of state and neutron star properties constrained by nuclear physics and observation. ApJ. (2013) 773:11–25. doi: 10.1088/0004-637X/773/1/11
179. Antoniadis J, Freire PCC, Wex N, Tauris TM, Lynch RS, van Kerkwijk MH, et al. A massive pulsar in a compact relativistic binary. Science. (2013) 340:6131. doi: 10.1126/science.1233232
180. Cromartie HT, Fonseca E, Ransom SM, Demorest PB, Arzoumanian Z, Blumer H, et al. Relativistic Shapiro delay measurements of an extremely massive millisecond pulsar. Nat Astron. (2019). doi: 10.1038/s41550-019-0880-2
181. Lattimer JM, Prakash M. Neutron star structure and the equation of state. ApJ. (2001) 550:426–42. doi: 10.1086/319702
182. Miyatsu T, Saito K, Cheoun MK. Equation of state for neutron stars with hyperons and quarks in the relativistic hartree - fock approximation. Astrophys J. (2015) 813:2–15. doi: 10.1088/0004-637X/813/2/135
183. Mishra RN, Sahoo HS, Panda PK, Barik N, Frederico T. Hyperon stars in a modified quark meson coupling model. Phys Rev C. (2016) 94:035805. doi: 10.1103/PhysRevC.94.035805
185. Vidana I. Hyperons in neutron stars. J Phys Conf Ser. (2016) 668:012031. doi: 10.1088/1742-6596/668/1/012031
186. Rapaj E, Roggero A, Holt JW. Microscopically constrained mean-field models from chiral nuclear thermodynamics. Phys Rev C. (2016) 93:065801. doi: 10.1103/PhysRevC.93.065801
187. Endrizzi A, Logoteta D, Giacomazzo B, Bombaci I, Kastaun W, Ciolfi R. Effects of chiral effective field theory equation of state on binary neutron star mergers. arXiv:1806.09832 [astro-ph.HE] (2018). doi: 10.1103/PhysRevD.98.043015
Keywords: nuclear forces, chiral effective field theory, symmetry energy, neutron skin thickness, neutron stars
Citation: Sammarruca F and Millerson R (2019) Nuclear Forces in the Medium: Insight From the Equation of State. Front. Phys. 7:213. doi: 10.3389/fphy.2019.00213
Received: 29 September 2019; Accepted: 21 November 2019;
Published: 10 December 2019.
Edited by:
Laura Elisa Marcucci, University of Pisa, ItalyReviewed by:
Constança Providência, University of Coimbra, PortugalFiorella Burgio, National Institute of Nuclear Physics (INFN), Italy
Copyright © 2019 Sammarruca and Millerson. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Francesca Sammarruca, ZnNhbW1hcnJAdWlkYWhvLmVkdQ==
 Francesca Sammarruca
Francesca Sammarruca Randy Millerson
Randy Millerson