All-Dielectric Nanoresonators for χ(2) Nonlinear Optics

Introduction

Light manipulation at the nanoscale has been a central topic in nanophotonics for the last two decades. The control of light–matter interaction through subwavelength-resonating elements has led to the possibility of engineering the optical properties of nanopatterned materials, and, in turn, this has led to peculiar phenomena and opportunities for striking applications, including optical magnetism, negative refraction [1, 2], epsilon-near-zero [3, 4], hyperbolic metamaterials [5], sub-wavelength focusing [6], cloaking, wavefront shaping, and flat lenses [7, 8].

Many of these applications originated from the observation of a magnetic response produced by subwavelength structures. In metallic nanostructures, the response to external electromagnetic excitation arises from surface plasmon polaritons or localized surface plasmons. The resonant behavior of these nanostructures allows for the imprint of an abrupt phase discontinuity to propagating light. Control over optical properties allows for the design of 2D arrays of resonators with a spatially varying phase response and, consequently, the fabrication of metasurfaces for beam shaping [7–10].

Nanophotonics has also attracted the interest of the scientific community for intensity-dependent phenomena. Tight field confinement boosts nonlinear generation efficiency in the medium, allowing for the presence of subwavelength nonlinear light sources with amplitude and phase control [11–14]. However, due to their nature, surface plasmons are always accompanied by losses, which limits their application at optical frequencies.

An alternative way to solve this problem is offered by all-dielectric nanostructures. According to Mie theory, high-refractive-index dielectric nanoparticles exhibit strong electric and magnetic resonances, demonstrated for the first time in the visible spectral range with silicon nanoparticles [15, 16]. Control over the phase of the diffracted beam through a 2D array of all-dielectric elements was already proven in 1998 with local effective index modulation in blazed-binary diffractive elements [17, 18].

The linear resonant behavior of high-refractive-index dielectric nanoparticles is typically obtained via multipolar decomposition of the scattered electromagnetic fields, which consists of the approximation of complex charge distributions with point multipoles [19]. This approach reproduces the observable scattering cross section of the nanoparticles fairly well as it considers the dominant excited multipole moments. However, more accurate methods exist that calculate the scattering cross section from the natural eigenstate basis of the considered open cavity, whose elements are called quasinormal-modes (QNMs) [20–23].

For nonlinear generation processes in the visible range, high-refractive-index nanoparticles are even more advantageous than their plasmonic counterparts due to (a) the absence of ohmic losses and (b) strong field confinement inside the resonator volume, thus enabling the exploitation of the large bulk nonlinearity of these materials. These features are promising for the integration of flat metasurfaces in optoelectronic devices for efficient parametric generation of light with controlled amplitude, phase, and polarization. In this context, the first relevant results have been obtained with third harmonic generation (THG) in silicon nanodisks. In 2014, Shcherbakov et al. demonstrated that local enhancement of an electromagnetic field in silicon nanodisks, due to the magnetic resonance response in the near IR, gives rise to two-order-of-magnitude enhancement of THG with respect to bulk silicon [24], immediately establishing this as an ideal building block for ultra-fast optical switching in integrated photonics [25]. All-dielectric resonators can be thought of as optical cavities with losses. If, on one hand, this makes them attractive as engineerable nonlinear light sources, their nonlinear generation efficiency is, on the other hand, strongly limited by the poor quality factor of resonating modes. In this respect, nanoresonator performances can be boosted by exploiting the multi-mode interference [26], resulting, for example, in Fano resonances [27, 28] or non-radiative anapole modes [29].

Since second-order bulk nonlinear processes are inhibited in centrosymmetric materials like silicon, the quest for high-χ⁽²⁾ nonlinear Mie resonators drew the attention on non-centrosymmetric III-V alloys. Among them, promising results have been obtained with aluminum gallium arsenide (AlGaAs) [30, 31] and gallium phosphide (GaP) [32].

This review focuses on three axes of AlGaAs Mie nanoresonators. Firstly, we illustrate two state-of-the-art methods for deriving the linear scattering cross section: multipolar decomposition, and QNM. Secondly, we report on two tools to predict the second harmonic generation (SHG): the first (numerical) consists of finite-elements (FEM) calculations followed by multipolar decomposition, and the second (analytical) relies on Green's functions. Finally, we focus on SHG shaping by highlighting several experimental works.

Scattering Properties of AlGaAs Mie-Resonators

AlGaAs is a zinc-blend alloy exhibiting a high refractive index in the visible/near-IR range (n > 3.2), a bandgap that is both larger than GaAs (ℏω_g ~ 1.42 eV), tunable with Al concentration, and has high quadratic nonlinear susceptibility (χ⁽²⁾ ~ 200 pm/V) [33]. Its physical properties, combined with a mature technological process, make this material an attractive choice in the framework of III-V nonlinear optical devices. AlGaAs nonlinear Mie-nanoresonators were first investigated by Carletti et al. [34] with Al_0.18Ga_0.82As nanocylinders. This alloy composition prevents two-photon absorption in the telecom range while preserving a high refractive index [35]. As an example, take the response of a resonator with radius r = 225 nm and h = 400 nm that is suspended in air to an electromagnetic plane wave with wavevector k parallel to the cylinder axis, as is reported in Figure 1A.

FIGURE 1

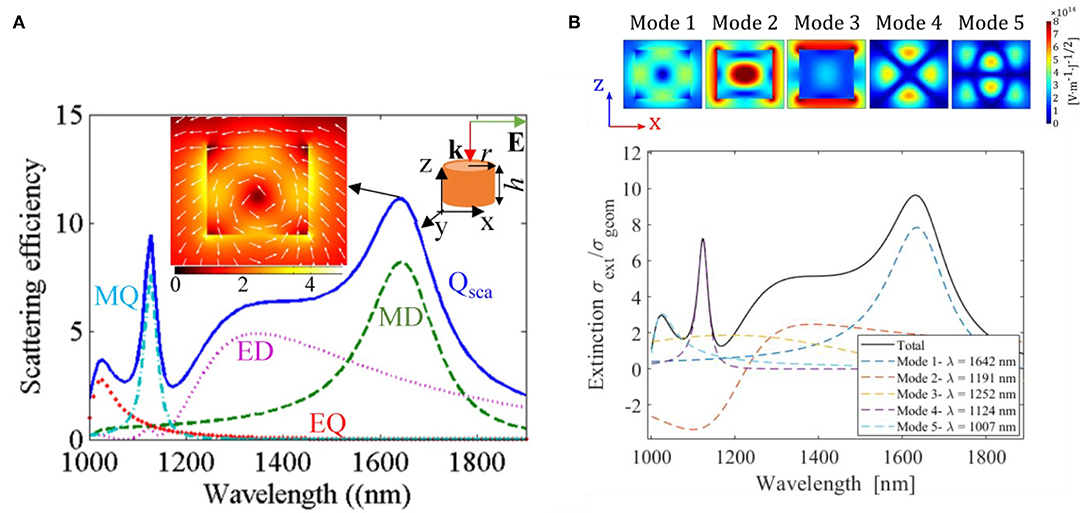
Figure 1. AlGaAs nanocylinder scattering efficiency computed with COMSOL for radius r = 225 nm and height h = 400 nm. External excitation is approximated with a plane wave with the k vector parallel to the cylinder axis (see inset). Blue solid line represents total scattering, while dashed line is the expansion on spherical harmonics multipoles: electric and magnetic dipoles (ED and MD, respectively) and quadrupoles (EQ and MQ, respectively). Reprinted with permission from Carletti et al. [34]. (B) QNM expansion of AlGaAs nanocylinder linear scattering for the same geometry and excitation conditions as in (A). Black solid line reports the total scattering, considering that just five QNMs. Colored dashed lines report the contribution of each QNM separately. Values in nm reported in the legend refer to the real part of the eigenfrequency of every mode. Inset: Electric field distributions in the xz plane of the five QNMs used for linear scattering reconstruction.

The inset of the same figure reports the electric field distribution inside the resonator at λ = 1640 nm, which testifies to the presence of rotating displacement currents typical of a magnetic dipole. A quantitative understanding of this resonant behavior can be obtained by replacing the complex distribution of charges and currents with an equivalent set of point multipoles generating the same fields [19]. Numerically, this operation is performed by projecting the current distributions originating the scattered field on the basis of spherical harmonics, which leads to the scattering cross section expansion at a given frequency:

$\begin{array}{ll}{\sigma }_S=\frac{\pi }{k^2}{\displaystyle \sum _{l=1}^{\infty }}{\displaystyle \sum _{m=-l}^l}\left(2l+1\right)\left[|a_E\left(l,m\right){|}^2+|a_M\left(l,m\right){|}^2\right].& (1)\end{array}$

The lowest-order multipole contributions to this expansion are reported as dashed lines in Figure 1A, which confirms that a strong MD resonance dominates the scattering at λ = 1640 nm.

In Figure 1A, each resonance of the scattering spectrum is dominated by a multipolar response, which depends on the driving field. At normal incidence, it turns out that the fundamental resonance includes ED and MD contributions. Thus, the multipolar expansion reproduces the scattering cross section of the nanostructure for a given excitation fairly well. However, resonances in the scattering spectrum exhibit contributions not only from the dominant multipole moments that are excited and captured in the decomposition but also from other resonant modes of the considered open cavity. Recently, several numerical tools have been proposed to study radiative and dissipative systems in their proper eigenstate basis [20–23]. In the following section, we demonstrate the deconvolution of extinction spectra of the same system in Figure 1A through the method proposed in [23]. In this case, the electromagnetic field in the nanostructure is expanded on the natural basis of the nanoresonator eigenstates, called quasinormal-modes (QNMs), which are solutions to the source-free Maxwell's equations:

$\begin{array}{ll}\left[\begin{array}{cc}0& -\text{i}{\mu }_0^{-1}\nabla \times \\ i\text{ε}({\tilde{\omega }}_{\text{m}})\nabla \times & 0\end{array}\right]\left[\begin{array}{l}{\tilde{\text{H}}}_{\text{m}}\hfill \\ {\tilde{\text{E}}}_{\text{m}}\hfill \end{array}\right]={\tilde{\omega }}_{\text{m}}\left[\begin{array}{l}{\tilde{\text{H}}}_{\text{m}}\hfill \\ {\tilde{\text{E}}}_{\text{m}}\hfill \end{array}\right]& (2)\end{array}$

This is a non-Hermitian eigenvalue problem. QNMs are therefore modes of an open system with a complex eigenfrequency ${\tilde{\omega }}_m$. The scattered electric field can be expanded as [22]:

$\begin{array}{ll}{\text{E}}_S(r,\omega )={\displaystyle \sum _m}{\alpha }_m(\omega ){\tilde{\text{E}}}_m(r)& (3)\end{array}$

where ${\tilde{\text{E}}}_m(r)$ is the m-th QNM electric field distribution and the α_m coefficients are known analytically. The scattering spectrum in Figure 1A can be accurately reconstructed using five QNMs, see Figure 1B. For the normalization and implementation of this method we refer the reader to [23]. This reconstruction offers several advantages: (a) a robust formalism relying on a proper orthonormal basis; (b) a piece of software implemented in COMSOL Multiphysics; and (c) a gain in terms of computational costs for reconstructing the scattered field irrespective of the incident field.

The proposed case immediately shows the potential of highlighting constructive or destructive interference among QNMs, thereby enabling a good understanding of the physics of the resonating behavior of nanoantennas. It is not surprising to see negative contributions to the total scattering as this is the footprint of interference between quasinormal modes. It is important to appreciate the change in paradigm from multipole expansion to QNM: in the case of the former, once computed, the scattered field was projected on multipoles distributions; in the latter case, instead, eigenmodes of the structures, i.e., independent of the external source, are analyzed, and then the response to an incident field is retrieved. Furthermore, the electric field distribution of every QNM in the near and far field can be studied separately, which offers a powerful opportunity to apply coupled-mode theory and study mode overlap in the frequency generation processes.

Theoretical Analysis of SHG in Aluminum Gallium Arsenide Mie-Resonators

The exhaustive comprehension of linear properties enabled the development of models for nonlinear optical phenomena in nanoantennas. In the following section, we have focused on second harmonic generation in AlGaAs resonators. They can be studied numerically with FEM, reducing the analysis to a two-step scattering problem: (1) an external excitation at the fundamental frequency (FF) ω is imposed, and electric fields in the nanostructure are retrieved; and (2) a second-harmonic (SH) polarization vector is computed as P^SH(r, 2ω) = χ⁽²⁾:[E(r, ω)⊗E(r, ω)], and Maxwell's equations are solved in the presence of a known current-source distribution J^SH(r, 2ω)=i2ωP^SH (r, 2ω). At variance with bulk crystals or microresonators, sub-wavelength resonators cannot benefit from phase-matching conditions. Then SHG efficiency depends on electric-field confinement at FF and SH as well as the overlap of these fields mediated by the nonlinear susceptibility tensor [34].

The above requirements imply that having highly resonant modes at FF and SH is necessary, but this is not enough if their distributions do not spatially overlap with respect to symmetry conditions imposed by the χ⁽²⁾ tensor. Indeed, it is immediately possible to highlight that, when moving to shorter wavelengths, the number of excited modes increases. An example is summarized in Figure 1S: for [100] grown AlGaAs pillars, crystal symmetry imposes that the magnetic dipole excited at FF by a normally incident beam effectively couples just with SH modes with zero emission in the normal direction. While this constraint might appear as an intrinsic limitation of AlGaAs for applications, it actually illustrates the possibility of exploiting the richness of resonant modes to shape the SHG radiation pattern, polarization, or phase of nonlinear light sources. Taking the same example of a cylindrical resonator with r = 225 nm and h = 400 nm, it was shown that different resonances at SH could be excited by changing the pump polarization or the incident angle [36].

A different strategy to study the SHG efficiency from high-index dielectric nanoparticles (resumed in Figure 2S) relies on the Green's function method [37]. This technique, where the SH far field can be calculated via the dyadic Green's function $\widehat{\text{G}}$ of a sphere, has the advantage of showing the selection rules associated with mode coupling based on the symmetry of multipole moments and the crystalline structure. However, it is analytical only in the case of spherical particles and bulk sources. Finally, as an alternative to Green's function, the multipolar coefficients of the SH fields can also be calculated using the Lorentz lemma [38].

Shaping SHG from AlGaAs Nanoantennas: Model and Experimental Observations

The numerical model treated in the previous section enables the investigation of resonance overlap at FF and SH to optimize the nanoantennas design for enhanced SHG. Although the theoretical analyses reported above refer to air-suspended nanocylinders, two slightly different types of (100) high-contrast AlGaAs nanoantennas on a low refractive index have been studied the most: (a) a monolithic device on an aluminum oxide substrate with n ≈ 1.6 [30] and (b) a device embedded in BCB with n ≈ 1.35 [31]. In particular, it was shown [30] that by tuning a magnetic dipole resonance at FF in the telecom range (around λ_FF = 1.55 μm), a SHG efficiency up to 6·10⁻⁵ could be expected for a nanocylinder pumped with a field intensity of 1 GW/cm² at normal incidence. This numerical prediction was confirmed experimentally. Please notice that no SHG occurs under normal incidence on (100) bulk zinc-blend crystals, other than a contribution from surface χ⁽²⁾ that is negligible for FF below half bandgap. Furthermore, experimental results for nanocylinders with radii ranging from 175 to 225 nm pumped at telecom wavelengths displayed good agreement with a theoretical model considering just bulk χ⁽²⁾ contribution. A summary of those result is reported in Figure 3S, and the experimental setup is sketched and detailed in Figure 4S. This outcome is all the more interesting in that it highlights one of the advantages of dielectric structures over their plasmonic counterparts: strong field confinement inside the volume of the resonator allows for the exploitation of the large bulk nonlinear susceptibility as it yields to about three-order-of-magnitude SHG enhancement with respect to metallic antennas reported in [39] (${\gamma }_{SHG}\cong 1.5\times 10^{-7}{W}^{-1}$ for the former, instead of ${\gamma }_{SHG}\cong 5\times 10^{-10}{W}^{-1}$ for the latter).

The same outcome also holds for polarization properties, as summarized in Figure 5SA where the multipolar expansion based on FEM calculations shows that, as the cylinder radius is varied, SHG is dominated by entirely different resonances. More specifically, as the radius is increased, SH polarization passes from co-polarized to cross-polarized with respect to the polarization of the pump [40].

Similar results regarding the polarization properties of SHG in AlGaAs nanocylinders were detailed by Camacho-Morales et al. [31] (Figure 5SB). In that case, the resonators were embedded in a transparent benzocyclobutene (BCB) layer with refractive index n≈1.35, allowing for both a higher refractive index contrast and the possibility of characterizing the device in transmission. In this case, back-focal-plane imaging, enabled via the insertion of a Bertrand lens in the camera detection line, highlighted a strong correlation between the emission direction and SH polarization state. Forward and backward emissions revealed the same features, and, in both cases, the experimental results confirmed full-wave numerical predictions neglecting the contribution of surface χ⁽²⁾. The comprehension of single element SHG properties, in terms of polarization and directionality, successfully enabled the development of antenna arrays for the controlled generation of SH polarization states [41].

A quite different landscape was explored by Liu et al. [42], which involved working with GaAs resonators on aluminum-gallium oxide. In this case, the dimension of nanoantennas were smaller in order to ensure a magnetic dipole resonance around a pump wavelength of 1020 nm, as detailed in Figure 6S.

In contrast to the previous cases, the SH polarization pattern could not be exhaustively explained when considering just bulk χ⁽²⁾ contribution. This is the case particularly when it involves resonances at FF that exhibit strong field intensity close to the resonator surface or when the SH signal is above the energy bandgap, as is displayed in Figure 6S, and the SHG contribution from the bulk is strongly absorbed. On the other hand, the introduction of a surface χ⁽²⁾ contribution remains quantitatively challenging due to the unexplored value of this quantity, thereby urging for further and deeper investigations.

Even if these reviewed works confirm three-order-of-magnitude higher SHG efficiency in AlGaAs nanocylinders compared to plasmonic structures [39], SH normal emission is forbidden due to the symmetry of the nonlinear tensor and the nanoparticle shape. This might compromise the development of integrated optical devices. As shown in previous sections, several strategies exist to overcome the limitations of χ⁽²⁾ symmetry in [100] grown AlGaAs.

In reference [36], it was numerically predicted that a tilted excitation breaks the electric field symmetry inside the resonator, thereby redirecting SH emission. In that case, for a tilted pump wavevector, different resonating modes exhibiting, for example, normal emission dominate the scattering. This highlights one of the possible mechanisms used to control the SH emission pattern of the nanoscatterer by playing with the excitation of different resonating modes or on the interference between them. These numerical investigations proved that there are a large number of features offered by subwavelength dielectric particles, which rely on the high density of leaky resonant modes in this region of the spectrum. This idea was adopted in Carletti et al. [43] to study the control of the emission pattern of monolithic AlGaAs nanocylinders on an AlOx substrate in the backward direction (see Figure 2A). It was shown that changing the incident angle had a strong impact both on multipoles dominating the FF and on SH resonator scattering properties. In particular, with an experimental setup similar to that one of Figure 4S, an s-polarized beam at 1570 nm with normal incidence was used to excite an in-plane MD resonance of a 220 nm radius and 400 nm height AlGaAs nanocylinder. When moving to higher angles thanks to the off-axis lateral translation of the microscope objective, the out-of-plane MD contribution increases, breaking the field symmetry in the resonator. At the SH frequency, this results in a change from a mainly “electric-quadrupole like” field distribution with radiation lobes at large angles and a minimum along the normal axis to an “electric-dipole like” one with two main lobes in the forward and backward directions that point along the cylinder axis (see Figure 2A). Exploiting these features, the backward-collected SH can be increased by about one order of magnitude with respect to the two-lobe SH field generated upon normal incidence of the FF pump. Conversely, a p-polarized beam would excite, in nearly the same way, the different FF resonances regardless of the incident angle that was chosen. This results in a quasi-invariant emission, meaning a small enhancement in collected power (see Figures 2B–E).

FIGURE 2

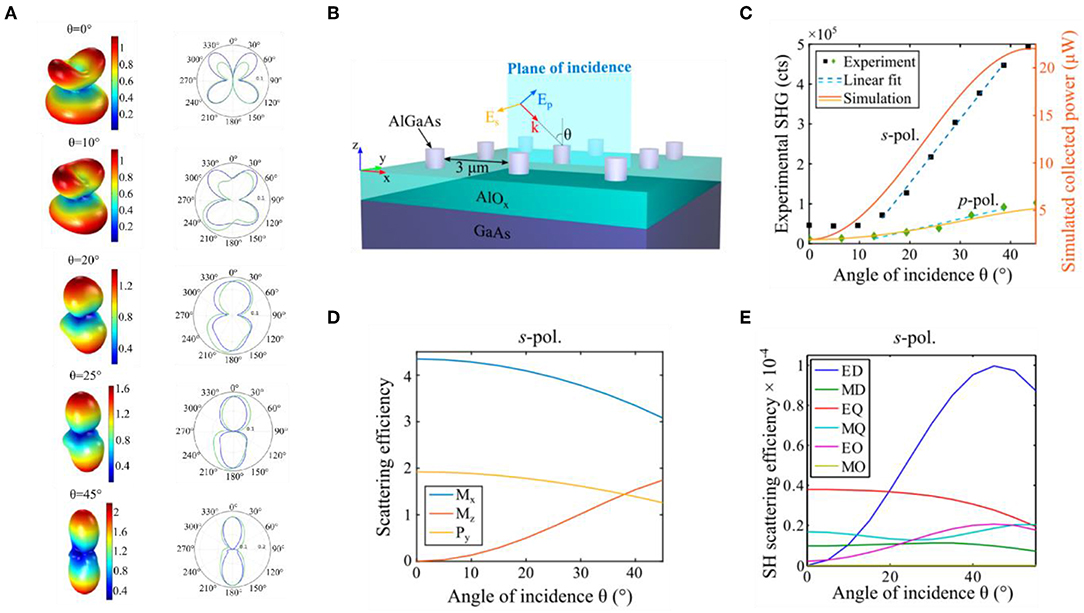
Figure 2. (A) Numerical analysis of SHG in AlGaAs nanocylinders when varying the FF beam incident angle: far-field when moving from a normal incident excitation and s-polarized along [100] to a tilted s-polarized excitation oriented at 45° from the normal. Reprinted with permission from Carletti et al. [36]. (B) SHG in AlGaAs nanopillars for tilted excitation. Sketch of the analyzed experiment. A plane wave with incidence angle θ impinges on a single pillar with radius 220 nm and height 400 nm. (C) Numerical and experimental results of back-collected SH when varying θ for linearly s and p polarized FF. (D) Cartesian coordinate multipoles expansion of linear scattering at 1,570 nm. Three main contributions are reported here: magnetic dipoles along x and z (solid blue and red lines, respectively) and electric dipole along y (solid yellow line). (E) Spherical harmonics multipole expansion calculated from SH displacement current distribution. Reprinted with permission from Carletti et al. [43].

A different approach that maintains normal excitation consists of the integration of a dielectric grating around a nanoparticle so as to control the phase of the nonlinear generation [44]. As explained before, SHG in large-angle lobes is detrimental for the use of on-axis applications. Instead of working on nanoantenna resonances, it is possible to make the in-plane nonlinear emission interact locally with a diffraction grating to reshape the far field (Figure 7S for sample images and experimental results). Due to the symmetry of nonlinear displacement currents, the resonator emission at SH exhibits two main lobes with a π-phase shift, meaning that simply redirecting them to the normal would result in destructive interference. The problem is solved by introducing an asymmetry in grating design in order to further π-shift one lobe with respect to the other. Exploiting this technique an increase by two order of magnitude in the backward collected power with respect to the bare nanocylinder was demonstrated.

An alternative solution to the absence of normal SHG is to rotate the AlGaAs crystalline structure, and thus the χ⁽²⁾ tensor, by fabricating nanoantennas from (111)-GaAs [45]. This change of symmetry of the crystalline structure allows superior forward directionality compared to its (100)-counterparts. The shaping of the SHG radiation pattern via FF polarization was also shown in this case (results are summarized in Figure 8S).

Conclusion

Advances in integrated photonics require nonlinear compact devices, like metasurfaces, with high conversion efficiencies and tailorable emission features. After having drawn the attention of the scientific community on the subject of linear applications, nanopatterned dielectric materials have become promising also for nonlinear optics. Here, we reviewed recent progress in high-index dielectric χ⁽²⁾ nanoresonators, which proved advantageous over their plasmonic counterparts because of lower optical losses and a higher conversion efficiency stemming from to the overlap of cavity modes with a strong bulk χ⁽²⁾. Since their multi-resonant behavior enabled the background-free nonlinear displacement current distribution to be tailored locally, a complete understanding of their features is imperative for the SH wavefront design. In this respect, we benchmarked the numerical calculations of the linear scattering cross section against the QNM theory. The latter provides complementary physical insight into Mie-like resonances in complex structures that cannot be studied analytically. We then focused on fully vectorial numerical calculations, which allowed to model nonlinear effects in good agreement with experimental results. In conclusion, we would like to stress that a better understanding of the relative contribution of bulk vs. surface nonlinear susceptibility would significantly help future progress regarding subwavelength frequency conversion devices. Finally, when compared to their guided-wave counterparts, nanoresonators offer a larger number of spatial degrees of freedom for the engineering of nonlinear generation processes. The development of more powerful design tools, combined with the technological advances of the last years, will probably lead to the creation of unprecedented nonlinear photonic devices.

Author Contributions

CG and GM wrote the paper draft. GL was the scientific supervisor. All the others have contributed to its evolution to the final form.

Funding

GL and PL acknowledge the NOMOS project (ANR-18CE24-0026) for financial support.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The handling editor declared a past co-authorship with one of the authors GL.

Acknowledgments

The authors thank C. De Angelis, L. Carletti, D. Rocco, and T. Wu for fruitful discussions.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2019.00221/full#supplementary-material

References

1. Shalaev VM, Cai W, Chettiar UK, Yuan H, Sarychev AK, Drachev VP, et al. Negative index of refraction in optical metamaterials. Opt Lett. (2005) 30:3356–8. doi: 10.1364/FIO.2005.FTuC2

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Zhang S, Fan W, Panoiu NC, Malloy KJ, Osgood RM, Brueck SRJ. Experimental demonstration of near-infrared negative-index metamaterials. Phys Rev Lett. (2005) 95:1–4. doi: 10.1103/PhysRevLett.95.137404

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Ziolkowski RW. Propagation in and scattering from a matched metamaterial having a zero index of refraction. Phys Rev E. (2004) 70:1–12. doi: 10.1103/PhysRevE.70.046608

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Garcia N, Ponizovskaya EV, Xiao JQ. Zero permittivity materials: band gaps at the visible. Appl Phys Lett. (2002) 80:1120–2. doi: 10.1063/1.1449529

CrossRef Full Text | Google Scholar

5. Segovia P, Marino G, Krasavin AV, Olivier N, Wurtz GA, Belov PA, et al. Hyperbolic metamaterial antenna for second-harmonic generation tomography. Opt Expr. (2015) 23:30730–8. doi: 10.1364/OE.23.030730

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Pendry JB. Negative refraction makes a perfect lens. Phys Rev Lett. (2000) 85:3966–9. doi: 10.1103/PhysRevLett.85.3966

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Aieta F, Patrice G, Kats M, Yu N, Blanchard R, Gaburro Z, et al. Aberration-free ultrathin flat lenses and axicons at telecom wavelengths based on plasmonic metasurfaces. Nano Lett. (2012) 12:4932–6. doi: 10.1021/nl302516v

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Yu N, Genevet P, Kats MA, Aieta F, Tetienne J-P, Capasso F, et al. Light propagation with phase discontinuities: generalized laws of reflection and refraction. Science. (2011) 334:333–7. doi: 10.1126/science.1210713

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Ni X, Kildishev AV, Shalaev VM. Metasurface holograms for visible light. Nat Commun. (2013) 4:1–6. doi: 10.1038/ncomms3807

CrossRef Full Text | Google Scholar

10. Kildishev AV, Boltasseva A, Shalaev VM. Planar photonics with metasurfaces. Science. (2013) 339:1–6. doi: 10.1126/science.1232009

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Almeida E, Bitton O, Prior Y. Nonlinear metamaterials for holography. Nat Commun. (2016) 7:1–7. doi: 10.1038/ncomms12533

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Keren-Zur S, Avayu O, Michaeli L, Ellenbogen T. Nonlinear beam shaping with plasmonic metasurfaces. ACS Photon. (2016) 3:117–23. doi: 10.1021/acsphotonics.5b00528

CrossRef Full Text | Google Scholar

13. Li G, Chen S, Pholchai N, Reineke B, Wong PWH, Pun EYB, et al. Continuous control of the nonlinearity phase for harmonic generations. Nat Mater. (2015) 14:607–12. doi: 10.1038/nmat4267

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Tymchenko M, Gomez-Diaz JS, Lee J, Nookala N, Belkin MA, Alù A. Gradient nonlinear pancharatnam-berry metasurfaces. Phys Rev Lett. (2015) 115:1–5. doi: 10.1103/PhysRevLett.115.207403

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Evlyukhin AB, Novikov SM, Zywietz U, Eriksen RL, Reinhardt C, Bozhevolnyi SI, et al. Demonstration of magnetic dipole resonances of dielectric nanospheres in the visible region. Nano Lett. (2012) 12:3749–55. doi: 10.1021/nl301594s

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Kuznetsov AI, Miroshnichenko AE, Fu YH, Zhang J, Lukyanchukl B. Magnetic light. Sci Rep. (2012) 2:1–6. doi: 10.1038/srep00492

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Lalanne P. Waveguiding in blazed-binary diffractive elements. J Opt Soc Am A. (1999) 16:2517–20. doi: 10.1364/JOSAA.16.002517

CrossRef Full Text | Google Scholar

18. Lalanne P, Astilean S, Chavel P, Cambril E, Launois H. Design and fabrication of blazed binary diffractive elements with sampling periods smaller than the structural cutoff. J Opt Soc Am A. (1999) 16:1143–56. doi: 10.1364/JOSAA.16.001143

CrossRef Full Text | Google Scholar

19. Grahn P, Shevchenko A, Kaivola M. Electromagnetic multipole theory for optical nanomaterials. New J Phys. (2012) 14:1–11. doi: 10.1088/1367-2630/14/9/093033

CrossRef Full Text | Google Scholar

20. Powell DA. Resonant dynamics of arbitrarily shaped meta-atoms. Phys Rev B Condens Matter Mater Phys. (2014) 90:1–10. doi: 10.1103/PhysRevB.90.075108

CrossRef Full Text | Google Scholar

21. Powell DA. Interference between the modes of an all-dielectric meta-atom. Phys Rev Appl. (2017) 7:1–13. doi: 10.1103/PhysRevApplied.7.034006

CrossRef Full Text | Google Scholar

22. Bai Q, Perrin M, Sauvan C, Hugonin J-P, Lalanne P. Efficient and intuitive method for the analysis of light scattering by a resonant nanostructure. Opt Expr. (2013) 21:27371–82. doi: 10.1364/OE.21.027371

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Yan W, Faggiani R, Lalanne P. Rigorous modal analysis of plasmonic nanoresonators. Phys Rev B. (2018) 97:1–9. doi: 10.1103/PhysRevB.97.205422

CrossRef Full Text | Google Scholar

24. Shcherbakov MR, Neshev DN, Hopkins B, Shorokhov AS, Staude I, Melik-Gaykazyan EV, et al. Enhanced third-harmonic generation in silicon nanoparticles driven by magnetic response. Nano Lett. (2014) 14:6488–92. doi: 10.1021/nl503029j

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Shcherbakov MR, Vabishchevich PP, Shorokhov AS, Chong KE, Choi DY, Staude I, et al. Ultrafast all-optical switching with magnetic resonances in nonlinear dielectric nanostructures. Nano Lett. (2015) 15:6985–90. doi: 10.1021/acs.nanolett.5b02989

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Smirnova D, Kivshar YS. Multipolar nonlinear nanophotonics. Optica. (2016) 3:1241–52. doi: 10.1364/OPTICA.3.001241

CrossRef Full Text | Google Scholar

27. Yang Y, Wang W, Boulesbaa A, Kravchenko II, Briggs DP, Puretzky A, et al. Nonlinear fano-resonant dielectric metasurfaces. Nano Lett. (2015) 15:7388–93. doi: 10.1021/acs.nanolett.5b02802

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Hopkins B, Miroshnichenko AE, Kivshar YS. All-dielectric nanophotonic structures: exploring the magnetic component of light. In: Agrawal A, Benson T, De La Rue R, Wurtz G, editors. Recent Trends in Computational Photonics. Springer Series in Optical Sciences, Vol. 204. Cham: Springer (2017).

Google Scholar

29. Grinblat G, Li Y, Nielsen MP, Oulton RF, Maier SA. Enhanced third harmonic generation in single germanium nanodisks excited at the anapole mode. Nano Lett. (2016) 16:4635–40. doi: 10.1021/acs.nanolett.6b01958

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Gili VF, Carletti L, Locatelli A, Rocco D, Finazzi M, Ghirardini L, et al. Monolithic AlGaAs second-harmonic nanoantennas. Opt Expr. (2016) 24:15965–71. doi: 10.1364/OE.24.015965

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Camacho-Morales R, Rahmani M, Kruk S, Wang L, Xu L, Smirnova DA, et al. Nonlinear generation of vector beams from AlGaAs nanoantennas. Nano Lett. (2016) 16:7191–7. doi: 10.1021/acs.nanolett.6b03525

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Cambiasso J, Grinblat G, Li Y, Rakovich A, Cortés E, Maier SA. Bridging the gap between dielectric nanophotonics and the visible regime with effectively lossless gallium phosphide antennas. Nano Lett. (2017) 17:1219–25. doi: 10.1021/acs.nanolett.6b05026

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Ohashi M, Kondo T, Ito R, Fukatsu S, Shiraki Y, Kumata K, et al. Determination of quadratic nonlinear optical coefficient of AlxGa1-xAs system by the method of reflected second harmonics. J Appl Phys. (1993) 74:596–601. doi: 10.1063/1.355272

CrossRef Full Text | Google Scholar

34. Carletti L, Locatelli A, Stepanenko O, Leo G, De Angelis C. Enhanced second-harmonic generation from magnetic resonance in AlGaAs nanoantennas. Opt Expr. (2015) 23:26544–50. doi: 10.1364/OE.23.026544

PubMed Abstract | CrossRef Full Text | Google Scholar

35. Gehrsitz S, Reinhart FK, Gourgon C, Herres N, Vonlanthen A, Sigg H. The refractive index of AlxGa1-xAs below the band gap: accurate determination and empirical modeling. J Appl Phys. (2000) 87:7825–37. doi: 10.1063/1.373462

CrossRef Full Text | Google Scholar

36. Carletti L, Locatelli A, Neshev D, De Angelis C. Shaping the radiation pattern of second-harmonic generation from AlGaAs dielectric nanoantennas. ACS Photon. (2016) 3:1500–7. doi: 10.1021/acsphotonics.6b00050

CrossRef Full Text | Google Scholar

37. Frizyuk K, Volkovskaya I, Smirnova D, Poddubny A, Petrov M. Second-harmonic generation in Mie-resonant dielectric nanoparticles made of noncentrosymmetric materials. Phys Rev B. (2019) 99:1–15. doi: 10.1103/PhysRevB.99.075425

CrossRef Full Text | Google Scholar

38. Smirnova D, Smirnov AI, Kivshar YS. Multipolar second-harmonic generation by Mie-resonant dielectric nanoparticles. Phys Rev A. (2018) 97:1–11. doi: 10.1103/PhysRevA.97.013807

CrossRef Full Text | Google Scholar

39. Celebrano M, Wu X, Baselli M, Großmann S, Biagioni P, Locatelli A, et al. Mode matching in multiresonant plasmonic nanoantennas for enhanced second harmonic generation. Nat Nanotechnol. (2015) 10:412–7. doi: 10.1038/nnano.2015.69

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Ghirardini L, Carletti L, Gili V, Pellegrini G, Duò L, Finazzi M, et al. Polarization properties of second-harmonic generation in AlGaAs optical nanoantennas. Opt Lett. (2017) 42:559–62. doi: 10.1364/OL.42.000559

PubMed Abstract | CrossRef Full Text | Google Scholar

41. Gigli C, Marino G, Suffit S, Patriarche G, Beaudoin G, Pantzas K, et al. Polarization- and diffraction-controlled second-harmonic generation from semiconductor metasurfaces. J Opt Soc Am B. (2019) 36:E55–63. doi: 10.1364/JOSAB.36.000E55

CrossRef Full Text | Google Scholar

42. Liu S, Sinclair MB, Saravi S, Keeler GA, Yang Y, Reno J, et al. Resonantly enhanced second-harmonic generation using III-V semiconductor all-dielectric metasurfaces. Nano Lett. (2016) 16:5426–32. doi: 10.1021/acs.nanolett.6b01816

PubMed Abstract | CrossRef Full Text | Google Scholar

43. Carletti L, Marino G, Ghirardini L, Gili VF, Rocco D, Favero I, et al. Nonlinear goniometry by second harmonic generation in AlGaAs nanoantennas. ACS Photon. (2018) 5:4386–92. doi: 10.1021/acsphotonics.8b00810

CrossRef Full Text | Google Scholar

44. Ghirardini L, Marino G, Gili VF, Favero I, Rocco D, Carletti L, et al. Shaping the nonlinear emission pattern of a dielectric nanoantenna by integrated holographic gratings. Nano Lett. (2018) 18:6750–5. doi: 10.1021/acs.nanolett.8b02432

PubMed Abstract | CrossRef Full Text | Google Scholar

45. Sautter JD, Xu L, Miroshnichenko AE, Lysevych M, Volkovskaya I, Smirnova DA, et al. Tailoring second-harmonic emission from (111)-GaAs nanoantennas. Nano Lett. (2019) 19:3905–11. doi: 10.1021/acs.nanolett.9b01112

PubMed Abstract | CrossRef Full Text | Google Scholar