A Deep Learning Approach to Predict Abdominal Aortic Aneurysm Expansion Using Longitudinal Data

An abdominal aortic aneurysm (AAA) is a gradual enlargement of the aorta that can cause a life-threatening event when a rupture occurs. Aneurysmal geometry has been proved to be a critical factor in determining when to surgically treat AAAs, but, it is challenging to predict the patient-specific evolution of an AAA with biomechanical or statistical models. The recent success of deep learning in biomedical engineering shows promise for predictive medicine. However, a deep learning model requires a large dataset, which limits its application to the prediction of the patient-specific AAA expansion. In order to cope with the limited medical follow-up dataset of AAAs, a novel technique combining a physical computational model with a deep learning model is introduced to predict the evolution of AAAs. First, a vascular Growth and Remodeling (G&R) computational model, which is able to capture the variations of actual patient AAA geometries, is employed to generate a limited in silico dataset. Second, the Probabilistic Collocation Method (PCM) is employed to reproduce a large in silico dataset by approximating the G&R simulation outputs. A Deep Belief Network (DBN) is then trained to provide fast predictions of patient-specific AAA expansion, using both in silico data and patients' follow-up data. Follow-up Computer Tomography (CT) scan images from 20 patients are employed to demonstrate the effectiveness and the feasibility of the proposed model. The test results show that the DBN is able to predict the enlargements of AAAs with an average relative error of 3.1%, which outperforms the classical mixed-effect model by 65%.

1. Introduction

The aorta is a major artery in which blood flows through the circulatory system. To consider an enlargement of an aorta as an aneurysm, a relative criterion can be used such as that the enlargement of the aorta is greater than 50% of the normal diameter. On the other hand, an absolute criterion can also be used. For example, in the region of the infrarenal aorta, which lies between the renal branches and the iliac bifurcation, an aorta with maximum diameter greater than 3 cm is considered an Abdominal Aortic Aneurysm (AAA). Because the risk from open surgery or endovascular repair outweighs the risk of AAA rupture, surgical treatments are not recommended with AAAs less than 5.5 cm in diameter [1].

Traditionally, the maximum diameter has been considered a significant risk factor of AAA rupture and has been commonly used as the criterion for screening, surveillance, and intervention decision making. Current clinical practices for diameter measurement methods, however, vary depending on parameters such as plane of acquisition, axis of measurement, position of callipers, and selected diameter [2]. A consensus on the best diameter measurement method has not yet been reached. Recently, a new diameter measurement method, which is called the inscribed sphere method, has been proposed to enhance growth prediction capability by the automatic selection of the maximum diameter using three-dimensional imaging [3]. In this study, the inscribed sphere method is employed to provide a solid foundation for the patient-specific predictions of AAAs.

In recent years, notable advances in statistical tools have been implemented to predict the maximum diameter with longitudinal AAA scanning data. Sweeting and Thompson [4] developed a hierarchical linear growth model utilizing a zero-mean Gaussian distributed random-effects term to simulate the growth effects of aneurysms. Others have used linear and quadratic hierarchical growth models to make predictions of the evolution of aneurysms [5, 6]. Do et al. [7] tested a method of dynamic Gaussian process to predict three-dimensional surface evolution and its uncertainty using patient follow-up images. Nevertheless, due to the limited sample size and large measurement error of longitudinal data from patients, all these statistical predictive tools are not accurate enough to aid in clinical treatment. To cope with this problem, in this paper, a novel predictive tool is designed using a deep learning algorithm, which holds promise for clinical treatment and recommendation.

Deep learning and deep architectures in general have been applied in an enormous number of research areas, with the majority being in computer vision [8] and natural language processing [9]. Deep learning has also been widely applied in risk prediction based on electronic health records [10], image labeling [11], traffic flow prediction [12], image segmentation [13], medical image segmentation [14], stress estimation [15], and many other fields. Deep architecture has been investigated since 1980 [16] and proved to be more effective and requires fewer resources than a shallow structure of the same size, i.e., same number of nodes. The merits of deep structure come from its ability to improve efficiency by distributing different kinds of tasks through different layers [14]. For instance, the low layers can perform low level tasks like gradients computation or edge detection while the higher layers can perform classification or regression. However, as the networks are constructed in deeper layers, the training becomes prohibitively slow due to the problem of “vanishing gradients” [17]. In particular, when the error is back-propagated from the output layer, it is multiplied by the derivatives of the activation function, which is near zero for those saturation nodes. Consequently, the error, as the driving force for the gradient decent algorithm, is dramatically dissipated which results in an extremely slow training rate for those nodes behind the saturated node.

The training problem remained until 2007 when Hinton proposed a two-stage learning scheme based on the Restricted Boltzmann Machine (RBM) [18]. After that, other methods, such as Rectifier Networks [19], drop out technique [20], and Convolutional Neural Network [21] have been further developed and improved to solve the training problem. Research has shown that deep structure yields a high level of generalization and a low test error only when it is trained on a large training set. For instance, LeCun et al. [22] utilized a MNIST [23] dataset of hand-written numbers with 60,000 samples to train a 3-layer deep network. Unfortunately, such a large dataset of longitudinal AAA images is unavailable. Therefore, the applications of deep structure in medical data are limited to medical image segmentation.

The two main contributions of this work are as follows. First, to address the fundamental problem of the limited longitudinal data size, a massive in silico dataset is generated using a physics-based computational model and an approximation algorithm. Second, a novel predictive tool using a deep learning algorithm is established to combine both in silico and measured longitudinal data.

To achieve these contributions, we employ a Deep Belief Network (DBN) to predict the AAA shape in a regression framework. In section 2 of this study, the inscribed sphere method [3] is employed to translate the 3D spatial images of patient AAAs into 2D curves. To cope with the limited dataset, a small in silico dataset is generated by a computational Growth and Remodeling (G&R) model that can simulate the evolutionary process of AAAs. In section 3, the Probability Collocation Method (PCM) is introduced as an approximation method to reproduce a large amount of in silico data based on the G&R simulation outputs, which enables a computationally efficient data generation process. In section 4, inspired by Hinton [18], a two-stage learning scheme is employed to train the DBN. Briefly, the network is first pre-trained with the in silico data by the RBM in an unsupervised manner. The network is then fine-tuned with the labeled patient data. The data processing and model testing results are shown in section 5, which is followed by the discussion and conclusion in section 6. A basic schematic drawing of the overall flow is shown in Figure 1. To the best of our knowledge, this is the first effort to adapt a deep structure coupled with a G&R computational model to predict AAA enlargement.

FIGURE 1

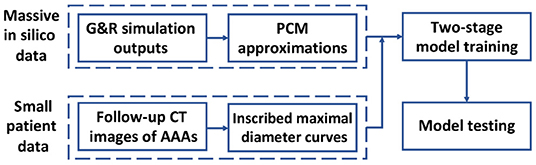
Figure 1. Diagram of overall methodology. A massive number of in silico data and a small number of patient data are generated and processed, respectively, which is followed by a two-stage model training and a model testing.

2. Data

Two kinds of data, including patient data and in silico data, are produced as training data for the predictive model. In particular, we combine a G&R code of AAA and a PCM approximation code to generate massive in silico data to pre-train the deep structure, and compute IMDCs from follow-up CT images of AAAs to fine-tune the deep structure.

2.1. Patient Data

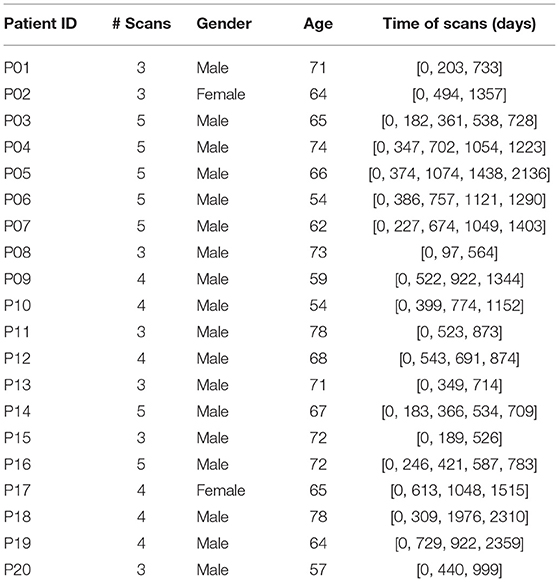
The longitudinal patient dataset is collected from multiple CT images taken from 20 patients at the Seoul National University Hospital. The demography is shown in Table 1. However, patient data cannot be fed into the deep structure directly. We need to transfer the 3D AAA images to shape curves that represent the diameters at different locations on AAAs.

TABLE 1

Table 1. Demographic data of patients.

There are various ways of measuring the maximum diameter of an AAA [24]. In this study, we calculate shape curves of aortas, i.e., Inscribed Maximal Diameter Curves (IMDCs), utilizing an inscribed sphere method from the work of Gharahi et al. [3]. Specifically, the calculation using the inscribed sphere method is initialized with a 3D point cloud of the AAA wall, and a maximally inscribed sphere is defined as the largest sphere within the outer arterial surface. Next, by moving the maximally inscribed sphere from the iliac bifurcation point to the end point at the lowest renal artery, we obtain the centerline of a AAA formed by the spheres' center points.

As a result, the IMDC of an AAA image is obtained. The IMDC incorporates the maximum diameters (d) of the maximally inscribed spheres and the associated centerline (s). Figure 2A provides an example that illustrates five IMDCs from a patient's follow-up CT images. By applying the inscribed sphere method on all patients' longitudinal data of AAAs, we obtain the proper patient data to train the deep structure.

FIGURE 2

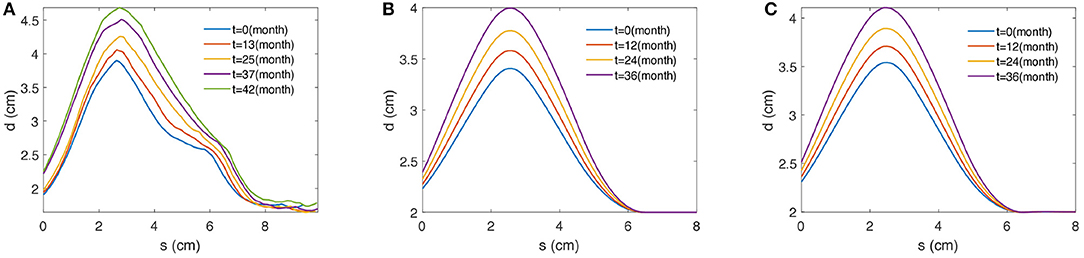
Figure 2. Examples of 2D profile curves of maximal diameters over the centerline obtained from (A) a patient, (B) the G&R computational model, and (C) the PCM approximation. s (cm) defines the length along the centerline of AAA and d (cm) stands for the associated maximal diameter measured by the maximally inscribed sphere method [3].

2.2. In silico Data

2.2.1. Growth and Remodeling Computational Model

We utilize a G&R computational model, which is based on the Finite Element Method (FEM), to generate in silico data to pre-train the deep framework. The G&R model integrates the advanced understanding of the mechanical properties and the stress-mediated adaptation of vascular tissues to capture the long-term changes of geometrical features in AAAs [25–27]. In our G&R simulations, the aortic tissue is considered a mixture of multiple structural constituents, such as elastin and collagen fibers, with different microstructural properties at the reference configuration. Moreover, a Constrained Mixture Method (CMM) is utilized to homogenize multiple constituents in the G&R model to enable FEM simulations. Additionally, in order to capture the long-term adaptation of blood vessels, we assume that constituents continuously generate and degrade in response to the changes of aortic wall stress. Along with the assumption that the elastin degradation initially induces the local dilation of AAA, our G&R code is capable of simulating long term changes of the geometrical features of AAA. The energy form of aortic wall materials and FEM implementation are briefly summarized in Appendix A. The readers refer to Baek et al. [25], Zeinali-Davarani et al. [28], and Farsad et al. [29] for details of the G&R model framework.

Elastin contributes resilience and elasticity to the aortic tissue, but it degenerates over time and is irreplaceable. The degeneration in elastin causes a localized dilation of the aorta, leading to the weakening of the aortic wall as well as the increase of aortic diameter and wall stress. This study utilizes an axisymmetric FEM model to generate in silico data, i.e., a two-dimensional profile curve represented by a set of diameters against the centerline of an AAA [30, 31]. As a result, the damage function can be expressed as the amount of elastin degradation at different spatial locations on the centerline (s), which can be specified by a Gaussian form function:

$\begin{array}{ll}dmg(s)=\text{exp}\left[-\frac{{(s-{\mu }_d)}^2}{2{\sigma }_d^2}\right],& (1)\end{array}$

where μ_d represents the mean of the Gaussian function estimated from image data of each patient; σ_d defines the standard deviation of the Gaussian function, which controls the area of degraded elastin. In particular, σ_d determines the initial loss of elastin, which further affects the stress-stretch and the geometrical state of the AAA, causing various geometrical features of the AAA.

The collagen fiber family is suggested to be an important material in supporting the main aortic wall [32]. It is continuously removed and produced throughout human life, thus changing the mechanical properties of the aorta. Moreover, given the initial degradation of elatin, the aortic wall stress increases, causing a faster accumulation rate of collagen fiber, which plays a compensation role for the loss of elastin. In our G&R computational model, it assumes that the generation rate of collagen fiber changes from its basal value in response to the stress, which is given by

$\begin{array}{ll}{m}^k(t)=\frac{M^c(t)}{M^c(0)}(K_g({\sigma }^k(t)-{\sigma }_h^c)+m_{basal}^k),& (2)\end{array}$

where M^c(t) is mass density at time t; M^c(0) represents the mass density of collagen fiber in a healthy aorta at reference time 0; σ^k(t) is stress on fiber family k at time t; ${\sigma }_h^c$ is the basal value of fiber stress; m^k(t) is the stress-mediated mass production rate; $m_{basal}^k$ is a basal production rate of fiber family k. Here, the parameter K_g controls the magnitude of the stress-mediated mass production rate, so a larger K_g implies that the aorta is able to produce more collagen fiber to maintain the stability of mechanical properties under elastin degeneration. Therefore, K_g plays a decisive role in controlling the self-repairing and evolutionary process of an aneurysm.

Those three parameters {K_g, σ_d, μ_d} directly affect the large time-scale enlargement of the aneurysm; thus, each unique group of the three parameters yields a unique outcome of the axisymmetric G&R code. One example is shown in Figure 2B. All the other parameters used in the G&R code are given by Seyedsalehi et al. [33].

2.2.2. PCM Approximation Model

One common disadvantage of the G&R model is that it is time-consuming. Therefore, it is not the optimal option for generating a massive dataset for the deep structure. In this study, we utilize a PCM method to reproduce a massive dataset by approximating a small dataset from the G&R simulation outputs. The details of the PCM are discussed in section 3 and an example is shown in Figure 2C.

3. Probabilistic Collocation Method

3.1. Deterministic Input

The G&R model takes a group of parameters γ = {K_g, σ_d, μ_d}¹ as input and generates the 2D profile curve y as output.

$\begin{array}{ll}y=\eta (\gamma ),& (3)\end{array}$

where η(.) represents the G&R computational code. Due to the high demand of computational resource and time during the simulation, we shall approximate η(.) by utilizing a set of N basis functions {g_i(γ)}, with i = 1, ⋯ , N, such that

$\begin{array}{ll}ŷ={\displaystyle \sum _{i=0}^N}{\beta }_i{g}_i(\gamma ),& (4)\end{array}$

where N is the order of approximation and β_i are the regression coefficients. Given a set of functions {g_i(γ)}, the regression coefficients {β_i} can be solved as follow.

The residual between the truth and the approximation is defined as

$\begin{array}{ll}R\left(\left\{{\beta }_i\right\},\gamma \right)=ŷ(\gamma )-y(\gamma ).& (5)\end{array}$

By applying the ordinary least squares estimation to (4), the optimal set of coefficients β_i is formulated in

$\begin{array}{ll}\langle g_i(\gamma ),R\left(\left\{{\beta }_i\right\},\gamma \right)\rangle ={\displaystyle {\int }_{\gamma }}{g}_i(\gamma )R\left(\left\{{\beta }_i\right\},\gamma \right)d\gamma =0,& (6)\end{array}$

where i = 1, ⋯ , N and 〈., .〉 represents the dot product between two deterministic functions. (6) can be solved by the idea of Gaussian quadrature [34], which approximates the integral as

$\begin{array}{ll}{\displaystyle {\int }_{\gamma }}R\left(\left\{{\beta }_i\right\},\gamma \right)g_i(\gamma )d\gamma \simeq {\displaystyle \sum _{j=1}^N}{v}_{j}R\left(\left\{{\beta }_i\right\},{\tilde{\gamma }}_j\right)g_i({\tilde{\gamma }}_j)=0,& (7)\end{array}$

where v_j are weights and ${\tilde{\gamma }}_j$ are abscissas, respectively. If the weights and the basis functions are chosen such that ${\prod }_{i,j}{v}_j{g}_i({\tilde{\gamma }}_j)>0$ for all i and j, the summation in (7) can be further approximated as

$\begin{array}{ll}R\left(\left\{{\beta }_i\right\},{\tilde{\gamma }}_j\right)=0,j=0,\cdots ,N.& (8)\end{array}$

Note that the quadrature points ${\tilde{\gamma }}_j$ are also the collocation points. Equation (8) can be used to find the coefficients {β_i} by running the model at N + 1 different collocation points and solving a system of N + 1 equations.

3.2. Stochastic Input

Suppose that the input γ is a random vector with a known probability density function (PDF) π(γ), (6) can be transformed into the probability space as

$\begin{array}{ll}{\displaystyle {\int }_{\gamma }}\pi (\gamma )R\left(\left\{{\beta }_i\right\},\gamma \right)g_i(\gamma )d\gamma =0.& (9)\end{array}$

Similarly, with the proper choice of v_j and g_i(γ), (8) becomes

$\begin{array}{ll}\pi (\gamma )R\left(\left\{{\beta }_i\right\},{\tilde{\gamma }}_j\right)=0,& (10)\end{array}$

where j = 0, ⋯ , N. Since the PDF function π(γ) is always positive, (8) can be used to find the coefficients in the stochastic case.

3.3. Selection of Base Functions and Collocation Points

Theorem 3.1. Consider a quadrature formula:

$\begin{array}{ll}{\displaystyle {\int }_{\gamma }}W(\gamma )F(\gamma )d\gamma \simeq {\displaystyle \sum _{j=1}^N}{w}_{j}F({\gamma }_j),& (11)\end{array}$

where w_j are weights and γ_j are abscissas. Given a weight function W(γ) = γ^α(1 − γ)^β, an optimal choice of N quadrature points can be found based on the correct integration using the highest order of the polynomial expansion of F(γ). The optimal quadrature points are the zeros of the polynomial of degree (N + 1), i.e., P_{N + 1}(γ), that satisfy the orthogonality condition

$\begin{array}{ll}{\displaystyle {\int }_{\gamma }}W(\gamma ){\gamma }^j{P}_{N+1}(\gamma )d\gamma =0,\text{for }j=0,\cdots ,N.& (12)\end{array}$

The detailed proof of Theorem 3.1 is provided in Chap 3 of Villadsen and Michelsen [35]. In short, the choice of collocation points as the roots of the next order orthogonal polynomial lets the collocation method approximation close to Galerkin's method. As a result, it outperforms other methods of weighted residual (MWR) [35].

Corollary 3.2. Consider the same quadrature formula in Theorem 3.1, and a set of N + 1 orthogonal polynomial functions {g_i(γ)}, if the set of functions satisfy the condition

$\begin{array}{ll}{\displaystyle {\int }_{\gamma }}\pi (\gamma )g_i(\gamma )g_{N+1}(\gamma )d\gamma =0,i=1,\cdots ,N,& (13)\end{array}$

they also satisfy condition (12), and the zeros of g_{N + 1}(γ) are the optimal quadrature points.

The proof of Corollary 3.2 is provided in Appendix B. If we choose the weight function to be the PDF of γ, i.e., W(γ) = π(γ), (13) can be used to generate the set {g_i(γ)} in a recursive manner as follows.

In practice, we define the initial conditions

$\begin{array}{l}\begin{array}{l}{g}_{-1}=0,\\ g_0=1,\end{array}\end{array}$

and the orthogonal polynomials can be obtained recursively by solving the equations

$\begin{array}{ll}{\displaystyle {\int }_{\gamma }}\pi (\gamma )g_i(\gamma )g_{i+1}(\gamma )d\gamma =0,i=1,\cdots ,N.& (14)\end{array}$

However, solving for high order polynomials (13) is time-consuming and error-prone. Thus, we use Favard theorem to compute the set of basis functions more efficiently.

Theorem 3.3. (Favard Theorem) If a sequence of polynomials {P_i(γ)}, where i = 1, ⋯ , N, satisfies the recurrence relation

$\begin{array}{l}{P}_i(\gamma )=(\gamma -c_i)P_{i-1}(\gamma )-d_i{P}_{i-2}(\gamma ),\\ \begin{array}{c}{P}_{-1}=0,P_0=1,\end{array}& (15)\end{array}$

where c_i and d_i are real numbers, then {P_i(γ)} are orthogonal polynomials.

In this study, we utilized c_i = 〈γg_{i − 1}, g_{i − 1}〉 and $d_i=\sqrt{\langle g_{i-1},g_{i-1}\rangle }$ by referring the work of [36]. The overall PCM algorithm is shown in Figure 3. Furthermore, though the PCM has been widely used for approximation of univariate prediction target, i.e., y is scalar, in our approach we extend it to be a multivariate approximation.

FIGURE 3

Figure 3. The algorithm of the PCM, which consisting of the computation of collation points (part 1), the realizations of physical-based model at collocation points (part 2), the computation of coefficients (part 3), and the generalization of approximated outputs (part 4).

4. Deep Learning

In this section, we introduce the constructing and training of DBN. A standard structure of the DBN [37] with two layers of RBM [38] is utilized as shown in Figure 4.

FIGURE 4

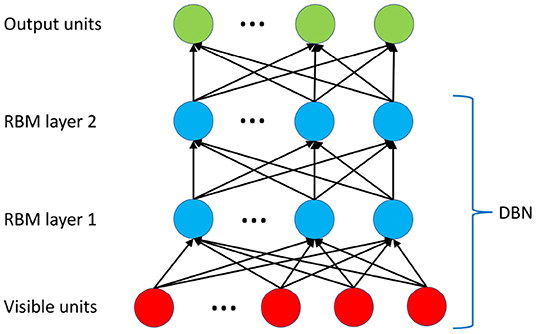
Figure 4. The deep architecture of the DBN. Two layers of RBM are trained in an unsupervised manner (pre-trained) using CD-1 algorithm. The top layer utilizes a neural network sigmoid regression for the prediction.

Assume that we have two types of variables: the visible unit (x) and the hidden unit (h). The two variables are governed by an energy function E(x, h). Given that both visible and hidden units follow binomial distribution, a Boltzmann Machine is defined as an energy-based model using a second-order polynomial [39]

$\begin{array}{l}E(\text{x},\text{h}|\theta )=-{\text{b}}^T\text{x}-{\text{c}}^T\text{h}-{\text{h}}^{T}W\text{x}-{\text{x}}^{T}U\text{x}-{\text{h}}^{T}V\text{h},\end{array}$

where θ is the collection of b, c, W, U, and V. Thus, any probability density function (PDF) of visible layer P(x), as well as joint and conditional PDFs, can be easily represented by a normalized form of the energy function. For instance, the PDF of x can be computed as

$\begin{array}{ll}P(\text{x})={\displaystyle \sum _{\text{h}}}\frac{e^{-E(\text{x},\text{h})}}{Z},& (16)\end{array}$

where $Z=\sum _{\tilde{\text{x}}}\sum _{\text{h}}{e}^{-E(\tilde{\text{x}},\text{h})}$ is the normalization factor and $\tilde{\text{x}}$ can be all possible values of the visible vector x. The realization of $\tilde{\text{x}}$ can be considered as reconstructed visible units.

The parameter θ is estimated using the maximum likelihood estimation. However, the energy-based PDF in this study requires sampling of two conditional probabilities: P(h|x) and P(x, h). Although this can be done via the Markov chain Monte Carlo (MCMC) sampling [40], it is highly computationally expensive. Therefore, contrastive divergence (CD), an alternative way of finding the log-likelihood, is utilized to provide a more efficient solution.

The RBM is introduced by posting an additional restriction: U = 0 and V = 0. In other words, there is no connection between the units in the same layer, either visible or hidden. Note that there is no link among units in the same layer in Figure 4. Furthermore, to incorporate the real-valued values, we specifically assume that the visible units follow Gaussian distribution, i.e., $x_i~{N}(a_i,{\sigma }_i)$, and the hidden units follow binomial distribution, i.e., h_j ∈ {0, 1}. Thus, the modified energy function is defined as [38]

$\begin{array}{ll}\begin{array}{l}E(\text{x},\text{h}|\theta )=-{\displaystyle \sum _{i=1}^{{V}}}\frac{{(x_i-a_i)}^2}{2{\sigma }_i^2}-{\displaystyle \sum _{j=1}^{{H}}}{c}_j{h}_j-{\displaystyle \sum _{i=1}^{{V}}}{\displaystyle \sum _{j=1}^{{H}}}{w}_{ij}\frac{x_i}{{\sigma }_i}{h}_j.\\ \end{array}& (17)\end{array}$

The conditional PDF of the visible units given the hidden units can be computed as

$\begin{array}{l}P(\text{x}|\text{h},\theta )=\frac{e^{-E(\text{x},\text{h}|\theta )}}{{\displaystyle {\sum }_{\text{x}}}{e}^{-E(\text{x},\text{h}|\theta )}}.\end{array}$

Note that P(h|x, θ) can be computed in the same manner. Using E(x, h|θ) in (17), we have

$\begin{array}{ll}\begin{array}{l}P(h_j=1|\text{x},\theta )=\text{sigm }\left({\displaystyle \sum _{i=1}^{{V}}}{w}_{ij}{x}_i+c_j\right),\\ P(x_i=x|\text{h},\theta )={N}\left(a_i+{\sigma }_i{\displaystyle \sum _{j=1}^{{H}}}{h}_j{w}_{ij},{\sigma }_i^2\right),\\ \end{array}& (18)\end{array}$

where $\mathrm{\text{sigm}}(x)=\frac{1}{1+\text{exp}(-x)}$ is the sigmoid function.

The likelihood gradient can be computed by taking the derivative of P(x) in (16) with respect to θ, and we have

$\begin{array}{ll}\begin{array}{l}\frac{\text{log }P(\text{x})}{\partial \theta }\\ =-\frac{1}{{\displaystyle {\sum }_{\text{h}}}{e}^{-E(\text{x},\text{ h})}}{\displaystyle \sum _{\text{h}}}{e}^{-E(\text{x},\text{ h})}\frac{\partial E(\text{x},\text{ h})}{\partial \theta }\\ +\frac{1}{Z}{\displaystyle \sum _{\tilde{\text{x}}}}{\displaystyle \sum _{\text{h}}}{e}^{-E(\tilde{\text{x}},\text{ h})}\frac{\partial E(\tilde{\text{x}},\text{ h})}{\partial \theta }\\ =-{\displaystyle \sum _{\text{h}}}P(\text{h}|\text{x})\frac{\partial E(\text{x},\text{ h})}{\partial \theta }+{\displaystyle \sum _{\tilde{\text{x}}}}{\displaystyle \sum _{\text{h}}}P(\tilde{\text{x}},\text{ h})\frac{\partial E(\tilde{\text{x}},\text{ h})}{\partial \theta }\\ =-{𝔼}_{P(\text{h}|\text{x})}\left[\frac{\partial E(\text{x},\text{ h})}{\partial \theta }\right]+{𝔼}_{P(\tilde{\text{x}},\text{ h})}\left[\frac{\partial E(\tilde{\text{x}},\text{ h})}{\partial \theta }\right].\end{array}& (19)\end{array}$

The expectation 𝔼_P(h|x)[.] is also called positive phase distribution or data distribution while the other expectation ${𝔼}_{P(\tilde{\text{x}},\text{h})}\left[.\right]$ is called negative phase or model distribution [39].

Optimization of (19) involves sampling from $P(\tilde{\text{x}},\text{h})$ and it can be realized by running a Gibbs sampling until it reaches equilibrium, which is extremely time consuming. Alternatively, Hinton [41] suggested the CD learning which minimizes the difference between the data distribution and the one-step reconstructed distribution rather than directly minimizing the difference between the data and the model distribution. The approximation of (19) and its derivation using CD are provided in Appendix C. Empirical studies have shown that the CD method is efficient and effective enough to make the DBN unsupervised learning practical.

Given the approximation to the derivative of P(x), we can pre-train the DBN by updating the weights iteratively using the in silico data in an unsupervised manner. The training is performed throughout the DBN structure shown in Figure 4. We consider this step, i.e., the pre-training of the DBN, as the first step of the two-stage learning scheme, enabling the DBN to capture the changes of geometrical features simulated by the G&R of AAA expansion.

After the pre-training, the DBN is unfolded into a Neural Network (NN), which is further trained in a supervised manner. This supervised learning, i.e., fine-tuning, is considered the second step of the two-stage learning scheme. Specifically, during the fine-tuning, the pre-trained weights of the unfolded DBN are properly adjusted for a better ability in capturing patient-specific features of aortic enlargement from the patient data.

Our proposed two-step training model could be interpreted as a deep learning version of the Bayesian approach, where computer-generated data act as a prior distribution and the patient data for fine-tuning can be viewed as new measurements to compute the posteriori distribution for prediction [42–44]. We also would like to remind that the Bayesian approach is normally used for prediction with the limited sized data (by leveraging the prior distribution), which is well suited for our case.

5. Data Processing and Results

In this section, we introduce the data processing step and demonstrate the effectiveness of our proposed predictive model using observations of patient-specific CT images.

5.1. Data Processing

Given CT images of AAAs taken from a patient, we can obtain IMDCs with regular time intervals. Let f_t,i be an IMDC of the ith AAA obtained at certain scan time noted as t. A collection of f generated at different times, i.e., t − 2, t − 1, t, and t + 1, provides us a timeline growth of the AAA. Note that the time intervals between IMDCs are fixed as the same constant. For each data point, we choose the feature vector x_i as the collection of the three adjacent IMDCs, and the prediction target y_i as the IMDC at the next time step in the future,

$\begin{array}{l}\begin{array}{l}{x}_i=\left[f_{t-2,i},f_{t-1,i},f_{t,i}\right],\\ y_i=f_{t+1,i}.\end{array}\end{array}$

Following Table 1, however, we realize that the time intervals between patient follow-up CT scans are not constants. To address this problem, a fixed-time interval of 270 days is chosen and all patient data are linearly interpolated by this fixed-time interval. Generally, we obtain 55 sets of interpolated patient data as collections of {x_i, y_i} from 20 patients. Specifically, 6 sets of the patient data from 6 different patients are randomly selected as testing data while the others are employed for pre-training.

Given the multiple sets of G&R input parameters γ = [K_g, σ_d, μ_d], the G&R model associated with the PCM approximation can produce a large number of longitudinal 2D profile curves to capture the enlargement of AAAs during a time span, which can be transformed into the in silico data, i.e., artificially generated collections of {x_i, y_i}. In this study, we focus on predicting the aneurysm growth; hence, only those in silico data with maximum diameters ranging from 3 to 8.5 cm are accepted into the training dataset. After random samplings and rejections, 32,900 sets of in silico data {x_i, y_i} are collected in the training dataset.

In order to assimilate patient data and in silico data together with the same dimensionality of data, we trim all both patient data and in silico data into regions where the coordinate along the centerline ranges 0 to 8 cm. Next, each shape curve is discretized by a grid size of 81, meaning that the dimension of x_i and y_i are 243 and 81, respectively. Additionally, it has been shown that it is much simpler to train the RBM by the data with a zero mean and unit variance [38]. Thus, we normalize the training data before training the deep learning model. Specifically, a scale factor of 8.5 cm is selected for the normalization, based on the fact that the largest diameters of all our patient data are significantly smaller than 8.5 cm (also immediately recommended for surgical options [5]). As a result, all diameters obtained from both the patient data and the simulated results are normalized into the range [0, 1] before the training.

As described in section 4, the 32,900 sets of normalized in silico data are utilized to pre-train the DBN in an unsupervised manner. Next, the selected patient data are employed to further update the deep structure in a supervised manner. Finally, during the model testing, we can collect the predicted IMDCs, which are then transformed back to the normal scale as the final prediction results. The overall method is depicted in Figure 5.

FIGURE 5

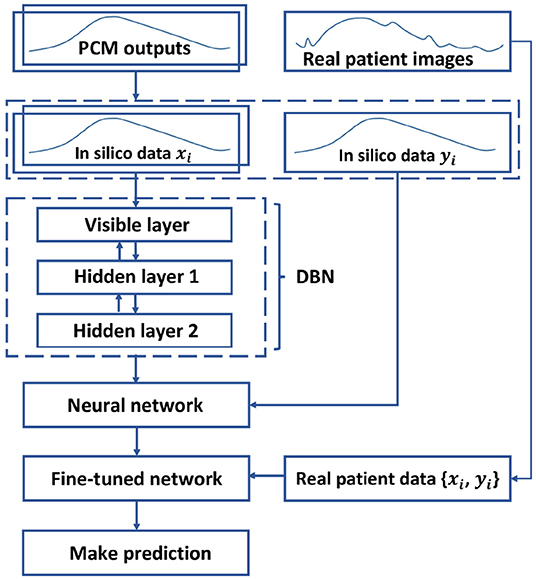
Figure 5. Diagram of the model training. The DBN is pre-trained by in silico data in an unsupervised manner, and is unfolded into a neural network. Next, the neural network is fine-tuned with the patient data in a supervised manner to predict the AAA expansion.

5.2. Test Set-Up

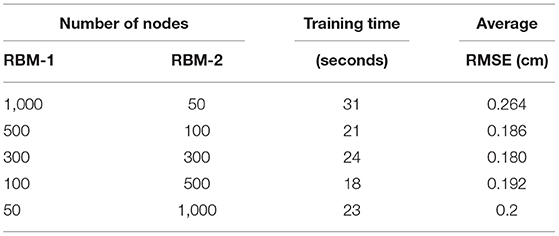
For a deep structure, parameters, such as the number of hidden units and the number of epochs², are important factors in determining the model performance. To avoid over-fitting, as a rule of thumb for the generative models using the high-dimensional data, the number of parameters is constrained [38]. In our case, the data dimensionality (243) is significantly lower than the size of training samples (32,900). In order to test the effect of the number of nodes within each layer, we construct a number of 2-layer DBNs with different sets of hidden nodes in each layer. In particular, since there is a remarkable difference in the dimensions of the data and the label, i.e., 243 vs. 81, we test the DBNs of three structures: increasing width, decreasing width and equal width. As shown in Table 2, as the number of input or output layer nodes decreases, it becomes harder for the model to capture the representative features in the data. Note that in Table 2, the prediction error is quantified by the discrepancy between the predicted IMDC and the patient IMDC using the standard root mean squared error (RMSE), and the average RMSE is calculated from of 6 test samples. We then conclude from the test set-up that 300 nodes in each layer leads to the smallest prediction error among all tested configurations.

TABLE 2

Table 2. Effect of the number of nodes in a 2-layer DBN on the model testing.

As aforementioned, one of the problems in the DBN approach is that the pre-training generates a large in silico dataset (32,900 samples), while the patient data for fine-tuning are limited (49 samples). To better employ both datasets, we fix the epoch of the pre-training process to be 1 while changing the number of epochs of the fine-tuning process. The RMSE and training time for different epochs (ranged from 1 to 1,000) is shown in Figure 6. As the number of epochs reaches 400, the error is not reduced any more as the model-fitting shows the over-fitting of the fine-tuning data and eventually the generalization capacity is reduced.

FIGURE 6

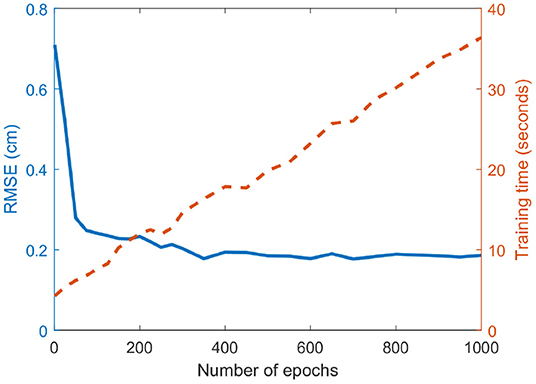
Figure 6. Effect of the number of epochs on the prediction error. The RMSE and the fine-tuning training time are plotted in solid blue and dashed red lines, respectively. The training time increases linearly with the number of epochs, while the RMSE rapidly decreases at the beginning but converges at around 400 epochs.

5.2.1. Mixed-Effect Model

The performance of our proposed method is compared to the nonlinear mixed-effects model, which has been used extensively as a powerful growth hierarchical model over the decades [4–6]. For the mixed-effects model, a basic form of the growth function is selected as:

$\begin{array}{l}{y}_{i,j}={\alpha }_0+({\alpha }_1+b_1)t_{i,j}+({\alpha }_2+b_2)t_{i,j}^2+{ϵ}_{i,j},\end{array}$

where y_i,j and t_i,j are the diameter and the associated time at the jth measurement of ith patient, b = [b₁, b₂] is the random-effects terms and $\text{b}~{N}(0,{\Sigma }_b)$, α = [α₀, ⋯ , α₂] is the parameters vector, and ϵ_i,j is the independent error term, i.e., ${ϵ}_{i,j}~{N}(0,{\sigma }_w^2)$. b and α are fitted to the data via the fminsearch function in MATLAB.

5.3. Test Prediction Results

As it is shown in Table 2, a DBN with 300 nodes in both layers is selected for model testing. The absolute prediction error and relative prediction error for selected samples are shown in Table 3, and are compared with those from a mixed-effect model. A comparison of prediction results is shown in Figure 7. The proposed method outperforms the mix-effects method with a 65% reduction in RMSE. The overall prediction is relatively accurate because the relative error of each prediction only ranges from 2.3% to 4.3%, which is negligible.

TABLE 3

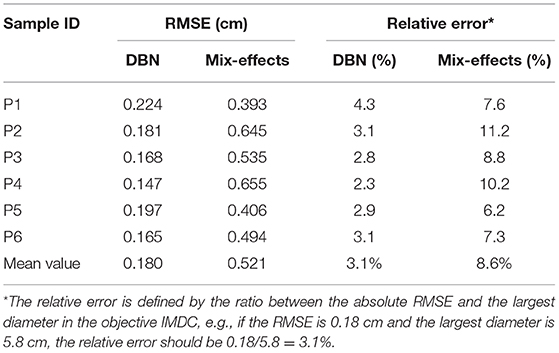
Table 3. The absolute and relative prediction errors of 6 testing samples under DBN and Mix-effects model.

FIGURE 7

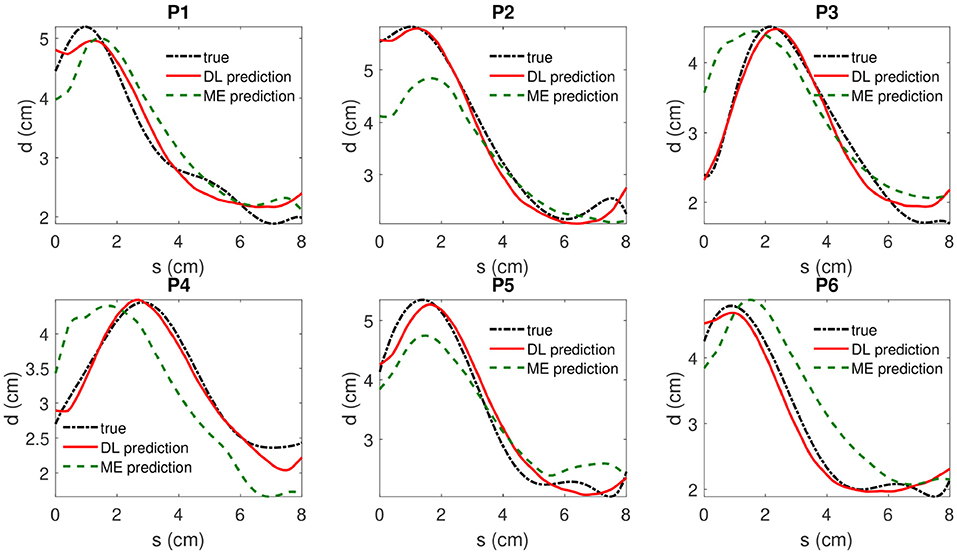
Figure 7. The true value, the DBN model prediction and mixed-effects model prediction of IMDCs are shown in dotted dashed black (“true”), solid red(“DL prediction”), and dashed green lines(“ME prediction”), respectively. s denotes the coordinate of location along the centerline of AAA and d represents the associated maximum diameter measured by inscribed sphere method.

The deep learning model, which is implemented on the MATLAB, can be trained within 30 s on a PC with a 3.3 GHz 10-core CPU and a 64 GB RAM (Table 2). This period of time is short enough to provide insight in aiding clinicians to make surgical decision of AAAs.

5.4. Monte-Carlo Cross-Validation

A Monte-Carlo cross-validation method is performed to show the robustness of the proposed deep learning model. As the first step, 13 sets of eligible testing data, i.e., {x_i, y_i}, are collected from 20 patients' CT images. There are two criteria for choosing eligible data from a patient. The first criterion is that the eligible {x_i, y_i} should be the last set of data of the patient. The second criterion is that the number of raw CT images of the patient is at least four. As the second step, the cross-validation trials are independently performed 100 times under the deep structure of 2-layers DBN with 300 nodes on each layer. In each trial, we randomly choose 3 sets of test data out of the whole eligible dataset and leave the other sets of eligible data as training data to be used in the fine-tuning step. As a result of the Monte-Carlo cross-validation, 100 prediction errors (RMSEs) are independently collected, of which the mean and the standard deviation are 0.196 cm and 0.051 cm. The standard deviation is so small relative to the mean that it guarantees the robustness of the proposed method. Moreover, as a comparison, the average testing RMSE (0.18 cm) falls into the range of the standard deviation of the cross-validation result, thus supporting the test results shown in Table 3.

6. Discussion and Conclusion

This study utilized a physical G&R computational model combined with follow-up image data from 20 patients to predict the shape evolution of AAAs represented by IMDCs. To our knowledge, this is the first study that utilizes the deep learning technique to predict the shapes of AAAs in an evolutionary scheme based on a small dataset of follow-up images. The main difficulty in applying deep learning to predict AAA enlargement is the limited size of the training dataset, i.e., follow-up images of AAAs. In this study, we overcame this difficulty by proposing a work-flow, in which the DBN is pre-trained by massive in silico data. The accurate predictions demonstrate that deep learning holds promise for capturing evolutionary features of individual soft tissue with numerical simulations. It gives deep learning techniques a new application in biomedical engineering, other than surrogates [15], image segmentation [14], etc.

Besides combining deep learning and AAA prediction, the proposed study also contributes by making fast and accurate predictions of AAA enlargement. Following Table 2, the model training time takes approximately 24 s, which is significantly faster than other statistical models [7, 30]. Additionally, the efficiency of data generation is significantly improved by the PCM approximation, which generates tens of thousands of IMDCs in 20 s. As a comparison, the G&R computational model takes 30 min to generate one set of data, meaning that it would take more than 1 year to provide the same amount of training data.

Additionally, due to the high complexity of physics in patient-specific predictions of AAA, even high-fidelity physical models cannot promise to make accurate predictions. To enable accurate predictions, in this paper, we proposed a two-stage training approach: first, we pre-train our deep learning model with a computationally generated sizable dataset; second, we fine-tune the deep structure with the patient data for patient-specific predictions. In this study, the average prediction error is 0.180 cm, which is significantly small compared to the AAA diameters (3–8.5 cm). The results shown in Figure 7 and Table 3 also indicate that the proposed method indeed provides effective predictions, which outperform the classical mixed-effect model [4–6] by 65% in terms of the average relative error. Also, a Monte-Carlo cross-validation, which is a standard and widely recognized validating approach commonly used in machine learning studies, also provides similar prediction results compared with the test results, thus showing the effectiveness and robustness of the proposed study. Therefore, although the in silico data are limited by the G&R which cannot capture all marginal situations, the two-stage DBN method still shows its promise in predicting patient-specific geometries.

In our previous paper [7], we proposed a patient-specific prediction method using Kalman filter, which has been widely used for time series analysis. However, Do et al. was not capable of capturing the patient-specific characteristics since it is only based on individual shape of AAAs. As a time-series approach, the prediction cannot be improved by adding more datasets as a prior for pre-training. To cope with these problems, in this study, we proposed the DBN-based framework for patient-specific predictions that successfully tackled these limitations. In Zhang et al. [30], a Bayesian model are employed to predict AAA enlargement. This model, however, did not use massive in silico data and multiple patient data together for training, so restricting their predictive effects. In contrast, our proposed DBN is efficiently trained by a large amount of data, meaning that it can generate more effective predictions.

The maximum diameter, the largest value in an IMDC, is one of the most important factors to help decide whether to perform surgery or not in clinical practice, e.g., performing surgery if the maximum diameter is larger than 5.5 cm [45]. Figure 7 shows that the deep learning algorithm is able to predict the maximum diameter with negligible error. Moreover, the predicted IMDCs, which represent the 2D profile shapes of AAAs, are close to those of real cases. The DBN code successfully captured different patient-specific AAA shapes with negligible error on the boundary sections. Therefore, our study shows strong evidence that the proposed algorithm is feasible to be applied in clinical practice.

Additionally, we also utilized another method, i.e., the drop out technique from Hinton et al. [20], to further improve the prediction of the DBN code. However, it did not show a significant increase of the accuracy for the prediction outputs, partly because of the simple 2-layer network, which was employed to avoid over-fitting.

There are also limitations in this study. The first limitation is that because the patient-specific IMDCs are 2D profile curves, we choose to generate the simulation data using a simple axisymmetric G&R model which also gives 2D profile curves. The use of an the axisymmetric G&R model is acceptable because it can predict reasonable patient-specific growth of AAAs under normal conditions, but it cannot capture the special features caused by aortic bending, such as proximal neck bend. Fortunately, the bending has little effect on the center parts of AAA and the simulation of maximum diameter, so it does not affect the key prediction results. In the future, 2D profile curves can be replaced with 3D patient-specific geometries in order to provide more accurate patient-specific predictions.

The second limitation is that the G&R code does not take other factors into account, such as hemodynamics, thrombus and surrounding tissues [46–51], which may also contribute to the patient-specific AAA expansion. For example, Zambrano et al. [50] has illustrated that there exist mutual effects among hemodynamics forces, intraluminal thrombus and the expansion rate of AAA. However, in this study, the G&R was only responsible for providing in silico data for the pre-training. And the G&R is fully competent in capturing those geometrical features by simulating stress-mediated expansions [25–28]. Meanwhile, other confounding factors, such as aortic flow, thrombus, and surrounding tissues, are probably considered as patient-specific features that are captured during the second step of the learning, i.e., fine-tuning, using patient data. Additionally, due to the relatively simple structure of the G&R code, it is highly efficient to provide a large number of in silico training data, which is essential for training a deep structure. Otherwise, it may take days or even weeks to perform one simulation with more biomechanical factors included; thus inhibiting its integration to deep learning.

The third limitation is that we have to interpolate patient CT images into the in silico training data with constant time intervals to train and test the model, which may restrict the applications of the proposed method. We plan to solve this problem by introducing additional data points or more complex data structure to represent the patient-specific time gap between CT scans.

In the future, we expect to further enrich the variability of the training data by improving the physical models or collecting more patient data to incorporate the marginal situations. Specifically, we generate a large amount of data by varying three parameters in the computational G&R simulations, which may not be enough to capture all the different features in actual AAA evolution, e.g., intraluminal thrombus [50, 52, 53], other morphological parameters [54, 55], and influence of surrounding tissues [56, 57]. Hence, more parameters and more complex models will be carefully selected in the future to provide better simulation-based training data. Furthermore, considering the importance of hemodynamics, we would like to replace our G&R model by a Fluid-Solid-Growth model which is capable of capturing the geometrical change of AAAs caused by both wall stress and hemodynamics [58]. Based on that, the in silicon data can incorporate information of AAA expansion caused by hemodynamics, thus increasing the effectiveness of pre-training. Additionally, given a larger set of training data, we can further increase the number of layers in the DBN and test for better predictions.

Data Availability Statement

The datasets generated for this study are available on request to the corresponding author.

Ethics Statement

The studies involving human participants were reviewed and approved by the Institutional Review Boards at Seoul National University Hospital and at Michigan State University. Written informed consent for participation was not required for this study in accordance with the national legislation and the institutional requirements because the data was collected for a retrospective study.

Author Contributions

SB and JC designed the probabilistic model and the deep learning framework. ZJ and HD carried out the implementation and calculation. ZJ and HD wrote the manuscript with input from all authors. SB, JC, and WL conceived the study and were in charge of overall direction and planning.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

This work has been supported in part by the National Heart, Lung, and Blood Institute of the National Institutes of Health (R01HL115185 and R21HL113857), National Science Foundation CAREER Award (CMMI-1150376), the National Research Foundation of Korea (NRF) grant funded by the Korea government (MSIT) (2018R1A4A1025986) and the Vietnam Education Foundation. The content is solely the responsibility of the authors and does not necessarily represent the official views of the NIH. Note that this study includes the content which first appeared in the dissertation from one of the authors [59].

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2019.00235/full#supplementary-material

Footnotes

1. ^For the sake of notational simplicity, we also denote {K_g, σ_d, μ_d} as {γ^[1], γ^[2], γ^[3]}.

2. ^Epochs are the number of times that the model is trained through the whole training set.

References

1. Paraskevas KI, Mikhailidis DP, Andrikopoulos V, Bessias N, Bell SPRF. Should the size threshold for elective abdominal aortic aneurysm repair be lowered in the endovascular era? Yes. Angiology. (2010) 61:617–9. doi: 10.1177/0003319710375084

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Long A, Rouet L, Lindholt JS, Allaire E. Measuring the maximum diameter of native abdominal aortic aneurysms: review and critical analysis. Eur J Vasc Endovasc Surg. (2012) 43:515–24. doi: 10.1016/j.ejvs.2012.01.018

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Gharahi H, Zambrano BA, Lim C, Choi J, Lee W, Baek S. On growth measurements of abdominal aortic aneurysms using maximally inscribed spheres. Med Eng Phys. (2015) 37:683–91. doi: 10.1016/j.medengphy.2015.04.011

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Sweeting MJ, Thompson SG. Making predictions from complex longitudinal data, with application to planning monitoring intervals in a national screening programme. J R Stat Soc Ser A (Stat Soc). (2012) 175:569–86. doi: 10.1111/j.1467-985X.2011.01005.x

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Brady AR, Thompson SG, Fowkes FGR, Greenhalgh RM, Powell JT, et al. Abdominal aortic aneurysm expansion risk factors and time intervals for surveillance. Circulation. (2004) 110:16–21. doi: 10.1161/01.CIR.0000133279.07468.9F

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Eriksson P, Jormsjö-Pettersson S, Brady AR, Deguchi H, Hamsten A, Powell JT. Genotype–phenotype relationships in an investigation of the role of proteases in abdominal aortic aneurysm expansion. Brit J Surg. (2005) 92:1372–6. doi: 10.1002/bjs.5126

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Do HN, Ijaz A, Gharahi H, Zambrano B, Choi J, Lee W, et al. Prediction of abdominal aortic aneurysm growth using dynamical Gaussian process implicit surface. IEEE Trans Biomed Eng. (2019) 66:609–22. doi: 10.1109/TBME.2018.2852306

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Memisevic R, Hinton GE. Unsupervised learning of image transformations. In: 2007 IEEE Conference on Computer Vision and Pattern Recognition. Minneapolis, MN: IEEE (2007). p. 1–8. doi: 10.1109/CVPR.2007.383036

CrossRef Full Text | Google Scholar

9. Collobert R, Weston J. A unified architecture for natural language processing: deep neural networks with multitask learning. In: Proceedings of the 25th international conference on Machine learning. Helsinki: ACM (2008). p. 160–7. doi: 10.1145/1390156.1390177

CrossRef Full Text | Google Scholar

10. Cheng Y, Wang F, Zhang P, Hu J. Risk prediction with electronic health records: a deep learning approach. In: Proceedings of the 2016 SIAM International Conference on Data Mining Miami, FL (2016). doi: 10.1137/1.9781611974348.49

CrossRef Full Text | Google Scholar

11. He X, Zemel RS, Carreira-Perpiñán MÁ. Multiscale conditional random fields for image labeling. In: Computer Vision and Pattern Recognition, 2004. CVPR 2004. Proceedings of the 2004 IEEE computer society conference on. Vol. 2. Washington, DC: IEEE (2004). p. II–695.

Google Scholar

12. Huang W, Song G, Hong H, Xie K. Deep architecture for traffic flow prediction: deep belief networks with multitask learning. IEEE Trans Intell Transport Syst. (2014) 15:2191–201. doi: 10.1109/TITS.2014.2311123

CrossRef Full Text | Google Scholar

13. Long J, Shelhamer E, Darrell T. Fully convolutional networks for semantic segmentation. In: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA (2015). p. 3431–40. doi: 10.1109/CVPR.2015.7298965

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Lai M. Deep learning for medical image segmentation. arXiv:150502000 (2015).

Google Scholar

15. Liang L, Liu M, Martin C, Sun W. A deep learning approach to estimate stress distribution: a fast and accurate surrogate of finite-element analysis. J R Soc Interface. (2018) 1:15. doi: 10.1098/rsif.2017.0844

CrossRef Full Text | Google Scholar

16. Fukushima K. Neocognitron: a self-organizing neural network model for a mechanism of pattern recognition unaffected by shift in position. Biol Cybernet. (1980) 36:193–202. doi: 10.1007/BF00344251

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Bengio Y, Simard P, Frasconi P. Learning long-term dependencies with gradient descent is difficult. IEEE Trans Neural Netw. (1994) 5:157–66. doi: 10.1109/72.279181

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Hinton GE. Learning multiple layers of representation. Trends Cogn Sci. (2007) 11:428–34. doi: 10.1016/j.tics.2007.09.004

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Glorot X, Bordes A, Bengio Y. Deep sparse rectifier neural networks. In: Proceedings of the Fourteenth International Conference on Artificial Intelligence and Statistics, Fort Lauderdale, FL (2011).

Google Scholar

20. Hinton GE, Srivastava N, Krizhevsky A, Sutskever I, Salakhutdinov RR. Improving neural networks by preventing co-adaptation of feature detectors. CoRR. abs/1207.0580 (2012). Available online at: http://arxiv.org/abs/1207.0580

Google Scholar

21. Meng F, Lu Z, Wang M, Li H, Jiang W, Liu Q. Encoding source language with convolutional neural network for machine translation. In: Proceedings of the 53rd Annual Meeting of the Association for Computational Linguistics and the 7th International Joint Conference on Natural Language Processing (Volume 1: Long Papers). Beijing: Association for Computational Linguistics (2015). p. 20–30. Available online at: https://www.aclweb.org/anthology/P15-1003

Google Scholar

22. LeCun Y, Bottou L, Bengio Y, Haffner P. Gradient-based learning applied to document recognition. Proc IEEE. (1998) 86:2278–324. doi: 10.1109/5.726791

CrossRef Full Text | Google Scholar

23. LeCun Y, Cortes C, Burges CJ. The MNIST database of handwritten digits, New York, NY (1998). Available online at: http://yann.lecun.com/exdb/mnist/

Google Scholar

24. Kontopodis N, Metaxa E, Gionis MN, Papaharilaou Y, Ioannou CV. Discrepancies in determination of abdominal aortic aneurysms maximum diameter and growth rate, using axial and orhtogonal computed tomography measurements. Eur J Radiol. (2013) 82:1398–403. doi: 10.1016/j.ejrad.2013.04.031

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Baek S, Rajagopal KR, Humphrey JD. A theoretical model of enlarging intracranial fusiform aneurysms. Trans ASME J Biomech Eng. (2006) 128:142. doi: 10.1115/1.2132374

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Watton P, Hill N. Evolving mechanical properties of a model of abdominal aortic aneurysm. Biomech Model Mechanobiol. (2008) 8:25–42. doi: 10.1007/s10237-007-0115-9

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Volokh K, Vorp D. A model of growth and rupture of abdominal aortic aneurysm. J Biomech. (2008) 41:1015–21. doi: 10.1016/j.jbiomech.2007.12.014

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Zeinali-Davarani S, Sheidaei A, Baek S. A finite element model of stress-mediated vascular adaptation: application to abdominal aortic aneurysms. Comput Methods Biomech Biomed Eng. (2011) 14:803–17. doi: 10.1080/10255842.2010.495344

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Farsad M, Zeinali-Davarani S, Choi J, Baek S. Computational growth and remodeling of abdominal aortic aneurysms constrained by the spine. J Biomech Eng. (2015) 137:091008. doi: 10.1115/1.4031019

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Zhang L, Jiang Z, Choi J, Lim CY, Maiti T, Baek S. Patient-specific prediction of abdominal aortic aneurysm expansion using Bayesian calibration. IEEE J Biomed Health Inform. 23:2537–50. doi: 10.1109/JBHI.2019.2896034

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Kwon ST, Rectenwald JE, Baek S. Intrasac pressure changes and vascular remodeling after endovascular repair of abdominal aortic aneurysms: review and biomechanical model simulation. J Biomech Eng. (2011) 133:011011. doi: 10.1115/1.4003134

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Choke E, Cockerill G, Wilson WRW, Sayed S, Dawson J, Loftus I, et al. A review of biological factors implicated in abdominal aortic aneurysm rupture. Eur J Vasc Endovasc Surg. (2005) 30:227–44. doi: 10.1016/j.ejvs.2005.03.009

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Seyedsalehi S, Zhang L, Choi J, Baek S. Prior distributions of material parameters for Bayesian calibration of growth and remodeling computational model of abdominal aortic wall. J Biomech Eng. (2015) 137:101001. doi: 10.1115/1.4031116

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Stroud AH, Secrest D. Gaussian quadrature formula. Math Comput. (1966) 21:125–126. doi: 10.2307/2003493

CrossRef Full Text | Google Scholar

35. Villadsen J, Michelsen ML. Solution of Differential Equation Models by Polynomial Approximation. vol. 7. Englewood Cliffs, NJ: Prentice-Hall (1978).

Google Scholar

36. Zhou Y, Wan Y, Roy S, Taylor C, Wanke CR, Ramamurthy D, et al. Multivariate probabilistic collocation method for effective uncertainty evaluation with application to air traffic flow management. IEEE Trans Syst Man Cybernet. (2014) 44:1347–63. doi: 10.1109/TSMC.2014.2310712

CrossRef Full Text | Google Scholar

37. Hinton GE, Osindero S, Teh YW. A fast learning algorithm for deep belief nets. Neural Comput. (2006) 18:1527–54. doi: 10.1162/neco.2006.18.7.1527

PubMed Abstract | CrossRef Full Text | Google Scholar

38. Hinton GE. A practical guide to training restricted Boltzmann machines. Momentum. (2010) 9:926.

Google Scholar

39. Bengio Y. Learning deep architectures for AI. Found Trends Mach Learn. (2009) 2:1–127. doi: 10.1561/2200000006

CrossRef Full Text | Google Scholar

40. Hinton GE, Sejnowski TJ, Ackley DH. Boltzmann Machines: Constraint Satisfaction Networks That Learn. Pittsburgh, PA: Carnegie-Mellon University, Department of Computer Science (1984).

Google Scholar

41. Hinton GE. Training products of experts by minimizing contrastive divergence. Neural Comput. (2002) 14:1771–800. doi: 10.1162/089976602760128018

PubMed Abstract | CrossRef Full Text | Google Scholar

42. Neal RM. Priors for infinite networks. In: Bayesian Learning for Neural Networks. Lecture Notes in Statistics, Vol. 118. New York, NY: Springer (1996).

Google Scholar

43. Williams CKI. Computing with infinite networks. In: Proceedings of the 9th International Conference on Neural Information Processing Systems. NIPS'96. Cambridge, MA: MIT Press (1996). p. 295–301. Available online at: http://dl.acm.org/citation.cfm?id=2998981.2999023

Google Scholar

44. Lee J, Bahri Y, Novak R, Schoenholz S, Pennington J, Sohl-Dickstein J. Deep neural networks as Gaussian processes. arXiv: 1711.00165 (2017).

Google Scholar

45. Budtz-Lilly J, Venermo M, Debus S, Behrendt CA, Altreuther M, Beiles B, et al. Assessment of international outcomes of intact abdominal aortic aneurysm repair over 9 years. Eur J Vasc Endovasc Surg. (2017) 54:13–20. doi: 10.1016/j.ejvs.2017.03.003

PubMed Abstract | CrossRef Full Text | Google Scholar

46. Dua M, Dalman R. Hemodynamic influences on abdominal aortic aneurysm disease: application of biomechanics to aneurysm pathophysiology. Vasc Pharmacol. (2010) 53:11–21. doi: 10.1016/j.vph.2010.03.004

PubMed Abstract | CrossRef Full Text | Google Scholar

47. Sheidaei A, Hunley S, Zeinali-Davarani S, Raguin L, Baek S. Simulation of abdominal aortic aneurysm growth with updating hemodynamic loads using a realistic geometry. Med Eng Phys. (2010) 33:80–8. doi: 10.1016/j.medengphy.2010.09.012

PubMed Abstract | CrossRef Full Text | Google Scholar

48. Arzani A, Suh GY, Dalman R, Shadden S. A longitudinal comparison of hemodynamics and intraluminal thrombus deposition in abdominal aortic aneurysms. Am J Physiol Heart Circul Physiol. (2014) 10:307. doi: 10.1152/ajpheart.00461.2014

CrossRef Full Text | Google Scholar

49. Poelma C, Watton P, Ventikos Y. Transitional flow in aneurysms and the computation of haemodynamic parameters. J R Soc Interface R Soc. (2015) 4:12. doi: 10.1098/rsif.2014.1394

CrossRef Full Text | Google Scholar

50. Zambrano BA, Gharahi H, Lim C, Jaberi FA, Choi J, Lee W, et al. Association of intraluminal thrombus, hemodynamic forces, and abdominal aortic aneurysm expansion using longitudinal CT images. Ann Biomed Eng. (2016) 44:1502–14. doi: 10.1007/s10439-015-1461-x

PubMed Abstract | CrossRef Full Text | Google Scholar

51. Salman H, Ramazanli B, Yavuz M, Yalcin H. Biomechanical investigation of disturbed hemodynamics-induced tissue degeneration in abdominal aortic aneurysms using computational and experimental techniques. Front Bioeng Biotechnol. (2019) 7:111. doi: 10.3389/fbioe.2019.00111

PubMed Abstract | CrossRef Full Text | Google Scholar

52. Piechota-Polanczyk A, Jozkowicz A, Nowak W, Eilenberg WH, Neumayer C, Malinski T, et al. The abdominal aortic aneurysm and intraluminal thrombus: current concepts of development and treatment. Front Cardiovasc Med. (2015) 2:19. doi: 10.3389/fcvm.2015.00019

PubMed Abstract | CrossRef Full Text | Google Scholar

53. Martufi G, Lindquist Liljeqvist M, Sakalihasan N, Panuccio G, Hultgren R, Roy J, et al. Local diameter, wall stress, and thrombus thickness influence the local growth of abdominal aortic aneurysms. J Endovasc Ther. (2016) 23:957–66. doi: 10.1177/1526602816657086

PubMed Abstract | CrossRef Full Text | Google Scholar

54. Pappu S, Dardik A, Tagare H, Gusberg RJ. Beyond fusiform and saccular: a Novel Quantitative Tortuosity Index May Help Classify Aneurysm Shape and Predict Aneurysm Rupture Potential. Ann Vasc Surg. (2008) 22:88–97. doi: 10.1016/j.avsg.2007.09.004

PubMed Abstract | CrossRef Full Text | Google Scholar

55. Raut SS, Chandra S, Shum J, Finol EA. The role of geometric and biomechanical factors in abdominal aortic aneurysm rupture risk assessment. Ann Biomed Eng. (2013) 41:1459–77. doi: 10.1007/s10439-013-0786-6

PubMed Abstract | CrossRef Full Text | Google Scholar

56. Kwon ST, Burek W, Dupay AC, Farsad M, Park EA, Lee W, et al. Interaction of expanding abdominal aortic aneurysm with surrounding tissue: Retrospective CT image studies. J Nat Sci. (2015) 1:e150. Available online at: www.jnsci.org/content/150

PubMed Abstract | Google Scholar

57. Nguyen TT, Le NT, Doan QH. Chronic contained abdominal aortic aneurysm rupture causing vertebral erosion. Asian Cardiovasc Thoracic Ann. (2019) 27:33–5. doi: 10.1177/0218492318773237

PubMed Abstract | CrossRef Full Text | Google Scholar

58. Figueroa C, Baek S, Taylor C, Humphrey J. A computational framework for fluid-solid-growth modeling in cardiovascular simulations. Comput Methods Appl Mech Eng. (2009) 198:3583–602. doi: 10.1016/j.cma.2008.09.013

PubMed Abstract | CrossRef Full Text | Google Scholar

59. Do HN. Predictive Models for Robotics and Biomedical Applications. East Lansing, MI: Michigan State University (2017).

Google Scholar