Time-Dependent Approaches to Open Quantum Systems

Couplings of a system to other degrees of freedom (that is, environmental degrees of freedom) lead to energy dissipation when the number of environmental degrees of freedom is large enough. Here, we discuss quantal treatments for such energy dissipation. To this end, we discuss two different time-dependent methods. One is to introduce an effective time-dependent Hamiltonian, which leads to a classical equation of motion as a relationship among expectation values of quantum operators. We apply this method to a heavy-ion fusion reaction and discuss the role of dissipation on the penetrability of the Coulomb barrier. The other method is to start with a Hamiltonian with environmental degrees of freedom and derive an equation that the system degree of freedom obeys. For this, we present a new efficient method to solve coupled-channels equations that can be easily applied even when the dimension of the coupled-channels equations is huge.

1. Introduction

Open quantum systems are ubiquitous in many branches of science. In general, a system is never isolated but couples to other degrees of freedom, which are often referred to as the environment. The couplings to the environmental degrees of freedom can strongly affect the dynamics of the system. When the number of environmental degrees of freedom is huge, the couplings lead to energy dissipation. It has been demonstrated by Caldeira and Leggett that such couplings suppress the tunneling rate [1, 2], going into a transition from quantum to classical regimes. In nuclear physics, it has been well known that a large amount of the relative energy and angular momentum is dissipated during collisions of heavy nuclei at energies close to the Coulomb barrier, known as deep inelastic collisions [3]. In this case, the dissipation occurs due to the couplings between the relative motion of two colliding nuclei and nucleonic degrees of freedom in those nuclei. A classical Langevin equation [4] has been successfully applied to describe such collisions [3]. The Langevin approach has also been employed in order to discuss fusion reactions for syntheses of superheavy elements [5–11].

The classical Langevin approach, by definition, is not applicable at energies around the Coulomb barrier, at which quantum effects play an important role [12, 13]. One can then ask: what is a quantum model that, in the classical Limit, is equivalent to a classical Langevin equation? There are two approaches to address this question. One is to use a phenomenological quantum friction model in which the expectation values of operators obey the classical equation of motion with friction [14–17]. Recently, we solved such quantum friction Hamiltonians with a time-dependent wave packet approach in order to discuss the effect of friction on quantum tunneling [18]. The other approach to a quantum Langevin equation is to start from a system-plus-bath Hamiltonian, that is, a Hamiltonian that consists of the system and the environmental degrees of freedom and eliminates the environmental degrees of freedom. For instance, one can employ the Caldeira-Leggett Hamiltonian [1] since the classical Langevin equation can be derived from it [3, 4]. This approach is more microscopic, and a computation would thus be more involved than the quantum friction model. It has been known that, in the Markovian limit, the time evolution for the reduced density matrix for the system degree of freedom in general takes the so-called Lindblad form [19, 20].

In this paper, we discuss both of these approaches for open quantum systems from the point of view of the time-dependent method. In the next section, we first discuss the phenomenological quantum friction models using a time-dependent wave packet approach. We apply them to heavy-ion fusion reactions around the Coulomb barrier and discuss a role of friction in fusion dynamics. In section III. we solve the Calderira-Leggett Hamiltonian using a time-dependent coupled-channels approach. Using a quantum damped harmonic oscillator, we discuss how one can deal with a large number of degrees of freedom. A summary of the paper is then given in section IV.

2. Phenomenological Quantum Friction Models

We first considered a phenomenological approach to quantum friction. In this approach, one treats the environmental degrees of freedom implicitly and introduce a phenomenological Hamiltonian with which the classical equation of motion with a frictional force is reproduced as expectation values. For this purpose, several model Hamiltonians have been proposed so far [14–17]. Among these, we focused in this paper on the one introduced by Kostin [16].

Consider a particle of mass m moving in a one-dimensional space q under the influence of a potential V(q). With a friction coefficient γ, the phenomenological Schrödinger equation in the Kostin model is given by [16]:

$\begin{array}{ll}i\hslash \frac{\partial }{\partial t}\psi (q,t)=\left[-\frac{{\hslash }^2}{2m}\frac{{\partial }^2}{\partial q^2}+V(q)+\gamma S(q,t)\right]\psi (q,t),& (1)\end{array}$

where S(q, t) is the phase of the wave function, ψ(q, t) = |ψ(q, t)| exp(iS(q, t)/ℏ). From this equation, it is easy to confirm that one can derive the equation of motion with a frictional force:

$\begin{array}{ll}\frac{d}{dt}\langle p\rangle =-\gamma \langle p\rangle -\langle \frac{dV}{dq}\rangle ,& (2)\end{array}$

as is desired. Here, the expectation value of an operator ${O}$ is denoted as $\langle {O}\rangle =\int dq{\psi }^{*}(q,t){O}\psi (q,t)$, and p is the momentum operator.

When one simulates an energy dissipation in heavy-ion collisions by means of friction, a frictional force should be active only when the colliding nuclei are close to each other. In other words, one needs to deal with a coordinate-dependent friction coefficient, γ = γ(q). An extension of the Kostin model along this line has been proposed in Immele et al. [21], Bargueno and Miret-Artes [22], with which the modified Schrödinger equation is given by:

$\begin{array}{l}i\hslash \frac{\partial }{\partial t}\psi (q,t)=[-\frac{{\hslash }^2}{2m}\frac{{\partial }^2}{\partial q^2}+V(q)\\ +{{\displaystyle \int }}^{q}d{q}_1\gamma (q_1)\frac{\partial }{\partial q_1}S(q_1,t)]\psi (q,t).& (3)\end{array}$

To apply the phenomenological model to realistic collision problems, one further needs an extension to a three-dimensional space, $\overrightarrow{q}=\overrightarrow{q}(r,\theta ,\varphi )$. To this end, we first must expand the wave function with the Legendre polynomials P_l(x) as $\psi (\overrightarrow{q},t)=\sum _{l=0}^{\infty }{u}_l(r,t)P_l(cos\theta )/r$. One can then modify the Schrödinger equation for u_l(r, t) in the same way as Equation (3) to incorporate a frictional force,

$\begin{array}{l}i\hslash \frac{\partial }{\partial t}{u}_l(r,t)=[-\frac{{\hslash }^2}{2m}\frac{{\partial }^2}{\partial r^2}+\frac{{\hslash }^2}{2m}\frac{l(l+1)}{r^2}\\ +V(r)+{{\displaystyle \int }}^{r}d{r}_1\gamma (r_1)\frac{\partial }{\partial r_1}{S}_l(r_1,t)]u_l(r,t),& (4)\end{array}$

where S_l(r, t) is the phase of the radial wave function u_l(r, t) = |u_l(r, t)|exp(iS_l(r, t)/ℏ). We have here assumed a spherically symmetric potential, $V(\overrightarrow{q})=V(r)$. Notice that only the radial friction is taken into account here, while the angular momentum dissipation is neglected.

In applying Equation (4) to scattering problems, one needs to use the time-dependent approach since the Hamiltonian depends explicitly on time. To this end, we propagate a wave packet and observe how it bifurcates after it crosses the potential region. Since a wave packet is a superposition of various energy waves, one has to choose the initial condition carefully to get scattering quantities at certain initial energy. Notice that the energy projection approach [23] is inapplicable for our purpose since the energy is not conserved.

In the initial condition, the width of the energy distribution must be small enough to get reasonable results. In this context, the energy refers to the expectation value of the asymptotic Hamiltonian, H₀. If we restrict to the s-wave scattering, l = 0, and if V(r) rapidly vanishes as r → ∞, one can simply take the kinetic energy operator as H₀, that is, $H_0=-{\hslash }^2/2m({\partial }^2/\partial r^2)$. The minimum uncertainty wave packet in this case has been discussed in Bracher [24], which reads:

$\begin{array}{ll}{u}_0^{\text{min}}(r,t=0)\propto r{e}^{-{(r-r_0)}^2/4{\sigma }_r^2}{e}^{i{k}_{0}r},& (5)\end{array}$

where r₀ and σ_r are related to the mean position and the width of the wave function in the coordinate space, respectively, and k₀ is related to the mean initial energy.

In heavy-ion collisions, on the other hand, the potential is a sum of the nuclear potential V_N and the Coulomb potential $V_C(r)=Z_P{Z}_T{e}^2/r$ with the projectile charge Z_P and the target charge Z_T. Since the Coulomb potential is a long range potential, the asymptotic Hamiltonian H₀ has to include it: $H_0=-{\hslash }^2/2m({\partial }^2/\partial r^2)+V_C$. Thus, the minimum uncertainty wave packet in the form of Equation (5) would not be efficient in this case. Instead, one needs to construct a wave packet from the energy distribution, f_C(E), of H₀ in the presence of the Coulomb potential. In analogy to the spherical Bessel functions, we find that this can be achieved as:

$\begin{array}{ll}{u}_0^C(r,t=0)\propto {\displaystyle {\int }_0^{\infty }}dk{F}_0(\eta ,kr)e^{ik{r}_0}\sqrt{k{f}_C(E)},& (6)\end{array}$

with E = ℏ²k²/2m, where $\eta =m{Z}_P{Z}_T{e}^2/{\hslash }^{2}k$ is the Sommerfeld parameter and F₀(η, kr) is the regular Coulomb wave function.

With the initial condition given by Equation (6), we compute the penetrability of the Coulomb barrier for the ¹⁶O + ²⁰⁸Pb system in the presence of friction. For the nuclear potential, we employ the optical potential in Evers et al. [25]:

$\begin{array}{ll}{V}_N(r)=\frac{V_0}{1+exp((r-R_{\text{v}})/a_{\text{v}})}+i\frac{W_0}{1+exp((r-R_{\text{w}})/a_{\text{w}})},& (7)\end{array}$

with V₀ = −901.4 MeV, R_v = 8.44 fm, a_v = 0.664 fm, W₀ = −30 MeV, R_w = 6.76 fm, and a_w = 0.4 fm. With this potential, the Coulomb barrier height V_B is 74.5 MeV.

For a friction coefficient γ(r), we employ the surface friction model [3],

$\begin{array}{ll}\gamma (r)=\frac{{\gamma }_0}{m}{\left(V_B\frac{d{f}_{\text{WS}}}{dr}\right)}^2,& (8)\end{array}$

with the Woods-Saxon from factor f_WS = 1/(1 + exp ((r − R_v)/a_v)). This is a general form of the friction coefficient obtained perturbatively [26], and it has successfully been applied to the above barrier fusion reactions and to deep inelastic scatterings [3]. We arbitrarily set ${\gamma }_0=4.7\times 10^{-23}$ s/MeV, and this is used in the classical calculations. We compute the phase of the wave function in the same way as in Tokieda and Hagino [18].

For the initial energy distribution in Equation (6), we assume the Gaussian form,

$\begin{array}{ll}{f}_C(E)=\frac{1}{\sqrt{2\pi {\sigma }_E^2}}{e}^{-{(E-E_0)}^2/2{\sigma }_E^2}.& (9)\end{array}$

where E₀ and σ_E are the mean and the width of the initial energy distribution. We have confirmed that σ_E = 0.5 MeV is sufficient in the present parameter set.

Figure 1 compares the penetrability obtained with and without friction. One finds that the penetrability with friction is shifted to higher energies around the barrier. That is, in the presence of friction, a particle needs additional energy to penetrate the barrier, which originates from the energy dissipation. One can also see that the penetrability does not reach unity at high energies, but it is almost saturated at around 0.9. This means that the exit channel is in a quantum superposition state of absorption and reflection even at sufficiently above-barrier energies. Notice that, in classical mechanics without a random force, the penetrability can be only 0 or 1. In this sense, this is peculiar to the quantum friction model.

FIGURE 1

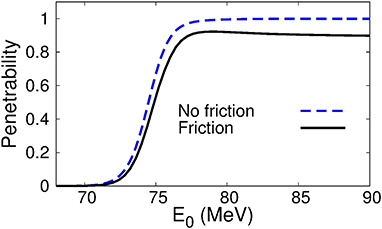
Figure 1. Energy dependence of the penetrability of the Coulomb barrier for the ¹⁶O+²⁰⁸Pb reaction. The dashed line shows the result without friction, while the solid line is for the result with friction.

For a practical application to fusion reactions, one needs to take into account explicitly low-lying collective excitations, as they play a crucial role [27]. This can be achieved by extending the above method to the coupled-channels formalism. In that treatment, low-lying collective excitations are taken into account explicitly, while other degrees of freedom, such as non-collective excitations and nucleon transfers, are treated by means of a frictional force.

In Tokieda and Hagino [28], we have applied the method to the ¹⁶O+²⁰⁸Pb system. The nuclear potential is the Woods-Saxon form as Equation (7). For low-lying collective states, the first excited state of both ¹⁶O and ²⁰⁸Pb were taken into account. The channel-coupling effect was treated in the same way as the CCFULL code, and the iso-centrifugal approximation was adopted [29]. The surface friction model was employed for a friction coefficient [with a replacement of V_B with V₀ in Equation (8)], treating γ₀ as an adjustable parameter. See Tokieda and Hagino [28] and reference therein for details of the parameters.

To compute the penetrability at certain energy, we used the same initial condition as Equation (9). It has turned out that σ_E = 0.5 MeV was sufficient for the employed parameter set. By taking a sum of the penetrability at each angular momentum, one could calculate fusion cross sections, which could then be compared with experimental data.

In Figure 2, we compare the energy dependence of fusion cross sections. Notice that the present method is reduced to the conventional coupled-channels method when friction is turned off. Thus, the no-friction result is nothing but the result of the conventional coupled-channels approach. To reproduce the experimental data, we set ${\gamma }_0=0.6\times 10^{-23}$ s/MeV. In the left panel of Figure 2, on one hand, one finds that the fusion cross sections at above barrier energies are suppressed in the friction model (the solid line) compared to that in the no-friction model (the dashed line). In the right panel of Figure 2, on the other hand, one sees that the sub-barrier fusion cross sections in both the models give almost the same result. Considering overall energies, the present friction model provided a more consistent description of fusion reactions around the Coulomb barrier as compared to the conventional coupled-channels approach. In this calculation, the same behavior as in Figure 1 has been found, and this may be a key to achieve a consistent description [28].

FIGURE 2

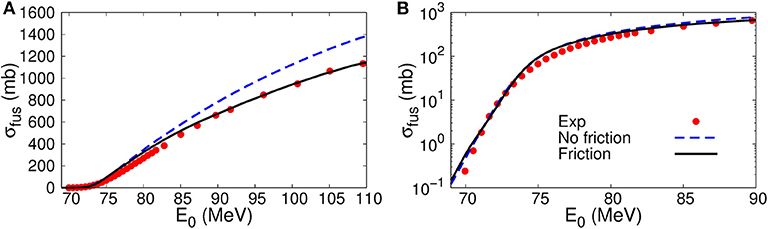
Figure 2. Energy dependence of fusion cross sections for the ¹⁶O + ²⁰⁸Pb system. The results with and without friction are shown by the solid and the dashed lines, respectively, while the experimental data are shown by the circles. The left panel (A) is in the linear scale, while the right panel (B) is in the logarithmic scale. The experimental data are taken from Morton et al. [30].

In comparison with the classical Langevin approach, the present method did not contain a random force originating from thermal fluctuation. For the ¹⁶O+²⁰⁸Pb system, the compound nucleus was formed once the projectile and the target nuclei touched each other, and the fluctuation played a much more minor role compared to the massive systems. In that situation, fusion cross sections were given as an averaged quantity, and it was expected that the presence of a random force does not change the result much. However, when one deals with phenomena in which thermal fluctuation plays a crucial role, such as deep inelastic scattering or a synthesis of superheavy elements, the thermal fluctuation should be explicitly taken into account. One could in fact directly add a random force to the Schrödinger equation Equation (1) as was done in the original paper [16]. Alternatively, friction and fluctuation will naturally emerge by explicitly treating environmental degrees of freedom, which we have discussed in the next section.

3. System-Plus-Bath Model

We next considered a more microscopic model for quantum friction, employing a system-plus-bath model. To be more specific, we considered the Caldeira-Leggett model [1, 2], whose Hamiltonian is given by,

$\begin{array}{ll}{H}_{\text{tot}}=H_S+{\displaystyle \sum _i}\hslash {\omega }_i{a}_i^{†}{a}_i+h(q){\displaystyle \sum _i}{d}_i(a_i^{†}+a_i),& (10)\end{array}$

$\begin{array}{lll}\equiv & H_S+H_B+V_{\text{coup}},& (11)\end{array}$

where H_S and H_B are the Hamiltonians for the system and the bath degrees of freedom, respectively, while V_coup is the coupling Hamiltonian between the system and the bath. Here, the bath degree of freedom is assumed to be a set of harmonic oscillators, whose creation and annihilation operators are denoted by an $a_i^{†}$ and a_i. The coupling Hamiltonian is assumed to be separable between the system and the bath degrees of freedom. In there, d_i is the coupling strength, and h(q) is the coupling form factor, where q is the coordinate of the system.

There are several ways to solve the Calderira-Leggett Hamiltonian. In Caldeira and Leggett [1, 2], the bath degrees of freedom were integrated out using the path integral in order to obtain an effective action for the system degree of freedom [see also Takigawa and Bertsch [31]]. One can also introduce the influence functional [32]. Here we discussed the coupled-channels approach [33].

In the conventional coupled-channels approach [27], one expands the total wave function in terms of the eigen-wave functions of H_B:

$\begin{array}{ll}{\Psi }_{\text{tot}}(q,t)={\displaystyle \sum _{\left\{n_i\right\}}{\psi }_{\left\{n_i\right\}}}(q,t)|\{n_i\}\rangle ,& (12)\end{array}$

where the basis states |{n_i}〉 are given by:

$\begin{array}{ll}|\{n_i\}\rangle ={\displaystyle \prod _i\frac{1}{\sqrt{n_i!}}}{\left(a_i^{†}\right)}^{n_i}|0\rangle .& (13)\end{array}$

Here, |0〉 is the vacuum state defined as a_i|0〉 = 0. One can derive the coupled equations for ψ_{ni}(q, t) by evaluating the equation:

$\begin{array}{ll}\langle \left\{n_i\right\}|i\hslash \frac{\partial }{\partial t}|{\text{Ψ}}_{\text{tot}}\rangle =\langle \left\{n_i\right\}\left|H_{\text{tot}}\right|{\text{Ψ}}_{\text{tot}}\rangle ,& (14)\end{array}$

that is,

$\begin{array}{l}i\hslash \frac{\partial }{\partial t}{\psi }_{\{n_i\}}(q,t)=\left(H_S+{\displaystyle \sum _i{n}_i}\hslash {\omega }_i\right){\psi }_{\{n_i\}}(q,t)\\ \hfill +{\displaystyle \sum _{\{{n^{\prime }}_i\}}\langle \{}{n}_i\}|V_{\text{coup}}|\{{n^{\prime }}_i\}\rangle {\psi }_{\{{n^{\prime }}_i\}}(q,t).& (15)\end{array}$

The coupled-channels equations, Equation (15), can be numerically solved when the number of the oscillator modes is not large [27, 29]. However, in general, the number of the oscillator modes can be huge, or the distribution of the frequency of the oscillator may even be given as a continuous function. In that situation, it is almost hopeless to solve the coupled-channels equations directly. In order to overcome this problem, we introduced a more efficient basis to expand the total wave function [33]. To this end, we first expanded the function exp(−iωt) with a finite basis set as:

$\begin{array}{ll}{e}^{-i\omega t}~{\displaystyle \sum _{k=1}^K}{\eta }_k(\omega )u_k(t),& (16)\end{array}$

where u_k(t) is a known function such as a Bessel function, and η_k(ω) is the expansion coefficient. We then introduced a new phonon creation operator as:

$\begin{array}{ll}{b}_k^{†}={\displaystyle \sum _i}\frac{d_i}{\hslash }{\eta }_k({\omega }_i)a_i^{†}.& (17)\end{array}$

Notice that the number of k is finite, k running from 1 to K, even though the number of i may be infinite. We then constructed the basis states using the operators $b_k^{†}$ and expanded the total wave function with them. That is, instead of Equation (12), we expanded the total wave function as:

$\begin{array}{ll}{\Psi }_{\text{tot}}(q,t)={\displaystyle \sum _{\{{\tilde{n}}_k\}}{\tilde{\psi }}_{\{{\tilde{n}}_k\}}}(q,t)|\{{\tilde{n}}_k\}\rangle ,& (18)\end{array}$

with,

$\begin{array}{ll}|\{{\tilde{n}}_k\}\rangle ={\displaystyle \prod _{k=1}^K\frac{1}{\sqrt{{\tilde{n}}_k!}}}{\left(b_k^{†}\right)}^{{\tilde{n}}_k}|0\rangle .& (19)\end{array}$

One can then obtain the coupled-channels equations similar to Equation (15):

$\begin{array}{l}i\hslash \frac{\partial }{\partial t}{\tilde{\psi }}_{\{{\tilde{n}}_k\}}(q,t)=H_S{\tilde{\psi }}_{\{{\tilde{n}}_k\}}(q,t)\\ +{\displaystyle \sum _{\{{\tilde{n}}_k^{\prime }\}}}\langle \{{\tilde{n}}_k\}|H_B+V_{\text{coup}}|\{{\tilde{n}}_k^{\prime }\}\rangle {\tilde{\psi }}_{\{{\tilde{n}}_k^{\prime }\}}(q,t).& (20)\end{array}$

We once again emphasize that the dimension of the coupled-channels equations, Equation (20), is much smaller than that of the original equations, Equation (15).

The structure of the coupled-channels equations, Equation (20), becomes simple when the basis functions u_k(t) satisfy the following two conditions.

1. The matrix D defined as:

$\begin{array}{ll}{D}_{k{k}^{\prime }}\equiv \frac{1}{{\hslash }^2}{\displaystyle \sum _i}{d}_i^2{\eta }_k(\omega ){\eta }_{k^{\prime }}^{*}(\omega ),& (21)\end{array}$

is diagonal with respect k and k′. That is, $D_{k{k}^{\prime }}={\lambda }_k{\delta }_{k,k^{\prime }}$. Notice that the matrix D can be expressed also as:

$\begin{array}{ll}{D}_{k{k}^{\prime }}\equiv \frac{1}{\hslash }{\displaystyle {\int }_{-\infty }^{\infty }}d\omega J(\omega ){\eta }_k(\omega ){\eta }_{k^{\prime }}^{*}(\omega ),& (22)\end{array}$

with the spectral density given by:

$\begin{array}{ll}J(\omega )=\frac{1}{\hslash }{\displaystyle \sum _i}{d}_i^2\delta (\omega -{\omega }_i).& (23)\end{array}$

2. The basis function u_k(t) is closed under differentiation:

$\begin{array}{ll}\frac{d{u}_k(t)}{dt}={\displaystyle \sum _{k^{\prime }=1}^K}{C}_{k{k}^{\prime }}{u}_{k^{\prime }}(t).& (24)\end{array}$

Notice that Bessel functions satisfy this condition since the following relation holds,

$\begin{array}{ll}\frac{d}{dx}{J}_k(x)=-\frac{1}{2}{J}_{k+1}(x)+\frac{1}{2}{J}_{k-1}(x),& (25)\end{array}$

(with $J_{-k}(x)={(-1)}^k{J}_k(x)$ for an integer value of k).

See Equation (31) in Tokieda and Hagino [33] for the explicit form of the coupled-channels equations, Equation (20). Tokieda and Hagino [33] also provides an alternative derivation of the coupled-channels equations, which used the influence functional of the path integral method. This allows one to extend the present formalism to finite temperatures.

Before the present method is applied to heavy-ion collisions, we should make sure that it works in principle. To this end, we considered a damped harmonic oscillator in which the exact solution can be obtained easily [33]. The Hamiltonian for the system, H_S in Equation (10), is now given by:

$\begin{array}{ll}{H}_S=\frac{p^2}{2M}+\frac{1}{2}M{\omega }_S^2{q}^2+h^2(q){\displaystyle \sum _i}\frac{d_i^2}{\hslash {\omega }_i},& (26)\end{array}$

where M and ω_S are the mass and the frequency of the system, respectively, and the last term represents the so-called counter term. In the following, we measured the length of the system in units of the oscillator length q_S defined by $q_S\equiv \sqrt{\hslash /M{\omega }_S}$, and took the coupling form factor, h(q), to be h(q) = q/q_S. We assumed that the bath oscillators are distributed according to the spectral density (see Equation 23) as:

$\begin{array}{ll}J(\omega )=V_I\frac{\omega }{\Omega }\sqrt{1-{\left(\frac{\omega }{\Omega }\right)}^2}.& (27)\end{array}$

In the numerical calculations shown below, we took ℏω_S = 2 eV, V_I = 1 eV and ℏΩ = 4 eV.

At t = 0, we assumed that ${\tilde{\psi }}_{\{{\tilde{n}}_k\}}(q,t=0)=0$ for $N\equiv \sum _{k=1}^K{\tilde{n}}_k\ne 0$. For N = 0, that is, for ñ_k = 0 for all k, we assumed that the wave function is given by:

$\begin{array}{ll}{\tilde{\psi }}_{N=0}(q,t=0)=\frac{1}{\sqrt[4]{2\pi {\sigma }_0^2}}{e}^{-{(q-q_0)}^2/4{\sigma }_0^2}{e}^{i{p}_{0}q/\hslash },& (28)\end{array}$

with q₀/q_S = −1, ${\sigma }_0/q_S=1/\sqrt{2}$, and p₀q_S/ℏ = 0.

Figures 3, 4 show the time evolution. The upper panel of Figure 3 shows the norm for each phonon state N as a function of ω_St. Here, the norm is defined as:

$\begin{array}{ll}{{N}}_N(t)\equiv {\displaystyle \sum _{\{{\tilde{n}}_k\}}}{\displaystyle \int }dq|{\tilde{\psi }}_{\{{\tilde{n}}_k\}}(q,t){|}^2{\delta }_{{\displaystyle {\sum }_k}{\tilde{n}}_k,N}.& (29)\end{array}$

FIGURE 3

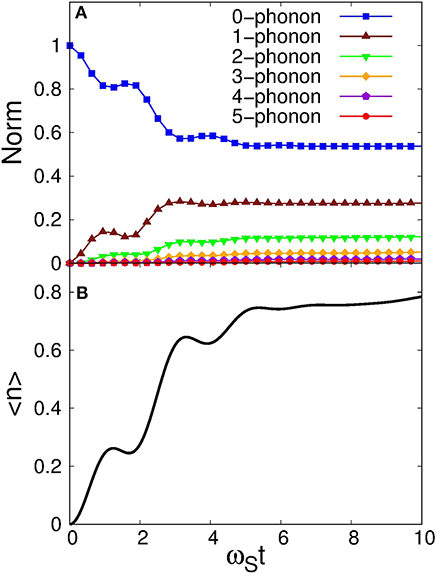
Figure 3. (A) The norm for each phonon number, $N=\sum _{k=1}^K{\tilde{n}}_k$. The solid line with squares, triangles, inverted triangles, diamonds, pentagons, and circles are for N = 0, 1, 2, 3, 4, and 5, respectively. These are obtained by solving the coupled-channels equations with the phonon states up to N_max = 5, for which the phonon operators are defined with the Bessel function basis with K = 20. (B) The expectation value of the number of phonon.

FIGURE 4

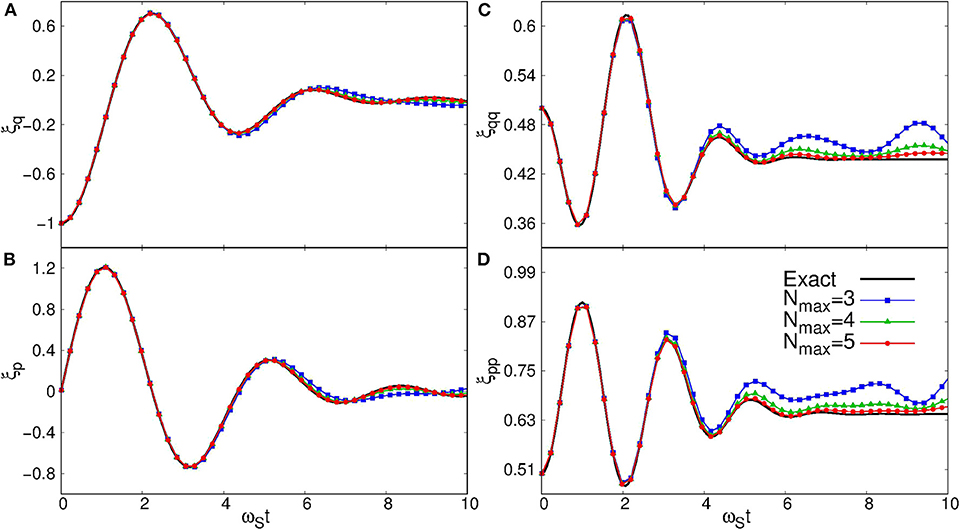
Figure 4. Comparison between the present method and the exact results for the expectation values of several quantities, that is, (A) ξ_q = 〈q〉/q_S, (B) ξ_p = 〈p〉 q_S/ℏ, (C) ${\xi }_{qq}=\langle {(q-\langle q\rangle )}^2\rangle /q_S^2$, and (D) ${\xi }_{pp}=\langle {(p-\langle p\rangle )}^2\rangle q_S^2/{\hslash }^2$. The solid lines show the exact results, while the solid lines with squares, triangles, and circles are the results of the present method with N_max = 3, 4, and 5, respectively.

To draw this figure, we took Bessel functions, J_k(Ωt), for u_k(t) in Equation (16) with K = 20. A new basis was then constructed by diagonalizing the matrix D in Equation (21). With this basis, we solved the coupled-channels equations by including the phonon states with N ≤ 5. The expectation value of the norm was also shown in the lower panel. As is expected, the number of phonons in the bath gradually increases as a function of time. Notice that the contribution of the 5-phonon states is small in the whole time range shown in the figure. This justifies the truncation at N_max = 5 for the present parameter set. One can also see that the contribution of each phonon reaches its equilibrium at around ω_St = 6.

Figure 4 compares the results of the present method with the exact solution for the quantum damped harmonic oscillator. To this end, we evaluated the expectation values for the following four quantities: ξ_q ≡ 〈q〉 /q_S, ξ_p ≡ 〈p〉 q_S/ℏ, ${\xi }_{qq}\equiv \langle {(q-\langle q\rangle )}^2\rangle /q_S^2$, and ${\xi }_{pp}\equiv \langle {(p-\langle p\rangle )}^2\rangle q_S^2/{\hslash }^2$. We carried out the calculations with three different values of N_max, that is, N_max = 3, 4, and 5, and compare them with the exact results shown by the solid lines. One can see that all of the calculations with N_max = 3, 4, and 5 reproduce the exact results up to ω_St ~ 5, for which J₂₀(Ωt) is negligibly small, and the expansion in Equation (16) with Bessel functions up to K = 20 [that is, up to J₁₉(Ωt)] is therefore reasonable. The deviation from the exact results becomes significant for larger values of ω_St, especially for the second order moments, ξ_qq and ξ_pp. This is a natural consequence of the fact that the larger number of phonon states are required to describe the finer structures.

We would like to make a few comments on an application of the present method to heavy-ion collisions. Unlike the phenomenological quantum friction models discussed in the previous section, the total energy conservation was assured with the Hamiltonian given by Equation (10). Therefore, one can utilize the energy projection method [23] to calculate the penetrability for a given energy. In the present method, the number of N_max required to achieve convergence was an important parameter that controlled the numerical cost. We expected that N_max was small for collision problems since the system-bath coupling was active only while a wave packet overlapped with the potential region. Another issue in an application to heavy-ion collisions was that one needs to model properly the environmental degrees of freedom. Note that they are described solely by the spectral density (see Equation 23) in the Caldeira-Leggett model. That is, one needs to model a suitable spectral density for heavy-ion collisions. A similar problem has already been discussed in the linear response approach to heavy-ion collisions [34] as well as to fission reactions [35]. We anticipate that these approaches provide a useful means for our future works of an application of the present method to heavy-ion reactions.

4. Summary

We have discussed two time-dependent methods for quantum friction. The first method was based on an effective Hamiltonian, which was constructed so that expectation values of operators obey a classical equation of motion with friction. Such Hamiltonian is in general time-dependent, and we have solved it with a time-dependent wave packet method. The other method is to start with a total Hamiltonian with both the system and the environmental degrees of freedom and then eliminate the environmental degree of freedom to derive an equation that the system degree of freedom obeys. For this approach, we have presented a new efficient basis for coupled-channels equations. These two methods were complimentary to each other. In the first method, whereas several parameters had to be determined phenomenologically, a required computational time was much shorter than the second method. On the other hand, the second method was based on a more microscopic Hamiltonian, and fewer empirical inputs were thus required even though the computational time may have been large. By combining these two approaches appropriately, one may be able to achieve a quantum description of heavy-ion deep inelastic collisions as well as fusion reactions to synthesize superheavy elements.

Data Availability Statement

The datasets generated for this study are available on request to the corresponding author.

Author Contributions

All authors listed have made a substantial, direct and intellectual contribution to the work, and approved it for publication.

Funding

This work was supported by Tohoku University Graduate Program on Physics for the Universe (GP-PU) and JSPS KAKENHI Grant Numbers JP18J20565 and 19K03861.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

We would like to thank Denis Lacroix and Guillaume Hupin for useful discussions.

References

1. Caldeira AO, Leggett AJ. Influence of dissipation on quantum tunneling in macroscopic systems. Phys Rev Lett. (1981) 46:211. doi: 10.1103/PhysRevLett.46.211

CrossRef Full Text | Google Scholar

2. Caldeira AO, Leggett AJ. Quantum tunnelling in a dissipative system. Ann Phys. (1983) 149:374. doi: 10.1016/0003-4916(83)90202-6

CrossRef Full Text | Google Scholar

3. Fröbrich P, Lipperheide R. Theory of Nuclear Reactions. Oxford: Oxford University Press (1996).

Google Scholar

4. Abe Y, Ayik S, Reinhard PG, Suraud E. On stochastic approaches of nuclear dynamics. Phys Rep. (1996) 275:49. doi: 10.1016/0370-1573(96)00003-8

CrossRef Full Text | Google Scholar

5. Abe Y, Boilley D, Giraud BG, Wada T. Diffusion over a saddle with a Langevin equation. Phys Rev E. (2000) 61:1125. doi: 10.1103/PhysRevE.61.1125

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Shen CW, Kosenko G, Abe Y. Two-step model of fusion for the synthesis of superheavy elements. Phys Rev C. (2002) 66:061602(R). doi: 10.1103/PhysRevC.66.061602

CrossRef Full Text | Google Scholar

7. Aritomo Y, Ohta M. Dynamical calculation for fusion - fission probability in superheavy mass region, where mass symmetric fission events originate. Nucl Phys. (2004) A744:3–14. doi: 10.1016/j.nuclphysa.2004.08.009

CrossRef Full Text | Google Scholar

8. Swiatecki WJ, Siwek-Wilczynska K, Wilczynski J. Fusion by diffusion. Acta Phys Pol B. (2003) 34:2049–71.

Google Scholar

9. Swiatecki WJ, Siwek-Wilczynska K, Wilczynski J. Fusion by diffusion. II. Synthesis of transfermium elements in cold fusion reactions. Phys Rev C. (2005) 71:014602. doi: 10.1103/PhysRevC.71.014602

CrossRef Full Text | Google Scholar

10. Zagrebaev VI, Greiner W. Cross sections for the production of superheavy nuclei. Nucl Phys. (2015) A944:257–307. doi: 10.1016/j.nuclphysa.2015.02.010

CrossRef Full Text | Google Scholar

11. Hagino K. Hot fusion reactions with deformed nuclei for synthesis of superheavy nuclei: an extension of the fusion-by-diffusion model. Phys Rev C. (2018) 98:014607. doi: 10.1103/PhysRevC.98.014607

CrossRef Full Text | Google Scholar

12. Takigawa N, Ayik S, Washiyama K, Kimura S. Quantum effect in the diffusion along a potential barrier: Comments on the synthesis of superheavy elements. Phys Rev C. (2004) 69:054605. doi: 10.1103/PhysRevC.69.054605

CrossRef Full Text | Google Scholar

13. Ayik S, Yilmaz B, Gokalp A, Yilmaz O, Takigawa T. Quantum statistical effects on fusion dynamics of heavy ions. Phys Rev C. (2005) 71:054611. doi: 10.1103/PhysRevC.71.054611

CrossRef Full Text | Google Scholar

14. Caldirola P. Forze non conservative nella meccanica quantistica. Nuovo Cimento. (1941) 18:393–400.

Google Scholar

15. Kanai E. On the quantization of the dissipative systems. Prog Theor Phys. (1948) 3:440–2. doi: 10.1143/ptp/3.4.440

CrossRef Full Text | Google Scholar

16. Kostin MD. On the Schrodinger-Langevin equation. J Chem Phys. (1972) 57:3589. doi: 10.1063/1.1678812

CrossRef Full Text | Google Scholar

17. Albrecht K. A new class of Schrodinger operators for quantized friction. Phys Lett B. (1975) 56:127–9. doi: 10.1016/0370-2693(75)90283-X

CrossRef Full Text | Google Scholar

18. Tokieda M, Hagino K. Quantum tunneling with friction. Phys Rev C. (2017) 95:054604. doi: 10.1103/PhysRevC.95.054604

CrossRef Full Text | Google Scholar

19. Lindblad G. On the generators of quantum dynamical semigroups. Commun Math Phys. (1976) 48:119–130.

Google Scholar

20. Pearle P. Simple derivation of the Lindblad equation. Euro J Phys. (2012) 33:805. doi: 10.1088/0143-0807/33/4/805

CrossRef Full Text | Google Scholar

21. Immele JD, Kan KK, Griffin JJ. Special examples of quantized friction. Nucl Phys. (1975) A241:47–60. doi: 10.1016/0375-9474(75)90364-4

CrossRef Full Text | Google Scholar

22. Bargueno P, Miret-Artes S. The generalized Schrodinger-Langevin equation. Ann Phys. (2014) 346:59–65. doi: 10.1016/j.aop.2014.04.004

CrossRef Full Text | Google Scholar

23. Yabana K. Low energy reactions of halo nuclei in a three-body model. Prog Theor Phys. (1997) 97:437–50. doi: 10.1143/PTP.97.437

CrossRef Full Text | Google Scholar

24. Bracher C. Uncertainty relations for angular momentum eigenstates in two and three spatial dimensions. Am J Phys. (2011) 79:313. doi: 10.1119/1.3534840

CrossRef Full Text | Google Scholar

25. Evers M, Dasgupta M, Hinde DJ, Gasques L. Systematic study of the nuclear potential diffuseness through high precision back-angle quasi-elastic scattering. Phys Rev C. (2008) 78:034614. doi: 10.1103/PhysRevC.78.034614

CrossRef Full Text | Google Scholar

26. Gross DHE, Kalinowski H. Friction model of heavy-ion collisions. Phys Rep. (1978) 45:175–210. doi: 10.1016/0370-1573(78)90031-5

CrossRef Full Text | Google Scholar

27. Hagino K, Takigawa N. Subbarrier fusion reactions and many-particle quantum tunneling. Prog Theo Phys. (2012) 128:1061–106. doi: 10.1143/PTP.128.1061

CrossRef Full Text | Google Scholar

28. Tokieda M, Hagino K. Quantum surface friction model for fusion reactions around the Coulomb barrier. to be published in the proceeding of the International Conference on Nucleus-Nucleus collisions (NN2018).

Google Scholar

29. Hagino K, Rowley N, Kruppa AT. A program for coupled-channel calculations with all order couplings for heavy-ion fusion reactions. Comp Phys Comm. (1999) 123:143–52. doi: 10.1016/S0010-4655(99)00243-X

CrossRef Full Text | Google Scholar

30. Morton CR, Berriman AC, Dasgupta M, Hinde DJ, Newton JO, Hagino K, et al. Coupled-channels analysis of the ¹⁶O+²⁰⁸Pb fusion barrier distribution. Phys Rev C. (1999) 60:044608. doi: 10.1103/PhysRevC.60.044608

CrossRef Full Text | Google Scholar

31. Takigawa N, Bertsch GF. Semiclassical theory of quantum tunneling in multidimensional systems. Phys Rev C. (1984) 29:2358. doi: 10.1103/PhysRevC.29.2358

CrossRef Full Text | Google Scholar

32. Balantekin AB, Takigawa N. Path integral approach to multidimensional quantum tunnelling. Ann Phys. (1985) 160:441–76. doi: 10.1016/0003-4916(85)90152-6

CrossRef Full Text | Google Scholar

33. Tokieda M, Hagino K. A new approach for open quantum systems based on a phonon number representation of a harmonic oscillator bath. Ann Phys. (2020) 412:168005. doi: 10.1016/j.aop.2019.168005

CrossRef Full Text | Google Scholar

34. Adamian GG, Jolos RV, Nasirov AK, Muminov AI. Friction coefficient for deep-inelastic heavy-ion collisions. Phys Rev C. (1997) 56:373. doi: 10.1103/PhysRevC.56.373

CrossRef Full Text | Google Scholar

35. Ivanyuk FA, Hofmann H. Pairing and shell effects in the transport coefficients of collective motion. Nucl Phys. (1999) A657:19–58. doi: 10.1016/S0375-9474(99)00324-3

CrossRef Full Text | Google Scholar