Optical Solutions of Schrödinger Equation Using Extended Sinh–Gordon Equation Expansion Method

In this paper, we investigated the non-linear Schrödinger equation (NLS) to extract optical soliton solutions by implementing the extended Sinh–Gordon equation expansion method (ShGEEM). Optical soliton solutions included bright, dark, combined bright-dark, singular soliton combined singular soliton solutions, and singular periodic wave solutions. Our new results have been compared to these in the literature. Also, graphical analysis was presented with 3D and contour graphs to understand the physics of obtained solutions.

Introduction

In recent years, soliton propagation in non-linear optical fiber has become the most extensive topic of research in the field of non-linear sciences. In non-linear optical fiber, the study of the non-linear Schrödinger equation (NLS) plays an important role in order to understand the dynamical behavior of optical soliton. NLS helps to provide exact soliton solutions in non-linear fiber optics. During the last few years, in the study of optical solitons, many new research developments have taken place, which is a great achievement in the field of soliton [1–15]. However, there are a lot of problems that need to be solved.

Many new methods have been developed to tackle complicated problems in a very smooth manner and provide exact soliton solutions of these problems such as the modified simple equation method [16, 17], the extended trial equation method [18, 19], the tan$\left(\frac{\varphi (\xi )}{2}\right)$-expansion method [20, 21], and many others.

In this paper, our main focus is the study of NLS [22]. This equation has large physical importance in non-linear optics.

$\begin{array}{ll}i{V}_t-V_{xx}+{2\left|V\right|}^{2}V-2{\sigma }^{2}V=0,i=\sqrt{-1},& (1)\end{array}$

where V(x, t) is a complex function and σ is a constant. It should also be noted that, for σ = 0, Equation (1) reduces to the non-Kerr law non-linearity as

$\begin{array}{ll}{V}_t-V_{xx}+{2\left|V\right|}^{2}V=0,i=\sqrt{-1}& (2)\end{array}$

To study Equation (1), we consider the following wave transformation:

$\begin{array}{ll}V(x,t)=p(\xi )e^{i\varphi (x,t)},\xi =\rho x-\upsilon t,\phi =-kx+\varpi t+\theta & (3)\end{array}$

where φ(x, t) is the phase component, and k, ϖ, θ, and υ represent the frequency, wave number, phase constant, and velocity of the soliton. By substituting Equation (3) into Equation (1), we obtain the following real and imaginary equations:

$\begin{array}{ll}\left(\frac{d^2}{d{\xi }^2}\phi (\xi )\right){\rho }^2+\varphi (\xi )\left(k^2-2{\sigma }^2-\varpi \right)-2{(\varphi (\xi ))}^3=0,& (4)\end{array}$

$\begin{array}{ll}\nu =2k\rho ,& (5)\end{array}$

Algorithm of Extended ShGEEM

To describe the mechanism of the extended Sinh–Gordon equation method (SGEM) for differential equations, we consider the equation [23]

$\begin{array}{ll}{{\rm Y}}_{xt}=\varrho \text{ sinh }({\rm Y}),& (6)\end{array}$

where Υ = Υ(x, t) and ϱ is a nonzero constant.

Applying the traveling wave transformation Υ(x, t) = Φ(ζ), ζ = λ(x − μt), to Equation (6), we acquire the following form of non-linear ODE:

$\begin{array}{ll}{\Phi }^{″}=-\frac{\varrho }{{\lambda }^2\mu }\text{sinh}(\Phi ),& (7)\end{array}$

where Φ = Φ(ζ), λ is a wave number, and μ is the velocity of the traveling wave. By applying the integration procedure, Equation (7) can be found in a simplified form:

$\begin{array}{ll}{\left[\frac{\left({\Phi }^{\prime }\right)}{2}\right]}^2=-\frac{\varrho }{{\lambda }^2\mu }{\text{sinh}}^2\left(\frac{\Phi }{2}\right)+r,& (8)\end{array}$

where r is the constant of integration. Setting $v(\zeta )=\frac{\Phi }{2},$ and $\theta =-\frac{\varrho }{{\lambda }^2\mu }$, into Equation (8) yields

$\begin{array}{ll}{v}^{\prime }(\zeta )=\sqrt{\theta {\text{ sinh}}^2\left(v\right)+r},& (9)\end{array}$

Equation (9) has the following set of solutions, by substituting different values for given parameters θ and r.

Set I:

If we substitute r = 0, θ = 1 in Equation (9), we obtain

$\begin{array}{ll}{v}^{\prime }(\zeta )=\text{sin }h(v),& (10)\end{array}$

Simplifying Equation (10), we acquire the following solutions:

$\begin{array}{ll}\text{sin }h(v(\zeta ))=\pm csch(\zeta ),or\text{ sin }h(v(\zeta ))=\pm isech(\zeta ),& (11)\end{array}$

and

$\begin{array}{ll}\text{cos }h(v(\zeta ))=\pm coth(\zeta ),or\text{ cos }h(v(\zeta ))=\pm tanh(\zeta )!,& (12)\end{array}$

where $i=\sqrt{-1}.$

Set II:

If we substitute r = 1, θ = 1 in Equation (9), we have the following equation:

$\begin{array}{ll}{v}^{\prime }(\zeta )=\text{cos }h(v),& (13)\end{array}$

After simplification in Equation (13), we have the following solutions:

$\begin{array}{ll}\text{sin }h(v(\zeta ))=\text{tan}(\zeta ),or\text{ sin }h(v(\zeta ))=-cot(\zeta ),& (14)\end{array}$

and

$\begin{array}{ll}\text{cos }h(v(\zeta ))=\pm sec(\zeta ),or\text{ cos }h(v(\zeta ))=\pm tan(\zeta ),& (15)\end{array}$

To obtain the different wave solutions of non-linear partial differential equations (NPDEs), we consider the equation in the following form:

$\begin{array}{ll}\complement ({\rm Y},{{\rm Y}}_t,{{\rm Y}}_x,{{\rm Y}}_{xx},{{\rm Y}}_{xt},{{\rm Y}}_{tt},\dots )=0,& (16)\end{array}$

Step I: By using wave transformation Υ(x, t) = Φ(ζ), ζ = λ(x − μt), we first transform Equation (16) into the following NODE:

$\begin{array}{ll}H(\Phi ,{\Phi }^{\prime },{\Phi }^{″},{{\Phi }^2\Phi }^{\prime },\dots )=0,& (17)\end{array}$

Step II: We suppose that Equation (17) has a new ansatz solution in the following form:

$\begin{array}{ll}\Phi (v)={\displaystyle \sum _{\kappa =1}}{\left[{{B}}_{\kappa }sinh(v(\zeta ))+A_{\kappa }cosh(v(\zeta ))\right]}^{\kappa }+{\AA }_0,& (18)\end{array}$

where ${\AA }_0,{\AA }_{\kappa },{{B}}_{\kappa },(\kappa =1,\dots ,n)$ are constants to be determined later. The value of can be determined by balancing the highest order dispersive term with the non-linear term in Equation (17).

Step III: We substitute Equation (18) for the fixed value of in Equation (17) to obtain a polynomial form of equation in v^′f sinh^g (v) cosh^ι (v), (f = 0, 1 and g, ι = 0, 1, 2……). We get the system of algebraic equations by equating the coefficients of v^′f sinh^g (v) cosh^ι (v) to be all zero. We extract the values of coefficients ${\AA }_0,{\AA }_{\kappa },{{B}}_{\kappa },\lambda ,\mu$ by solving the system of algebraic equations with the help of MAPLE 2016.

Step IV: Substituting the values of ${\AA }_0,{\AA }_{\kappa },{{B}}_{\kappa },\mu$ in Equations (19)–(22), we obtain the following wave solutions to the non-linear Equation (16):

$\begin{array}{ll}\Phi (\zeta )={\displaystyle \sum _{\kappa =1}^N}{\left[\pm {{B}}_{\kappa }isech(\zeta )\pm {\AA }_{\kappa }\text{tanh}(\zeta )\right]}^{\kappa }+{\AA }_0,& (19)\end{array}$

$\begin{array}{ll}\Phi (\zeta )={\displaystyle \sum _{\kappa =1}^N}{\left[\pm {{B}}_{\kappa }csch(\zeta )\pm {{B}}_{\kappa }\text{coth}(\zeta )\right]}^{\kappa }+{\AA }_0,& (20)\end{array}$

$\begin{array}{ll}\Phi (\zeta )={\displaystyle \sum _{\kappa =1}^N}{\left[{{B}}_{\kappa }\text{sec}(\zeta )+{\AA }_{\kappa }\text{tan}(\zeta )\right]}^{\kappa }+{\AA }_0,& (21)\end{array}$

and

$\begin{array}{ll}\Phi (\zeta )={\displaystyle \sum _{\kappa =1}^N}{\left[{{B}}_{\kappa }\text{csc}(\zeta )-{\AA }_{\kappa }\text{cot}(\zeta )\right]}^{\kappa }+{\AA }_0,& (22)\end{array}$

Application of Extended ShGEEM to Equation (1)

In this section, Extended ShGEEM [24–29] is implemented to Equation (1).

Considering a homogeneous balance between Φ″ and Φ³ in Equation (4) yields N = 1. And setting the value of N in Equations (18)–(22), we obtain

$\begin{array}{ll}\Phi (v)={{B}}_{1}sinh(v(\zeta ))+{\AA }_{1}cosh(v(\zeta ))+{\AA }_0,& (23)\end{array}$

$\begin{array}{ll}\Phi (\zeta )=\pm {{B}}_{1}isech(\zeta )\pm {\AA }_{1}tanh(\zeta )+{\AA }_0,& (24)\end{array}$

$\begin{array}{ll}\Phi (\zeta )=\pm {{B}}_{1}csch(\zeta )\pm {\AA }_{1}coth(\zeta )+{\AA }_0,& (25)\end{array}$

$\begin{array}{ll}\Phi (\zeta )=\pm {{B}}_{1}sec(\zeta )+{\AA }_{1}tan(\zeta )+{\AA }_0,& (26)\end{array}$

$\begin{array}{ll}\Phi (\zeta )=\pm {{B}}_{1}csc(\zeta )-{\AA }_{1}cot(\zeta )+{\AA }_0,& (27)\end{array}$

Substituting Equation (23) together with its derivatives in Equation (4), we get a polynomial equation in v^′f sinh^g (v) cosh^ι (v), (f = 0, 1 and g, ι = 0, 1, 2……). Using some hyperbolic identities, we acquire a system of algebraic equations by setting the coefficients of v^′f sinh^g (v) cosh^ι (v) equal to zero. After simplifying the system of equations, we obtain the values of ${\AA }_0,{\AA }_{\kappa },{{B}}_{\kappa },\rho ,k,\lambda$ with the help of Maple 16. Subsisting all the values of ${\AA }_0,{\AA }_{\kappa },{{B}}_{\kappa },\rho ,k,\lambda$ in any of Equations (24)–(27), we found numerous different types of soliton solutions of Equation (1).

Result I:

$\begin{array}{ll}{\AA }_0=0,{\AA }_1=\pm \frac{1}{2}\rho ,{{B}}_1=\pm \frac{1}{2}\rho ,\varpi =k^2+\frac{1}{2}{\rho }^2-2{\sigma }^2,& (28)\end{array}$

Result II:

$\begin{array}{ll}{\AA }_0=0,{\AA }_1=0,{{B}}_1=\pm \rho ,\varpi =k^2-{\rho }^2-2{\sigma }^2,& (29)\end{array}$

Result III:

$\begin{array}{ll}{\sigma }^2{\AA }_0=0,{\AA }_1=\pm \rho ,{{B}}_1=0,\varpi =k^2{+2\rho }^2-2{\sigma }^2,& (30)\end{array}$

Result IV:

$\begin{array}{ll}{\AA }_0=0,{\AA }_1=0,{{B}}_1=\pm \rho ,\rho =\sqrt{k^2-2{\sigma }^2-\varpi },& (31)\end{array}$

Result V:

$\begin{array}{ll}{\AA }_0=0,{\AA }_1=\rho ,{{B}}_1=0,\rho =\frac{1}{2}\sqrt{-2k^2+4{\sigma }^2+2\varpi },& (32)\end{array}$

Result VI:

$\begin{array}{ll}{\AA }_0=0,{\AA }_1=\frac{1}{2}\rho ,{{B}}_1=\frac{1}{2}\rho ,\rho =\sqrt{-2k^2+4{\sigma }^2+2\varpi },& (33)\end{array}$

Result VII:

$\begin{array}{ll}{\AA }_0=0,{\AA }_1=\mp \frac{1}{2}\rho ,{{B}}_1=\pm \frac{1}{2}\rho ,\varpi =k^2-\frac{1}{2}{\rho }^2-2{\sigma }^2,& (34)\end{array}$

Result VIII:

$\begin{array}{ll}{\AA }_0=0,{\AA }_1=\frac{1}{2}\rho ,{{B}}_1=\frac{1}{2}\rho ,\rho =\sqrt{2k^2-4{\sigma }^2-2\varpi },& (35)\end{array}$

Substituting the values of the above given results in Equations (24)–(27), we get the following solutions.

Case I: Bright Optical Solitons

Substituting the values of the parameters given in Results II and IV into Equation (24):

$\begin{array}{ll}{V}_1(x,t)=\pm i\rho sech\left(\rho x-2tk\rho \right)e^{i(-kx+t(k^2-{\rho }^2-2{\sigma }^2)+\theta )},& (36)\end{array}$

$\begin{array}{l}{V}_2(x,t)=\pm i\sqrt{k^2-2{\sigma }^2-\varpi }\text{ sech}(-2tk\sqrt{k^2-2{\sigma }^2-\varpi }\\ +\sqrt{k^2-2{\sigma }^2-\varpi }x)\times e^{i(-kx+t\varpi +\theta )}& (37)\end{array}$

where (k² − 2σ² − ϖ) > 0, for valid solutions.

Case II: Dark Optical Solitons

Substituting the values of the parameters given in Results III and V into Equation (24):

$\begin{array}{ll}{V}_3(x,t)=\pm \rho \text{ tanh}(-2tk\rho +\rho x)e^{i(-kx+t(k^2+2{\rho }^2-2{\sigma }^2)+\theta )},& (38)\end{array}$

$\begin{array}{l}{V}_4(x,t)=\left(\begin{array}{c}\frac{1}{2}\sqrt{-2k^2+4{\sigma }^2+2\varpi }\\ \text{tanh}\left(-tk\sqrt{-2k^2+4{\sigma }^2+2\varpi }+\frac{1}{2\sqrt{-2k^2+4{\sigma }^2+2\varpi }x}\right)\\ \end{array}\right)\\ e^{i(-kx+t\varpi +\theta )}& (39)\end{array}$

where (−2k² + 4σ² + 2ϖ) > 0, for valid solutions.

Case III: Combined Dark-Bright Optical Soliton Solutions

Using the values of the parameters given in Results I and VI into Equation (24):

$\begin{array}{l}{V}_5(x,t)=\pm \frac{1}{2}\rho (isech(\rho x-2tk\rho )+\text{tanh}(\rho x-2tk\rho ))\\ e^{i(-kx+t(k^2+\frac{1}{2}{\rho }^2-2{\sigma }^2)+\theta )},& (40)\end{array}$

$\begin{array}{l}{V}_6(x,t)=\left(\begin{array}{c}\frac{i}{2}\sqrt{2\varpi -2k^2+4{\sigma }^2}\\ \text{sech}\left(-2tk\sqrt{2\varpi -2k^2+4{\sigma }^2}+\sqrt{2\varpi -2k^2+4{\sigma }^2}x\right)\\ \end{array}\right)\\ +\left(\begin{array}{c}\frac{1}{2}\sqrt{2\varpi -2k^2+4{\sigma }^2}\\ \text{tanh}(-2tk\sqrt{2\varpi -2k^2+4{\sigma }^2}+\sqrt{2\varpi -2k^2+4{\sigma }^2}x)\\ \end{array}\right)\\ \times e^{i(-kx+t\varpi +\theta )}.& (41)\end{array}$

where (2ϖ − 2k² + 4σ²) > 0, for valid solutions.

Case IV: Singular Soliton Solutions

Using the values of the parameters given in Results II, III, IV, and V into Equation (25):

$\begin{array}{ll}{V}_7(x,t)=\pm \rho csch(-2tk\rho +\rho x)e^{i(-kx+t(k^2-{\rho }^2-2{\sigma }^2)+\theta )},& (42)\end{array}$

$\begin{array}{ll}{V}_8(x,t)=\pm \rho \text{coth}(-2tk\rho +\rho x)e^{i(-kx+t(k^2+2{\rho }^2-2{\sigma }^2)+\theta )}& (43)\end{array}$

$\begin{array}{l}{V}_9(x,t)=\pm \sqrt{k^2-2{\sigma }^2-\varpi }csch(-2tk\sqrt{k^2-2{\sigma }^2-\varpi }\\ +\sqrt{k^2-2{\sigma }^2-\varpi }x)\times e^{i(-kx+t\varpi +\theta )}& (44)\end{array}$

where (k² − 2σ² − ϖ) > 0, for valid solutions.

$\begin{array}{l}{V}_{10}(x,t)=\left(\begin{array}{c}\frac{1}{2}\sqrt{2\varpi -2k^2+4{\sigma }^2}\\ \text{coth}\left(-tk\sqrt{2\varpi -2k^2+4{\sigma }^2}+\frac{1}{2}\sqrt{2\varpi -2k^2+4{\sigma }^2}x\right)\\ \end{array}\right)\\ \times e^{i(-kx+t\varpi +\theta )},& (45)\end{array}$

where (2ϖ − 2k² + 4σ²) > 0, for valid solutions.

Case V: Combined Singular Solitons

Substituting the values of the parameters given in Results I and VI into Equation (25):

$\begin{array}{l}{V}_{11}(x,t)=\pm \left(\frac{1}{2}\rho csch(-2tk\rho +\rho x)-\frac{1}{2}\rho \text{coth}(-2tk\rho +\rho x)\right)\\ \times e^{i(-kx+t(k^2+\frac{1}{2}{\rho }^2-2{\sigma }^2)+\theta )},& (46)\end{array}$

$\begin{array}{l}{V}_{12}(x,t)=\left(\begin{array}{c}\frac{1}{2}\sqrt{-2k^2+4{\sigma }^2+2\varpi }\\ \times csch\left(-2tk\sqrt{-2k^2+4{\sigma }^2+2\varpi }+\sqrt{-2k^2+4{\sigma }^2+2\varpi }x\right)\\ +\frac{1}{2}\sqrt{-2k^2+4{\sigma }^2+2\varpi }\\ \times \text{coth}\left(-2tk\sqrt{-2k^2+4{\sigma }^2+2\varpi }+\sqrt{-2k^2+4{\sigma }^2+2\varpi }x\right)\\ \end{array}\right)\\ \times e^{i(-kx+t\varpi +\theta )},& (47)\end{array}$

where (−2k² + 4σ² + 2ϖ) > 0, for valid solutions.

Case VI: Singular Periodic Wave Solitons

Substituting the values of the parameters given in Result VII into Equations (26), (27):

$\begin{array}{l}{V}_{13}(x,t)=\frac{1}{2}\rho (\pm \text{sec}(-2tk\rho +\rho x)\mp \text{tan}(-2tk\rho +\rho x))\\ e^{i(-kx+t(k^2-\frac{1}{2}{\rho }^2-2{\sigma }^2)+\theta )},& (48)\end{array}$

$\begin{array}{l}{V}_{14}(x,t)=\left(\left(\begin{array}{c}\frac{1}{2}\sqrt{2k^2-4{\sigma }^2-2\varpi }\\ \times \text{sec}\left(-2tk\sqrt{2k^2-4{\sigma }^2-2\varpi }+\sqrt{2k^2-4{\sigma }^2-2\varpi }x\right)\\ +\frac{1}{2}\sqrt{2k^2-4{\sigma }^2-2\varpi }\\ \times \text{tan}\left(-2tk\sqrt{2k^2-4{\sigma }^2-2\varpi }+\sqrt{2k^2-4{\sigma }^2-2\varpi }x\right)\\ \end{array}\right)\right)\\ \times e^{i(-kx+t\varpi +\theta )},& (49)\end{array}$

where (2k² − 4σ² − 2ϖ) > 0, for valid solutions.

Substituting the values of the parameters given in Result VIII into Equations (26), (27):

$\begin{array}{l}{V}_{15}(x,t)=\frac{1}{2}(\pm \rho \text{csc}(-2tk\rho +\rho x)\pm \rho \text{cot}(-2tk\rho +\rho x))\\ e^{i(-kx+t(k^2-\frac{1}{2}{\rho }^2-2{\sigma }^2)+\theta )},& (50)\end{array}$

$\begin{array}{l}{V}_{16}(x,t)=\left(\begin{array}{c}\frac{1}{2}\sqrt{2k^2-4{\sigma }^2-2\varpi }\\ \text{csc}\left(-2tk\sqrt{2k^2-4{\sigma }^2-2\varpi }+\sqrt{2k^2-4{\sigma }^2-2\varpi }x\right)\\ -\frac{1}{2}\sqrt{2k^2-4{\sigma }^2-2\varpi }\\ \text{cot}\left(-2tk\sqrt{2k^2-4{\sigma }^2-2\varpi }+\sqrt{2k^2-4{\sigma }^2-2\varpi }x\right)\\ \end{array}\right)\\ \times e^{i(-kx+t\varpi +\theta )},& (51)\end{array}$

where (2k² − 4σ²− 2ϖ) > 0, for valid solutions.

Graphs and Discussions

In this section, we presented some of our obtained solutions in the following figures.

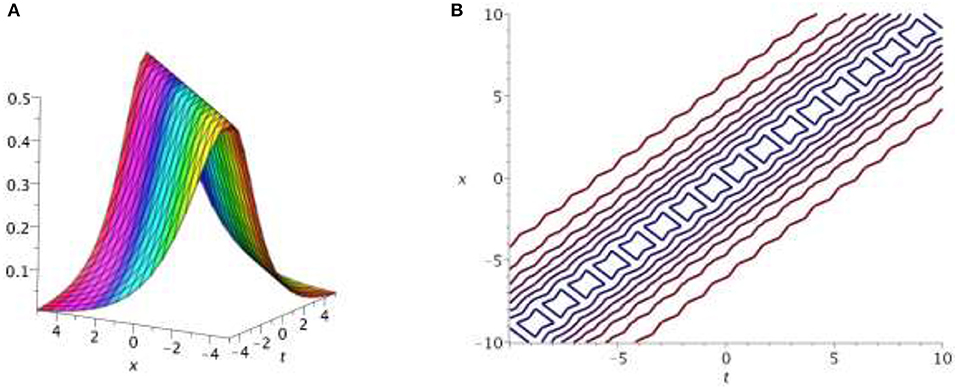
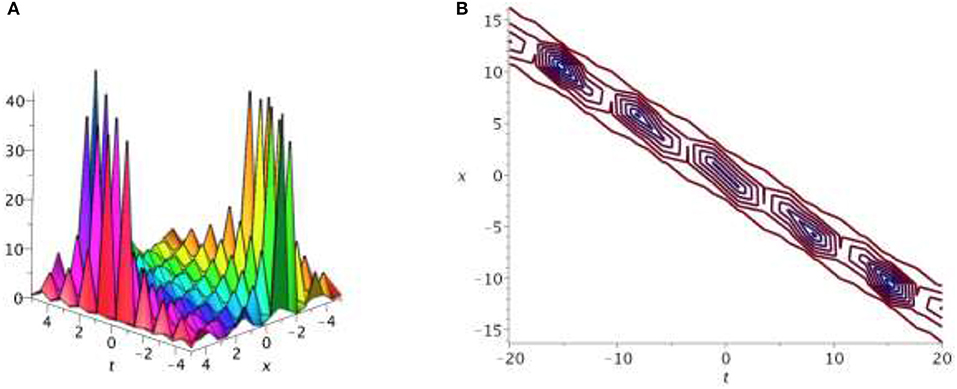
Solutions V₁, V₂ of Equation (1) depict the bright optical soliton solutions. Figure 1 represents the 3D surface of the bright soliton solution of Equation (36) with a contour plot for given parametric values ρ = 0.5, θ = 0.5, σ = 0.5, k = 0.5.

FIGURE 1

Figure 1. (A) Bright soliton Equation (36). (B) Contour plot.

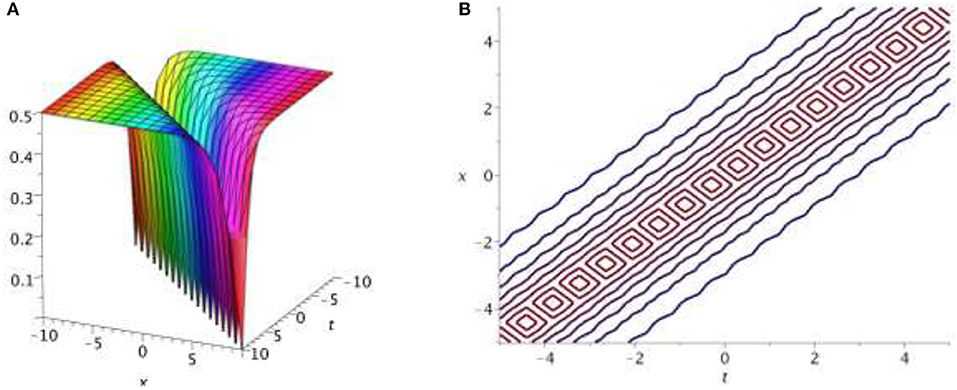
Solutions V₃, V₄ of Equation (1) show the dark optical soliton solutions. Figure 2 represents the 3D surface of the dark optical soliton solution of Equation (38) with a contour plot for given parametric values ρ = 0.5, θ = 0.5, σ = 0.5, k = 0.5.

FIGURE 2

Figure 2. (A) Dark soliton solution Equation (38). (B) Contour plot.

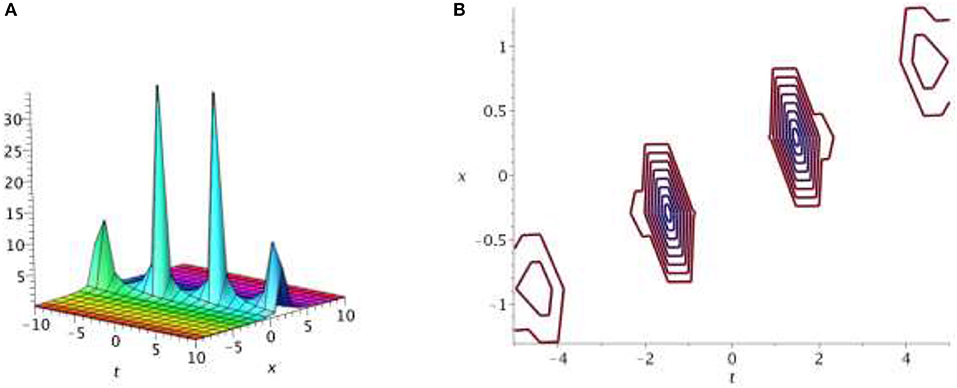
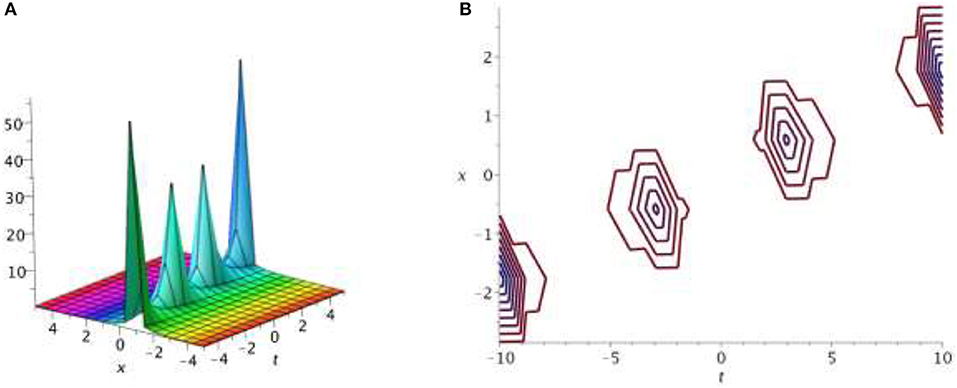
Figures 3, 4 represent the singular and combined singular soliton solutions of Equation (1), obtained from solutions of V₈ and V₁₂[Equations (38), (47)] for ρ = 0.065, θ = 1, σ = 0.09, k = 0.095 and ϖ = 0.05, θ = 5, σ = 0.05, k = 0.09.

FIGURE 3

Figure 3. (A) Singular solution Equation (43). (B) Contour plot.

FIGURE 4

Figure 4. (A) Combined singular solution Equation (47). (B) Contour plot.

Solutions V₁₃, V₁₄, V₁₅, V₁₆ of Equation (1) represent the singular periodic wave solutions. Figure 5 illustrates the 3D surface of the singular periodic wave solution of Equation (50) with a contour plot for given parametric values ρ = 2.5, θ = 0.2, σ = 0.2, k = 7.5. For convenience, some other figures are not reported.

FIGURE 5

Figure 5. (A) Singular periodic soliton Equation (50). (B) Contour plot.

Comparisons

In Cheemaa and Younis [22], Nadia Cheema and Muhammad Younis investigated the traveling wave solutions of NLSE by applying the extended Fan sub-equation method. The obtained solutions V₃, V₄, V₈, V₁₀, V₁₁, V₁₂, V₁₅, V₁₆ in this paper are equivalent to the solutions q₁, q₂, q₆, q₁₅, q₁₆. found in Cheemaa and Younis [22] for non-linear Schrödinger's equation. The extended Sinh–Gordon equation expansion method provides a large variety of optical soliton solutions [24–29]. By means of the extended Sinh–Gordon equation expansion method, we found some new more generalized exact solutions. Therefore, these new exact solutions are not reported before for this equation in the literature.

Conclusions

We have implemented the extended Sinh–Gordon equation expansion method to solve the non-linear Schrodinger equation for exact optical soliton solutions. The types of solutions we reported include singular periodic wave solutions, bright, dark, combined bright-dark, singular, and combined singular soliton solutions. The non-linear Schrodinger equation is one of the very major equations arising in the field of optic fibers. Its new solutions are expected to help engineers and scientists working in the field. It is worth mentioning that the solutions obtained by us are more generalized. That is, we have recovered not only many already existing solutions but also many unreported solutions. These new solutions are expected to help scientists working in the fields of optic fiber to understand the phenomenon governed by the non-linear Schrodinger equation. All the solutions have been verified for their exactness. Wherever the reported solutions have been recovered, they have been compared with their counterparts in the literature.

Data Availability Statement

The datasets generated for this study are available on request to the corresponding author.

Author Contributions

The formulation of the problem was done by UK and AI. Non-dimensionalization of the nanofluid models by using invertible transformations done by NA. Mathematical analysis and the graphical results plotted and discussed by SM-D and IK. E-SS revised the whole manuscript and checked the typo mistakes.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

Researchers Supporting Project number (RSP-2019/33), King Saud University, Riyadh, Saudi Arabia.

References

1. Khalique CM, Mhlanga IE. Travelling waves and conservation laws of a. (2 + 1)-dimensional coupling system with Korteweg-de Vries equation. Appl Math Nonlinear Sci. (2018) 3:241–54. doi: 10.21042/AMNS.2018.1.00018

CrossRef Full Text | Google Scholar

2. Biswas A, Yildirim Y, Yasar E, Triki H, Alshomrani AS, Ullah MZ, et al. Optical soliton perturbation with Gerdjikov–Ivanov equation by modified simple equation method. Optik. (2018) 157:1235–40. doi: 10.1016/j.ijleo.2017.12.101

CrossRef Full Text | Google Scholar

3. Eskitaşçioglu EI, Aktaş MB, Baskonus HM. New complex and hyperbolic forms for Ablowitz–Kaup–Newell–Segur wave equation with fourth order. Appl Math Nonlinear Sci. (2019) 4:93–100. doi: 10.2478/AMNS.2019.1.00010

CrossRef Full Text | Google Scholar

4. Mathobo M, Atangana A. Analysis of exact groundwater model within a confined aquifer: new proposed model beyond the Theis equation. Eur Phys J Plus. (2018) 133:415. doi: 10.1140/epjp/i2018-12205-9

CrossRef Full Text | Google Scholar

5. Inc M, Aliyu AI, Yusuf A, Baleanu D. Optical solitons for biswas-milovic model in nonlinear optics by sine-gordon equation method. Optik. (2018) 157:267–74. doi: 10.1016/j.ijleo.2017.11.061

CrossRef Full Text | Google Scholar

6. Biswas A, Yildirim Y, Yasar E, Triki H, Alshomrani AS, Ullah MZ, et al. Optical soliton perturbation for complex Ginzburg–Landau equation with modified simple equation method. Optik. (2018) 158:399–415. doi: 10.1016/j.ijleo.2017.12.131

CrossRef Full Text | Google Scholar

7. Biswas A, Yildirim Y, Yasar E, Zhou Q, Moshokoa SP, Belic M. Optical solitons for Lakshmanan–Porsezian–Daniel model by modified simple equation method. Optik. (2018) 160:24–32. doi: 10.1016/j.ijleo.2018.01.100

CrossRef Full Text | Google Scholar

8. Biswas A, Yildirim Y, Yasar E, Triki H, Alshomrani AS, Ullah MZ, Zhou Q, Moshokoa SP, Belic M Optical soliton perturbation with full nonlinearity for Kundu–Eckhaus equation by modified simple equation method. Optik. (2018) 157:1376–80. doi: 10.1016/j.ijleo.2017.12.108

CrossRef Full Text | Google Scholar

9. Biswas A, Yildirim Y, Yasar E, Zhou Q, Moshokoa SP, Belic M. Optical soliton perturbation with resonant nonlinear schrödinger's equation having full nonlinearity by modified simple equation method. Optik. (2018) 160:33–43. doi: 10.1016/j.ijleo.2018.01.098

CrossRef Full Text | Google Scholar

10. Tariq KU, Seadawy AR. Optical soliton solutions of higher order nonlinear Schrödinger equation in monomode fibers and its applications. Optik. (2018) 154:785–98. doi: 10.1016/j.ijleo.2017.10.063

CrossRef Full Text | Google Scholar

11. Jawad AJM, Abu-AlShaeer MJ, Biswas A, Zhou Q, Moshokoa S, Belic M. Optical solitons to Lakshmanan-Porsezian-Daniel model for three nonlinear forms. Optik. (2018) 160:197–202. doi: 10.1016/j.ijleo.2018.01.121

CrossRef Full Text | Google Scholar

12. Jawad AJM, Abu-AlShaeer MJ, Majid FB, Biswas A, Zhou Q, Belic M. Optical soliton perturbation with exotic non-Kerr law nonlinearities. Optik. (2018) 158:1370–9. doi: 10.1016/j.ijleo.2017.12.184

CrossRef Full Text | Google Scholar

13. Bulut H, Sulaiman TA, Baskonus HM, Aktürk T. On the bright and singular optical solitons to the (2 + 1)-dimensional NLS and the Hirota equations. Opt Quantum Electron. (2018) 50:134. doi: 10.1007/s11082-018-1411-6

CrossRef Full Text | Google Scholar

14. Baskonus HM, Bulut H, Atangana A. On the complex and hyperbolic structures of the longitudinal wave equation in a magneto-electro-elastic circular rod. Smart Mater Struct. (2016) 25:1–8. doi: 10.1088/0964-1726/25/3/035022

CrossRef Full Text | Google Scholar

15. Amkadni M, Azzouzi A, Hammouch Z On the exact solutions of laminar MHD flow over a stretching flat plate. Commun Nonlinear Sci. (2008) 13:359–68. doi: 10.1016/j.cnsns.2006.04.002

CrossRef Full Text | Google Scholar

16. Arnous AH, Ullah MZ, Asma M, Moshokoa SP, Zhou Q, Mirzazadeh M, et al. Dark and singular dispersive optical solitons of Schrödinger–Hirota equation by modified simple equation method. Optik. (2017) 136:445–50. doi: 10.1016/j.ijleo.2017.02.051

CrossRef Full Text | Google Scholar

17. El-Borai MM, El-Owaidy HM, Ahmed HM, Arnous AH, Moshokoa S, Biswas A, et al. Dark and singular optical solitons with spatio-temporal dispersion using modified simple equation method. Optik. (2017) 130:324–31. doi: 10.1016/j.ijleo.2016.10.105

CrossRef Full Text | Google Scholar

18. Biswas A, Ekici M, Sonmezoglu A, Triki H, Zhou Q, Moshokoa SP, et al. Dispersive optical solitons with differential group delay by extended trial equation method. Optik. (2018) 158:790–98. doi: 10.1016/j.ijleo.2017.12.193

CrossRef Full Text | Google Scholar

19. Foroutan M, Zamanpour I, Manafian J. Applications of IBSOM and ETEM for solving the nonlinear chains of atoms with long-range interactions. Eur Phys J Plus. (2017) 132:421. doi: 10.1140/epjp/i2017-11681-7

CrossRef Full Text | Google Scholar

20. Manafian J, Lakestani M. Abundant soliton solutions for the Kundu–Eckhaus equation via tan[φ(ξ)]-expansion method. Optik. (2016) 127:5543–51. doi: 10.1016/j.ijleo.2016.03.041

CrossRef Full Text | Google Scholar

21. Ahmed N, Irshad A, Mohyud-Din ST, Khan U. Exact solutions of perturbed nonlinear schrödinger's equation with kerr law nonlinearity by improved tan(2) -expansion method. Opt Quantum Electron. (2018) 50:1–27. doi: 10.1007/s11082-017-1314-y

CrossRef Full Text | Google Scholar

22. Cheemaa N, Younis M. New and more general traveling wave solutions for nonlinear schrödinger equation. Waves Random and Complex Media. (2016) 26:30–41. doi: 10.1080/17455030.2015.1099761

CrossRef Full Text | Google Scholar

23. Yan Z. A sinh-Gordon equation expansion method to construct doubly periodic solutions for nonlinear differential equations. Chaos Solitons Fractals. (2003) 16:291–7. doi: 10.1016/S0960-0779(02)00321-1

CrossRef Full Text | Google Scholar

24. Cattani C, Sulaiman TA, Baskonus HM, Bulut H. Solitons in an inhomogeneous Murnaghan's rod. Eur Phys J Plus. (2018) 133:228. doi: 10.1140/epjp/i2018-12085-y

CrossRef Full Text | Google Scholar

25. Baskonus HM, Sulaiman TA, Bulut H. On the new wave behavior to the Klein–Gordon–Zakharov equations in plasma physics. Indian J Phys. (2019) 93:393–9. doi: 10.1007/s12648-018-1262-9

CrossRef Full Text | Google Scholar

26. Cattani C, Sulaiman TA, Baskonus HM, Bulut H. On the soliton solutions to the Nizhnik-Novikov-Veselov and the Drinfel'd-Sokolov systems. Opt Quantum Electron. (2018) 50:138. doi: 10.1007/s11082-018-1406-3

CrossRef Full Text | Google Scholar

27. Bulut H, Sulaiman TA, Baskonus HM. Dark, bright optical and other solitons with conformable space-time fractional second-order spatiotemporal dispersion. Optik. (2018) 163:1–7. doi: 10.1016/j.ijleo.2018.02.086

CrossRef Full Text | Google Scholar

28. Bulut H, Sulaiman TA, Baskonus HM, Rezazadeh H, Eslami M, Mirzazadeh M. Optical solitons and other solutions to the conformable space–time fractional Fokas–Lenells equation. Optik. (2018) 172:20–7. doi: 10.1016/j.ijleo.2018.06.108

CrossRef Full Text | Google Scholar

29. Baskonus HM, Sulaiman TA, Bulut H. Bright, dark optical and other solitons to the generalized higher-order NLSE in optical fibers. Opt Quantum Electr. (2018) 50:253. doi: 10.1007/s11082-018-1522-0

CrossRef Full Text | Google Scholar