AME: A Cross-Scale Constellation of CubeSats to Explore Magnetic Reconnection in the Solar–Terrestrial Relation

Introduction

Magnetic reconnection is a fundamental process of plasma transport and energy conversion, with applications in the near-Earth space, solar plasmas, astrophysical systems, as well as in the laboratory. Magnetic reconnection regulates the energy transfer in the solar–terrestrial connection. In the solar corona, magnetic reconnection explosively releases energy and sets off solar eruptions such as the coronal mass ejections and solar flares. In the Earth's magnetosphere, the dayside and night-side magnetic reconnection regulates the energy flow and energy release within the magnetosphere.

Intrinsically, magnetic reconnection is a multi-scale plasma process, involving global-scale, meso-scale, and kinetic-scale structure and processes. The “breaking” and “reconnection” of magnetic field lines occur in a limited region. The consequence and the impact of reconnection on the near-Earth space, however, are of a global nature. The Earth's magnetosphere is an ideal laboratory for in situ exploration of magnetic reconnection. Existing spacecraft constellation missions, such as Cluster and MMS, focused on measurements of magnetic reconnection on ion and electron kinetic scales. Cross-scale and macro-scale physics of reconnection, which is crucial for a precise characterization of its role in the context of space weather, remains to be explored. Generally, at least four spacecraft are needed to distinguish between spatial and temporal variations, and to measure gradients in the observed system. However, a large number of spacecraft is needed for multiple-scale measurements. While usage of standard spacecraft may imply a huge cost for a constellation mission, a CubeSat Constellation provides a cost-effective approach to achieve multiple-scale measurements.

With the above considerations, we propose a CubeSat Constellation “AME” (self-Adaptive Magnetic reconnection Explorer), which aims to make simultaneous cross-scale in situ measurements of space plasmas. In this paper, we describe the science rationale and the proposed mission profile of AME. The organization of the paper is as follows. The Magnetic Reconnection in Solar–Terrestrial Relation section presents an overview of magnetic reconnection in the context of space weather. The Scientific Rationale for Cross-Scale Constellation Missions section describes existing constellation missions and the need for future cross-scale constellation missions. The Self-adaptive Magnetic Reconnection Explorer section presents the science opportunity, mission profile, and payload of the AME mission. The Summary section gives the summary and conclusions.

Magnetic Reconnection in Solar–Terrestrial Relation

A major part of solar–terrestrial relations, responsible in particular for space weather phenomena, is the transport of energy, mass, and momentum into the near-Earth space during the interaction between the solar wind and Earth's magnetosphere. One of the most important modes of the solar–wind–magnetosphere interactions is magnetic reconnection. Simply speaking, magnetic reconnection refers to the “cut” and “reconnection” of magnetic field lines in magnetized plasmas. This process is usually accompanied with energy conversion and transport of plasmas of different origins, responsible for explosive energy release phenomena such as solar flares, CMEs, and geomagnetic storms (e.g., [1]).

In the near-Earth space, magnetic reconnection regulates the energy entry and energy release within the magnetosphere. As illustrated in Figure 1, two primary sites for magnetic reconnection in the magnetosphere are the sub-solar point on the dayside and the rear magnetotail on the night-side. The dayside magnetopause reconnection enables the entry of magnetic flux and energy from the solar wind into the magnetosphere. This is the key process of the solar–terrestrial connection. The transfer of solar wind energy into the near-Earth space is a driver of geomagnetic activity. The night-side magnetic reconnection regulates the release of energy within the magnetosphere. The stretched magnetotail stores the energy from the solar wind. Magnetic reconnection releases the stored energy explosively within the magnetosphere and drives geomagnetic storms and substorms [3–5], producing various space weather effects such as enhanced relativistic electron fluxes in the radiation belts, increase in the ionospheric scale height, induced currents on ground power transmission lines, and bright auroras.

FIGURE 1

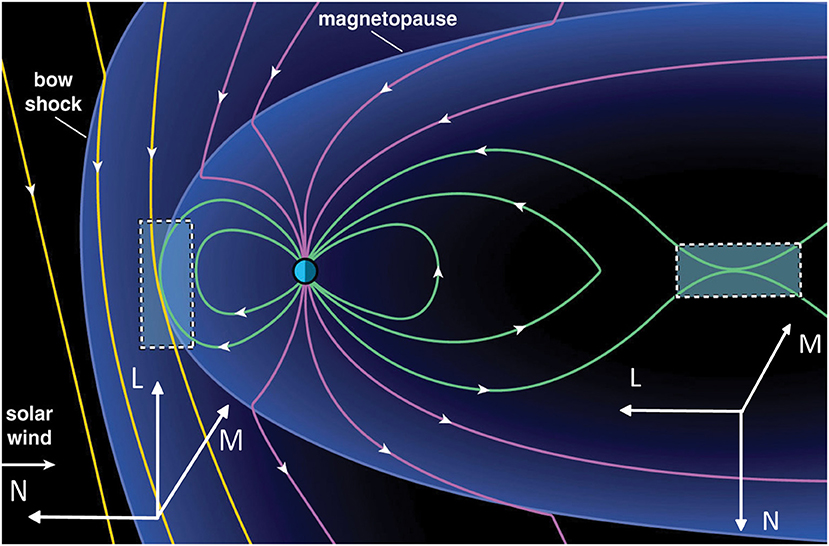
Figure 1. Magnetic reconnection in the magnetosphere during southward magnetic field in the solar wind. Reconnection sites are indicated by two box areas. The LMN coordinate system represents the local normal boundary coordinate system for reconnection at different locations: L is the direction of the reconnecting magnetic field line, M is tangential to the normal and in the direction of the electric current, and N is the normal direction to the boundary layer. The figure is modified from Figure 1 of Burch et al. [2] under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/).

Scientific Rationale for Cross-Scale Constellation Missions

Magnetic reconnection is a spectacular example of a physical system dominated by multi-scale physics. In the large-scale region outside the site of where magnetic field lines “reconnect,” the so-called MHD (magnetohydrodynamic) approximation applies. Plasma elements connected at one time by a single magnetic field line remain connected at subsequent times. The magnetic field lines appear to be “frozen-in” with the plasma motion. Magnetic reconnection is possible only where the MHD approximation breaks down, which happens in a thin non-MHD layer of electron-kinetic scales.

Understanding the nature of reconnection relies on the knowledge of both large-scale and kinetic-scale plasma properties. In the context of solar–terrestrial relation, one of the most important questions for reconnection is how much of the incoming solar wind plasma reconnects and flows into the magnetosphere, vs. how much of it flows around the magnetosphere without reconnecting [6]? This is substantially equivalent to the question of what determines the rate of magnetic flux transfer into the Earth's magnetosphere (reconnection rate). Whether the reconnection rate is determined primarily by the properties of the non-MHD layer in the reconnection site or, on the contrary, by the global dynamics and boundary conditions that govern the large-scale plasma flow is a question debated since the earliest studies of reconnection and still not conclusively settled. Another important question of reconnection is what determines the reconnection onset. Since the initial theoretical studies of large-scale reconnection [e.g., [7]], it is expected that the onset and evolution of the reconnection process becomes governed not only by the physics of the diffusion region but also by the large-scale external magnetic fields and plasmas. The onset of reconnection must involve special conditions in thin current sheets—otherwise, it would occur all the time, which it does not. Similarly, the cessation of reconnection must involve interactions with a changing external environment; otherwise, it would continue forever. To date, we know neither what these conditions are nor where and when they occur, but it is exceedingly likely that their occurrence is shaped by the large-scale regions separated by the reconnecting layers.

In the near-Earth space, existing constellation missions such as Cluster, THEMIS, and MMS have fulfilled their science goals with four or five spacecraft placed at key positions or key separation distances from each other. The characteristic scales of previous and existing constellation mission in the magnetosphere are summarized in Figure 2. Cluster initially addressed plasma processes at the ion-scale and then measured two scales at the same time with two spacecraft separated from a few kilometers up to a few tens of thousands of kilometers. In such a case, however, the 3-D tetrahedron scale was lost with only four spacecraft. THEMIS addressed the storm and substorm process, and showed that magnetic reconnection in the near-Earth region was responsible for the initiation of magnetic energy release and the subsequent energy transport to the inner magnetosphere and ionosphere [3, 4]. The three inner THEMIS spacecraft were measuring fluid scales (Earth radii), while the other two spacecraft were at 10 and 20 R_E away down the tail, covering the global scale. However, the five THEMIS probes were not in the form of a tetrahedron. Again, ion and electron scales could not be measured simultaneously, and the kinetic processes were not studied using multi-spacecraft. More recently, MMS focused on reconnection process at the electron scale with the four spacecraft in a tetrahedron shape and in the range of 7–50 km [2]. The electron diffusion region could be thus recognized and appropriately studied (e.g., [8–10]).

FIGURE 2

Figure 2. Schematic showing the spatial scales of past magnetosphere constellation missions and proposals since year 2000.

The next step forward to advance the physics of reconnection is, therefore, to measure simultaneously the electron-scale and ion-scale processes in the reconnection layer and their effect on the magnetosphere at fluid and global scales. It is timely to embark now on the questions of how the reconnection microphysics shapes the large-scale space environment and how the latter feeds back on the former. Answering this question requires a multi-scale observational approach.

A cross-scale mission allows putting magnetic reconnection process into the context of solar–terrestrial relation. Such a mission will answer how reconnection facilitates energy conversion on large scales and how this conversion couples to the dynamics of the small electron diffusion region. It can further address the critical question of why reconnection operates in small bursts at times and in large eruptions at others. It will furthermore shed light on the puzzle of whether large eruptions are a collection of small bursts occurring together, or whether they are a different, organized, type of reconnection altogether [11]. Understanding when and how these disruptions occur is also critical to predict the harmful effects on the space environment, which are collectively referred to as “space weather” [12].

The Self-Adaptive Magnetic Reconnection Explorer (AME) Mission

Mission Overview

Previous and existing constellation missions of space plasma, for instance, Cluster [13], MMS [8, 14], and THEMIS [15], consist of four to five identical spacecraft. In principle, four spacecraft are needed to distinguish spatial and temporal variation at one specific scale. Such a constellation mission can provide detailed measurements at a single spatial scale. Owing to the limited number of spacecraft in previous constellations, however, the connection of pace plasma process across multiple scales cannot be fully explored.

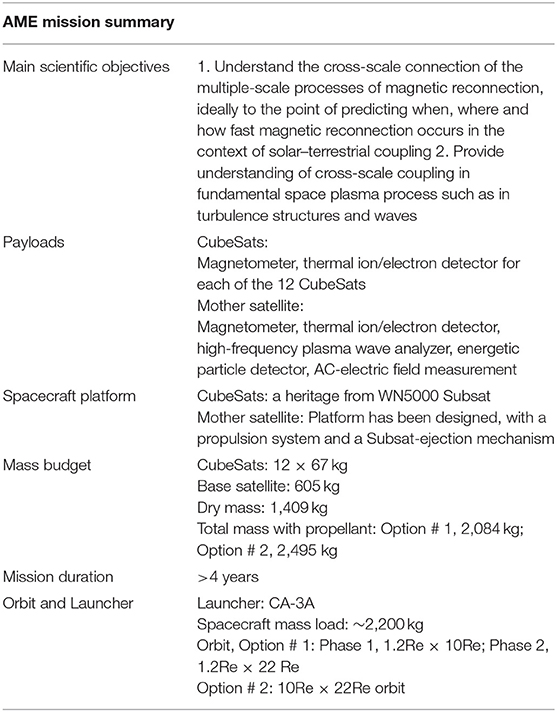
The proposed self-Adaptive Magnetic reconnection Explorer (AME) mission consists of a base satellite and a constellation of 12 small CubeSats. The basic concept of the mission is to employ a constellation of spacecraft to take simultaneous measurements at differential spatial scales, exploring processes and structures from kinetic-scale to macro-scale in space plasmas. The AME mission proposal is currently in the stage of pre-phase A in the Strategic Priority Research Program on Space Science II, Chinese Academy of Sciences. In Table 1, we present a summary of the AME mission profile.

TABLE 1

Table 1. AME mission profile overview.

Scientific Objectives

The scientific rationale for cross-scale constellation missions has been well-described in the previous section. With the achievement of previous constellation mission at individual scale, many fundamental questions of magnetic reconnection remain to be explored. With all the above considerations in mind, we propose the following science objective for the cross-scale AME mission.

Science objective # 1. Understand the cross-scale connection of the multiple-scale processes of magnetic reconnection, ideally to the point of predicting when, where, and how fast magnetic reconnection occurs in the context of solar–terrestrial coupling.

The investigation of fundamental aspects of reconnection, such as when, where, and how fast it occurs, requires the understanding of the cross-scale coupling and the global aspect of reconnection. Answers to these questions are necessary for quantitative prediction of the role of reconnection in the context of space weather. Magnetic reconnection is usually studied in LMN (local-normal-boundary) coordinate system (see the description of LMN in Figure 1). In the following, we specify the science questions in this LMN coordinate.

Magnetic reconnection occurs in the thin current layer associated with magnetic field shear. However, magnetic field shear does not necessarily imply magnetic reconnection is occurring. Current layers without signatures of magnetic reconnection abound in space plasmas. Predicting when reconnection occurs relies on the understanding on the sequence of processes related to reconnection onset. Figure 3 shows the observational signals related to the onset of magnetic reconnection. These signatures of reconnection are considered to be detected in the LN plane in the LMN coordinate system.

FIGURE 3

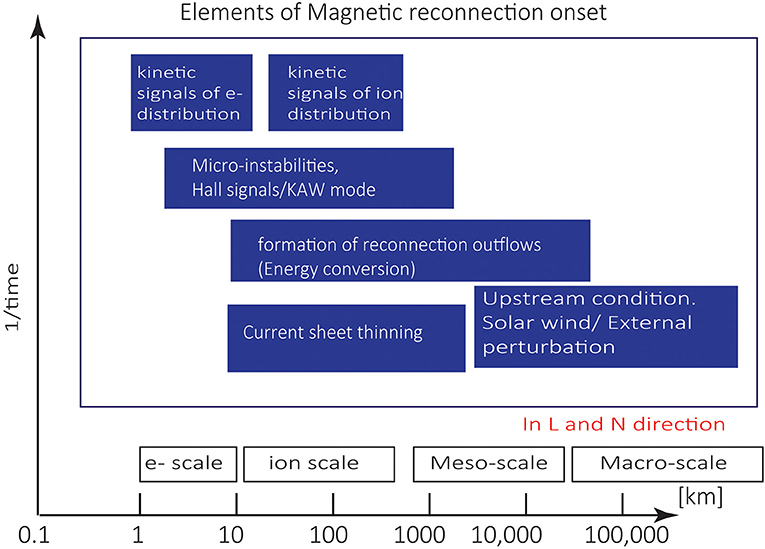
Figure 3. Science questions of AME mission. Schematic of the scales of physical processes in the reconnection onset problem. This includes but not limited to upstream conditions, solar wind/external perturbation, current sheet thinning, reconnection outflows, Kinetic Alfven Waves (KAW)/Hall signals, micro-instabilities, kinetic signals of electron/ion distributions.

At the largest spatial and time scales, the upstream conditions are considered to affect the pre-condition of onset. The upstream plasma beta (the ratio of particle pressure to magnetic pressure), combined with the magnetic field shear angle, is believed to be an important parameter to determine if reconnection can occur for a certain current layer (e.g., [16]). On a smaller scale, the thinning of the current layer to an ion-scale is considered as a pre-onset signal in reconnection models. The thinning of the current sheet enhances the free energy for reconnection to occur. Thin current sheets can be unstable to a variety of plasma instabilities, including the lower-hybrid drift instability and the collisionless tearing mode instability (e.g., [17–19]). In addition, thin current layers down to the ion scale are also favorable for introducing two-fluid effects and fast reconnection (e.g., [20]). On ion scales to macro scale, the formation of diverging ion outflows from the reconnection site is the most definite signal for the occurrence of magnetic reconnection (e.g., [21, 22]). On the ion kinetic scale to the meso scale, the Hall fields and current, which have been also interpreted as an kinetic Alfven mode [23–25] or whistler mode [26], are considered as a key element for fast collisionless reconnection [20, 27]. On the electron kinetic scale, off-diagonal terms of the electron pressure tensor are expected to be related to the reconnection electric field [28, 29]. Similarly, off-diagonal terms of the ion pressure tensor are considered to balance the reconnection electric field on the ion-scale as well (e.g., [30–32]). Kinetic signals of reconnection at the electron-scale also include the crescent-like distributions, as was recently observed by the MMS mission (e.g., [8]). As described above, processes related to the reconnection onset occur at multiple scales. It would require a cross-scale constellation mission to resolve the relation and the time sequence of these processes. Such cross-scale measurements can be directly compared with particle-in-cell (PIC) and MHD-PIC simulation models (e.g., [33–35]).

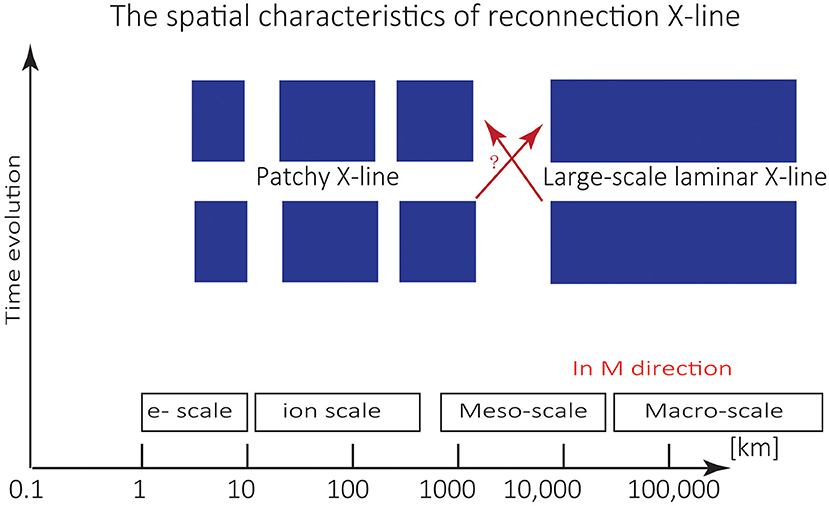
In simple terms, the reconnection site where magnetic field lines “reconnect” takes the shape of an “X-line” along the direction of the electric current (in the M direction in LMN coordinate system). The extent of the “X-line” characterizes the spatial scale of reconnection in space. On the largest scale, a case study in the solar wind indicates that the X-line can be as large as several hundred Re [36]. Measurements in the magnetosphere suggest that the X-line of magnetopause reconnection may extend from several Re to tens of Re along the magnetopause [37, 38]. The magnetopause X-line may also appear patchy or of limited extent as inferred from in situ and ground-based measurements ([39] JGR; [40]). Compared with existing in situ multipoint missions, a cross-scale constellation would have much larger spatial coverage in terms of number of measurement points. As illustrated in Figure 4, such a constellation would allow systematic investigations of the spatial characteristics of the X-line.

FIGURE 4

Figure 4. Science questions of AME mission. Spatial scales of magnetic reconnection X-line.

A central question of magnetic reconnection is how fast it occurs [41, 42]. The meaning of “how fast reconnection occurs” includes at least two elements, the magnetic topology changes and the energy conversion. This is illustrated in Figure 5. In the scale of the reconnection diffusion region, the change in magnetic topology allows the mixture of plasmas from different origins. On the global-scale, magnetic flux transfer produced by magnetic reconnection is a crucial element in the global evolution of the magnetosphere [43]. Energy conversion occurs in a limited diffusion region in the Sweet–Parker model and also in the extended ion exhaust region downstream. In the Petschek model, the diffusion is limited, and energy conversion mostly occurs in switch-off shock at the boundary [42]. Recent observations suggest that coherent structures, for instance reconnection fronts and flux ropes, play an important role in energy conversion following reconnection onset [44, 45]. These coherent structures occur over a wide range of spatial scales. A cross-scale constellation mission can study the relation between different energy conversion processes at different scales.

FIGURE 5

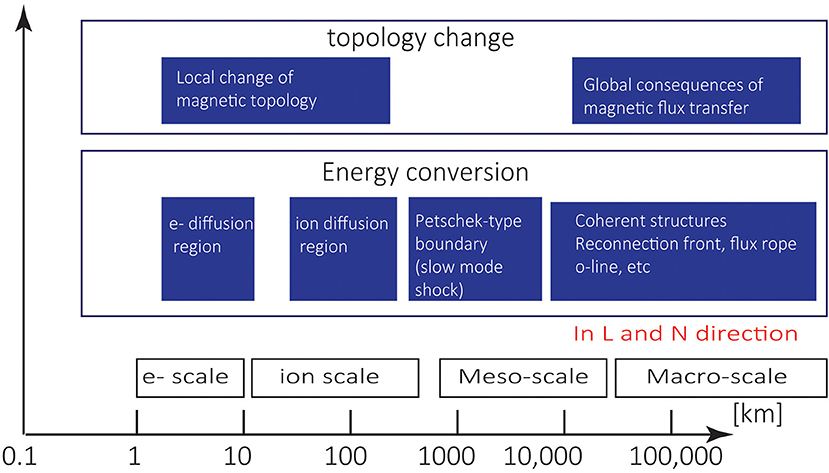
Figure 5. Science questions of AME mission. Spatial scales of physical processes in the energy conversion and topology changes in reconnection.

Science objective #2. Provide understanding of cross-scale coupling in fundamental space plasma process such as in turbulence, structures, and waves.

In addition to studying magnetic reconnection, a cross-scale constellation can provide multi-scale investigations on a variety of phenomena in space plasmas, including, but not limited to, turbulence, shock waves, current sheets, Kelvin Helmholtz instability, various types of discontinuities, flux ropes, dipolarization fronts, fast ion busty bulk flows, plasma waves, etc.

Turbulence and coherent structures universally exist in space plasmas. Kinetic-scale turbulence is strongly coupled to dissipative processes such as magnetic reconnection and shocks [46–48]. One form of turbulence in space plasmas is flow eddies. Recent MMS spacecraft provide detailed observation of electron-scale vortices [49, 50] and larger-scale flow vortices [51].

Current sheets (CSs) are widely spread in space plasmas and play an important role in storage and release of magnetic energy in the magnetosphere. Multiple-scale physics is a key ingredient of the formation of CSs. Observations and theoretical analysis revealed that multiple current–layer structures could form within a CS (e.g., [52–54]).

Kelvin–Helmholtz instability (KHI) often occurs on the Earth's magnetopause. Rolled-up K.-H. waves and the mixing of magnetosheath and magnetospheric were observed as Cluster was skimming the magnetopause around the apogee (e.g., [55]). Such a large-scale structure as K.-H. waves would require cross-scale simultaneous measurements, with spacecraft at fluid scale, ion scale, and electron scale in order to be further understood (e.g., [56–58]).

The bursty bulk flow (BBF) in the magnetotail and the associated dipolarization front exhibit a multiple-scale nature, as revealed by multiple spacecraft measurements. At MHD scale, flow patterns of BBFs participate in the large-scale magnetosphere–ionosphere coupling process (e.g., [59, 60]). At ion scale and electron scale, kinetic signatures of dipolarization fronts have been resolved by Cluster [61], THEMIS [62], and MMS (e.g., [63, 64]).

Plasma waves in the magnetosphere occur over a broad range of temporal and spatial scales. They can contribute to particle acceleration, scattering, and energy transport, which can modify magnetic reconnection and plasma boundaries. Plasma waves of a variety of scales are frequently observed in relation to reconnection, ranging from low-frequency kinetic Alfvén waves (KAW), to intermediate-frequency lower hybrid and whistler-mode waves, electrostatic broadband and solitary waves, as well as the high-frequency upper hybrid, Langmuir, and electron Bernstein waves [65].

Studies of structures and waves from four-point measurements usually rely on the assumption of linear interpolation and laminar structure at scales of spacecraft separation [66]. Studies of turbulence usually need to apply Taylor's hypothesis or equivalent assumptions to convert timescale to spatial scales. With a cross-scale constellation mission, some assumptions of the four-point/single-point analysis method can be relaxed or replaced. New multi-point analysis method, such as non-linear interpolation [67], may be applied to shed new insights in studies of turbulence, structures, and waves.

Scientific Payload

The magnetometer and thermal plasma (ion/electron) detectors are embarked on the main spacecraft and all the 12 CubeSats. In addition to these three payloads, a high-frequency plasma wave analyzer, an energetic particle detector, and a DC electric field instrument are employed on the main spacecraft.

The Magnetometer (MAG)

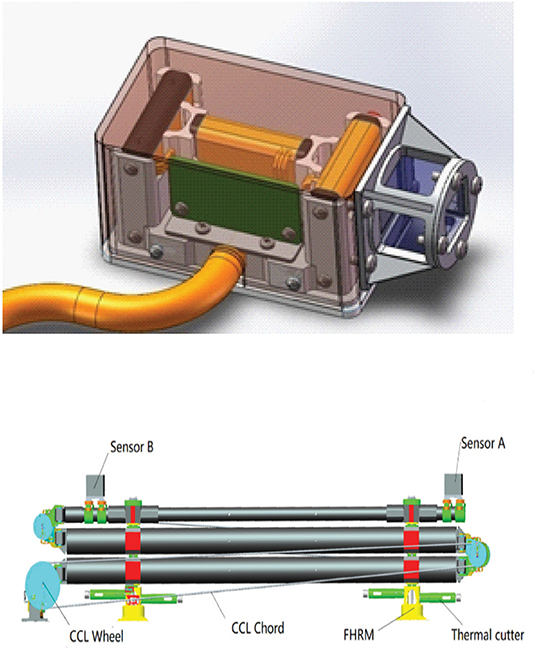
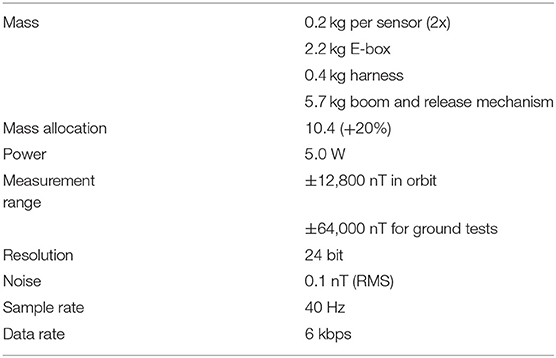
The vector magnetometer measures the three-dimensional magnetic field vector in the frequency range from DC to 40 Hz. The configuration of MAG sensor and its deployable boom are shown in Figure 6. The MAG is a heritage from the payload for the CAS-ESA joint SMILE mission. Its specifications are shown in Table 2. The range of measurement for MAG is from −12,800 nT to +12,800 nT. The noise level is 0.1 nT (RMS). The mass of the MAG instrument, itself (without the deployable boom), is around 3.2 kg, and the boom is 5.7 kg. Its power is 5.0 W.

FIGURE 6

Figure 6. Configuration of MAG: (Top) the MAG sensor; (Bottom) boom.

TABLE 2

Table 2. Summary of the performance of MAG.

25 ev−30 keV Thermal Plasma (Ion/Electron) Detector

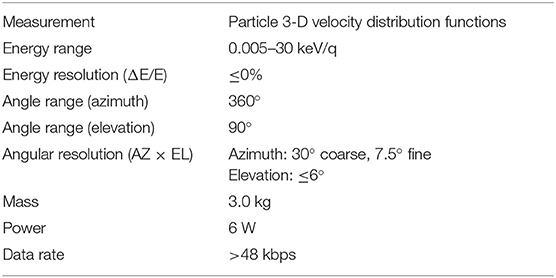
The thermal plasma (ion/electron) detector measures the three-dimensional particle distribution and its corresponding moments in the range of 5 eV−30 keV. The instrument includes two electrostatic analyzers, which take measurements for ions and electrons, respectively. The payload has a heritage from the light ion analyzer (LIA) for the CAS-ESA joint SMILE mission. The configuration of one electrostatic analyzer and electronic box is shown in Figure 7. The specifics of the plasma (ion/electron) detector are presented in Table 3. The energy resolution is 10%. The energy range is 5 eV−30 keV. The angle range of the detector is 360° in the azimuthal direction and 90° in the elevation direction. To make a measurement of the full 4Π solid space, either a spinning spacecraft or two identical sensors are needed. For a time cadence of 0.5 s, the data rate for each instrument is 48 kbps. The mass and power for each instrument is 3 kg and 6.0 W, respectively. The investigation to miniaturize the plasma detector is underway.

FIGURE 7

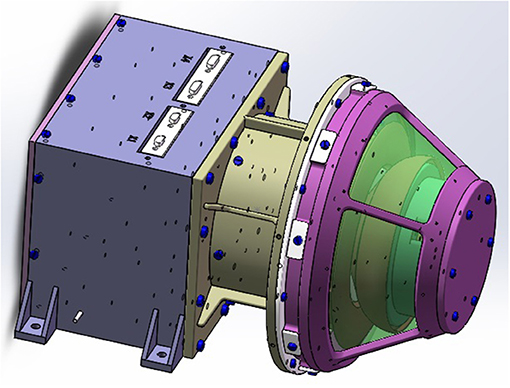
Figure 7. The configuration of the thermal plasma (ions) detector, including the sensor and the electronic box.

TABLE 3

Table 3. Summary of the performance of thermal plasma (ion/electron) detector.

Electric Field Measurement

The double-probe electric field instrument uses the potential difference between two conducting spheres separated by booms to measure the electric field. The electric field is obtained by dividing the potential difference by the length between the probes. Since the main spacecraft is not spinning, and the length of the boom is limited (10 m for each boom), only the AC-electric field is measured as required. Spinning mother spacecraft and longer electric field boom will also be considered to implement accurate measurements of Dc and low-frequency electric fields. The specifications of the electric field measurement areas follow. The dynamic range of the electric field measurement is ±1,000 mV/m. The electric field resolution is 15 μV/m. The frequency band of the measurement is from 10 Hz to 5 kHz. The range of the voltage on the probe is −100 V~ + 100 V. The resolution of the voltage on the probe is 3 mV. The mass and power is 1.5 kg and 2.5 W for each pair of the probes. The study of the possibility to employ a third pair of booms in the direction perpendicular to the spacecraft plane is underway.

High-Frequency Plasma Wave Analyzer

The high-frequency plasma wave analyzer employ a tri-axial search-coil magnetometer (SCM) to measure the 3D wave magnetic field vector in the frequency range from 10 Hz to 10 kHz. The noise level is of the designed SCM and is <5 × 10⁻³nT/$\sqrt{}\text{Hz}$ at 10 Hz, 2.5 × 10⁻⁴nT/$\sqrt{}\text{Hz}$ at 200 Hz, 5 × 10⁻⁵nT/$\sqrt{}\text{Hz}$ at 2 kHz, 6 × 10⁻⁵ nT/$\sqrt{}\text{Hz}$ at 10 KHz. The waveform provided by the SCM, together with electric field data provided by the double-probe measurement, is processed inside the digital signal processor of the high-frequency plasma wave analyzer. A deployable boom would be necessary to avoid perturbations from the spacecraft on the measurements.

Energetic Particle Measurement

The energetic particle detector measures the energy spectra and the pitch angle of the energetic protons and electrons. The energetic particle detector includes three sets of sensors and one electronic box. Each set of sensors include one proton sensor and one electron sensor. The energy range of the measured proton is 50 keV−4 MeV, the field-of-view is 40°, and the energy resolution is 20%. The energy range of the electrons is 50 keV−400 keV, the field-of-view is 30°, and the energy resolution is 20%.

Spacecraft, Orbit, and Launcher

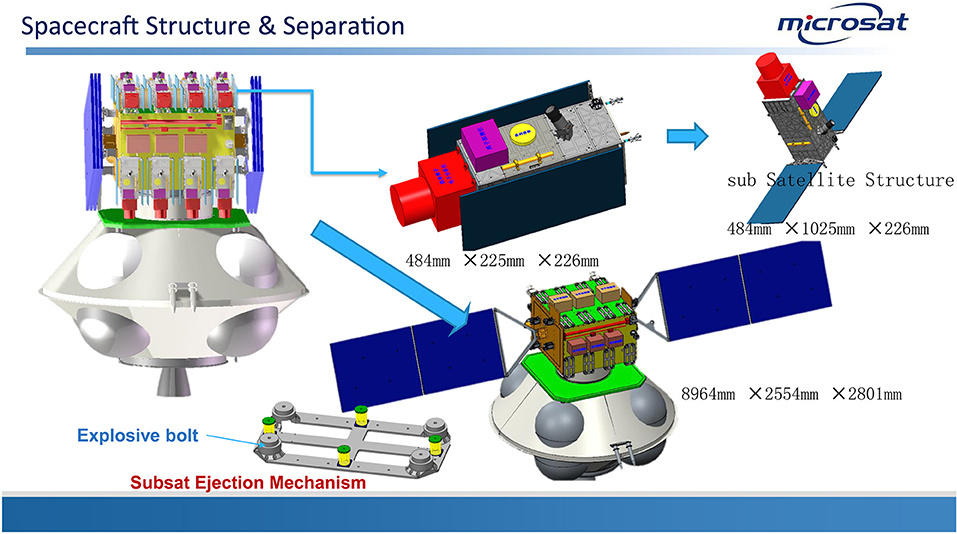
The spacecraft configuration is shown in Figure 8. The left side shows the configuration of the combination of the AME constellation fleet. The 12 CubeSats are installed at the top of the main spacecraft. A release mechanism will deploy each CubeSat when the spacecraft reaches the nominal orbit. The design of the CubeSats is shown in the middle top of the figure. The dimension of each CubeSat before (after) the deployment is 484 mm × 225 mm × 226 mm (484 mm × 1,025 mm × 226 mm). The main spacecraft dimensions, after unfolding solar panels, are 8,964 mm × 2,554 mm × 2,801 mm.

FIGURE 8

Figure 8. The configuration of the main spacecraft and the CubeSats of the AME mission.

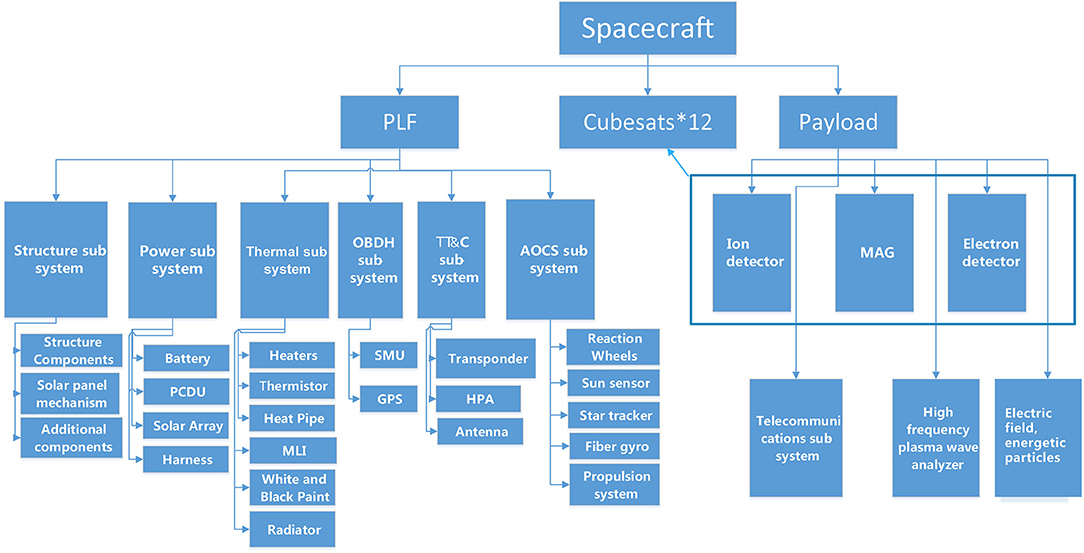
The spacecraft product tree is presented in Figure 9. The main spacecraft includes the Platform (PLF) consisting of six sub-systems. The structure sub-system includes the structure components, the solar panel mechanism and additional components. The power sub-system includes the batteries, the power control unit (PCDU), and the solar array and harness. The thermal sub-system includes the heaters, thermistor, heat pipe, multi-layer insulation (MLI), white and black paint, and radiator. The onboard data handling (OBDH) sub-system include the global position system (GPS) and solid state memory unit (SMU). The telemetry, tracking, and commanding (TT&C) sub-subsystem includes the transponder, high-power amplifier (HPA), and antenna. The TT&C system is responsible for uploading the telemetry commands, downloading all telemetry data, and ranging and tracking of the satellite. We rely on the inter-satellite communication system to transmit science data from CubeSats to the mother satellite. All the data are then transmitted from the mother satellite to ground stations via a high-gain antenna and a Ka band transmitter. The TM and TC data rate are 8,192 and 2,000 bps, respectively. For the inter-satellite communication system, a broad-beam UHF antenna and a UHF transmitter are essential. The main specifications for the UHF antenna are frequency, 436 MHz; bandwidths, Δf ≥ 2 MHz; gain, G ≥ −3 dBi (within Beam range); polarization mode, linear. The specifications for the UHF transmitter are frequency, 436 MHz; output power, >6 W; data rate, 4 kbps; carrier modulation, OQPSK; data coding, differential coding of the NRZ-L type; channel coding, convolutional coding (7, 1/2), of constraint length 7 and ratio 1/2. The configuration of UHF antenna and transmitter is feasible and has been widely used for inter-satellite communication missions, for instance, xx-6 and Kuai Xiang mission at the Innovation Academy for Microsatellites. The Attitude and Orbit Control System (AOCS) sub-system includes the reaction wheels, the sun sensor, star tracker, Fiber Gyro, and propulsion system. The average power for the platform and payload of the main satellite is 200 and 180 W, respectively. The average power for the platform and payload of each CubeSat satellite is 67 and 30 W, respectively.

FIGURE 9

Figure 9. The spacecraft product tree of the main spacecraft and CubeSats.

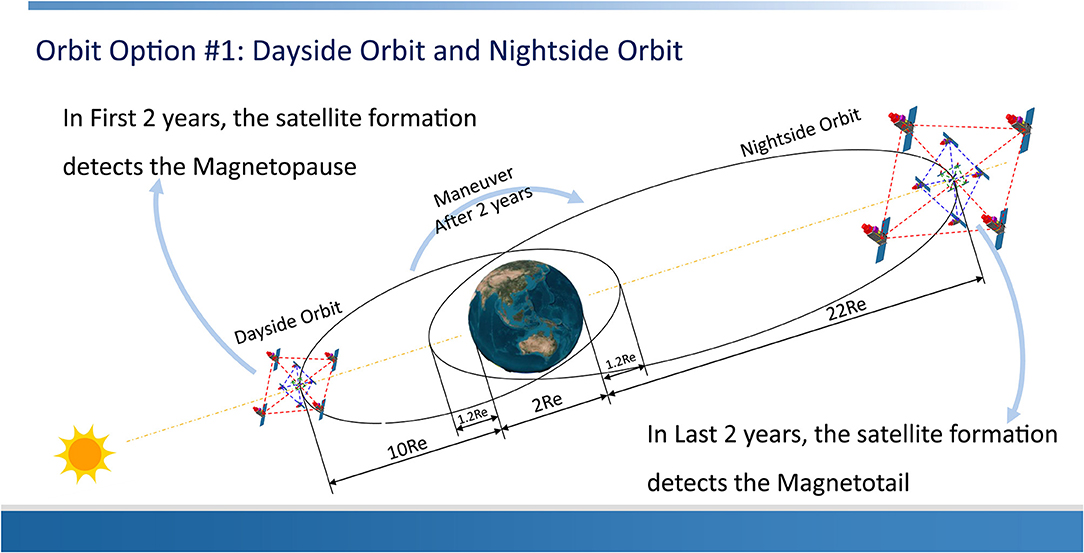
Two of the spacecraft orbits are envisaged to fulfill the science requirement to measure the reconnection near the dayside magnetopause and in the night-side magnetotail. The orbit option # 1 is shown in Figure 10.

FIGURE 10

Figure 10. The configuration of the spacecraft orbit in option # 1.

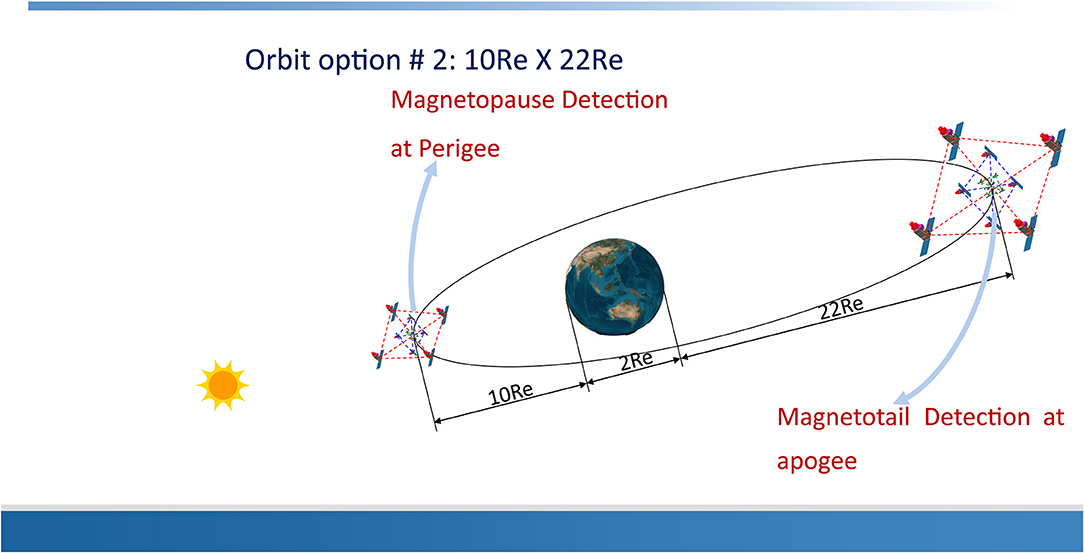
Option #1 includes a dayside phase of 2 years and a night-side phase of 2 years. In the first dayside phase of the mission, the perigee is 1.2Re, the apogee is 10Re in the dayside, and the inclination is 23.5°. In the night-side phase, the perigee is 1.2Re, the apogee is 22Re in the night-side, and the inclination is 23.5°. Option # 2 is an optional orbit that can measure the magnetopause reconnection near the perigee and magnetotail reconnection at the apogee. Option #2 is shown in Figure 11. The parameter of the orbit is as follows. The perigee is 10Re, the apogee is 22Re, and the inclination is 23.5°.

FIGURE 11

Figure 11. The configuration of the spacecraft orbit in option # 2.

The main satellite and the 12 CubeSats form multiple tetrahedrons around the main satellite. The baseline option of the satellite formation (formation #1) is to divide the 12 CubeSats into three four-satellite groups. Each four-satellite group forms a tetrahedron at a specific scale. The three tetrahedra have three different scales, at 1–10 km (electron scale), 100–1,000 km (ion scale), and 1–3Re (macro scale). Another optional formation (formation #2) is to divide the 12 CubeSats into four three-satellite groups. Each group of three CubeSats, together with the main spacecraft, forms a tetrahedron. The fleet forms four tetrahedron at 1–10 km (electrons scale), 100 km (ion scale), 1,000–10,000 km (meso scale), and 3–5Re (macro scale). In either formation, the configuration of each tetrahedron is self-adjustable to form a suitable configuration in the LMN coordinate system. The input for adjusting the configuration is based on either real-time measurement data or advance planning. The propulsion system of the CubeSats will have sufficient fuel to maintain and adjust the tetrahedral formation.

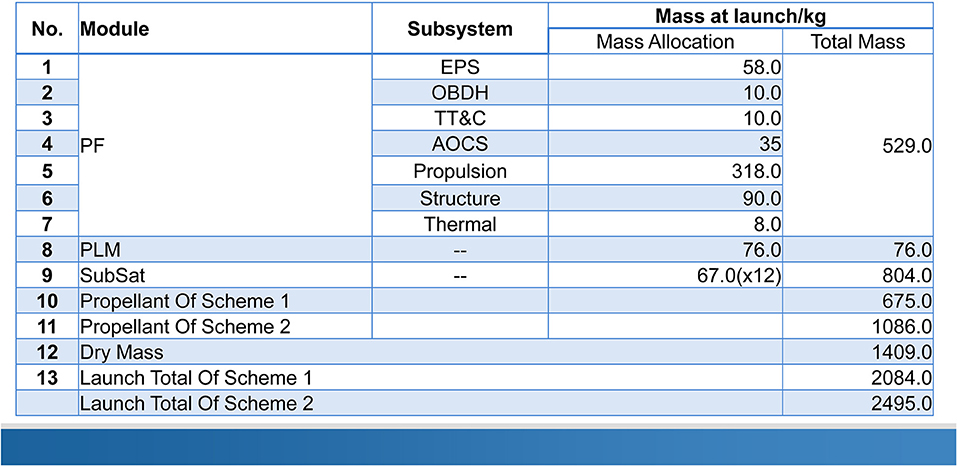
The mass budget of the mission is shown in Figure 12. The platform (PF) part of the main satellite is 529 kg. The payload (PLM) part of the main satellite is 76 kg. The mass of each CubeSat is 67 kg, including 26 kg of payload and 9.5 kg of propulsion system. The total dry mass for the main satellite and the 12 CubeSats is 1,409 kg. The Launcher is Long March CZ-3A, which has the capacity to carry a spacecraft mass of 2,200 kg with a maximum envelope of 3,350 ^* 8,887 mm. Including the propellant, the total mass for launch is 2,084 kg for option # 1 and 2,495 kg for option # 2. The launch site is expected to be at Xichang. The ground stations are Sanya and Miyun.

FIGURE 12

Figure 12. The mass budget of the AME mission.

Summary

A cross-scale constellation mission allows investigating the global-scale consequences of magnetic reconnection in the near-Earth space and its coupling to the micro-scale physics in the reconnection layer. Such a constellation mission makes it possible to put the investigation of magnetic reconnection into the context of solar–terrestrial relations and space weather.

A constellation of four spacecraft is needed to make measurements at one specific scale. A multiple-scale constellation thus requires a large number of spacecraft. To provide a cost-effective approach to achieve such multiple-scale measurements, we propose the AME Constellation consisting of 12 small CubeSats surrounding a base satellite. This constellation enables simultaneous space plasma measurements at different spatial scales ranging from kinetic-scale to macro-scale. In this paper, we have described the scientific rationale and the profile of the proposed AME mission. This is a logical next step forward to advance the understanding of reconnection in the context of solar–terrestrial relations.

Data Availability Statement

All datasets generated for this study are included in the article/supplementary material.

Author Contributions

All authors participated on the discussions of the results and commented on the paper. LD, CW, PE, VA, MH, WG, VV, ZC, DG, HF, RN, MD, and QL contributed to the writing and editing of the paper.

Funding

The mission name AME was formerly known as SAME, which has been presented in the ISSI-BJ forum. This work was supported by NNSFC grants (41874175 and 41731070), the Specialized Research Fund for State Key Laboratories of China and China–Brazil Joint Laboratory for Space Weather, and the Strategic Pioneer Program on Space Science II, Chinese Academy of Sciences, grants XDA15350201 and XDA15052500.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The reviewer GL declared a past co-authorship with the authors LD and DG to the handling editor.

References

1. Gonzalez WD, Joselyn JA, Kamide Y, Kroehl HW, Rostoker G, Tsurutani BT, et al. What is a geomagnetic storm? J Geophys Res Space Phys. (1994) 99:5771–92. doi: 10.1029/93JA02867

CrossRef Full Text | Google Scholar

2. Burch JL, Moore TE, Torbert RB, Giles BL. Magnetospheric multiscale overview and science objectives. Space Sci Rev. (2016) 199:5–21. doi: 10.1007/978-94-024-0861-4_2

CrossRef Full Text | Google Scholar

3. Angelopoulos V, Artemyev A, Phan TD, Miyashita Y. Near-Earth magnetotail reconnection powers space storms. Nat. Phys. (2020) 16:317–21. doi: 10.1038/s41567-019-0749-4

CrossRef Full Text | Google Scholar

4. Angelopoulos V, McFadden JP, Larson D, Carlson CW, Mende SB, Frey H, et al. Tail Reconnection triggering substorm onset. Science. (2008) 321:931. doi: 10.1126/science.1160495

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Fu HS, Xu Y, Vaivads A, Khotyaintsev YV. Super-efficient electron acceleration by an isolated magnetic reconnection. Astrophys J Lett. (2019) 870:L22. doi: 10.3847/2041-8213/aafa75

CrossRef Full Text | Google Scholar

6. Vasyliunas VM. Fundamentals of planetary magnetospheres. In: Schriver CJ, Siscoe GL, editors. Heliophysics: Plasma Physics of the Local Cosmos. New York, NY: Cambridge University Press (2009) 256–294.

Google Scholar

7. Axford WI. The polar wind and the terrestrial helium budget. J Geophys Res. (1968) 73:6855–9. doi: 10.1029/JA073i021p06855

CrossRef Full Text | Google Scholar

8. Burch JL, Torbert RB, Phan TD, Chen LJ, Moore TE, Ergun RE, et al. Electron-scale measurements of magnetic reconnection in space. Science. (2016) 352:aaf2939. doi: 10.1126/science.aaf2939

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Chen LJ, Hesse M, Wang S, Gershman D, Ergun R, Pollock C, et al. Electron energization and mixing observed by MMS in the vicinity of an electron diffusion region during magnetopause reconnection. Geophys Res Lett. (2016) 43:6036–43. doi: 10.1002/2016GL069215

CrossRef Full Text | Google Scholar

10. Phan TD, Eastwood PJ, Shay MA, Drake JF, Sonnerup BUÖ, Fujimoto M, et al. Electron magnetic reconnection without ion coupling in Earth's turbulent magnetosheath. Nature. (2018) 557:202–6. doi: 10.1038/s41586-018-0091-5

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Hesse M, Cassak PA. Magnetic reconnection in the space sciences: past, present, and future. J Geophys Res. (2020) 125:e2018JA025935. doi: 10.1029/2018JA025935

CrossRef Full Text | Google Scholar

12. Cassak PA. Inside the black box: magnetic reconnection and the magnetospheric multiscale mission. Space Weather. (2016) 14:186–97. doi: 10.1002/2015SW001313

CrossRef Full Text | Google Scholar

13. Escoubet CP, Fehringer M, Goldstein M. The cluster mission. Ann Geophys. (2001) 19:1197–200. doi: 10.5194/angeo-19-1197-2001

CrossRef Full Text | Google Scholar

14. Burch JL, Torbert RB. Preface. Space Sci Rev. (2016) 199:1–3. doi: 10.1007/978-94-024-0861-4_1

CrossRef Full Text | Google Scholar

15. Angelopoulos V. The THEMIS mission. Space Sci Rev. (2008) 141:5–34. doi: 10.1007/s11214-008-9336-1

CrossRef Full Text | Google Scholar

16. Phan TD, Gosling JT, Paschmann G, Pasma C, Drake JF, Øieroset M, et al. The dependence of magnetic reconnection on plasma β and magnetic shear: evidence from solar wind observations. Astrophys J Lett. (2010) 719:L199. doi: 10.1088/2041-8205/719/2/L199

CrossRef Full Text | Google Scholar

17. Coppi B, Furth HP, Rosenbluth MN, Sagdeev RZ. Drift instability due to impurity ions. Phys Rev Lett. (1966) 17:377. doi: 10.1103/PhysRevLett.17.377

CrossRef Full Text | Google Scholar

18. Huba JD, Gladd NT, Drake JF. On the role of the lower hybrid drift instability in substorm dynamics. J Geophys Res Space Phys. (1981) 86:5881–4. doi: 10.1029/JA086iA07p05881

CrossRef Full Text | Google Scholar

19. Daughton W, Lapenta G, Ricci P. Nonlinear evolution of the lower-hybrid drift instability in a current sheet. Phys Rev Lett. (2004) 93:105004. doi: 10.1103/PhysRevLett.93.105004

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Hesse M, Kuznetsova M, Hoshino M. The structure of the dissipation region for component reconnection: particle simulations. Geophys Res Lett. (2002) 29:4-1-4-4. doi: 10.1029/2001GL014714

CrossRef Full Text | Google Scholar

21. Hones EW Jr, Bame SJ, Asbridge JR. Proton flow measurements in the magnetotail plasma sheet made with Imp 6. J Geophys Res. (1976) 81:227–34. doi: 10.1029/JA081i001p00227

CrossRef Full Text | Google Scholar

22. Paschmann GBUO, Sonnerup BÖ, Papamastorakis I, Sckopke N, Haerendel G, Bame SJ, et al. Plasma acceleration at the Earth's magnetopause: evidence for reconnection. Nature. (1979) 282:243. doi: 10.1038/282243a0

CrossRef Full Text | Google Scholar

23. Dai L. Collisionless magnetic reconnection via Alfvén eigenmodes. Phys Rev Lett. (2009) 102:245003. doi: 10.1103/PhysRevLett.102.245003

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Shay MA, Drake JF, Eastwood JP, Phan ET. Super-Alfvénic propagation of substorm reconnection signatures and poynting flux. Phys. Rev. Lett. (2011) 107:065001. doi: 10.1103/PhysRevLett.107.065001

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Dai L, Wang C, Zhang Y, Lavraud B, Burch J, Pollock C, et al. Kinetic Alfven wave explanation of the Hall fields in magnetic reconnection. Geophys Res Lett. (2017) 44:634–40. doi: 10.1002/2016GL071044

CrossRef Full Text | Google Scholar

26. Mandt ME, Denton RE, Drake JF. Transition to whistler mediated magnetic reconnection. Geophys Res Lett. (1994) 21:73–6. doi: 10.1029/93GL03382

CrossRef Full Text | Google Scholar

27. Birn J, Drake JF, Shay MA, Rogers BN, Denton RE, Hesse M, et al. Geospace Environmental Modeling (GEM) magnetic reconnection challenge. J Geophys Res Space Phys. (2001) 106:3715–9. doi: 10.1029/1999JA900449

CrossRef Full Text | Google Scholar

28. Vasyliunas VM. Theoretical models of magnetic field line merging. Rev Geophys. (1975) 13:303–36. doi: 10.1029/RG013i001p00303

CrossRef Full Text | Google Scholar

29. Hesse M, Schindler K, Birn J, Kuznetsova M. The diffusion region in collisionless magnetic reconnection. Phys Plasmas. (1999) 6:1781–95. doi: 10.1063/1.873436

CrossRef Full Text | Google Scholar

30. Cai HJ, Ding DQ, Lee LC. Momentum transport near a magnetic X line in collisionless reconnection. J Geophys Res Space Phys. (1994) 99:35–42. doi: 10.1029/93JA02519

CrossRef Full Text | Google Scholar

31. Henderson PD, Owen CJ, Lahiff AD, Alexeev IV, Fazakerley AN, Lucek E, et al. Cluster PEACE observations of electron pressure tensor divergence in the magnetotail. Geophys Res Lett. (2006) 33:L22106. doi: 10.1029/2006GL027868

CrossRef Full Text | Google Scholar

32. Dai L, Wang C, Angelopoulos V, Glassmeier KH. In situ evidence of breaking the ion frozen-in condition via the non-gyrotropic pressure effect in magnetic reconnection. Ann Geophys. (2015) 33:1147–53. doi: 10.5194/angeo-33-1147-2015

CrossRef Full Text | Google Scholar

33. Drake JF, Swisdak M, Schoeffler KM, Rogers BN, Kobayashi S. Formation of secondary islands during magnetic reconnection. Geophys Res Lett. (2006) 33:L13105. doi: 10.1029/2006GL025957

CrossRef Full Text | Google Scholar

34. Tóth G, Jia X, Markidis S, Peng IB, Chen Y, Daldorff LKS, et al. Extended magnetohydrodynamics with embedded particle-in-cell simulation of Ganymede's magnetosphere. J Geophys Res. (2016) 121:1273–93. doi: 10.1002/2015JA021997

CrossRef Full Text | Google Scholar

35. Lu QM, Wang HY, Huang K, Wang RS, Wang S. Formation of power law spectra of energetic electrons during multiple X line magnetic reconnection with a guide field. Phys Plasmas. (2018) 25:072126. doi: 10.1063/1.5034012

CrossRef Full Text | Google Scholar

36. Phan TD, Gosling JT, Davis MS, Skoug RM, Øieroset M, Lin RP, et al. A magnetic reconnection X-line extending more than 390 Earth radii in the solar wind. Nature. (2006) 439:175–8. doi: 10.1038/nature04393

PubMed Abstract | CrossRef Full Text | Google Scholar

37. Phan TD, Kistler LM, Klecker B, Haerendel G, Paschmann G, Sonnerup BÖ, et al. Extended magnetic reconnection at the Earth's magnetopause from detection of bi-directional jets. Nature. (2000) 404:848–50. doi: 10.1038/35009050

PubMed Abstract | CrossRef Full Text | Google Scholar

38. Dunlop MW, Zhang QH, Bogdanova YV, Lockwood M, Pu Z, Hasegawa H, et al. Extended magnetic reconnection across the dayside magnetopause. Phys Rev Lett. (2011) 107:025004. doi: 10.1103/PhysRevLett.107.025004

PubMed Abstract | CrossRef Full Text | Google Scholar

39. Milan SE, Lester M, Cowley SWH, Brittnacher M. Convection and auroral response to a southward turning of the IMF: PolarUVI, CUTLASS, and IMAGE signatures of transient magnetic flux transfer at the magnetopause. J Geophys Res. (2000) 105:15741–55. doi: 10.1029/2000JA900022

CrossRef Full Text | Google Scholar

40. Walsh BM, Komar CM, Pfau-Kempf Y. Spacecraft measurements constraining the spatial extent of a magnetopause reconnection X line. Geophys Res Lett. (2017) 44:3038–46. doi: 10.1002/2017GL073379

CrossRef Full Text | Google Scholar

41. Parker EN. Sweet's mechanism for merging magnetic fields in conducting fluids. J Geophys Res. (1957) 62:509–20. doi: 10.1029/JZ062i004p00509

CrossRef Full Text | Google Scholar

42. Petschek HE. Magnetic field annihilation. In: Hess WN, editor. Proceedings of AAS-NASA Symposium on the Physics of Solar Flares. Greenbelt, MD: NASA (1964). p. 425–439.

Google Scholar

43. Dungey JW. Interplanetary magnetic field and the auroral zones. Phys Rev Lett. (1961) 6:47. doi: 10.1103/PhysRevLett.6.47

CrossRef Full Text | Google Scholar

44. Angelopoulos V, Runov A, Zhou XZ, Turner DL, Kiehas SA, Li SS, et al. Electromagnetic energy conversion at reconnection fronts. Science. (2013) 341:1478–82. doi: 10.1126/science.1236992

PubMed Abstract | CrossRef Full Text | Google Scholar

45. Fu HS, Vaivads A, Khotyaintsev YV, André M, Cao JB, Olshevsky V, et al. Intermittent energy dissipation by turbulent reconnection. Geophys Res Lett. (2017) 44:37–43. doi: 10.1002/2016GL071787

CrossRef Full Text | Google Scholar

46. Retinò A, Sundkvist D, Vaivads A, Mozer F, André M, Owen CJ. In situ evidence of magnetic reconnection in turbulent plasma. Nat Phys. (2007) 3:236–8. doi: 10.1038/nphys574

CrossRef Full Text | Google Scholar

47. Karimabadi H, Roytershteyn V, Vu HX, Omelchenko YA, Scudder J, Daughton W, et al. The link between shocks, turbulence, and magnetic reconnection in collisionless plasmas. Phys Plasmas. (2014) 21:06230. doi: 10.1063/1.4882875

CrossRef Full Text | Google Scholar

48. Khotyaintsev YV, Graham DB, Steinvall K, Alm L, Vaivads A, Johlander A, et al. Electron heating by debye-scale turbulence in guide-field reconnection. arXiv. (2019) 1908:09724. doi: 10.1103/PhysRevLett.124.045101

CrossRef Full Text | Google Scholar

49. Huang SY, Sahraoui F, Yuan ZG, He JS, Zhao JS, Contel OL, et al. Magnetospheric Multiscale observations of electron vortex magnetic hole in the turbulent magnetosheath plasma. Astrophys J Lett. (2017) 836:L27. doi: 10.3847/2041-8213/aa5f50

CrossRef Full Text | Google Scholar

50. Zhong ZH, Tang RX, Zhou M, Deng XH, Pang Y, Paterson WR, et al. Evidence for secondary flux rope generated by the electron Kelvin-Helmholtz instability in a magnetic reconnection diffusion region. Phys Rev Lett. (2018) 120:075101. doi: 10.1103/PhysRevLett.120.075101

PubMed Abstract | CrossRef Full Text | Google Scholar

51. Zhang LQ, Baumjohann W, Dai L, Khotyaintsev YV, Wang C. Measurements of the vorticity in the bursty bulk flows. Geophys Res Lett. (2019) 46:10322–9. doi: 10.1029/2019GL084597

CrossRef Full Text | Google Scholar

52. Runov A, Sergeev VA, Nakamura R, Baumjohann W, Zhang TL, Asano Y, et al. Reconstruction of the magnetotail current sheet structure using multi-point Cluster measurements. Planet Space Sci. (2005) 53:237–43. doi: 10.1016/j.pss.2004.09.049

CrossRef Full Text | Google Scholar

53. Zelenyi LM, Malova HV, Popov VY, Delcourt DC, Ganushkina NY, Sharma AS. “Matreshka” model of multilayered current sheet. Geophys Res Lett. (2006) 33:L05105. doi: 10.1029/2005GL025117

CrossRef Full Text | Google Scholar

54. Grigorenko EE, Zelenyi LM, DiBraccio G, Ermakov VN, Shuvalov SD, Malova HV, et al. Thin current sheets of sub-ion scales observed by MAVEN in the Martian magnetotail. Geophys Res Lett. (2019) 46:6214–2. doi: 10.1029/2019GL082709

CrossRef Full Text | Google Scholar

55. Hasegawa H, Fujimoto M, Phan TD, Reme H, Balogh A, Dunlop MW, et al. Transport of solar wind into Earth's magnetosphere through rolled-up Kelvin–Helmholtz vortices. Nature. (2004) 430:755–8. doi: 10.1038/nature02799

PubMed Abstract | CrossRef Full Text | Google Scholar

56. Hwang KJ, Kuznetsova MM, Sahraoui F, Goldstein ML, Lee E, Parks GK. Kelvin-Helmholtz waves under southward interplanetary magnetic field. J Geophys Res Space Phys. (2011) 116:7282–7286. doi: 10.1029/2011JA016596

CrossRef Full Text | Google Scholar

57. Huang C, Lu Q, Guo F, Wu M, Du A, Wang S. Magnetic islands formed due to the Kelvin-Helmholtz instability in the outflow region of collisionless magnetic reconnection. Geophys Res Lett. (2015) 42:7282–6. doi: 10.1002/2015GL065690

CrossRef Full Text | Google Scholar

58. Lin D, Wang C, Li W, Tang B, Guo X, Peng Z. Properties of Kelvin-Helmholtz waves at the magnetopause under northward interplanetary magnetic field: statistical study. J Geophys Res Space Phys. (2014) 119:7485–94. doi: 10.1002/2014JA020379

CrossRef Full Text | Google Scholar

59. Nakamura R, Baumjohann W, Mouikis C, Kistler LM, Runov A, Volwerk M, et al. Spatial scale of high-speed flows in the plasma sheet observed by cluster. Geophys Res Lett. (2004) 31:L09804. doi: 10.1029/2004GL019558

CrossRef Full Text | Google Scholar

60. Panov EV, Nakamura R, Baumjohann W, Angelopoulos V, Petrukovich AA, Retinò A, et al. Multiple overshoot and rebound of a bursty bulk flow. Geophys Res Lett. (2010) 37:L08103. doi: 10.1029/2009GL041971

CrossRef Full Text | Google Scholar

61. Fu HS, Khotyaintsev YV, Vaivads A, André M, Huang SY. Electric structure of dipolarization front at sub-proton scale. Geophys Res Lett. (2012) 39:L06105. doi: 10.1029/2012GL051274

CrossRef Full Text | Google Scholar

62. Runov A, Angelopoulos V, Zhou X-Z, Zhang X-J, Li S, Plaschke F, et al. A THEMIS multicase study of dipolarization fronts in the magnetotail plasma sheet. J Geophys Res. (2011) 116:A05216. doi: 10.1029/2010JA016316

CrossRef Full Text | Google Scholar

63. Liu CM, Fu HS, Xu Y, Khotyaintsev YV, Burch JL, Ergun RE, et al. Electron-scale measurements of dipolarization front. Geophys Res Lett. (2018) 45:4628–38. doi: 10.1029/2018GL077928

CrossRef Full Text | Google Scholar

64. Pan DX, Khotyaintsev YV, Graham DB, Vaivads A, Zhou XZ, André M, et al. Rippled electron-scale structure of a dipolarization front. Geophys Res Lett. (2018) 45:12:116–24. doi: 10.1029/2018GL080826

CrossRef Full Text | Google Scholar

65. Khotyaintsev YV, Graham DB, Norgren C, Vaivads A. Collisionless magnetic reconnection and waves: progress review. Front Astron Space Sci. (2019) 6:70. doi: 10.3389/fspas.2019.00070

CrossRef Full Text | Google Scholar

66. Fu HS, Vaivads A, Khotyaintsev YV, Olshevsky V, André M, Cao JB, et al. How to find magnetic nulls and reconstruct field topology with MMS data? J Geophys Res Space Phys. (2015) 120:3758–82. doi: 10.1002/2015JA021082

CrossRef Full Text | Google Scholar

67. Liu Y, Fu H, Olshevsky V, Pontin D, Liu C, Wang Z, et al. SOTE: a nonlinear method for magnetic topology reconstruction in space plasmas. Astrophys J Suppl Ser. (2019) 244:31. doi: 10.3847/1538-4365/ab391a

CrossRef Full Text | Google Scholar