- Department of Physics and Astronomy, The University of Texas at San Antonio, San Antonio, TX, United States
In this article, the Brownian dynamics fluctuation-dissipation theorem (BD-FDT) is applied to the study of transport of neutral solutes across the cellular membrane of Plasmodium berghei (Pb), a disease-causing parasite. Pb infects rodents and causes symptoms in laboratory mice that are comparable to human malaria caused by Plasmodium falciparum (Pf). Due to the relative ease of its genetic engineering, P. berghei has been exploited as a model organism for the study of human malaria. P. berghei expresses one type of aquaporin (AQP), PbAQP, and, in parallel, P. falciparum expresses PfAQP. Either PbAQP or PfAQP is a multifunctional channel protein in the plasma membrane of the rodent/human malarial parasite for homeostasis of water, uptake of glycerol, and excretion of some metabolic wastes across the cell membrane. This FDT-study of the channel protein PbAQP is to elucidate how and how strongly it interacts with water, glycerol, and erythritol. It is found that erythritol, which binds deep inside the conducting pore of PbAQP/PfAQP, inhibits the channel protein's functions of conducting water, glycerol, etc. This points to the possibility that erythritol, a sugar substitute, may inhibit the malarial parasites in rodents and in humans.
Introduction
The fluctuation-dissipation theorem (FDT) is a corner stone of statistical mechanics. Since the Einstein relation for the Brownian motion [1], it has been fully established with a great many variations and applications. See, e.g., [2–10]. Amazingly and exactly, FDT relates the dissipative characteristics of a non-equilibrium system (such as diffusivity for mass flux in response to a concentration gradient and conductivity for electric current in response an electric field) to the equilibrium fluctuations of the corresponding microscopic quantities (velocities and currents, respectively). The former (diffusivity/conductivity) gives how a system responds to a perturbation imposed on the system while the latter represents the statistics of the microscopic quantities (velocities/currents) that constantly fluctuate even in an equilibrium state. In theoretical-computational studies, we can calculate diffusivity via the Einstein relation from the time-correlation function of the particle velocities sampled in molecular dynamics simulations. We can also compute conductivity via the Kubo formula from the time-correlation function of the microscopic current densities. Conversely, in this paper, I aim to elucidate the equilibrium properties of a system from how the system respond to a prescribed set of perturbations (condition changes) imposed on the system. Namely, the goal of this study is to compute the Gibbs free energies under biochemically different conditions: when a relevant small molecule is bound to a protein (bound state) and when that small molecule is far away from the protein (apo state). Specifically, the protein of interest here is the membrane protein, aquaglyceroporin PbAQP, that facilitates transport of water, glycerol, ammonia, and several other small neutral molecules across the plasma membrane of Plasmodium berghei. The strategy of this study is to force/pull the relevant small molecules from the bound state to the apo state in all-atom simulations and quantify how the system respond to such imposed perturbations, from which the Gibbs free energies of binding will be extracted.
Plasmodium falciparum infects humans and causes the most severe form of malaria leading to several 100 thousands of deaths per year even today [11]. Plasmodium berghei infects rodents and causes malarial symptoms that are comparable to P. falciparum malaria. Since genetic engineering in P. berghei is more achievable, P. berghei has been exploited as model organism for the study of P. falciparum malaria in humans. For example, P. berghei aquaglyceroporin (PbAQP) gene knock-out has been conducted to determine the essential roles played by this channel protein in the liver and blood stages of the parasite infection in laboratory mice [12, 13].
Maintenance of hydrohomeostasis, uptake of nutrients, and excretion of metabolic wastes across the cell membrane are essential for all cells to proliferate or even to survive. Some of these essential tasks are accomplished by two subfamilies of aquaporins (AQPs) [14–20]: the water channel proteins (aquaporins) and the glycerol channel proteins (aquaglyceroporins) that also conduct water. In fact, the human body expresses a total of 13 types of AQPs, having multiple types of AQPs in a single cell of various tissues to redundantly fulfill the essential tasks of conducting water, glycerol, etc. Intriguingly, P. berghei only expresses a single type of AQP, the multifunctional aquaglyceroporin PbAQP for the multiple essential tasks and so does P. falciparum [21–28]. In a recent study [13], Promeneur et al. determined the role played by PbAQP in the liver stage of P. berghei, adding to their previous study in the blood stage [12]. They elucidated that PbAQP facilitates the uptake of exogenous glycerol for the rapid phospholipid syntheses in hepatic merozoites. PbAQP-null parasites are less virulent than the wild type: Delayed prepatent period, slower replication, and smaller merosomes. These findings highlight the possibility of curing malaria by inhibiting P. berghei/falciparum with PbAQP/PfAQP inhibitors.
In this article, we present an atomistic computational study of PbAQP to elucidate how and how strongly this channel protein interacts with water, glycerol, erythritol, etc. The computed results show that glycerol and erythritol both bind deep inside the conducting pore of PbAQP near the Asn-Leu-Ala (NLA) and Asn-Pro-Ser (NPS) motifs, inhibiting the channel protein's functions of conducting water and excreting ammonia etc. Analyzing the fluctuations and the interactions with the channel, erythritol is shown to fit better than glycerol to the intra-channel space near the NLA-NPS motifs. Consequently, erythritol's affinity of binding is 50 folds stronger than glycerol. Therefore, erythritol competitively inhibits glycerol uptake through PbAQP in addition to its inhibition of water conduction and ammonia excretion through this channel protein. This prediction of erythritol inhibiting PbAQP based on the homology modeling is consistent with earlier studies of two other aquaglyceroporins based on their crystal structure, PfAQP and the Escherichia coli aquaglyceroporin GlpF [21, 23, 29–34]. In particular, the computational studies of PfAQP showed that the free-energy landscape of water was flat throughout this protein channel [30, 34–36] in accordance with its high permeability [21]. The glycerol-PfAQP affinity was computed to be in the low to sub mM range [34, 37] which is sufficiently strong to interfere with water transport through the channel [38]. The erythritol-PfAQP affinity was computed to be many folds stronger than glycerol [34] and thus prediction was made that erythritol inhibits PfAQP's multiple functions from water conduction to glycerol uptake. All these insights consistently point to the possibility that erythritol, a sugar substitute, may inhibit the malarial parasite in rodents and in humans.
Methods
Theoretical Formulation
Biophysical/biochemical processes occur down the Gibbs free energy gradient. Therefore, it is necessary and effective to map out the free energy profile in terms of the potential of mean force (PMF) that is defined as the Gibbs free energy of the entire system when a small number of degrees of freedom selected to characterize a process (namely, the reaction coordinates) are located at a set of given values. The PMF gradients (or changes) along a relevant path give a quantitative characterization of the biophysical/biochemical process. The PMF is a function of state. The PMF difference between two states (State A and State B) should be independent of the paths connecting A and B. This basic property allows for non-equilibrium sampling of forced paths connecting A and B in the computation of the PMF change, ΔPMF = PMF(B) − PMF(A). In this paper, we employ the Brownian dynamics fluctuation-dissipation theorem (BD-FDT) [39] to compute the PMF differences from the non-equilibrium work done to the system when the system is forced along a given path from A to B and the same from B to A:
Here kB is the Boltzmann constant. T is the absolute temperature of the thermal bath the system is coupled to (via the stochastic random forces in the Brownian or Langevin dynamics). WA→B is the work done to the system when it goes from A to B. Likewise, WB→A for B to A. The brackets indicate statistical mean over the paths sampled between A and B. In the Supplementary Material 1, we give mathematical details of an exactly solvable model system to illustrate the validity of BD-FDT. The focus of this paper, however, is the application of BD-FDT to the biophysical processes facilitated by PbAQP. It is noted that the BD-FDT formula has been proven for quasi-static paths connecting A and B sampled by slow pulling and for arbitrary non-equilibrium paths sampled by fast pulling as well [39].
System Setup
This study was based on an all-atom model of PbAQP embedded in the cell membrane. Using the PfAQP crystal structure (PDB code: 3C02) without the ligands, a homology model of PbAQP was built using the SWISS-MODEL workspace [40] (modeling details given in the Supplementary Material 2). Following the well-tested steps of the literature [e.g., [30, 32, 41, 42]], the PbAQP tetramer, was embedded in a patch of fully hydrated palmitoyloleylphosphatidyl-ethanolamine (POPE) bilayer. The PbAQP-POPE complex was sandwiched by two layers of water, each of which is ~40 Å thick. The system was then neutralized and salinated with Na+ and Cl− ions to a salt concentration of 150 mM. The entire system, consisting of 145,302 atoms, was 108 Å × 107 Å × 119 Å in dimension when fully equilibrated (illustrated in Figure S1). The Cartesian coordinates were chosen such that the origin is at the geometric center of the PbAQP tetramer. The xy-plane is parallel to the lipid-water interface and the z–axis is pointing from the periplasm to the cytoplasm. The PbAQP-membrane system with a glycerol in each of the four channels of the PbAQP tetramer was built by replacing the pore-filling waters in the NLA-NPS regions with glycerol molecules. Likewise, the system with an erythritol in each of the tetrameric channels.
Simulation Parameters
All the simulations of this work were performed using NAMD 2.13 [43]. The all-atom CHARMM36 parameters [44, 45] were adopted for inter- and intra-molecular interactions. The pressure and the temperature were maintained at 1 bar and 298.15 K, respectively. The Langevin damping coefficient was chosen to be 5/ps. The periodic boundary conditions were applied to all three dimensions, and the particle mesh Ewald (grid level: 128 × 128 × 128) was used for the long-range electrostatic interactions. The time step of 1 fs was used for short-range interactions and 4 fs was used for long-range forces. The cut-off for long-range interactions was set to 10 Å with a switching distance of 9 Å. In all simulations, the alpha carbons on the trans-membrane helices of PbAQP were fixed to their respective z-coordinates after the systems were fully equilibrated (their x- and y-degrees of freedom are not constrained, free to fluctuate in the xy-planes parallel to the membrane).
Free-Energy Profiles and Affinities
The free-energy profile of water/glycerol/erythritol, in terms of the PMF as a function of the center-of-mass z-coordinate of the molecule, was computed from steered molecular dynamics (SMD) runs over multiple sections as described in [33] except that, in each section, the z-coordinate is advanced by 1.0 Å at a slower SMD speed of 1.0 Å/ns. This slow pulling speed was used so that the computed results converge with known accuracy. The dissociation constant (inverse binding affinity) of glycerol/erythritol was computed from the PMF difference between dissociated state (when the molecule is in the cytoplasm away from the protein) and the bound state (when it is inside the channel near the NLA-NPS motifs), the z-fluctuations at the binding site, and the xy-fluctuations at the cytoplasmic orifice of the channel (shown in Figures S2, S3). At the binding site, the small molecule fluctuates as governed by the free stochastic Brownian/Langevin dynamics with no constraints. However, the interactions with the channel-lining residues of PbAQP confine its x- and y-coordinates and larger fluctuations along the z-axis. At the cytoplasmic orifice (z = 10 A), the z-coordinate was fixed while the x- and y-coordinates can freely fluctuate but they are confined by the interactions with the PbAQP residues. All these fluctuations give rise to normal diffusion [10] within the available domains bounded by the channel protein.
Results and Discussion
PbAQP Conducts Water and Small Polar Molecules
The top panel of Figure 1 shows how waters interact with the pore-lining residues that form a PbAQP channel. The coordinates are from the last frame of the 60 ns equilibrium molecular dynamics (MD) run of the PbAQP-membrane system without glycerol/erythritol after 20 ns initial run of setting up the systems. Movie 1 illustrates the dynamic behavior during the 40 ns MD run starting from the last frame of the 60 ns MD run. Like in all other AQPs (especially PfAQP), waters line up in a single file inside each PbAQP channel. Even though there are rooms near the NLA-NPS motifs where the two half transmembrane helices meet (1Å < z < 6Å in Figure 1), waters stay in single file due to hydrogen-bond networks with themselves and with the pore-lining residues of the channel. All these are in agreement with the literature of water and glycerol-conducting aquaglyceroporins [21, 29, 30], which indicates accuracy of our homology modeling.
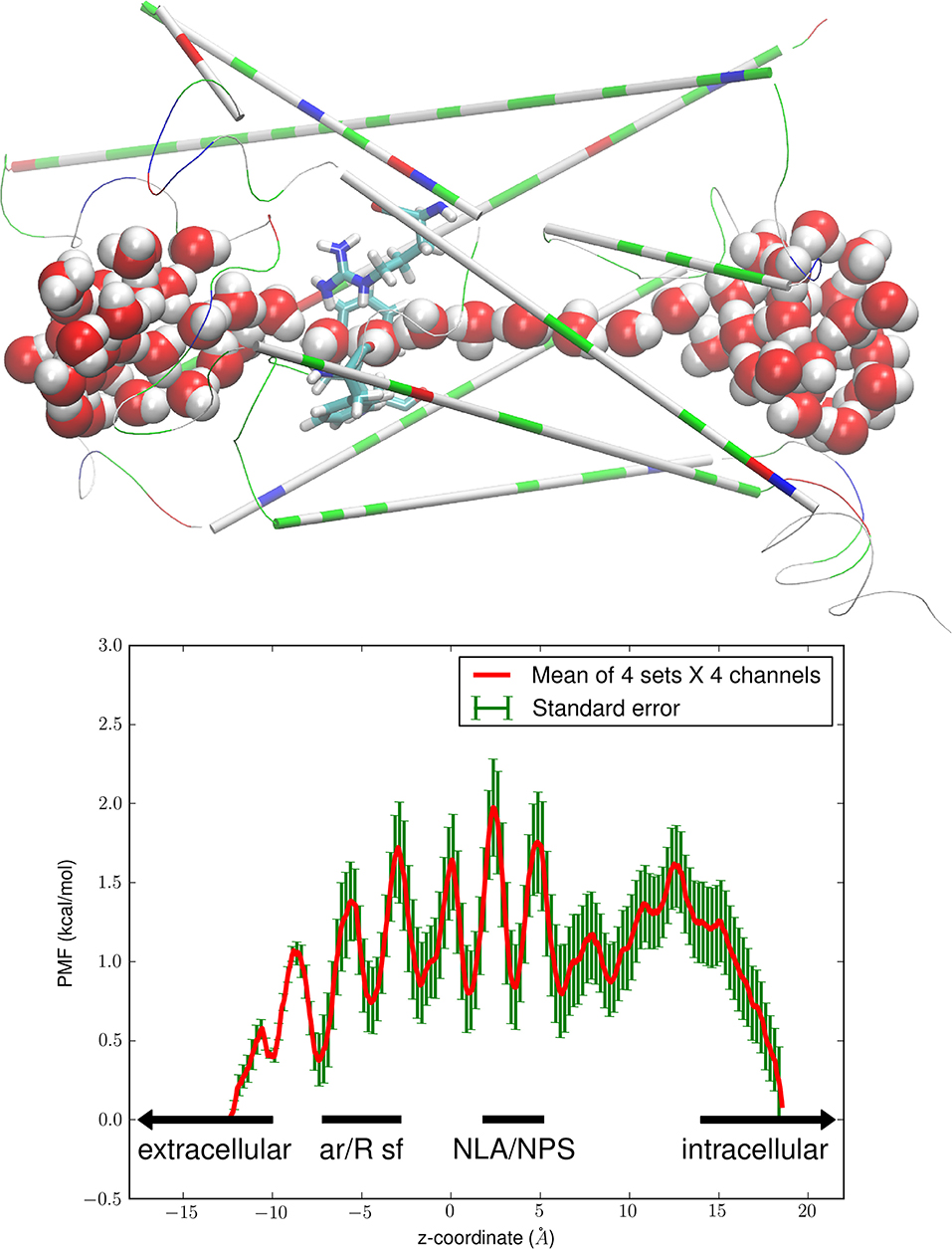
Figure 1. Water-PbAQP interactions. The (Top panel) shows the single file of waters inside the PbAQP channel. The protein monomer (constituting one channel) is shown in thin cartoons colored by residue types (hydrophilic, green; hydrophobic, white; positively charged, blue; negatively charged, red). The ar/R selectivity filter residues (Arg 196, Phe 190, Trp 50) are shown in licorices colored by atoms (H, white; O, red; C, cyan; N, blue). Waters inside or near the channel are shown in large spheres colored by atoms. Graphics here and in the rest of the paper were rendered with VMD [46]. The (Bottom panel) shows the free-energy profile of water conduction through PbAQP. The PMF of water is plotted as a function of the z-coordinate along the channel axis of PbAQP. The ar/R SF and the NLA-NPS motifs regions are so marked. The mean values and the standard errors are over 16 sets of data (four sets of forward and reverse paths in each of the four channels of the PbAQP tetramer).
The bottom panel of Figure 1 shows the Gibbs free energy of the system, namely, the PMF as a function of a water molecule's z-coordinate when it traverses the PbAQP channel. This free-energy profile correlates exactly with the single-file lining of waters inside the channel (Figure 1, top panel). The seven minima in the PMF curve are located at the single-file lining of waters (−8Å < z < 10Å). Quantitatively, the difference between the highest PMF peak and the deepest PMF well inside the channel is <2.0 kcal/mol. This very low free-energy barrier means that water can traverse the PbAQP channel as efficiently as free diffusion, in agreement with the current literature that aquaglyceroporins conduct water as well as (or better than) the water-specific AQPs [47].
It is worth noting that ammonia, a metabolic waste, is similar to water in size and polarity. It can move through PfAQP as easily as water [26, 34, 37, 48] and thus is expected to permeate PbAQP because PbAQP is exactly parallel (in channel characteristics) to PfAQP [21, 23] and GlpF [29, 30]: Lining waters up in single file and disallowing them to pass over one another inside the channel despite their dynamic fluctuations [47].
Glycerol or Erythritol Clogs up the PbAQP Channel
To illustrate the glycerol-PbAQP interaction, we took the full equilibrated structure of the PbAQP-membrane system, deleted the waters near the NLA-NPS motifs, placed a glycerol inside each of the tetrameric PbAQP channels, and ran MD for 120 ns. After the initial 20 ns, the channel characteristics of PbAQP (illustrated in Figure 2 and Movie 2) remain unaltered, in close resemblance of the PfAQP channel characteristics: Waters remain in single file and glycerol stays inside the channel fluctuating near the NLA-NPS motifs. The glycerol so dwelling inside a channel does not cause distortions to the pore-lining residues but completely severs the single-file line of waters into two. Therefore, it inhibits PbAQP's function of conducting water and other small polar solutes including ammonia, which is similar to what was computed for PfAQP [34]. This close resemblance is because PbAQP is 62% identical to PfAQP in amino-acid sequence. In functional assays, PfAQP was found to conduct water, ammonia, glycerol, etc. [21, 26]. In the crystal structure of PfAQP, a glycerol was located inside each channel near the NLA-NPS motifs interrupting the single-file lining of waters [23]. Here, we observe that PbAQP acts likewise.
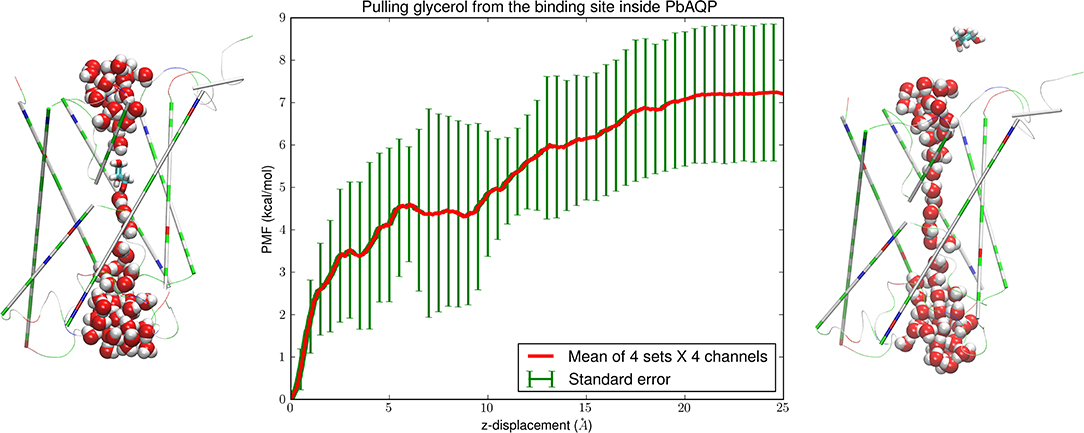
Figure 2. Glycerol-PbAQP interactions. (Left) glycerol bound inside PbAQP near the NLA-NPS motifs interrupts the single file of waters through the channel. (Right) glycerol is held outside the channel and waters line up in single file throughout the channel. The representation and color schemes are identical to Figure 1 except that glycerol is shown in licorices. (Central) the PMF along the dissociation path of glycerol from the binding site to the intracellular side. The mean values and the standard errors are over 16 sets of data (four sets of forward and reverse paths in each of the four channels of the PbAQP tetramer).
To quantify the glycerol-PbAQP interaction, we computed the Gibbs free energy of binding, namely, the difference in the free energies of the system when the glycerol resides inside the PbAQP channel (shown in the left panel of Figure 2) and when it is in dissociated state (shown in the right panel of Figure 2). The binding free energy involves the PMF along the dissociation path of pulling a glycerol from the bound state to the dissociated state (shown in the central panel of Figure 2) and the fluctuations of a glycerol when inside the channel (shown in Figure 3). The entire dissociation path over a z-displacement of 25 Å was sampled as 25 sections of 1.0 Å each. Over each section, four forward paths of pulling a glycerol along the z-axis at a speed of 1.0 Å/ns and four reverse paths of pulling a glycerol along the opposite direction at the same speed. At each end point of the 25 sections, the system was equilibrated for 4.0 ns while the z-coordinate of a glycerol was held constant. Altogether, we conducted 300 ns SMD runs for the PMF curve shown in Figure 2. The PMF and the fluctuations (shown in Figure 3) combined to give the Gibbs free energy of glycerol-PbAQP binding at −5.55 ± 2.07 kcal/mol.
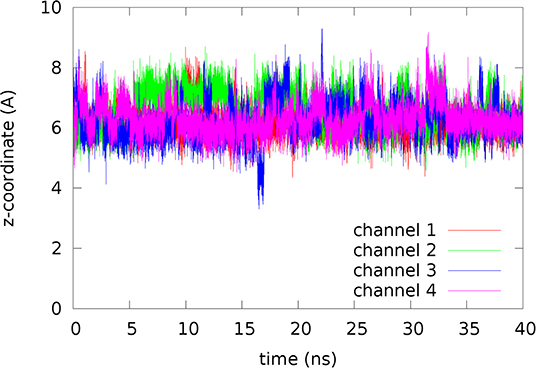
Figure 3. Fluctuations of glycerol inside the channel. The coordinates represent the last 40 ns of the 120 ns MD run.
Replacing the four glycerols inside the tetrameric PbAQP channels with four erythritols, the 120 ns MD run showed that erythritol is also stable at the same binding site near the NLA-NPS motifs (shown in the left panel of Figure 4 and Movie 3). Like glycerol, an erythritol located inside the channel does not cause distortions to the pore-lining residues but occludes the channel from conducting water or small solutes. Unlike glycerol, the fluctuations of erythritol are smaller (compare Figure 5 with Figure 3), indicating that erythritol inhibits PbAQP's conduction of water and ammonia more effectively than glycerol.
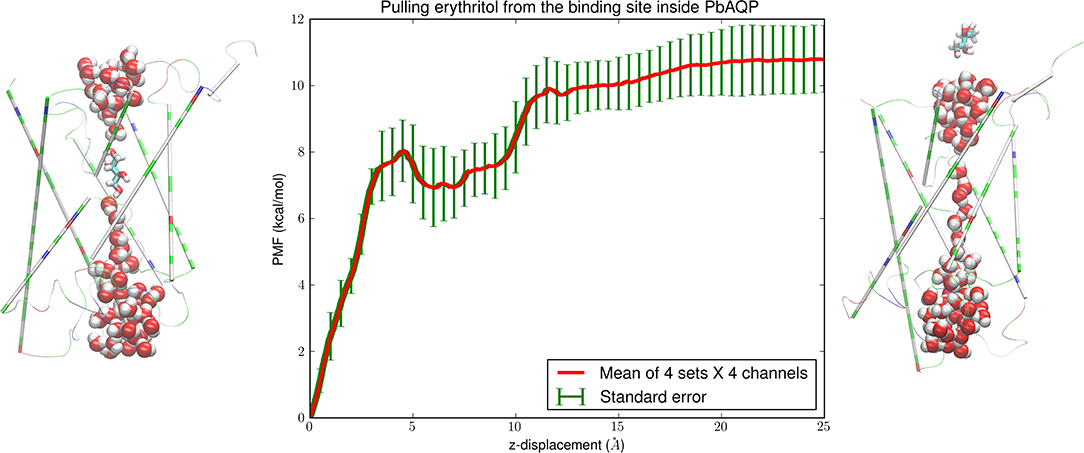
Figure 4. Erythritol-PbAQP interactions. (Left) erythritol bound inside PbAQP near the NLA-NPS motifs interrupts the single file of waters through the channel. (Right) erythritol is held outside the channel and waters line up in single file throughout the channel. The representation and color schemes are identical to Figure 1 except that erythritol is shown in licorices. (Central) the PMF along the dissociation path of erythritol from the binding site to the intracellular side. The mean values and the standard errors are over 16 sets of data (four sets of forward and reverse paths in each of the four channels of the PbAQP tetramer).
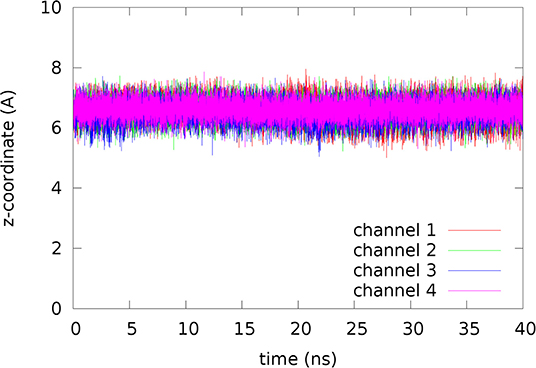
Figure 5. Fluctuations of erythritol inside the channel. The coordinates represent the last 40 ns of the 120 ns MD run.
The SMD runs for computing the erythritol PMF are parallel to the case of pulling glycerols for 300 ns. The central panel of Figure 4 shows the PMF along the path of dissociating erythritol from the binding site (Figure 4, left panel) to the intracellular space (Figure 4, right panel). The PMF (shown in Figure 4) and the fluctuations (shown in Figure 5) combined to give the Gibbs free energy of erythritol-PbAQP binding at −7.87 ± 1.55 kcal/mol.
Erythritol Competitively Inhibits Glycerol Uptake Through PbAQP
Recent experiments of Promeneur et al. [13] showed that P. berghei relies on the PbAQP channel for efficient infection and proliferation. The parasite uses PbAQP for glycerol uptake required by its high demand of lipids. Inhibiting PbAQP with an inhibitor that has a higher affinity than glycerol would be similar to knocking out the PbAQP gene to disable the parasite's uptake of glycerol and excretion of ammonia through its sole aquaglyceroporin PbAQP. Therefore, it is interesting to compare the glycerol-PbAQP affinity and the erythritol-PbAQP affinity for the possibility that erythritol competitively inhibits glycerol uptake through PbAQP as they have the same binding site (Figures 2, 4, 6).
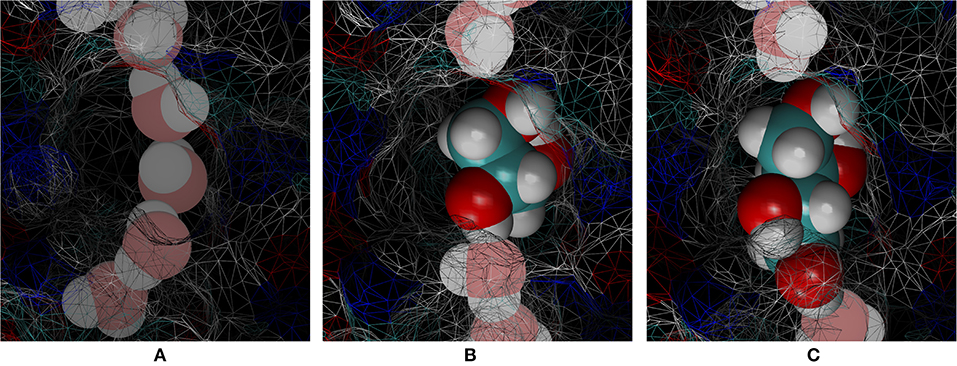
Figure 6. Cavity of the binding site inside the PbAQP channel near the NLA-NPS motifs. (A) Waters line up in single file occupying a smaller portion of the cavity. (B) Glycerol fits loosely in the cavity but totally interrupts the single file of waters. (C) Erythritol fits snuggly in the cavity and totally interrupts the single file of waters. Waters are shown in large spheres chalk colored by atoms. Glycerol and erythritol are shown in large spheres brightly colored by atoms. The protein is partially shown as wireframe surface colored by atoms.
In Table 1, we summarize the glycerol- and erythritol-PbAQP interactions. Erythritol's binding free energy is −2.3 kcal/mol stronger than glycerol, which is outside (but not far from) the margin of error. Correspondingly, the erythritol-PbAQP affinity (dissociation constant kD = 2 μM) is ~50 times the glycerol-PbAQP affinity (kD = 0.1 mM). It is reasonable to conclude that erythritol competitively inhibits glycerol uptake through PbAQP. At a typical blood glycerol level, e.g., 0.1 mM, erythritol at 1.0 mM concentration would inhibit PbAQP's conduction of glycerol to <1%.
Atomistic Interactions and Steric Fit
Analyzing the relevant atomistic interactions, we can see how and how strongly a glycerol/erythritol interacts with the protein and its aqueous environments. We can also see that the uncertainties of this computational work are probably lower than what might be suggested by the margins of error in the computed free energies (Table 1).
First, the hydrogen bonds. Glycerol (erythritol) is hydrophilic. Away from the protein where a glycerol (erythritol) molecule is surrounded by waters, it can form six (eight) hydrogen bonds with the surrounding waters. When it is inside the protein channel, it forms two hydrogen bonds with waters and one or two hydrogen bonds with the pore-lining residues. This seems to suggest that hydrogen-bond interactions favor the unbound state of glycerol (erythritol) where it has three (four) more hydrogen bonds to its three (four) hydroxyl groups, if we ignore the hydrogen bonds between waters. When a glycerol (erythritol) is inside the channel, it displaces two or three (three or four) waters that are bonded to each other and to the pore-lining residues by three or four (five or six) hydrogen bonds. Namely, in the bound state, a glycerol (erythritol) breaks four (six) hydrogen bonds to waters. In the dissociated state, a glycerol (erythritol) displaces four (five) waters from the volume it occupies and thus disrupts 10 (12.5) hydrogen bonds between the waters if assuming 2.5 hydrogen bonds per water in the aqueous bulk. Altogether, the system has six (6.5) more hydrogen bonds when a glycerol (erythritol) is inside the protein than in the aqueous bulk. Therefore, hydrogen-bond interactions favor the binding of a glycerol (erythritol) inside the channel.
Second, the entropic forces. There is enough room inside the channel near the NLA-NPS motifs to accommodate a glycerol (erythritol). In fact, the dihedral energy of a glycerol (erythritol), shown in Figure 7, simply fluctuates around the same level along the dissociation path leading from the NLA-NPS region to cytoplasmic bulk. Otherwise, the dihedral energy would be significant higher in the bound state inside the channel than in the dissociated state outside the protein. Not surprisingly, the glycerol fluctuations at the binding site is higher than erythritol (the root mean square fluctuation values, RMSF, are shown in Table 1). The room there is greater than the volume a glycerol occupies but is nearly a perfect fit to accommodate an erythritol. In this aspect, the entropic contribution to the free energy of binding favors glycerol over erythritol by −1.1 ± 0.3 kcal/mol (which is estimated as with values given in Table 1).
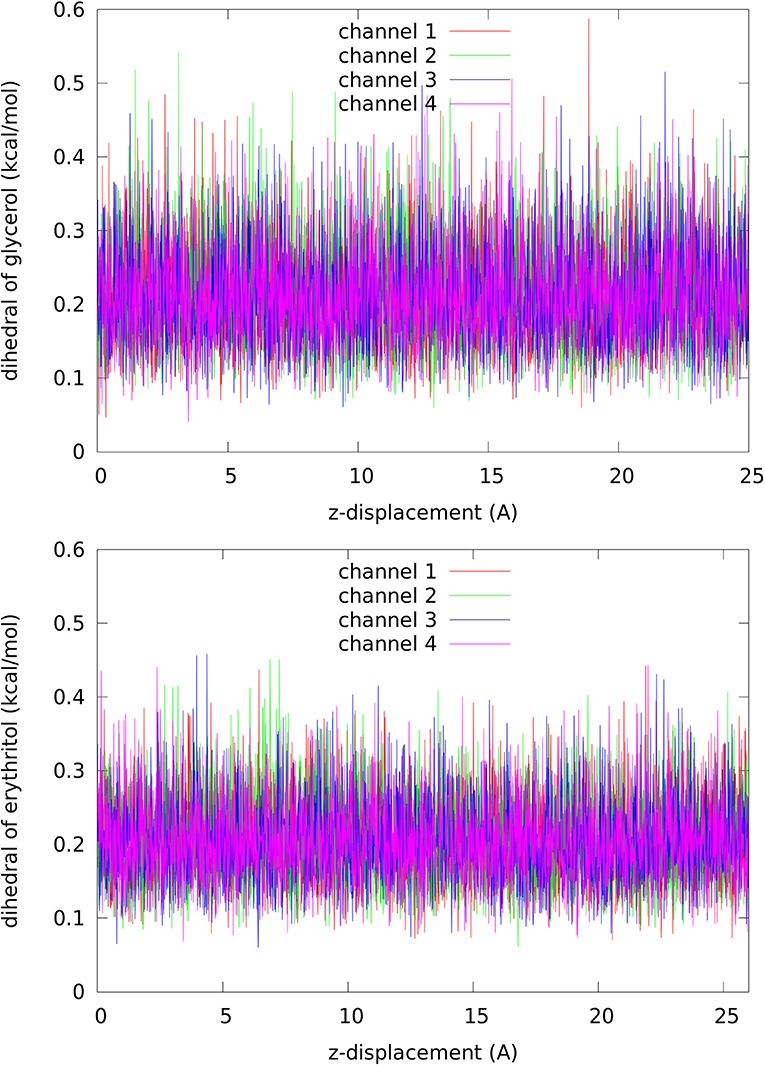
Figure 7. Dihedral energy of glycerol (Top panel, per each of the 27 dihedrals)/erythritol (Bottom panel, per each of the 37 dihedrals) along the dissociation path from inside the channel to the cytoplasmic bulk.
Third, the van der Waals (vdW) interactions. These forces were computed with the smallest uncertainties in this work. In fact, the vdW interactions between a glycerol (erythritol) and the protein are all attractive. The erythritol-PbAQP attraction is −18.60 ± 1.29 kcal/mol and the glycerol-PbAQP attraction is −14.80 ± 1.01 kcal/mol. The separation between these two vdW attractions are far outside the margins of error.
Overall, both glycerol and erythritol bind inside the PbAQP near the NLA-NPS motifs mostly due to the vdW interactions and the hydrogen-bond compensations. The erythritol-PbAQP vdW attraction is stronger than the glycerol-PbAQP vdW attraction by 3.8 kcal/mol, which is the dominant factor leading to the 50 folds stronger affinity of erythritol than glycerol.
Based on the computed binding free energy of erythritol, −7.87 ± 1.55 kcal/mol (Table 1), the possible values of its kD range from 0.15 to 27 μM. Therefore, at a concentration in the low or sub mM range, erythritol should strongly inhibit P. berghei. It is particularly interesting that erythritol is a sugar substitute generally regarded as safe. If proven effective to inhibit P. berghei in laboratory rodents, it is expected to inhibit P. falciparum in humans without significant adverse side effects.
Data Availability Statement
The datasets including all the parameters, coordinates and scripts to reproduce the results of this study is available from the Harvard Dataverse: https://doi.org/10.7910/DVN/ZOAQJW.
Author Contributions
The author conducted the simulations, analyzed the data, and wrote the manuscript.
Funding
The author acknowledges NIH Grant #GM121275.
Conflict of Interest
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
The author acknowledges the Texas Advanced Computing Center for computing resources.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2020.00119/full#supplementary-material
References
1. Einstein A. Über die von der molekularkinetischen Theorie der Wärme geforderte Bewegung von in ruhenden Flüssigkeiten suspendierten Teilchen. Annalen Phys. (1905) 322:549–60. doi: 10.1002/andp.19053220806
2. Nyquist H. Thermal agitation of electric charge in conductors. Phys Rev. (1928) 32:110–3. doi: 10.1103/PhysRev.32.110
3. Onsager L. Reciprocal relations in irreversible processes. I. Phys Rev. (1931) 37:405–26. doi: 10.1103/PhysRev.37.405
4. Callen HB, Welton TA. Irreversibility and generalized noise. Phys Rev. (1951) 83:34–40. doi: 10.1103/PhysRev.83.34
5. Weber J. Fluctuation dissipation theorem. Phys Rev. (1956) 101:1620–6. doi: 10.1103/PhysRev.101.1620
6. Kubo R. Statistical-mechanical theory of irreversible processes. I. General theory and simple applications to magnetic and conduction problems. J Phys Soc Jpn. (1957) 12:570–86. doi: 10.1143/JPSJ.12.570
7. Ruelle D. General linear response formula in statistical mechanics, and the fluctuation-dissipation theorem far from equilibrium. Phys Lett A. (1998) 245:220–4. doi: 10.1016/S0375-9601(98)00419-8
8. Marconi UMB, Puglisi A, Rondoni L, Vulpiani A. Fluctuation-dissipation: response theory in statistical physics. Phys Rep. (2008) 461:111–95. doi: 10.1016/j.physrep.2008.02.002
9. Colangeli M, Rondoni L, Vulpiani A. Fluctuation-dissipation relation for chaotic non-Hamiltonian systems. J Stat Mech Theory Exp. (2012) 2012:L04002. doi: 10.1088/1742-5468/2012/04/L04002
10. Oliveira FA, Ferreira RMS, Lapas LC, Vainstein MH. Anomalous diffusion: a basic mechanism for the evolution of inhomogeneous systems. Front Phys. (2019) 7:18. doi: 10.3389/fphy.2019.00018
11. WHO. Malaria. (2017). Available online at: http://www.who.int/malaria/en/
12. Promeneur D, Liu Y, Maciel J, Agre P, King LS, Kumar N. Aquaglyceroporin PbAQP during intraerythrocytic development of the malaria parasite Plasmodium berghei. Proc Natl Acad Sci USA. (2007) 104:2211–6. doi: 10.1073/pnas.0610843104
13. Promeneur D, Mlambo G, Agre P, Coppens I. Aquaglyceroporin PbAQP is required for efficient progression through the liver stage of Plasmodium infection. Sci Rep. (2018) 8:655. doi: 10.1038/s41598-017-18987-3
14. Agre P, Bonhivers M, Borgnia MJ. The aquaporins, blueprints for cellular plumbing systems. J Biol Chem. (1998) 273:14659–62. doi: 10.1074/jbc.273.24.14659
15. Engel A, Stahlberg H. Aquaglyceroporins: channel proteins with a conserved core, multiple functions, and variable surfaces. In: Thomas Zeuthen WDS, editor. International Review of Cytology. New York, NY: Academic Press (2002). p. 75–104.
16. Carbrey JM, Agre P. Discovery of the aquaporins and development of the field. In: Beitz E, editor. Aquaporins. Handbook of Experimental Pharmacology. Vol. 190. Berlin; Heidelberg: Springer.
17. Hedfalk K, Pettersson N, Oberg F, Hohmann S, Gordon E. Production, characterization and crystallization of the Plasmodium falciparum aquaporin. Protein Express Purif. (2008) 59:69–78. doi: 10.1016/j.pep.2008.01.004
18. Lee JK, Khademi S, Harries W, Savage D, Miercke L, Stroud RM. Water and glycerol permeation through the glycerol channel GlpF and the aquaporin family. J Synchrotron Radiat. (2004) 11:86–8. doi: 10.1107/S0909049503023872
19. Benga G. On the definition, nomenclature and classification of water channel proteins (aquaporins and relatives). Mol Aspects Med. (2012) 33:514–7. doi: 10.1016/j.mam.2012.04.003
20. Verkman AS, Anderson MO, Papadopoulos MC. Aquaporins: important but elusive drug targets. Nat Rev Drug Discov. (2014) 13:259–77. doi: 10.1038/nrd4226
21. Hansen M, Kun JF, Schultz JE, Beitz E. A single, bi-functional aquaglyceroporin in blood-stage Plasmodium falciparum malaria parasites. J Biol Chem. (2002) 277:4874–82. doi: 10.1074/jbc.M110683200
22. Beitz E, Pavlovic-Djuranovic S, Yasui M, Agre P, Schultz JE. Molecular dissection of water and glycerol permeability of the aquaglyceroporin from Plasmodium falciparum by mutational analysis. Proc Natl Acad Sci USA. (2004) 101:1153–8. doi: 10.1073/pnas.0307295101
23. Newby ZE, O'Connell J, Robles-Colmenares Y, Khademi S, Miercke LJ, Stroud RM. Crystal structure of the aquaglyceroporin PfAQP from the malarial parasite Plasmodium falciparum. Nat Struct Mol Biol. (2008) 15:619–25. doi: 10.1038/nsmb.1431
24. Song J, Almasalmeh A, Krenc D, Beitz E. Molar concentrations of sorbitol and polyethylene glycol inhibit the Plasmodium aquaglyceroporin but not that of E. coli: involvement of the channel vestibules. Biochim Biophys Acta. (2012) 1818:1218–24. doi: 10.1016/j.bbamem.2012.01.025
25. Holm L, Jahn TP, Møller ALB, Schjoerring JK, Ferri D, Klaerke DA, et al. NH3 and NH4+ permeability in aquaporin-expressing Xenopus oocytes. Pflügers Archiv. (2005) 450:415–28. doi: 10.1007/s00424-005-1399-1
26. Zeuthen T, Wu B, Pavlovic-Djuranovic S, Holm LM, Uzcategui NL, Duszenko M, et al. Ammonia permeability of the aquaglyceroporins from Plasmodium falciparum, Toxoplasma gondii and Trypansoma brucei. Mol Microbiol. (2006) 61:1598–608. doi: 10.1111/j.1365-2958.2006.05325.x
27. Laforenza U, Bottino C, Gastaldi G. Mammalian aquaglyceroporin function in metabolism. Biochim Biophys Acta Biomembr. (2016) 1858:1–11. doi: 10.1016/j.bbamem.2015.10.004
28. Kenthirapalan S, Waters AP, Matuschewski K, Kooij TW. Flow cytometry-assisted rapid isolation of recombinant Plasmodium berghei parasites exemplified by functional analysis of aquaglyceroporin. Int J Parasitol. (2012) 42:1185–92. doi: 10.1016/j.ijpara.2012.10.006
29. Fu D, Libson A, Miercke LJ, Weitzman C, Nollert P, Krucinski J, et al. Structure of a glycerol-conducting channel and the basis for its selectivity. Science. (2000) 290:481–6. doi: 10.1126/science.290.5491.481
30. de Groot BL, Grubmüller H. Water permeation across biological membranes: mechanism and dynamics of Aquaporin-1 and GlpF. Science. (2001) 294:2353–7. doi: 10.1126/science.1062459
31. Tajkhorshid E, Nollert P, Jensen MØ, Miercke LJ, O'Connell J, Stroud RM, et al. Control of the selectivity of the aquaporin water channel family by global orientational tuning. Science. (2002) 296:525–30. doi: 10.1126/science.1067778
32. Zhu F, Tajkhorshid E, Schulten K. Theory and simulation of water permeation in aquaporin-1. Biophys J. (2004) 86:50–7. doi: 10.1016/S0006-3495(04)74082-5
33. Chen LY. Glycerol modulates water permeation through Escherichia coli aquaglyceroporin GlpF. Biochim Biophys Acta Biomembr. (2013) 1828:1786–93. doi: 10.1016/j.bbamem.2013.03.008
34. Chen LY. Erythritol predicted to inhibit permeation of water and solutes through the conducting pore of P. falciparum aquaporin. Biophys Chem. (2015) 198:14–21. doi: 10.1016/j.bpc.2015.01.004
35. Aponte-Santamaria C, Hub JS, de Groot BL. Dynamics and energetics of solute permeation through the Plasmodium falciparum aquaglyceroporin. Phys Chem Chem Phys. (2010) 12:10246–54. doi: 10.1039/c004384m
36. Hub JS, de Groot BL. Mechanism of selectivity in aquaporins and aquaglyceroporins. Proc Natl Acad Sci USA. (2008) 105:1198–203. doi: 10.1073/pnas.0707662104
37. Chen LY. Glycerol inhibits water permeation through Plasmodium falciparum aquaglyceroporin. J Struct Biol. (2013) 181:71–6. doi: 10.1016/j.jsb.2012.10.007
38. Song J, Mak E, Wu B, Beitz E. Parasite aquaporins: current developments in drug facilitation and resistance. Biochim Biophys Acta Gen Subj. (2014) 1840:1566–73. doi: 10.1016/j.bbagen.2013.10.014
39. Chen LY. Nonequilibrium fluctuation-dissipation theorem of Brownian dynamics. J Chem Phys. (2008) 129:144113. doi: 10.1063/1.2992153
40. Biasini M, Bienert S, Waterhouse A, Arnold K, Studer G, Schmidt T, et al. SWISS-MODEL: modelling protein tertiary and quaternary structure using evolutionary information. Nucl Acids Res. (2014) 42:W252–8. doi: 10.1093/nar/gku340
41. Zhu F, Tajkhorshid E, Schulten K. Collective diffusion model for water permeation through microscopic channels. Phys Rev Lett. (2004) 93:224501. doi: 10.1103/PhysRevLett.93.224501
42. Freites JA, Németh-Cahalan KL, Hall JE, Tobias DJ. Cooperativity and allostery in aquaporin 0 regulation by Ca2+. Biochim Biophys Acta Biomembr. (2019) 1861:988–96. doi: 10.1016/j.bbamem.2019.02.007
43. Phillips JC, Braun R, Wang W, Gumbart J, Tajkhorshid E, Villa E, et al. Scalable molecular dynamics with NAMD. J Comput Chem. (2005) 26:1781–802. doi: 10.1002/jcc.20289
44. Best RB, Zhu X, Shim J, Lopes PEM, Mittal J, Feig M, et al. Optimization of the additive CHARMM all-atom protein force field targeting improved sampling of the backbone φ, ψ and side-chain χ1 and χ2 dihedral angles. J Chem Theory Comput. (2012) 8:3257–73. doi: 10.1021/ct300400x
45. Vanommeslaeghe K, Hatcher E, Acharya C, Kundu S, Zhong S, Shim J, et al. CHARMM general force field: a force field for drug-like molecules compatible with the CHARMM all-atom additive biological force fields. J Computat Chem. (2010) 31:671–90. doi: 10.1002/jcc.21367
46. Humphrey W, Dalke A, Schulten K. VMD: visual molecular dynamics. J Mol Graph. (1996) 14:33–8. doi: 10.1016/0263-7855(96)00018-5
47. Wambo TO, Rodriguez RA, Chen LY. Computing osmotic permeabilities of aquaporins AQP4, AQP5, and GlpF from near-equilibrium simulations. Biochim Biophys Acta Biomembr. (2017) 1859:1310–6. doi: 10.1016/j.bbamem.2017.04.022
Keywords: Brownian dynamics, malarial parasite, aquaglyceroporin, channel-transport regulation, binding affinity
Citation: Chen LY (2020) Application of the Brown Dynamics Fluctuation-Dissipation Theorem to the Study of Plasmodium berghei Transporter Protein PbAQP. Front. Phys. 8:119. doi: 10.3389/fphy.2020.00119
Received: 14 February 2020; Accepted: 25 March 2020;
Published: 17 April 2020.
Edited by:
Fernando A. Oliveira, University of Brasilia, BrazilReviewed by:
Luciano Calheiros Lapas, Universidade Federal da Integração Latino-Americana, BrazilMatteo Colangeli, University of L'Aquila, Italy
Copyright © 2020 Chen. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Liao Y. Chen, bGlhby55LmNoZW5AZ21haWwuY29t
 Liao Y. Chen
Liao Y. Chen