- 1Department of Applied Mathematics, Huainan Normal University, Huaina, China
- 2School of Mathematics and Physics, Guangxi University for Nationalities, Nanning, China
In this paper, neural network (NN) control of the fractional-order Duffing system (FODS) by using a backstepping method within finite time in the presence of input saturation has been investigated. A fractional-order filter with an order lying on the interval (1,2) was used to estimate the virtual input together with its fractional derivative, and this showed that the estimation error tends to a small region in some finite time. Fractional-order law is designed for the parameter of the NN, and an adaptive NN controller was given. The proposed method drives the tracking error, tending to an arbitrary small region within a finite time. The simulation results verify the validity of the proposed method.
1. Introduction
It is a well-known fact that classical differential operators are local operators and cannot describe some complex properties. For example, Brownian motion, viscoelastic materials, anomalous diffusion, and irregular fluctuations in the turbulent velocity field have memory problems. Fractional-order differential operators are non-local and can well-characterize memory, genetic, and global correlation in the real world. The physical process is an important tool for describing physical processes and complex mechanics [1, 2]. In fact, fractional derivatives exhibit several advantages over integer derivatives: (1) fractional derivatives have a global correlation and can reflect the historical dependence of function development in the system; (2) the fractional derivative model is more consistent with the experimental results when simulating some complex properties, and the effect is better; and (3) when simulating complex mechanics and physical process problems, the expression of fractional-order model is more concise and the meaning is clearer [3, 4]. In view of these three advantages of fractional derivative, scholars have gradually used fractional differential equations to describe some practical problems. In recent decades, fractional calculus and fractional differential equations have developed rapidly and have gradually matured, and they have also been applied in other disciplines, such as quantum mechanics, economics and finance, turbulence, viscoelasticity theory, and superconductivity. A large number of papers on fractional calculus and fractional differential equations and works and so on have appeared [5–10]. The research contents include the theory and application of fractional calculus, the existence and uniqueness of solutions to the Cauchy problem, stability, controllability, the existence and uniqueness of solutions to boundary value problems, analytical solutions, and numerical algorithms. However, some research methods in integer-order differential equations cannot be directly applied to the study of fractional-order differential equations, and new theories and methods need to be sought. There are many research fields for integer-order differential equations, and research fields for fractional-order differential equations are limited, and the solution mapping of fractional-order differential equations does not have a semigroup property. Therefore, there are many difficulties in the study of fractional differential equations.
On the other hand, it is well-known that chaos control is a research hot topic and has some successful applications. With the in-depth study of chaotic systems, people began to try to migrate the synchronization method of integer-order chaotic systems to the synchronization of fractional-order chaotic systems (FOCSs). This natural idea is not easy to implement. For this reason, some people try to use the Laplace transform method and time-frequency domain transformation method. By solving the sα by using the Laplace transform method, finite time control was investigated in Tavazoei and Haeri [5]. Up to now, many control methods have been used to control or synchronize FOCSs, for example, adaptive robust control, adaptive fuzzy control (AFC), adaptive neural network control (ANNC), sliding mode control (SMC), command filtered control (CFC), etc. [11–18]. In Pham et al. [19], a three-dimensional FOCS that had no equilibrium was introduced and investigated, and it was shown that the system shows chaotic phenomenon when the order <2.7. In Zhang et al. [20], the lag projective synchronization of FOCSs with time-varying delays was considered by using a comparison principle of linear fractional equation. In Liu et al. [16], the NN was used to control FOCSs in the presence of input faults. It should be mentioned that above works do not consider the finite time stability is. Up to now, the finite time control of the FOCS has rarely been investigated [21–23].
Inspired with above discussion, we will address the finite time NN control of the fractional-order Deffuing system (FODS) with input saturation. Take some related works, such as Liu et al. [16] and Ha et al. [24, 25], the our work has included several features: (1) a fractional-order filter whose order lies on (1,2), designed to evaluate the immediate controller and its fractional derivative within some finite time. However, a fractional filter was also used in Liu et al. [16] and Ha et al. [25] whose order lies on (0, 1), and, in addition, the finite-time stability cannot be guaranteed; (2) to cancel the estimation error of the filter, a fractional-order compensated signal was proposed. Compared with the compensated signals proposed in Ha et al. [24], our method can obtain a more rapid convergence; and (3) in the FOCS's mode, we have considered the case of input saturation.
2. Preliminaries
2.1. Description of the NN
The NN with three layers is expressed as
where n, h, andm ∈ ℕ+ denote the amount of neurons three layers (input, middle, and output), , and . vji denotes a weight whose value is on the interval [−1, 1]. Usually, φ(·) can be defined by
Then, the NN is given as
with , and . Suppose that f(ℏ), ℏ ∈ ℝn is unknown, then it can be approximated by the NN as
with ε(ℏ) denoting the optimal approximation error, where
with .
2.2. Basic Lemmas
The q-th fractional integral for a function g(t) is defined as
with Γ(·) representing Euler's function, and the q-th fractional-order derivative for a function g(t), which has a k-th continuous derivative, is
where k−1 ≤ q < k (k ∈ ℕ). The following always assumes that 0 < q ≤ 1 for convenience. The fractional-order calculus has the following properties.
Lemma 1. [16] For a smooth function x(t), it holds that
Lemma 2. [22] Let V(ζ) be a smooth function satisfying , , , and 0 < α2 < 1. Then, one can find , which holds that V(ζ) begins within Ω2 will reach a sufficient small region in some finite time T*.
Lemma 3. [23] Assume g1, g2 > 0, 0 < g3 < 1, and
where ζ ∈ ℝn. Then, the system is finite time stable.
Lemma 4. [23] Consider
where ζ(t) ⊂ ℝ, . Let
Then, ê1 and ê2 are finite time stable.
3. Main Results
The integer-order Duffing system is written as
where a, b are parameters. Denote x1(t) = y(t), x2(t) = ẏ(t), and . By putting the fractional calculus into system (9) and considering the input saturation, the controlled FODS is written as
in which sat : u(t) → sat(u(t)) is called a saturator. It can be expressed as:
with ur > 0, ul < 0. Denoting the term that exceeds the saturation limiter as γ(t):
For the target, let x1(t) track a known smooth signal xd(t) ∈ ℝ in finite time. In this paper, we have used the backstepping method. Define e1(t) = x1(t) − xd(t), and let us construct a virtual input α(t), giving us
with , and being α(t)'s estimation. Noting the estimation error is hard to be canceled, we have designed a compensated signal to solve this problem. Let
where β2(t) is given later, k1, c1 > 0, and β(0) = 0. Using Lemma 4, we can estimate α(t) and as
Thus, (15) and Lemma 4 imply that and within finite time. Let
where . Then the victual signal is designed as
with , ν ∈ (0, 1). Define , according to Lemma 1, and its fractional-order derivative is
It follows from (10), (11), (12), and (16) that
with Θ(t) = γ(t) + d(t) + f(x(t)), being driven from (15). The unknown function Θ(x) in (19) can be approximated by the NN as
Let the optimal parameter of NN be . Define , and . In fact, according to universal approximation theorem of the NN, we know that, for any continuous non-linear function defined on a compact set, there is a NN in order for the optimal to be as small as possible [16, 26, 27]. Thus, it is possible for us to assume the optimal estimation error is bounded, i.e., where is a constant. We then have
To meet the control objective, we can design the compensated signal as
with k2, c2 > 0. Then, let us construct the final input as
where σ, a2 > 0, and can be satisfied. It follows from (22) and (23) into (19) that
Then, (24) implies
Define
According to (18), (25), and (26), we have
The fractional-order adaptation law is
with κ1, κ2 > 0.
The following theorem provides a conclusion for the discussion.
Theorem 1. Let the immediate controller be (17) with the fractional filter (15). Let the compensated signal be (14) and (22). Then, the NN controller (23) with adaptation law (28) drive e1(t) to be arbitrary small in finite time.
Proof. Let
Then, based on (27), (28), and (29), we obtain
Then, (30) implies
If , it is easy to know that
On the contrary, if , one has
Thus, it follows from (32) and (33) that
Substituting (34) into (31) yields
with and , and κmin = min{κ1, κ2}. As a result, (35) can be arranged as
According to (36) and Lemma 3, when , e1(t) will tend to the region
in some finite time. Since e1(t) = ẽ1(t) + β1(t), e2(t) = ẽ2(t) + β2(t), if β1(t) and β2(t) are bounded, then all signals are bounded. Let Then, (14) and (22) imply
where . Then, it follows from (15) and Lemma 4 that is bounded in finite time. As a result, we have
where k = 2 min{k1, k2}, c = min{c1, c2}, and . Thus, (38) and Lemma 3 imply that β1(t) and β2(t) are finite time bounded. This concludes our proof.■
Remark 1. In this paper, the finite-control of fractional-order Duffing system was considered. It can be seen from the system model (10) that the non-linear function f(x) is Lipschitz continuous. In addition, under the proposed controller (23), for any initial condition, the solution to the fractional-order Duffing system exists and is unique. In addition, from Theorem 1, it is obvious that all the signals in the closed loop system keep bounded. Thus, the solution of the controlled system (10) is stable.
Remark 2. In should be emphasized that the proposed fractional-order finite-time filter has very convergence ability compared with some related works, such as Liu et al. [16] and Ha et al. [25], where only the following class of lower filter (the order of the filter lying on (0,1)) is used:
where k > 0. The fractional-order filter (39) can also guarantee that the approximation errors of the virtual input and its fractional converge to a small region of zero; however, the finite-time convergence cannot be guaranteed. In addition, to drive the approximation smaller, larger design parameter k should be used, which usually results in the signal z(t) being too big. However, the proposed filter (15) has no such problems. To show the effectiveness of the proposed high order filter, some comparisons have been given in the following section.
4. Simulation Results
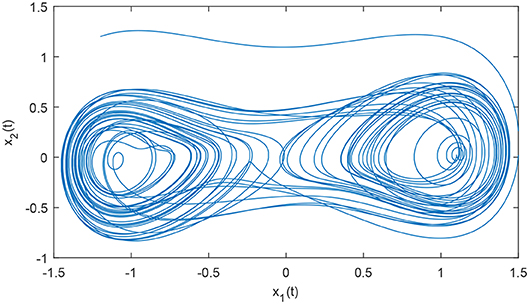
In system (10), let parameters a = 0.15, b = 0.23, and the initial conditions be x1(0) = −1.2, x2(0) = 1.2. When d(t) = u(t) = 0, under above parameters and initial conditions, system (10) exhibits chaotic phenomenon, as shown in Figure 1.
In the simulation, let x1(0) = 2, x2(0) = 0, and let the reference signal be
The design parameters are k1 = k2 = 0.9; a1 = a2 = 1, c1 = c2 = 1, κ1 = κ2 = 1, ν = 0.70, b1 = b2 = 1. The NN uses x1(t), x2(t) as input variables with θ(0) = 0 ∈ ℝ81. The saturation parameters are ul = −5, ur = 5.
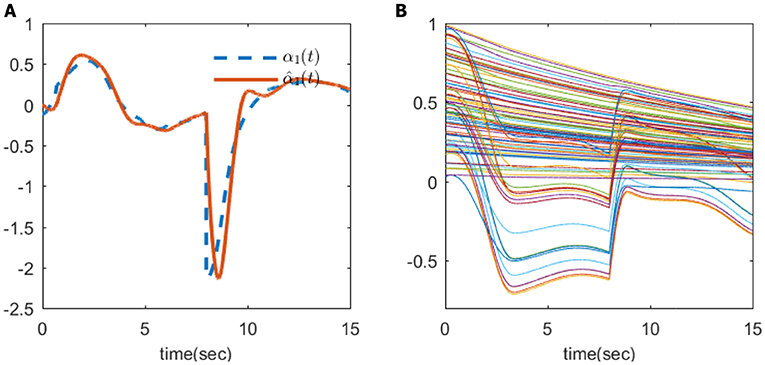
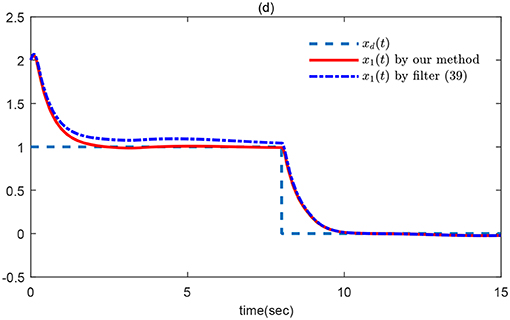
Then, the simulation results can be seen in Figures 2–4. The tracking errors e1(t) and e2(t) are given in Figure 2A, and we can see that the tracking error converges quickly. The compensated tracking errors are given in Figure 2B, where the proposed filter has very good approximation ability. The control input is given in Figure 2C. The tracking performance is in Figure 2D. The virtual input and its approximation is given in Figure 3A, and the NN parameters are shown in Figure 3B.
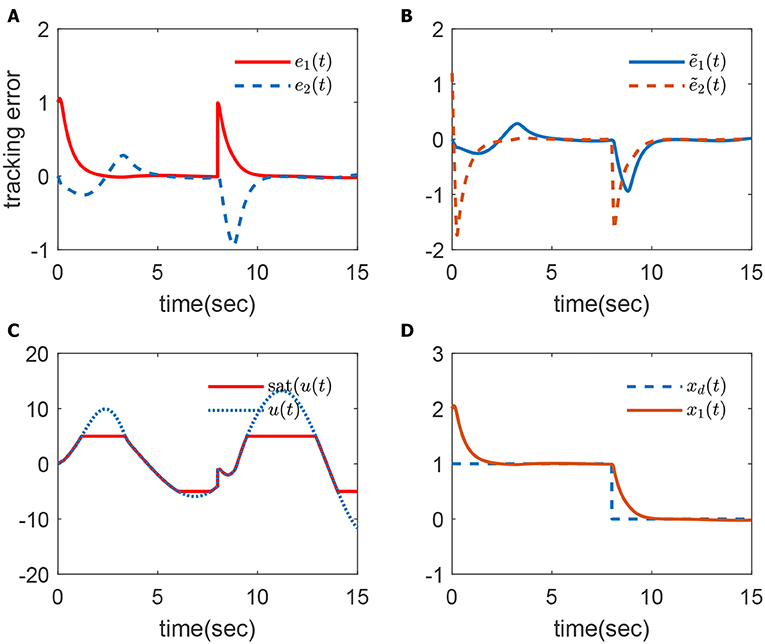
Figure 2. Simulation1 results in (A) e1(t) and e2(t); (B) ẽ1(t) and ẽ2(t); (C) u(t) and sat(u(t)); (D) xd(t) and x1(t).
To show the rapid convergence speed of the proposed high-order filter, some comparative simulation results will be given here. Noting that in Liu et al. [16] and Ha et al. [25], the lower filter (39) was used. The simulation results under our filter (15) and (39) are given in Figure 4; in order to make a fair comparison, the design parameters in (39) are taken as 0.9 just the same as the value we took above. Obviously, compared with the lower filter (39), our method can guarantee a quicker convergence speed.
5. Conclusions
This paper addressed the finite time control of an unknown disturbed FODS in the presence of input saturation. By using the backstepping technique, a high order fractional filter with the order lying on (1,2) is proposed, and thus, the virtual input and its fractional derivative can be approximated. It is proven that the filter's approximation error can be enough small and can converge to the small region in some finite time. Then, an adaptive NN controller is given. The stability is proven strictly. In addition, the robustness of the proposed method is shown in simulation results. Our future research directions including how to design sliding mode surface for FODS and how to construct a high-order filter.
Data Availability Statement
All datasets generated for this study are included in the article/supplementary material.
Author Contributions
HL and XZ contributed the conception of the study. HL wrote the study and organized the literature. XZ wrote the simulation programs. All authors contributed to the manuscript revision, read, and approved the submitted version.
Funding
This work was supported by the Basic Ability Promotion Project for Young and Middle-aged Teachers of Guangxi Colleges and Universities (2020KY04022), the Key Natural Science Research Projects in Anhui Universities (KJ2019A0695), and the Xiangsihu Young Scholars Innovative Research Team of Guangxi University for Nationalities (2019RSCXSHQN02).
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
1. Monje CA, Chen Y, Vinagre BM, Xue D, Feliu-Batlle V. Fractional-Order Systems and Controls: Fundamentals and Applications. London: Springer Science & Business Media Verlag (2010).
2. Luo Y, Chen YQ, Wang CY, Pi YG. Tuning fractional order proportional integral controllers for fractional order systems. J Process Control. (2010) 20:823–31. doi: 10.1016/j.jprocont.2010.04.011
3. Munoz-Pacheco J, Zambrano-Serrano E, Volos C, Tacha O, Stouboulos I, Pham VT. A fractional order chaotic system with a 3D grid of variable attractors. Chaos Solit Fract. (2018) 113:69–78. doi: 10.1016/j.chaos.2018.05.015
4. Liu H, Pan Y, Cao J. Composite learning adaptive dynamic surface control of fractional-order nonlinear systems. IEEE Trans Cybern. (2019). doi: 10.1109/TCYB.2019.2938754. [Epub ahead of print].
5. Tavazoei MS, Haeri M. Chaotic attractors in incommensurate fractional order systems. Phys D Nonlin Phenom. (2008) 237:2628–37. doi: 10.1016/j.physd.2008.03.037
6. Liu H, Pan Y, Cao J, Zhou Y, Wang H. Positivity and stability analysis for fractional-order delayed systems: a T-S fuzzy model approach. IEEE Trans Fuzzy Syst. (2020). doi: 10.1109/TFUZZ.2020.2966420. [Epub ahead of print].
7. Liu H, Pan Y, Li S, Chen Y. Adaptive fuzzy backstepping control of fractional-order nonlinear systems. IEEE Trans Syst Man Cybern Syst. (2017) 47:2209–17. doi: 10.1109/TSMC.2016.2640950
8. Gallegos JA, Aguila-Camacho N, Duarte-Mermoud M. Vector Lyapunov-like functions for multi-order fractional systems with multiple time-varying delays. Commun Nonlin Sci Numer Simul. (2020) 83:105089. doi: 10.1016/j.cnsns.2019.105089
9. Tlelo-Cuautle E, Pano-Azucena AD, Guillén-Fernández O, Silva-Juárez A. Synchronization and applications of fractional-order chaotic systems. In: Azar AT, Vaidyanathan S, editors. Analog/Digital Implementation of Fractional Order Chaotic Circuits and Applications. Cham: Springer (2020). p. 175–201. doi: 10.1007/978-3-030-31250-3_6
10. Yuan L, Yang Q. Parameter identification of fractional-order chaotic systems without or with noise: reply to comments. Commun Nonlin Sci Numer Simul. (2019) 67:506–16. doi: 10.1016/j.cnsns.2018.07.032
11. Marir S, Chadli M. Robust admissibility and stabilization of uncertain singular fractional-order linear time-invariant systems. IEEE/CAA J Autom Sinica. (2019) 6:685–92. doi: 10.1109/JAS.2019.1911480
12. Wei Y, Wang J, Liu T, Wang Y. Sufficient and necessary conditions for stabilizing singular fractional order systems with partially measurable state. J Frank Inst. (2019) 356:1975–90. doi: 10.1016/j.jfranklin.2019.01.022
13. Boroujeni EA, Momeni HR. Non-fragile nonlinear fractional order observer design for a class of nonlinear fractional order systems. Signal Process. (2012) 92:2365–70. doi: 10.1016/j.sigpro.2012.02.009
14. Efe MÖ. Fractional order systems in industrial automation-a survey. IEEE Trans Ind Inform. (2011) 7:582–91. doi: 10.1109/TII.2011.2166775
15. Boulkroune A, Bouzeriba A, Bouden T, Azar AT. Fuzzy adaptive synchronization of uncertain fractional-order chaotic systems. In: Azar AT, Vaidyanathan S, editors. Advances in Chaos Theory and Intelligent Control. Cham: Springer (2016). p. 681–97. doi: 10.1007/978-3-319-30340-6_28
16. Liu H, Pan Y, Cao J, Wang H, Zhou Y. Adaptive neural network backstepping control of fractionial-order nonlinear systems with actuator faults. IEEE Trans Neural Netw Learn Syst. (2020). doi: 10.1109/TNNLS.2020.2964044. [Epub ahead of print].
17. Bouzeriba A, Boulkroune A, Bouden T. Projective synchronization of two different fractional-order chaotic systems via adaptive fuzzy control. Neural Comput Appl. (2016) 27:1349–60. doi: 10.1007/s00521-015-1938-4
18. Mirzajani S, Aghababa MP, Heydari A. Adaptive control of nonlinear fractional-order systems using T-S fuzzy method. Int J Mach Learn Cybern. (2019) 10:527–40. doi: 10.1007/s13042-017-0733-1
19. Pham VT, Ouannas A, Volos C, Kapitaniak T. A simple fractional-order chaotic system without equilibrium and its synchronization. AEU Int J Electron Commun. (2018) 86:69–76. doi: 10.1016/j.aeue.2018.01.023
20. Zhang W, Cao J, Wu R, Alsaadi FE, Alsaedi A. Lag projective synchronization of fractional-order delayed chaotic systems. J Frank Inst. (2019) 356:1522–34. doi: 10.1016/j.jfranklin.2018.10.024
21. Thanh NT, Phat VN. Improved approach for finite-time stability of nonlinear fractional-order systems with interval time-varying delay. IEEE Trans Circuits Syst II Express Briefs. (2018) 66:1356–60. doi: 10.1109/TCSII.2018.2880777
22. Yang S, Yu J, Hu C, Jiang H. Finite-time synchronization of memristive neural networks with fractional-order. IEEE Trans Syst Man Cybern Syst. (2019). doi: 10.1109/TSMC.2019.2931046. [Epub ahead of print].
23. Liang J, Wu B, Liu L, Wang YE, Li C. Finite-time stability and finite-time boundedness of fractional order switched systems. Trans Inst Meas Control. (2019) 41:3364–71. doi: 10.1177/0142331219826333
24. Ha S, Liu H, Li S. Adaptive fuzzy backstepping control of fractional-order chaotic systems with input saturation. J Intell Fuzzy Syst. (2019) 37:6513–25. doi: 10.3233/JIFS-182623
25. Ha S, Liu H, Li S, Liu A. Backstepping-based adaptive fuzzy synchronization control for a class of fractional-order chaotic systems with input saturation. Int J Fuzzy Syst. (2019) 21:1571–84. doi: 10.1007/s40815-019-00663-5
26. Xu W, Hu G, Ho DW, Feng Z. Distributed secure cooperative control under denial-of-service attacks from multiple adversaries. IEEE Trans Cybern. (2019). doi: 10.1109/TCYB.2019.2896160. [Epub ahead of print].
Keywords: finite time control, fractional-order system, fractional filter, adaptive neural network control, chaos control
Citation: Lv H and Zhang X (2020) Finite-Time Neural Network Backstepping Control of an Uncertain Fractional-Order Duffing System With Input Saturation. Front. Phys. 8:122. doi: 10.3389/fphy.2020.00122
Received: 14 February 2020; Accepted: 27 March 2020;
Published: 05 May 2020.
Edited by:
Muhammad Javaid, University of Management and Technology, Lahore, PakistanReviewed by:
Lin Zhao, Qingdao University, ChinaPeijun Wang, Anhui Normal University, China
Shumin Ha, Shaanxi Normal University, China
Copyright © 2020 Lv and Zhang. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Xiulan Zhang, eGx6aGFuZ0BneHVuLmVkdS5jbg==
 Hui Lv
Hui Lv Xiulan Zhang
Xiulan Zhang