l1-Embeddability Under Gate-Sum Operation of Two l1-Graphs

1. Introduction

A computer network is a group of computer systems and other computing hardware devices that are linked together through communication channels to facilitate communication and resource-sharing among a wide range of users. Networks are usually visualized as a graph, with the computers or devices being represented by vertices and the connections between vertices shown as edges. Graham and Pollak [1] were concerned with message switching in interconnected loops of computers, and they studied the problem of addressing graphs with a ternary alphabet {0, 1, δ} such that any graph may be addressed with an edge distance of unity for some address length n. Blake and Gilchrist [2] restricted attention to the binary alphabet. They formulated a routing algorithm for message switching in computer networks that simplifies the computation of the minimum-length path between any two vertices. An l₁-graph is one in which the vertices can be labeled by binary vectors such that the Hamming distance between two binary addresses is, to scale, the distance in the graph of corresponding vertices [3]. The graph operation can construct a new graph from a given graph, and some properties can be inherited under these operations. Our motivation for this study was to determine which operations can inherit the l₁-embeddability. Thus, the purpose of this work is to determine the l₁-embeddability of the gate-sum graph of two l₁-graphs.

Let G = (V, E) be a connected simple graph. The distance between two vertices u and v of G, denoted by d_G(u, v), is the length of a shortest u–v path in G. Then [V(G), d_G] is a graphic metric space associated with G [3]. A subgraph H of G is an isometric subgraph if d_H(u, v) = d_G(u, v) for any u, v ∈ H. A subgraph of G is convex if, for any two vertices, it includes all of the shortest paths between them. Obviously, a convex subgraph of G is an isometric subgraph. Let S⊂V(G) be any subset of vertices of G. The induced subgraph G[S] is the graph that has the vertex set S and the edge set consisting of all edges in E for which both ends are in S [4].

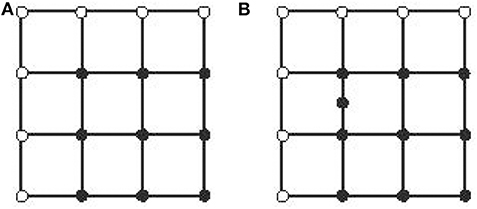
Bandelt and Chepoi [5] introduced the definition of a gate subgraph. A subgraph H of a graph G is a gate subgraph if, for every vertex v ∈ V(G), there exists a unique vertex x ∈ V(H) such that x lies on the shortest path between v and any vertex u ∈ V(H); x is called the gate of v. Hammack et al. [6] showed that a gate subgraph is convex, but that a convex subgraph may not be a gate subgraph. For example, each subgraph induced by the black vertices in Figures 1A,B is a convex subgraph in each graph. The subgraph shown in Figure 1A is a gate subgraph, whereas that in Figure 1B is not.

FIGURE 1

Figure 1. Examples of a convex subgraph (A) and a gate subgraph (B).

If u and v are two vertices of a path, the subsequence of this path starting with u and ending with v is the segment of this path from u to v. The shortest path P_xy is the path connecting x to y that has the fewest edges. Clearly, the segment of a shortest path is still a shortest path [7].

The l₁-space is the metric space of sequences whose series is absolutely convergent, denoted by (X, d₁). Thus, X is the set of all real sequences x = (x₁, x₂, …) such that $\sum _{k=1}^{\infty }\left|x_k\right|<\infty$, and the distance function is defined as $d_1(x,y)=\sum _{k=1}^{\infty }|x_k-y_k|$ for any x, y ∈ X. A graph G is an l₁-graph if (V(G), d_G) is isometrically embeddable into some l₁-space. That is, there is a distance-preserving mapping φ from V(G) into X such that d_G(x, y) = d₁(φ(x), φ(y)).

The n-dimensional hypercube Q_n is the graph whose vertices are ordered n-tuples of 0s and 1s, two vertices being joined if and only if they differ in exactly one coordinate.

Assouad and Deza [8] showed that a graph G is an l₁-graph if and only if G is scale-λ-embeddable into a hypercube Q_n for some positive integers λ and n, meaning that there exists a mapping ϕ:V(G) → V(Q_n) such that

λ·d_G(x, y) = d_Qn(ϕ(x), ϕ(y))

for any x, y ∈ V(G). The integer λ is the scale of G. The smallest such integer λ is called the minimum scale of G. According to Shpectorov [9], the minimum scale λ of G is equal to 1 or is even. In particular, if λ = 1, G is an isometric subgraph of Q_n, also called a partial cube.

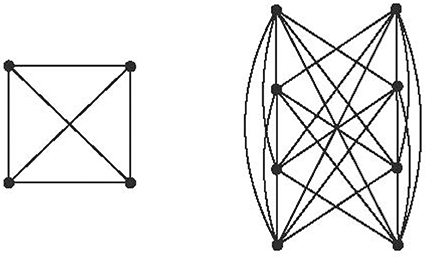
Shpectorov [9] and Deza and Grishukhin [10] showed that a graph G is an l₁-graph if and only if it is an isometric subgraph of the Cartesian product of cocktail party graphs and half-cubes. The cocktail party graph K_{n × 2} is a complete multipartite graph with n parts, each of cardinality 2, which is equivalent to a complete graph K_2n deleting a perfect matching, as shown in Figure 2. The hypercube Q_n is a bipartite graph, and the half-cube $\frac{1}{2}{Q}_n$ is the graph defined on one of two parts of this hypercube, with two vertices being joined if the distance between them in Q_n is 2.

FIGURE 2

Figure 2. The complete graph K₄ and the cocktail graph K_{4 × 2}.

An l₁-rigid graph is an l₁-graph that essentially admits a unique l₁-embedding. Shpectorov [9] showed that every l₁-rigid graph G is an isometric subgraph of a half-cube. He also proved that every l₁-rigid graph has scale 1 or 2. Deza and Laurent [11] proved that the complete graph K_n (n ≥ 4) and the cocktail graph K_{n × 2} (n ≥ 4) are not l₁-rigid, where the variety of l₁-embeddings of K_{n × 2} all come from that of the complete graph K_n. The half-cube graph $\frac{1}{2}{Q}_n$ (n = 3, 4) is l₁-rigid. Hence, they claim that, if G is not l₁-rigid, the variety of its l₁-embeddings arises from that of the complete graph. Deza and Tuma [12] and Chepoi et al. [13] studied the forbidden subgraphs of an l₁-rigid graph. They determined that an l₁-graph is l₁-rigid if and only if it is K₄-free.

Deza and Laurent [11] proved that the graph obtained by identifying single vertices from two l₁-graphs is also an l₁-graph. Wang and Zhang [14] proved that the graph obtained by gluing two l₁-graphs along an edge is also an l₁-graph if at least one of the original graphs is bipartite. However, for two non-bipartite graphs, this is not always the case. They also determined that even for two bipartite l₁-graphs, gluing a convex subgraph cannot guarantee the l₁-embeddability of the obtained graph. Naturally, we wondered if this result could be generalized.

Suppose that H_i is a subgraph of G_i, i = 1, 2. If H₁ is isomorphic to H₂, their vertices can be identified under some isomorphism as a new graph H such that the incidence relationship between vertices and edges remains. The resulting graph is called the H-sum of G₁ and G₂, denoted by G₁∪_HG₂. In particular, if H is a single vertex v or an edge e = uv, the H-sum is called the 1-sum or the 2-sum, denoted by G₁∪_vG₂ and G₁∪_uvG₂, respectively. Additionally, if G₁ and G₂ are isometric in G₁∪_HG₂, and H is a gate subgraph of at least one of G₁ and G₂, then G₁∪_HG₂ is called a gate-sum of G₁ and G₂, denoted by $G_1{\cup }_H^g{G}_2$. Both G₁ and G₂ are isometric subgraphs of G₁∪_HG₂ if and only if d_G1(x, y) = d_G2(x, y) for any x, y ∈ H.

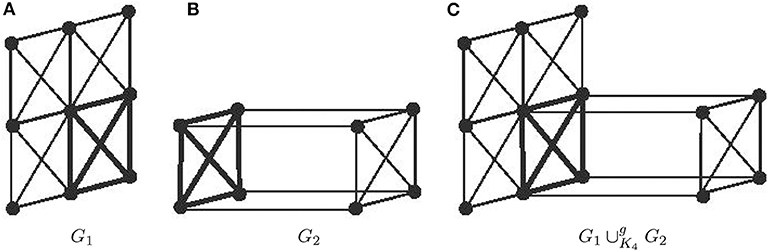
For example, see the graph in Figure 3, where the marked K₄ is an isomorphic subgraph of G₁ and G₂. The K₄-sum graph G₁∪_K4G₂, shown in Figure 3C, is obtained by identifying these two marked K₄ as the same subgraph. In particular, in Figure 3B, the marked K₄ is a gate subgraph of G₂. Obviously, both G₁ and G₂ are isometric subgraphs of G₁∪_K4G₂. Therefore, it can be seen as a gate-sum graph $G_1{\cup }_{K_4}^g{G}_2$ of G₁ and G₂ with respect to K₄.

FIGURE 3

Figure 3. The gate-sum graph $G_1{\cup }_{K_4}^g{G}_2$ of G₁ and G₂ with respect to K₄.

In this paper, we have shown that the gate-sum graph of two l₁-graphs G₁ and G₂ is also an l₁-graph. The remainder of this article is organized as follows. In section 2, we have introduced the concept of convex cuts of graphs, which are used to characterize the l₁-graphs. We have proven that the collection of convex cuts of the gate-sum graph $G_1{\cup }_H^g{G}_2$ can be expanded by those of G₁ and G₂. We have then proven the main theorem. For the sake of brevity, we obtained the main result by omitting the proofs of certain lemmas. In section 3, we have presented detailed proofs of those lemmas that were not proved in section 2. Finally, we have presented our conclusions to this study in section 4.

2. Convex Cuts and Main Results

Deza and Tuma [12] introduced the concept of convex cuts, which can be used to characterize l₁-graphs. A cut {A, B} of G is a partition of V(G) into two nonempty parts. If both A and B are convex sets, then the cut {A, B} is a convex cut. A cut {A, B} of G cuts an edge uv if u ∈ A and v ∈ B. An edge cut of G is a subset of E(G) of the form $\left[S,\overline{S}\right]$, where S is a nonempty proper subset of V(G), $\overline{S}=V\backslash S$, and $\left[S,\overline{S}\right]$ is the set of edges with one end in S and the other in $\overline{S}$. Similarly, we say that a cut {A, B} of G cuts a subgraph H if [A∩V(H), B∩V(H)] is an edge cut of H.

Deza and Tuma [12] and Deza et al. [15] proved the following theorem.

Theorem 2.1. ([12, 15]) A graph G is scale-λ-embeddable into a hypercube if and only if there exists a collection ${C}(G)$ of (not necessarily distinct) convex cuts of G such that every edge of G is cut by exactly λ cuts from ${C}(G)$.

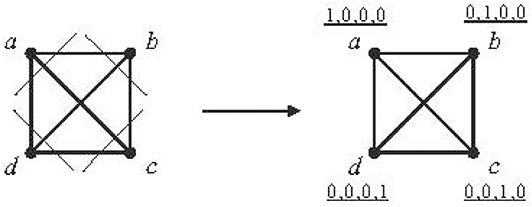
For example, in the graph K₄ in Figure 4, the cuts {{a}, {b, c, d}}, {{b}, {a, c, d}}, {{c}, {a, b, d}}, {{d}, {a, b, c}} are convex cuts. Every edge of K₄ is cut by exactly 2 cuts of {{a}, {b, c, d}}, {{b}, {a, c, d}}, {{c}, {a, b, d}}, and {{d}, {a, b, c}}. By Theorem 2.1, the graph K₄ is scale-2-embeddable into the hypercube Q₄.

FIGURE 4

Figure 4. Convex cuts and binary address of K₄.

Furthermore, Wang and Zhang [14] showed that the scale of an l₁-graph can be proportionally amplified.

Lemma 2.2. ([14]) If a graph G is scale-λ-embeddable into a hypercube, then, for any positive integer r, G is scale-rλ-embeddable into a hypercube.

Let G₁ and G₂ be two l₁-graphs and $G_1{\cup }_H^g{G}_2$ be a gate-sum graph of G₁ and G₂. Without loss of generality, suppose that G₁ is scale-λ-embeddable into some hypercube and G₂ is scale-η-embeddable into some hypercube. By Theorem 2.1, there are two collections ${C}(G_1)$ and ${C}(G_2)$ such that every edge of G₁ and G₂ is cut by exactly λ and η cuts, respectively. According to Theorem 2.1 and Lemma 2.2, to prove $G_1{\cup }_H^g{G}_2$ is an l₁-graph, it is sufficient to construct a collection ${C}(G_1{\cup }_H^g{G}_2)$ of convex cuts of $G_1{\cup }_H^g{G}_2$ such that every edge of $G_1{\cup }_H^g{G}_2$ is cut by exactly the same number of cuts. Now, we construct a collection of convex cuts of $G_1{\cup }_H^g{G}_2$ from the convex cuts of ${C}(G_1)$ and ${C}(G_2)$.

We now define the expansion of convex cuts. Suppose that H is a subgraph of G and {A, B} is a convex cut of H. If G has a convex cut {A′, B′} such that A ⊆ A′ and B ⊆ B′, then we say that the convex cut {A, B} of H expands the convex cut {A′, B′} of G. We say that the collection ${C}(H)$ expands a collection ${C}(G)$ if every convex cut of ${C}(H)$ can expand a convex cut of G. We also say that the collection ${C}(H)$ is the restriction of ${C}(G)$ on the subgraph H.

To enhance the readability of this paper, we list the following three lemmas without proofs. Their proofs have been given in section 3.

Lemma 2.3. Suppose that $G_1{\cup }_H^g{G}_2$ is a gate-sum graph of two l₁-graphs G₁ and G₂. Then, a convex cut of G₁ (or G₂) not cutting H can expand a convex cut of $G_1{\cup }_H^g{G}_2$.

Next, we will prove that two convex cuts of G₁ and G₂ can expand a convex cut of $G_1{\cup }_H^g{G}_2$ if they cut the same edges of H. Suppose that the convex cut {A₁, B₁} of G₁ is cutting H and that the cut {A₂, B₂} is that of G₂. Then, {A₁, B₁} and {A₂, B₂} cut the same edges of H. If A₁∩A₂ ≠ ∅, then A₁∩B₂ = ∅. If not, A₁∩A₂ ≠ ∅ and A₁∩B₂ ≠ ∅, which contradicts the assertion that {A₁, B₁} and {A₂, B₂} cut the same edges of H. Similarly, we have B₁∩B₂ ≠ ∅ and B₁∩A₂ = ∅. Because A_i∪B_i = V(G_i) (i = 1, 2) and V(G₁)∩V(G₂) = V(H), we know that A₁∩V(H) = A₁∩(A₁∪B₁)∩(A₂∪B₂) = A₁∩A₂ and A₂∩V(H) = A₁∩A₂. Similarly, B₁∩V(H) = B₁∩B₂ = B₂∩V(H). Furthermore, we have that V(H) = V(G₁)∩V(G₂) = (A₁∪B₁)∩(A₂∪B₂) = [A₁∩(A₂∪B₂)]∪[B₁∩(A₂∪B₂)] = [A₁∩A₂]∪[B₁∩B₂]. We denote V(H_A) = A₁∩A₂ and V(H_B) = B₁∩B₂. Then, V(H_A)∪V(H_B) = V(H), and we have the following lemma.

Lemma 2.4. Suppose that $G_1{\cup }_H^g{G}_2$ is a gate-sum graph of two l₁-graphs G₁ and G₂. Assume that {A₁, B₁} is a convex cut of G₁ and {A₂, B₂} is that of G₂. If H is l₁-rigid, {A₁, B₁} and {A₂, B₂} cut the same edges of H. Then, {A₁, B₁} and {A₂, B₂} can together expand a convex cut {A₁∪_V(HA)A₂, B₁∪_V(HB)B₂} of $G_1{\cup }_H^g{G}_2$.

If H is not l₁-rigid, then it has more than one kind of collection of convex cuts. Any two collections ${C}(G_1)$ and ${C}(G_2)$ may not be equal on H. Therefore, the convex cuts of ${C}(G_1)$ and ${C}(G_2)$ may not cut the same edges of H.

To solve this problem, we have proven that any kind of collection of convex cuts of H can expand two new collections of convex cuts of G₁ and G₂, respectively, such that they are equal on H.

Lemma 2.5. Let H be an isometric subgraph of an l₁-graph G. If H is not l₁-rigid, each collection ${C}(H)$ of H can expand a collection ${C}(G)$ of G.

We will now prove the main theorem of this work.

Theorem 2.6. Suppose that $G_1{\cup }_H^g{G}_2$ is a gate-sum graph of G₁ and G₂. If G₁ and G₂ are l₁-embeddable, then $G_1{\cup }_H^g{G}_2$ is also l₁-embeddable.

Proof: Without loss of generality, suppose that H is a gate subgraph of G₁. Because a gate subgraph is a convex subgraph, H is a convex subgraph of G₁. Then, H is an l₁-graph. Suppose that G₁ is scale-λ-embeddable into some hypercube and G₂ is scale-η-embeddable into some hypercube. By Theorem 2.1, there are two collections ${C}(G_1)$ and ${C}(G_2)$ such that every edge of G₁ and G₂ is cut by exactly λ and η cuts, respectively.

If H is l₁-rigid, H has only one kind of collection of convex cuts. Then, ${C}(G_1)$ and ${C}(G_2)$ have the same restriction on H (which means that λ = η).

If H is not l₁-rigid, the restriction on H of ${C}(G_1)$ is not equal to that of ${C}(G_2)$. Suppose that λ ≠ η. By Lemma 2.2, G₂ is scale-λη-embeddable into some hypercube. Then, G₂ has a collection ${{C}}^{\prime }(G_2)$ such that every edge of G₂ is cut by exactly λη cuts. By Lemma 2.5, every ${C}(H)$ can expand a collection ${C}(G_1)$. Obviously, the restriction on H of ${{C}}^{\prime }(G_2)$ is a kind of ${C}(H)$. Thus, it can expand a new collection ${{C}}^{\prime }(G_1)$ of G₁ such that every edge of G₁ is cut by exactly λη cuts.

Hence, there always are two collections ${{C}}^{\prime }(G_1)$ and ${{C}}^{\prime }(G_2)$ for which the restrictions of them on H are equal, and every edge of G₁ and G₂ is cut by exactly λη cuts.

As ${{C}}^{\prime }(G_1)$ and ${{C}}^{\prime }(G_2)$ are equal on H, there are the same number of convex cuts of ${{C}}^{\prime }(G_1)$ and ${{C}}^{\prime }(G_2)$ cutting H. Denote the convex cuts of ${{C}}^{\prime }(G_1)$ that are cutting H as {A₁, B₁}, ..., {A_h, B_h} and those of ${{C}}^{\prime }(G_2)$ as $\left\{A_1^{\prime },B_1^{\prime }\right\},...,\left\{A_h^{\prime },B_h^{\prime }\right\}$. Because the restrictions on H of ${{C}}^{\prime }(G_1)$ and ${{C}}^{\prime }(G_2)$ are equal, each convex cut of {A₁, B₁}, ..., {A_h, B_h} must equal one of $\left\{A_1^{\prime },B_1^{\prime }\right\},...,\left\{A_h^{\prime },B_h^{\prime }\right\}$ on H. Without loss of generality, we assume that each pair of {A_i, B_i} and $\left\{A_i^{\prime },B_i^{\prime }\right\}$ cut the same edges of H (1 ≤ i ≤ h). By Lemma 2.4, each pair of convex cuts {A_i, B_i} and $\left\{A_i^{\prime },B_i^{\prime }\right\}$ can together expand a convex cut $\left\{A_i\cup A_i^{\prime },B_i\cup B_i^{\prime }\right\}$ of $G_1{\cup }_H^g{G}_2$ (1 ≤ i ≤ h). Then, every edge of H is cut by $\left\{A_i\cup A_i^{\prime },B_i\cup B_i^{\prime }\right\}$ to give exactly λη cuts (1 ≤ i ≤ h).

By Lemma 2.3, the convex cuts of ${{C}}^{\prime }(G_1)$ and ${{C}}^{\prime }(G_2)$ that do not cut H can expand the convex cuts of $G_1{\cup }_H^g{G}_2$ that do not cut H.

Now, the convex cuts $\left\{A_i\cup A_i^{\prime },B_i\cup B_i^{\prime }\right\}$ for 1 ≤ i ≤ h, together with the convex cuts of ${{C}}^{\prime }(G_1)$ and ${{C}}^{\prime }(G_2)$ that do not cut H, form a collection of convex cuts of $G_1{\cup }_H^g{G}_2$, such that every edge of $G_1{\cup }_H^g{G}_2$ is cut by λη convex cuts. Therefore, by Theorem 2.1, the graph $G_1{\cup }_H^g{G}_2$ is scale-λη-embedded into some hypercube. This completes the proof.

Note that, for any graph, a single vertex is a gate subgraph. A cycle is a closed path that originates and terminates at the same vertex. A graph is bipartite if and only if it contains no odd cycles [4]. Therefore, for any edge e = uv of a bipartite graph, there is no vertex a such that d(u, a) = d(v, a). The subgraph induced by an edge is then a gate subgraph in a bipartite graph. Obviously, both G₁ and G₂ are isometric subgraphs of the graphs G₁∪_vG₂ and G₁∪_uvG₂. The following corollaries can be immediately obtained from Theorem 2.6.

Corollary 2.7. ([11]). Let G₁ and G₂ be two l₁-graphs. G₁∪_vG₂ is an l₁-graph.

Corollary 2.8. ([14]). Let G₁ and G₂ be two l₁-graphs. If at least one of them is bipartite, G₁∪_uvG₂ is an l₁-graph.

3. Proofs of Lemmas 2.3–2.5

3.1. Proof of Lemma 2.3

First, we need the following lemma.

Lemma 3.1. Suppose that $G_1{\cup }_H^g{G}_2$ is a gate-sum graph of G₁ and G₂. If H is a gate subgraph of G₁, then G₂ is a convex subgraph of $G_1{\cup }_H^g{G}_2$.

Proof: If G₂ is not a convex subgraph of $G_1{\cup }_H^g{G}_2$, there are two vertices x₁ and x₂ lying in G₂ such that the shortest path P_x1x2 passes through a vertex v₃ of G₁. As this shortest path must pass through the vertices of the gate subgraph H of G₁, there are two vertices $x_1^{\prime }$ and $x_2^{\prime }$ of H on the x₁, v₃-path and x₂, v₃-path of P_x1x2, respectively. Note that both G₁ and G₂ are isometric subgraphs of $G_1{\cup }_H^g{G}_2$. It is clear that the segment from $x_1^{\prime }$ to $x_2^{\prime }$ of P_x1x2 is a shortest path $P_{x_1^{\prime }{x}_2^{\prime }}$. Then, we have $P_{x_1^{\prime }{x}_2^{\prime }}=P_{x_1^{\prime }{v}_3}+P_{v_3{x}_2^{\prime }}$.

As H is a gate subgraph of G₁, there exists a unique gate a₃ of v₃ in H such that $P_{x_1^{\prime }{v}_3}=P_{x_1^{\prime }{a}_3}+P_{a_3{v}_3}$ and $P_{x_2^{\prime }{v}_3}=P_{x_2^{\prime }{a}_3}+P_{a_3{v}_3}$. Then, we have that $P_{x_1^{\prime }{x}_2^{\prime }}=P_{x_1^{\prime }{v}_3}+P_{v_3{x}_2^{\prime }}=P_{x_1^{\prime }{a}_3}+P_{a_3{v}_3}+P_{x_2^{\prime }{a}_3}+P_{a_3{v}_3}>P_{x_1^{\prime }{a}_3}+P_{a_3{x}_2^{\prime }}$, which contradicts the assertion that $P_{x_1^{\prime }{x}_2^{\prime }}$ is a shortest path. Thus, G₂ is a convex subgraph of $G_1{\cup }_H^g{G}_2$.

Proof of Lemma 2.3. Without loss of generality, suppose that H is a gate subgraph of G₁. We need only prove that a convex cut of G₁ or G₂ that does not cut H can expand a convex cut of $G_1{\cup }_H^g{G}_2$.

Case 1. A convex cut of G₁ that does not cut H can expand that of $G_1{\cup }_H^g{G}_2$.

Suppose {A, B} is a convex cut of G₁ that does not cut H. Without loss of generality, we assume that V(H) ⊆ B. We now prove that {A, B∪_V(H)V(G₂)} is a convex cut of $G_1{\cup }_H^g{G}_2$ that does not cut H and is expanded by {A, B}.

If A is not a convex set of $G_1{\cup }_H^g{G}_2$, there are two vertices v₁ and v₂ belonging to A such that P_v1v2 of $G_1{\cup }_H^g{G}_2$ passes through a vertex v₃ of G[B]∪_HG₂. Therefore, P_v1v2 = P_v1v3 + P_v3v2. If all vertices of P_v1v2 lie entirely in G₁, A cannot be a convex set of G₁. Without loss of generality, suppose that v₃ lies in G₂. Note that H is a gate subgraph of G₁. There are two gates x₁ of v₁ and x₂ of v₂ in H, and these two gates lie in P_v1v3 and P_v3v2, respectively. Then, we have that P_v1v2 = P_v1x1 + P_x1v3 + P_v3x2 + P_x2v2. As G₁ is an isometric subgraph of $G_1{\cup }_H^g{G}_2$, there is some P_x1x2 that lies entirely in G₁, and its length equals that of P_x1x2 of G₂. Then, P_v1v2 = P_v1x1 + P_x1x2 + P_x2v2, and P_v1v2 lies entirely in G₁. As P_v1v2 passes through the vertices of H, and H belongs to B, A cannot be a convex set of G₁. Therefore, A is a convex set of $G_1{\cup }_H^g{G}_2$.

If B∪_V(H)V(G₂) is not a convex set of $G_1{\cup }_H^g{G}_2$, there are two vertices v₄ and v₅ belonging to B∪_V(H)V(G₂) such that P_v4v5 passes through a vertex v₆ in A and P_v4v5 = P_v4v6 + P_v6v5. Obviously, the path P_v4v6 does not intersect with P_v6v5 at any internal vertices. The segment of a shortest path is still a shortest path. This means that v₆ has two internally disjoint paths P_v6v4 and P_v6v5 that connect with the vertices in H. Thus, v₆ has at least two gates, which contradicts the statement that the gate is unique.

Both A and B∪_V(H)V(G₂) are convex sets of $G_1{\cup }_H^g{G}_2$, and they contain all vertices of $G_1{\cup }_H^g{G}_2$. Thus, {A, B∪_V(H)V(G₂)} is a convex cut of $G_1{\cup }_H^g{G}_2$. Furthermore, note that A = A and B ⊆ B ∪ _V(H)V(G₂), and so the convex cut {A, B ∪ _V(H)V(G₂)} is expanded by the convex cut {A, B} of G₁.

Case 2. A convex cut of G₂ that does not cut H can expand that of $G_1{\cup }_H^g{G}_2$.

Suppose that {C, D} is a convex cut of G₂ that does not cut H. Without loss of generality, we assume that H ⊆ D. We now prove that the cut {C, D ∪ _V(H)V(G₁)} is a convex cut of $G_1{\cup }_H^g{G}_2$ and is expanded by {C, D}.

By Lemma 3.1, it is obvious that C is a convex set of $G_1{\cup }_H^g{G}_2$ because C is a convex set of G₂ and G₂ a convex subgraph of $G_1{\cup }_H^g{G}_2$.

Suppose that the vertex set D ∪ _V(H)V(G₁) is not a convex set of $G_1{\cup }_H^g{G}_2$. There will be two vertices v₁, v₂ of D ∪ _V(H)V(G₁) such that the shortest path P_v1v2 passes through a vertex v₃ of C. Let P_v1v3 and P_v3v2 denote the two segments of P_v1v2 divided by v₃. Because the vertices v₁, v₂ belong to D ∪ _V(H)V(G₁), we can find two vertices $v_1^{\prime },v_2^{\prime }$ of D such that $v_1^{\prime }\in P_{v_1{v}_3}$ and $v_2^{\prime }\in P_{v_3{v}_2}$. Note that both G₁ and G₂ are isometric subgraphs of $G_1{\cup }_H^g{G}_2$. It is clear that the segment from $v_1^{\prime }$ to $v_2^{\prime }$ of the path P_v1v2 is a shortest path, and it passes through the vertex v₃ of C, which contradicts the assertion that D is a convex set of G₂. Therefore, D ∪ _V(H)V(G₁) is a convex set of G.

As C and D ∪ _V(H)V(G₁) are convex sets of $G_1{\cup }_H^g{G}_2$, {C, D ∪ _V(H)V(G₁)} is a convex cut of G and its two convex sets contain C and D, respectively. It follows that the convex cut {C, D} of G₂ that does not cut H expands the convex cut {C, D ∪ _V(H)V(G₁)} of $G_1{\cup }_H^g{G}_2$. This completes the proof.

□

3.2. Proof of Lemma 2.4

Proof: Let G₁ and G₂ be two l₁-graphs and $G_1{\cup }_H^g{G}_2$ be the gate-sum graph of G₁ and G₂. By Theorem 2.1, there are two collections ${C}(G_1)$ and ${C}(G_2)$ such that every edge of G₁ and G₂ is cut by exactly λ and η cuts, respectively, as H is l₁-rigid, ${C}(G_1)$ and ${C}(G_2)$ must be equal on H. For any convex cut {A₁, B₁} of ${C}(G_1)$, we can find a convex cut {A₂, B₂} of ${C}(G_2)$ that cuts the same edge of H.

Without loss of generality, suppose that H is a gate subgraph of an l₁-graph G₁. Suppose that x₁ of V(H) is the gate of v₁ in G₁. If v₁ and x₁ belong to different convex sets, assume that v₁ lies in A₁ and x₁ belongs to B₁∩V(H). There will be a vertex u in A₁∩V(H) such that the shortest path P_v1u must pass through the vertices of B₁, which contradicts the assertion that A₁ is a convex set. Then, both v₁ and x₁ belong to the same convex set A₁ or B₁.

Without loss of generality, suppose that v₁ and x₁ belong to A₁. We now show that {A₁ ∪_V(HA)A₂, B₁ ∪ _V(HB)B₂} is a convex cut of $G_1{\cup }_H^g{G}_2$. First, we prove that A₁ ∪ _V(HA)A₂ is a convex set of $G_1{\cup }_H^g{G}_2$. Consider two vertices v₁ and v₂ that belong to A₁ ∪ _V(HA)A₂.

Case 1. Both v₁ and v₂ lie in A₂.

As A₂ is a convex subset of G₂ and G₂ is a convex subgraph of $G_1{\cup }_H^g{G}_2$, A₂ is a convex subset of $G_1{\cup }_H^g{G}_2$. Obviously, P_v1v2 lies entirely in A₂.

Case 2. The vertex v₁ lies in A₁ and v₂ lies in A₂.

Because v₁ lies in A₁ and v₂ lies in A₂, the gate x₁ of v₁ belongs to A₁∩V(H). As {A₁, B₁} and {A₂, B₂} cut the same edges of H, we have that A₁∩V(H) = A₂∩V(H) and x₁ also belongs to A₂. Therefore, the shortest path P_v1v2 must pass through the vertices of H.

If P_v1v2 passes through the gate x₁ of v₁, we have that P_v1v2 = P_v1x1 + P_x1v2. Note that both G₁ and G₂ are isometric subgraphs of $G_1{\cup }_H^g{G}_2$. As both v₁ and x₁ belong to A₁ and A₁ is a convex set, the path P_v1x1 lies entirely in A₁. Similarly, v₂ and x₁ belong to A₂, which is a convex set. Hence, P_v2x1 lies entirely in A₂. Thus, the shortest path P_v1v2 lies entirely in A₁ ∪ _V(HA)A₂.

If there is a shortest path P_v1v2 that does not pass through the gate x₁ of v₁, P_v1v2 will pass through a vertex x₃ of V(H), which is not the gate of v₁, and P_v1v2 = P_v1x3 + P_x3v2.

We now prove that x₃ belongs to A₁∩V(H). If this is not the case, then x₃ lies in B₁∩V(H), and so P_v1x3 = P_v1x1 + P_x1x3 and P_x1v2 < P_x1x3 + P_x3v2. Furthermore, P_v1x3 + P_x3v2 = P_v1x1 + P_x1x3 + P_x3v2 > P_v1x1 + P_x1v2, which contradicts the assertion that P_v1v2 passes through x₃, but does not pass through the gate x₁.

As v₁ and x₃ belong to A₁, and x₃ and v₂ belong to A₂, we have that P_v1x3 lies entirely in A₁ and P_x3v2 lies entirely in A₂. Therefore, P_v1v2 = P_v1x3 + P_x3v2 lies entirely in A₁ ∪ _V(HA)A₂.

Hence, for any vertex v₁ of A₁ and any vertex v₂ of A₂, P_v1v2 lies entirely in A₁ ∪ _V(HA)A₂. This proves case 2.

Case 3. Both v₁ and v₂ lie in A₁.

If P_v1v2 does not pass through the vertices of G₂, then P_v1v2 lies in G₁. Note that A₁ is a convex subgraph of G₁, and P_v1v2 lies in A₁. If P_v1v2 passes through the vertices of G₂, it must pass through a vertex v₃ of A₂. From case 2, we know that both P_v1v3 and P_v3v2 lie in A₁ ∪ _V(HA)A₂ and that P_v1v2 lies entirely in A₁ ∪ _V(HA)A₂.

Summarizing the above three cases, for any two vertices v₁ and v₂ of A₁ ∪ _V(HA)A₂, we have that the shortest path P_v1v2 lies entirely in A₁ ∪ _V(HA)A₂. It follows that A₁ ∪ _V(HA)A₂ is a convex set of $G_1{\cup }_H^g{G}_2$.

A similar proof shows that the set B₁ ∪ _V(HB)B₂ is also a convex set of $G_1{\cup }_H^g{G}_2$. Then, {A₁ ∪ _V(HA)A₂, B₁ ∪ _V(HB)B₂} is a convex cut of $G_1{\cup }_H^g{G}_2$, and its two convex sets contain vertex sets A₁, A₂ and B₁, B₂, respectively. Thus, {A₁, B₁} of G₁ and {A₂, B₂} of G₂ together expand the convex cut {A₁ ∪ _V(HA)A₂, B₁ ∪ _V(HB)B₂} of $G_1{\cup }_H^g{G}_2$.

3.3. Proof of Lemma 2.5

To study the expansion of the collection of convex cuts, we have introduced a new characteristic of l₁-graphs. Shpectorov [9] and Deza and Grishukhin [10] characterized l₁-graphs as follows:

Theorem 3.2. ([9, 10]) A graph G is an l₁-graph if and only if it is an isometric subgraph of the Cartesian product of cocktail party graphs and half-cubes.

Suppose that H is an isometric subgraph of an l₁-graph G; H is also an l₁-graph. By Theorem 3.2, H is an isometric subgraph of the Cartesian product of some cocktail party graphs and half-cubes, and G is that of larger cocktail party graphs and larger half-cubes. To expand the collection of convex cuts of H to G, we need only expand the collection of convex cuts of the cocktail party graph and half-cube to a larger cocktail party graph and a larger half-cube, respectively. As the half-cube is l₁-rigid, it has a unique collection of convex cuts. Note that $\frac{1}{2}{Q}_m$ is a subgraph of $\frac{1}{2}{Q}_n$. Thus, we have that any collection ${C}(\frac{1}{2}{Q}_m)$ of $\frac{1}{2}{Q}_m$ can expand a collection ${C}(\frac{1}{2}{Q}_n)$ of $\frac{1}{2}{Q}_n$ (m ≤ n). We need only examine whether any collection ${C}(K_{m\times 2})$ can expand a collection ${C}(K_{n\times 2})$ (m ≤ n).

We require the definition of a vertex-transitive graph. An automorphism of a (simple) graph G is a permutation π of V(G) that has the property that (u, v) is an edge of G if and only if (π(u), π(v)) is an edge of G. The set of all automorphisms of G, with the composition operation, is a group. This group is called the automorphism group of G. A graph G is vertex-transitive if the automorphism group of G acts transitively on V(G) [16, 17].

In other words, a vertex-transitive graph is a graph G such that, given any two vertices v₁ and v₂ of G, there is some automorphism f:V(G) → V(G) such that f(v₁) = v₂.

For a complete graph K_n, we constructed its collection of convex cuts. Without loss of generality, assume that V(K_n) = {v₁, ..., v_n}. From Theorem 3.2, K_n is an l₁-graph. Suppose that K_n is scale-λ-embeddable into a hypercube. Theorem 2.1 implies that there is a collection ${C}(K_n)$ such that every edge uv is cut by λ cuts (u, v belong to K_n and λ is even). We assume that {S₁, V(K_n) − S₁} is a convex cut of ${C}(K_n)$, and that both S₁ and V(K_n) − S₁ are convex sets of V(K_n) (|S₁| = q). As the complete graph is vertex-transitive, each S_i constructs a convex cut of K_n of the form S_i ⊆ V(K_n), |S_i| = q ($(1\le i\le \left(\frac{n}{q}\right))$). Then, we have that all convex cuts {S_i, V(K_n) − S_i}, |S_i| = q $(1\le i\le (\frac{n}{q}))$, form a collection of convex cuts of K_n such that every edge of K_n is cut by the same cuts.

Obviously, there are $\left(\frac{n}{q}\right)$ different convex cuts, and each convex cut acts on q(n − q) edges. Note that the complete graph K_n has $\frac{n(n-1)}{2}$ edges and is vertex-transitive. Thus, we have that $\lambda =\frac{\left(\frac{n}{q}\right)q(n-q)}{\frac{n(n-1)}{2}}=2\left(\frac{n-2}{q-1}\right)$.

For m ≤ n, we can now prove that the collection ${C}(K_{m\times 2})$ of K_{m × 2} can expand a collection ${C}(K_{n\times 2})$ of K_{n × 2}.

Theorem 3.3. Let K_{n × 2} be a cocktail party graph and K_{m × 2} be a cocktail party subgraph of K_{n × 2}. Every collection ${C}(K_{m\times 2})$ of K_{m × 2} can expand a collection ${C}(K_{n\times 2})$ of K_{n × 2}.

Proof: Obviously, the cocktail party graph K_{n × 2} has a complete subgraph K_n. Without loss of generality, assume that V(K_n) = {v₁, ..., v_n}, $V(K_n^{\prime })=\left\{v_1^{\prime },...,v_n^{\prime }\right\}$, and $V(K_{n\times 2})=\left\{v_1,...,v_n,v_1^{\prime },...,v_n^{\prime }\right\}$ such that $d_{K_{n\times 2}}(v_j,v_j^{\prime })=2$ (1 ≤ j ≤ n), $d_{K_{n\times 2}}(v_i,v_j)=d_{K_{n\times 2}}(v_i,v_j^{\prime })=1$ (i ≠ j). If the vertex set S is a subset of V(K_{n × 2}), then the vertex set S′ = {x′|x ∈ S} is a subset of $V(K_{n\times 2}^{\prime })$.

First, we prove that every convex cut of K_{n × 2} has only two forms: $\left\{S\cup (V(K_n^{\prime })-S^{\prime }),S^{\prime }\cup (V(K_n)-S)\right\}$ and $\left\{V(K_n),V(K_n^{\prime })\right\}$.

Suppose that {A, B} is a convex cut of K_{n × 2}. If x belongs to A, x′ will belong to B. If not, both x and x′ belong to A, and A is a convex subset of V(K_{n × 2}); all vertices of V(K_{n × 2}) will then belong to A. Furthermore, B is an empty set, which contradicts both A and B being nonempty. We now have that the vertex sets S and S′ belong to different convex sets of {A, B}. Without loss of generality, suppose that S ⊆ A and S′ ⊆ B. If V(K_n) − S ⊆ A, then $V(K_n^{\prime })-S^{\prime }\subseteq B$ and $\left\{A,B\right\}=\left\{V(K_n),V(K_n^{\prime })\right\}$. If V(K_n) − S ⊆ B, then $V(K_n^{\prime })-S^{\prime }\subseteq A$ and $\left\{A,B\right\}=\{S\cup (V(K_n^{\prime })-S^{\prime }$), $S^{\prime }\cup (V(K_n)-S)\}$.

Thus, the convex cut of K_{n × 2} has only two forms, $\left\{S\cup (V(K_n^{\prime })-S^{\prime }),S^{\prime }\cup (V(K_n)-S)\right\}$ and $\left\{V(K_n),V(K_n^{\prime })\right\}$.

Second, we prove that the collection of convex cuts $\left\{S_i\cup (V(K_n^{\prime })-S_i^{\prime }),S_i^{\prime }\cup (V(K_n)-S_i)\right\}$, |S_i| = q ($(1\le i\le \left(\frac{n}{q}\right))$), together with some $\left\{V(K_n),V(K_n^{\prime })\right\}$ make the cocktail graph K_{n × 2} embeddable into some cubes.

For every edge uv in K_n, uv is cut by the convex cut $\left\{S_i\cup (V(K_n^{\prime })-S_i^{\prime }),S_i^{\prime }\cup (V(K_n)-S_i)\right\}$. We have that $u\in (S_i\cup (V(K_n^{\prime })-S_i^{\prime }))\cap V(K_n)=S_i$ and $v\in (S_i^{\prime }\cup (V(K_n)-S_i))\cap V(K_n)=V(K_n)-S_i$, or u ∈ V(K_n) − S_i and v ∈ S_i. Note that |S_i| = q and V(K_n) has n vertices, so the number of convex cuts that cut edge uv is $2\left(\frac{n-2}{q-1}\right)$. This is similar to each edge u′v′ of $K_n^{\prime }$.

If u ∈ K_n and $v^{\prime }\in K_n^{\prime }$, uv′ is cut by the convex cut $\left\{S_i\cup (V(K_n^{\prime })-S_i^{\prime }),S_i^{\prime }\cup (V(K_n)-S_i)\right\}$. We have that $u\in (S_i\cup (V(K_n^{\prime })-S_i^{\prime }))\cap V(K_n)=S_i$, $v^{\prime }\in (S_i^{\prime }\cup \left\{V(K_n)-S_i\right\})\cap V(K_n^{\prime })=S_i^{\prime }$, $u^{\prime }\in S_i^{\prime }$, and v ∈ S_i, or $u\in (S_i^{\prime }\cup \left\{V(K_n)-S_i\right\})\cap V(K_n)=V(K_n)-S_i$, $v^{\prime }\in (S_i\cup (V(K_n^{\prime })-S_i^{\prime }))\cap V(K_n^{\prime })=V(K_n^{\prime })-S_i^{\prime }$, $u^{\prime }\in V(K_n^{\prime })-S_i^{\prime }$, and v ∈ V(K_n) − S_i. Note that $\left|S_i\right|=\left|S_i^{\prime }\right|=q$ and $|V(K_n)-S_i|=|V(K_n^{\prime })-S_i^{\prime }|=n-q$, so the number of convex cuts that cut edge uv′ is $\left(\frac{n-2}{q-2}\right)+\left(\frac{n-2}{n-q-2}\right)=\left(\frac{n-2}{q-2}\right)+\left(\frac{n-2}{q}\right)$.

As $\frac{n-\sqrt{n}}{2}\le q\le \frac{n+\sqrt{n}}{2}$, $2\left(\frac{n-2}{q-1}\right)\ge \left(\frac{n-2}{q-2}\right)+\left(\frac{n-2}{q}\right)$. If $2\left(\frac{n-2}{q-1}\right)=\left(\frac{n-2}{q-2}\right)+\left(\frac{n-2}{q}\right)$, every edge of K_{n × 2} is cut by $2\left(\frac{n-2}{q-1}\right)$ cuts.

If $2\left(\frac{n-2}{q-1}\right)>\left(\frac{n-2}{q-2}\right)+\left(\frac{n-2}{q}\right)$, then $\frac{n-\sqrt{n}}{2}<q<\frac{n+\sqrt{n}}{2}$. Obviously, $\left\{V(K_n),V(K_n^{\prime })\right\}$ is a convex cut of K_{n × 2}, which only cuts the edges with one end vertex in K_n and the other one in $K_n^{\prime }$. Then, the collection $\left\{S_i\cup (V(K_n^{\prime })-S_i^{\prime }),S_i^{\prime }\cup (V(K_n)-S_i)\right\}$ ($(1\le i\le \left(\frac{n}{q}\right))$) together with $\left\{V(K_n),V(K_n^{\prime })\right\}$ form a new collection ${{C}}^{\prime }(K_{n\times 2})$ such that every edge of K_{n × 2} is cut by $2\left(\frac{n-2}{q-1}\right)$ cuts.

Let $2\left(\frac{n-2}{q-1}\right)<\left(\frac{n-2}{q-2}\right)+\left(\frac{n-2}{q}\right)$. If n is even, choose T_i ⊆ V(K_n) such that $\left|T_i\right|=\frac{n}{2}$ ($(1\le i\le \left(\frac{n}{\frac{n}{2}}\right))$. If n is odd, choose T_i ⊆ V(K_n) such that $\left|T_i\right|=\frac{n+1}{2}$ $(1\le i\le (\frac{n}{\frac{n+1}{2}}))$. Then, $\left\{T_i\cup (V(K_n^{\prime })-T_i^{\prime }),T_i^{\prime }\cup (V(K_n)-T_i)\right\}$ is a convex cut of K_{n × 2}. Obviously, the number of edges with both vertices in V(K_n) (or $V(K_n^{\prime })$) that are cut by $\left\{T_i\cup (V(K_n^{\prime })-T_i^{\prime }),T_i^{\prime }\cup (V(K_n)-T_i)\right\}$ is greater than the number of edges that are cut by the same cut with one end vertex in K_n and the other vertex in $K_n^{\prime }$. Thus, the collection $\left\{S_i\cup (V(K_n^{\prime })-S_i^{\prime }),S_i^{\prime }\cup (V(K_n)-S_i)\right\}$ ($(1\le i\le \left(\frac{n}{q}\right))$) together with $\{T_i\cup (V(K_n^{\prime })-T_i^{\prime }),$ $T_i^{\prime }\cup (V(K_n)-T_i)\}$ $(1\le i\le \left(\frac{n}{\frac{n}{2}}\right)$ $(\mathrm{\text{or}}\left(\frac{n}{\frac{n+1}{2}}\right)))$) and $\left\{V(K_n),V(K_n^{\prime })\right\}$ form a new collection ${{C}}^{\prime }(K_{n\times 2})$ such that every edge of K_{n × 2} is cut by $2\left(\frac{n-2}{q-1}\right)+2a\left(\frac{n-2}{\frac{n}{2}-1}\right)$ cuts. The constant a is the minimal number such that $2\left(\frac{n-2}{q-1}\right)+2a\left(\frac{n-2}{\frac{n}{2}-1}\right)\ge \left(\frac{n-2}{q-2}\right)+\left(\frac{n-2}{q}\right)+a(\left(\frac{n-2}{\frac{n}{2}-2}\right)+(\frac{n-2}{\frac{n}{2}}))$.

Third, we prove that every collection of convex cuts of K_{m × 2} can expand that of K_{n × 2} (m ≤ n).

Similarly, each convex cut of K_{m × 2} has only two forms: $\left\{A\cup (V(K_m^{\prime })-A^{\prime }),A^{\prime }\cup (V(K_m)-A)\right\}$, and $\left\{V(K_m),V(K_m^{\prime })\right\}$.

Obviously, (V(K_m) − A) ⊆ (V(K_n) − A) and $(V(K_m^{\prime })-A^{\prime })\subseteq (V(K_n^{\prime })-A^{\prime })$. Then, each convex cut $\left\{A\cup (V(K_m^{\prime })-A^{\prime }),A^{\prime }\cup (V(K_m)-A)\right\}$ of ${C}(K_{m\times 2})$ can expand a convex cut $\left\{A\cup (V(K_n^{\prime })-A^{\prime }),A^{\prime }\cup (V(K_n)-A)\right\}$ of ${C}(K_{n\times 2})$. Similarly, the convex cut $\left\{V(K_m),V(K_m^{\prime })\right\}$ expands the cut $\left\{V(K_n),V(K_n^{\prime })\right\}$.

Assume that |A_i| = |A_j| is true for all convex cuts of ${C}(K_{m\times 2})$ except the convex cut $\left\{V(K_m),V(K_m^{\prime })\right\}$. This means that $\left\{A_i\cup (V(K_m^{\prime })-A_i^{\prime }),A_i^{\prime }\cup (V(K_m)-A_i)\right\}$, |A_i| = q ($(1\le i\le \left(\frac{m}{q}\right))$). Then, all of the cuts together with $\left\{V(K_m),V(K_m^{\prime })\right\}$ expand a collection of convex cuts of K_{n × 2}, in the form $\left\{A_i\cup (V(K_n^{\prime })-A_i^{\prime }),A_i^{\prime }\cup (V(K_n)-A_i)\right\}$, |A_i| = q ($(1\le i\le \left(\frac{n}{q}\right))$), together with $\left\{V(K_n),V(K_n^{\prime })\right\}$. By the second part, $\left\{A_i\cup (V(K_n^{\prime })-A_i^{\prime }),A_i^{\prime }\cup (V(K_n)-A_i)\right\}$, |A_i| = q ($(1\le i\le \left(\frac{n}{q}\right))$), together with $\left\{V(K_n),V(K_n^{\prime })\right\}$ ensure that every edge of the graph K_{n × 2} is cut by the same cuts.

Let |A_i| ≠ |A_j| for some i and j of the convex cuts of ${C}(K_{m\times 2})$. Without loss of generality, suppose that ${C}(K_{m\times 2})$ has three kinds of convex cuts, formed as $\left\{A_i\cup (V(K_n^{\prime })-A_i^{\prime }),A_i^{\prime }\cup (V(K_n)-A_i)\right\}$, |A_i| = q ($(1\le i\le \left(\frac{n}{q}\right))$), and $\left\{B_i\cup (V(K_n^{\prime })-B_i^{\prime }),B_i^{\prime }\cup (V(K_n)-B_i)\right\}$, |B_i| = p ($(1\le i\le \left(\frac{n}{p}\right))$), together with $\left\{V(K_n),V(K_n^{\prime })\right\}$. By the above discussion, all of the convex cuts $\left\{A_i\cup (V(K_n^{\prime })-A_i^{\prime }),A_i^{\prime }\cup (V(K_n)-A_i)\right\}$, |A_i| = q ($(1\le i\le \left(\frac{n}{q}\right))$), together with $\left\{V(K_n),V(K_n^{\prime })\right\}$ expand a collection ${{C}}_1(K_{n\times 2})$ of convex cuts of K_{n × 2} such that every edge of K_{n × 2} is cut by the same cuts. Similarly, all of the convex cuts $\left\{B_i\cup (V(K_n^{\prime })-B_i^{\prime }),B_i^{\prime }\cup (V(K_n)-B_i)\right\}$, |B_i| = p ($(1\le i\le \left(\frac{n}{p}\right)$), together with $\left\{V(K_n),V(K_n^{\prime })\right\}$ expand a collection ${{C}}_2(K_{n\times 2})$ of convex cuts of K_{n × 2} such that every edge of K_{n × 2} is cut by the same cuts.

Obviously, the collection ${{C}}_1(K_{n\times 2})$ together with the collection ${{C}}_2(K_{n\times 2})$ is still a collection of convex cuts of K_{n × 2} such that every edge of K_{n × 2} is cut by the same cuts.

Therefore, every collection ${C}(K_{m\times 2})$ of K_{m × 2} can expand a collection ${C}(K_{n\times 2})$ such that every edge of K_{n × 2} is cut by the same number of cuts.

We have that, for each cocktail party graph and half-cube, the collection ${C}(\frac{1}{2}{Q}_m)$ can expand a collection ${C}(\frac{1}{2}{Q}_n)$, and the collection ${C}(K_{m\times 2})$ can expand a collection ${C}(K_{n\times 2})$ (m ≤ n). By Theorem 3.2, we can prove that the collection of convex cuts of an l₁-graph can expand that of a larger l₁-graph.

Hammack et al. [6] introduced the Cartesian product G□H of two graphs G and H as the graph whose vertex set is the Cartesian product V(G) × V(H). Two vertices (u, v) and (u′, v′) are adjacent in G□H if and only if u = u′ and v is adjacent to v′ in H, or v = v′ and u is adjacent to u′ in G. Thus,

    V(G□H) = {(u, v)|u ∈ V(G) and v ∈ V(H)}

    E(G□H) = {(u, v)(u′, v′)|u = u′, vv′ ∈ E(H), or uu′ ∈

    E(G), u = u′}

The graphs G and H are called factors of the product G□H. Hammack et al. proved the following lemmas.

Lemma 3.4. ([6]) A subgraph W of G = G₁□⋯□G_n is convex if and only if W = W₁□⋯□W_n, where each W_i is convex in G_i.

Lemma 3.5. ([6]) If G = G₁□⋯□G_n and x, y ∈ V(G), then

$d_G(x,y)={\displaystyle \sum _{i=1}^n}{d}_{G_i}(p_i(x),p_i(y))$

For any index 1 ≤ i ≤ n, p_i is a projection map p_i:G₁□⋯□G_n → G_i, defined as p_i(x₁, x₂, ..., x_n) = x_i.

We can now prove that the convex cut of a Cartesian product can be represented by the convex cuts of all factors.

Theorem 3.6. The cut {A, B} is a convex cut of a graph G = G₁□⋯□G_n if and only if {A, B} has the form {V(G₁) × ⋯ × V(G_{i − 1}) × A_i × V(G_i+1) × ⋯ × V(G_n), V(G₁) × ⋯ × V(G_{i − 1}) × B_i × V(G_i+1) × ⋯ × V(G_n)} in which {A_i, B_i} is a convex cut of G_i for 1 ≤ i ≤ n.

Proof: ⇐= Suppose that G = G₁□⋯□G_n. If {A_i, B_i} is a convex cut of G_i, then G_i[A_i] and G_i[B_i] are convex subgraphs of G_i (1 ≤ i ≤ n). By Lemma 3.4, G[A_i] = G₁□⋯□G_{i − 1}□G_i[A_i]□G_i+1□⋯□G_n is a convex subgraph of G. Similarly, G[B_i] = G₁□⋯□G_{i − 1}□G_i[B_i]□G_i+1□⋯□G_n is also a convex subgraph of G.

Without loss of generality, suppose that

$\begin{array}{l}\hfill V(G)=\left\{(x_1,...,x_i,...,x_n)|x_i\in V(G_i)\right\}\hfill \\ \hfill V(G\left[A_i\right])=\left\{(x_1,...,x_{i-1},y_i,x_{i+1},...,x_n)\right|x_j\hfill \\ \hfill \in V(G_j),j\ne i,y_i\in A_i\}\hfill \\ \hfill =\{V(G_1)\times \cdots \times V(G_{i-1})\times A_i\times V(G_{i+1})\hfill \\ \hfill \times \cdots \times V(G_n)\}\hfill \\ \hfill V(G\left[B_i\right])=\left\{(x_1,...,x_{i-1},y_i,x_{i+1},...,x_n)\right|x_j\hfill \\ \hfill \in V(G_j),j\ne i,y_i\in B_i\}\hfill \\ \hfill =\{V(G_1)\times \cdots \times V(G_{i-1})\times B_i\hfill \\ \hfill \times V(G_{i+1})\times \cdots \times V(G_n)\}.\hfill \end{array}$

As {A_i, B_i} is a convex cut of G_i and the vertex y_i belongs to either A_i or B_i, we have that the cut {V(G[A_i]), V(G[B_i])} = {A, B} is a partition of V(G), and {A, B} is a convex cut of G.

⇒ Suppose that {A, B} is a convex cut of G. Then, both G[A] and G[B] are convex subgraphs of G, and B = Ā = V(G) − A. By Lemma 3.4, G[A] = G₁[A₁]□⋯□G_n[A_n] and each G_i[A_i] is a convex subgraph of G_i (1 ≤ i ≤ n).

We now prove that only one A_i is a proper subset of V(G_i). If there are two proper subsets, without loss of generality, suppose that A₁ is a proper subset of V(G₁), A₂ is that of V(G₂), and A_i = G_i (3 ≤ i ≤ n), V(G_j) − A_j = B_j (1 ≤ j ≤ n). Then, we have that

$\begin{array}{l}\begin{array}{c}A=\left\{(x_1,x_2,...,x_n)|x_i\in V(G_i),i\ne 1,2,x_1\in A_1,x_2\in A_2\right\}\hfill \\ =\left\{A_1\times A_2\times V(G_3)\times \cdots \times V(G_n)\right\}\hfill \end{array}\end{array}$

and

$\begin{array}{l}\begin{array}{c}Ā=B=\{(x_1,x_2,...,x_n)|x_i\in V(G_i),i\ne 1,2,x_1\notin A_1,x_2\in A_2,\hfill \\ \text{ or }{x}_1\in A_1,x_2\notin A_2,\text{ or }{x}_1\notin A_1,x_2\notin A_2\}\hfill \\ =\{\left[(B_1\times A_2)\cup (A_1\times B_2)\cup (B_1\times B_2)\right]\times V(G_3)\hfill \\ \times \cdots \times V(G_n)\}.\hfill \end{array}\hfill \end{array}$

Suppose that x₁ ∈ A₁, x₂ ∈ A₂, y₁ ∈ B₁, y₂ ∈ B₂, and x_i ∈ G_i (3 ≤ i ≤ n). We have two vertices (y₁, x₂, x₃, x₄, ..., x_n) ∈ B₁ × A₂ × V(G₃) × ⋯ × V(G_n) and (x₁, y₂, x₃, x₄, ..., x_n) ∈ A₁ × B₂ × V(G₃) × ⋯ × V(G_n). By Lemma 3.5, the distance between them is

$\begin{array}{l}\begin{array}{c}{d}_G((y_1,x_2,x_3,x_4,...,x_n),(x_1,y_2,x_3,x_4,...,x_n))=d_{G_1}(y_1,x_1)\hfill \\ +d_{G_2}(x_2,y_2)\hfill \\ =d_G((y_1,x_2,x_3,x_4,...,x_n),(x_1,x_2,x_3,x_4,...,x_n))\hfill \\ +d_G((x_1,x_2,x_3,x_4,...,x_n),(x_1,y_2,x_3,x_4,...,x_n)).\hfill \end{array}\hfill \end{array}$

However, vertex (x₁, x₂, x₃, x₄, ..., x_n) belongs to A₁ × A₂ × V(G₃) × ⋯ × V(G_n), which means that there are two vertices in B and a shortest path between them through a vertex in A. Therefore, B is not a convex subset of V(G), which contradicts the assertion that {A, B} is a convex cut of G.

Thus, only one A_i is a proper subset of V(G_i), and we have that

$\begin{array}{l}\begin{array}{c}A=\left\{(x_1,...,x_{i-1},y_i,x_{i+1},...,x_n)|x_j\in V(G_j),j\ne i,y_i\in A_i\right\}\\ =\left\{V(G_1)\times \cdots \times V(G_{i-1})\times A_i\times V(G_{i+1})\times \cdots \times V(G_n)\right\}.\hfill \\ \end{array}\end{array}$

Similarly, note that V(G_j) − A_j = B_j (1 ≤ j ≤ n), and so

$\begin{array}{l}\begin{array}{c}B=\left\{(x_1,...,x_{i-1},y_i,x_{i+1},...,x_n)|x_j\in V(G_j),j\ne i,y_i\notin A_i\right\}\\ =\left\{V(G_1)\times \cdots \times V(G_{i-1})\times B_i\times V(G_{i+1})\times \cdots \times V(G_n)\right\}.\hfill \end{array}\end{array}$

As G[A] and G[B] are convex subgraphs of G, by Lemma 3.4, both G_i[A_i] and G_i[B_i] are convex subgraphs of G_i. Then, A_i and B_i are convex subsets of V(G_i), and {A_i, B_i} is a convex cut of G_i (1 ≤ i ≤ n).

Proof of Lemma 2.5. Let G be an l₁-graph and H be an isometric subgraph of G. By Theorem 2.1, there is a collection ${C}(G)$ such that every edge of G is cut by exactly λ cuts.

As H is not l₁-rigid, H has another l₁-embedding. By Theorem 3.2, G is an isometric subgraph of the Cartesian product of cocktail party graphs and half-cubes. Let $\widehat{G}=K_{m_1\times 2}\square \cdots \square K_{m_p\times 2}\square \frac{1}{2}{Q}_{n_1}\square \cdots \square \frac{1}{2}{Q}_{n_q}$ be a Cartesian product that contains G as an isometric subgraph, such that each factor of Ĝ is minimal and the number of factors is minimal. Without loss of generality, we assume that m_i ≤ m_j and n_i ≤ n_j (i < j).

Because H is an isometric subgraph of G and G is an l₁-graph, H is an l₁-graph. By Theorem 3.2, H has a minimal Cartesian product $\widehat{H}=K_{m_1^{\prime }\times 2}\square \cdots \square K_{m_s^{\prime }\times 2}\square \frac{1}{2}{Q}_{n_1^{\prime }}\square \cdots \square \frac{1}{2}{Q}_{n_t^{\prime }}$.

As H is an isometric subgraph of G and G is an isometric subgraph of Ĝ, H is an isometric subgraph of Ĝ. Because Ĥ may not be equal to Ĝ, we have that s ≤ p, t ≤ q, and $m_i^{\prime }\le m_i$, $n_j^{\prime }\le n_j$ (1 ≤ i ≤ s, 1 ≤ j ≤ t).

It is obvious that $\frac{1}{2}{Q}_{n_i^{\prime }}$ is a convex subgraph of $\frac{1}{2}{Q}_{n_i}$ (1 ≤ i ≤ t) and $K_{m_i^{\prime }\times 2}$ is an isometric subgraph of K_{mi × 2} (1 ≤ i ≤ s).

As $\frac{1}{2}{Q}_n$ is l₁-rigid, the collection ${C}(\frac{1}{2}{Q}_{n_i^{\prime }})$ can expand a collection ${C}(\frac{1}{2}{Q}_{n_i})$ for 1 ≤ i ≤ t.

By Theorem 3.3, every collection ${C}(K_{m_i^{\prime }\times 2})$ can expand a collection ${C}(K_{m_i\times 2})$ (1 ≤ i ≤ s).

Without loss of generality, suppose that every collection of ${C}(K_{m_j\times 2})$ (1 ≤ j ≤ s) and ${C}(\frac{1}{2}{Q}_{n_k})$ (1 ≤ k ≤ t) cuts the edges of the corresponding factors K_{mj × 2} and $\frac{1}{2}{Q}_{n_k}$ exactly λ₁, λ₂, ..., λ_s+t times, respectively. Take the least common multiple λ = [λ₁, λ₂, ..., λ_s+t]. By Lemma 2.2, we have a list of collections ${{C}}^{\prime }(K_{m_j\times 2})$ (1 ≤ j ≤ s) and ${{C}}^{\prime }(\frac{1}{2}{Q}_{n_k})$ (1 ≤ k ≤ t) such that every edge of factors K_{mj × 2} and $\frac{1}{2}{Q}_{n_k}$ is cut by exactly λ cuts.

By Theorem 3.6, each convex cut {A_ji, B_ji} of ${{C}}^{\prime }(K_{m_j\times 2})$ (1 ≤ j ≤ s) can expand a convex cut {A, B} of G such that {p_j(A), p_j(B)} = {A_ji, B_ji}. This is similar to any convex cut {A_ki, B_ki} of ${{C}}^{\prime }(\frac{1}{2}{Q}_{n_k})$ (1 ≤ k ≤ t).

All such {A, B} expanded by {A_ji, B_ji} of ${{C}}^{\prime }(K_{m_j\times 2})$ (1 ≤ j ≤ s) and {A_ki, B_ki} of ${{C}}^{\prime }(\frac{1}{2}{Q}_{n_k})$ (1 ≤ k ≤ t) form a collection ${C}(G)$ and every edge of G is cut by exactly λ cuts of ${C}(G)$. This completes the proof. □

4. Conclusion

In this study, we investigated the l₁-embeddability of the gate-sum graph of two l₁-graphs. We have shown that the gate-sum graph of two l₁-graphs G₁ and G₂ is still an l₁-graph.

Data Availability Statement

The original contributions presented in the study are included in the article/supplementary materials, further inquiries can be directed to the corresponding author/s.

Author Contributions

GW contributed the conception of gate-sum of the study. GW and CL contributed to the convex cuts of the gate-sum of two l₁-graphs. CL and FW organized the literature. FW performed the design of figures. All authors contributed to manuscript revision and read and approved the submitted version.

Funding

This work was supported by NSFC (Grant Nos. 11861032 and 11961026).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

1. Graham RL, Pollak HO. On the addressing problem for loop switching. Bell Syst Tech J. (1972) 50:2495–519. doi: 10.1002/j.1538-7305.1971.tb02618.x

CrossRef Full Text | Google Scholar

2. Blake I, Gilchrist J. Addresses for graphs. IEEE Trans Inf Theory. (1973) 19:683–8. doi: 10.1109/TIT.1973.1055087

CrossRef Full Text | Google Scholar

3. Deza M, Laurent M. Geometry of Cuts and Metrics. Berlin: Springer-Verlag (1997).

Google Scholar

4. Diestel R. Graph Theory. Heidelberg: Springer-Verlag (2006).

Google Scholar

5. Bandelt H, Chepoi V. Decomposition and l₁-embedding of weakly median graphs. Eur J Combin. (2000) 21:701–14. doi: 10.1006/eujc.1999.0377

CrossRef Full Text | Google Scholar

6. Hammack R, Imrich W, Klavzar S. Handbook of Product Graphs. Bosa Roca: CRC Press (2011).

Google Scholar

7. Bondy J, Murty U. Graph Theory. New York, NY: Springer-Verlag (2008).

Google Scholar

8. Assouad P, Deza M. Espaces metriques plongeables dans un hypercube: aspects combinatories. Ann Discret Math. (1980) 8:197–210. doi: 10.1016/S0167-5060(08)70874-4

CrossRef Full Text | Google Scholar

9. Shpectorov S. On scale embeddings of graphs into hypercubes. Eur J Combin. (1993) 14:117–30.

Google Scholar

10. Deza M, Grishukhin V. Hypermetric graphs. Q J Math. (1993) 44:393–433. doi: 10.1093/qmath/44.4.399

CrossRef Full Text | Google Scholar

11. Deza M, Laurent M. l₁-rigid graphs. J Algebr Combin. (1994) 3:153–75.

Google Scholar

12. Deza M, Tuma J. A note on l₁-rigid planar graphs. Eur J Combin. (1996) 17:157–60. doi: 10.1006/eujc.1996.0014

CrossRef Full Text | Google Scholar

13. Chepoi V, Deza M, Grishukhin V. Clin d'oeil on l₁-embeddable planar graphs. Discret Appl Math. (1997) 80:3–19. doi: 10.1016/S0166-218X(97)00066-8

CrossRef Full Text | Google Scholar

14. Wang G, Zhang H. l₁-embeddability under the edge-gluing operation on graphs. Discret Math. (2013) 313:2115–8. doi: 10.1016/j.disc.2013.04.032

CrossRef Full Text | Google Scholar

15. Deza M, Grishukhin V, Shtogrin M. Scale-Isometric Polytopal Graphs in Hypercubes and Cubic Lattices. London: Imperical College Press (2004).

Google Scholar

16. Biggs N. Algebraic Graph Theory. Cambridge, UK: Cambridge University Press (1993).

Google Scholar

17. Godsil C, Royle G. Algebraic Graph Theory. New York, NY: Springer-Verlag (2001).

Google Scholar