New Soliton Applications in Earth's Magnetotail Plasma at Critical Densities

New plasma wave solutions of the modified Kadomtsev Petviashvili (MKP) equation are presented. These solutions are written in terms of some elementary functions, including trigonometric, rational, hyperbolic, periodic, and explosive functions. The computational results indicate that these solutions are consistent with the MKP equation, and the numerical solutions indicate that new periodic, shock, and explosive forms may be applicable in layers of the Earth's magnetotail plasma. The method employed in this paper is influential and robust for application to plasma fluids. In order to depict the propagating soliton profiles in a plasma medium, the MKP equation must be solved at critical densities. In order to achieve this, the Riccati-Bernoulli sub-ODE technique has been utilized in solutions. The research findings indicate that a number of MKP solutions may be applicable to electron acoustics appearing in the magnetotail.

AMS subject classifications: 35A20, 35A99, 35C07, 35Q51, 65Z05

1. Introduction

The existence of electron acoustic solitary excitations (EAs) in plasmas has been noticed in laboratories [1, 2]. Different observations in space have confirmed propagations of EAs in magnetospheres, auroral zones, broadband electrostatic noise (BEN), heliospheric shock, and geomagnetic tails [3–10]. The concept of EAs was generated by Fried and Gould [11]. It is principally an acoustic-type of wave with inertia given by the mass of cold electrons and restoring force expressed by hot electron thermal pressure [12]. Abdelwahed et al. [10] inspected the modulation of characteristics of EAs in non-isothermal electron plasmas [13] using a time-fractional modified non-linear equation. Pakzad studied [14] cylindrical EAs by hot non-extensive electrons, and found through numerical simulations that the spherical amplitude is greater than the cylindrical in EAs. Non-thermal critical geometrical EA plasmas were studied using a Gardner-type equation in Shuchy et al. [15]. Contributions of solitons to science have been discussed in many research works, some of which may be listed as [16–23]. The observed BEN emission bursts in auroras and the Earth's magnetotail regions indicate small and large amplitude electric fields with some explosive and rational domains at critical density. These wave structures appear to be prevalent in some parts of these regions [16, 17]. Therefore, we aim to obtain the solutions that confirm the existence of the electrostatic field in our model.

Let us consider the non-linear partial differential equation

$\begin{array}{ll}H(\phi ,{\phi }_x,{\phi }_t,{\phi }_{xx},{\phi }_{xt},{\phi }_{tt},...)=0,& (1.1)\end{array}$

where φ(x, t) is an unknown function. Using the wave transformation

$\begin{array}{ll}\phi (x,t)=\phi (\xi ),\xi =kx-ct,& (1.2)\end{array}$

Equation (1.1) is converted to an ODE:

$\begin{array}{ll}E(\phi ,{\phi }^{\prime },{\phi }^{″},{\phi }^{‴},...)=0.& (1.3)\end{array}$

Many models in physics, fluid mechanics, and engineering are written in the form of (1.1), and this form may be transformed into the ODE:

$\begin{array}{ll}{\alpha }_1{\phi }^{″}+{\alpha }_2{\phi }^3+{\alpha }_3\phi =0,& (1.4)\end{array}$

(see for instance [24–35], and so on). Equation (1.3) is quite significant and useful in our computations, and we employ a robust and unified method known as the Riccatti-Bernoulli (RB) sub-ODE method [36]. The RB sub-ODE method has been used as a box solver for many systems of equations arising in applied science and physics. There are other powerful analytical methods that solve such ODEs; an important example is the Lie algebra method (see [37, 38]).

Next, we describe the RB sub-ODE method briefly.

2. The RB Sub-ODE Method

According to the RB sub-ODE method [36], the solution of Equation (1.3) is

$\begin{array}{ll}{\phi }^{\prime }=a{\phi }^{2-m}+b\phi +c{\phi }^m,& (2.1)\end{array}$

where a, b, c, and n are constants that will be determined later. From Equation (2.1), we get

$\begin{array}{l}{\phi }^{″}=ab(3-m){\phi }^{2-m}+a^2(2-m){\phi }^{3-2m}+m{c}^2{\phi }^{2m-1}\\ +bc(m+1){\phi }^m+(2ac+b^2)\phi ,& (2.2)\end{array}$

$\begin{array}{l}{\phi }^{‴}=\phi \prime [ab(3-m)(2-m){\phi }^{1-m}+a^2(2-m)(3-2m){\phi }^{2-2m}\\ +m(2m-1)c^2{\phi }^{2m-2}+bcn(m+1){\phi }^{m-1}+(2ac+b^2)].& (2.3)\end{array}$

The solitary solutions φ_i(ξ) of Equation (2.1) are given by

1. At m = 1

$\begin{array}{ll}\phi (\xi )=\varsigma e^{(a+b+c)\xi }.& (2.4)\end{array}$

2. At m ≠ 1, b = 0, and c = 0

$\begin{array}{ll}\phi (\xi )={(a(m-1)(\xi +\varsigma ))}^{\frac{1}{m-1}}.& (2.5)\end{array}$

3. At m ≠ 1, b ≠ 0, and c = 0

$\begin{array}{ll}\phi (\xi )={(\frac{-a}{b}+\varsigma e^{b(m-1)\xi })}^{\frac{1}{m-1}}.& (2.6)\end{array}$

4. At m ≠ 1,a ≠ 0, and b² − 4ac < 0

$\begin{array}{ll}\phi (\xi )={\left(\frac{-b}{2a}+\frac{\sqrt{4ac-b^2}}{2a}tan\left(\frac{(1-m)\sqrt{4ac-b^2}}{2}(\xi +\varsigma )\right)\right)}^{\frac{1}{1-m}}& (2.7)\end{array}$

and

$\begin{array}{ll}\phi (\xi )={\left(\frac{-b}{2a}-\frac{\sqrt{4ac-b^2}}{2a}cot\left(\frac{(1-m)\sqrt{4ac-b^2}}{2}(\xi +\varsigma )\right)\right)}^{\frac{1}{1-m}}.& (2.8)\end{array}$

5. At m ≠ 1,a ≠ 0, and b² − 4ac > 0

$\begin{array}{ll}\phi (\xi )={\left(\frac{-b}{2a}-\frac{\sqrt{b^2-4ac}}{2a}coth\left(\frac{(1-m)\sqrt{b^2-4ac}}{2}(\xi +\varsigma )\right)\right)}^{\frac{1}{1-m}}& (2.9)\end{array}$

and

$\begin{array}{ll}\phi (\xi )={\left(\frac{-b}{2a}-\frac{\sqrt{b^2-4ac}}{2a}tanh\left(\frac{(1-m)\sqrt{b^2-4ac}}{2}(\xi +\varsigma )\right)\right)}^{\frac{1}{1-m}}.& (2.10)\end{array}$

6. At m ≠ 1, a ≠ 0, and b² − 4ac = 0

$\begin{array}{ll}\phi (\xi )={\left(\frac{1}{a(m-1)(\xi +\varsigma )}-\frac{b}{2a}\right)}^{\frac{1}{1-m}}.& (2.11)\end{array}$

2.0.1. Bäcklund Transformation

If φ_r−1(ξ) and φ_r(ξ)(φ_r(ξ) = φ_r(φ_r−1(ξ))) are the solutions of Equation (2.1), we have

$\begin{array}{l}\frac{d{\phi }_r(\xi )}{d\xi }=\frac{d{\phi }_r(\xi )}{d{\phi }_{r-1}(\xi )}\frac{d{\phi }_{r-1}(\xi )}{d\xi }\\ =\frac{d{\phi }_r(\xi )}{d{\phi }_{r-1}(\xi )}(a{\phi }_{r-1}^{2-m}+b{\phi }_{r-1}+c{\phi }_{r-1}^m),\end{array}$

namely

$\begin{array}{ll}\frac{d{\phi }_r(\xi )}{a{\phi }_r^{2-m}+b{\phi }_r+c{\phi }_r^m}=\frac{d{\phi }_{r-1}(\xi )}{a{\phi }_{r-1}^{2-m}+b{\phi }_{r-1}+c{\phi }_{r-1}^m}.& (2.12)\end{array}$

Integrating Equation (2.12) once with respect to ξ, we get the Bäcklund transformation of Equation (2.1) as follows:

$\begin{array}{ll}{\phi }_r(\xi )={\left(\frac{-c{L}_1+a{L}_2{({\phi }_{r-1}(\xi ))}^{1-m}}{b{L}_1+a{L}_2+a{L}_1{({\phi }_{r-1}(\xi ))}^{1-m}}\right)}^{\frac{1}{1-m}},& (2.13)\end{array}$

where L₁ and L₂ are arbitrary constants. Equation (2.13) gives the infinite solutions of Equations (2.1) and (1.1).

3. Unified Solver

In this section, we will describe the practical implementation of the concept of a unified solver.

$\begin{array}{ll}{\alpha }_1{\phi }^{″}+{\alpha }_2{\phi }^3+{\alpha }_3\phi =0,& (3.1)\end{array}$

Substituting Equation (2.2) into Equation (3.1), we obtain

$\begin{array}{l}{\alpha }_1(ab(3-m){\phi }^{2-m}+a^2(2-m){\phi }^{3-2m}+m{c}^2{\phi }^{2m-1}\\ +bc(m+1){\phi }^m+(2ac+b^2)\phi )+{\alpha }_2{\phi }^3+{\alpha }_3\phi =0.& (3.2)\end{array}$

Making m = 0, Equation (3.2) is reduced to

$\begin{array}{ll}{\alpha }_1(3ab{u}^2+2a^2{\phi }^3+bc+(2ac+b^2)\phi )+{\alpha }_2{\phi }^3+{\alpha }_3\phi =0.& (3.3)\end{array}$

Setting each coefficient of φⁱ(i = 0, 1, 2, 3) to zero, we get

$\begin{array}{ll}{\alpha }_{1}bc=0,& (3.4)\end{array}$

$\begin{array}{ll}{\alpha }_1(2ac+b^2)+{\alpha }_3=0,& (3.5)\end{array}$

$\begin{array}{ll}3{\alpha }_{1}ab=0,& (3.6)\end{array}$

$\begin{array}{ll}2{\alpha }_1{a}^2+{\alpha }_2=0.& (3.7)\end{array}$

Solving Equations (3.4)–(3.7) yields

$\begin{array}{ll}b=0,& (3.8)\end{array}$

$\begin{array}{ll}c=\mp \frac{{\alpha }_3}{\sqrt{-2{\alpha }_1{\alpha }_2}},& (3.9)\end{array}$

$\begin{array}{ll}a=\pm \sqrt{\frac{-{\alpha }_2}{2{\alpha }_1}}.& (3.10)\end{array}$

Hence, we present the following possible cases for solutions of Equations (3.1) and (1.1).

1. When b = 0 and c = 0 (α₃ = 0), the solution of Equation (3.1) is

$\begin{array}{ll}{\phi }_1(x,t)={\left(\mp \sqrt{\frac{-{\alpha }_2}{2{\alpha }_1}}(\xi +\varsigma )\right)}^{-1},& (3.11)\end{array}$

where ς is an arbitrary constant.

2. When $\frac{{\alpha }_3}{{\alpha }_1}<0$, substituting Equations (3.8)–(3.10) and (1.2) into Equations (2.7) and (2.8), the trigonometric function solutions of Equation (1.1) are then given by

$\begin{array}{ll}{\phi }_{2,3}(x,t)=\pm \sqrt{\frac{{\alpha }_3}{{\alpha }_2}}tan\left(\sqrt{\frac{-{\alpha }_3}{2{\alpha }_1}}(\xi +\varsigma )\right)& (3.12)\end{array}$

$\begin{array}{ll}{\phi }_{4,5}(x,t)=\pm \sqrt{\frac{{\alpha }_3}{{\alpha }_2}}cot\left(\sqrt{\frac{-{\alpha }_3}{2{\alpha }_1}}(\xi +\varsigma )\right),& (3.13)\end{array}$

where ς is an arbitrary constant.

3. When $\frac{{\alpha }_3}{{\alpha }_1}>0$, substituting Equations (3.8)–(3.10) and (1.2) into Equations (2.9) and (2.10), the hyperbolic function solutions of Equation (1.1) are,

$\begin{array}{ll}{\phi }_{6,7}(x,t)=\pm \sqrt{\frac{-{\alpha }_3}{{\alpha }_2}}tanh\left(\sqrt{\frac{{\alpha }_3}{2{\alpha }_1}}(\xi +\varsigma )\right)& (3.14)\end{array}$

and

$\begin{array}{ll}{\phi }_{8,9}(x,t)=\pm \sqrt{\frac{-{\alpha }_3}{{\alpha }_2}}coth\left(\sqrt{\frac{{\alpha }_3}{2{\alpha }_1}}(\xi +\varsigma )\right),& (3.15)\end{array}$

where ς is an arbitrary constant.

4. Mathematical Model

We use stretched τ = ϵ³t, ξ = ϵ(x − λt), η = ϵ²y, where ϵ is an arbitrarily small number and λ is the speed of EA. Elwakil et al. [17] examined two-dimensional propagation of EAs in plasma with cold fluid of electrons and two different ion temperatures within the framework of Poisson equations:

$\begin{array}{ll}\frac{{\partial }^2\varphi }{\partial x^2}+\frac{{\partial }^2\varphi }{\partial y^2}=(n_e-n_{il}-n_{ih}),& (4.1)\end{array}$

$\begin{array}{ll}{n}_{il}=\mu exp(\frac{-\varphi }{\nu \beta +\mu }),n_{ih}=\gamma exp(\frac{-\beta \varphi }{\nu \beta +\mu }).& (4.2)\end{array}$

where T_l is the low ion temperature at equilibrium density μ, T_h is the high ion temperature at equilibrium density γ, and $\beta =\frac{T_l}{T_h}.$ The computational results indicate that the system reaches critical density μ_c which makes non-linearity vanish. At μ = μ_c, the modified KP equation was given:

$\begin{array}{l}\frac{\partial }{\partial \xi }\left(\frac{\partial }{\partial \tau }\varphi +G{\varphi }^2\frac{\partial }{\partial \xi }\varphi +R\frac{{\partial }^3}{\partial {\xi }^3}\varphi \right)+Q\frac{{\partial }^2}{\partial {\eta }^2}\varphi =0\end{array}$

with

$\begin{array}{ll}{\mu }_c=\frac{{\beta }^2{\lambda }^4-{\lambda }^4\pm (\beta -1){\lambda }^2\sqrt{{\beta }^2{\lambda }^4+2\beta {\lambda }^4+{\lambda }^4-12\beta }-6{\beta }^2+6\beta }{2(-3{\beta }^2+6\beta -3)},& (4.3)\end{array}$

$\begin{array}{ll}G=\frac{1}{2}\lambda (-\frac{3\nu {\beta }^2}{2{(\mu +\beta \nu )}^2}-\frac{3\mu }{2{(\mu +\beta \nu )}^2}-\frac{3}{{\lambda }^4}),& (4.4)\end{array}$

$\begin{array}{l}R=\frac{{\lambda }^3}{2},Q=\frac{\lambda }{2}.\end{array}$

We use a similarity transformation in the form:

$\begin{array}{ll}\chi =L\xi +M\eta -\tau ({\upsilon }_1+{\upsilon }_2),& (4.5)\end{array}$

$\begin{array}{ll}\varphi (\chi )=\varphi (x,y,t)& (4.6)\end{array}$

$\begin{array}{ll}\tau =t,& (4.7)\end{array}$

where L and M are directional cosines of x and y axes.

The MKP equation transformed to the ODE form is:

$\begin{array}{ll}-3(v-s)\varphi +\delta {\varphi }^3+3\sigma \frac{d^2\varphi }{d{\chi }^2}=0.& (4.8)\end{array}$

Equation (4.8) gives a stationary soliton in the form of

$\begin{array}{ll}{\varphi }_c=\sqrt{6(\frac{v-S}{\delta })}\text{sech}\left(\frac{\sqrt{\frac{v-S}{\delta }}}{\sqrt{\frac{\sigma }{\delta }}}\chi \right),& (4.9)\end{array}$

$\begin{array}{ll}S=\frac{M^{2}Q}{L}-u,& (4.10)\end{array}$

$\begin{array}{ll}\delta =GL,\sigma =R{L}^3,& (4.11)\end{array}$

where u and v are traveling speeds in both directions.

5. Results and Discussion

Comparing Equation (4.8) with the general form (3.1) gives α₁ = 3σ, α₂ = δ, and α₃ = −3(υ − s). According to the unified solver given in section 3, solutions of Equation (4.8) are expressed as follows.

5.1. Rational Function Solutions: (When υ = s)

The rational solutions of Equation (4.8) are.

$\begin{array}{ll}{\varphi }_{1,2}(x,t)={\left(\mp \sqrt{\frac{-\delta }{6\sigma }}(\chi +\varsigma )\right)}^{-1}.& (5.1)\end{array}$

5.2. Trigonometric Function Solution: (When $\frac{\upsilon -s}{\sigma }>0$)

The trigonometric solutions of Equation (4.8) are

$\begin{array}{ll}{\varphi }_{3,4}(x,t)=\pm \sqrt{\frac{-3(\upsilon -s)}{\delta }}tan\left(\sqrt{\frac{\upsilon -s}{2\sigma }}(\chi +\varsigma )\right)& (5.2)\end{array}$

and

$\begin{array}{ll}{\varphi }_{5,6}(x,t)=\pm \sqrt{\frac{-3(\upsilon -s)}{\delta }}cot\left(\sqrt{\frac{\upsilon -s}{2\sigma }}(\chi +\varsigma )\right).& (5.3)\end{array}$

5.3. Hyperbolic Function Solution: (When $\frac{\upsilon -s}{\sigma }<0$)

The hyperbolic solutions of Equation (4.8) are.

$\begin{array}{ll}{\varphi }_{7,8}(x,t)=\pm \sqrt{\frac{3(\upsilon -s)}{\delta }}tanh\left(\sqrt{\frac{s-\upsilon )}{2\sigma }}(\chi +\varsigma )\right)& (5.4)\end{array}$

and

$\begin{array}{ll}{\varphi }_{9,10}(x,t)=\pm \sqrt{\frac{3(\upsilon -s)}{\delta }}coth\left(\sqrt{\frac{s-\upsilon }{2\sigma }}(\chi +\varsigma )\right).& (5.5)\end{array}$

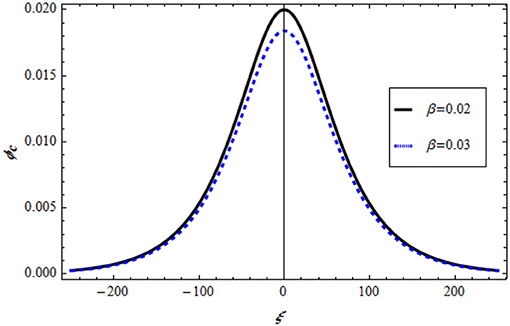
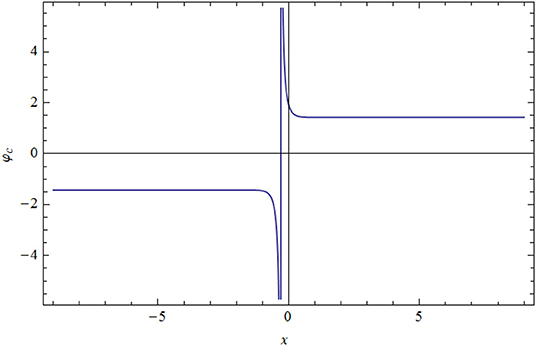
Two-dimensional propagation of solitary non-linear EAs has been examined in a plasma mode using parameters related to sheet layers of plasmas of the Earth's magnetotail [16, 17]. At a certain ion density value called the criticality value, the equation obtained cannot describe the mode. Hence, the new stretching produced by the MKP equation describes the critical system under investigation. Equation (4.8) represents a soliton with stationary behavior, as shown in Figure 1. At the critical point, many solitary forms are concerned with the behavior of EAs using the Riccati-Bernoulli solver for the MKP equation.

FIGURE 1

Figure 1. Variation of ϕ_c against χ, β for u = 0.01, v = 0.01, L = 0.95.

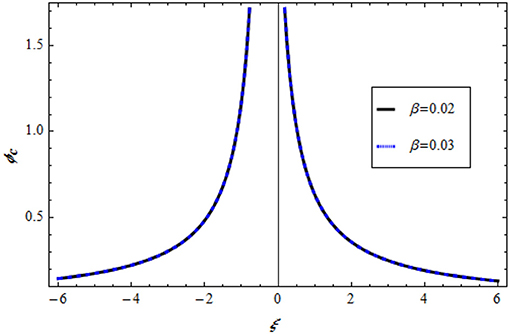
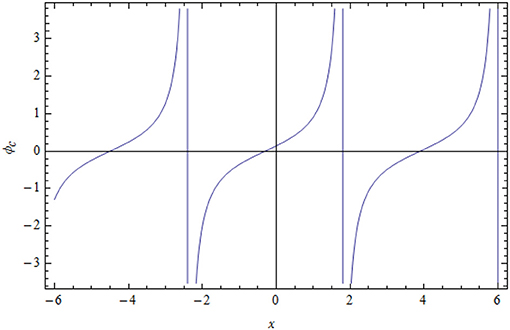
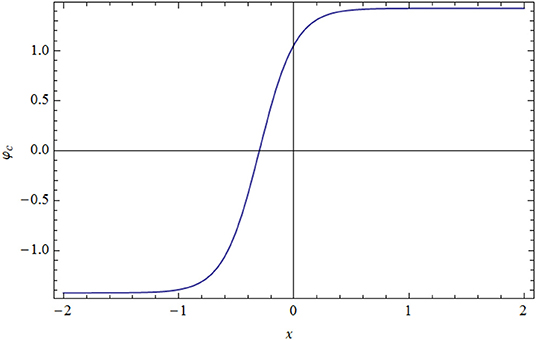
Solution (5.1) is a solitary wave type called explosive type, which has rapidly increasing amplitude, as depicted in Figure 2. Solution (5.2) has a blow-up periodic shape, as shown in Figure 3. Dissipative behaviors are also produced in Figures 4, 5. In the solution of (5.4), the shock wave is propagated in the medium, as shown in Figure 4. Finally, the explosive shock profile is obtained for solution (5.5), as shown in Figure 5.

FIGURE 2

Figure 2. Variation of rational ϕ_c against χ, β for u = 0.01, v = 0.01, L = 0.95.

FIGURE 3

Figure 3. Variation of periodic ϕ_c against χ for β = 0.05, u = 0.02, v = 0.5, L = 0.92.

FIGURE 4

Figure 4. Variation of shock ϕ_c against χ for β = 0.02, u = 0.02, v = 0.5, L = 0.5.

FIGURE 5

Figure 5. Variation of explosive shock ϕ_c against χ for β = 0.02, u = 0.02, v = 0.5, L = 0.5.

6. Conclusions

We have devoted major effort to examining the adequate description of the new type solutions at critical density in plasma layers of the Earth's magnetotail. The application of perturbation theory leads to the modified MKP equation. An RB sub-ODE solver gives new solitary excitations for the MKP equation, including periodic, explosive, and shock types. The new explosive shocks represent the wave motion of plasma solitons. Moreover, these new exact solitonic and other solutions to the MKP equation supply guidelines for the classification of the new types of waves according to the model parameters and can introduce the following types: (a) solitary and hyperbolic solutions, (b) periodic solutions, (c) explosive solutions, (d) rational solutions, (e) shock waves, and (f) explosive shocks. The application of this model could be used in the verification of the broadband and observations of magnetotail electrostatic waves.

Data Availability Statement

The datasets generated for this study are available on request to the corresponding author.

Author Contributions

All authors listed have made a substantial, direct and intellectual contribution to the work, and approved it for publication.

Funding

This project was supported by the deanship of scientific research at Prince Sattam Bin Abdulaziz University under the research project No. 10259/01/2019.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

1. Henry D, Treguier JP. Propagation of electronic longitudinal modes in a non-Maxwellian plasma. J Plasma Phys. (1972) 8:311–9. doi: 10.1017/S0022377800007169

CrossRef Full Text | Google Scholar

2. Ikezawa S, Nakamura Y. Observation of electron plasma waves in plasma of two-temperature electrons. J Phys Soc Jpn. (1981) 50:962–7. doi: 10.1143/JPSJ.50.962

CrossRef Full Text | Google Scholar

3. Dubouloz N, Pottelette R, Malingre M, Treumann RA. Generation of broadband electrostatic noise by electron acoustic solitons. Geophys Res Lett. (1991) 18:155–8. doi: 10.1029/90GL02677

CrossRef Full Text | Google Scholar

4. Singh SV, Lakhina GS. Generation of electron-acoustic waves in the magnetosphere. Planet Space Sci. (2001) 49:107–14. doi: 10.1016/S0032-0633(00)00126-4

CrossRef Full Text | Google Scholar

5. Dubouloz N, Treumann R, Pottelette R, Malingre MJ. Turbulence generated by a gas of electron acoustic solitons. Geophys Res. (1993) 98:17415–22. doi: 10.1029/93JA01611

CrossRef Full Text | Google Scholar

6. Gill TS, Kaur H, Bansal S, Saini NS, Bala P. Modulational instability of electron-acoustic waves: an application to auroral zone plasma. Eur Phys J D. (2007) 41:151–6. doi: 10.1140/epjd/e2006-00198-7

CrossRef Full Text | Google Scholar

7. Demiray H. Modulation of electron-acoustic waves in a plasma with kappa distribution. Phys Plasmas. (2016) 23:032109. doi: 10.1063/1.4943279

CrossRef Full Text | Google Scholar

8. Devanandhan S, Singh SV, Lakhina GS, Bharuthram R. Electron acoustic waves in a magnetized plasma with kappa distributed ions. Phys Plasmas. (2012) 19:082314. doi: 10.1063/1.4743015

CrossRef Full Text | Google Scholar

9. Williams G, Verheest F, Hellberg MA, Anowar MGM, Kourakis I. A Schamel equation for ion acoustic waves in superthermal plasmas. Phys Plasmas. (2014) 21:092103. doi: 10.1063/1.4894115

CrossRef Full Text | Google Scholar

10. Abdelwahed HG. Higher-order corrections to broadband electrostatic shock noise in auroral zone. Phys Plasmas. (2015) 22:092102. doi: 10.1063/1.4929793

CrossRef Full Text | Google Scholar

11. Fried BD, Gould RW. Longitudinal ion oscillations in a hot plasma. Phys Fluids. (1961) 4:139. doi: 10.1063/1.1706174

CrossRef Full Text | Google Scholar

12. Watanabe K, Taniuti T. Electron-acoustic mode in a plasma of two-temperature eelectrons. J Phys Soc Jpn. (1977) 43:1819–20. doi: 10.1143/JPSJ.43.1819

CrossRef Full Text | Google Scholar

13. Abdelwahed HG, El-Shewy EK, Mahmoud AA. Cylindrical electron acoustic solitons for modified time-fractional nonlinear equation. Phys Plasmas. (2017) 24:082107. doi: 10.1063/1.4996569

CrossRef Full Text | Google Scholar

14. Pakzad HR. Cylindrical and spherical electron acoustic solitary waves with nonextensive hot electrons. Phys Plasmas. (2011) 18:082105. doi: 10.1063/1.3622207

CrossRef Full Text | Google Scholar

15. Shuchy ST, Mannan A, Mamun AA. Cylindrical and spherical electron-acoustic Gardner solitons and double layers in a two-electron-temperature plasma with nonthermal ions. JETP Lett. (2012) 95:282. doi: 10.1134/S0021364012060094

CrossRef Full Text | Google Scholar

16. Matsumoto H, Kojima H, Miyatake T, Omura Y, Okada M, Nagano I, et al. Electrostatic solitary waves (ESW) in the magnetotail: BEN wave forms observed by GEOTAIL. Geophys Res Lett. (1994) 21:2915. doi: 10.1029/94GL01284

CrossRef Full Text | Google Scholar

17. Elwakil SA, El-hanbaly AM, El-Shewy EK, El-Kamash IS. Electron acoustic soliton energy of the Kadomtsev-Petviashvili equation in the Earth's magnetotail region at critical ion density. Astrophys Space Sci. (2014) 349:197–203. doi: 10.1007/s10509-013-1613-0

CrossRef Full Text | Google Scholar

18. Aliyu AI, Li Y, Qi L, Inc M, Baleanu D, Alshomrani AS. Lump-type and bell-shaped soliton solutions of the time-dependent coefficient Kadomtsev-Petviashvili equation. Front Phys. (2020) 7:242. doi: 10.3389/fphy.2019.00242

CrossRef Full Text | Google Scholar

19. Abdo NF. Effect of non Maxwellian distribution on the dressed electrostatic wave and energy properties. J Taibah Univ Sci. (2017) 11:617–22. doi: 10.1016/j.jtusci.2016.06.001

CrossRef Full Text | Google Scholar

20. El-Shewy EK, Abdelwahed HG, Abdo NF, Yousef MS. On the modulation of ionic velocity in electron-positron-ion plasmas. J Taibah Univ Sci. (2017) 11:1267–74. doi: 10.1016/j.jtusci.2017.03.003

CrossRef Full Text | Google Scholar

21. Alharbi AR, Almatrafi MB. Numerical investigation of the dispersive long wave equation using an adaptive moving mesh method and its stability. Results Phys. (2020) 16:1028702. doi: 10.1016/j.rinp.2019.102870

CrossRef Full Text | Google Scholar

22. Alharbi AR, Abdelrahman MAE, Almatrafi MB. Analytical and numerical investigation for the DMBBM equation. Comput Model Eng Sci. (2020) 122:743–56. doi: 10.32604/cmes.2020.07996

CrossRef Full Text | Google Scholar

23. Abdelrahman MAE, Almatrafi MB, Alharbi AR. Fundamental solutions for the coupled KdV system and its stability. Symmetry. (2020) 12:429. doi: 10.3390/sym12030429

CrossRef Full Text | Google Scholar

24. Abdelrahman MAE, Sohaly MA. The development of the deterministic nonlinear PDEs in particle physics to stochastic case. Results Phys. (2018) 9:344–50. doi: 10.1016/j.rinp.2018.02.032

CrossRef Full Text | Google Scholar

25. Abdelrahman MAE, Sohaly MA. On the new wave solutions to the MCH equation. Indian J Phys. (2019) 93:903–11. doi: 10.1007/s12648-018-1354-6

CrossRef Full Text | Google Scholar

26. Abdelrahman MAE, Sohaly MA. Solitary waves for the nonlinear Schrödinger problem with the probability distribution function in stochastic input case. Eur Phys J Plus. (2017) 132:339. doi: 10.1140/epjp/i2017-11607-5

CrossRef Full Text | Google Scholar

27. Abdelrahman MAE, Moaaz O. New exact solutions to the dual-core optical fibers. Indian J Phys. (2019) 94:705–11. doi: 10.1007/s12648-019-01503-w

CrossRef Full Text | Google Scholar

28. Abdelrahman MAE, Sohaly MA, Alharbi A. The new exact solutions for the deterministic and stochastic (2+1)-dimensional equations in natural sciences. J Taibah Univ Sci. (2019) 13:834–43. doi: 10.1080/16583655.2019.1644832

CrossRef Full Text | Google Scholar

29. Wazwaz AM. A sine-cosine method for handling nonlinear wave equations. Math Comput Model. (2004) 40:499–508. doi: 10.1016/j.mcm.2003.12.010

CrossRef Full Text | Google Scholar

30. Baskonus HM, Bulut H. New wave behaviors of the system of equations for the ion sound and Langmuir waves. Waves Random Complex Media. (2016) 26:613–25. doi: 10.1080/17455030.2016.1181811

CrossRef Full Text | Google Scholar

31. Liu C. Exact solutions for the higher-order nonlinear Schrödinger equation in nonlinear optical fibres. Chaos Solit Fract. (2005) 23:949–55. doi: 10.1016/S0960-0779(04)00345-5

CrossRef Full Text | Google Scholar

32. Zhang S. Exp-function method for solving Maccari's system. Phys Lett A. (2007) 371:65–71. doi: 10.1016/j.physleta.2007.05.091

CrossRef Full Text | Google Scholar

33. El Achab A, Amine A. A construction of new exact periodic wave and solitary wave solutions for the 2D Ginzburg-Landau equation. Nonlinear Dyn. (2017) 91:995–9. doi: 10.1007/s11071-017-3924-0

CrossRef Full Text | Google Scholar

34. Hosseini K, Kumar D, Kaplan M, Bejarbaneh EY. New exact traveling wave solutions of the unstable nonlinear Schrödinger equations. Commun Theor Phys. (2017) 68:761–7. doi: 10.1088/0253-6102/68/6/761

CrossRef Full Text | Google Scholar

35. Bulut H, Sulaiman TA, Baskonus HM. Optical solitons to the resonant nonlinear Schrödinger equation with both spatio-temporal and inter-modal dispersions under Kerr law nonlinearity. Optik. (2018) 163:49–55. doi: 10.1016/j.ijleo.2018.02.081

CrossRef Full Text | Google Scholar

36. Yang XF, Deng ZC, Wei Y. A Riccati-Bernoulli sub-ODE method for nonlinear partial differential equations and its application. Adv Differ Equat. (2015) 1:117–33. doi: 10.1186/s13662-015-0452-4

CrossRef Full Text | Google Scholar

37. Shang Y. A Lie algebra approach to susceptible-infected-susceptible epidemics. Electron J Differ Equat. (2012) 2012:1–7.

Google Scholar

38. Shang Y. Lie algebraic discussion for affinity based information diffusion in social networks. Open Phys. (2017) 15:705–11. doi: 10.1515/phys-2017-0083

CrossRef Full Text | Google Scholar