- 1Dipartimento di Fisica, Politecnico di Milano, Milan, Italy
- 2Dipartimento di Scienze Matematiche, Fisiche e Informatiche, Università di Parma, Parma, Italy
- 3PSH, UR 1115, INRAE, Avignon, France
- 4Center for Nano Science and Technology@PoliMi, Istituto Italiano di Tecnologia, Milan, Italy
- 5Division of Computational Mathematics and Engineering, Institute for Computational Science, Ton Duc Thang University, Ho Chi Minh City, Vietnam
- 6Faculty of Finance and Banking, Ton Duc Thang University, Ho Chi Minh City, Vietnam
- 7Dipartimento di Fisica, Università di Modena e Reggio Emilia, Modena, Italy
We review the main results from the literature on the consequences of link and node removal in real social networks. We restrict our review to only those works that adopted the two most common measures of network robustness, i.e., the largest connected component (LCC) and network efficiency (Eff). We consider both binary and weighted network approaches. We show that the study of the response of social networks subjected to link/node removal turns out to be extremely useful for managing a number of real problems. For instance, we show that the consequences of the imposition of social distancing in many states to control the spread of COVID-19 could be analyzed within the framework of social network analysis. Our mini-review outlines that in social networks, it is necessary to consider the weight of links between persons to perform reliable analyses. Finally, we propose promising lines for future research in social network science.
Introduction
In the last few decades, a number of studies investigated the response of real networks to link/node removal (LNR) in what is called “network attack analysis” because it simulates the consequences of an attack on the network [1–8]. These studies found application in very different fields of science such as biology [9–11], ecology [12–15], transport and infrastructure science [16–21], informatics [22, 23], neurology [24], economics [25, 26], and social networks [27–30]. These studies aimed to (i) assess network robustness, a measure that indicates the capacity of the system to maintain its functions after LNR [6, 31], and (ii) identify the LNRs that trigger the greatest amount of damage in the systems, thus revealing the links/nodes that act as key players in network functioning [5, 31].
In this mini-review, we focus on LNR in real social networks describing relationships between individuals, groups, organizations, societies, etc. [32]. We will summarize the main results from the literature and elucidate real applications.
Binary and Weighted Networks
Despite the fact that some of the preliminary works on social networks considered the link weights [33], most of the LNR in the last two decades used binary (topological) models in which links are only present or absent [31]. The binary network approach has the advantages of simplicity and low computational cost and is straight-forward in gathering information to describe the network. Nonetheless, recent analyses showed that a thorough description of real networks should consider the heterogeneity of the links-interactions [34–37]. In fact, almost all real networks are characterized by links with different “weights” indicating the strength of the interaction among nodes. For instance, in airport networks, the weight of a link identifies the number of passengers flowing between two airports [34], in neural networks, it identifies the number or the strength of connections among neurons [38, 39], and in ecological networks, it quantifies the amount of energy (or matter) flowing between species [40]. In real social networks, the link weight has been measured as the strength of friendship [32, 33, 41], face-to-face contact time [42], co-appearance in films [43], or the number of co-authored papers among scientists [30]. In the following, we review the main findings on social networks obtained by both a binary and a weighted description of the networks.
The Network Functioning Measures
Many measures have been used to evaluate the robustness of network functioning under LNR [44]. Here, we summarize the studies that have adopted two widely used indicators, i.e., the largest connected component (LCC) and the network efficiency (Eff). The LCC, also called “giant cluster,” represents the maximum number of connected nodes in the network [5, 6, 31, 45]. Considering all the network clusters, i.e., the sub-networks of connected nodes, the LCC can be defined as:
where Sj is the size (number of nodes) of the j-th cluster.
Spreading processes, such as information propagation among users of an online social network or the diffusion of pathogens among individuals, are dynamical phenomena occurring in social networks [46]. The LCC furnishes a simple and heuristic static snapshot of the network spreading entities by providing the maximum number of nodes that are in contact among them. The LCC can be used to evaluate both binary and weighted networks under LNR. Nonetheless, the LCC may be an imprecise functioning indicator in weighted networks. Consider a comparison of two removal strategies, A and B, that trigger a similar LCC decrease, but strategy A removes higher weighted links (strong links) in the network. Strategy A is likely to induce more damage than B, but the LCC is not able to discriminate the difference. Further, one can remove many strong links, which may play an important systemic role, and yet leave the nodes connected and the LCC size constant (Figures 1A,B). Even in this case, the LCC is not able to evaluate the network functioning decrease, probably underestimating its damage. For these reasons, even when adopted in weighted networks, the LCC returns a pure topological description, neglecting to evaluate the underlying weighted structure [34–37].
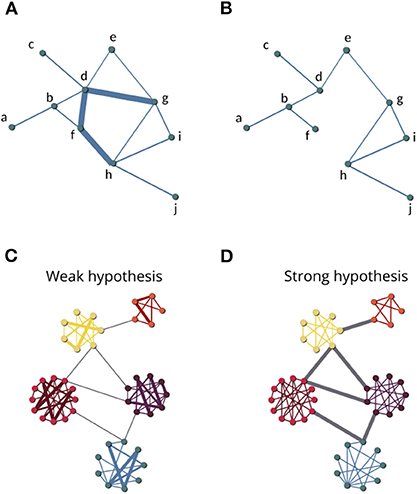
Figure 1. Network model with 10 nodes before (A) and after (B) the removal of the three highest-weight links. (C) Network model representing the “weak link” hypothesis where weak acquaintance links are more likely to bridge social sub-community modules. (D) Network model representing the opposite case with local neighborhoods mainly consist of weak links, whereas strong links that bridge social sub-community modules are more important for overall connectivity.
Differently, the network efficiency (Eff) works properly with both binary and weighted structures, being able to consider the difference in link weights for the network functioning. The efficiency measure is based on the shortest paths (also called geodesic path) between two nodes, i.e., the minimum number of links used to travel from one node to another [47].
The network efficiency is [48]:
where N is the total number of nodes of network G, and d(i,j) is the shortest path between nodes i and j. In the case where the network is weighted, the efficiency is based on the weighted shortest path. The weighted shortest path is computed as the minimum sum of the inverse link weights to travel among nodes [44]. Computing the inverse of link weight is a standard procedure for considering strong links as shorter routes with higher spreading capacity. Eff decreases with an increase in the nodes' shortest paths, thus defining as a more efficient networks with closer nodes. Eff performs a more granular evaluation of the network functioning after LNR by considering the elongation of shortest paths when the nodes are still connected (Figures 1A,B) and by giving more importance to the removal of strong links that play a major role in routing the shortest paths and the system spreading capacity [37, 49]. We remark that spreading is a dynamic process and that LCC and Eff are “static” indicators summarizing in a single value the extent of dynamic processes occurring in networks.
Link Removal in Social Networks
One of the first link removal analyses was originally conceived for social networks. In the classic “The Strength of Weak Ties” study [33], which arguably contains the most influential sociological theory of networks, Granovetter described the complex social networks of individual interpersonal relationships (links or ties) by grading their weight as “strong,” “weak,” or “absent.” Granovetter referred to strong links as friends and weak links as acquaintances. A strong link occurs between a person and her/his close circle of family or friends, thus joining together people with a great deal of similarity. On the other hand, weak links are more tenuous acquaintance connections bringing together different groups of individuals. The “weak link hypothesis” describes a specific social network structure in which strong links are associated with dense neighborhoods (communities or groups), while weaker links act as bridges between them. Granovetter argues that contacts maintained through weak acquaintance links play the important role of holding together groups with low levels of similarity, thus providing access to novel information (Figure 1C). In that study emerged the seminal idea of using node connectivity as an indicator of social network information spreading, an insight that is formalized in the LCC notion [3, 45]. In other words, LCC connectivity, supporting the overall information spreading in social systems, would be most threatened by the removal of weak links [33].
Technical progress has made it easier to collect data on complex social systems, and in the last two decades, many studies expanded the Granovetter framework to different social network databases. Onnela et al. [28] built a social network collecting mobile phone call records by describing the nodes-individuals and their phone calls links-interactions, weighting the phone call links by their duration [28]. Corroborating the “weak link hypothesis,” the authors found that the phone call network LCC is more vulnerable to weak link removal, revealing a networked structure where longer-duration calls (strong links) generally occur within communities whereas shorter-duration calls (weaker links) take place from individuals of different communities. In complex socio-economic networks, a weighted link was assigned between two nodes representing different stocks according to the cross-correlation between the return time series of each stock in the New York Stock Exchange. Garas et al. [25] show that the removal of weak connections decreases the LCC significantly more than the removal of strong links. These studies confirm the “weak link hypothesis” (Figure 1C), outlining the role of the weak links-interactions in supporting the overall connectivity and the information spreading of the network [25, 27, 28].
Searching for further evidence of the “weak link hypothesis,” Pan and Saramaki [30] analyzed the co-authorship network in the field of physics. The network is formed by nodes (scientists) and links weighted by the number of co-authored papers. In distinction from what occurred in other social networks, the LCC of the scientific network shrinks faster when the strongest links are removed first [30]. This analysis revealed a specific topological-weight coupling of the science co-authorship network, with dense local neighborhoods mainly consisting of weaker links but strong links joining senior scientists leading different research groups (Figure 1D).
Following these results, Pajevic and Plenz [43] performed a comprehensive analysis of science co-authorship and cinema collaboration social network robustness. They found that the LCCs of all four science co-authorship networks are more vulnerable to strong link removal. These outcomes would falsify the “weak link hypothesis” for this specific class of social networks [30, 43]. In contrast, for the other two social networks of cinema collaborations, in which the nodes represent actors and the link weights represent the number of movies in which they appeared together, the LCC was more vulnerable to weak link removal.
A recent study expanded the investigation concerning social network robustness by comparing the effect of new link removal strategies based on different network properties, with the classic weak/strong link removals [37]. The authors found that the removal strategy based on the binary betweenness centrality (BC) of the links is the most efficient way to disrupt the LCC. The BC is a widely used measure of link/node importance in social network analyses, and it is based on the shortest paths between a pair of nodes, e.g., the minimum number of links to travel from one node to the other [44, 47]. The BC is a measure for the number of shortest paths from any node couple passing along that link, indicating links with higher BC as more important articulation routes for the network communication paths [44, 47]. For this reason, the results of Bellingeri et al. [37] provide an interesting insight into the long-standing debate about weak-strong link importance started by Granovetter, indicating that the links playing the main role in sustaining system connectivity are neither the strong nor the weak but are those of highest BC.
All of the studies mentioned above used the LCC as an indicator of the robustness of network functioning. Nonetheless, different indicators rely on different rationales, thus furnishing quite different interpretations of system functioning. For this reason, a more comprehensive description of the social network response to link removals should include the adoption and the comparison of different indicators. With this aim, Bellingeri et al. [35] performed link removal over science co-authorship [30] and UK faculty friendship [41] social networks, finding that removing a small fraction of strong links quickly reduced the efficiency (Eff) despite the LCC remaining roughly unaltered. The removal of strong interactions left the real social systems in a “connected but inefficient” network state (Figures 2A–D). In this response state, the real social networks undergo a heavy decrease in information spreading capacity but are still well-connected. Since the most likely link removal in real social systems may occur with the network still connected, such as in the case of scholars breaking up scientific collaborations in pursuit of others, the end of friendships, or the interruption of working relationships, the findings of Bellingeri et al. [35] outlined that in order to properly evaluate the information spreading robustness in real social networks, it is necessary to include weighted measures of network functioning.
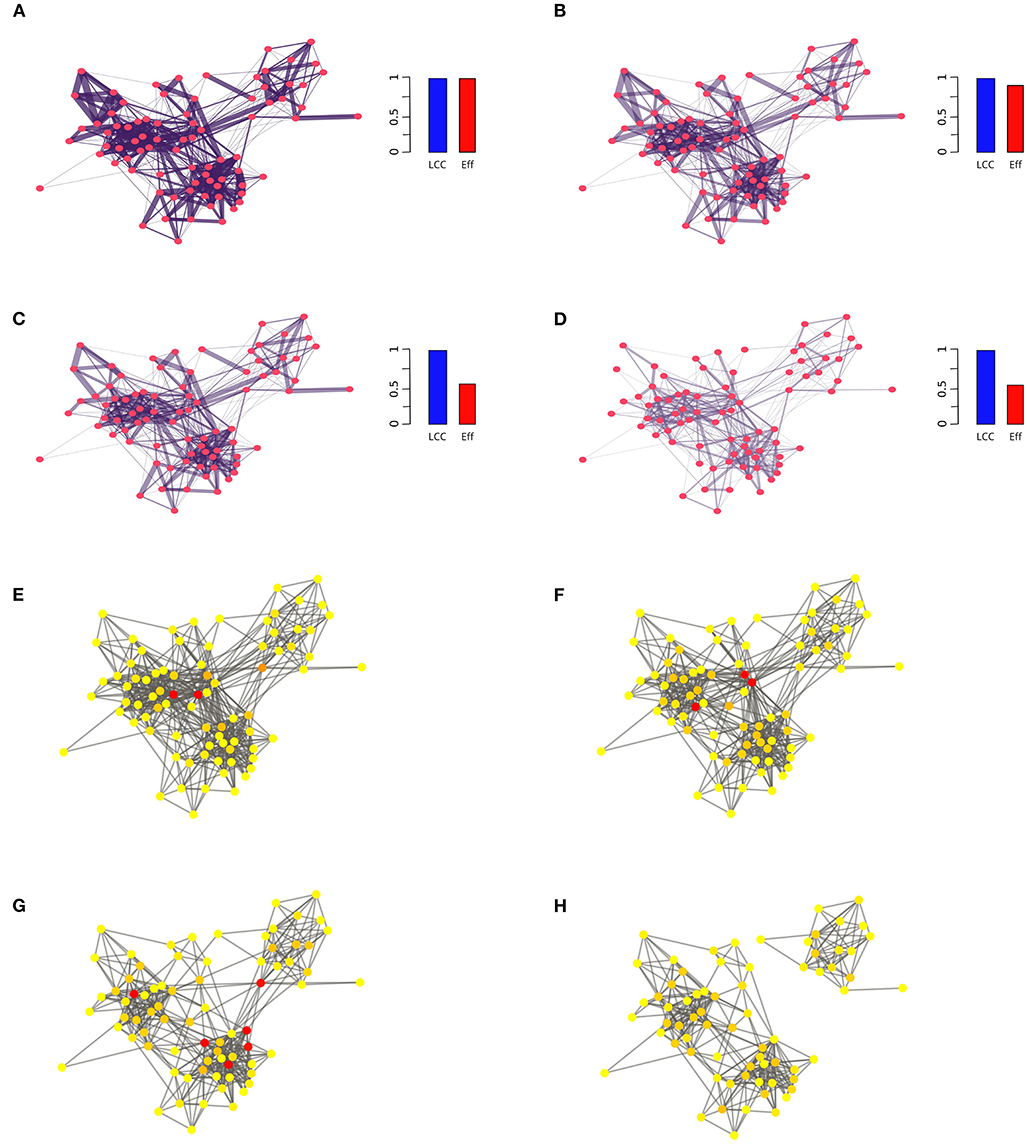
Figure 2. (A–D) Link removal process of the links with the highest weight over the UK faculty friendship social network [41] composed of 81 nodes and 817 links. We progressively remove the strong links in the network to reach the removal of 20% of the total number of links. Strong link removal (thick black lines = strong links) quickly decreases the network efficiency (Eff) with no network node disconnection, e.g., LCC does not decrease. The Eff and LCC measures are normalized by the initial value, e.g., before any removals. Strong link removal may severily slow down the pace of spreading in the network without disconnecting the nodes. (E–H) The UK faculty network subjected to the process of removal of the nodes with highest betweenness centrality (red nodes). The red nodes in each panel represent the nodes removed at each step; the total number of removed nodes is 11. The node removal fragments the network into two isolated components, halting the information spreading among nodes.
Node Removal in Social Networks
Classic results focusing on the problem of node removal indicated that many real networks show a “robust yet fragile” nature, i.e., they are robust to random node removal but very fragile to attack of the nodes with the highest number of links [1–4]. Following these seminal findings, a plethora of attack strategies were proposed to determine the sequence of node removal that maximizes the damage to the networks [5, 6, 50–55]. A proper understanding of how the node removal affects real social systems has many practical applications. In social networks, node removal may predict how the abandoning of individuals affects the information spread in the network. This can be useful for identifying the most important network nodes, with very different interpretations. On one side of the coin, in science co-authorship networks, determining which node removals produce higher information spreading reduction may help us to understand who are the nodes/scientists making the greatest contribution to knowledge and idea spreading [30, 56, 57]. These findings may furnish useful tools for designing policies facilitating the activities of these scholars, who act as “influential spreaders” in the network. On the other side, these analyses can be useful for finding which criminals play a major role in shaping information delivery in criminal networks, thus providing knowledge for investigative policies [58, 59].
From another perspective, if the network in question is a social contact network on which a disease can spread, it is critical to understand how node removal through vaccination affects the spread of the disease [60–65]. This is of great importance within network epidemiology: how should a population be vaccinated in the case of limited resources (vaccines, times, doctors, or funding) to efficiently prevent an epidemic? This is tantamount to finding the set of nodes whose removal causes the fastest LCC disruption (Figures 2E–H). Many studies have proposed strategies for minimizing the number of attacked nodes, such as removing articulation points [52], equal graph partitioning [64, 65], influence maximization [50], combined attacks [6, 51], and many others [5, 31, 53, 66–68]. A recent large comparison of node attack strategies demonstrated that the old and well-known notion in social network theory of node betweenness centrality more effective in determining the node sequence producing the fastest LCC dismantling [31].
However, node attack models using the LCC neglect to investigate the effect of link weight heterogeneity on information spreading. Dall'Asta et al. [34] showed that introducing link weights into the US airport network would decrease its robustness with respect to classic topological frameworks. The authors demonstrated that when removing highly connected nodes, the total “outreach” (e.g., the product of the link weight and the Euclidean distance between airports) of the US airport network decreased more rapidly than its LCC [34]. Following this finding, Bellingeri et al. [35] compared the LCC and Eff indicators under the removal of a few nodes (1–5 removals) and discovered a much faster Eff decrease. These outcomes outlined how the simple adoption of binary measurements like the widely used LCC may overestimate the robustness of real social networks [34, 35].
Bellingeri and Cassi [36] showed how the network robustness response to node attacks changes according to the measures of system functioning considered, i.e., weighted or binary. The authors traced the network functioning under different node attack strategies, finding that the node set triggering the greatest amount of damage may change when switching from the LCC to the Eff measure. This result elucidates that the ensemble of important nodes identified via binary-topological indicators (LCC) may yield misleading information about node importance [36]. Take the above example of a social network where the link weights account for the contact duration between individuals and consequently determines the probability that a susceptible individual is infected after having been in contact with an infectious individual. In this network, research using the node sequence to arrive at the best vaccination strategies (i.e., the best in fragmenting the LCC) would neglect the underlying weighted structure of the network and not provide the best node selection. For example, we know from the literature that vaccinating hubs, i.e., more highly linked nodes, is efficient for disrupting the LCC and is arguably a good vaccination strategy [60, 61]; in this case, vaccinating nodes with higher binary connectivity may select false hub-nodes, e.g., nodes with many weak links of negligible contact time and low probability of infection.
Node removal optimal strategies hold for those cases where a vaccine is available. On the other hand, when no vaccine is available, measures such as social distancing act on the weights of the network links, possibly reducing them to zero when a link is removed. This is the case of the novel disease COVID-19 [69–71]. The control policies applied all over the world, with different intensity levels, from the beginning of 2020 to halt disease spread follow this criterion: confining people at home; closing schools, conferences, museums, and events; suppressing trains, flights, and shipping; closing streets and national borders [72]. All of these measures are equivalent to the removal of (suppression of) links in social networks. For this reason, when no vaccine is available, as is true for emerging diseases, link removal (attack) analyses [37] would be the preferential benchmark frameworks to model the disease spread in social networks and consequently to investigate policies for preventing a pandemic. Thus, the main problem within network epidemiology should be reframed: which contacts within a population should be suppressed to most effectively prevent the spread of the disease?
Conclusions
We summarized the main results in the field of social networks, showing how LNR in networks can describe different real situations. First, this review outlines that, although binary-topological analyses present an advantage for furnishing simple baseline frameworks, to perform more exhaustive network descriptions, it is necessary to account for heterogeneity in link weights. Second, the works mentioned in this review do not consider the network reorganization after damage. In reality, networks may be able to react to LNR by reorganizing their structure, e.g., by forming new links (rewiring) [73–75]. For example, ecological network species are able to switch their prey (trophic link rewiring), dampening the decrease in ecosystem functioning after species extinction [73]. For this reason, it would be very interesting to test whether the indicators of social network robustness presented here (LCC and Eff) are sensitive to rewiring. Last, the LNR mentioned here is based on a complete knowledge of the network. Nonetheless, real problems are often poorly described. For this reason, it is recommended to perform sensitivity analysis to test the robustness of the LNR results in the presence of uncertainty about the structural features of the network.
Author Contributions
All authors listed have made a substantial, direct and intellectual contribution to the work, and approved it for publication.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
MB and FS acknowledge financial support from Fondazione Cariplo, grant n° 2018-0979. QN acknowledges financial support from Vietnam National University Ho Chi Minh City (VNU-HCM), Ho Chi Minh City, Vietnam, under grant number B2018-42-01. This project has received funding from the Vietnam Ministry of Science and Technology (MOST) under the Vietnam-Italy scientific and technological cooperation program for the period 2020–2022. This project has received funding from the European Research Council (ERC) under the European Union's Horizon 2020 Research and Innovation Program (grant agreement No. [816313]). We thank Aaron M. Ross for helpful suggestions. We thank the two reviewers for useful suggestions that greatly improved the mini-review.
References
1. Albert R, Jeong H, Barabasi A. Error and attack tolerance of complex networks. Nature. (2000) 406:378–82. doi: 10.1038/35019019
2. Callaway DS, Newman ME, Strogatz SH, Watts DJ. Network robustness and fragility: percolation on random graphs. Phys Rev Lett. (2000) 85:5468–71. doi: 10.1103/PhysRevLett.85.5468
3. Albert R, Barabási A. Statistical mechanics of complex networks. Rev Mod Phys. (2002) 74:47. doi: 10.1103/RevModPhys.74.47
4. Holme P, Kim BJ, Yoon CN, Han SK. Attack vulnerability of complex networks. Phys Rev E. (2002) 65:056109. doi: 10.1103/PhysRevE.65.056109
5. Iyer S, Killingback T, Sundaram B, Wang Z. Attack robustness and centrality of complex networks. PLoS ONE. (2013) 8:e59613. doi: 10.1371/journal.pone.0059613
6. Bellingeri M, Cassi D, Vincenzi S. Efficiency of attack strategies on complex model and real-world networks. Phys A Stat Mech its Appl. (2014) 414:174–80. doi: 10.1016/j.physa.2014.06.079
7. Ren XL, Gleinig N, Helbing D, Antulov-Fantulin N. Generalized network dismantling. Proc Natl Acad Sci USA. (2019) 116:6554–9. doi: 10.1073/pnas.1806108116
8. Zou Z, Xiao Y, Gao J. Robustness analysis of urban transit network based on complex networks theory. Kybernetes. (2013) 42:383–99. doi: 10.1108/03684921311323644
9. Jeong H, Albert R, Ottval ZN, Barabási AL. The large scale organization of metabolic networks. Nature. (2000) 407:651–4. doi: 10.1038/35036627
10. Azevedo H, Moreira-Filho CA. Topological robustness analysis of protein interaction networks reveals key targets for overcoming chemotherapy resistance in glioma. Sci Rep. (2015) 5:1–13. doi: 10.1038/srep16830
11. Smart AG, Amaral LAN, Ottino JM. Cascading failure and robustness in metabolic networks. Proc Natl Acad Sci USA. (2008) 105:13223–8. doi: 10.1073/pnas.0803571105
12. Solé R V, Montoya JM. Complexity and fragility in ecological networks. Proc Biol Sci. (2001) 268:2039–45. doi: 10.1098/rspb.2001.1767
13. Bellingeri M, Bodini A. Threshold extinction in food webs. Theor Ecol. (2013) 6:143–52. doi: 10.1007/s12080-012-0166-0
14. Bellingeri M, Bodini A. Food web's backbones and energy delivery in ecosystems. Oikos. (2016) 125:586–94. doi: 10.1111/oik.02244
15. Bellingeri M, Cassi D, Vincenzi S. Increasing the extinction risk of highly connected species causes a sharp robust-to-fragile transition in empirical food webs. Ecol Modell. (2013) 251:1–8. doi: 10.1016/j.ecolmodel.2012.12.011
16. Bellingeri M, Lu ZM, Cassi D, Scotognella F. Analyses of the response of a complex weighted network to nodes removal strategies considering links weight: the case of the Bejing urban road system. Mod Phys Lett B. (2018) 32:1850067. doi: 10.1142/S0217984918500677
17. Bellingeri M, Bevacqua D, Scotognella F, Lu ZM, Cassi D. Efficacy of local attack strategies on the Beijing road complex weighted network. Phys A Stat Mech Appl. (2018) 510:316–28. doi: 10.1016/j.physa.2018.06.127
18. Cuadra L, Salcedo-Sanz S, Del Ser J, Jiménez-Fernández S, Geem ZW. A critical review of robustness in power grids using complex networks concepts. Energies. (2015) 8:9211–65. doi: 10.3390/en8099211
19. Berche B, Von Ferber C, Holovatch T, Holovatch Y. Transportation network stability: a case study of city transit. Adv Complex Syst. (2012) 15:1–19. doi: 10.1142/S0219525912500634
20. Yang Y, Nishikawa T, Motter AE. Small vulnerable sets determine large network cascades in power grids. Science. (2017) 358:eaan3184. doi: 10.1126/science.aan3184
21. Lordan O, Sallan JM, Simo P, Gonzalez-prieto D. Robustness of the air transport network. Transp Res Part E. (2014) 68:155–63. doi: 10.1016/j.tre.2014.05.011
22. Cohen R, Erez K, ben-Avraham D, Havlin S. Breakdown of the internet under intentional attack. Phys Rev Lett. (2001) 86:3682–5. doi: 10.1103/PhysRevLett.86.3682
23. Wang J, Jiang C, Qian J. Robustness of Internet under targeted attack: a cascading failure perspective. J Netw Comput Appl. (2014) 40:97–104. doi: 10.1016/j.jnca.2013.08.007
24. Stam CJ. Modern network science of neurological disorders. Nat Publ Gr. (2014) 15:683–95. doi: 10.1038/nrn3801
25. Garas A, Argyrakis P, Havlin S. The structural role of weak and strong links in a financial market network. Eur Phys J B. (2008) 63:265–71. doi: 10.1140/epjb/e2008-00237-3
26. Martinazzi S, Flori A. The evolving topology of the Lightning Network: centralization, efficiency, robustness, synchronization, and anonymity. PLoS ONE. (2020) 15:1–18. doi: 10.1371/journal.pone.0225966
27. Onnela JP, Saramäki J, Hyvönen J, Szabó G, De Menezes MA, Kaski K, et al. Analysis of a large-scale weighted network of one-to-one human communication. New J Phys. (2007) 9:1–25. doi: 10.1088/1367-2630/9/6/179
28. Onnela JP, Saramäki J, Hyvönen J, Szabó G, Lazer D, Kaski K, et al. Structure and tie strengths in mobile communication networks. Proc Natl Acad Sci USA. (2007) 104:7332–6. doi: 10.1073/pnas.0610245104
29. Boldi P, Rosa M, Vigna S. Robustness of social networks: comparative results based on distance distributions. Soc Informatics. (2011) 6984:8–21. doi: 10.1007/978-3-642-24704-0_7
30. Pan RK, Saramäki J. The strength of strong ties in scientific collaboration networks. EPL. (2012) 97:018007. doi: 10.1209/0295-5075/97/18007
31. Wandelt S, Sun X, Feng D, Zanin M, Havlin S. A comparative analysis of approaches to network-dismantling. Sci Rep. (2018) 8:1–15. doi: 10.1038/s41598-018-31902-8
32. Borgatti SP, Mehra A, Brass DJ, Labianca G. Network analysis in the social sciences. Science. (2009) 323:892–5. doi: 10.1126/science.1165821
34. Dall'Asta L, Barrat A, Barthélemy M, Vespignani A. Vulnerability of weighted networks. J Stat Mech Theory Exp. (2006) 2006:04006. doi: 10.1088/1742-5468/2006/04/P04006
35. Bellingeri M, Bevacqua D, Scotognella F, Cassi D. The heterogeneity in link weights may decrease the robustness of real-world complex weighted network. Sci Rep. (2019) 8:10692. doi: 10.1038/s41598-019-47119-2
36. Bellingeri M, Cassi D. Robustness of weighted networks. Phys A Stat Mech Appl. (2018) 489:47–55. doi: 10.1016/j.physa.2017.07.020
37. Bellingeri M, Bevacqua D, Scotognella F, Alfieri R, Cassi D. A comparative analysis of link removal strategies in real complex weighted networks. Sci Rep. (2020) 10:1–15. doi: 10.1038/s41598-020-60298-7
38. Watts DJ, Strogatz SH. Collective dynamics of “small-world” networks. Nature. (1998) 393:440–2. doi: 10.1038/30918
39. Arenas A, Fernández A, Gómez S. A complex network approach to the determination of functional groups in the neural system of C. elegans. Lect Notes Comput Sci. (2008) 5151:9–18. doi: 10.1007/978-3-540-92191-2_2
40. Jordan F, Scotti M. Weighting, scale dependence and indirect effects in ecological networks : a comparative study. Ecol Complexity. (2007) 4:148–59. doi: 10.1016/j.ecocom.2007.05.002
41. Nepusz T, Petróczi A, Négyessy L, Bazsó F. Fuzzy communities and the concept of bridgeness in complex networks. Phys Rev E Stat Nonlin Soft Matter Phys. (2008) 77:1–12. doi: 10.1103/PhysRevE.77.016107
42. Vanhems P, Barrat A, Cattuto C, Pinton JF, Khanafer N, Régis C, et al. Estimating potential infection transmission routes in hospital wards using wearable proximity sensors. PLoS ONE. (2013) 8:e73970. doi: 10.1371/journal.pone.0073970
43. Pajevic S, Plenz D. The organization of strong links in complex networks. Nat Phys. (2012) 8:429–36. doi: 10.1038/nphys2257
44. Boccaletti S, Latora V, Moreno Y, Chavez M, Hwang DU. Complex networks: structure and dynamics. Phys Rep. (2006) 424:175–308. doi: 10.1016/j.physrep.2005.10.009
45. Erdos P, Renyi A. On the evolution of random graphs. Publ Math Inst Hung Acad Sci. (1960) 5:17–60.
46. Salehi M, Sharma R, Marzolla M, Magnani M, Siyari P, Montesi D. Spreading processes in multilayer networks. IEEE Transactions on Network Science and Engineering. (2015):2:65–83. doi: 10.1109/TNSE.2015.2425961
48. Latora V, Marchiori M. Efficient behavior of small-world networks. Phys Rev Lett. (2001) 87:198701. doi: 10.1103/PhysRevLett.87.198701
49. Newman MEJ. Analysis of weighted networks. Phys Rev E Stat Nonlin Soft Matter Phys. (2004) 70:1–9. doi: 10.1103/PhysRevE.70.056131
50. Gallos LK, Cohen R, Argyrakis P, Bunde A, Havlin S. Stability and topology of scale-free networks under attack and defense strategies. Phys Rev Lett. (2005) 94:188701. doi: 10.1103/PhysRevLett.94.188701
51. Nie T, Guo Z, Zhao K, Lu ZM. New attack strategies for complex networks. Phys A Stat Mech Appl. (2015) 424:248–53. doi: 10.1016/j.physa.2015.01.004
52. Tian L, Bashan A, Shi DN, Liu YY. Articulation points in complex networks. Nat Commun. (2017) 8:1–9. doi: 10.1038/ncomms14223
53. Nguyen Q, Pham HD, Cassi D, Bellingeri M. Conditional attack strategy for real-world complex networks. Phys A Stat Mech Appl. (2019) 530:121561. doi: 10.1016/j.physa.2019.121561
54. Morone F, Makse H. Influence maximization in complex networks through optimal percolation. Nature. (2015) 524:65–8. doi: 10.1038/nature14604
55. Schneider CM, Mihaljev T, Herrmann HJ. Inverse targeting —an effective immunization strategy. EPL. (2012) 98:46002. doi: 10.1209/0295-5075/98/46002
56. Kitsak M, Gallos LK, Havlin S, Liljeros F, Muchnik L, Stanley HE, et al. Identification of influential spreaders in complex networks. Nat Phys. (2010) 6:888–93. doi: 10.1038/nphys1746
57. Ahajjam S, Badir H. Identification of influential spreaders in complex networks using HybridRank algorithm. Sci Rep. (2018) 8:1–10. doi: 10.1038/s41598-018-30310-2
58. Agreste S, Catanese S, De Meo P, Ferrara E, Fiumara G. Network structure and resilience of Mafia syndicates. Inf Sci. (2016) 351:30–47. doi: 10.1016/j.ins.2016.02.027
59. da Cunha BR, Gonçalves S. Topology, robustness, and structural controllability of the Brazilian Federal Police criminal intelligence network. Appl Netw Sci. (2018) 3:1–20. doi: 10.1007/s41109-018-0092-1
60. Holme P. Efficient local strategies for vaccination and network attack. Europhys Lett. (2004) 68:908–14. doi: 10.1209/epl/i2004-10286-2
61. Wang Z, Zhao DW, Wang L, Sun GQ, Jin Z. Immunity of multiplex networks via acquaintance vaccination. EPL. (2015) 112:48002. doi: 10.1209/0295-5075/112/48002
62. Schneider CM, Mihaljev T, Havlin S, Herrmann HJ. Suppressing epidemics with a limited amount of immunization units. Phys Rev E. (2011) 84:061911. doi: 10.1103/PhysRevE.84.061911
63. Bellingeri M, Agliari E, Cassi D. Optimization strategies with resource scarcity: from immunization of networks to the traveling salesman problem. Mod Phys Lett B. (2015) 29:1550180. doi: 10.1142/S0217984915501808
64. Chen Y, Paul G, Havlin S, Liljeros F, Stanley H. Finding a better immunization strategy. Phys Rev Lett. (2008) 101:058701. doi: 10.1103/PhysRevLett.101.058701
65. Hadidjojo J, Cheong SA. Equal graph partitioning on estimated infection network as an effective epidemic mitigation measure. PLoS ONE. (2011) 6:e22124. doi: 10.1371/journal.pone.0022124
66. Da Cunha BR, González-Avella JC, Gonçalves S. Fast fragmentation of networks using module-based attacks. PLoS ONE. (2015) 10:1–15. doi: 10.1371/journal.pone.0142824
67. Zdeborová L, Zhang P, Zhou HJ. Fast and simple decycling and dismantling of networks. Sci Rep. (2016) 6:2–7. doi: 10.1038/srep37954
68. Braunstein A, Dall'Asta L, Semerjian G, Zdeborová L. Network dismantling. Proc Natl Acad Sci USA. (2016) 113:12368–73. doi: 10.1073/pnas.1605083113
69. Zhao S, Lin Q, Ran J, Musa SS, Yang G, Wang W, et al. Preliminary estimation of the basic reproduction number of novel coronavirus (2019-nCoV) in China, from 2019 to 2020: a data-driven analysis in the early phase of the outbreak. Int J Infect Dis. (2020) 92:214–17. doi: 10.1016/j.ijid.2020.01.050
70. Lourenço J, Paton R, Ghafari M, Kraemer M, Thompson C, Klenerman P, et al. Fundamental principles of epidemic spread highlight the immediate need for large-scale serological surveys to assess the stage of the SARS-CoV-2 epidemic. medRxiv. (2020) 1–7. doi: 10.1101/2020.03.24.20042291
71. Ferguson NM, Laydon D, Nedjati-gilani G, Imai N, Ainslie K, Baguelin M, et al. Report 9 : Impact of non-pharmaceutical interventions (NPIs) to reduce COVID-19 mortality and healthcare demand. Imperial College COVID-19 Response Team (2020).
72. Prin M, Bartels K. Social distancing: implications for the operating room in the face of COVID-19. Can J Anesth. (2020) 67:789–97. doi: 10.1007/s12630-020-01651-2
73. Alelio DD, Mele BH, Libralato S, Jordán F. Rewiring and indirect effects underpin modularity reshuffling in a marine food web under environmental shifts. Ecol Evol. (2019) 9:11631–46. doi: 10.1002/ece3.5641
74. Kim J, Kim I, Han SK, Bowie JU, Kim S. Network rewiring is an important mechanism of gene essentiality change. Sci Rep. (2012) 2:900. doi: 10.1038/srep00900
Keywords: social network, network attack, information spreading, network robustness and resiliency, link (node) removal
Citation: Bellingeri M, Bevacqua D, Scotognella F, Alfieri R, Nguyen Q, Montepietra D and Cassi D (2020) Link and Node Removal in Real Social Networks: A Review. Front. Phys. 8:228. doi: 10.3389/fphy.2020.00228
Received: 08 April 2020; Accepted: 26 May 2020;
Published: 21 July 2020.
Edited by:
Elena Agliari, Sapienza University of Rome, ItalyReviewed by:
Andreas Nold, Max Planck Institute for Brain Research, GermanyFabio Sartori, Max Planck Institute for Brain Research, Germany, in collaboration with reviewer AN
Ferenc Jordan, Balaton Limnological Research (MTA), Hungary
Copyright © 2020 Bellingeri, Bevacqua, Scotognella, Alfieri, Nguyen, Montepietra and Cassi. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Michele Bellingeri, bWljaGVsZS5iZWxsaW5nZXJpQHBvbGltaS5pdA==
 Michele Bellingeri1,2*
Michele Bellingeri1,2* Daniele Bevacqua
Daniele Bevacqua Francesco Scotognella
Francesco Scotognella Davide Cassi
Davide Cassi