Studying Snow Failure With Fiber Bundle Models

Introduction

Studying snow failure and its dependency on the rate of the applied load or of displacement is of particular interest for snow avalanche formation. Among the various types of avalanches, dry-snow slab avalanches are the most hazardous and cause the largest number of fatalities—at least about 200 per year worldwide (e.g., [1]). Slab avalanches start by a failure nucleating under mixed-mode loading in a weak layer below a cohesive slab. Once this so-called initial crack reaches a critical size it propagates within the weak layer across the slope, leading to detachment and downhill sliding of the slab provided the slope-parallel gravitational force overcomes friction (e.g., [2]). The formation of this initial crack is still not fully understood for the case of spontaneously releasing avalanches and a crucial point for modeling avalanche release.

Snow is a highly porous material constituted by an ice matrix formed by ice grains welded together whereas the pore space is filled with air. The mechanical properties of snow are determined by its microstructure and the mechanical properties of ice. The loading or displacement rate dependency of the mechanical and failure properties of snow are believed to be due to two ice properties: ice sintering—i.e., ice bonds form on contact immediately with bond strength increasing with time—and the viscous deformation of ice (e.g., [3]).

Fiber bundle models have been widely used for studying snow failure (e.g., [4, 5]). Moreover, since FBMs replicate the macroscopic mechanical properties and failure behavior of materials through a large set of single elements with simple mechanical properties, they are an ideal choice for studying the micromechanical drivers of snow failure. We provide a review of the use of the fiber bundle model in snow science. We first describe the FBMs that have been used for simulating snow failure. Then we describe the inclusion of fiber healing and viscous fibers in FBM and discuss the effects of these properties on the bundle mechanics and failure dynamics. In a third part, we demonstrate how FBMs can reproduce the results of snow failure experiments. Finally, we introduce the use of FBMs to study the effects of sound wave attenuation and of acoustic emissions (AE) for snow failure prediction and application of AE to provide early warnings for snow avalanche prediction.

Fiber Bundle Models

Originally developed for studying the strength of cotton yarns [6, 7] fiber bundle models (FBM) are a family of statistical models widely used for studying the failure of heterogeneous materials [8, 9]. In a FBM the material consists of a set of single elements (fibers) with heterogeneous strengths (Figure 1). An external load or displacement is applied to the fiber bundle and the single fibers fail when the load exceeds the strength. For load-controlled FBMs the load of the failing fibers is redistributed to intact fibers possibly causing a cascade of further fiber failures. The complex damage process of the bulk material arises from the interaction of multiple fibers (load redistribution) and the heterogeneous fiber strengths representing the material disorder. In the classical FBM the fibers are assumed to respond in a linearly elastic manner. The influence of local microscopic mechanisms on the global failure (i.e., failure of the whole system) can be investigated by changing the mechanical properties of the fibers [10]. There exist numerous applications as the study of local load distribution (e.g., Hansen and Hemmer [11] Hidalgo et al. [12]), creep failure [13, 14], or fatigue [15]. Moreover, FBMs are used to analyze the failure process in the context of critical phenomena and phase transitions [9, 16].

FIGURE 1

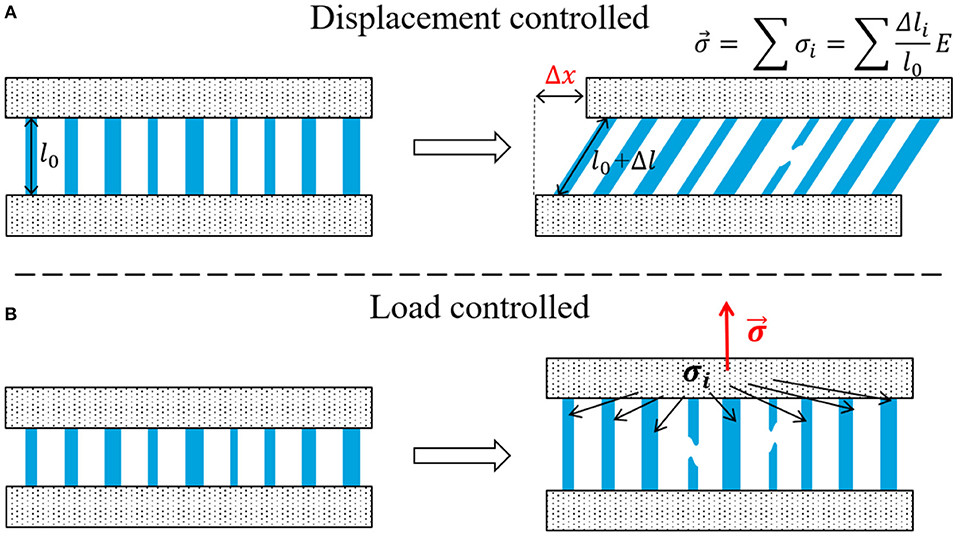
Figure 1. Schematic representation of (A) displacement-controlled FBM in shear [4] and (B) load-controlled FBM in tension [5]. The fiber width illustrates the variability in fiber strength.

Snow

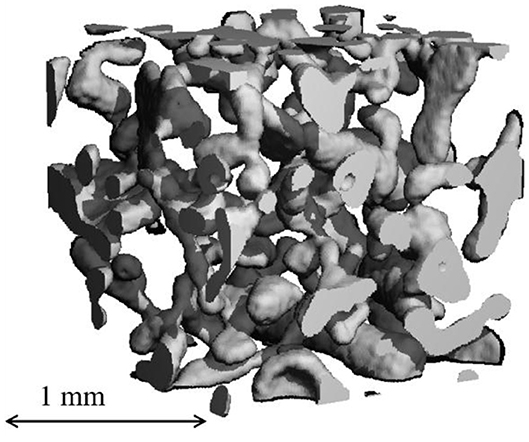
Snow is a highly porous material (porosity 0.5–0.95) consisting of an ice matrix with air filling the connected pore space¹. The ice matrix is a continuous structure, as shown by micro-CT images (Figure 2; e.g., [17]), consisting of welded discrete ice elements (grains). The snow microstructure (e.g., size, form and connectivity of the ice matrix elements) strongly influences the snow mechanical properties (e.g., [18, 19]). Moreover, the high homologous temperature (i.e., temperature near to the melting point) of ice under natural conditions leads to peculiar material properties. The ice matrix undergoes a continuous recrystallization known as snow metamorphism. The type and speed of metamorphism depends on meteorological conditions. At isothermal conditions the crystal shape is first transformed from dendritic to small rounded particles and later from smaller to larger round particles, as the water vapor pressure is higher with higher curvature of the ice surface. This type of metamorphism generally increases the strength of snow [20–22]. Faceting (or temperature gradient) metamorphism is induced by the temperature gradients typically caused by snow surface cooling due to emission of longwave radiation. Temperature gradients cause vapor transport from warmer to the cooler ice surfaces leading to the growth of large faceted and depth hoar crystals if the vapor flow persists (e.g., [23]). Faceting metamorphism generally reduces snow strength and can lead to the formation of weak layers. Simultaneously, the gravitational load induced by the overlaying snow can contribute to compaction of the snowpack (settlement) and increase of snow strength.

FIGURE 2

Figure 2. Micro-computed tomography image of a snow sample (Snow Physics Group, SLF).

The large range in porosity and microstructure of snow leads to corresponding large differences in physical properties. For example, the elastic modulus spans over several orders of magnitude depending on density and snow type (e.g., [18]). Therefore, a great challenge for finding a unified model for describing the snow microstructure is given by the broad range of density and snow types. Moreover, the ice particles bond immediately on contact (sintering) and the bond strength increases with time [24, 25] allowing to heal damage in the snow. The increase of bond strength with time is initially fast, then gradually slows down, but nevertheless continues with time leading to the increase of strength and stiffness over several days for new or sieved snow (e.g., [19, 22]).

Finally, the ice is subjected to viscous deformation or creep (e.g., [26, 27]) leading to snow creep and relaxation of localized stress. These phenomena result in the highly rate dependent failure behavior of snow. Whereas under high strain rates ($\stackrel{\cdot }{ϵ}>$ 10⁻³ s⁻¹) snow fails in a brittle manner with very little deformation before fracture, at low strain rates ($\stackrel{\cdot }{ϵ}<$ 10⁻³ s⁻¹) snow can sustain large strain and undergoes ductile failure—i.e., large irreversible deformation occurs before failure or the snow does not fail at all [28]. Sintering is considered one of the driving mechanism of the rate dependence of snow failure by some authors [4, 29, 30]. On the other hand, Kirchner et al. [31] used an open foam model including viscous deformation and a ductile-to-brittle transition in ice (at much lower strain rates $\stackrel{\cdot }{ϵ}=10^{-6}$ s⁻¹) to reproduce the ductile-to-brittle transition in snow. Moreover, the stress and time dependent creep deformation of ice may cause the relaxation of local load concentrations and influence the damage process. More recently Löwe et al. [3] developed a scalar model with rate-dependent, elastoplastic constitutive law and sintering that correctly reproduces mechanical experiments. Hence, a combination of the above-mentioned effects contributes to the ductile-to-brittle transition observed for snow.

Slab Avalanche Formation

Snow avalanches are a serious hazard for human life and infrastructures in snow-covered mountainous regions around the world; they cause on average about 100 fatalities annually in the European Alps [32]. The majority of avalanche accidents are due to dry-snow slab avalanches (see Figure 3A) [33]. For the release of a slab avalanche a so-called weak layer below cohesive slab layers is necessary. Weak layers typically consist of large poorly bonded crystals (Figure 3B, mainly faceted crystals and depth hoar, surface hoar, or new snow layers [34]). After an initial crack of sufficient size has formed in the weak layer, the crack propagates below the slab due to the stress concentrations at the crack tip, which is caused by lack of support of the weight of the overlaying slab over the cracked area. The critical crack size when rapid self-propagation starts, depends on both weak layer and slab properties, primarily the specific fracture energy of the weak layer and the thickness, density and stiffness of the slab layers [35, 36]. Crack propagation in the weak layer arrests by slope perpendicular fracture through the slab (Figure 3B). Once the slab is detached, it slides downslope if the gravitational force overcomes the friction, generally for slope angles >30° [37], and an avalanche is released (Figure 3A).

FIGURE 3

Figure 3. (A) Dry-snow slab avalanche (R. Pajarola). (B) Snow weak layer (surface hoar) buried below a cohesive slab. On the right side the weak layer is intact. On the left side the weak layer failed leading to volumetric collapse of the porous structure. The black lines are a schematic representation of the FBM. Reprinted from the Journal of Glaciology with permission of the International Glaciological Society [4].

In case of artificially triggered avalanches the initial crack is caused by rapid near-surface loading due to e.g., a skier or an explosion. For natural (spontaneous) avalanches the load increase is much slower (additional weight due to precipitation or snow drift by wind), and the initial crack is believed to be the result of a progressive damage process at the microscale [34]. The exact processes involved in initial crack formation are, however, not well-understood. It is therefore fundamental to increase our understanding of snow avalanche formation by modeling snow failure.

Models in Snow Mechanics

Snow failure leading to avalanche release is a process involving different scales with different types of heterogeneity—going from the snow microstructure, through the vertical variation in snow properties (stratigraphy), to the spatial variability at the slope-scale. Modeling snow and avalanche formation requires dealing with these heterogeneities at the different respective scales. Generally different models are applied at the different scales. The microscopic snow structure and ice properties must be considered for modeling snow mechanical properties and failure initialization. Snow stratigraphy and mechanical properties of snow need to be considered for modeling crack propagation (e.g., [36, 38, 39]). At the slope-scale, spatial variations of snow stratigraphy and terrain are essential to model avalanche release (e.g., [40, 41]). More recently, Gaume et al. [2] introduced a model based on the material point method that can cope with both snow stratigraphy and terrain variability covering the multi-scale processes involved in avalanches: from failure initiation and crack propagation to avalanche flow [42, 43]. However, even these advanced models rely on appropriate parametrizations of snow including correct failure behavior and rate-dependent response.

Models aiming to reproduce the mechanical behavior of snow and the failure process have to take into account both the snow microstructure as well as the mechanical properties of ice. These models can be grouped into (i) Continuum models that include some parametrization of the microstructure – e.g. the snow viscosity model of Bartelt and von Moos [44], the open-cell foam model for snow [45, 46], or other models considering damage healing [3, 47, 48]. (ii) Models reproducing the microstructure in simplified form with discrete elements (beams, spheres) with some random variations such as the discrete element models [49–51]. (iii) Models that use the full 3-D representation of the microstructure obtained by micro-tomography as input for a finite-element model (e.g., [52–54]). Statistical models as the FBM belong to the second group of models.

Fiber Bundle Models Applied to Snow

The FBM was first applied to snow by Reiweger et al. [4]. Incorporating healing of broken fibers representing the fast sintering of broken bonds in snow, they were able to reproduce the characteristics of displacement-controlled snow failure experiments for different strain rates. Capelli et al. [5] introduced a load-controlled FBM including both healing of broken fibers and viscous deformation and described the effects of these two mechanisms on the failure behavior. With the same model it was possible to reproduce the mechanical characteristics and the concurrent acoustic emissions (AE) characteristics of load-controlled snow failure experiments with different loading rates spanning over the ductile-to-brittle transition [55]. Acoustic emissions are acoustic waves generated by the occurrence of damage in solid materials. An example of AE is the crackling noise produced by wood under load (e.g., [56]). AE are widely used for monitoring the damage process of heterogeneous materials (e.g., [57]). Attenuation of acoustic waves is a limitation for the application of AE for early warning, since it reduces the detection range and alters the AE signature. Attenuation in snow is particularly high due to the high porosity (e.g., [58]). The attenuation of AE is therefore particularly critical for applications aiming at using AE for early warning of snow avalanches. Faillettaz et al. [59] used a FBM for studying the effects of attenuation of AE on the failure prediction and proposed to use co-detection of AE for natural hazard early warning. Their FBM results were supported by AE data from snow failure experiments. In the following sections, we recap the working principle of the FBMs applied to snow.

Fiber Strength Distribution

The intrinsic disorder of heterogeneous materials (such as snow) is represented in the FBM by a large number of fibers with varying strengths (Figure 1). The Weibull distribution, which is commonly used for strength distributions in statistical models [8], was also employed in snow models for fiber strength [4, 5, 55]. The density function for the fiber strength σ_th is given by:

$\begin{array}{ll}p({\sigma }_{\text{th}}|\mu ,k)=k{\mu }^{-k}{{\sigma }_{\text{th}}}^{k-1}{e}^{-{\left(\frac{{\sigma }_{\text{th}}}{\mu }\right)}^k},& (1)\end{array}$

where μ is a scaling factor and k controls the amount of damage in the system (lower k correspond to larger amount of disorder). The disorder parameter k should depend on the snow microstructure. There is, however, no measurement method that allows determining k, so k must be assumed. Reiweger et al. [4] looked at the sensitivity to k in the range of 0.5 to 3 on the FBM and used k= 0.7 for fitting their mechanical experiments. Further studies used the value k = 1.1 [5, 55].

Displacement-Controlled FBM

In the displacement-controlled model presented by Reiweger et al. [4] a constant shear rate is imposed (Figure 1A). Assuming elastic fibers, the stress on the single fibers increases linearly with fiber strain. If the stress on a fiber reaches its strength, the fiber fails. Thus, the total stress on the fiber bundle decreases. When half of the fibers failed, the entire bundle is considered as broken. Reiweger et al. [4] introduced a variation to the classical FBM. They assumed that the fibers are subjected to shear perpendicular to the initial direction. The fiber elongation Δl is then:

$\begin{array}{ll}\Delta l=\sqrt{l_0^2+{\Delta x}^2}-l_0,& (2)\end{array}$

where Δx is the shear deformation of the bundle and l₀ is the fiber length. The stress is then given by:

$\begin{array}{ll}\sigma =Eϵ=E\frac{\Delta l}{l_0},& (3)\end{array}$

where E is the elastic modulus. Introducing shear deformation shifts the stress-strain curve toward higher deformations [4], since initially the fiber stress increase is slower than for the FBM with displacement parallel to the fibers (Equations 2, 3).

Load-Controlled FBM

In case of load-controlled FBMs [5, 55], the load on the fibers is increased step wise to the strength of the weakest fiber that consequently fails. As a fiber fails, its load is distributed to the other surviving fibers according to a redistribution rule (Figure 1B). For the FBM described by Capelli [5] a “democratic” or “equal” load-sharing rule was used. Meaning that the load was redistributed equally to the surviving fibers. This is equivalent to the assumption of stiff plates clamping the fibers and makes the spatial position of the fibers irrelevant (0 dimensional material). Other models use local load-sharing rules, where the load is distributed to the neighboring fibers only [59]. With local load-sharing rules the fiber position becomes relevant (one or more dimensional material). Distributing the load of failing fibers among the surviving fibers can cause a cascade of failures. The number of fibers failing in a cascade following a failure due to load increase is expressed as the burst size S. For linear elastic fibers the bundle strain ϵ_J is obtained from the sum of the strain increase at each load increase step up to the step J:

$\begin{array}{ll}{ϵ}_J(\sigma )={\sum }_{\text{j}=0}^J\Delta {ϵ}_{el,\text{j}}={\sum }_{\text{j}=0}^J{\displaystyle \underset{\text{load increase}}{{\displaystyle \underbrace{\frac{1}{U_{\text{j}}E}\Delta {\sigma }_{\text{j}}}}}}+{\displaystyle \underset{\text{redistribution}}{{\displaystyle \underbrace{\frac{1}{U_{\text{j}}E}{\displaystyle \sum _{\text{k}ϵs_{\text{j}}}}{\sigma }_{\text{k},\text{j}}}}}},& (4)\end{array}$

where U_j is the fraction of intact fibers, σ_{k, j} is the load of the fiber k, and S_j is the set of fibers that failed at the load step j.

FBM With Healing Fibers

When two ice particles are brought in contact, a bond is immediately created with increasing bond strength with increasing time [25, 60]. This process, known as sintering, allows damage in snow to heal with time. The FBM is well-suited to study the effects of healing on the mechanical properties of snow as implementing a healing mechanism is quite straight forward. Healing has been incorporated in FBMs in different ways in the past, e.g., in the stick-slip FBM the fibers regain strength immediately after failure [61, 62].

Reiweger et al. [4] were the first to apply a FBM to snow that included healing of broken fibers (Figure 4A). In their displacement-controlled FBM at each time step Δt a broken fiber regains strength with the probability p_s depending on the number of brocken fiber N_b available for forming a new bond with ${\mathrm{\text{p}}}_{\text{s}}=p_{max}\frac{N_{\text{b}}}{N}$. The strength of a new bond is initially zero but increases with time:

$\begin{array}{ll}{\sigma }_{\text{th},\text{i}}(t)=\left(1-e^{\frac{-t}{{\text{t}}_{\text{s}}-\text{t}}}\right){\sigma }_{\text{th},\text{i},\text{final}}& (5)\end{array}$

for t < t_s where t_s is the sintering time and σ_{th, i, final} is drawn from the same initial distribution.

Similarly, fiber healing has been implemented in the load-controlled FBM with the probability of a broken fiber to regain strength during the time Δt being:

$\begin{array}{ll}{\text{p}}_{\text{s}}(\Delta t)=\left(1-e^{\frac{-\Delta t}{{\text{t}}_{\text{p}}}}\right)\frac{N_b}{N}& (6)\end{array}$

with the characteristic time t_p [5]. In this case, it was assumed that the fibers regain full strength immediately.

The fiber healing speed is higher with either lower characteristic time or lower loading rate. If the characteristic time in the model by Capelli et al. [5] is compared to that of Reiweger et al. [4], then the sintering probability in Reiweger et al. [4] is linear with $p_{max}=\frac{\Delta t}{{\mathrm{\text{t}}}_{\mathrm{\text{p}},\text{Reiw}.}}.$ The characteristic time used by Reiweger et al. [4] for fitting the model to mechanical experiments was ${\mathrm{\text{t}}}_{\mathrm{\text{p}},\text{Reiw}.}=\frac{\Delta \mathrm{\text{t}}}{{\mathrm{\text{p}}}_{max}}=$ 0.66 s. Capelli et al. [55] reported a larger characteristic time of healing t_{p, Cap.} = 20 s. The difference in time scale may be due to the different snow type and testing mode (displacement- vs. load-controlled). Additionally, in the model by Reiweger et al. [4] the strength of the new bonds increases with time. The speed of the strength increase is controlled by the sintering time t_s= 1.09 s (Equation 7). A DEM model for snow including bond sintering on contact with increasing bond strength using a similar sintering time t_s= 1 s was proposed by Mulak and Gaume [50].

FIGURE 4

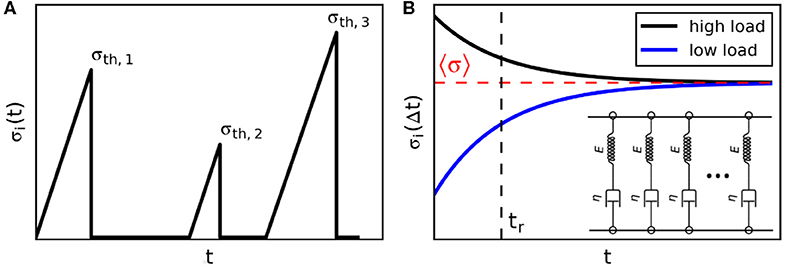
Figure 4. (A) Load evolution for a single fiber when healing is included. The load increases until the strength σ_{th, 1} is reached and the fiber fails. After a certain random time, the fiber heals and is assigned a new strength σ_{th, 2} independent of the previous strength; subsequently it may fail and sinter again. (B) Relaxation of load on the single fibers toward the mean load 〈σ〉 for the FBM assuming viscoelastic fibers (schematic in inset). The speed of the load relaxation is controlled by the characteristic loading time t_r. Figures adapted from [5].

Effect of Healing on Mechanical Behavior and Failure Dynamics

For both displacement- and load-controlled FBMs healing results in higher stress at equal strain and in higher stress and strain at failure [4, 5]. Healing counterweighs the damage process as broken fibers regain strength. The number of intact fibers in the bundle increases so that they can support a higher load or, equivalent, a higher load is needed for equal deformation. Therefore, the material becomes stiffer and has higher strength.

The effects on the failure behavior differ between displacement- and load-controlled FBMs. For the displacement-controlled FBM, Reiweger et al. [4] reproduced the ductile-to-brittle transition of snow with the introduction of healing. For large displacement rates the healing process is slower than the damage process and does not affect the bundle's failure. After reaching the bundle strength the stress rapidly decreases and all fibers fails (brittle failure). For low strain rates, as the damage in the bundle increases and steady-state is reached (i.e., the damage process is compensated by healing of fibers), the number of broken fibers remaine constant with increasing strain and ductile failure is observed (Figure 5). The type of the stress-strain curve in the steady-state regime is controlled by the fiber strength distribution. With higher disorder (Weibull parameter k ≤ 1), strain strengthening and creep (increase of strain at constant stress) is observed. Whereas, with low disorder (k≥ 1) failure (stress peak) is followed by strain softening and final creep.

FIGURE 5

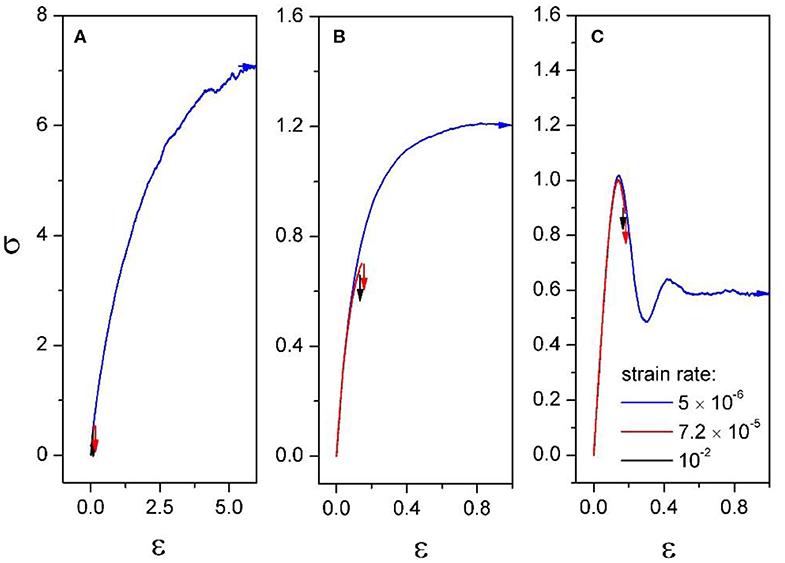
Figure 5. FBM simulation results with varying shape factor k for the Weibull distributions of single fiber strength: (A) k = 0.5; (B) k = 1; and (C) k = 3. For each shape factor, stress–strain curves for three different strain rates (1 × 10⁻², 7.2 × 10⁻⁵, and 5 × 10⁻⁶ s⁻¹) are given. The vertical arrows mark the point where the bundle fractures, while the horizontal arrows indicate that the bundle is still intact but the simulation was stopped. Reprinted from the Journal of Glaciology with permission of the International Glaciological Society [4].

For the load-controlled FBM the steady state is not “visible” since when the imposed stress exceeds the bundle strength (stress peak in displacement-controlled strain-stress curve) all fibers fail. On the other hand, stress control allows observing the failure dynamics arising as the load sharing causes a catastrophic cascade of fiber ruptures resulting in the complete failure of the bundle. In the load-controlled FBM the damage process diverges approaching failure (e.g., [9, 16]). The fiber failure rate $\frac{dS}{d\sigma }$, which is commonly known as susceptibility, diverges approaching failure at σ_c with $\frac{dS}{d\sigma }~{({\sigma }_c-\sigma )}^{-\alpha }$. The order parameter O(σ) = U(σ_c)−U(σ) approaches zero following a power law with $O(\sigma )={({\sigma }_c-\sigma )}^{\kappa }$, where U(σ) is the fraction of broken fibers. With healing the amount of damage (portion of broken fibers) immediately before failure is lower. Moreover, with healing the exponent α decreases, whereas the exponent κ increases (Figure 6) indicating that the period before failure, where the damage process accellerate, is shorter—a sign of increased brittleness. For the FBM the bursts size S is generally power-law distributed with P(S) ~S^−b, similarly to the Gutenberg–Richter law for earthquakes (e.g., [9]). Generally, an apparent decrease of the exponent b toward failure is observed. This is explained by a truncated power-law distribution $P(S)~S^{-\tau }exp(\frac{S}{S_0})$ with diverging cut-off burst size $S_0~{\Delta }^{-\gamma }$ and $\Delta =\frac{{\sigma }_c-\sigma }{{\sigma }_c}$ (e.g., [63, 64]). The exponents are linked by $b=\tau +\frac{1}{\gamma }$. Capelli et al. [5] reported a decrease of b with increasing healing rate when all events were considered, whereas near to failure the exponent was unaffected by healing. This is equivalent to a constant exponent τ whereas the exponent γ increases with increasing healing rate (Figure 6). In the context of failure prediction, faster acceleration and lower apparent decrease of exponent b means that that time lag for prediction decreases and prediction becomes more difficult, yet not impossible.

FIGURE 6

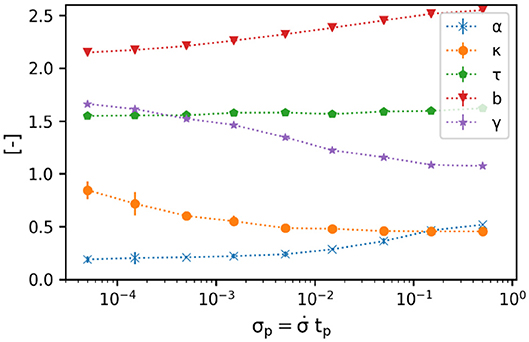
Figure 6. Critical exponents for different increasing healing speeds. The healing speed increases with decreasing healing load ${\sigma }_{\mathrm{\text{p}}}=\stackrel{\cdot }{\sigma }{t}_{\mathrm{\text{p}}}$.

FBM With Viscous Fibers

As ice is a viscous material, Capelli et al. [5] introduced ice viscosity in their FBM assuming that the fibers are Maxwell elements (Figure 4B) with the corresponding constitutive equation:

$\begin{array}{ll}{\stackrel{\cdot }{ϵ}}_{\text{i}}=\frac{{\sigma }_{\text{i}}}{\eta }+\frac{{\stackrel{\cdot }{\sigma }}_{\text{i}}}{E}& (7)\end{array}$

where σ_i is the stress on a single fiber, E is the fiber's elastic modulus and η its viscosity. Incorporating viscosity results in the relaxation of load inhomogeneity in the bundle with time. The load is redistributed from the older fibers carrying more load to the younger ones carrying less load. The load of the single fiber i converges exponentially toward the mean load with:

$\begin{array}{ll}{\sigma }_{\text{i}}(t+\Delta t)=\langle \sigma \rangle +({\sigma }_{\text{i}}(t)-\langle \sigma \rangle )e^{-\frac{\Delta t}{{\text{t}}_{\text{r}}}},& (8)\end{array}$

where 〈σ〉 is the intact fiber mean load, and the ratio between elastic modulus E and viscosity η is the characteristic relaxation time ${\mathrm{\text{t}}}_{\mathrm{\text{r}}}=\frac{E}{\eta }$ determinig the speed of relaxation (Figure 4B). In the model by Capelli et al. [5] the load inhomogeneity is due to the healing process, since new fibers initially do not carry load. If fiber viscosity is included, a viscous term is added to Equation (4) for the bundle strain ϵ_J:

$\begin{array}{l}{ϵ}_J(\sigma )={\displaystyle \sum _{\text{j}=0}^J}(\Delta {ϵ}_{el,\text{j}}+\Delta {ϵ}_{\text{visc},\text{j}})=\stackrel{\text{elastic part}}{\overbrace{{\displaystyle \sum _{\text{j}=0}^J}{\displaystyle \underset{\text{load increase}}{{\displaystyle \underbrace{\frac{1}{U_{\text{j}}E}\Delta {\sigma }_{\text{j}}}}}}+{\displaystyle \underset{\text{redistribution}}{{\displaystyle \underbrace{\frac{1}{U_{\text{i}}E}{\displaystyle \sum _{kϵs_{\text{j}}}}{\sigma }_{k,\text{j}}}}}}}}\\ +\stackrel{\text{viscous part}}{\overbrace{{\displaystyle \sum _{\text{j}=0}^J}\frac{1}{\eta }\frac{{\langle \sigma \rangle }_{\text{j}}}{U_{\text{i}}}\Delta t_{\text{j}}}},& (9)\end{array}$

The magnitude of the effects of viscosity can be expressed with the characteristic load ${\sigma }_r=\stackrel{\cdot }{\sigma }{\mathrm{\text{t}}}_{\mathrm{\text{r}}}=\stackrel{\cdot }{\sigma }\frac{\eta }{E}$. Load relaxation and viscous deformation are higher for low characteristic loads σ_r.

Effect of Viscous Fibers on Mechanical Behavior

If viscosity is added to the FBM, fiber deformation can be divided in an elastic and a viscous part. With the Maxwell model for viscoelasticity, the elastic deformation takes place immediately as the load is applied, whereas the viscous deformation increases linearly in time with the strain rate depending on the applied load (Equation 7). For high values of viscosity or high loading rate, the bundle deformation is mainly elastic. For lower values of loading rate or viscosity, the deformation is predominantly viscous and strain at equal stress is larger than with primarily elastic deformation (Figure 7A and [5]).

FIGURE 7

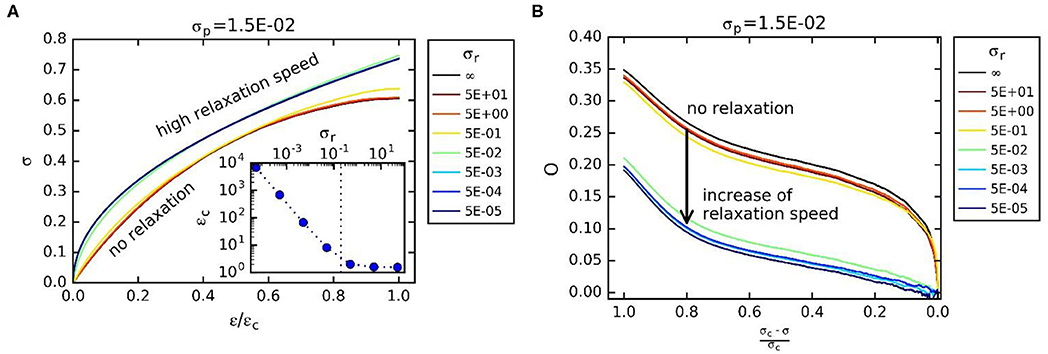
Figure 7. (A) Stress-strain relations of FBM for different relaxation characteristic loads σ_r and a constant sintering characteristic load σ_p= 1.5 × 10⁻². The strain was scaled with the strain at failure ϵ_c. The inset shows the strain at failure ϵ_c as a function of the relaxation characteristic load σ_r. (B) Evolution of the order parameter O toward failure for different σ_r and constant σ_p = 1.5 × 10⁻². The characteristic times t_r/p were scaled to characteristic loads with ${\sigma }_{r/p}=\stackrel{\cdot }{\sigma }{t}_{r/p}$. Reprinted from [5].

Effect of Viscous Fibers on Failure Dynamics

Fiber viscosity also has consequences for the internal distribution of fiber load. The viscous deformation rate is higher for fibers carrying higher load. Therefore, the fiber load relaxes toward the mean fiber load, transferring load from fibers carrying high loads to fibers carrying low loads. This is equivalent to a load transfer from older fibers to newly healed fibers, since with equal load-sharing fiber healing is the only source of load inhomogeneity. The load inhomogeneity in the bundle decreases for lower t_r leading to a more efficient distribution of load resulting in a bundle strength increase [5]. Load relaxation has a large effect on the failure dynamics. For high load relaxation speed the acceleration of damage prior to failure is suppressed (Figure 7A). No divergence of strain rate and fiber failure $\frac{dS}{d\sigma }$ is observed; the order parameter O(σ) develops from a power law decrease approaching failure at σ_c with $O(\sigma )={({\sigma }_c-\sigma )}^{\kappa }$ to a linear decrease (Figure 7B). Fiber failure burst size distribution is also affected by load relaxation. Both exponents b and τ of the burst size distribution P(S) increase with increasing load relaxation speed indicating a shift to a larger share of small failure bursts.

The absence of damage acceleration suggests that load relaxation changes the type of transition at failure from continuous to abrupt indicating a change of the universality class. This interpretation is supported by the change of the power law exponent τ. Load relaxation causes a shift in the distribution of fiber strength with increasing main strength and decreasing disorder. Therefore, the fibers are likely to fail abruptly as a critical load is reached. A similar change in the type of transition at failure was reported by Biswas and Sen [65] for a FBM where the load of failing fibers was redistributed according to the fiber strength.

Reproducing Snow Failure Experiments

The FBMs presented above were used to reproduce snow failure experiments with the aim to investigate the micromechanical principles governing the macroscopic mechanical behavior of snow. In particular the FBM allowed to study the rate dependent mechanical response of snow with the well-known ductile-to-brittle transition [28].

Displacement-Controlled Experiments

With the FBM including healing Reiweger et al. [4] reproduced the displacement-controlled snow failure experiments at different strain rates presented by Schweizer [66]. Their FBM very well-captured the observed ductile-to-brittle transition (Figure 8) and reproduced the higher strength and strain at failure with decreasing strain rate. Both, snow samples and fiber bundle, showed brittle failure behavior for high strain rates (>3 × 10⁻⁴ s⁻¹) and for low strain rates ductile failure followed by strain softening and creep. The stress-strain relations obtained with the FBM had a convex form at low strain. The convexity is due to the arrangement of the fibers relative to the load. When the fibers are loaded in shear the fiber stress initially increases just slowly (Equation 2). The experimental curves did not show any convexity. The simple spatial arrangement of the fibers in the FBM can obviously not fully reproduce the complex structure of the ice matrix. A FBM with load parallel to the fibers (pure tension) would better fit the experimental results. Indeed, recent DEM studies suggest that under mixed-mode loading (compression and shear) the ice matrix mainly failed in tension [67]. The FBM results support this view.

FIGURE 8

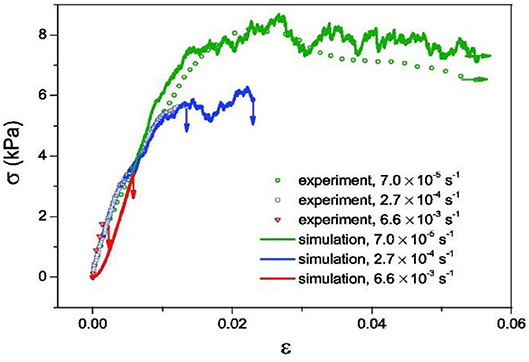
Figure 8. Comparison of FBM and experimental results for displacement-controlled conditions. Reprinted from the Journal of Glaciology with permission of the International Glaciological Society [4].

Load-Controlled Experiments and Concurrent Acoustic Emissions

Capelli et al. [55] applied the FBM including healing of broken fibers and viscous fibers for modeling load-controlled snow failure experiments at different loading rates (32, 128, and 400 Pa s⁻¹) and the concurrent acoustic emissions [68]. Using parameters in agreement with the snow values reported in the literature, they reproduced the main features of the experimental results. The stress-strain relations found in experiments and obtained with their FBM were similar with higher stress and strain at failure and higher strain at equal stress for lower loading rates (Figure 9). Capelli et al. [55] compared the energy of the AE with the elastic energy released at fiber failure—i.e., they assumed that the elastic energy stored in the fiber failing in a failure burst $U=\frac{\sum _j{\sigma }_j^2}{2E}$ is equivalent to the energy of measured AE. The FBM exhibited features similar to the loading rate dependent AE signatures observed for the snow failure experiments. For both, FBM and experiments, the AE energy rate increased toward failure and the energy distribution exponent τ was higher for the fast loading rates (Figure 10). Also, Pradhan et al. [69] claim that the elastic energy exhibits a peak prior to failure that can be used to predict the failure point of FBM. The elastic energy is, however, difficult to quantify for the snow experiments since the displacement measured includes elastic as well as viscous deformation. However, there were also differences between FBM and experimental results. For the FBM an apparent decrease of the exponent b, indicating a divergence of the cut-off energy of a truncated power law (see section FBM With Healing Fibers) was present for all loading rates. For the experiments, the apparent decrease of b was not observed for the low loading rates, although the exponent at failure τ was higher for low loading rates (Figure 10A). Moreover, the divergence in the damage process at failure for high loading rates, that is visible in the strain rate and the energy rate $\frac{dU}{d\sigma }$, was not observed in the experimental results.

FIGURE 9

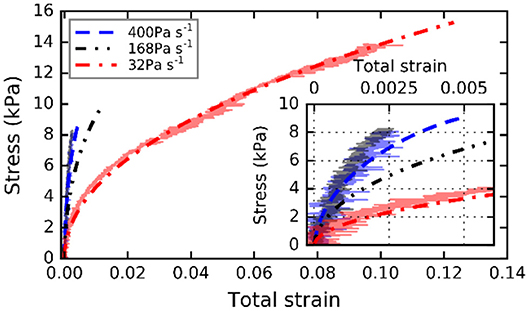
Figure 9. FBM and experimental results for load-controlled conditions. The dotted line indicates the FBM results. Reprinted from [55].

FIGURE 10

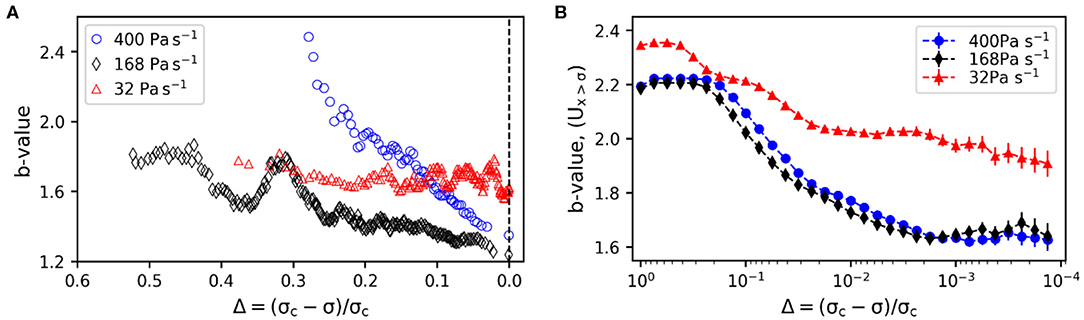
Figure 10. Evolution of b-value with increasing load σ up to failure at σ_c for three different loading rates for: the AE energy E_AE (A) and the FBM burst elastic energy U (B). Adapted from [55].

The substantial differences in the failure dynamics of snow for different loading rates could only be reproduced with the FBM by including both healing of broken fibers and viscous deformation with resulting load relaxation. It follows that both, healing and load relaxation, are essential for understanding and modeling snow failure and should be taken into account in future models, which aim at reproducing snow behavior at low loading rates.

Attenuation of AE and Consequences for Failure Prediction

The amplitude of acoustic waves propagating in natural media decreases with distance from the source due to geometrical spreading, absorption and scattering. Faillettaz et al. [59] introduced signal attenuation into the load-controlled FBM with equal and local load-sharing, which was developed by Faillettaz and Or [70]. The amplitude attenuation was computed for each fiber failure burst (i) assuming that the amplitude is proportional to the burst size S and (ii) accounting for geometrical spreading only (decrease of amplitude with $A(r)~\frac{1}{r}$ for the distance from the source r). The attenuated amplitude A_a of the burst S_j measured at the sensor at position x_sensor is then: $A_a=\sum _{{i\in S}_j}\frac{1}{\left|\right|x_i-x_{\text{sensor}}\left|\right|}$, with x_i being the position of the failing fiber i. Faillettaz et al. [59] showed that attenuation changes the frequency distribution of the recorded fiber failure bursts. The apparent decrease of the power law exponent (b → τ) is less pronounced when signal attenuation is taken into account. The decrease of the power law exponent is considered useful for assessing the stability of geological structures (e.g., [63]).

However, for real cases where attenuation is present the decrease is less prominent and occasionally hard to detect. Therefore, using the decrease of the exponent as precursor to failure for early warning purposes is limited. To overcome this problem Faillettaz et al. [59] proposed the number of co-detections (event detected by multiple sensor) as precursor to catastrophic failure, since small events are generally detected by nearby sensors only, whereas large events may be detected also by sensors at larger distances. Faillettaz et al. [59] tested the co-detection method with AE data from laboratory snow failure experiments [71]. An increase of the AE maximum amplitude was registered one second before failure, whereas a significant increase in the number of co-detections was recorded 10 s before failure increasing the early warning time lag by a factor 10.

Conclusions

The fiber bundle model (FBM) consists of a large number of fibers with variable strengths following simple mechanical laws (e.g., elastic or viscoelastic). Through the disorder and load sharing (fiber interaction) a complex behavior arises. FBMs are used to reproduce failure of heterogeneous materials and to study effects of micromechanical processes on global failure. For these reasons, the FBM is well-suited for studying the failure of snow. The displacement or loading rate dependence of snow failure observed experimentally, in particular the ductile-to-brittle transition, was reproduced. Whereas, displacement-controlled experiments were reproduced by including healing, for reproducing load-controlled experiment both healing and load relaxation (viscosity) were necessary. In particular, the loading rate dependent failure dynamics revealed by the AE signature preceding snow failure were reproduce only with both healing and load relaxation. Therefore, the results of the FBM studies on snow point out the importance of considering healing and viscosity for modeling snow, especially at low displacement or loading rates. The FBM with healing and load relaxation shows that for low loading rates there is a lack of failure precursors suggesting that in some cases failure prediction is not possible.

The similarity between the fiber failure bursts in FBMs and the AE produced prior to failure is useful not just for interpreting the AE signatures, but can also be used for studying the effects of acoustic wave attenuation of the recorded AE. Using a FBM Faillettaz et al. [59] showed that the attenuation reduces the applicability of AE as precursor to failure. As alternative they suggested to use co-detection of AE for early warning and demonstrated the working principle with a FBM [59].

Simplicity is a strength of the FBM since it allows to study the effects of simple micromechanical drivers on failure. However, reproducing the complex 3D microstructure of snow is not possible. Nevertheless, it is important to include the findings obtained with FBM into models able to reproduce the 3D snow microstructure, such as the discrete element model (DEM). Rate dependent snow failure experiments at different temperatures in combination with FBM may be used for separating the effects of healing and viscosity since both ice sintering and viscosity are temperature dependent. The understanding of the damage process in snow gained with FBM should be applied to slope-scale models for studying natural avalanche release. The snow FBM may be even incorporated into a slope scale model as it has been done for modeling landslide release [72].

Author Contributions

AC wrote the original draft of the manuscript. IR and JS provided feedback and edited the manuscript. All authors contributed to the article and approved the submitted version.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Footnotes

1. ^For wet snow at 0°C, we additionally have water within the pore space. Within this paper, we consider dry snow only.

References

1. Schweizer J, Bartelt P, van Herwijnen A. Chapter 12 - Snow Avalanches. In: Shroder JF, Haeberli W, Whiteman C, Editors. Snow and Ice-Related Hazards, Risks and Disasters Academic Press (2015). p. 395–436. doi: 10.1016/B978-0-12-394849-6.00012-3

CrossRef Full Text | Google Scholar

2. Gaume J, Gast T, Teran J, van Herwijnen A, Jiang C. Dynamic anticrack propagation in snow. Nat Commun. (2018) 9:3047. doi: 10.1038/s41467-018-05181-w

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Löwe H, Zaiser M, Mösinger S, Schleef S. Snow mechanics near the ductile-brittle transition: compressive stick-slip and snow microquakes. Geophys Res Lett. (2020) 47:e2019GL085491. doi: 10.1029/2019GL085491

CrossRef Full Text | Google Scholar

4. Reiweger I, Schweizer J, Dual J, Herrmann HJ. Modelling snow failure with a fiber bundle model. J Glaciol. (2009) 55:997–1002. doi: 10.3189/002214309790794869

CrossRef Full Text | Google Scholar

5. Capelli A, Reiweger I, Lehmann P, Schweizer J. Fiber bundle model with time-dependent healing mechanisms to simulate progressive failure of snow. Phys Rev E. (2018) 98:023002. doi: 10.1103/PhysRevE.98.023002

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Peirce FT. Tensile tests for cotton yarns v. - “The weakest link” theorems on the strength of long and of composite specimens. J Text Inst Trans. (1926) 17:T355–68. doi: 10.1080/19447027.1926.10599953

CrossRef Full Text | Google Scholar

7. Daniels HE. The statistical theory of the strength of bundles of threads. Proc R Soc A Math Phys Eng Sci. (1945) 183:405–35. doi: 10.1098/rspa.1945.0011

CrossRef Full Text | Google Scholar

8. Herrmann HJ, Roux S. Statistical Models for the Fracture of Disordered Media. Amsterdam: Elsevier Science Publishers. (1990).

Google Scholar

9. Alava MJ, Nukalaz PKVV, Zapperi S. Statistical models of fracture. Adv Phys. (2006) 55:349–476. doi: 10.1080/00018730300741518

CrossRef Full Text | Google Scholar

10. Kun F, Hidalgo RC, Raischel F, Herrmann HJ. Extension of fibre bundle models for creep rupture and interface failure. Int J Fracture. (2006) 140:255–65. doi: 10.1007/s10704-005-2556-4

CrossRef Full Text | Google Scholar

11. Hansen A, Hemmer PC. Burst avalanches in bundles of fibers: local versus global load-sharing. Phys Lett A. (1994) 184:394–6. doi: 10.1016/0375-9601(94)90511-8

CrossRef Full Text | Google Scholar

12. Hidalgo RC, Moreno Y, Kun F, Herrmann HJ. Fracture model with variable range of interaction. Phys Rev E. (2002) 65:046148. doi: 10.1103/PhysRevE.65.046148

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Hidalgo RC, Kun F, Herrmann HJ. Creep rupture of viscoelastic fiber bundles. Phys Rev E. (2002) 65:032502. doi: 10.1103/PhysRevE.65.032502

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Kun F, Moreno Y, Hidalgo RC, Herrmann HJ. Creep rupture has two universality classes. Europhys Lett. (2003) 63:347–53. doi: 10.1209/epl/i2003-00469-9

CrossRef Full Text | Google Scholar

15. Kun F, Costa MH, Costa RN, Andrade JS, Soares JB, Zapperi S, et al. Fatigue failure of disordered materials. J Stat Mech Theor Exp. (2007) 2007:P02003. doi: 10.1088/1742-5468/2007/02/P02003

CrossRef Full Text | Google Scholar

16. Pradhan S, Hansen A, Chakrabarti BK. Failure processes in elastic fiber bundles. Rev Mod Phys. (2010) 82:499–555. doi: 10.1103/RevModPhys.82.499

CrossRef Full Text | Google Scholar

17. Coléou C, Lesaffre B, Brzoska J-B, Ludwig W, Boller E. Three-dimensional snow images by X-ray microtomography. Ann Glaciol. (2001) 32:75–81. doi: 10.3189/172756401781819418

CrossRef Full Text | Google Scholar

18. Shapiro LH, Johnson JB, Sturm M, Blaisdell GL. Snow mechanics - review of the state of knowledge and applications. In: CRREL Report 97-3. Hanover, NH: US Army Cold Regions Research and Engineering Laboratory (1997). doi: 10.21236/ADA330695

CrossRef Full Text | Google Scholar

19. Gerling B, Löwe H, van Herwijnen A. Measuring the elastic modulus of snow. Geophys Res Lett. (2017) 44:11088–96. doi: 10.1002/2017GL075110

CrossRef Full Text | Google Scholar

20. Perla R, Sommerfeld RA. On the metamorphism, morphology and microstructure of snow. In: Proceedings ISSW 1986 International Snow Science Workshop, Lake Tahoe, California, U.S.A. Homewood, AL: ISSW Workshop Committee (1987). p. 98–102.

Google Scholar

21. Kaempfer TU, Schneebeli M. Observation of isothermal metamorphism of new snow and interpretation as a sintering process. J Geophys Res Atmosph. (2007) 112:D24101. doi: 10.1029/2007JD009047

CrossRef Full Text | Google Scholar

22. van Herwijnen A, Miller DA. Experimental and numerical investigation of the sintering rate of snow. J Glaciol. (2013) 59:269–74. doi: 10.3189/2013JoG12J094

CrossRef Full Text | Google Scholar

23. Pinzer BR, Schneebeli M, Kaempfer TU. Vapor flux and recrystallization during dry snow metamorphism under a steady temperature gradient as observed by time-lapse micro-tomography. Cryosphere. (2012) 6:1141–55. doi: 10.5194/tc-6-1141-2012

CrossRef Full Text | Google Scholar

24. Gubler H. Strength of bonds between ice grains after short contact times. J Glaciol. (1982) 28:457–73. doi: 10.1017/S0022143000005050

CrossRef Full Text | Google Scholar

25. Szabo D, Schneebeli M. Subsecond sintering of ice. Appl Phys Lett. (2007) 90:151916. doi: 10.1063/1.2721391

CrossRef Full Text | Google Scholar

26. Sinha NK. Short-term rheology of polycrystalline ice. J Glaciol. (1978) 21:457–73. doi: 10.1017/S002214300003361X

CrossRef Full Text | Google Scholar

27. Schulson EM, Duval P. Creep and Fracture of Ice. Cambridge: Cambridge University Press (2009). doi: 10.1017/CBO9780511581397

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Narita H. Mechanical behaviour and structure of snow under uniaxial tensile stress. J Glaciol. (1980) 26:275–82. doi: 10.1017/S0022143000010819

CrossRef Full Text | Google Scholar

29. De Montmollin V. Shear tests on snow explained by fast metamorphism. J Glaciol. (1982) 28:187–98. doi: 10.1017/S0022143000011898

CrossRef Full Text | Google Scholar

30. Schweizer J. Review of dry snow slab avalanche release. Cold Reg Sci Technol. (1999) 30:43–57. doi: 10.1016/S0165-232X(99)00025-7

CrossRef Full Text | Google Scholar

31. Kirchner HOK, Michot G, Narita H, Suzuki T. Snow as a foam of ice: plasticity, fracture and the brittle-to-ductile transition. Philos Mag A. (2001) 81:2161–81. doi: 10.1080/01418610108217141

CrossRef Full Text | Google Scholar

32. Techel F, Jarry F, Kronthaler G, Mitterer S, Nairz P, Pavšek M, et al. Avalanche fatalities in the European Alps: long-term trends and statistics. Geogr Helv. (2016) 71:147–59. doi: 10.5194/gh-71-147-2016

CrossRef Full Text | Google Scholar

33. Jamieson JB, Johnston CD. Snowpack characteristics associated with avalanche accidents. Can Geotech J. (1992) 29:862–6. doi: 10.1139/t92-093

CrossRef Full Text | Google Scholar

34. Schweizer J, Jamieson JB, Schneebeli M. Snow avalanche formation. Rev Geophys. (2003) 41:1016. doi: 10.1029/2002RG000123

CrossRef Full Text | Google Scholar

35. Schweizer J, van Herwijnen A, Reuter B. Measurements of weak layer fracture energy. Cold Reg Sci Technol. (2011) 69:139–44. doi: 10.1016/j.coldregions.2011.06.004

CrossRef Full Text | Google Scholar

36. Gaume J, van Herwijnen A, Chambon G, Wever N, Schweizer J. Snow fracture in relation to slab avalanche release: critical state for the onset of crack propagation. Cryosphere. (2017) 11:217–28. doi: 10.5194/tc-11-217-2017

CrossRef Full Text | Google Scholar

37. van Herwijnen A, Heierli J. Measurement of crack-face friction in collapsed weak snow layers. Geophys Res Lett. (2009) 36:L23502. doi: 10.1029/2009GL040389

CrossRef Full Text | Google Scholar

38. Heierli J, Gumbsch P, Zaiser M. Anticrack nucleation as triggering mechanism for snow slab avalanches. Science. (2008) 321:240–3. doi: 10.1126/science.1153948

PubMed Abstract | CrossRef Full Text | Google Scholar

39. Rosendahl PL, Weissgraeber P. Modeling snow slab avalanches caused by weak-layer failure - part 1: slabs on compliant and collapsible weak layers. Cryosphere. (2020) 14:115–30. doi: 10.5194/tc-14-115-2020

CrossRef Full Text | Google Scholar

40. Fyffe B, Zaiser M. The effects of snow variability on slab avalanche release. Cold Reg Sci Technol. (2004) 40:229–42. doi: 10.1016/j.coldregions.2004.08.004

CrossRef Full Text | Google Scholar

41. Gaume J, Chambon G, Eckert N, Naaim M, Schweizer J. Influence of weak layer heterogeneity and slab properties on slab tensile failure propensity and avalanche release area. Cryosphere. (2015) 9:795–804. doi: 10.5194/tc-9-795-2015

CrossRef Full Text | Google Scholar

42. Gaume J, Van Herwijnen A, Gast T, Teran J, Jiang C. Investigating the release and flow of snow avalanches at the slope-scale using a unified model based on the material point method. Cold Reg. Sci. Technol. (2019) 168:102847. doi: 10.1016/j.coldregions.2019.102847

CrossRef Full Text | Google Scholar

43. Li X, Sovilla B, Jiang C, Gaume J. The mechanical origin of snow avalanche dynamics and flow regime transitions. Cryosphere Discuss. (2020) 2020:1–25. doi: 10.5194/tc-2020-83

CrossRef Full Text | Google Scholar

44. Bartelt PA, Von Moos M. Triaxial tests to determine a microstructure-based snow viscosity law. Ann Glaciol. (2000) 31:457–62. doi: 10.3189/172756400781819761

CrossRef Full Text | Google Scholar

45. Gibson LJ, Ashby MF. Cellular Solids: Structure and Properties. Cambridge: Cambridge University Press (1997). doi: 10.1017/CBO9781139878326

CrossRef Full Text | Google Scholar

46. Kirchner HOK. Brittle fracture of snow. In: Bouchaud E, Jeulin D, Prioul C and Roux S, editors. Physical Aspects of Fracture (Proceedings of the NATO Advanced Study Institute on Physical Aspects of Fracture, Cargèse, France, 5-17 June 2000) Dordrecht: Kluwer Academic Publishers (2001). p. 47–57.

Google Scholar

47. Louchet F. Creep instability of the weak layer and natural slab avalanche triggerings. Cold Reg Sci Technol. (2001) 33:141–6. doi: 10.1016/S0165-232X(01)00035-0

CrossRef Full Text | Google Scholar

48. Barraclough T, Blackford JR, Liebenstein S, Sandfeld S, Stratford TJ, Weinlander G, et al. Propagating compaction bands in confined compression of snow. Nat Phys. (2017) 13:272–5. doi: 10.1038/nphys3966

CrossRef Full Text | Google Scholar

49. Gaume J, Van Herwijnen A, Chambon G, Birkeland KW, Schweizer J. Modeling of crack propagation in weak snowpack layers using the discrete element method. Cryosphere. (2015) 9:1915–32. doi: 10.5194/tc-9-1915-2015

CrossRef Full Text | Google Scholar

50. Mulak D, Gaume J. Numerical investigation of the mixed-mode failure of snow. Comput Part Mech. (2019) 6:439–47. doi: 10.1007/s40571-019-00224-5

PubMed Abstract | CrossRef Full Text | Google Scholar

51. Bobillier G, Bergfeld B, Capelli A, Dual J, Gaume J, Van Herwijnen A, et al. Micromechanical modeling of snow failure. Cryosphere. (2020) 14:39–49. doi: 10.5194/tc-14-39-2020

CrossRef Full Text | Google Scholar

52. Schneebeli M. Numerical simulation of elastic stress in the microstructure of snow. Ann Glaciol. (2004) 38:339–42. doi: 10.3189/172756404781815284

CrossRef Full Text | Google Scholar

53. Hagenmuller P, Theile TC, Schneebeli M. Numerical simulation of microstructural damage and tensile strength of snow. Geophys Res Lett. (2014) 41:86–9. doi: 10.1002/2013GL058078

CrossRef Full Text | Google Scholar

54. Mede T, Chambon G, Hagenmuller P, Nicot F. Snow failure modes under mixed loading. Geophys Res Lett. (2018) 45:13351–8. doi: 10.1029/2018GL080637

CrossRef Full Text | Google Scholar

55. Capelli A, Reiweger I, Schweizer J. Modelling snow failure behavior and concurrent acoustic emissions signatures with a fiber bundle model. Geophys Res Lett. (2019) 46:6653–62. doi: 10.1029/2019GL082382

CrossRef Full Text | Google Scholar

56. Fuyuhiko K. An experiment on the progression of fracture (a preliminary report). J Acoust Emission. (1990) 9:177–80.

Google Scholar

57. Grosse CU, Ohtsu M. Acoustic Emission Testing. Berlin, Germany: Springer (2006).

PubMed Abstract | Google Scholar

58. Capelli A, Kapil JC, Reiweger I Or D, Schweizer J. Speed and attenuation of acoustic waves in snow: laboratory experiments and modelling with Biot's theory. Cold Reg Sci Technol. (2016) 125:1–11. doi: 10.1016/j.coldregions.2016.01.004

CrossRef Full Text | Google Scholar

59. Faillettaz J Or D, Reiweger I. Codetection of acoustic emissions during failure of heterogeneous media: new perspectives for natural hazard early warning. Geophys Res Lett. (2016) 43:1075–83. doi: 10.1002/2015GL067435

CrossRef Full Text | Google Scholar

60. Willibald C, Scheuber S, Löwe H, Dual J, Schneebeli M. Ice spheres as model snow: tumbling, sintering, and mechanical tests. Front Earth Sci. (2019) 7:229. doi: 10.3389/feart.2019.00229

CrossRef Full Text | Google Scholar

61. Halasz Z, Kun F. Fiber bundle model with stick-slip dynamics. Phys Rev E. (2009) 80:027102. doi: 10.1103/PhysRevE.80.027102

PubMed Abstract | CrossRef Full Text | Google Scholar

62. Halasz Z, Kun F. Slip avalanches in a fiber bundle model. Europhys Lett. (2010) 89:26008. doi: 10.1209/0295-5075/89/26008

CrossRef Full Text | Google Scholar

63. Amitrano D. Variability in the power-law distributions of rupture events - how and why does b-value change. Eur Phys J Spec Top. (2012) 205:199–215. doi: 10.1140/epjst/e2012-01571-9

CrossRef Full Text | Google Scholar

64. Amitrano D, Girard L. Fiber bundle model under fluid pressure. Phys Rev E. (2016) 93:033003. doi: 10.1103/PhysRevE.93.033003

PubMed Abstract | CrossRef Full Text | Google Scholar

65. Biswas S, Sen P. Maximizing the strength of fiber bundles under uniform loading. Phys Rev Lett. (2015) 115:155501. doi: 10.1103/PhysRevLett.115.155501

PubMed Abstract | CrossRef Full Text | Google Scholar

66. Schweizer J. Laboratory experiments on shear failure of snow. Ann Glaciol. (1998) 26:97–102. doi: 10.1017/S0260305500014634

CrossRef Full Text | Google Scholar

67. Gaume J, Löwe H, Tan S, Tsang L. Scaling laws for the mechanics of loose and cohesive granular materials based on baxter's sticky hard spheres. Phys Rev E. (2017) 96:032914. doi: 10.1103/PhysRevE.96.032914

PubMed Abstract | CrossRef Full Text | Google Scholar

68. Capelli A, Reiweger I, Schweizer J. Acoustic emissions signatures prior to snow failure. J Glaciol. (2018) 64:543–54. doi: 10.1017/jog.2018.43

CrossRef Full Text | Google Scholar

69. Pradhan S, Kjellstadli JT, Hansen A. Variation of Elastic Energy Shows Reliable Signal of Upcoming Catastrophic Failure. Front Phy. (2019) 7:106. doi: 10.3389/fphy.2019.00106

CrossRef Full Text | Google Scholar

70. Faillettaz J Or D. Failure criterion for materials with spatially correlated mechanical properties. Phys Rev E. (2015) 91:032134. doi: 10.1103/PhysRevE.91.032134

PubMed Abstract | CrossRef Full Text | Google Scholar

71. Reiweger I, Mayer K, Steiner K, Dual J, Schweizer J. Measuring and localizing acoustic emission events in snow prior to fracture. Cold Reg Sci Technol. (2015) 110:160–9. doi: 10.1016/j.coldregions.2014.12.002

CrossRef Full Text | Google Scholar

72. Fan LF Lehmann P Or D. Effects of hydromechanical loading history and antecedent soil mechanical damage on shallow landslide triggering. J Geophys Res Earth Surf. (2015) 120:1990–2015. doi: 10.1002/2015JF003615

CrossRef Full Text | Google Scholar