- 1Centre for THz Research, China Jiliang University, Hangzhou, China
- 2School of Information Science and Engineering, Hangzhou Normal University, Hangzhou, China
We numerically and experimentally demonstrated double Fano resonances in a simple S-shaped plasmonic metasurface in the terahertz frequency range. Apart from the electric-LC resonance and electric dipole (ED) resonance, two trapped modes are excited in two different types of asymmetric S-shaped structures in the frequency range 0.2–1.4 THz, which are mainly attributed to a magnetic dipole (MD) and an electric quadrupole (EQ). Thereafter, double Fano resonances [one Fano and one electromagnetically induced transparency (EIT) resonance] are achieved via the coupling of the two dark trapped modes and a broad bright ED at normal incidence of the metasurfaces. Furthermore, under oblique incidence, strong Fano responses can be observed; they are considerably enhanced in asymmetric structures, and even in a symmetric structure. The proposed S-shaped plasmonic metasurfaces are easy to fabricate and have potential applications in multi-wavelength optical switches, filters, and sensors.
Introduction
In the last decade, metamaterials (MMs) have been extensively studied because of their peculiar electromagnetic properties, such as negative index media, cloaking, and subwavelength resolution imaging [1–5], which cannot be obtained from naturally occurring materials. The fundamental characteristic of an MM is its electromagnetic resonance responses, one of which is the interesting trapped mode, which results from the anti-phased dipole resonance in an asymmetric plasmonic MM [6–10]. The trapped mode has a high Q factor because of its small radiation loss, so it can be used in sensor and modulator [11–15]. Researchers have focused on MMs containing a single trapped mode observed in simple one-meta-atom MMs for a long time, and in recent years, multiple trapped modes, usually excited in a complicated multi-meta-atom called metamolecule MMs, have attracted extensive attention due to their superior performance in terms of modifying resonant waveforms at multiple spectral locations simultaneously [16–20]. For example, two or more trapped modes are demonstrated in MMs with a double-chain meander wire array or two different lattices of metamolecules [19, 20]. On the other hand, trapped mode, as a dark resonance, can be coupled with a low-Q bright mode to generate Fano resonance or an EIT response [21–28]. Furthermore, multiple Fano resonances can be excited via multiple trapped modes in multi-meta-atom MMs [29–33], which could be useful in multi-wavelength optical switches, filters, and sensors. For example, only one Fano resonance is observed in a Z-shaped one-meta-atom plasmonic metasurface [26], but three Fano resonances have been observed in two different-sized asymmetric double-bar structures, where two Fano resonances are attributed to two individual meta-atoms, and one to their combinations or metamolecule MM [33]. However, the metamolecule structure will increase the size of the devices, which may not be conducive to practical applications.
In this work, we propose and experimentally demonstrate a metasurface with double trapped modes consisting of only one S-shaped plasmonic structure in the terahertz region. Furthermore, double Fano resonances were also observed in this type of one-meta-atom metasurface. This planar plasmonic metasurface is easy to fabricate and has potential applications in biochemical sensing, optical switching, and slow-light devices.
Design and Simulation Results
S-shaped Symmetric and Asymmetric Plasmonic Metasurfaces
The unit cell of the symmetric S-shaped plasmonic metasurface is similar to Refs. [34–36] and shown in Figure 1A, where the S-shaped aluminum structure (electric conductivity σ = 3.56 × 107 S/m) with a thickness of 200 nm is deposited on a 12-μm-thickness polyethylene terephthalate film (PET, permittivity ε = 3.2). The atom S exhibits inversion symmetry, and its geometrical dimensions are l1 = 100 μm, l2 = 80 μm, and w = 10 μm. The unit cells are periodically arranged in the x and y planes with identical lattice constants Px = Py = 200 μm. In addition, two different types of asymmetric S-shaped structures are considered, as shown in Figures 1B,C, respectively. In Case I, the symmetry of the S is broken by changing the lengths of the horizontal metal arms, and the degree of asymmetry is determined by d. In Case II, the lengths of the vertical arms are changed, and the degree of asymmetry is determined by g. To investigate the resonant properties of the metasurface, numerical simulations are carried out with commercial CST software. In our simulations, we utilize periodic boundary conditions in both x and y directions, and open boundary conditions are applied in the wave propagating direction z. In the simulation, a lossless substrate is assumed for PET.
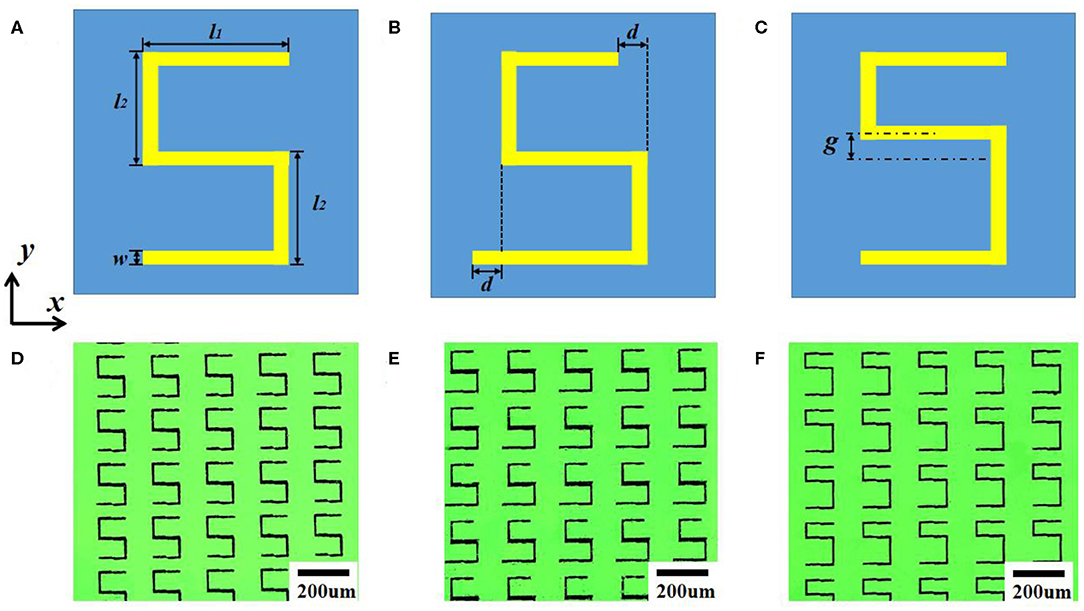
Figure 1. Unit cells of three S-shaped plasmonic metasurfaces and the corresponding fabricated samples. (A) Inversion symmetry, (B) Case I: Broken symmetry produced by changing the length of the horizontal arms, (C) Case II: Broken symmetry produced by changing the length of the vertical arms, (D–F) Microscopic images of the corresponding three fabricated metasurfaces, where d = 20 μm in (E) and g= 20 μm in (F).
Double Trapped Modes in Asymmetric Metasurfaces
At first, the metasurfaces are illuminated by a normally incident plane wave with the electric field along the y-axis. Figure 2 shows the simulated transmissions of three symmetric and asymmetric S-shaped plasmonic metasurfaces in the frequency range 0.2–1.4 THz. It is evident in Figure 2A that two strong resonances are located around 0.3 and 1.3 THz in the centrally symmetric S-shaped metasurface. From the surface current distributions (not shown here) at these two frequencies, we know that they are typical electric-LC and electrical dipole (ED) resonances, respectively. For an asymmetric S-shaped metasurface as in Case I, however, in addition to the two resonances at 0.3 and 1.3 THz, two new weak and narrow resonances can be clearly seen at 0.6 and 1.0 THz in Figure 2B, which are dependent on the related asymmetric value of d. As theoretical analysis has shown, the origin of the narrow spectral response in an asymmetry structure can be attributed to the so-called “trapped mode,” which is weakly coupled to free space [6, 23], and a larger asymmetric value of the structure corresponds to a stronger trapped resonance with a wider bandwidth [25–29, 33]. Similarly, two strong trapped modes at the same frequencies of 0.6 and 1.0 THz in Figure 2C can be observed in another asymmetric structure in Case II. The same dependence of the trapped modes on the asymmetry value g is also shown in Figure 2C. As g decreases from 30 to 10 μm, the Q-values of the trapped modes at 0.6 and 1.0 THz increase from 78 to 149, and from 72 to 203, respectively. And the Q factor of the trapped mode at 1.0 THz will reach up to 270 when g = 5 μm, but very sensitive to the loss of the substrate. Compared to Case I, the trapped modes in Case II are much stronger, which is related to their different excitation nature and discussed in the following.
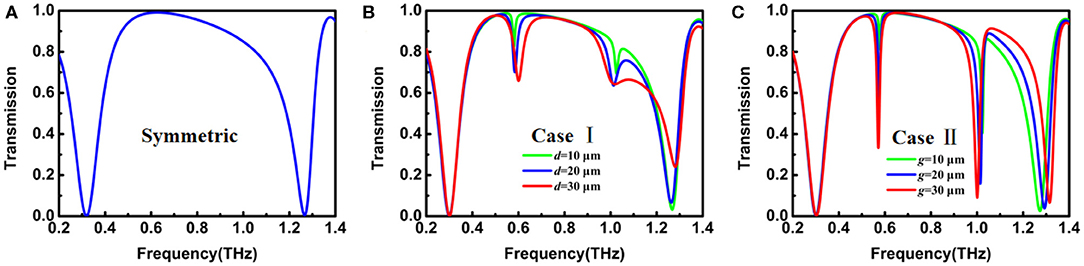
Figure 2. Simulated transmission spectra for (A) symmetric metasurface; (B) Case I with different values of d; (C) Case II with different values of g. The E-field of incident wave is polarized along the y-axis.
To explain the excitation nature of these two trapped modes, the structure S can be regarded as the splicing of double U-shaped sub-structures. Because of the anti-phase symmetry, the dipolar moments in them are in opposite directions, and perfectly canceled in the symmetric S-shaped metasurface, indicating that the modes are not excited and remain dark at 0.6 and 1.0 THz. However, the trapped modes can be excited when the symmetry of S is broken. The instantaneous current distributions at 0.6 and 1.0 THz are plotted in Figures 3A–D. Figures 3A,B show the surface current distributions at 0.6 THz in Case I and Case II, respectively. Due to the different size of the double U-shaped structures, the dipole momentums can't be completely canceled, meaning the balance of the anti-phase currents is destroyed, and thus the two clockwise circulating currents enhance the magnetic dipole (MD) and suppress the toroidal dipole (TD), which means this resonance is an MD resonance. On the other hand, the surface current distributions at 1.0 THz in Case I and Case II are given in Figures 3C,D, respectively. Strong currents can be observed in the top and bottom arms, as well as in the arms on both sides. Obviously, this is reminiscent of the electric quadrupole form (EQ).
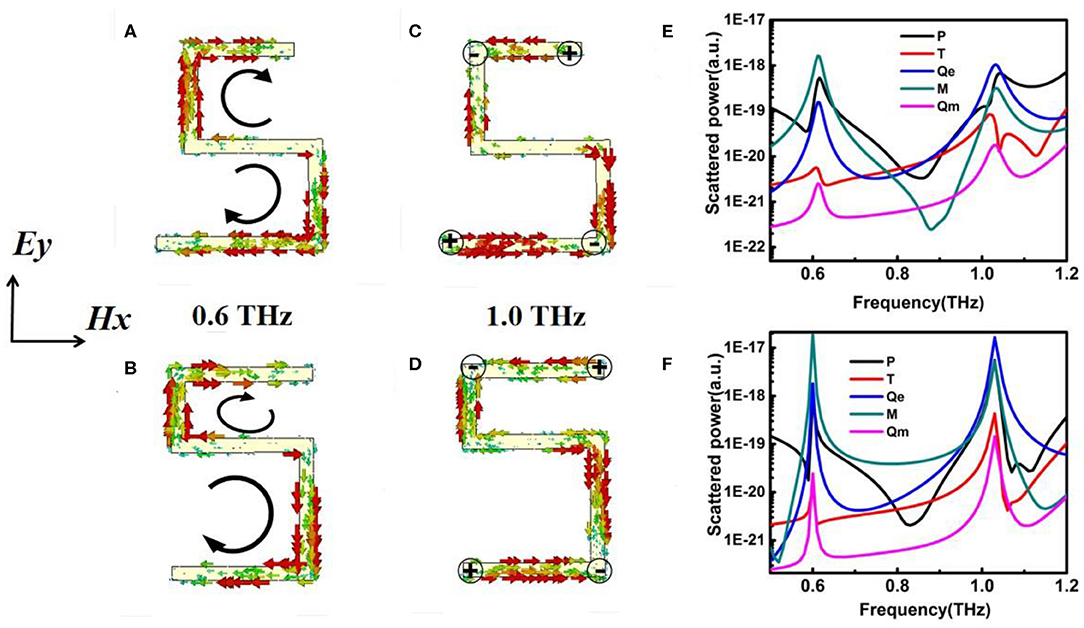
Figure 3. Simulated current distributions at resonant frequencies of (A) 0.6 THz in Case I, (B) 0.6 THz in Case II, (C) 1.0 THz in Case I, (D) 1.0 THz in Case II. Multipole decomposition results of the scattering spectrum by using the Cartesian coordinate system for (E) Case I when d = 20 μm and (F) Case II when g = 20 μm, where P, M, T, Qe, and Qm represent the ED, MD, TD, EQ, and magnetic quadrupole (MQ), respectively.
To further understand the nature of these two resonances, decomposed scattered powers for multipole moments are calculated based on the density of the induced current inside the metamolecules by using a Cartesian coordinate system [37–40]. Figures 3E,F plot the five strongest scattering powers of multipoles around the resonant frequencies of Case I and Case II, which include the ED P, MD M, TD T, EQ Qe, and magnetic quadrupole (MQ) Qm. For multipole moments of Case I around the resonant frequency of 0.6 THz, the magnetic dipole M increases greatly and dominates the other multipoles in far-field scattering power, which confirms that the resonant mode is an MD. The TD T appears weaker than the other multipoles, as previously analyzed from surface currents. At the frequency of 1.0 THz, it is evident that the electric quadrupole Qe occupies the dominant position, while the ED P is in the second position, which means this resonance is an EQ. Similar to Case I, the MD M and EQ Qe for Case II occupy the dominant positions at 0.6 and 1.0 THz, respectively, which indicates that the two trapped modes in Case I and Case II are identical.
Double Fano Resonances in Asymmetric Metasurfaces
For an incident wave polarized along the x-axis instead of the y-axis, the transmission spectra of three S-shaped metasurfaces are calculated and shown in Figure 4. The transmission of symmetric metasurface shown in Figure 4A displays a clear, broad resonance dip around 1.0 THz, which is a typical ED resonance from the surface current distribution (not shown here). However, once the symmetry of the S structure is broken as in Case I, we interestingly observe a distinct EIT-like resonance (shown in Figure 4B) in the vicinity of 1.0 THz. The EIT-like transparency peak coincidentally appears at the dip of the broad ED resonance shown in Figure 4A, and is consistent with the trapped EQ given in Figure 2B as well. Consequently, this EIT-like resonance can be interpreted as a destructive interference between the bright ED and the trapped EQ. Moreover, besides the EIT-like transparency window, a sharp Fano resonance appears at 0.6 THz that lies in the range of the broad ED resonance (Figure 4A) and coincides with the trapped MD resonance given in Figure 2B as well, which indicates that this Fano resonance is excited by optical coupling between the dark trapped MD and the bright ED mode. It is noteworthy that the large detuning between the bright ED (1.0 THz) and the trapped MD (0.6 THz) results in a Fano response rather than an EIT resonance; here, EIT is a special form of Fano resonance when the detuning between the two coupling bright and dark trapped modes is very small [20]. Furthermore, considering that Fano responses are related to the asymmetry of the structures, the transmission curves of the metasurface with different values of d are also calculated and shown in Figure 4B. As d decreases from 30 to 10 μm, the Q-values of the Fano resonance at 0.6 THz and EIT at 1.0 THz increase from 22 to 95, and from 12 to 54, respectively, but their central frequencies remain unchanged.
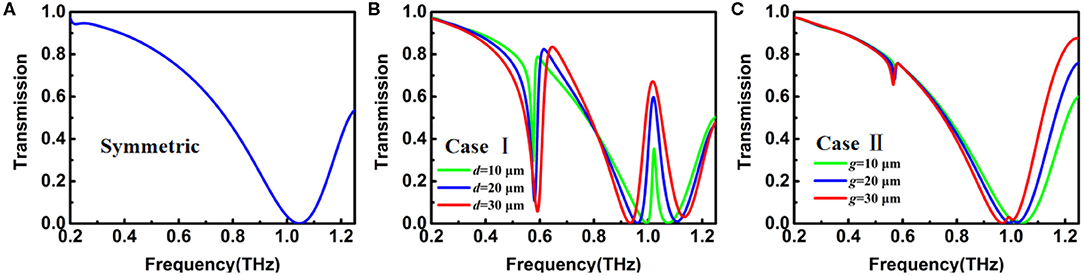
Figure 4. Simulated transmission spectra for (A) symmetric S-shaped metasurface, (B) Case I with different values of d, (C) Case II with different values of g. The E-field of incident wave is polarized along the x-axis.
However, the results for the other asymmetric metasurface of Case II shown in Figure 4C are quite different from those for Case I. The broad ED resonance with its dip at 1.0 THz is clearly observed, but two much weaker Fano resonances respectively appeared at 0.6 and 1.0 THz for the large asymmetric value g = 30 μm, and they can almost be neglected when g = 10 μm. Considering that two much stronger trapped modes are excited in Case II compared to Case I (shown in Figure 2), we can conclude that the coupling path between the bright and dark trapped modes, which is related to the asymmetric structure, plays an important role in the excitation of the Fano resonances.
Moreover, the frequencies of the two Fano resonances of the proposed metasurface can be easily designed and tuned by enlarging or reducing the size of the S-shaped structure. For example, when doubling the size of the structure, the two resonance frequencies will reduce to be half of the original.
Fano Resonances Under Oblique Incidence
We also explore the characteristics of the two trapped modes and two Fano resonances under off-normal incidence in the symmetric and asymmetric Case I (d = 20 μm) and Case II (g = 20 μm) S-shaped metasurfaces. Two different types of incident field polarizations are considered as shown in Figures 5A,B, and for each case, there are two oblique incidences in both the E-plane (the plane containing vectors E and k) and the H-plane (the plane containing vectors H and k); here, E, H, and k stand for the electric field, magnetic field, and wave vector, respectively. The calculated transmissions of three different metasurfaces under the field polarization of Figure 5A at 15° incidence are presented in Figures 5C,E. We can see that two trapped modes are excited around 0.6 and 1.0 THz in all three metasurfaces in both E-plane and H-plane oblique incidences. Unlike the normal incidence, the excitation of the two dark trapped modes in the symmetric structure becomes possible under off-normal incidence, which can be simply explained by the structure being geometrically symmetric but optically asymmetric under oblique incidence. When the field polarization of Figure 5B is used, we find that the responses under E-plane oblique incidence shown in Figure 5D are close to transmissions at normal incidence (shown in Figure 4) (i.e., two strong Fano resonances appear at 0.6 and 1.0 THz, respectively, in Case I, but much weakened in Case II, and disappear in the symmetric structure).
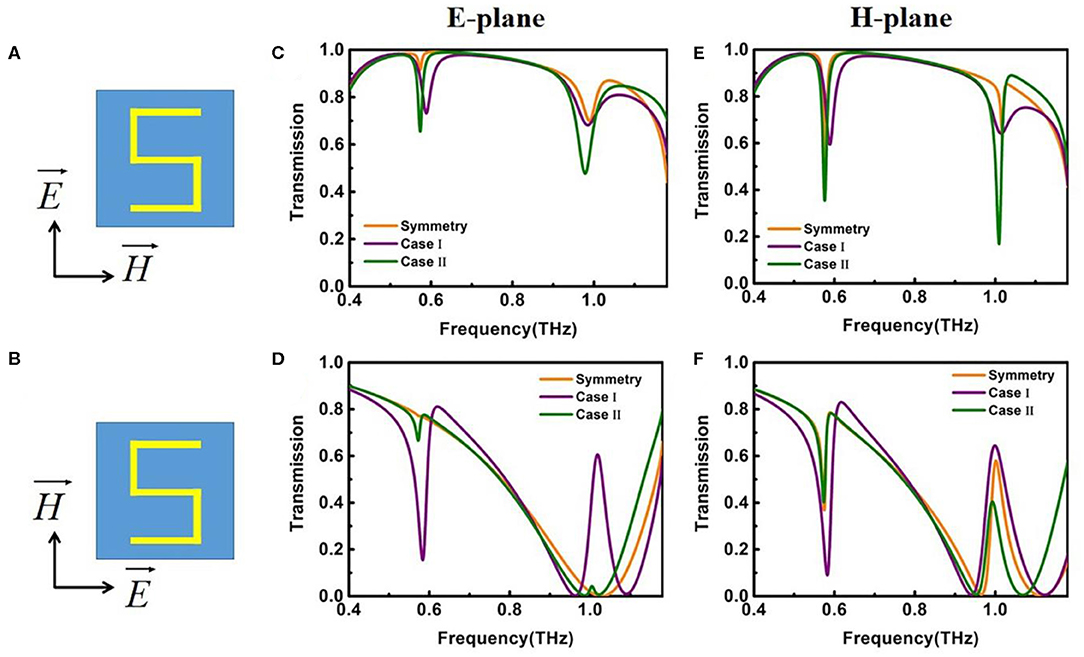
Figure 5. (A,B) Incident field polarizations for three S-shaped metasurfaces. (C–F) Computed transmission spectra at oblique incidence of 15° in E-plane and H-plane, respectively. Here, d = 20 μm, g = 20 μm for Case I and Case II, respectively.
However, under H-plane oblique incidence, Figure 5F shows that both strong Fano and EIT resonances can be excited in all three symmetric and asymmetric S-shaped metasurfaces, and the strengths of the resonances in Case I are the largest, the symmetric structure being second, and Case II third. Therefore, oblique incidence can not only make the excitation of the trapped mode possible even in symmetric metasurfaces, but can also enhance the coupling of the bright and trapped modes significantly as well.
Experimental Results
In the fabrication of our metasurface, we used the purchased composite of a PET-aluminum film as the raw material. This type of commercial aluminum foil is very cheap and often used in common food packaging. Positive photoresist was spin-coated on the film and baked on a hot plate. After cooling to room temperature, the samples were exposed by laser direct writing with a spatial light modulator (DMD, Digital Micromirror Device). Finally, wet etching was carried out in a mixed acidic solution. Figures 1D–F are the microscope images of the three fabricated symmetric and asymmetric Case I (d = 20 μm) and Case II (g = 20 μm) S-shaped metasurfaces. The size of the samples is 1 × 1 cm. The transmission spectra of the samples at normal incidence were measured using a terahertz time-domain spectroscopy (THz-TDS) system under both x- and y-polarized incidences, a Gaussian focused beam was used as the THz source, and the spectral resolution is 10 GHz. The measured transmissions for the three samples are shown as black curves in Figure 6, and simulations are also shown as red curves for lossy PET (loss tangent = 0.05). From Figures 6A–C, the measured electric-LC resonance at ~0.3 THz and ED resonance at ~1.3 THz at the y-polarized incidence are clearly seen for all three samples and are in good agreement with the simulations. The measured two trapped modes are located at 0.6 and 1.0 THz for asymmetric samples (Case I and Case II) as the simulations predicted, the Q factor of the trapped mode at 0.6 THz (shown in Figure 6C) reaches up to over 50, but they are much weaker than those for lossless substrates as shown in Figure 2. Other reason for the differences between measured and simulated results is the limited sample size or effective unit cells of the structure in the measurements, in contrast to the infinite unit cells in the simulations, which impacts the high-Q resonance more than the low-Q resonance. In addition, the imperfect fabrication geometry will produce a small difference as well. As the metasurfaces are illuminated by the x-polarized wave, the measured transmissions in Figure 6E show a clear Fano resonance at 0.6 THz and an EIT at 1.0 THz in the asymmetric sample in Case I, but Case II (Figure 6F) shows a very weak Fano and no EIT, which are basically consistent with the simulation results. Thus, the two trapped modes and two Fano resonances in the asymmetric S-shaped metasurfaces have been verified experimentally.
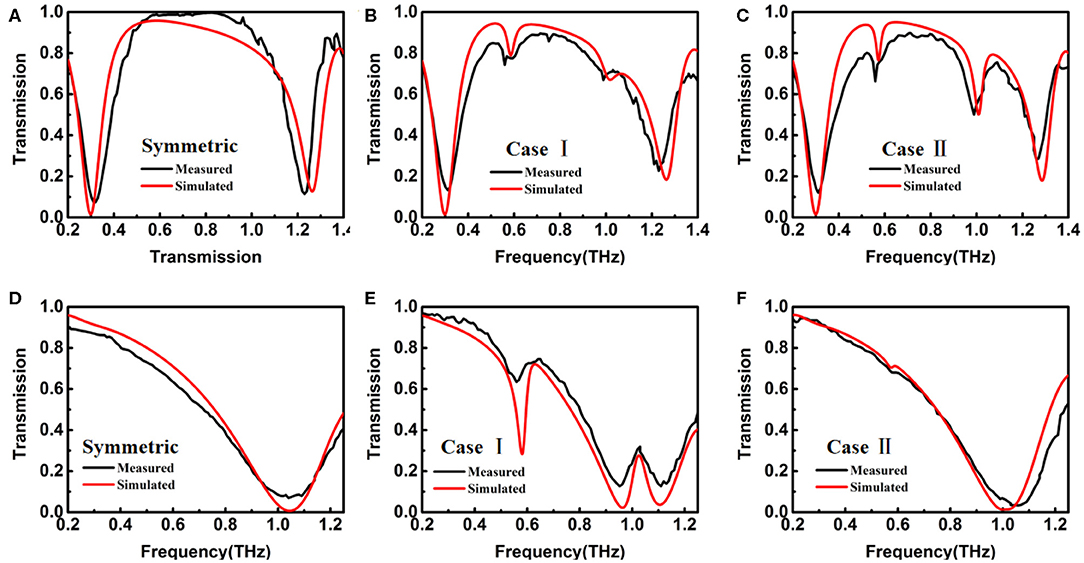
Figure 6. Measured transmission spectra (black line) for (A,D): symmetric metasurface; (B,E): Case I; (C,F): Case II. The E-field of the incident wave is polarized along (A–C): the y-axis; (D–F): the x-axis. Simulated curves (red line) are also given for the lossy substrate (loss tangent = 0.05).
Conclusion
In summary, we numerically and experimentally demonstrated double Fano resonances in simple S-shaped plasmonic metasurfaces in the terahertz spectral region. Transmissions of two types of asymmetric S-shaped structures were investigated under both normal and oblique incidences in the frequency range 0.2–1.4 THz. At normal incidence, apart from the electric-LC resonance at 0.3 THz and ED at 1.3 THz, two trapped modes at 0.6 and 1.0 THz are simultaneously excited in both the asymmetric structures, which are mainly attributed to the MD and the EQ, respectively. Furthermore, strong Fano and EIT resonances are achieved by coupling the two dark trapped modes with a broad ED in one asymmetric structure, but very weak resonances are observed for the other asymmetric structure. This indicates that the asymmetric structure plays an important role in the excitation of Fano resonances. Moreover, at oblique incidence, strong Fano responses can be observed and greatly enhanced in both the asymmetric metasurfaces, and even for inversion symmetry, which is impossible at normal incidence. The results measured by THz-TDS for the fabricated symmetric and asymmetric structures are in good agreement with calculations. The proposed S-shaped plasmonic metasurfaces have wide applications in biochemical sensing, optical switching, and slow-light devices.
Data Availability Statement
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author/s.
Author Contributions
ZH was the leader of the work. ZH and WX wrote the manuscript. WX, CS, and JL were responsible for experiment setting. LC and FZ were mainly engaged in picture editing and related data processing. All authors have made positive contributions to the work.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
Natural Science Foundation of China (NSFC) (61875179) and Zhejiang Province (LY17F010010 and LGG19F050004); Primary Research and Development Plan of Zhejiang Province (2019C03114).
References
1. Shelby RA, Smith DR, Schultz S. Experimental verification of a negative index of refraction. Science. (2001) 292:77–9. doi: 10.1126/science.1058847
2. Valentine J, Zhang S, Zentgraf T, Ulin-Avila E, Genov DA, Bartal G, et al. Three-dimensional optical metamaterial with a negative refractive index. Nature. (2008) 455:376–9. doi: 10.1038/nature07247
3. Schurig D, Mock JJ, Justice BJ, Cummer SA, Pendry JB, Starr AF, et al. Metamaterial electromagnetic cloak at microwave frequencies. Science. (2006) 314:977–80. doi: 10.1126/science.1133628
4. Khorasaninejad M, Chen WT, Devlin RC, Oh J, Zhu AY, Capasso F. Metalenses at visible wavelengths: diffraction-limited focusing and subwavelength resolution imaging. Science. (2016) 352:1190–4. doi: 10.1126/science.aaf6644
5. Yang S, Tang C, Liu Z, Wang B, Wang C, Li J, et al. Simultaneous excitation of extremely high-Q-factor trapped and octupolar modes in terahertz metamaterials. Opt Express. (2017) 25:15938–46. doi: 10.1364/OE.25.015938
6. Fedotov VA, Rose M, Prosvirnin SL, Papasimakis N, Zheludev NI. Sharp trapped-mode resonances in planar metamaterials with a broken structural symmetry. Phys Rev Lett. (2007) 99:147401. doi: 10.1103/PhysRevLett.99.147401
7. Singh R, Al-Naib IAI, Koch M, Zhang W. Asymmetric planar terahertz metamaterials. Opt Express. (2010) 18:13044–50. doi: 10.1364/OE.18.013044
8. Abdeddaim R, Ourir A, Rosny J. Realizing a negative index metamaterial by controlling hybridization of trapped modes. Phys Rev B. (2011) 83:033101. doi: 10.1103/PhysRevB.83.033101
9. Kabantsev AA, Driscoll CF, Hilsabeck TJ, O'Neil TM, Yu JH. Trapped-particle asymmetry modes in single-species plasmas. Phys Rev Lett. (2001) 87:225002. doi: 10.1103/PhysRevLett.87.225002
10. Yang S, Liu Z, Xia X, E Y, Tang C, Wang Y, et al. Excitation of ultrasharptrapped-mode resonances in mirror-symmetric metamaterials. Phys Rev B. (2016) 93:235407. doi: 10.1103/PhysRevB.93.235407
11. Mousavi SH, Kholmanov I, Alici KB, Purtseladze D, Arju N, Tatar K, et al. Inductive tuning of Fano-resonant metasurfaces using plasmonic response of graphene in the mid-infrared. Nano Lett. (2013) 13:1111–7. doi: 10.1021/nl304476b
12. Wu C, Khanikaev AB, Adato R, Arju N, Yanik AA, Altug H, et al. Fano-resonant asymmetric metamaterials for ultrasensitive spectroscopy and identification of molecular monolayers. Nat Mater. (2011) 11:69–75. doi: 10.1038/nmat3161
13. Chen CY, Un IW, Tai NH, Yen TJ. Asymmetric coupling between subradiant and superradiant plasmonic resonances and its enhanced sensing performance. Opt Express. (2009) 17:5372–80. doi: 10.1364/OE.17.015372
14. Fedotov VA, Tsiatmas A, Shi JH, Buckingham R, Groot PD, Chen Y, et al. Temperature control of Fano resonances and transmission in superconducting metamaterials. Opt Express. (2010) 18:9015–9. doi: 10.1364/OE.18.009015
15. Zhao W, Ju D, Jiang Y, Zhan Q. Dipole and quadrupole trapped modes within bi-periodic Silicon particle array realizing three-channel refractive sensing. Opt Express. (2014) 22:31277–85. doi: 10.1364/OE.22.031277
16. Zhao T, Xiao H, Li Y, Yang J, Jia H, Ren G, et al. Independently tunable double Fano resonances based on waveguide-coupled cavities. Opt Express. (2019) 44:3154–7. doi: 10.1364/OL.44.003154
17. Tuz VR, Novitsky DV, Mladyonov PL, Prosvirnin SL, Novitsky AV. Non-linear interaction of two trapped-mode resonances in a bilayer fish-scale metamaterial. J Opt Soc Am B. (2014) 31:2095–103. doi: 10.1364/JOSAB.31.002095
18. Zheng X, Zhao Z, Peng W, Zhang J, Zhao H, Shi W. Tuning the terahertz trapped modes of conductively coupled Fano-resonators in reflectional and rotational symmetry. Opt Mater Express. (2018) 8:105–18. doi: 10.1364/OME.8.000105
19. Tang X, Liu J, Zhang X, Zhu Y. Double trapped modes due to the hybridization effect in a composite meander wire array. J Phys D Appl Phys. (2014) 47:265304. doi: 10.1088/0022-3727/47/26/265304
20. Born N, Al-Naib I, Jansen C, Ozaki T, Morandotti R, Koch M. Excitation of multiple trapped-eigenmodes in terahertz metamolecule lattices. Appl Phys Lett. (2014) 104:101107. doi: 10.1063/1.4868420
21. Luk'yanchuk B, Zheludev NI, Maier SA, Halas NJ, Nordlander P, Giessen H, et al. The Fano resonance in plasmonic nanostructures and metamaterials. Nat Mater. (2010) 9:707–15. doi: 10.1038/nmat2810
22. Papasimakis N, Fu YH, Fedotov VA, Prosvirnin SL, Tsai DP, Zheludev NI. Metamaterial with polarization and direction insensitive resonant transmission response mimicking electromagnetically induced transparency. Appl Phys Lett. (2009) 94:211902. doi: 10.1063/1.3138868
23. Diao J, Han B, Yin J, Li X, Lang T, Hong Z. Analogue of electromagnetically induced transparency in an S-shaped all-dielectric metasurface. Photon J IEEE. (2019) 11:4601110. doi: 10.1109/JPHOT.2019.2920433
24. Zhao W, Leng X, Jiang Y. Fano resonance in all-dielectric binary nanodisk array realizing optical filter with efficient linewidth tuning. Opt Express. (2015) 23:6858–66. doi: 10.1364/OE.23.006858
25. Cao W, Singh R, Al-Naib IAI, He M, Taylor AJ, Zhang W. Low-loss ultra-high-Q dark mode plasmonic Fano metamaterials. Opt Lett. (2012) 37:3366–68. doi: 10.1364/OL.37.003366
26. Dhouibi A, Nawaz Burokur S, Lupu A, Lustrac AD, Priou A. Excitation of trapped modes from a metasurface composed of only Z-shaped meta-atoms. Appl Phys Lett. (2013) 103:184103. doi: 10.1063/1.4827880
27. Liu N, Weiss T, Mesch M, Langguth L, Eigenthaler U, Hirscher M, et al. Planar metamaterial analogue of electromagnetically induced transparency for plasmonic sensing. Nano Lett. (2010) 10:1103–7. doi: 10.1021/nl902621d
28. Cong L, Manjappa M, Xu N, Al-Naib I, Zhang W, Singh R. Fano resonances in terahertz metasurfaces: a figure of merit optimization. Adv Opt Mater. (2015) 3:1537–43. doi: 10.1002/adom.201500207
29. Wang J, Fan C, He J, Ding P, Liang E, Xue Q. Double Fano resonances due to interplay of electric and magnetic plasmon modes in planar plasmonic structure with high sensing sensitivity. Opt Express. (2013) 21:2236–44. doi: 10.1364/OE.21.002236
30. Zhang Q, Wen X, Li G, Ruan Q, Wang J, Xiong Q. Multiple magnetic mode-based fano resonance in split-ring resonator/disk nanocavities. ACS Nano. (2013) 7:11071–8. doi: 10.1021/nn4047716
31. Yan Z, Wen X, Gu P, Zhong H, Zhan P, Chen Z, et al. Double Fano resonances in individual metallic nanostructure for high sensing sensitivity. Nanotechnology. (2017) 28:475203. doi: 10.1088/1361-6528/aa8229
32. Le KQ, Alù A, Bai J. Multiple Fano interferences in a plasmonic metamolecule consisting of asymmetric metallic nanodimers. J Appl Phys. (2015) 117:023118. doi: 10.1063/1.4905619
33. Moritake Y, Kanamori Y, Hane K. Demonstration of sharp multiple Fano resonances in optical metamaterials. Opt Express. (2016) 24:9332–9. doi: 10.1364/OE.24.009332
34. Jung H, In C, Choi H, Lee H. Anisotropy modeling of terahertz metamaterials: polarization dependent resonance manipulation by meta-atom cluster. Sci Rep. (2014) 4:5214. doi: 10.1038/srep05217
35. Chen H, Ran L, Huang J, Zhang X, Chen K. Left-handed materials composed of only S-shaped resonators. Phys Rev E. (2004) 70:057605. doi: 10.1103/PhysRevE.70.057605
36. Nesimoglu T, Karaali M, Sabah C. Tuning the electric resonance of a metamaterial based single-sided S-Shaped resonator. In: 20th International Conference on Microwaves, Radar, and Wireless Communications. Gdansk, Poland (2014). doi: 10.1109/MIKON.2014.6899923
37. Basharin AA, Kafesaki M, Economou EN. Dielectric metamaterials with toroidal dipolar response. Phys Rev X. (2015) 5:011036. doi: 10.1103/PhysRevX.5.011036
38. Radescu EE, Vaman G. Exact calculation of the angular momentum loss, recoil force, and radiation intensity for an arbitrary source in terms of electric, magnetic, and toroid multipoles. Phys Rev E. (2002) 65:046609. doi: 10.1103/PhysRevE.65.046609
39. Han B, Li X, Sui C, Diao J, Jing X, Hong Z. Analog of electromagnetically induced transparency in an E-shaped all-dielectric metasurface based on toroidal dipolar response. Opt Mater Express. (2018) 8:2197–207. doi: 10.1364/OME.8.002197
Keywords: Fano resonance, metasurface, plasmonic, trapped mode, terahertz
Citation: Xu W, Chen L, Zhu F, Liu J, Sui C and Hong Z (2020) Double Fano Resonances in S-Shaped Plasmonic Metasurfaces in Terahertz Region. Front. Phys. 8:256. doi: 10.3389/fphy.2020.00256
Received: 13 April 2020; Accepted: 09 June 2020;
Published: 17 July 2020.
Edited by:
Olivier J. F. Martin, École Polytechnique Fédérale de Lausanne, SwitzerlandReviewed by:
Ranjan Singh, Nanyang Technological University, SingaporeYugui Peng, CUNY Advanced Science Research Center, United States
Maria Kafesaki, University of Crete, Greece
Copyright © 2020 Xu, Chen, Zhu, Liu, Sui and Hong. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Zhi Hong, aG9uZ3poaUBjamx1LmVkdS5jbg==
 Weihang Xu
Weihang Xu Lingling Chen1
Lingling Chen1 Zhi Hong
Zhi Hong