- 1Department of Mathematics, Huainan Normal University, Huainan, China
- 2School of Education Science, Guangxi University for Nationalities, Nanning, China
In this paper, the dynamical analysis of Ca2+ oscillations in astrocytes is theoretically investigated by the center manifold theorem and the stability theory of equilibrium point. The global structure of bifurcation and evoked Ca2+ dynamics are presented in a human astrocyte model from a mathematical perspective. Results show that the difference in appearance and disappearance of Ca2+ oscillations is partly due to two subcritical Hopf bifurcation points. In addition, the numerical simulations are performed to further verify the effectiveness of the proposed method.
Introduction
Ca2+ as an important second messenger in the cytosol is critical for synaptic neurons and glia cells in the brain [1]. The oscillatory changes in concentration of Ca2+ are called Ca2+ oscillations and play an active part in the transmission of chemical and electrical signaling process [2]. Astrocytes comprise approximately 50% of the volume of human brain and exhibit not only neuron-dependent Ca2+ oscillations but also spontaneous Ca2+ waves [3]. It was demonstrated that the frequencies and amplitudes of Ca2+ oscillations play key roles in Ca2+ signal transduction in the nervous system [4]. Recent results from experiment calcium release-activated calcium channel (CRAC) have shown that it is effective for the control in inhibiting neuronal excitability by enhancing calcium release from astrocytes [5].
It was generally considered that Ca2+ oscillations in astrocyte take place in response to external stimuli, inducing the release of neuro-active chemicals [6, 7]. This view began to change as several lines of evidence indicate that these oscillations can also be formed spontaneously [8]. Nevertheless, the mechanism and functional role involved in these stochastic spontaneous Ca2+ waves are still not well-understood. Basically, Ca2+ signal transmission of astrocytes in the brain may vary owing to certain bifurcation principles, and different chemical information is typically characterized by frequency, amplitude, and spatial Ca2+ propagation [9]. Dynamical mechanisms that underlie the Ca2+ waves have been investigated from both theoretical and experimental points of view in recent years [10–18]. Therefore, the stability and bifurcation analysis are fundamental to investigate the appearance and disappearance of spontaneous Ca2+ oscillations in astrocytes. In the last decades, existing mathematical models helped explore the possible dynamical mechanism of these oscillatory activities in neuronal excitability [19–23].
Stability of Equilibrium Point and Bifurcation Analysis
In the present work, we apply an extension of the one-pool model proposed by Lavrentovich and Hemkin as a specific example of the stability of equilibrium point and the bifurcation scenario. This model consists of three main variables: cytosol Ca2+ concentration (Cacyt), Ca2+ concentration in the endoplasmic reticulum (Caer), and IP3 concentration in cell (IP3). The equations and meanings of each expression in the model are given as follows:
where
The details of each parameter can be found in Table 1 and [4].
Analysis of Stability and Bifurcation of Equilibria
In the following, vin is chosen as the bifurcation parameter, corresponding to Ca2+ inflow into the cytosol through the astrocyte's membrane.
For convenience, let x = Cacyt, y = Caer, z = IP3, and r = vin, we first rewrite model (1) as the following form:
The equilibrium of system (2) meets the following equations:
Let x0, y0, and z0 be the roots of Equation (2) and x1 = x – x0, y1 = y – y0, and z1 = z – z0, we have the following representations:
The corresponding equilibrium is (0, 0, 0), and system (4) has the same properties with the equilibrium of system (2). With simple calculation, it is easy to calculate the Jacobian matrix of system (4),
where
And one can easily obtain the following characteristic equation:
where
After a simple calculation, we have the following equations:
where
Owing to the meaning of x, y, z and r, special conditions meet the needs whether there exists equilibrium of system (4) when r ∈ [0.02, 0.06].
We consider the Hurwitz matrix using coefficients Qi of the characteristic polynomial:
It is easy to verify that the eigenvalues of the linearized system are negative or have a negative real part if the determinants of the three Hurwitz matrices are positive:
Consider the stability and bifurcations of system (4) for varying parameter vin in the case of the following Routh–Hurwitz criteria:
The corresponding two values can be obtained:
After the computation based on the Routh–Hurwitz criteria, when we choose r1 = 0.02383,
As r2 = 0.05944,
It can be seen that all the two values satisfy the Routh–Hurwitz criteria. After using the normal form method, one can easily obtain the following conclusions:
(1) r < 0.02383, there is a stable node of system (4);
(2) r = 0.02383, and system (4) has a non-hyperbolic equilibrium O1 = (0.04766, 3.96096098, 0.0153858);
(3) 0.02383 < r < 0.05944, system (4) has an equilibrium (saddle);
(4) r = 0.05944, and there exists a non-hyperbolic equilibrium O2 = (0.11886, 0.6665221778, 0.0847979);
(5) r > 0.05944, there is a stable node.
Let r = r0, x1 = x – x0, y1 = y – y0, z1 = z – z0, and r1 = r – r0, the equilibrium of system (4) is (x0, y0, z0). In order to apply the center manifold theorem with bifurcation parameter vin, a new variable r1 is introduced in the original model. On the basis of dr1/dt = 0, we have the following:
r1 = 0, O(x1, y1, z1, r1) = (0, 0, 0, 0) is the equilibrium of system (5), which has a same conclusion as the one of system (2) in stability and bifurcations.
For r0 = 0.02383, the Jacobian matrix of system (4) has the following form:
We have the eigenvalues of equilibrium point O1 = (0, 0, 0, 0) of system (5): ξ1 = −68.3987, ξ2 = 0.0204i, ξ3 = −0.0204i, ξ4 = 0, and the eigenvectors have met the following matrix:
Suppose
where
System (5) has the following form
and
where
Furthermore,
where
Through calculation, we have the following equations:
On the basis of the center manifold theory, one can conclude that there exists a center manifold of system (5), and its form can be expressed as
Substituting Equation (7) into Equation (6), the following equations can be derived as:
Let h (v, w, s) = av2 + bw2 + cs2 + dvw + evs + fws + …, and the center manifold of system (5) is
Using the method of high-order partial derivatives, one can obtain the following equations:
Based on the center manifold theory, one can compute a = −0.00094, b = −0.12224, c = −1.15703, d = 0.03634, e = 0.10863, and f = −0.75265. So the system that is confined to this center manifold is as follows:
where
Hence, it is easy to verify that
From the discussion above, we summarize the following conclusions.
Conclusion 1: A subcritical Hopf bifurcation occurs when r passes through r0 = 0.02383 of system (2). r < r0, and the equilibrium O1 is stable. r > r0, and the equilibrium loses its stability; meanwhile, a stable periodic solution occurs, and system (2) begins to oscillate.
r0 = 0.05944, eigenvalues of equilibrium point O2 = (0, 0, 0, 0) of system (3) are ξ1 = −60.5573, ξ2 = 0.1029i, ξ3 = −0.1029i, and ξ4 = 0, respectively. System (5) has the following form:
where
And g1j(j = 1, …, 4) have the following different formulae:
which reduce to the following equations:
The center manifold of system (5) is
where
And thus, the following equation can be obtained:
We compute a = 1.073869652, b = 0.3254214051, c = 1.590904144, d = 0.8641549, e = 2.5838022, and f = 1.1901543. So the system confined to the center manifold of system (5) is
where
By computation, Conclusion 2 can be inferred as follows:
Conclusion 2: A subcritical Hopf bifurcation occurs when r passes through r0 = 0.05944 of system (2). r < r0, the equilibrium O2 is unstable, and system (2) begins to oscillate. r > r0, the equilibrium O2 is stable, and the global oscillations of system (2) vanish.
Numerical Simulations
In order to investigate the bifurcation phenomenon in different Ca2+ oscillation patterns, we study the generation process with respect to the parameter vin. The bifurcation diagram of the equilibrium of system (2) in the (Cacyt, vin)-plane [(Cacyt, vin)-plane)] is shown in Figures 1A,B. Each point of the curve (solid line) represents a stable equilibrium, and the dashed line represents an unstable equilibrium. The equilibrium undergoes the Hopf bifurcation twice, marked by points HB1 and HB2 with respect to the bifurcation parameter = 0.0238 μM/s and = 0.0594 μM/s. When vin < , there exists stable equilibrium of system (2). As vin increases, the stable equilibrium loses its stability at the point HB1 and returns to being stable at HB2.
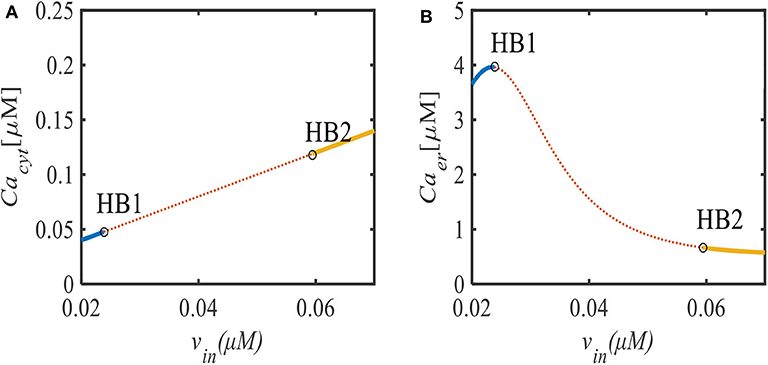
Figure 1. (A) Bifurcation diagram of the equilibrium of system (2) in the (vin, Cacyt)-plane. (B) Bifurcation diagram of the equilibrium of system (2) in the (vin, Caer)-plane. Points HB1 and HB2 are the Hopf bifurcation points.
In Figure 2, we shall present the time evolutions of cytosol Ca2+ concentration in this model for different values of the parameter vin by numerical simulation. The left panels represent time series of Cacyt comparison of parameter vin, and the right panels are the corresponding Cacyt-Caer-IP3 phase portrait. For example, there is a single peak in this type of oscillation for vin = 0.024 μM/s in Figure 2A, and the corresponding 3D phase-space is shown in Figure 2B. Around vin = 0.033 μM/s, it is seen that the number of peak counts and peak magnitude begin to increase, as shown in Figures 2C,D. Similarly, when vin = 0.052 μM/s, five peaks were obtained (Figures 2E,F). Moreover, it should be mentioned in Figures 2G,E, although the results for peak magnitude look very similar and in agreement with the peak counts, that the oscillatory vibration is significantly different (Figures 2G,H).
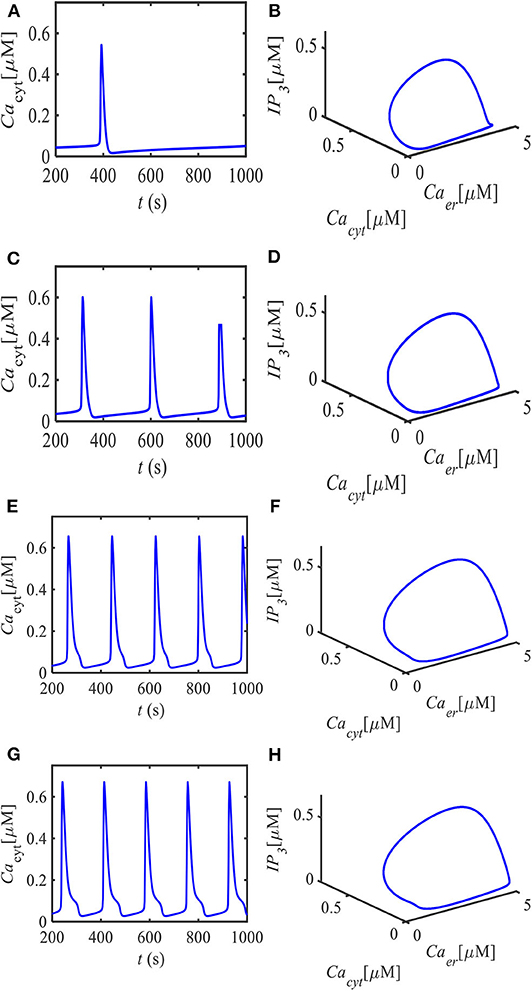
Figure 2. Spontaneous Ca2+ oscillations in astrocytes emerged at different parts of the curve in Figure 1 relative to points HB1 and HB2. The left panels denote the time evolution of Cacyt for different sets of parameter vin, and the right panels denote the corresponding Cacyt-Caer-IP3 phase portrait. (A) vin = 0.024 μM/s, (B) portrait diagram as vin = 0.024 μM/s, (C) vin = 0.033 μM/s, (D) portrait diagram as vin = 0.033 μM/s, (E) vin = 0.052 μM/s, (F) portrait diagram as vin = 0.052 μM/s, (G) vin = 0.0593 μM/s, and (H) portrait diagram as vin = 0.0593 μM/s.
Conclusion
In this paper, we have theoretically investigated the stability of equilibrium and bifurcation of spontaneous Ca2+ oscillations with a mathematical model in astrocytes. By choosing the flow of Ca2+ from the extracellular vesicles through the membrane and into the cytosol as the bifurcation parameter, we conclude that two subcritical Hopf bifurcation points play an important role in the occurrence of Ca2+ oscillations. By combining the theoretical analysis results in this paper, we numerically gave the Hopf bifurcations, which agree with the theoretical results. Our results may be instructive for better understanding the role of spontaneous Ca2+ oscillations in astrocytes. Because synchronization of different oscillatory patterns may relate to bifurcation, we will give detailed research in future.
Data Availability Statement
All datasets generated for this study are included in the article/supplementary material.
Author Contributions
HZ and MY contributed to the conception and design of the study. HZ organized the literature and wrote the first draft of the manuscript. MY performed the design of figures. All authors contributed to the manuscript revision and read and approved the submitted version.
Funding
This work was supported by the Natural Science Foundation of China under Grant No. 11872084 and the Natural Science Foundation of the Anhui Higher Education Institutions of China under Grant Nos. KJ2016SD54 and KJ2017A460.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
1. Scemes E, Giaume C. Astrocyte calcium waves: what they are and what they do. Glia. (2006) 54:716–25. doi: 10.1002/glia.20374
2. Nedergaard M, Ransom B, Goldman SA. New roles for astrocytes: redefining the functional architecture of the brain. Trends Neurosci. (2003) 26:523–30. doi: 10.1016/j.tins.2003.08.008
3. Agulhon C, Petravicz J, McMullen AB, Sweger EJ, Minton SK, Taves SR, et al. What is the role of astrocyte calcium in neurophysiology? Neuron. (2008) 59:932–46. doi: 10.1016/j.neuron.2008.09.004
4. Anwar H. Capturing intracellular Ca2+ dynamics in computational models of neurodegenerative diseases. Drug Discov Today Dis Models. (2016) 19:37–42. doi: 10.1016/j.ddmod.2017.02.005
5. Toth AB, Hori K, Novakovic MM, Bernstein NG, Lambot L, Prakriya M. CRAC channels regulate astrocyte Ca2+ signaling and gliotransmitter release to modulate hippocampal GABAergic transmission. Sci Signal. (2019) 12:eaaw5450. doi: 10.1126/scisignal.aaw5450
6. Volterra A, Meldolesi J. Astrocytes, from brain glue to communication elements: the revolution continues. Nat Rev Neurosci. (2005) 6:626–40. doi: 10.1038/nrn1722
7. Halnes G, Østby I, Pettersen KH, Omholt SW, Einevoll GT. Electrodiffusive model for astrocytic and neuronal ion concentration dynamics. PLoS Comput Biol. (2013) 9:e1003386. doi: 10.1371/journal.pcbi.1003386
8. Charles AC. Glia-neuron intercellular calcium signaling. Dev Neurosci. (1994) 16:196–206. doi: 10.1159/000112107
9. Matrosov VV, Kazantsev VB. Bifurcation mechanisms of regular and chaotic network signaling in brain astrocytes. Chaos. (2011) 21:023103. doi: 10.1063/1.3574031
10. Ji Q, Lu Y. Bifurcations and continuous transitions in a nonlinear model of intracellular calcium oscillations. Int J Bifurcat Chaos. (2013) 23:1350033. doi: 10.1142/S0218127413500338
11. Liu H, Pan Y, and Cao J. Composite learning adaptive dynamic surface control of fractional-order nonlinear systems. IEEE Trans Syst Man Cybernetics. (2019) 50:2557–67. doi: 10.1109/tcyb.2019.2938754
12. Liu H, Wang H, Cao J, Alsaedi A, Hayat T. Composite learning adaptive sliding mode control of fractional-order nonlinear systems with actuator faults. J Franklin Inst. (2019) 36:9580–99. doi: 10.1016/j.franklin.2019.02.042
13. Parri HR, Gould TM, Crunelli V. Spontaneous astrocytic Ca 2+ oscillations in situ drive NMDAR-mediated neuronal excitation. Nat Neurosci. (2001) 4:803–12. doi: 10.1038/90507
14. Ding X, Zhang X, Ji L. Contribution of calcium fluxes to astrocyte spontaneous calcium oscillations in deterministic and stochastic models. Appl Math Model. (2018) 55:371–82. doi: 10.1016/j.apm.2017.11.002
15. Li J, Tang J, Ma J, Du M, Wang R, Wu Y. Dynamic transition of neuronal firing induced by abnormal astrocytic glutamate oscillation. Sci Rep. (2016) 6:32343. doi: 10.1038/srep32343
16. Ji Q, Zhou Y, Yang Z, Meng X. Evaluation of bifurcation phenomena in a modified Shen–Larter model for intracellular Ca2+ bursting oscillations. Nonlinear Dyn. (2016) 84:1281–8. doi: 10.1007/s11071-015-2566-3
17. Oschmann F, Berry H, Obermayer K, Lenk K. From in silico astrocyte cell models to neuron-astrocyte network models: a review. Brain Res Bull. (2018) 136:76–84. doi: 10.1016/j.brainresbull.2017.01.027
18. Matrosov V, Gordleeva S, Boldyreva N, Ben-Jacob E, Kazantsev V, de Pitta M, et al. Emergence of regular and complex calcium oscillations by inositol 1,4,5-Trisphosphate signaling in astrocytes. Neurons Cogn. (2019) 151–76. doi: 10.1007/978-3-030-00817-8_6
19. Zhou A, Liu X, Yu P. Bifurcation analysis on the effect of store-operated and receptor-operated calcium channels for calcium oscillations in astrocytes. Nonlinear Dyn. (2019) 97:1–16. doi: 10.1007/s11071-019-05009-2
20. Engelborghs K, Luzyanina T, Roose D. Numerical bifurcation analysis of delay differential equations using DDE-BIFTOOL. ACM Trans Math Softw. (2002) 28:1–21. doi: 10.1145/513001.513002
21. Yu P, Leung AY. The simplest normal form of Hopf bifurcation. Nonlinearity. (2003) 16:277–300. doi: 10.1088/0951-7715/16/1/317
22. Yuan Y, Belair J. Stability and hopf bifurcation analysis for functional differential equation with distributed delay. Siam J Appl Dyn Syst. (2011) 10:551–81. doi: 10.1137/100794493
Keywords: astrocyte, equilibrium, Hopf bifurcation, center manifold, stability
Citation: Zuo H and Ye M (2020) Bifurcation and Numerical Simulations of Ca2+ Oscillatory Behavior in Astrocytes. Front. Phys. 8:258. doi: 10.3389/fphy.2020.00258
Received: 02 May 2020; Accepted: 10 June 2020;
Published: 14 August 2020.
Edited by:
Jia-Bao Liu, Anhui Jianzhu University, ChinaReviewed by:
Junqiang Wei, North China Electric Power University, ChinaYong Zhao, Henan Polytechnic University, China
Yong Lu, Harbin Engineering University, China
Copyright © 2020 Zuo and Ye. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Min Ye, bWlzc3llLTIwMDZAMTYzLmNvbQ==
 Hongkun Zuo1
Hongkun Zuo1 Min Ye
Min Ye