Transport Properties of the Simple Lennard-Jones/Spline Fluid I: Binary Scattering and High-Accuracy Low-Density Transport Coefficients

Inspired by recent work on the thermodynamic properties of the Lennard-Jones/spline (LJ/s) fluid [1], we have considered the transport properties of the simple LJ/s fluid. The binary scattering problem for LJ/s particles was solved numerically, and results were compared to the untruncated LJ fluid. The scattering dynamics are affected both by the restricted range of the LJ/s potential, and the stronger attraction between LJ/s particles at distances between the inflection point of the potential and the cutoff range. At small relative kinetic energies, it was found that the scattering cross section of the LJ/s particles is much smaller than that of the LJ particles. The shear viscosity, thermal conductivity, and the self-diffusion coefficient were calculated from the scattering cross sections by the Chapman-Enskog method, and a six-parameter equation with a worst case accuracy of roughly 1% over the temperature interval [0.1, 1000] in LJ units is provided. The smaller scattering cross section at low kinetic energies leads to transport coefficients of the LJ/s fluid to be greater than those of the LJ fluid at low temperatures, and were all found to be roughly 50% greater at T = 0.1, which is the lowest temperature considered.

1. Introduction

Knowledge of the transport properties of fluids is key to understanding a wide range of non-equilibrium behavior, such as thermal conduction, viscous flow, and diffusion. While the theory of non-equilibrium thermodynamics provides closure relations for describing fluxes in terms of thermodynamic driving forces, the functional dependence of the corresponding transport coefficients on thermodynamic variables must be supplied either from experiments, or calculated by means of statistical mechanics from a model interaction potential. The Lennard-Jones 12-6 potential (LJ) is a particularly ubiquitous and simple model potential that captures both the attraction between electrically neutral particles at long range, and their mutual repulsion at short range. The infinite range of this potential is, however, the cause of some problems in the application of periodic boundary conditions in direct molecular dynamics simulations. For this reason, the potential is often replaced in practical calculations by a truncated version with a finite range. One such potential is the Lennard-Jones/spline model (LJ/s) [2], which truncates the potential smoothly by means of a cubic spline. Recently, a detailed assessment was made on the effect of this type of truncation on the equilibrium thermodynamic properties of the resulting fluid [1]. Inspired by this work, it is of interest to see how this truncation affects non-equilibrium properties.

Transport properties of the untruncated Lennard-Jones fluid have been studied for nearly a century, and transport coefficients are known to a high degree of precision over a wide range of temperatures and densities. While the properties of the LJ and LJ/s fluids are expected to be similar, their difference may be of great importance in precise calculations of quantities of theoretical interest, such as the entropy generated by irreversible processes. In particular, the Chapman-Enskog values, which are expected to be accurate at low densities and low Knudsen numbers, are useful for several reasons—they supplement data from molecular dynamics in the low-density regime where the small number of particles gives low-quality statistics, and are also used as reference values in the modified Enskog theory [3], and for prediction through entropy scaling, as in e.g., [4]. High-accuracy calculations are therefore important as the basis for further work, such as the prediction of transport coefficients at higher densities, which will be the topic for a future paper.

2. Theory

2.1. Binary Scattering

The binary scattering problem of the Lennard-Jones fluid is already well-studied, and detailed recent analyses can be found in [5] and [6]. We consider instead the Lennard-Jones/spline potential

$\begin{array}{ll}V(r)=\{\begin{array}{ll}4\left(r^{-12}-r^{-6}\right)\hfill & r<r_s\hfill \\ a{\left(r-r_c\right)}^2+b{\left(r-r_c\right)}^3\hfill & r_s\le r\le r_c\hfill \\ 0\hfill & r>r_c\hfill \end{array}& (1)\end{array}$

which behaves like a Lennard-Jones potential up to a separation equal to the inflection point r = r_s. At longer separation, the potential drops smoothly to uniform at r = r_c by means of a cubic spline. The coefficients a and b are chosen such that V (r) and the force f (r) = −∇V (r) are continuous at r = r_s. Exact values of these parameters can be found in [1]. We consider here the case that the masses of the scattering particles are equal, and all quantities are dimensionless (Lennard-Jones units). The shape of the potential and the corresponding force is shown in Figure 1 along with the standard LJ potential. In a large part of the spline region, the force of attraction between LJ/s-particles is significantly larger than the corresponding force between LJ-particles. As we will see, this feature can lead to appreciable differences in the particle dynamics when collision trajectories are off-center.

FIGURE 1

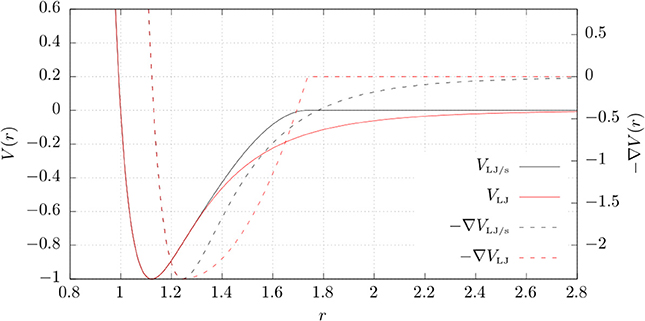
Figure 1. The Lennard-Jones/spline potential and the untruncated Lennard-Jones potential, plotted along with their corresponding forces.

We are interested in the shape of trajectories for different possible initial relative velocities and positions. Let θ be the angle between the particle positions with θ = 0 parallel to the initial relative velocity. A useful quantity is the relative angular momentum

$\begin{array}{ll}{p}_{\theta }=\frac{r^2}{2}\frac{\text{d}\theta }{\text{d}t}& (2)\end{array}$

which is a conserved quantity by virtue of V (r) being a central-force (θ-independent) potential. Since V (r) is also time-independent, the total energy

$\begin{array}{ll}E=\frac{1}{4}\left[{\left(\frac{\text{d}r}{\text{d}t}\right)}^2+r^2{\left(\frac{\text{d}\theta }{\text{d}t}\right)}^2\right]+V(r)& (3)\end{array}$

is also conserved. Let g be the initial relative velocity as the particles approach each other from infinity, and let the impact parameter ℓ be such that the initial (and constant) angular momentum is gℓ/2. The initial (and constant) total energy is then simply g²/4. Varying g and ℓ from 0 to ∞ then allow us to explore all possible trajectories during such an encounter. The trajectory may be found by solving the system

$\begin{array}{l}\frac{{\text{d}}^{2}r}{\text{d}{t}^2}=\frac{g^2{\ell }^2}{2r^3}+f(r)\\ \frac{\text{d}\theta }{\text{d}t}=\frac{g\ell }{r^2}& (4)\end{array}$

Conservation of energy allows us to integrate the radial equation from second to first order

$\begin{array}{ll}\frac{\text{d}r}{\text{d}t}=\sqrt{g^2\left(1-\frac{{\ell }^2}{r^2}\right)-4V(r)}& (5)\end{array}$

However, the sign is ambiguous, and care must be taken to avoid unphysical solutions. Solving for dt and multiplying by p_θ gives an equation for the trajectory

$\begin{array}{ll}\text{d}\theta =\frac{\ell \text{d}r}{r^2\sqrt{1-{\ell }^2{r}^{-2}-4g^{-2}V(r)}}& (6)\end{array}$

By spacetime inversion symmetry, the trajectory is symmetric about the line connecting the two particles when the interparticle distance is at the trajectory minimum r_m. Let the angular coordinate at this point be Φ. Since the particles approach from infinity, we have

$\begin{array}{ll}\text{Φ}={\displaystyle {\int }_{r_m}^{\infty }}\frac{\ell \text{d}r}{r^2\sqrt{1-{\ell }^2{r}^{-2}-4g^{-2}V(r)}}& (7)\end{array}$

The initial angle at infinity is π, and we are interested in the scattering angle Θ = π − 2Φ. The scattering angle as function of g and ℓ fully determines the contribution of binary collisions to the macroscopic hydrodynamical modes of the fluid in the low-density limit.

2.1.1. The Distance of Closest Approach

The piecewise nature of the LJ/s potential means that the equation determining r_m depends on whether or not r_m < r_s. In any case, the physical root must be the largest real root of dr/dt = 0 satisfying r_m ≤ r_c, where we restrict our attention to ℓ ≤ r_c. For ℓ > r_c, the particles will always remain out of range, so r_m = ℓ and trivially Θ = 0. Whether or not r_m < r_s depends on whether or not the relative kinetic energy of the particles can overcome any energy barrier along the way to r = r_s. The radial energy barrier is due to the centrifugal potential offset by the attractive potential. The height of this barrier is the maximum $V_{\text{eff}}^{\text{max}}$ of

$\begin{array}{ll}{V}_{\text{eff}}(r)={\left(\frac{g\ell }{2r}\right)}^2+V(r)& (8)\end{array}$

with r_max ≥ r_s. Then, r_m < r_s if and only if

$\begin{array}{ll}\frac{g^2}{4}>V_{\text{eff}}^{\text{max}}& (9)\end{array}$

If r_m ≥ r_s, we need to find the largest real r_m such that

$\begin{array}{ll}\frac{g^2}{4}\left(1-\frac{{\ell }^2}{r_m^2}\right)-a{(r_m-r_c)}^2-b{(r_m-r_c)}^3=0& (10)\end{array}$

or, equivalently, the smallest real u_m : = 1/r_m such that

$\begin{array}{ll}{c}_0+c_1{u}_m+c_2{u}_m^2+c_3{u}_m^3+u_m^5=0& (11)\end{array}$

with monomial coefficients

$\begin{array}{l}{c}_0=\frac{4b}{g^2{\ell }^2}{c}_1=\frac{4a-12b{r}_c}{g^2{\ell }^2}{c}_2=\frac{12b{r}_c^2-8a{r}_c}{g^2{\ell }^2}\\ \begin{array}{l}{c}_3=\frac{4a{r}_c^2-4b{r}_c^3-g^2}{g^2{\ell }^2}\end{array}& (12)\end{array}$

We solve this equation in two stages—first, we locate all the real roots of the equation by diagonalizing the companion matrix

$\begin{array}{ll}\text{C}=\left[\begin{array}{ccccc}0& 0& 0& 0& -c_0\\ 1& 0& 0& 0& -c_1\\ 0& 1& 0& 0& -c_2\\ 0& 0& 1& 0& -c_3\\ 0& 0& 0& 1& 0\end{array}\right]& (13)\end{array}$

such that |u_mI − C| = 0 is equivalent to (11). The true turning point is characterized by a positive radial acceleration. A secure way of computing the physical solution is then to diagonalize C and pick the largest real diagonal element that is smaller than r_c and gives a positive radial acceleration. The latter constraint is

$\begin{array}{ll}\frac{g^2{\ell }^2}{r_m^3}+2f(r_m)>0& (14)\end{array}$

If no such eigenvalue exists, we infer that r_m < r_s, in which case we need to find the largest real r_m such that

$\begin{array}{ll}\frac{g^2}{4}\left(1-\frac{{\ell }^2}{r_m^2}\right)-4\left(r_m^{-12}-r_m^{-6}\right)=0& (15)\end{array}$

or the smallest real u_m such that

$\begin{array}{ll}{b}_0+b_2{u}_m^2+b_6{u}_m^6+u_m^{12}=0& (16)\end{array}$

where

$\begin{array}{ll}{b}_0=-g^2/16b_2=g^2{\ell }^2/16b_6=-1& (17)\end{array}$

subject to the constraint that r_m < r_s. The computation of eigenvalues is restricted in precision by the conditioning of the companion matrices. Therefore, we introduce as a second calculation stage that the values obtained by this method be refined further by using them as initial guesses to a more precise root-finding algorithm. For this, we choose Halley's method

$\begin{array}{ll}{u}_{i+1}=u_i-\frac{2P(u_i)P^{\prime }(u_i)}{2|P^{\prime }(u_i){|}^2-P(u_i)P^{″}(u_i)}& (18)\end{array}$

where P is either of the polynomials (11) or (16), and the prime denotes the derivative with respect to the argument. The convergence criterion is that the absolute value of P (u_i) is smaller than some tolerance. This way of computing r_m ensures that we always obtain the physical solution. This can also be double-checked by direct integration of (4), which is a comparably inefficient two-particle molecular dynamics approach, but serves as a way to check the consistency of the obtained value of r_m.

2.1.2. The Scattering Angle

Having obtained accurate values of r_m, the next step is to find the scattering angle Θ by numerical integration of (7), where r_m appears as one of the integration limits. In this limit, the integrand has a singularity, which will need to be dealt with some care. Let $u:=r_m{r}^{-1}$, such that

$\begin{array}{ll}\text{Φ}={\displaystyle {\int }_0^1}\frac{\ell \text{d}u}{\sqrt{r_m^2-{\ell }^2{u}^2-4(r_m^2/g^2)V(r_m/u)}}& (19)\end{array}$

Let

$\begin{array}{ll}G(u)=\frac{\ell }{\sqrt{r_m^2-{\ell }^2{u}^2-4(r_m^2/g^2)V(r_m/u)}}& (20)\end{array}$

then, we apply a tanh-sinh type transformation, suitable for dealing with endpoint singularities

$\begin{array}{ll}{\displaystyle {\int }_0^1}\text{d}uG(u)=\frac{\pi }{2}{\displaystyle {\int }_0^{\infty }}\text{d}x\frac{\text{cosh }(x)}{{\text{cosh}}^2\left(\frac{\pi }{2}\text{sinh }(x)\right)}G\left(\text{tanh }\left(\frac{\pi }{2}\text{sinh }(x)\right)\right)& (21)\end{array}$

Applying the trapezoidal rule with spacing Δx, the quadrature is then

$\begin{array}{l}\text{Φ}={\displaystyle {\int }_0^1}\text{d}uG(u)\\ \begin{array}{l}\approx \frac{\pi \Delta x}{2}{\displaystyle \sum _{n=0}^{\infty }}\frac{\text{cosh}(n\Delta x)}{{\text{cosh}}^2\left(\frac{\pi }{2}\text{sinh}(n\Delta x)\right)}G\left(\text{tanh}\left(\frac{\pi }{2}\text{sinh}(n\Delta x)\right)\right)\end{array}& (22)\end{array}$

which is further approximated by truncating the sum. The singularity is smeared out over an unbounded interval, and the quadrature exhibits exponential convergence to the analytical solution [7]. The scattering angle is then Θ = π − 2Φ.

2.2. Transport Coefficients

The low-density, low-Knudsen number limit of the transport coefficients are obtained by solving the Boltzmann equation for the one-particle probability density, and then calculating the expectation values corresponding to the heat flux, pressure tensor, and the diffusion flux in order to obtain the thermal conductivity λ, the shear viscosity η, and the self-diffusion coefficient D, respectively. The bulk viscosity of the simple fluid is zero in this limit, because the particles have no internal degrees of freedom. We choose the Chapman-Enskog approach to solving the equation, which gives the following expressions for η and λ [3]

$\begin{array}{ll}\eta =T{b}_1\lambda =-\frac{5}{2}T{a}_1& (23)\end{array}$

where T is the reduced kinetic temperature, and the coefficients a₁ and b₁ satisfy the linear equations

$\begin{array}{ll}{\displaystyle \sum _{p=1}^{\infty }}{b}_p{{B}}_{pq}=\frac{5}{2}{\delta }_{1q}{\displaystyle \sum _{p=1}^{\infty }}{a}_p{{A}}_{pq}=-\frac{15}{4}{\delta }_{1q}& (24)\end{array}$

where the matrix elements ${{A}}_{pq}$ and ${{B}}_{pq}$ are

$\begin{array}{l}{{A}}_{pq}:=\left[S_{\frac{3}{2}}^{(p)}(c^2)\text{c},S_{\frac{3}{2}}^{(q)}(c^2)\text{c}\right]\\ \begin{array}{l}{{B}}_{pq}:=\left[S_{\frac{5}{2}}^{(p-1)}(c^2){\text{c}}^{◦}\text{c},S_{\frac{5}{2}}^{(q)}(c^2){\text{c}}^{◦}\text{c}\right]\end{array}& (25)\end{array}$

where $\text{c}=\delta \text{v}/\sqrt{2T}$, and δv is the reduced peculiar velocity, while $\text{c}\text{c}=\text{c}\text{c}-\text{I}{c}^2/3$. The Sonine polynomials are

$\begin{array}{ll}{S}_k^{(n)}(x)={\displaystyle \sum _{p=0}^n}{(-x)}^p{(k+n)}_{n-p}\frac{(n-p)!}{p!}& (26)\end{array}$

where the subscript means r_q = r (r − 1)(r − 2) … (r − q + 1). The brackets in (25) denote integrals that involve the scattering angles obtained by solving the binary scattering problem, and can be expressed as linear combinations of the well-known collision integrals Ω^(n,s) [3].

$\begin{array}{l}{\Omega }^{(n,s)}=\sqrt{\frac{T}{\pi }}{\displaystyle {\int }_0^{\infty }}\text{d}{g}^{\prime }\text{exp}\left(-{g^{\prime }}^2\right){g^{\prime }}^{(2s+3)}{\varphi }^{(n)}\\ \begin{array}{l}{\varphi }^{(n)}=2\pi {\displaystyle {\int }_0^{\infty }}\text{d}\ell (1-{\text{cos}}^n\Theta )\ell \end{array}& (27)\end{array}$

where ${\text{g}}^{\prime }=\text{g}/2\sqrt{T}$, with g the relative velocity, ℓ is the impact parameter defined in the preceding section, and Θ is the scattering angle. General expressions for the coefficients in these linear combinations were derived by Tompson et al. [8, 9], who also gave explicit calculations up to order 5.

In practice, the linear systems in (24) are solved approximately by truncating the sums at some finite number k and solving the resulting k × k linear systems, which is to truncate the series expansion of the Chapman-Enskog solution to the corresponding order in c². We consider also the self-diffusion coefficient, which can be obtained as the special case of the interdiffusion coefficient of a binary mixture when both components are actually the same. The interdiffusion coefficient D₁₂ of a binary mixture of particles with equal masses is [3]

$\begin{array}{ll}{D}_{12}=\frac{\sqrt{T}}{2}{x}_1{x}_2{d}_0& (28)\end{array}$

where d₀ is found from the solution to

$\begin{array}{ll}{\displaystyle \sum _{p=-\infty }^{\infty }}{d}_p{{A}}_{pq}^{\prime }=\frac{3\sqrt{T}}{2n}{\delta }_{q0}& (29)\end{array}$

with n the particle density, and x_i = n_i/n, where n_i is the number density of particles of component i. We are interested in the case of a simple fluid, where x₁ = x₂. Let c₁ and c₂ be the dimensionless peculiar velocities of components 1 and 2. Manipulation of the expressions given in [3] gives in that case

$\begin{array}{ll}\frac{{{{A}}^{\prime }}_{pq}}{x_1{x}_2}=\{\begin{array}{ll}{\left[S_{\frac{3}{2}}^{(p)}\left(c_1^2\right){\text{c}}_1,S_{\frac{3}{2}}^{(q)}\left(c_1^2\right){\text{c}}_1\right]}_{12}+{\left[S_{\frac{3}{2}}^{(p)}\left(c_1^2\right){\text{c}}_1,S_{\frac{3}{2}}^{(q)}\left(c_1^2\right){\text{c}}_1\right]}_1\hfill & p,q>0\hfill \\ {\left[S_{\frac{3}{2}}^{(p)}\left(c_2^2\right){\text{c}}_2,S_{\frac{3}{2}}^{(q)}\left(c_2^2\right){\text{c}}_2\right]}_{12}+{\left[S_{\frac{3}{2}}^{(p)}\left(c_2^2\right){\text{c}}_2,S_{\frac{3}{2}}^{(q)}\left(c_2^2\right){\text{c}}_2\right]}_2\hfill & p,q<0\hfill \\ {\left[S_{\frac{3}{2}}^{(p)}\left(c_1^2\right){\text{c}}_1,S_{\frac{3}{2}}^{(q)}\left(c_2^2\right){\text{c}}_2\right]}_{12}\hfill & q<0<p\hfill \end{array}& (30)\end{array}$

and

$\begin{array}{ll}\frac{{{{A}}^{\prime }}_{0q}}{x_1{x}_2}=\{\begin{array}{ll}{2}^{-1/2}{\left[{\text{c}}_1,S_{\frac{3}{2}}^{(q)}\left(c_1^2\right){\text{c}}_1\right]}_{12}\hfill & q>0\hfill \\ -2^{-1/2}{\left[{\text{c}}_2,S_{\frac{3}{2}}^{(q)}\left(c_2^2\right){\text{c}}_2\right]}_{12}\hfill & q<0\hfill \\ -2^{-1}{\left[{\text{c}}_1,{\text{c}}_2\right]}_{12}\hfill & q=0\hfill \end{array}& (31)\end{array}$

where the brackets are analogous to those in (25), with subscripts 1 and 2 denoting collisions between pairs of particles of types 1 and 2, respectively, and the subscript 12 denoting collision between the two different types. Treating x₁x₂d₀ as the coefficient to be determined, we need not worry about the exact values of x₁ and x₂. Only that they are equal. This gives a result that is independent of the values of x₁ and x₂, as it must be for the self-diffusion coefficient. We see in particular that since ${\left[{\text{c}}_1,{\text{c}}_2\right]}_{12}=-4{\Omega }^{(1,1)}$, we obtain the first approximation

$\begin{array}{ll}{x}_1{x}_2{d}_0^{(1)}=\frac{3\sqrt{T}}{4n{\Omega }^{(1,1)}}\Rightarrow D^{(1)}=\frac{3T}{8n{\Omega }^{(1,1)}}& (32)\end{array}$

which is a familiar result in the literature. Calculating higher-order collision integrals allows us to find correction terms to this result up to any desired order in the polynomial expansion. Such higher-order corrections are more important at higher temperatures, as the contributions from greater powers of c² become more significant. Again, expressions for the bracket integrals may be obtained from [8]. For convenience, the matrix elements ${{A}}_{pq}^{\prime }/x_1{x}_2$ have been calculated from the bracket integrals and are given in the Supplementary Material up to order 5. Since the collision integrals all depend only on the temperature, the quantity nD is a function of the temperature only.

3. Results and Discussion

3.1. Binary Scattering

Equations (11) and (16) were solved on a patchwork of uniform grids on the g, ℓ-plane numerically by implementation of a looping algorithm in C++, using the Eigen package [10] to calculate the eigenvalues of the companion matrices. Equation (7) was then solved for each grid point, by implementing the quadrature given in Equation (23), using the Boost C++ library [11]. Both r_m and Θ were calculated within an error tolerance of 10⁻¹⁴ in reduced units. The distance of closest approach and the scattering angle obtained for both LJ/s and LJ are shown as functions of g for a few values of ℓ in Figure 2.

FIGURE 2

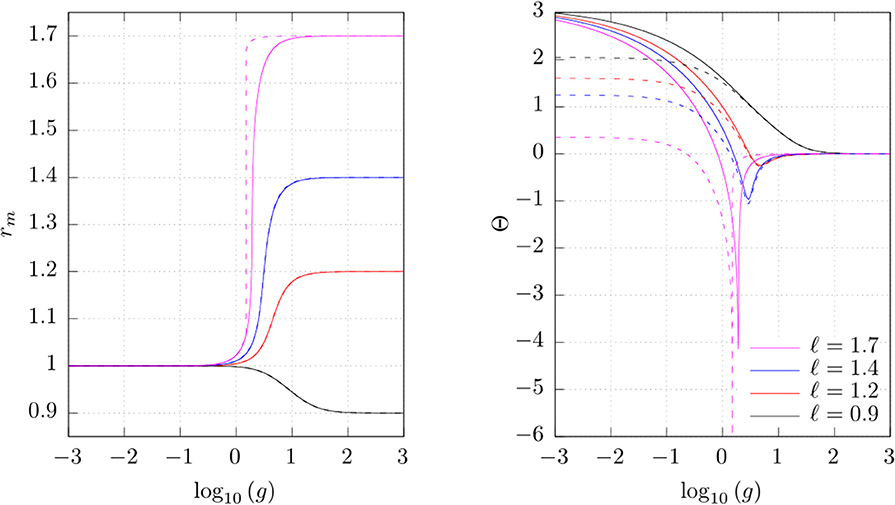
Figure 2. The distance of closest approach, r_m, and the scattering angle, Θ, from binary scattering of Lennard-Jones (solid lines) and Lennard-Jones/spline-particles (dashed lines) given as functions of the relative speed g for sampled values of the impact parameter ℓ.

We observe that when g is small, the dynamics are dominated by the potential energy of interaction, and r_m → 1 because that is the point where the mutual potential energy is equal to that at infinite separation. When g is large, r_m → ℓ as the energy barrier between the particles is dominated by the centrifugal force. The difference between the LJ and the LJ/s potential can be observed when ℓ approaches the cutoff radius, r_c, from below. The change in r_m is more sudden as a function of g for the LJ/s potential, because the particles only interact in a short window of time as the particles pass one another, and increasing g decreases the length of this time interval. This has a more pronounced effect on the scattering angle, where we see that when g is small and ℓ is large, the LJ/s-particles only deflect each other slightly from their initial paths, as their window of interaction becomes very short. We observe the singularity where Θ → −∞, where particles go into mutual orbit for an arbitrarily large number of revolutions before separating.

The total cross sections ϕ⁽ⁿ⁾ for n = 1, …, 6 were calculated from the scattering angles, and some of them are given as functions of g in Figure 3. For the Lennard-Jones particles, an error was introduced by truncating the calculations at an upper bound for ℓ. Using the estimate given by Equation (24) in [5], this error was kept below machine precision by choosing the upper bound for ℓ large enough. A discretization error was also introduced, and will be assessed by its effect on the transport coefficients.

FIGURE 3

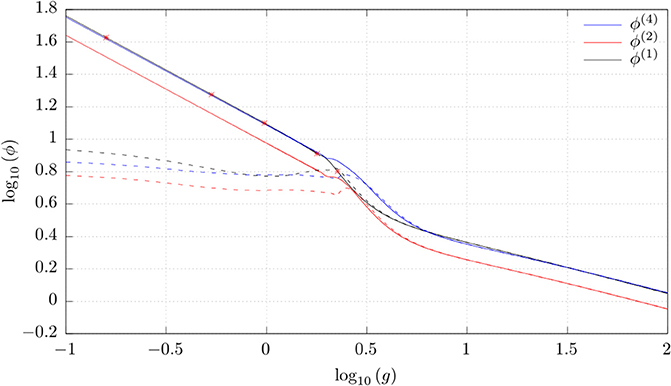
Figure 3. Samples of the total cross sections ϕ⁽ⁿ⁾ calculated for both Lennard-Jones (solid lines) and Lennard-Jones/spline (dashed lines) particles, as a function of the relative speed g. The stars are tabulated values of ϕ⁽¹⁾ for the LJ potential from [6].

At low velocities, the cross sections of the LJ particles are orders of magnitude greater than those of the LJ/s-particles, due to the infinite range of the LJ-potential. At high velocities, their cross sections converge because the repulsive part of the potential, which is the same for both types, dominates the dynamics in this regime. The cross sections fall off asymptotically as the inverse cube root of the relative speed, due to scattering events becoming more similar to hard-sphere collisions with an effective radius proportional to r_m. The distance of closest approach for head-on collisions is obtained by solving $g^2/4=V(r_m)$, assuming that r_m < r_s

$\begin{array}{ll}{r}_m={\left(\frac{1}{2}+\frac{1}{4}\sqrt{g^2+4}\right)}^{-1/6}\approx {\left(\frac{g}{4}\right)}^{-1/6}g>>1& (33)\end{array}$

so that the scattering cross section at high kinetic energy is approximately proportional to $r_m^2\propto g^{-1/3}$.

3.2. Transport Coefficients

Having obtained the cross sections from solving the scattering problem, the collision integrals Ω^(n,s) needed for calculating the transport coefficients may be obtained. The collision integrals suffer a truncation error from calculating to an upper bound g_s and a lower bound g_i for g, which is easily assessed by considering the asymptotic behavior of the cross sections. Since the cross sections fall off approximately as g^−1/3 at large g, and falls off even slower at small g, the truncation error is, approximately

$\begin{array}{l}{A}^{(n)}{T}^{-s-3/2}\left({\displaystyle {\int }_0^{g_i}}\text{d}g{e}^{-g^2/4T}{g}^{2s+3}+{\displaystyle {\int }_{g_{\text{s}}}^{\infty }}\text{d}g{e}^{-g^2/4T}{g}^{2s+8/3}\right)\end{array}$

where A⁽ⁿ⁾ is some n-dependent constant. This becomes very small for g_s >> 1 and g_i << 1, and was kept below machine precision by choosing g_s large enough and g_i small enough for the temperature range of interest. Having control over the truncation errors in the ℓ, g-plane, the transport coefficients still suffer from two additional sources of error—the error from discretizing the ℓ, g-plane, and the error from truncating the momentum-space polynomial expansion of the solution to the Boltzmann equation. To assess the former, the transport coefficients of the LJ/s fluid were calculated using different grid sizes, controlled by a size parameter N. For the latter, the coefficients were calculated with different truncation orders in momentum space. These different solutions were compared to the most accurate solution, to obtain upper bounds for the relative errors. This is summarized in Figure 4, where we see that the upper bound for the relative error due to discretization and truncation are both on the order 10⁻⁵ for the most accurate calculations that were carried out. The estimates are similar for the unmodified Lennard-Jones fluid.

FIGURE 4

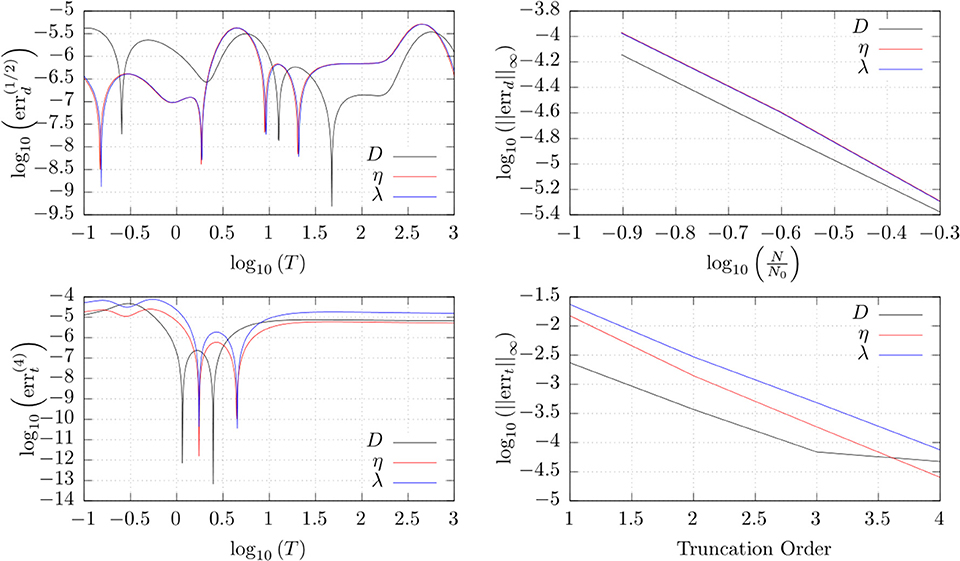
Figure 4. Discretization and truncation errors of the calculated transport coefficients of the Lennard-Jones/spline fluid. Top left: the estimated discretization error of a grid with half the number of points as the largest grid used. Top right: The variation of the inf-norm of the discretization error with the number of grid points, proportional to the size parameter N. Bottom left: the estimated truncation error by neglecting 5th order terms and higher (truncation order 4) in the Sonine polynomial expansions. Bottom right: The variation of the inf-norm of the truncation error with the truncation order.

The calculated values of η, λ, and nD of the LJ/s fluid are shown in Figure 5 as functions of the temperature. The lowest temperature considered here is 0.1, where the density has to be extremely low in order to stay away from the gas-liquid phase transition, see phase diagram in [1]. The highest temperature was chosen to be 1,000, to demonstrate the convergence to ordinary Lennard-Jones behavior at high temperatures. All transport coefficients appear to have two distinct power law regimes, separated by a sigmoidal region in the neighborhood of the critical temperature. This motivates a parameterization on the form

$\begin{array}{ll}\text{ln}(\psi )=a_0+a_1\text{ ln}(T)+\left(a_2+a_3\text{ ln}(T)\right)\text{ tanh}\left(\frac{\text{ln}(T)-a_4}{a_5}\right)& (34)\end{array}$

where ψ = η, λ, nD. The optimal parameters were found by a uniform search in the parameter space, applying Newton's method to approach the local optima. The best optimum found is assumed to be the global optimum. The relative errors of the optimal fitting are also given in Figure 5 as a function of temperature, and the numerical values of the optimal parameters for each of the transport coefficients are given in Table 1. The two asymptotical power law exponents are then a₁ ± a₃, while a₄ and a₅ are the position and width of the sigmoidal region. The remaining coefficients a₀ and a₂ are simply bias-correction coefficients adjusting the positions of the optimal curves along the ln (ψ)-axis.

FIGURE 5

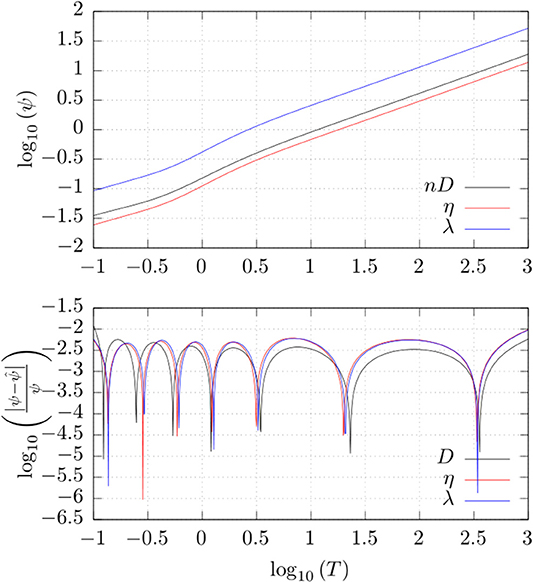
Figure 5. Logscale plot of transport coefficients against kinetic temperature. Bottom: Logscale plot of relative error in the optimized parameterization given by Equation (34).

TABLE 1

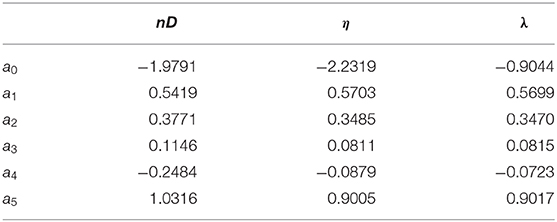
Table 1. Optimized numerical values of the parameters defined in Equation (34) for each of the transport coefficients.

We give also a comparison between the transport coefficients of the LJ/s fluid and those of the untruncated potential. As could be expected from the differences in the scattering cross sections at low velocities, the differences between the two fluids manifest themselves at low temperatures. At very low temperatures, the transport coefficients of the LJ/s fluid are significantly larger than those of the LJ fluid, around 50% at T = 0.1. In the Chapman-Enskog limit, that is, low density and low Knudsen number, the only mode of transport taken into account is that due to translation of particles, as opposed to transfer by collisions. Due to the truncated interaction range of the LJ/s particles, those particles generally move more freely at long range than LJ particles at the same temperature. At very low temperatures, the low kinetic energy of the average particles is more easily overcome by the infinite-ranged, though weak, attraction between LJ particles, while LJ/s particles are completely unaffected at distances greater than r_c, no matter how low the kinetic energy is. This leads to an overall more efficient transport of particles and their momenta in a given direction. At high temperatures, the differences between the two fluids are negligible.

4. Conclusions

We have provided an account of the properties of binary scattering events between LJ/s particles and their untruncated LJ counterparts. The main difference is that for LJ/s particles, the scattering angle is always zero when the impact parameter is greater than the cutoff radius of the potential, whereas the untruncated potential gives rise to a significant region of deflecting and oribiting collisions even at large impact parameters when the kinetic energy is small. The attractive force experienced by the LJ/s particles between the cutoff radius and the inflection point of the potential is stronger than that of the LJ particles, which leads to a slightly different scattering angle landscape in the region of orbital collisions. These differences lead to the LJ/s potential providing a much smaller scattering cross section than that provided by the untruncated potential, which again leads to significant differences in transport properties at low temperatures.

The shear viscosity η, the thermal conductivity λ, and the self-diffusion coefficient D have been calculated, by application of the Chapman-Enskog method, for temperatures between 0.1 and 1000 in LJ units, and a six-parameter equation (34) has been provided, with a worst-case accuracy of roughly 1% across the entire temperature range by using the coefficient values listed in Table 1. Such a model is useful for making quick calculations where an error of up to 1% is acceptable. It was observed that all transport coefficients appear to obey a power law as a function of the temperature at both high and low temperatures, with an intermediate transition region close to the critical temperature.

Comparisons were made between the LJ/s fluid and the untruncated LJ fluid, see Figure 6. At high temperatures, the transport properties are dominated by the repulsive part of the potential, which is identical for the two potentials. Therefore, the transport coefficients of the two fluids converge to the same values as the temperature is increased. At lower temperatures, the differences in the transport coefficients between the two fluids become significant. At temperatures below unity, the values diverge rapidly away from one another, with transport coefficients of the LJ/s being roughly 50% larger than those of the LJ fluid at T = 0.1, the lowest temperature considered in this work. When the LJ/s potential replaces the LJ potential for the sake of convenience in molecular dynamics simulations, it is important to be aware of these differences when considering subcritical temperatures. Further work will assess transport properties at increased densities, using the values obtained here in the low-density limit.

FIGURE 6

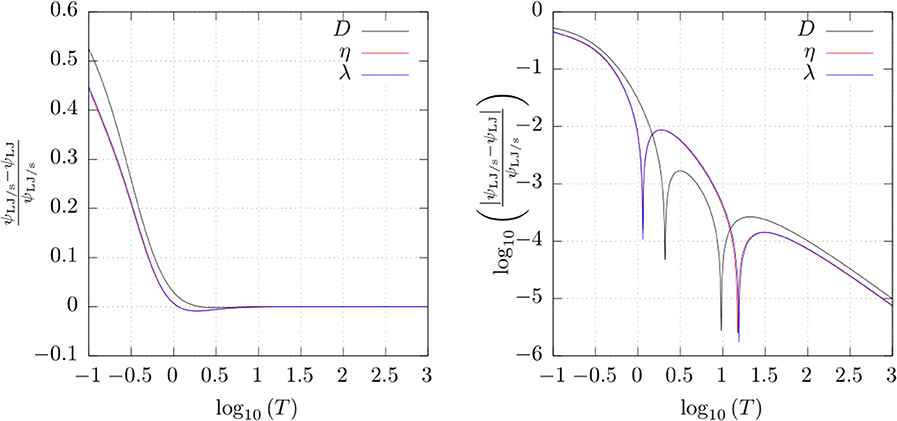
Figure 6. Comparison of the transport coefficients ψ = D, η, λ of the Lennard-Jones and Lennard-Jones/spline fluids at different temperatures T, where D is the self-diffusion coefficient, η is the shear viscosity, and λ is the thermal conductivity.

Data Availability Statement

The datasets generated for this study are available on request to the corresponding author.

Author Contributions

The author confirms being the sole contributor of this work and has approved it for publication.

Funding

Article processing charges are covered by the publishing fund of the Norwegian University of Science and Technology.

Conflict of Interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

The author is grateful to the Research Council of Norway through its Centers of Excellence funding scheme, project number 262644, PoreLab. Prof. Bjørn Hafskjold is thanked for fruitful discussions.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2020.00271/full#supplementary-material

References

1. Hafskjold B, Travis KP, Hass AB, Hammer M, Aasen A, Wilhelmsen Ø. Thermodynamic properties of the 3D Lennard-Jones/spline model. Mol Phys. (2019) 117:3754–69. doi: 10.1080/00268976.2019.1664780

CrossRef Full Text | Google Scholar

2. Holian BL, Evans DJ. Shear viscosities away from the melting line: a comparison of equilibrium and nonequilibrium molecular dynamics. J Chem Phys. (1983) 78:5147.

Google Scholar

3. Chapman S, Cowling T. The Mathematical Theory of Non-Uniform Gases. Cambridge, UK: Cambridge University Press (1952).

PubMed Abstract | Google Scholar

4. Hopp M, Gross J. Thermal conductivity of real substances from excess entropy scaling using PCP-SAFT. Ind Eng Chem Res. (2017) 56:4527–38. doi: 10.1021/acs.iecr.6b04289

CrossRef Full Text | Google Scholar

5. Kim S, Monroe C. High-accuracy calculations of sixteen collision integrals for Lennard-Jones (12-6) gases and their interpolation to parameterize neon, argon, and krypton. J Comp Phys. (2014) 273:358–73. doi: 10.1016/j.jcp.2014.05.018

CrossRef Full Text | Google Scholar

6. Khrapak SA. Accurate transport cross sections for the Lennard-Jones potential. Eur Phys J D. (2014) 68:276. doi: 10.1140/epjd/e2014-50449-y

CrossRef Full Text | Google Scholar

7. Takahasi H, Mori M. Double Exponential Formulas for Numerical Integration. Publ RIMS, Kyoto Univ. (1974).

Google Scholar

8. Tompson RV, Tipton EL, Loyalka SK. Chapman-Enskog solutions to arbitrary order in Sonine polynomials IV: summational expressions for the diffusion- and thermal conductivity-related bracket integrals. Eur J Mech B Fluids. (2009) 28:695–721. doi: 10.1016/j.euromechflu.2009.05.002

CrossRef Full Text | Google Scholar

9. Tompson RV, Tipton EL, Loyalka SK. Chapman-Enskog solutions to arbitrary order in Sonine polynomials V: summational expressions for the viscosity-related bracket integrals. Eur J Mech B Fluids. (2010) 29:153–79. doi: 10.1016/j.euromechflu.2009.10.002

CrossRef Full Text | Google Scholar

10. Guennebaud G, Jacob B. Eigen v3 (2010). Available online at: http://eigen.tuxfamily.org

11. Boost C++ Libraries. Available online at: http://www.boost.org/