Parallelized Monte Carlo Photon Transport Simulations for Arbitrary Multi-Angle Wide-Field Illumination in Optoacoustic Imaging

Optoacoustic imaging (OAI) or photoacoustic imaging can resolve the distribution of tissue chromophores and optical contrast agents deep inside tissue from the optoacoustic detection with multi-spectral illumination. The development of a fast and accurate modeling method for the photon transport in OAI is necessary to quantitatively evaluate the tissue optical parameters. This paper presents a parallelized Monte Carlo modeling method especially for OAI (MCOAI) to simulate photon transport in bio-tissues with arbitrary multi-angle wide-field illumination. The performance of the MCOAI method is verified by comparison with the graphics processing unit (GPU)-accelerated MCX method in the typical cases with the pencil beam and ring source illumination. The simulation results demonstrate the GPU-based MCOAI method has equivalent accuracy and significantly improved computation efficiency, compared to the MCX method. The simulations with cylindrical and hemispherical source illumination further illustrate that the MCOAI method can effectively implement three-dimensional photon transport simulation for typical illumination geometries of OAI systems. A cross-section of Digimouse is selected as a realistic heterogeneous phantom illuminated with six different light sources usually employed in OAI, in order to prove the necessity of establishing photon transport modeling in OAI for the quantitative visualization in deep tissues. The MCOAI method can provide a powerful tool to efficiently establish photon transport modeling with arbitrary illumination modes for OAI applications.

Introduction

Optoacoustic imaging (OAI) or photoacoustic imaging is a hybrid imaging modality that can provide multi-scale optical visualization with high depth-to-resolution ratio in biological tissues [1–6]. The distribution of the initial acoustic pressure or absorbed light energy density P₀, is generally reconstructed from optoacoustic signals detected by ultrasonic transducers in traditional OAI methods. The initial acoustic pressure P₀ is the product of optical absorption coefficient and light fluence in the irradiated region [7, 8]. Since light fluence in the tissue is attenuated along the penetration depth, the result of traditional OAI, i.e., the distribution of P₀, cannot directly reflect the optical properties of deep tissues, such as optical absorption coefficient [9, 10]. To accurately reveal the optical functional information of deep tissues, a precise photon transport modeling approach is necessary to be developed for offering assistance to quantitative OAI methods.

As the gold standard for predicting distribution of light fluence in the biological tissue, the Monte Carlo (MC) simulation with strong applicability is preferred for the precise modeling with multi-angle wide-field illuminations usually employed in OAI systems. MC simulation methods have been widely developed for optical imaging modalities [11–16]. The MCML and MCXYZ methods by Wang et al. have been used to study light propagation in multi-layered tissues [11, 12]. Several light source modes have been realized including the pencil beam and the finite beam with a fixed incident direction, as well as the isotropic beam. An accelerated MCML has been developed to reduce the computation time based on graphics processing unit (GPU) [13]. The MMC and GPU-based MCX methods by Fang et al. provide more light source modes, containing the slit beam, the planar beam, and the cone beam, with the option of sinusoidal modulated amplitude [14, 15]. For the multi-angle wide-field illumination modes usually employed in OAI systems, the conventional MC methods can not simultaneously and randomly generate the initial angles and positions of emitted photons using the GPU framework. Thus, the number of initial angles and positions is limited due to the low computation efficiency of the central processing unit (CPU) framework. The limited number of initial positions produces great challenges for efficient light transport modeling of arbitrary multi-angle wide-field illumination modes in OAI systems, such as ring, cylindrical and hemispherical sources for typical OAI systems.

In this work, we present a MC approach based on GPU to quickly and accurately establish light transport modeling for OAI systems with arbitrary multi-angle wide-field illuminations, termed as MCOAI. The incident angles and positions of emitted photons can be simultaneously and randomly generated from their pre-set probability distributions in MCOAI, allowing its effective performance for simulating arbitrary light sources with GPU acceleration. By comparing with the MCX method, the accuracy of MCOAI method is verified in the simulation with the pencil beam illumination. Comparison results using the ring source mode in optoacoustic tomography indicate that the MCOAI method performs higher efficiency and greater precision than the MCX method. The proposed MCOAI method can also effectively achieve three-dimensional (3D) light transport simulation for cylindrical and hemispherical illumination modes usually employed in OAI systems. Finally, several illumination modes are set up for a cross-section of Digimouse, illustrating the necessity of MCOAI for the quantitative OAI.

Method and Model

MCOAI Method

The MCOAI method can achieve simultaneous generation of both initial angles and positions of emitted photons by random numbers from pre-set probability distributions, or random selection from customized tables in the GPU framework. Owing to the sufficient number of initial angles and positions generated in the GPU framework, the MCOAI method can effectively conduct the precise photon transport modeling of arbitrary 3D media illuminated by arbitrary multi-angle wide-field light sources. In Cartesian coordinates, all objectives are uniformly divided into voxels. Optical properties of the media, such as absorption coefficient μ_a, scattering coefficient μ_s, scattering anisotropy factor g and refractive index n, are assigned to each voxel. The incident beam is simulated by emitting photon packets, whose trajectories are calculated in the media. Probability models and pseudorandom number generators are utilized to determine the initial position and direction, the path length between two adjacent scattering events, the scattering angle, transmission or reflection, as well as termination of the photon packet. As photons propagate from one voxel to the next, they deposit some energy (“weight”) into the voxel, depending on absorption coefficient μ_a of the voxel. Photons are tracked until terminated in Russian roulette or escaping from the media boundary. The deposited energy is digitally accumulated in a 3D matrix, and is normalized to output power at the end of the simulation. Figure 1 illustrates the flowchart of MCOAI for the multi-angle wide-field illumination mode.

FIGURE 1

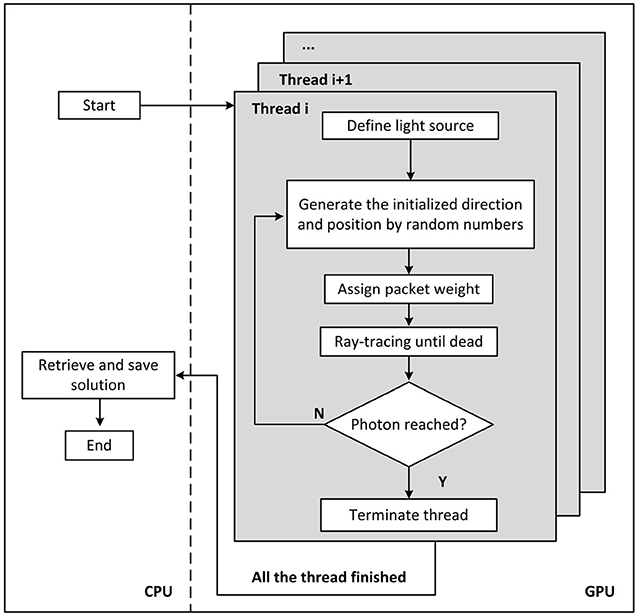
Figure 1. Diagram of the MCOAI simulation for photon transport. The multi-angle wide-field illumination mode is established through randomly generating initialized direction and position for each emitted photon.

In MCOAI, the random number is randomly generated in [0, 1]. For the ring source with the radius of r in the plane of z = z₀, a random number R₀ is used to obtain the longitude angle ϕ = 2πR₀ uniformly distributed in [0, 2π]. After an initialized direction ϕ is randomly generated, the initialized position r_s and the direction vector $\overrightarrow{v_s}$ can be expressed as

$\begin{array}{ll}\{\begin{array}{l}{r}_s=\left(r\cos (\text{2}\pi {\text{R}}_{\text{0}}),r\sin (\text{2}\pi {\text{R}}_{\text{0}}),z_{\text{0}}\right)\hfill \\ \overrightarrow{v_s}=\left(-\cos (\text{2}\pi {\text{R}}_{\text{0}}),-\sin (\text{2}\pi {\text{R}}_{\text{0}}),\text{0}\right)\hfill \end{array}.& (1)\end{array}$

For the cylindrical source with the radius of r and the height of H, a random number R₁ is employed to produce the longitude angle ϕ = 2πR₁, and another random number R₂ is used to compute the elevation position h = HR₂ randomly distributed in [0, H]. The initialized position r_s and the direction vector $\overrightarrow{v_s}$ can be expressed as

$\begin{array}{ll}\{\begin{array}{l}{r}_s=\left(r\cos (\text{2}\pi {\text{R}}_{\text{1}}),r\sin (\text{2}\pi {\text{R}}_{\text{1}}),H{R}_{\text{2}}\right)\hfill \\ \overrightarrow{v_s}=\left(-\cos (\text{2}\pi {\text{R}}_{\text{1}}),-\sin (\text{2}\pi {\text{R}}_{\text{1}}),\text{0}\right)\hfill \end{array}.& (2)\end{array}$

For the hemispherical source with the radius of r, two random numbers R₃ and R₄ are used to generate the longitude angle ϕ = 2πR₃ and latitude angle θ = πR₄/2, respectively. The initialized position r_s and direction vector $\overrightarrow{v_s}$ can be expressed as

$\begin{array}{ll}\{\begin{array}{l}{r}_s=(r\sin (\pi {\text{R}}_{\text{4}}/\text{2)}\cos (\text{2}\pi {\text{R}}_{\text{3}}),r\sin (\pi {\text{R}}_{\text{4}}\text{/2)}\sin (\text{2}\pi {\text{R}}_{\text{3}}),\\ r\cos (\pi {\text{R}}_{\text{4}}/2))\\ \overrightarrow{v_s}=(-\sin (\pi {\text{R}}_{\text{4}}/2)\cos (\text{2}\pi {\text{R}}_{\text{3}}),-\sin (\pi {\text{R}}_{\text{4}}/2)\sin (\text{2}\pi {\text{R}}_{\text{3}}),\\ -\cos (\pi {\text{R}}_{\text{4}}/2))\end{array}& (3)\end{array}$

For other types of source mode, the initial direction and position of emitted photon can be customized aforehand, and then the random extraction is adopted to randomly obtain these parameters based on the probability distributions. For light source models with uneven light intensity distribution, packet weights at different initialized positions can be prepared beforehand. The packet weight of emitted photon at a certain initialized position r_s is W(r_s), depending on the light intensity at the position r_s.

Simulation Set-Up

A total of 10⁸ photons are launched in the simulation of the proposed MCOAI method. One hundred and twenty-eight threads are set for parallel calculation. Four simulated samples are employed to validate the performance of the MCOAI method. The optical properties of the samples are set as the representative values in the optical window [16]. The MCOAI and MCX methods are run on the same computer with an NVIDIA GTX 750 GPU with 64 GB memory.

1) Sample 1: A homogeneous cube: A cubic domain of 60 mm × 60 mm × 60 mm is simulated shown in Figure 2. The volume is from −3 to +3 cm in x and y axis, and from 0 to 6 cm in z axis, with the number of grids in each axis of 60. The pencil beam is located at r_s = (30,30,0) with an incident direction vector $\overrightarrow{v_s}$ = (0,0,1); the medium is homogeneous with the absorption coefficient μ_a = 0.01 mm⁻¹, the scattering coefficient μ_s = 10 mm⁻¹, the refractive index n = 1.37 and the anisotropy g = 0.9.

2) Sample 2: A homogeneous cylinder: A cylinder sample with the center located at (6, 6, 8) mm has a radius of 5 mm and a height of 6 mm. The voxel size is 50 μm × 50 μm × 50 μm to build the accurate curved boundary. The optical properties for the cylinder are μ_a = 0.1 mm⁻¹, μ_s = 10 mm⁻¹, n = 1.37 and g = 0.9. A ring source with the radius of 5 mm is located at the plane of z = 8 mm, shown in Figure 3A. Figure 4A illustrates a 3D cylindrical illumination distributed around the cylinder boundary.

3) Sample 3: A homogeneous hemisphere: A hemisphere sample centered at (6, 6, 6) mm has a radius of 5 mm. The voxel size and optical properties of the hemisphere are the same as those of the Sample 2. Figure 4C shows a hemispherical illumination distributed around the hemisphere surface.

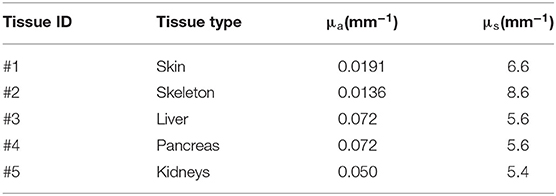
4) Sample 4: Cross-section of Digimouse: A cross-section of the widely-used Digimouse atlas has been chosen as a more realistic tissue sample. g = 0.9 and n = 1.37 are set to be homogeneous in the sample. μ_a and μ_s of the sample are shown in Table 1. Several types of light sources are simulated, including the finite-width light-sheet illumination from one side (left, right, top, or bottom) and four sides, as well as ring light-sheet illumination.

FIGURE 2

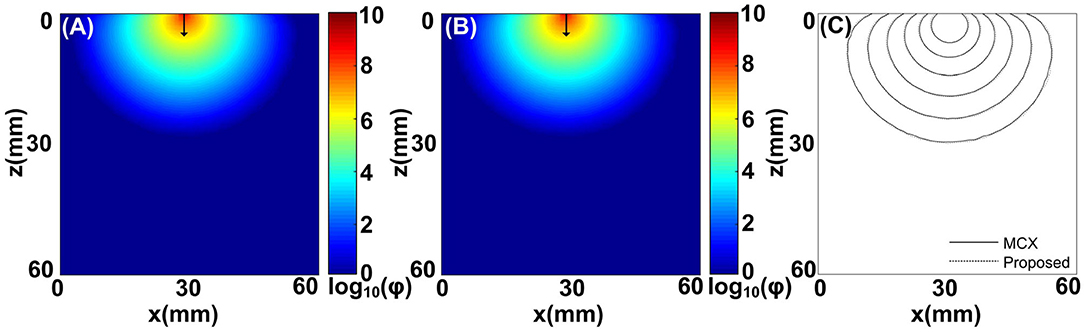
Figure 2. Comparisons between the MCOAI and MCX methods using the pencil beam to illuminate a cube (Sample 1): (A) the fluence map along the plane of y = 30 mm from the MCOAI result, (B) the fluence map along the plane of y = 30 mm from the MCX result, and (C) the fluence contours with 10 dB spacing along the plane of y = 30 mm. ϕ is the light fluence.

FIGURE 3

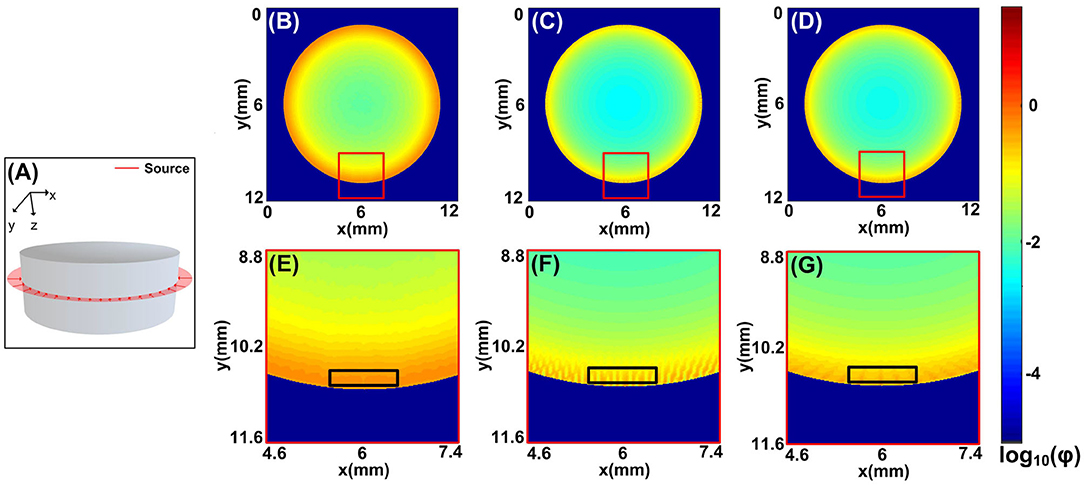
Figure 3. Comparisons between the MCOAI and MCX methods using the ring source to illuminate the cylinder sample (Sample 2): (A) the ring source located at the plane of z = 8 mm, (B) the fluence map at the plane of z = 8 mm from the MCOAI result, (C) the fluence map at the plane of z = 8 mm from the MCX result of 360 sources, (D) the fluence map at the plane of z = 8 mm from the MCX result of 720 sources, (E–G) the enlarged details of the fluence map in (B–D). ϕ is the light fluence.

FIGURE 4

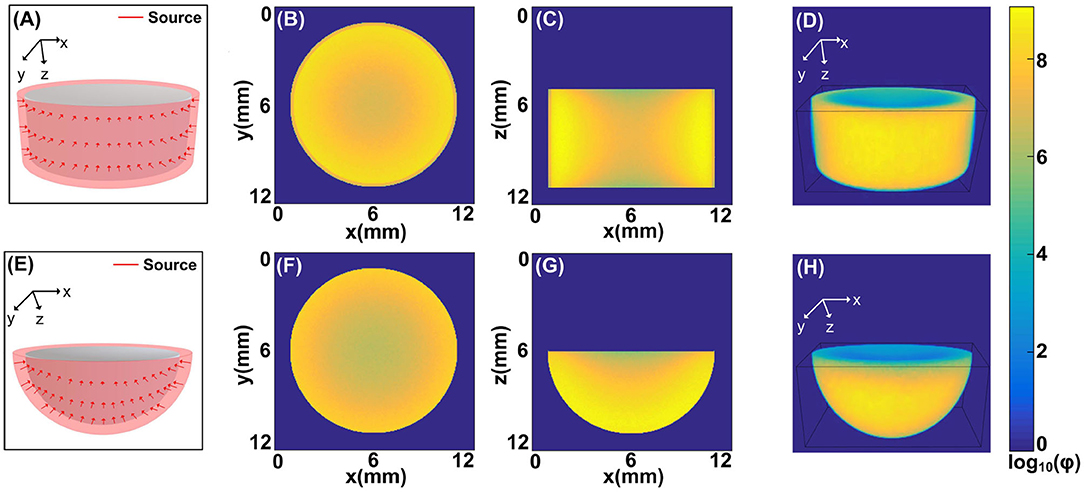
Figure 4. The illumination modes achieved by the MCOAI method: (A) the cylindrical source mode to illuminate the cylinder sample (Sample 2), (B) the fluence map at the plane of z = 9 mm from the MCOAI result, (C) the fluence map at the plane of y = 6 mm from the MCOAI result, and (D) the corresponding 3D view of the fluence map; (E) the hemispherical source mode to illuminate the hemisphere sample (Sample 3), (F) the fluence map at the plane of z = 6 mm from the MCOAI result, (G) the fluence map at the plane of y = 6 mm from the MCOAI result, and (H) the corresponding 3D view of the fluence map.

TABLE 1

Table 1. Optical properties of Sample 4.

Results and Discussion

To evaluate the accuracy of the MCOAI method, a comparison with the MCX method is implemented using the pencil beam to illuminate Sample 1. The fluence maps at the plane of y = 30 mm from the MCOAI and MCX results are presented in Figures 2A,B, respectively. The fluence contours with 10 dB spacing are also displayed in Figure 2C. The MCOAI result matches well with the MCX result in both fluence maps and contours, presenting the accurate performance of the MCOAI method. To quantitatively assess the accuracy of MCOAI result in Figure 2, the root mean square error (RMSE) has been calculated to show the difference between the MCOAI result and the MCX result. The RMSE is defined as

$\begin{array}{ll}\text{RMSE}=\sqrt{{\displaystyle \sum _{n=1}^N}{(r_{\text{MCX}}(n)-r_{\text{MCOAI}}(n))}^2/N},& (4)\end{array}$

where N is the total number of the image pixels, r_MCX(n) and r_MCOAI(n) are the values of fluence maps at the nth pixel in the MCX result and MCOAI result, respectively. The RMSE value between Figures 2A,B is 0.0008, indicating high consistency of the MCOAI result and the MCX result.

To demonstrate the fast and accurate modeling of the MCOAI method for the multi-angle wide-field illumination mode, a cylindrical sample (Sample 2) in Figure 3A has been chosen, with a ring source illumination usually employed in OAI. The calculation time of the MCOAI and MCX methods is illustrated in Table 2. The run time of MCOAI is 1.7 min. In the MCX method, amounts of pencil beam sources are set at the assigned positions around the cylinder boundary. The MCX simulations with 360 and 720 pencil beam sources (10⁸ photons for each beam) to form the ring illumination take the calculation time of 40 and 80 min, respectively. A total of 10⁸ photons are launched for the proposed MCOAI method. For each emitted photon, the initial angle and position are randomly generated. Thus, a total of 10⁸ initial angles and positions are randomly generated. With the sufficient number of photons (or the number of randomly generated initial angles and positions) and GPU acceleration, the computation time of the proposed MCOAI method is much faster than the MCX method.

TABLE 2

Table 2. Calculation time of the MCOAI and MCX methods.

The fluence maps at the plane of z = 3 mm from the MCOAI and MCX results are shown in Figures 3B–D. The zoom-in images at the curved boundary are, respectively, illustrated in Figures 3E–G. Although the distributions of fluence maps by the three MC simulations are generally similar in Figures 3B–D, the detailed image of fluence at the boundary in Figure 3E is obviously smoother and more authentic than the images in Figures 3F,G. Since 10⁸ photon packets are emitted at random initialized positions along the ring shape in the MCOAI method, the finite number of initialized positions set in the MCX method is much less than the number in the MCOAI method, resulting in the uneven fluence distributions at the boundary in the MCX results. The comparison results of the focused light illumination in Figure S1 are consistent with the results of the ring source in Figure 3. The standard deviation (SD) has been calculated to analyze the regional uniformity of the MCOAI and MCX results indicated by the black squares in Figures 3E–G. The SD is defined as

$\begin{array}{ll}\text{SD}(r)=\sqrt{{\displaystyle \sum _{n=1}^N}{(r(n)-r_{\text{mean}})}^2/N},& (5)\end{array}$

where r(n) is the value of fluence map at the nth pixel and r_mean is the mean value in the black square. The SD values of the MCOAI result, the MCX result of 360 sources and the MCX result of 720 sources are 0.0142, 0.0828, and 0.0520, respectively. The lowest SD value of the MCOAI result indicates the highest uniformity. The higher fidelity and efficiency of the MCOAI method can be attributed to introducing the random generation approach for the incident angle and position of each emitted photon into the parallel computing framework. Therefore, MCOAI method is more appropriate to accurately and quickly establish multi-angle wide-field illumination modes for optoacoustic tomography.

Furthermore, two typical 3D source modes (Figures 4A,E) usually existed in OAI are illustrated by MCOAI method. For the cylindrical illumination mode, the fluence maps at the planes of z = 9 mm, y = 6 mm and 3D view are presented in Figures 4B–D. For the hemispherical illumination mode, the fluence maps at the planes of z = 6 mm, y = 6 mm and 3D view are displayed in Figures 4F–H. The boundary and interior distributions of fluence maps in two homogeneous media are smooth and authentic owing to the sufficient incident positions generated randomly. The results demonstrate the light transport modeling in 3D simulation with multi-angle wide-field illumination modes can be efficiently and accurately established by the proposed MCOAI method.

This MCOAI approach is further used to simulate various light illumination modes on a cross-section of Digimouse (Sample 4) shown in Figure 5. The optoacoustic tomography technology has been widely employed for the whole-body small-animal imaging by integrating lots of cross-section images. The cross-section of Digimouse containing several main organs listed in Table 1 is selected.

FIGURE 5

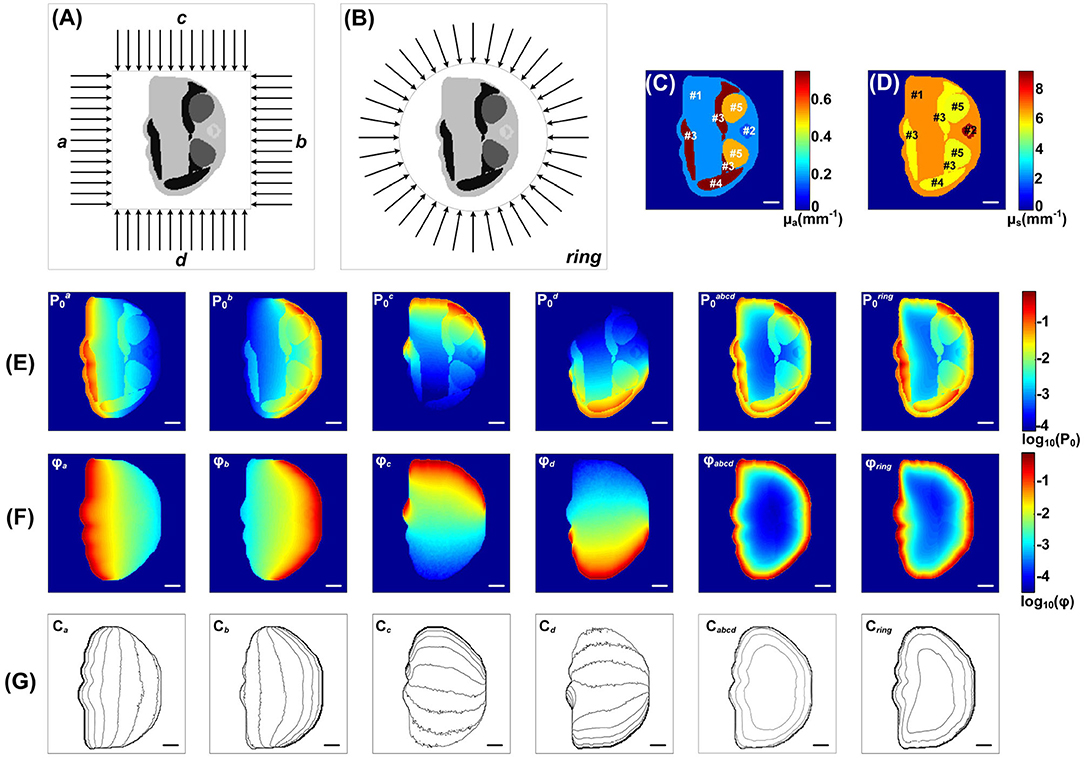
Figure 5. Simulation of the Sample 4 under different light illumination modes by the MCOAI method: (A) finite-width light-sheet illumination from left (a), right (b), top (c), and bottom (d) side, as well as four sides (abcd); (B) ring light-sheet illumination; (C) pseudo-color image of the absorption coefficient μ_a; (D) pseudo-color image of the scattering coefficient μ_s; (E) images of initial acoustic pressure P₀ under the finite-width light-sheet illumination from each side as well as four sides, and under the ring light-sheet illumination; (F) images of fluence ϕ under the finite-width light-sheet illumination from each side as well as four sides, and under the ring light-sheet illumination; (G) the corresponding fluence contours (with 10 dB spacing). Scale bar, 2 mm.

The MCOAI method was further utilized to illustrate the necessity for quantitatively evaluating functional information of biological tissue from OAI results. Figures 5C,D present the grayscale images of μ_a and μ_s of Sample 4, indicating the heterogeneity in different organs. Figure 5E shows the images of initial acoustic pressure P of Sample 4 using six different illumination modes. As displayed in the first four columns of Figure 5E using one-sided illumination, the intensity distribution of targets and background in the P images plummet when moving away the light source. In the last two columns of Figure 5E, due to the illumination modes are both full-angle wide-field, the P images are closer to the μ_a images while still presenting obvious differences. The results show the P image cannot directly reflect accurate quantitative distributions of μ_a in the sample, affected by the light attenuation along tissue depth. The fluence maps under these six different illumination modes are shown in Figure 5F, and the contours with 10 dB spacing are also displayed in Figure 5G. The light fluence ϕ in deep tissues is attenuated along the penetration depth, thus the fluence distributions in the region near the light source are higher than those in the region far from the light source. Under the finite-width light-sheet illumination modes only from one side, the heterogeneous distribution of ϕ is extremely evident. Under the four-sided light-sheet and ring light-sheet illumination modes, the Sample 4 receives full-angle wide-field irradiation, the fluence maps ϕ are attenuated from boundary to center. The results demonstrate the MCOAI method should be utilized to provide the fluence distribution of ϕ, in order to quantitatively recover the distribution of optical properties.

Conclusion

To quantitatively evaluate the optical properties of the biological tissues, it becomes essential to develop an efficient and precise photon transport modeling method for multi-angle wide-field illumination modes usually employed in OAI systems. In this work, we present the MCOAI method to randomly generate the incident angles and positions of emitted photons based on parallel computing framework for efficiently simulating arbitrary wide-field light sources. The MCOAI method can offer the same accuracy in the simulation using pencil beam as the MCX method. However, the MCOAI method for the multi-angle wide-field light sources, such as the ring source, is capable of providing more accurate and authentic distributions of light fluence in a few tenths of the time, compared to the MCX method. The GPU framework has been utilized in both the MCX method and the MCOAI method for acceleration. For the pencil beam and planar beam in the MCX method, the initial angles and positions of emitted photons are generated in the GPU framework. However, for the multi-angle wide-field illumination modes usually employed in OAI systems, the MCX method can not simultaneously and randomly generate the initial angles and positions of emitted photons in the GPU framework. The proposed MCOAI method can achieve simultaneous generation of both initial angles and positions of emitted photons by random numbers in the GPU framework, greatly reducing the running time. If the optical properties of samples at the selected wavelength in visible or near-infrared spectrum can be determined, the light transport modeling at any selected wavelength can be achieved by the proposed MCOAI method. The proposed method has been demonstrated with typical illumination modes and uniform light intensity, which can be explored on user-defined illumination modes and uneven light intensity for further study. The MCOAI method is able to precisely conduct the light transport modeling for all typical OAI systems, having great potential of contributing to the further investigation of quantitative OAI methods. In this work, the MCOAI method focuses on providing an accurate light transport simulation for the forward modeling in quantitative OAI, not involving the inverse problems. The MCOAI method is designed to be an open source for user-friendly employment.

Data Availability Statement

Publicly available datasets were analyzed in this study. The data of this article will be made available by the authors to any qualified researcher.

Author Contributions

JL and FG guided the work. TL did the simulation. TC, SM, SL, and XX gave the guide for analysis. JL and TL wrote the manuscript. All authors contributed to the article and approved the submitted version.

Funding

This work was supported by the grants from the National Natural Science Foundation of China (Grant Nos. 81771880, 81401453, 81671728, 81871393, and 81971656) and Tianjin Municipal Government of China (19JCQNJC12800).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2020.00283/full#supplementary-material

References

1. Wang LV, Yao J. A practical guide to photoacoustic tomography in the life sciences. Nat Methods. (2016) 13:627–38. doi: 10.1038/nmeth.3925

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Liu Y, Nie L, Chen X. Photoacoustic molecular imaging: from multiscale biomedical applications towards early-stage theranostics. Trends Biotechnol. (2016) 34:420–33. doi: 10.1016/j.tibtech.2016.02.001

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Zhou Y, Yao J, Wang LV. Tutorial on photoacoustic tomography. J Biomed Opt. (2016) 21:061007. doi: 10.1117/1.JBO.21.6.061007

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Wang LV. Multiscale photoacoustic microscopy and computed tomography. Nat Photonics. (2009) 3:503–9. doi: 10.1038/nphoton.2009.157

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Lu T, Wang Y, Zhang S, Li J. Photoacoustic mesoscopy:pushing toward the depth limit in the high-resolution optical imaging for biomedical applications and clinical potentials. Instrumentation. (2016) 3:29–42.

Google Scholar

6. Taruttis A, Ntziachristos V. Advances in real-time multispectral optoacoustic imaging and its applications. Nat Photonics. (2015) 9:219–27. doi: 10.1038/nphoton.2015.29

CrossRef Full Text | Google Scholar

7. Yuan Z, Jiang H. Quantitative photoacoustic tomography. Philos Trans A Math Phys Eng Sci. (2009) 367:3043–54. doi: 10.1098/rsta.2009.0083

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Cox B, Laufer JG, Arridge SR, Beard PC. Quantitative spectroscopic photoacoustic imaging: a review. J Biomed Opt. (2012) 17:061202. doi: 10.1117/1.JBO.17.6.061202

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Wang Y, He J, Li J, Lu T, Li Y, Ma W, et al. Toward whole-body quantitative photoacoustic tomography of small-animals with multi-angle light-sheet illuminations. Biomed Opt Express. (2017) 8:3778–95. doi: 10.1364/BOE.8.003778

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Zemp RJ. Quantitative photoacoustic tomography with multiple optical sources. Appl Opt. (2010) 49:3566–72. doi: 10.1364/AO.49.003566

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Wang LV, Jacques SL, Zheng L. MCML-Monte Carlo modeling of light transport in multi-layered tissues. Comput Methods Programs Biomed. (1995) 47:131–46. doi: 10.1016/0169-2607(95)01640-F

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Jacques SL. Coupling 3D Monte Carlo light transport in optically heterogeneous tissues to photoacoustic signal generation. Photoacoustics. (2014) 2:137–42. doi: 10.1016/j.pacs.2014.09.001

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Alerstam E, Svensson T, Andersson-Engels S. CUDAMCML: User Manual and Implementation Notes. Sweden: Department of Physics, Lund University (2009). p. 1–33.

Google Scholar

14. Fang Q. Mesh-based Monte Carlo method using fast ray-tracing in Plücker coordinates. Biomed Opt Express. (2010) 1:165–75. doi: 10.1364/BOE.1.000165

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Fang Q, Boas DA. Monte Carlo simulation of photon migration in 3D turbid media accelerated by graphics processing units. Opt Express. (2009) 17:20178–90. doi: 10.1364/OE.17.020178

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Hong G, Antaris AL, Dai H. Near-infrared fluorophores for biomedical imaging. Nat Biomed Eng. (2017) 1:1–22. doi: 10.1038/s41551-016-0010

CrossRef Full Text | Google Scholar