One-Step Calibration of AFM in Liquid

Introduction

Force measurements using atomic force microscopy (AFM) are becoming a standard and robust method to probe the mechanical properties of living cells, protein unfolding, and receptor-ligand bonds [1]. The first steps before any force measurement require the calibration of the spring constant of the cantilever (k) and the inverse of the optical lever sensitivity (InvOLS) and are crucial for accurate quantification of the measured and applied forces. Importantly, in biological applications, measurements are commonly carried out in liquid and require determination of the InvOLS in a liquid environment just before experiments.

The most established approach for AFM calibration currently consists of acquiring force-distance curves on a hard substrate and determining the slope of the contact part (OLS) or its inverse (invOLS, in units of nm/V). The spring constant is then calculated using the thermal method, acquiring the thermal noise spectrum of the cantilever deflection (d) of the fundamental mode of oscillation in liquid and invoking the equipartition theorem [2]

$\begin{array}{ll}\frac{1}{2}{k}_{B}T=\frac{1}{2}{k}_1\langle d^2\rangle & (1)\end{array}$

Where k_B is the Boltzmann constant and T, the absolute temperature. k₁ is the spring constant of the first, or fundamental, oscillation mode of the cantilever, in turn, related to the spring constant of the cantilever by a correction factor β = k/k₁, β = 0.971, for a rectangular cantilever [3]. The actual value of the mean square deflection of the fundamental mode (< d²>) is commonly calculated analytically, from the fit to the power spectral density (PSD) of the thermal fluctuations of the simple harmonic oscillator (SHO) or a related model, like the one developed by Pirzer and Huger for cantilevers in liquid [4–6].

Calibration of the spring constant has drawn most of the attention in the past, and much effort has been dedicated to developing different calibration methods [7–12]. One of the most common methods is the Sader method, which does not require the acquisition of a force-distance curve on a hard surface but only the plan view dimensions of a cantilever and the resonance frequency (f_R = ω_R/2π) and quality factor (Q) of the first flexural mode. Knowing these parameters allows us to determine k from

$\begin{array}{ll}k=0.1906\rho b^{2}LQ{\Gamma }_i({\omega }_R){\omega }_R^2& (2)\end{array}$

for rectangular shape cantilevers, being ρ is the density of the surrounding fluid, b and L are the width and length of the cantilever, respectively, and Γ_i(f _R), the imaginary part of the hydrodynamic function evaluated at the resonant frequency [9, 13]. The Sader method was originally developed for rectangular cantilevers and then extended to cantilevers of arbitrary shape [11]. This led to the idea of determining the spring constant of an uncalibrated cantilever using the parameters of a calibrated reference cantilever with the same geometry and dimensions. To reduce the uncertainty of the above equation, Sader et al. recently suggested using an averaged value of multiple reference cantilevers which evolved into a community-contributed approach. The global calibration initiative (GCI) was, thus, proposed by Sader et al. to standardize the calibration of AFM cantilevers using a virtual instrument consisting of an online database with parameters from reference cantilevers [14]. The GCI method takes advantage of the fact that, for any given cantilever type with the same plan view dimensions, a reference coefficient (A) can be defined to determine k from only the measured f _R and Q using

$\begin{array}{ll}k=AQ{f}_R^{1.3}& (3)\end{array}$

where the A-coefficient is determined from the community-driven average of multiple reference cantilevers, and is calculated as

$\begin{array}{ll}A=\frac{1}{N}{\sum }_{i=1}^N{A}_i=\frac{1}{N}{\sum }_{i=1}^N\frac{k_{\text{ref},\text{i}}}{Q_{\text{ref},\text{i}}{f}_{R,\text{ref},\text{i}}^{1.3}}& (4)\end{array}$

where k_ref, Q_ref, and f _R,ref, are the spring constant, quality factor, and resonance frequency of reference cantilevers uploaded by different users to the online database. The accuracy of this universal A-coefficient for a particular cantilever, i.e., of the calibration method, improves as the number of reference cantilevers uploaded by the community increases. In principle, both Sader and GCI methods are valid for cantilevers with high-Q, not the case for most cantilevers immersed in liquid as commonly used in AFM studies of biological systems. However, the Sader method has been also applied in liquid leading to satisfactory results [12].

Accurate calibration of the InvOLS is as much or even more critical than the calibration of the spring constant. However, little attention has been given to this parameter until recently. As mentioned before, the common calibration method of the InvOLS consists of obtaining force-distance curves (calibration curves) on a rigid substrate and calculating the resulting slope of the contact region. This method presents several drawbacks. First, it requires a rigid surface, which is not always accessible, for example, with tissue or confluent cell monolayers. Second, it requires a high contact force to obtain a linear deflection-distance relation free of artifacts associated to possible long-range forces, tip contamination, etc. Such a high contact force may damage the tip, especially if it is functionalized with biomolecules, as used in receptor-ligand or (un)folding measurements. Third, the possible uncertainty in the InvOLS propagates as 2-fold when using the thermal method to calibrate k. Thus, uncertainties associated with this method may be the main reason for inaccurate and variable force determination in AFM experiments, even for the same experimental system.

Higgins and coworkers proposed a non-contact approach to determine the InvOLS assuming that the spring constant remains unchanged in air and liquid [15]. The approach consists in calibrating the spring constant in air with the Sader method and calibrating the InvOLS from the thermal spectrum. It is important to note that the InvOLS obtained from the thermal of a freely vibrating cantilever (InvOLS_free) is not the same as that obtained from the contact-based approach. To convert from the free to end loaded (contact-based) InvOLS, a correction factor is required: $\chi =\frac{\text{InvOL}{\text{S}}_{\text{free}}}{\text{InvOLS}}$. For rectangular cantilevers, χ = 1.09 [11]. In their approach, the authors used the equipartition theorem (Equation 1) with d = d_V·InvOLS_free (being d_V the deflection in Volts) and reported accuracies of ~10%, as compared to the values obtained with the classical contact approach [15]. More recently, a series of experiments of the very same hydrogels and living cells was carried out across different laboratories in Europe, which aimed to establish a standardized approach for mechanical measurements. The authors used cantilevers with pre-calibrated spring constant, in this case using a vibrometer, then calibrating the InvOLS from the thermal spectrum with high accuracy. This standardized nanomechanical AFM procedure (SNAP) successfully reduced the variability in Young's modulus of the soft samples to ~1%, which is much lower than using the established contact approach, as it is more precise [16]. While the SNAP approach is advantageous, the possibility of using vibrometers to determine the spring constant of the cantilever is tedious and not available to most AFM laboratories. Thus, a method to calibrate both k and the InvOLS using standard AFM instrumentation in liquid would be a clear advance toward ease of use and applicability of AFM quantitative measurements. To reach this goal, given the shown precision and accuracy of using the thermal in liquid to calibrate the InvOLS, the main requirement would be to provide a robust method to calibrate the spring constant in liquid, thus on PSD featuring low-Q factor (~1), without knowledge of the InvOLS. While some AFM manufacturers already propose this one-step calibration approach using Sader's method, it requires knowledge of the cantilever geometry and dimensions. Thus, the GCI in liquid may be a more appropriate approach but it has not been assessed so far.

Here, we propose and validate two approaches to calibrate k and, then, the InvOLS from the same thermal spectrum in a liquid environment. The proposed one-step calibration approaches are based on the determination of the spring constant using the conventional Sader method and the recent GCI but in liquid. We also assess the influence of the PSD fitting model by comparing the SHO and Pirzer models to obtain the PSD parameters in liquid. Our results show that using the SHO model, the Sader, and GCI approach in liquid lead to similar calibration parameters, while the GCI appears to be more accurate and less prone to systematic errors.

Methods

Cantilever Characterization

To validate the two methods, we chose two types of rectangular cantilevers (Olympus AC10 and AC40) with similar spring constant ~0.1 N/m but different resonance frequency (~40 and ~500 kHz, in liquid) representing common cantilevers used in conventional and high-speed AFM [17]. A total of 20 AC10 and 25 AC40 cantilevers were used. The plan view dimensions (length and width) of at least 5 different cantilevers were determined from scanning electron microscopy images. Electron microscopy imaging was carried out on a JEOL 5910 (Japan) and a Teneo VS (FEI, The Netherlands) running in a high vacuum, at 10 kV and using an ETD secondary electrons detector.

Acquisition of Thermal Fluctuation Spectra

The thermal power spectral density of each cantilever was acquired away from any surface (>300 μm [18]) in air and liquid on an HS-AFM (RIBM, Japan), featuring an optical detection system of 20 MHz-bandwidth (MPR-1 AFM, Graviton, Japan) and a high-speed acquisition board system (PXI; National Instruments) at sampling rates up to 20 MS/s, using a custom made software developed in LabView. AC10 spectra in liquid and AC40 spectra in air and in liquid were acquired using a low-pass filter at 3 MHz.

Thermal Spectrum Analysis

The electronic 1/f noise was removed from the PSD by subtracting a linear fit of the data at f <10 kHz for AC10 and f <3 kHz for AC40 to minimize possible artifacts in the fit parameters [12, 19]. The range for fitting the PSD models was determined automatically by detecting the frequency at the resonance peak (f_max) within a predefined range expected for each cantilever type. We tested three different ranges of frequencies to fit the models [f_max/m, f_max·m] with m = 1.5, 2, and 3. After 1/f removal and range selection, the PSD was used to fit the damped SHO model

$\begin{array}{ll}{S}_{\text{SHO}}(f)=A_{\text{white}}^2+\frac{B^2{f}_R^4}{Q^2}{\left[{(f^2-f_R^2)}^2+\frac{f^2{f}_R^2}{Q^2}\right]}^{-1}& (5)\end{array}$

and the model proposed by Pirzer and Hugel [4], derived from the simple harmonic oscillator assuming a Lorentzian response to describe low-Q cantilevers

$\begin{array}{ll}{S}_{\text{L}}(f)=A_{\text{white}}^2+\frac{B^2{f}_R^2}{{4Q}^2}{\left[{(f-f_R)}^2+\frac{f_R^2}{4Q^2}\right]}^{-1}& (6)\end{array}$

where B is the amplitude of the thermal noise and A_white is white noise. From the fit, we extracted the f _R, Q, and B for each cantilever, which was then used to determine k and the InvOLS.

Spring Constant Determination

The fit of the SHO to thermal spectrum in air allowed us to extract f _R and Q of each cantilever. The spring constant in air (k_air) was then determined with the Sader method (Equation 2) and with the GCI method (Equations 3 and 4) separately. To obtain the average A-coefficient of the GCI method in air, we used our collection of reference cantilevers. The resulting spring constant (k_air) calculated using the Sader method, was used as the reference for each cantilever.

The thermal spectrum in liquid was fitted with both SHO and Pirzer models to extract f _R and Q. Then, the spring constant in liquid (k_liq) of each cantilever was determined with the Sader method (Equation 2) and with the GCI method (Equation 3) separately. In the GCI method, the average A-coefficient in liquid was calculated as

$\begin{array}{ll}{A}_{\text{liq}}=\frac{1}{N}{\sum }_{i=1}^N\frac{k_{\text{air},i}}{Q_{\text{liq},i}{f}_{R,\text{liq},i}^{1.3}}& (7)\end{array}$

where k_air is the spring constant determined in air for each cantilever using Sader method, and Q_liq, and f _R,liq, are the quality factor and resonance frequency of the same cantilever, respectively, but from the fits to the PSD in liquid. To notice, as in the original work by Higgins and coworkers, Equation 7 assumes that the spring constant remains unchanged in air and in liquid [15].

InvOLS Determination

Integrating Equations 5 and 6 we obtain the mean squared deflection of the cantilever for the SHO model

$\begin{array}{ll}\langle {\text{d}}_{\text{SHO}}^2\rangle =\frac{\pi {\text{B}}_{\text{m}}^2{\text{f}}_{\text{R}}}{2\text{Q}}& (8)\end{array}$

and for the Pirzer model

$\begin{array}{ll}\langle d_{Pirzer}^2\rangle =\frac{B_{\text{m}}^2{f}_R}{2Q}\left[\frac{\pi }{2}+{tan}^{-1}(2Q)\right]& (9)\end{array}$

The end loaded InvOLS in liquid (InvOLS_liq) was determined by replacing B_m, the amplitude of the thermal noise in units of length, with B·InvOLS_free in Equations 8 and 9, and using the equipartition theorem (Equation 1), for the SHO model considering the correction factors χ and β described before

$\begin{array}{ll}\text{InvOL}{\text{S}}_{\text{liq}}=\sqrt{\frac{\beta }{{\chi }^2}\frac{k_{B}T}{k}\frac{2Q}{\pi B^2{f}_R}}& (10)\end{array}$

and for the Pirzer model

$\begin{array}{ll}\text{InvOL}{\text{S}}_{\text{liq}}=\sqrt{\frac{\beta }{{\chi }^2}\frac{k_{B}T}{k}\frac{2Q}{\left[\frac{\pi }{2}+{tan}^{-1}(2Q)\right]B^2{f}_R}}& (11)\end{array}$

Notice that Equations 10 and 11 coincide for Q>>1 but differ up to 40% for Q~1, as in the case of soft cantilevers in liquid. The actual correction factors χ and β depend on the shape of the cantilever, and different values have been reported [2, 3, 11, 20, 21]. In this work, we have assumed the general values for a rectangular cantilever (χ = 1.09 and β = 0.971). Correction factors due to the tilt angle to mount the cantilever or the spot size and position were not considered in this work [4, 16, 22, 23].

One-Step Calibration Approach

To summarize, the one-step calibration approaches assessed in this work involved the following substeps using either SHO or Pirzer models to fit the PSD and Sader or GCI for spring constant calibration:

1) Acquisition of the thermal PSD in liquid;

2) Fitting SHO or Pirzer model to the PSD in liquid to extract f _R, Q, and B;

3) Calculation of k in liquid using Sader (Equation 2) or GCI (Equations 3 and 7);

4) Calculation of InvOLS in liquid using k_liq from substep 3 on Equation 10 (SHO) or Equation 11 (Pirzer).

Thus, all the parameters in the above procedure are determined from the PSD in liquid.

Results and Discussion

Representative examples of PSD with the corresponding fitted models are shown in Figure 1. Subtraction of the typical 1/f noise present at low frequencies did not influence substantially (≲0.02% for f _R and ≲0.06% for Q, see the table with all fitted parameters in the Supplementary Material) the extraction of f _R and Q for the two types of cantilevers used. This is likely due to the relatively high resonance frequency of these cantilever types (~30 and ~°500 kHz, for AC10 and AC40, respectively), leading to a resonance peak not importantly distorted by 1/f noise. However, the correction may be important in liquid for other cantilevers with lower f _R and helps in the automatic detection of the first resonance peak. Both models (Pirzer and SHO) fitted well the PSD over the frequency range [f _R/2, 2f _R] used for this study (Figure 1). Using other ranges [f _R/1.5, 1.5f _R] and [f _R/3, 3f _R] resulted in similar results (≲0.03% for f _R and ≲0.06% for Q, see Supplementary Material). The average dimensions and values of extracted parameters from the SHO fit in air from all the cantilevers used in this work are summarized in Table 1. The deviations in length and width of the cantilevers presented negligible variability (~2%), well-below the variability found on the spring constant or InvOLS parameters, thus having a minor influence in the results. In the air, the standard deviation across cantilevers for f _R and Q was of ~10%, and for k_air it was of ~16% using either Sader or GCI methods. This suggests that the primary source of variability in k_air was the actual variability across cantilevers. To notice, we assume the value of k_air as accurate, as it has been validated before against vibrometer calibration [11, 14]. Thus, we use k_air as the actual spring constant and reference to compare the spring constants calculated from GCI and Sader methods in liquid. Since the collection of cantilevers to obtain the reference A-coefficient for the GCI method is the same as used for the Sader estimation of k_air of each cantilever, the average spring constant in air using the two methods led virtually to the same value. Importantly, the A-coefficient obtained from our collection of cantilevers is in excellent agreement with the currently reported universal A-coefficient in the GCI website for both cantilever types (https://sadermethod.org).

FIGURE 1

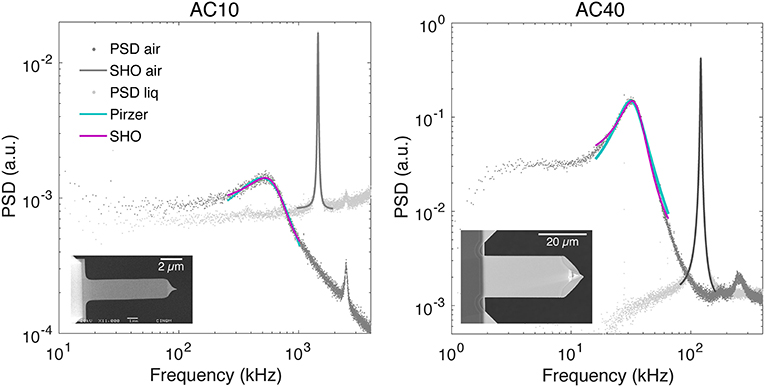
Figure 1. Representative examples of thermal spectra in air (light gray dots) and liquid (dark gray dots) with the corresponding fit of the SHO model in air (solid dark gray line with f _R = 1 453 kHz and Q = 56 for AC10, left, and f _R = 121 kHz and Q = 50 for AC40, right) and SHO model in liquid (solid magenta line, with f _R = 639 kHz, Q = 1.26 and χ² = 0.75 for AC10, left, and f _R = 34 kHz, Q = 2.1 and χ² = 5.8 for AC40, right) and the Pirzer model in liquid (solid cyan line, with f _R = 493 kHz, Q = 0.73 and χ² = 1.01 for AC10, left, and f _R = 31 kHz, Q = 1.8 and χ² = 8.2 for AC40, right). The insets show plan view electron micrographs of each cantilever type.

TABLE 1

Table 1. Summary of the cantilever parameters in air.

We applied the two proposed approaches (Sader and GCI) to calculate the AFM calibration parameters in liquid using both SHO and Pirzer models as described in section One-Step Calibration Approach. For each cantilever, we acquired the PSD in liquid, fitted the SHO, and Pirzer models to determine Q, f _R, and B and then calculate the spring constant in liquid (k_liq) using either Sader or GCI. Finally, the InvOLS_liq was calculated using the calculated k_liq in Equations 10 and 11, for SHO and Pirzer, respectively. To have a reference InvOLS_liq value, in the last step we used our reference k_air and the SHO parameters in liquid to obtain InvOLS_liq,_kair from Equation 10 (Table 2). This is the method originally proposed by Higgins et al. [15] and showed to lead to accurate results, close to the “standard” contact-based InvOLS_liq [15, 16]. The absolute values of both k_liq and InvOLS_liq using the different methods and PSD models are shown in Table 2. The absolute values of InvOLS_liq for all the individual cantilevers are shown in Figure 2 (left) vs. the corresponding reference values InvOLS_liq,_kair. Notice that all InvOLS values refer to liquid and only the PSD fitting model and/or the spring constant calibration approach changed.

TABLE 2

Table 2. Summary of the cantilever parameters in liquid.

FIGURE 2

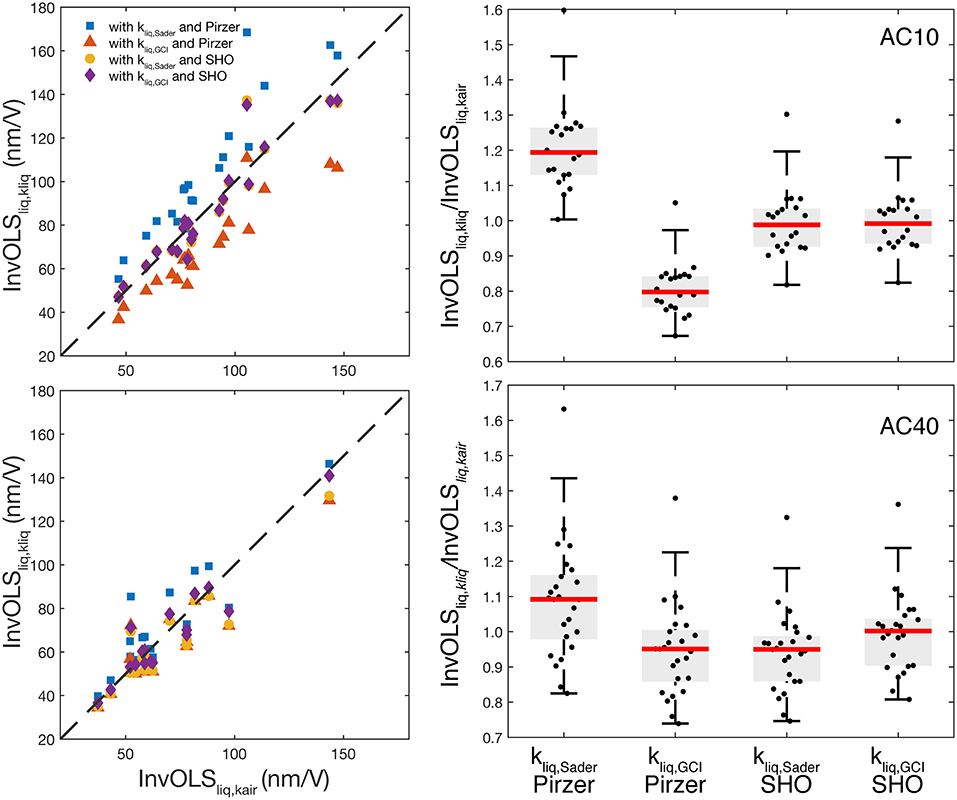
Figure 2. (Left) Scatter plot showing the individual InvOLS_liq values calculated using the different approaches and PSD models vs. the reference value InvOLS_liq,kair for AC10 (top), and AC40 (bottom). (Right) Boxplot of the InvOLS values in liquid normalized by the InvOLS in liquid using k_air, using either Sader and GCI calibration methods with either Pirzer and SHO models for AC10 (top) and AC40 (bottom). The red line is the median, the boxes show the 25th and 75th percentiles, and whiskers represent 2.7-times the standard deviation.

The standard deviation across cantilevers in k_liq using either method was ~20 and ~40% for AC10 and AC40, respectively, higher than that found in k_air (~15 and ~18%, respectively). This suggests possible uncertainties in the determination of f _R and Q in liquid as we address below. The standard deviation observed in our reference InvOLS_liq,_kair across cantilevers (~30% and ~70% for AC10 and AC40, respectively), was higher than that of k_air. This suggests other sources of variability added to the differences across cantilevers; likely the power of the laser source, the alignment of the laser spot on the cantilever, and/or the overall reflected light reaching the photodiode. Thus, this variability does not denote the low accuracy of the approach, but instead, indicates the effects of different experimental conditions.

It is important to assess the systematic uncertainties derived in the fitted parameters. The work of Sader et al. allowed us to determine the theoretical uncertainties in f _R, Q, and B using the SHO [5]. According to this work, standard deviation depends on the ratio between the white noise (A_w) and the amplitude of the thermal noise (B), as well as on the measurement duration (at least 1 s in our case), and the width of the fit window (we conservatively considered the range ± 1/2 f _R). Using the exact formulas for any Q and window width (SI in [5]), we obtained uncertainties of 5 and 20% for B, 5, and 20% for Q and 0.1 and 0.4% for f _R, for AC10 and AC40, respectively. After error propagation, we found that the relative contribution of the uncertainty in f _R was negligible both to determine k_liq and InvOLS_liq. Regarding the determination of k_liq, as expected, determination of the quality factor introduces the largest uncertainty. Since both Sader and GCI equations for k_liq (Equations 2 and 3) depend proportionally on Q, error propagation results in a corresponding uncertainty of ~5 and ~20% for AC10 and AC40, respectively, which adds to the variability across cantilevers. This results in a higher standard deviation of k_liq compared to k_air, as we observed. In the case of the InvOLS_liq, error propagation resulted in a relative contribution of the uncertainty in Q of ~20%, while uncertainties in B are the most important, with a relative contribution of ~80%. Thus, the corresponding overall uncertainty in InvOLS_liq was of ~6 and ~20% for AC10 and AC40, respectively, and also adds to the variability across cantilevers and experimental conditions. The above estimation of uncertainty is theoretical and other sources of error may influence the determination of the fitted parameters, such as proximity of the cantilever to the sample surface and experimental acoustic noise [24–26].

As shown in Figure 1, both SHO and Pirzer models fitted well to the PSD in liquid resulting in Q~1 in both cases. In the case of the PSD in air, SHO or Pirzer models lead to the same values of f _R and Q within 0.03 and 0.3%, respectively. In the case of soft cantilevers in liquid, i.e., with Q≲O (1), it has been suggested that the quality factor extracted from the SHO is only qualitative, as the equation is an approximation of the response for f ~f _R, valid for high Q [13]. The Pirzer model was proposed to better describe the frequency response of low-Q cantilevers. As shown in Table 2, the values of f _R and Q estimated by the Pirzer model were systematically lower than those estimated with the SHO (~60% for AC10 and ~20% for AC40). This considerable difference in both f _R and Q when using different models was observed for each cantilever, and it is inherent to the models. This brings into question what are the actual values of f _R and Q in liquid for these cantilevers and what is, thus, the contribution of the chosen PSD model in the estimation of the spring constant in liquid. The results reported in Table 3 allowed us to further assess this point.

TABLE 3

Table 3. Summary of the normalized cantilever parameters in liquid.

The first stage toward a one-step calibration is to evaluate the accuracy and precision in the determination of the spring constant in liquid (Tables 2, 3). Compared to the spring constant calibrated in air (k_air), the spring constant calculated with the Sader method in liquid (k_{liq, Sader}) was systematically lower using the Pirzer model (~50% for AC10 and 17% for AC40), while it was slightly higher using the SHO model (~4% for AC10 and ~17% for AC40). This suggests that in the chosen model, to fit the PSD is important and that Pirzer's model may underestimate the spring constant when using the Sader method in liquid. In contrast, using the GCI calibration in liquid provided average k_liq,GCI values varying from k_air between 4 and 8% when using Pirzer and between 3 and 5% when using the SHO and with a standard deviation between 15 and 25%, similar to that found in air. Therefore, in liquid, the GCI method seemed to be more accurate (≲8%) and more precise (≲25%) than the Sader method, findings similar to that reported using other methods (10–20%) [12]. The SHO model also seems to lead to more accurate results across approaches than Pirzer's, with values closer to k_air. Importantly, the GCI model appears to be less sensitive to the model chosen to fit the PSD, provided the same model is always applied, suggesting that GCI method is less prone to systematic uncertainties. Nevertheless, the results of the GCI approach should be taken cautiously because the collection of cantilevers to obtain the average A-coefficient was the same as the sample pool, which is addressed later in this article.

To determine the InvOLS from the PSD in liquid, we used the calibrated spring constants with Sader and GCI methods in liquid, using either SHO or Pirzer models (Equations 10 and 11). The results are shown in Table 3 and Figure 2, and after normalization with the reference InvOLS_liq,kair in Table 2 and Figure 2. As expected from the results in the spring constant calibration, using k_Sader,liq with Pirzer parameters, led to a deviation from InvOLS_liq,kair of ~20% for AC10 and ~9% for AC40, while with SHO parameters, the deviation (accuracy) was only of ~1 and 6%, respectively. Using k_GCI,liq with Pirzer parameters led to a difference of ~20% for AC10 and ~5% for AC40, while with SHO parameters, the difference was <1% for both cantilevers, remarkably smaller. Despite this, the accuracy in the determination of the InvOLS using the thermal spectrum was higher than the accuracy in the determination of k_liq, as has been suggested before [15, 16]. Thus, overall the use of the Pirzer model to determine f _R and Q seemed to introduce a systematic bias in the calibration of k_liq and InvOLS_liq: with spring constants in liquid 4% higher than k_air using the GCI method, but ~50% lower, using the Sader method, and variations up to ~20% but with the opposite trend in the InvOLS_liq. This was not the case with the SHO model. This suggests that, compared to Pirzer's, the SHO model described more accurately the response of low Q cantilevers, perhaps due to its simplicity. Importantly, since the systematic bias introduced using the Pirzer model may, in Equation 7, cancel out the GCI approach, as the associated uncertainty seems to be less important when applying this approach.

Taken together, our results show that using the GCI method with the SHO model to determine k_liq,GCI leads to a value closer to k_air (within 5%) showing the higher accuracy of the approach. They also show less dispersion (~20%), suggesting higher precision. Thus, using k_liq,GCI, and the SHO parameters to determine InvOLS_{liq, GCI} resulted in a value that was also more accurate (as k_liq,GCI is more accurate and more precise). This was reflected in Table 3, were the InvOLS_liq,CI using SHO was closer to InvOLS_liq,kair (within 1%) and less scattered (~10%) Thus, the most accurate one-step AFM calibration approach to determine k_liq and InvOLS_liq in liquid involves using the SHO model to estimate f _R, Q and B together with the GCI method.

As mentioned above, the GCI approach requires a collection of well-calibrated cantilevers that are used as a reference to determine the average A-coefficient (Equations 4 and 7 for air and liquid, respectively). As the number of reference calibrated cantilevers increases, the accuracy in A-coefficient improves. To evaluate the actual uncertainty and convergence of the average A-coefficient in liquid as a function of the number of reference cantilevers used, we applied a bootstrapping approach. Figure 3 shows 17 repetitions with each point representing the average A-coefficient calculated form N random reference cantilevers chosen without replacement from our collection of cantilevers. As a reference, we report the data for the A-coefficient in air using the same approach. In air, after ~10 cantilevers for AC10 and ~15 cantilevers for AC40, the average A-coefficient seemed to converge to the average value (solid blue line) of all the N cantilevers and the variability remained relatively constant. Similar results were obtained in liquid (results using SHO). In both cases, the relative spread of the values decreases as increasing N. It is important to note that the relative spreading was much lower in air than in liquid, suggesting that a larger number of reference cantilevers in liquid would be required to obtain comparable precision than in air.

FIGURE 3

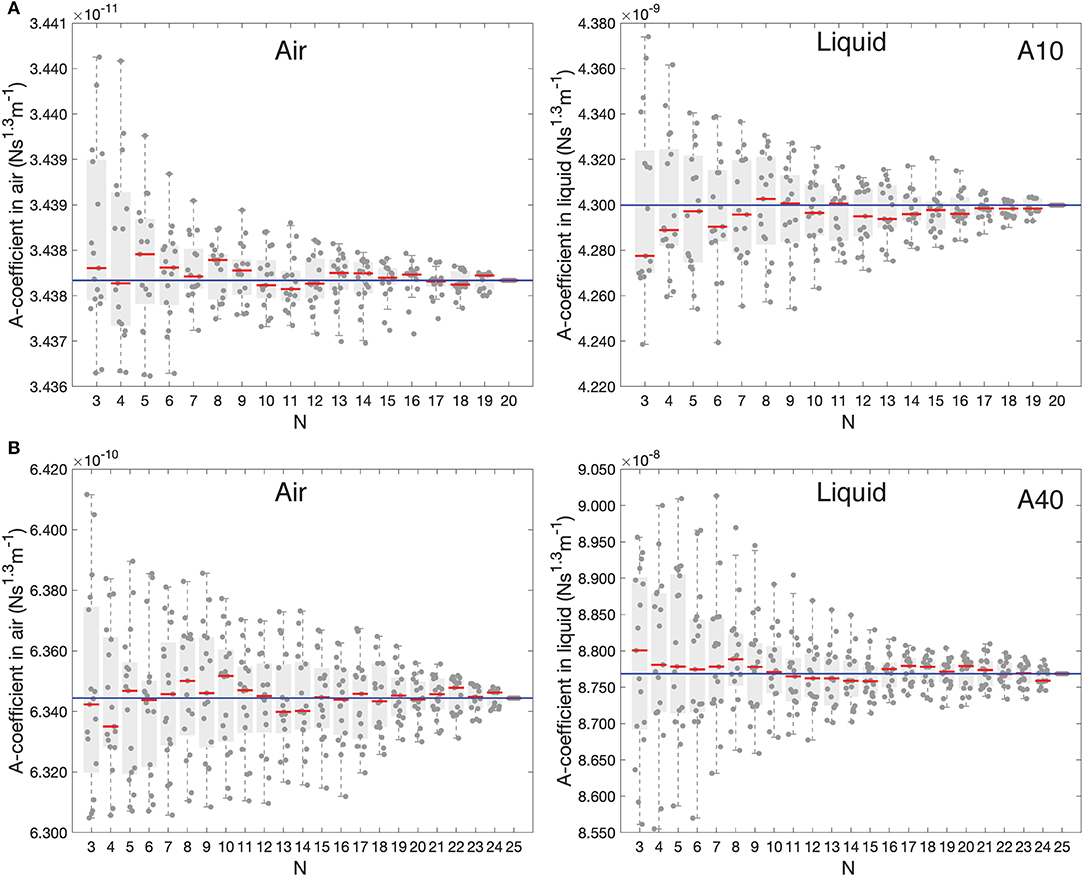
Figure 3. Boxplots showing the 17 repetitions (symbols) of the average A-coefficient calculated using N random reference cantilevers from our pool. The Red line is the median, boxes show the 25th and 75th percentiles, and whiskers represent the most extreme values not considered as outliers. The blue solid line is the average A-coefficient with all N considered. (A) AC10 cantilevers (B) AC40 cantilevers.

Conclusions

In this work, we have assessed two different approaches that allow the one-step calibration of AFM in liquid. These two approaches were based on the Sader and GCI methods to determine both k_liq and InvOLS_liq from the thermal spectrum in liquid using the parameters f _R, Q and B extracted from the first flexural mode using either SHO or Pirzer's model. First, the spring constant was obtained by using Sader and GCI methods, while the InvOLS_liq was determined from the equipartition theorem. Our results showed that using the Pirzer model may induce a bias in the calibration of k_liq via the Sader method as high as 2-fold compared to k_air. This bias was reduced to 3–5% using the SHO model together with the GCI method. Similarly, using Pirzer with the Sader method in liquid introduced a bias up to 20% in the calibration of the InvOLS_liq, which was reduced to ≲1% using SHO with the GCI model. Therefore, the GCI method using the SHO model provided the most accurate results, as compared to the non-contact calibration in air, both in the spring constant (~4%) and InvOLS (~1%). Moreover, GCI was less prone to possible bias in the PSD fitted parameters as it resulted in k_liq closer to k_air, independently of the used PSD model.

Thus, the proposed one-step calibration will involve the following procedure:

• Acquisition of the thermal PSD in liquid;

• Fitting the SHO model to the PSD in liquid to extract f _R, Q, and B;

• Calculation of k in liquid using GCI (Equations 3 and 7);

• Calculation of InvOLS in liquid using Equation 10 (SHO).

Notice the importance of using the SHO model to extract the PSD parameters. The obvious drawback of the GCI approach in liquid is the prerequisite of a collection of reference cantilevers. However, this turns out to be an advantage as, being a global initiative, it will improve the accuracy of the calibration as the number of users increases. Moreover, it will allow, if necessary, future corrections of published data provided the A-coefficient, f _R, and Q parameters are reported. Furthermore, the GCI approach does not require a priori knowledge of geometry and the dimensions of the cantilever, which may be difficult to model in some cases, for example in paddle shape or V-shaped cantilevers. Cantilever manufacturers start to commercialize cantilevers with the spring constant calibrated using vibrometers, which facilitates the establishment of the GCI database. This opens the door to the rapid implementation of the proposed GCI method in liquid on cantilevers of arbitrary shape. Thus, the proposed one-step calibration of AFM in liquid is the foundation for fast, robust, accurate, and standardized quantitative force measurements on biological samples.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors upon reasonable request.

Author Contributions

FS and FR designed the research. FS and NH collected and analyzed the data. All authors wrote the paper.

Funding

This project has received funding from the Agence National de la Recherche (ANR, grant No. BioHSFS ANR-15-CE11-0007) and the European Research Council (ERC, grant agreement No. 772257).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

The authors acknowledge Brian Todd for distributing the Matlab code for the application of the Sader method. FR thanks John E Sader for fruitful discussions. Scanning electron microscopy was performed in the clean room facility PLANETE CT-PACA (CINaM, Marseille, France), and on the PiCSL-FBI core facility (Nicolas BROUILLY, IBDM, AMU, Marseille), member of the France-BioImaging national research infrastructure (ANR-10-INBS-04).

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2020.00301/full#supplementary-material

References

1. Krieg M, Fläschner G, Alsteens D, Gaub BM, Roos WH, Wuite GJL, et al. Atomic force microscopy-based mechanobiology. Nat Rev Phys. (2019) 1:41. doi: 10.1038/s42254-018-0001-7

CrossRef Full Text | Google Scholar

2. Hutter JL, Bechhoefer J. Calibration of atomic-force microscope tips. Rev Sci Instrum. (1993) 64:1868–73.

Google Scholar

3. Butt HJ, Jaschke M. Calculation of thermal noise in atomic force microscopy. Nanotechnology. (1995) 6:1–7.

Google Scholar

4. Pirzer T, Hugel T. Atomic force microscopy spring constant determination in viscous liquids. Rev Sci Instruments. (2009) 80:035110–6. doi: 10.1063/1.3100258

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Sader JE, Yousefi M, Friend JR. Uncertainty in least-squares fits to the thermal noise spectra of nanomechanical resonators with applications to the atomic force microscope. Rev Sci Instruments. (2014) 85:025104. doi: 10.1063/1.4864086

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Nørrelykke SF, Flyvbjerg H. Power spectrum analysis with least-squares fitting: Amplitude bias and its elimination, with application to optical tweezers and atomic force microscope cantilevers. Rev Sci Instruments. (2010) 81:075103. doi: 10.1063/1.3455217

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Gibson CT, Watson GS, Myhra S. Determination of the spring constants of probes for force microscopy/spectroscopy. Nanotechnology. (1996) 7:259–62.

Google Scholar

8. Cleveland JP, Manne S, Bocek D, Hansma PK. A nondestructive method for determining the spring constant of cantilevers for scanning force microscopy. Rev Sci Instrum. (1993) 64:403–5.

Google Scholar

9. Sader JE, Chon JWM, Mulvaney P. Calibration of rectangular atomic force microscope cantilevers. Rev Sci Instruments. (1999) 70:3967–9. doi: 10.1063/1.1150021

CrossRef Full Text | Google Scholar

10. Sader JE. Parallel beam approximation for V-shaped atomic force microscope cantilevers. Rev Sci Instrum. (1995) 66:4583–7.

Google Scholar

11. Sader JE, Sanelli JA, Adamson BD, Monty JP, Wei X, Crawford SA, et al. Spring constant calibration of atomic force microscope cantilevers of arbitrary shape. Rev Sci Instruments. (2012) 83:103705. doi: 10.1063/1.4757398

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Burnham NA, Chen X, Hodges CS, Matei GA, Thoreson EJ, Roberts CJ, et al. Comparison of calibration methods for atomic-force microscopy cantilevers. Nanotechnology. (2003) 14:1–6. doi: 10.1088/0957-4484/14/1/301

CrossRef Full Text | Google Scholar

13. Sader JE. Frequency response of cantilever beams immersed in viscous fluids with applications to the atomic force microscope. J Appl Phys. (1998) 84:64–76.

Google Scholar

14. Sader JE, Borgani R, Gibson CT, Haviland DB, Higgins MJ, Kilpatrick JI, et al. A virtual instrument to standardise the calibration of atomic force microscope cantilevers. Rev Sci Instruments. (2016) 87:093711. doi: 10.1063/1.4962866

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Higgins MJ, Proksch R, Sader JE, Polcik M, Mc Endoo S, Cleveland JP, et al. Noninvasive determination of optical lever sensitivity in atomic force microscopy. Rev Sci Instruments. (2006) 77:013701. doi: 10.1063/1.2162455

CrossRef Full Text | Google Scholar

16. Schillers H, Rianna C, Schäpe J, Luque T, Doschke H, Wälte M, et al. Standardized nanomechanical atomic force microscopy procedure (SNAP) for measuring soft and biological samples. Sci Rep. (2017) 7:5117. doi: 10.1038/s41598-017-05383-0

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Valotteau C, Sumbul F, Rico F. High-speed force spectroscopy: microsecond force measurements using ultrashort cantilevers. Biophys Rev. (2019) 11:689–99. doi: 10.1007/s12551-019-00585-4

PubMed Abstract | CrossRef Full Text | Google Scholar

18. te Riet J, Katan AJ, Rankl C, Stahl SW, van Buul AM, Phang IY, et al. Interlaboratory round robin on cantilever calibration for AFM force spectroscopy. Ultramicroscopy. (2011) 111:1659–69. doi: 10.1016/j.ultramic.2011.09.012

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Kennedy SJ, Cole DG, Clark RL. Note: Curve fit models for atomic force microscopy cantilever calibration in water. Rev Sci Instruments. (2011) 82:116107. doi: 10.1063/1.3661130

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Stark RW, Drobek T, Heckl WM. Thermomechanical noise of a free v-shaped cantilever for atomic-force microscopy. Ultramicroscopy. (2001) 86:207–15. doi: 10.1016/s0304-3991(00)00077-2

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Ohler B. Application note 94: practical advice on the determination of cantilever spring constants. Science. (1994) 264:415–7.

Google Scholar

22. Hutter JL. Comment on tilt of atomic force microscope cantilevers: effect on spring constant and adhesion measurements. Langmuir. (2005) 21:2630–2. doi: 10.1021/la047670t

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Proksch R, Schaffer TE, Cleveland JP, Callahan RC, Viani MB. Finite optical spot size and position corrections in thermal spring constant calibration. Nanotechnology. (2004) 15:1344–50. doi: 10.1088/0957-4484/15/9/039

CrossRef Full Text | Google Scholar

24. Mascaro A, Miyahara Y, Dagdeviren OE, Grütter P. Eliminating the effect of acoustic noise on cantilever spring constant calibration. Appl Phys Lett. (2018) 113:233105. doi: 10.1063/1.5063992

CrossRef Full Text | Google Scholar

25. Benmouna F, Johannsmann D. Hydrodynamic interaction of AFM cantilevers with solid walls: An investigation based on AFM noise analysis. Euro Phys J E. (2002) 9:435–41. doi: 10.1140/epje/i2002-10096-x

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Matei GA, Thoreson EJ, Pratt JR, Newell DB, Burnham NA. Precision and accuracy of thermal calibration of atomic force microscopy cantilevers. Rev Sci Instruments. (2006) 77:083703. doi: 10.1063/1.2336115

CrossRef Full Text | Google Scholar