- 1Department of Physics, University at Albany (SUNY), Albany, NY, United States
- 2Department of Physics, Georgetown University, Washington, DC, United States
Recent experimental advances in ultrafast phenomena have triggered renewed interest in the dynamics of correlated quantum systems away from equilibrium. We review non-equilibrium dynamical mean-field theory studies of both the transient and the steady states of a DC field-driven correlated quantum system. In particular, we focus on the non-equilibrium behavior and how it relates to the fluctuation-dissipation theorem. The fluctuation-dissipation theorem emerges as an indicator for how the system thermalizes and for how it reaches a steady state. When the system thermalizes in an infinite temperature steady state it can pass through a succession of quasi-thermal states that approximately obey the fluctuation-dissipation theorem. We also discuss the Wigner distribution and what its evolution tells us about the non-equilibrium many-body problem.
1. Introduction
Strongly correlated systems include some of the most technologically promising materials of our time. The same quantum-mechanical complexity behind their most intriguing properties also renders them challenging to study. Much of the interest is motivated by recent experimental successes. For example, trapping and manipulating ultracold atomic gases in optical lattices provides a new platform for the controlled examination of strongly correlated systems in and out equilibrium [1, 2]. In electronics, device miniaturization leads to the creation of nanoscale devices in which electrons experience strong electric fields and thus cannot be well-approximated by linear-response theories [3, 4]. Additionally, pump-probe spectroscopy offers a new avenue for the exploration of available electronic states in correlated materials [5]. These advances have revived interest in the fundamental behavior of quantum systems away from equilibrium.
There are many unanswered questions. How does an equilibrium quantum system that is suddenly driven out of equilibrium, subsequently relax to a thermal state [6–9]? What governs the non-equilibrium driving of a system into a metastable state that is not found among known equilibrium phases [10, 11]? Answering these questions requires an accurate theoretical approach. Non-equilibrium dynamical mean-field theory [12] is a powerful tool to address these pressing questions.
In equilibrium, dynamical mean-field theory (DMFT) [13–16] treats spatial correlations in a mean-field fashion, while treating temporal correlations exactly. It is one of the most commonly used and successful methods for studying strongly correlated systems. It has also been extended to non-equilibrium [12, 17, 18].
Field-driven correlated systems display non-trivial dynamics. When a DC electric field is applied, the system responds by creating an electric current that flows. That current also leads to Joule heating, which, if left unchecked, will heat the system to infinite temperature (where the current vanishes and the heating ultimately stops). The heating can also stop prematurely, with the system reaching a metastable (or possibly even thermal) state. Indeed, several scenarios for this relaxation process can occur depending on the specific details of the system [9]. In many of these situations, the fluctuation-dissipation theorem is no longer rigorously valid. However, it still remains an important concept in non-equilibrium, because it can be used to tell us when a system settles into a thermal steady state [19–22]. We review non-equilibrium DMFT manifestations of these properties in a mixture of heavy and light fermionic particles described by the Falicov–Kimball model [23, 24] that starts in equilibrium and then has a DC electric field suddenly turned on.
The review is organized as follows. In section 2, we present a brief description of the non-equilibrium Green's functions and introduce the Falicov–Kimball model as it relates to the Hubbard model. In section 3, we describe the non-equilibrium DMFT solution first for the transient and then for the steady state. In section 4, we present a set of results that include manifestations of the fluctuation-dissipation theorem and provide insights into the rich dynamics of the field-driven strongly correlated quantum system.
2. Non-equilibrium Green's Functions
The many-body formalism for the non-equilibrium problem is similar to that of the equilibrium problem. All essential requirements for perturbation theory still hold away from equilibrium, except for the identification of the state at long times being identical to the state for the earliest times. Instead, it becomes necessary to evolve the system according to the Heisenberg representation for operators: start from the distant past, evolve forward to the time of physical interest and then evolve backward to the distant past (because of the Hermitian conjugate of the evolution operator in the Heisenberg representation) [25, 26]. This gives rise to the Kadanoff–Baym–Keldysh contour illustrated in Figure 1; the contour-ordered Green's functions has time ordering performed with respect to the advance along the contour. It is defined via
where is the contour-ordered Heaviside function, which orders time with respect to the contour. It is equal to 1 if t is ahead of t′ on the contour and is equal to 0 if t is behind t′ on the contour. Hence, the non-equilibrium formalism automatically includes several different Green's functions depending on the location of each time argument on the contour. The lesser (t on lower, t′ on upper), greater (t on upper, t′ on lower), time-ordered (t and t′ on upper), anti-time-ordered (t and t′ on lower) Green's functions are respectively defined by the following when both time arguments of the contour-ordered Green's function are real:
From these Green's functions, we can construct the so-called retarded and advanced Green's functions via
Here and ckσ (t) are respectively the Heisenberg representation of the creation and the destruction operators for an electron of momentum k and spin σ at time t; θ is the ordinary Heaviside function, i. e., θ(t − t′) = 0 if t < t′ and θ(t, t′) = 1 otherwise; is the anticommutator of operators and . The symbol is the expectation value taken of the operator with respect to the initial thermal state:
where is the initial Hamiltonian before any field is turned on. Several additional Green's functions are included in the formalism when at least one time argument is on the imaginary spur of the contour. These include the imaginary-time (or Matsubara) Green's functions with both times on the imaginary time vertical branch and the mixed-time Green's functions where one of the times is on the horizontal branch while the other is on the vertical branch (formulas not explicitly shown here). The non-equilibrium many-body formalism works directly with the contour-ordered Green's functions [12]. All other Green's functions can then be extracted from it.
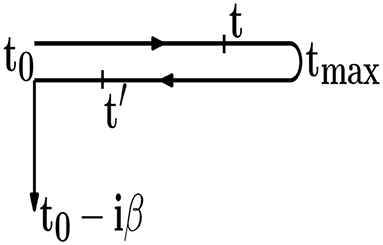
Figure 1. Kadanoff–Baym–Keldysh contour. The arrows indicate the direction of time ordering. In this example, t occurs before t′ on the contour, even though t > t′, when thought of as real numbers.
Note that these Green's functions are not all independent and are related by various identities and symmetries. One choice for two independent ones is the lesser and the retarded Green's functions, G< and GR. These determine most physical quantities. In particular, the retarded Green's function is related to the quantum states while the lesser Green's function is directly related to how those states are occupied by fermions.
We are interested in the dynamics of a strongly correlated system that starts initially in thermal equilibrium and then is driven out of equilibrium by turning on an external DC electric field. We describe how the fluctuation-dissipation theorem manifests itself and how it can be utilized in characterizing relaxation through transient states to the (long-time) steady-state.
As an example, we consider a generalized Hubbard model for strongly correlated systems with spin-dependent hopping:
Here 〈ij〉 represents unique nearest-neighbor pairs for sites i and j; Jijσ is the nearest-neighbor hopping integral; μ is the chemical potential; is the number operator for electrons of spin σ at site i; and U is the on-site repulsion for doubly occupied sites.
When , we obtain the conventional Hubbard model, which is believed to contain the essential elements for high-temperature superconductivity in the cuprates and for this reason has been the subject of intense research activity. Despite its deceptive simplicity, the model remains unsolved except in one dimension [27] and in the limit of infinite dimensions [13]. But, when we have Jij↓ = J and Jij↑ = 0, i.e., if the electrons with spin up are held static while those with spin down are allowed to hop between nearest-neighbor sites, we obtain the Falicov–Kimball model, which can also be viewed as describing a mixture of heavy and light fermions on a lattice. This model has the advantage of displaying a Mott transition while also being more amenable to numerical methods than the Hubbard model. We will study this model at half-filling when there are as many electrons with spin up as spin down (or, equivalently, as many light, ↓, as heavy, ↑, fermions) and, in total, as many electrons as there are lattice sites.
3. Non-equilibrium DMFT
Dynamical mean-field theory was introduced to address strongly correlated systems in equilibrium and has been used successfully to describe key aspects of strongly correlated systems such as the metal-to-Mott insulator transition [13–16]. The method has successfully been adapted to studies of non-equilibrium systems [12, 17, 18]. It maps the lattice model onto an impurity embedded in a self-consistently determined bath as illustrated in Figure 2. The method then relies on an accurate solution of the impurity problem and has been implemented with a multitude of impurity solvers with varied levels of success. These solvers include diagrammatic perturbative approaches [28, 29], Quantum Monte Carlo [30] and exact diagonalization [31, 32]. The Falicov–Kimball model considered in this case has the advantage of being able to be solved exactly, as shown below.

Figure 2. The dynamical mean-field theory maps the lattice problem (here, a square lattice with hoping integral J between nearest-neighboring sites and Coulomb interaction U for doubly occupied sites) onto that of an impurity embedded into a self-consistently determined bath with a hybridization function Λ(t, t′). In equilibrium, the hybridization function only depends on the relative time t − t′.
3.1. Transient Non-equilibrium DMFT
Here we consider a system on a hypercubic lattice in the limit of infinite spatial dimensions (d → ∞) with a constant electric field E applied at a specific time and oriented along a diagonal of the lattice. The dynamical mean-field theory employs a local self-energy such that
In the case of a system initially in equilibrium at an initial temperature T = 1/β, the symbol in Equations (2–7) is synonymous with , where is the initial Hamiltonian and is the corresponding partition function.
The contour-ordered Green's function obeys the Dyson equation given by
where is the non-interacting (U = 0) Green's function [also defined by Equations (2–7), but with a Hamiltonian that has U = 0]. The integrals each range over the entire Kadanoff–Baym–Keldysh contour. Prior to the electric field being turned on, the non-interacting Hamiltonian is
Here, ϵk is the band structure for the lattice electrons. When the electrons move on a hypercubic lattice in infinite dimensions, the band energy is given by:
where a is the lattice spacing (and is set equal to 1); the nearest-neighbor hopping is rescaled via and t* is the unit of energy. In the paramagnetic phase, the spin index may be dropped.
The system is driven out of equilibrium by an applied electric field E(r, t) which can be expressed in terms of a scalar potential ϕ(r, t) and a vector potential A(r, t) via
We choose the Hamiltonian gauge (Φ = 0), so that the electric field is completely determined by the vector potential. The electric field then enters into the Hamiltonian via the Peierls' substitution which modifies the hopping amplitude with a time-dependent phase [33]:
We will be working with a spatially uniform, but time-varying electric field, which is given by a spatially uniform vector potential A(t). In this case, the problem remains translationally invariant, but note that a spatially uniform but time-varying electric field does mildly violate Maxwell's equations. We ignore those magnetic-field effects since they are small.
The non-interacting Green's function obeys the equation:
where is a generalization of the Dirac delta function onto the contour.
When the field is constant and is turned on at time t = 0, the vector potential becomes A(t) = −cEtθ(t) and the Peierls' substitution results in the transformation in the Hamiltonian. The non-interacting Green's function then depends on the band energy ϵk and on the band velocity in the direction of the electric field. Setting ℏ = 1 and c = 1, this leads to the following expression [34]:
which becomes
The dressed lattice Green's function is constructed from the non-interacting Green's function and the self-energy following Equation (10). The local Green's function is found by summing the momentum-dependent dressed Green's function over all momentum, or, equivalently integrating over the joint density of states, . In the non-equilibrium DMFT formalism, the hybridization of the impurity to the dynamical mean field is given by
where we suppressed the spin indices.
To complete the self-consistency loop, we calculate the local Green's function from the dynamical mean field and use Dyson's equation (on the contour) to extract the self-energy. This is usually the bottleneck in the DMFT formalism. But in the case of the Falicov–Kimball model, this step can be determined analytically. We start from the spinless Falicov–Kimball model in the absence of a field
where wi = 0, 1 is the occupation number operator of a localized fermions at site i. The corresponding impurity problem is solved by
where is the initial (equilibrium) filling of the localized fermions. Note that the Green's function is represented by sum of the matrix inverses of two continuous matrix operators.
3.2. Non-equilibrium Steady State DMFT
The main shortcoming of the above non-equilibrium DMFT solution is that even in cases such as that of the Falicov-Model, where we can write an exact expression for the impurity Green's function, the non-equilibrium DMFT implementation remains computationally expensive both in terms of memory and time (the compute-intensive step is determining the local Green's function from the self-energy). It is for this reason that most studies are limited to examining the short-time transient only. One may alternatively be interested in studying the system after it has undergone its relaxation from an initial state and settled into its steady state. In this case, a steady-state non-equilibrium DMFT formalism can be formulated directly to study the steady-state regime. In this situation, we can use a non-interacting initial state with its non-interacting contour-ordered Green's function given by:
Switching to Wigner coordinates, as illustrated in Figure 3, with the relative time and average time , we obtain:
in the long-time limit (t ≫ ton and , with ton the time the field is initially turned on). We denote the Green's function in Wigner coordinates by . From Equation (22), it is easy to show that
or, equivalently
when the system is driven by a DC field.
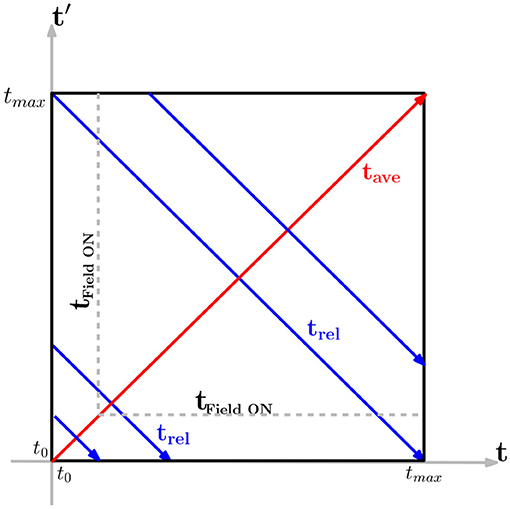
Figure 3. Schematic representation of the transformation of time coordinates (t, t′) on the contour into the Wigner coordinates of average and relative time . The dashed gray line represents the time at which the system is driven away from equilibrium by switching on the electric field (above and to the right of the dashed lines is where the field is turned on). The average time axis is illustrated by the red line across the diagonal and each average time has an associated set of relative times identified by points running along the blue lines.
Using the steady state assumption (in the long-time limit) that Σ(t, t′) = Σ(t − t′), one obtains that the dressed Green's functions also satisfy the expressions in Equations (24) and (25). For the choice of τ = (t + t′)/2, we obtain . The local Green's function is , which, in terms of the relative time, becomes
Note how gk depends on k only through ϵk and leading to
with the joint density of states [13] given by
This means that in frequency space, the local Green's function is obtained from
One can similarly show that in the long-time limit, we have or equivalently, i.e., gk is periodic with respect to tave with period 2π/E; this is the Bloch-Zener periodicity and νn = nE (with n an integer) are the Bloch frequencies. There is a subtle issue going on here, because we are working in this long-time limit. The formulas stated here hold when both times are much larger than ton. Nevertheless, the Green's function has a periodic average time dependence in this long-time limit, and this is what we are describing here. As a result, Fourier transforming gk(trel, tave) in this long-time limit, gives
where ω is a continuous variable while νl is quantized and the integral over tave can be restricted to be taken over just one Bloch period. In frequency space, the Dyson equation can then be written in the form
The periodicity in this long-time limit, maps the system to behave exactly as a many-body Floquet system acts. We now describe how to solve the steady-state problem within such a Floquet formalism, using discrete matrices within the Dyson equation for the Green's function defined within a frequency range determined by the Floquet period. We start by choosing a finite frequency range over which the Green's function has non-zero spectral weight. Next, we choose an integer L ≫ 1 such that Σ(ω) ≠ 0 only for ω ∈ [−νL, νL] and let ϕ be a real variable allowed to vary continuously between −E/2 and E/2. Equation (31) for (ω, νl) = (ϕ + ν−L + p, νp) can be rewritten as follows:
and one can immediately see that the frequency ϕ is coupled only to frequencies shifted by integer multiples of the Bloch frequency. Here we have defined
with i, j, p being integer indices. Equation (32) provides a convenient way to solve the Dyson equation. For this purpose, it is necessary to obtain the Fourier transform of the non-interacting Green's function in Equation (22) to frequency space. The result is
with
and
where Ja(x) is the Bessel function of the first kind and denotes the principal value. The different variables are defined by , , r′ = r/E, and .
Note that the integer indices i, j, and p in Equation (32), are chosen such that i, j, p = 0, 1, 2, ⋯L, for the quantized frequencies νi, νj, and νp, which combine with the real variable ϕ ∈ [−E/2, E/2] to produce a dependence on a single continuous frequency that varies within the range of non-zero spectral weight [−νL, νL]. This single variable is relabeled as ω.
To complete the self-consistency loop for this non-equilibrium steady-state DMFT algorithm, the only missing ingredient is the impurity solver. In the case of the Falicov–Kimball model [which is initially described by the Hamiltonian in Equation (19)], the dressed Green's function is related to the non-interacting Green's function via
Combining this with the Dyson equation yields
The self-consistency loop is now complete and proceeds as follows:
1. For a given Σ(ω), solve the Dyson equation for ;
2. Next, solve Equation (29) for the local Green's function;
3. Then, solve Equation (41) for Σ(ω);
4. Repeat steps 1 − 3 until convergence is achieved.
This formalism is equivalent to using Floquet theory to solve the steady-state problem for a field driven system [20, 21, 35, 36]. It allows the characterization of the steady state for a given electric field and interaction strengths. In particular, one can obtain the local density of states (DOS) from ρ(ω) = −Im[g(ω)]/π.
4. Relaxation Dynamics and Fluctuation Dissipation Theorem
4.1. Steady-State Density of States
In order to be able to describe the effects of the electric field, it is instructive to start by looking at the equilibrium local density of states (DOS) in Figure 4 obtained by the DMFT algorithm in equilibrium [16]. As the interaction strength is increased, we see a transition from a broadened Gaussian-like DOS in the weak-interaction regime to a gapped spectrum with two peaks in the strong-interaction regime. The spectral gap at ω = 0 is characteristic of the Mott-insulating regime, with the critical U occurring at . Note that the DOS of the Falicov–Kimball model, in the normal state, does not depend on temperature.

Figure 4. Local density of states of the Falicov–Kimball model solution in equilibrium for U = 0.5 (A), U = 1.50 (B), U = 2.0 (C), U = 3.0 (D). The system develops a Mott-insulating gap as the interaction is increased with the transition occurring when .
The non-equilibrium steady state DOS shows much richer behavior than in equilibrium. Figures 5, 6 show the steady-state DOS for electric fields E = 0.5 and E = 1.0, respectively, for the same interaction strengths as the equilibrium DOS in Figure 4. In the weak-interaction regime, the DOS displays the Wannier–Stark ladder [37–39] with peaks centered around ω = nE with n = 0, ±1, ±2, ... and the amplitude is sharply suppressed away from the central peak. The peaks are broadened by a width governed by the interaction strength and the central peak has a dip separated by two side peaks at ±U/2. As the interaction is further increased, the initial peaks eventually merge, while preserving the central dip that arises from strong correlations. With stronger interactions this dip does not however become the full width of the gap due to the presence of “in gap” states created by the electric field.
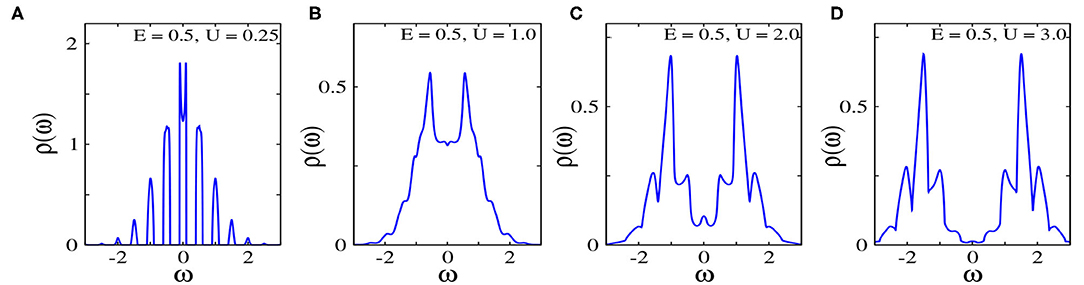
Figure 5. Local density of states of the field-driven system in its steady state for E = 0.5 and U = 0.25 (A), U = 1.0 (B), U = 2.0 (C), U = 3.0 (D).
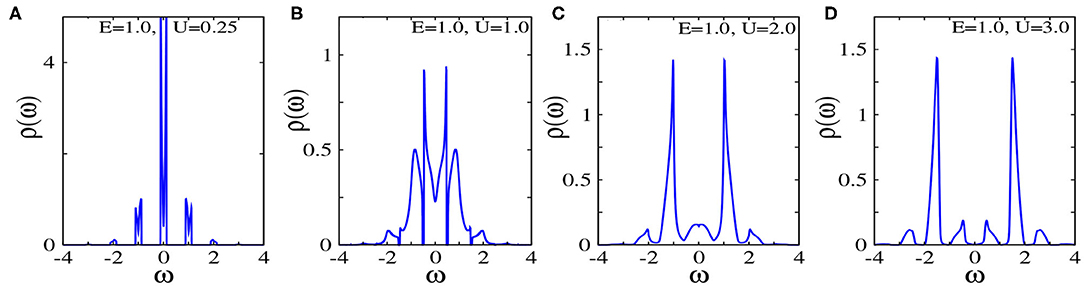
Figure 6. Local density of states of the field-driven system in its steady state for E = 1.0 and U = 0.25 (A), U = 1.0 (B), U = 2.0 (C), U = 3.0 (D).
In both the equilibrium and the steady-state regime, the system obeys the fluctuation-dissipation theorem and the lesser Green's function satisfy the relation
Where fT(ω) is the Fermi distribution function at temperature T. It is interesting to now ask how do the dynamics transiently take us from equilibrium to the steady state?
4.2. Monotonic Thermalization
In earlier work, we examined the transient dynamics of correlated quantum systems when they are driven away from equilibrium by a DC electric field [9]. Key findings included the fact that the DOS is only constrained by causality and takes its steady-state value as soon as the field is turned on (seeing this in the frequency domain takes a little longer, because one needs the retarded Green's function behavior to hold for a long-enough relative time span that a Fourier transformation can be performed). Since the system is isolated and the electric field remains constant after it is switched on, Joule heating should lead to an infinite-temperature state, if the system thermalizes. Without assuming the system to be thermal, an effective temperature at a time t can be obtained by comparing the energy of the system to that of the corresponding equilibrium system (in other words, using a thermometer based on the energy as a scale, without determining if the system has actually thermalized). The evolution of the effective temperature as a function of time is presented in Figure 7. We found that for some parameter regimes, this infinite-heating scenario did take place. Sometimes the infinite-temperature limit was approached monotonically, sometimes it was approached in an oscillatory fashion, with the effective temperature alternating between positive and negative temperatures en route to T = ∞.
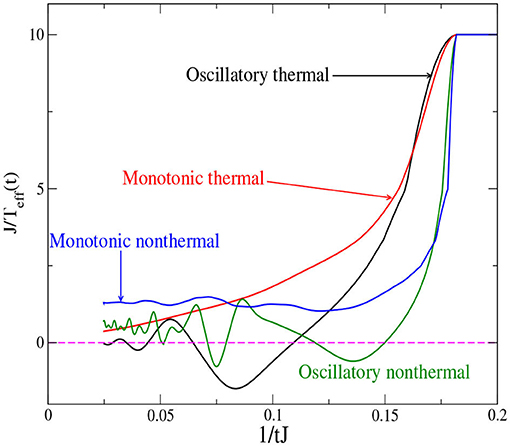
Figure 7. Effective temperature Teff as a function of time for the field-driven system. The dashed magenta line corresponds to infinite temperature and the data is plotted so that the vertical axis shows the inverse of the effective temperature while the horizontal axis displays the inverse of time. Along with the temperature, the dynamics of several physical quantities are used to identify different relaxation scenarios by examining different parameters (different field strength and interaction values). We observe monotonic thermal (red), oscillatory thermal (black), monotonic non-thermal (blue), and oscillatory non-thermal (green) relaxation. Non-thermal relaxation is characterized by not going to the infinite-temperature limit at long times. Reprinted figure with permission from H. F. Fotso, K. Mikelsons and J. K. Freericks, Scientific Reports 4, 4699 (2014).
We focus on the case of monotonic relaxation toward the infinite-temperature thermal state as it exhibits interesting manifestations of the fluctuation-dissipation theorem. Besides the effective temperature from an energy thermometer, several other quantities are used in characterizing the relaxation. These include the real part of the frequency-dependent lesser Green's function (Figure 8, left panel), and the current, the kinetic, potential and total energy (Figure 8, right panel). If the system is in a thermal state, then the lesser Green's function and the retarded Green's function satisfy the fluctuation-dissipation theorem. Namely, in frequency space, they obey Equation (42).
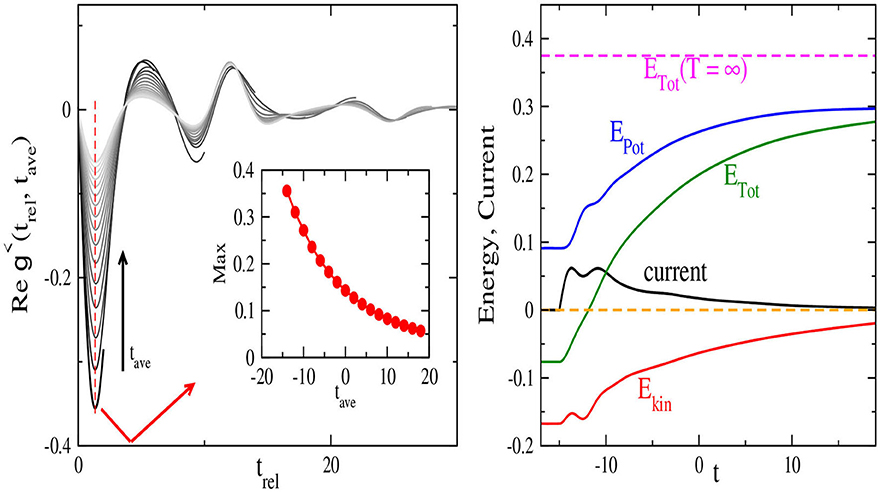
Figure 8. Physical indication of the monotonic evolution of the system toward an infinite temperature thermal state for E = 0.5 and U = 1.5 evolving from a system initially in equilibrium at temperature T = 0.1. The left panel shows the real part of the lesser Green's function as a function of trel for successive average times (the field is turned on at ton = −15); a grayscale is used with lighter shades indicating later average times. The inset shows the maximum (or absolute value of the minimum) of as a function of average time. The panel on the right shows the total energy (ETot, green), the potential energy (EPot, blue), kinetic energy (EKin red) and the current (black) as functions of time. The dashed line indicates the total energy at infinite temperature for the same interaction strength. Reprinted figure with permission from H. F. Fotso, K. Mikelsons and J. K. Freericks, Scientific Reports 4, 4699 (2014).
In this case, the lesser Green's function has a vanishing real part both in time and in frequency space. Figure 8, left panel, shows that the real part of the lesser Green's function relaxes monotonically toward zero (its infinite-temperature value). Additionally, it is easy to evaluate the total energy at infinite temperature. This is given by the dashed magenta line in Figure 8, right panel. To evaluate the transient total energy of the system, one starts from the known equilibrium energy at the initial temperature T = 0.1. Next, we integrate the inner product 〈j(t)〉·E up to time t to obtain the energy added to the system by Joule heating [here j (t) is the current at time t]. Adding this Joule heating energy to the initial energy produces the total energy of the system at time t. In Figure 8, one can see that in this case the total energy in the transient calculation approaches this limit monotonically, as the current also decays monotonically toward zero.
This decay of the current toward zero is to be expected at infinite temperature where particles are equally likely to move in opposite directions. The potential and kinetic energy also monotonically approach their infinite-temperature values. In this monotonic thermalization scenario, we find that even before reaching the infinite-temperature thermal state, the system appears to follow an evolution through successive quasi-thermal states approximately satisfying the fluctuation-dissipation theorem. This is illustrated in Figure 9 for the lesser Green's function as a function of frequency and average time. After the field is turned on, g< switches from its equilibrium value (green line) to different transient values. Their evolution is pictured in grayscale with lighter shades indicating later average times. At infinite average time, g< is expected to adopt the infinite-temperature fluctuation-dissipation result (blue dashed line). It is seen in the graph that at the last available simulation times, the transient already follows the fluctuation-dissipation theorem: the red line is the fluctuation-dissipation theorem at the effective temperature (using energy as the thermometer scale) corresponding to this average time and shows good agreement with the transient.
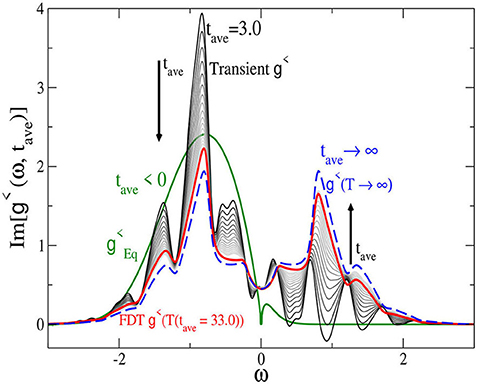
Figure 9. Imaginary part of the lesser Green's function as a function of frequency for initial temperature T = 0.1, U = 1.5 and E = 0.5 corresponding to a monotonic, thermalized case. The green line indicates the equilibrium curve before the electric field is turned on. The evolution of the non-equilibrium lesser Green's function, after the early transient, is shown by the grayscale plots with lighter shades indicating later average times. As the lesser Green's function evolves toward its infinite-temperature steady-state value (blue dashed curve), it is shown to be well-matched by the fluctuation-dissipation-theorem result, after an early transient. This is illustrated with the fluctuation-dissipation theorem curve at the latest average time (red curve) for a system at the corresponding effective temperature (as determined by the energy thermometer). While not perfectly matching the fluctuation-dissipation theorem result, it is quite close. Reprinted figure with permission from H. F. Fotso, K. Mikelsons and J. K. Freericks, Scientific Reports 4, 4699 (2014).
Another window into the relaxation of the field driven system is through the distribution function [40]. For the non-interacting system in equilibrium, this is simply the Fermi-Dirac distribution function. This equilibrium distribution function is modified by many-body effects for finite U values although the lineshape is essentially preserved as shown in Figure 10. We envision this situation as corresponding to fermionic atoms of two different masses trapped in a mixture on an optical lattice [24].
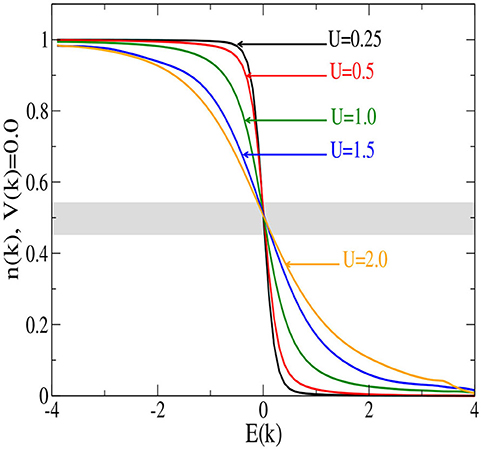
Figure 10. Plot of nk as a function of E(k) for V(k) = 0.0 and for different values of U; the shaded area represents the range [0.45, 0.55] over which nk is plotted in Figures 11, 12. The deviation from the Fermi-Dirac distribution in equilibrium for T = 0.1 comes from the many-body effects of the interactions between the two types of atoms. Reprinted figure with permission from H. F. Fotso, J. C. Vicente and J. K. Freericks, Phys. Rev. A 90, 053630 (2014). Copyright 2020 by the American Physical Society.
For the interacting system away from equilibrium, the distribution function is given by the gauge-invariant Wigner distribution [41]. Here, nk(t) represents the occupation of states in momentum space. The dependence on k is recast into a dependence on the band energy and the band velocity. Prior to the electric field being switched on, the system is in equilibrium at a temperature T = 0.1 and the Wigner distribution in momentum space is shown in Figure 11 for U = 0.25 and is similar for other interaction strengths.
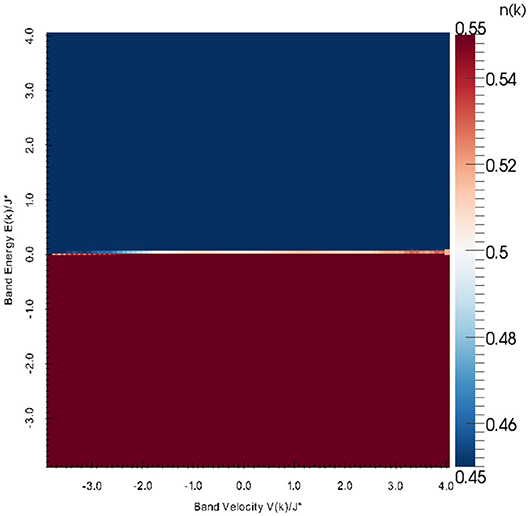
Figure 11. False-color image of the initial equilibrium Wigner distribution function at temperature T = 0.1. The graph shows nk as a function of E(k) ≡ ϵk and for U = 0.25. When the distribution function is larger than 0.55, it is plotted with the color at 0.55 and similarly when it is smaller than 0.45. Reprinted figure with permission from H. F. Fotso, J. C. Vicente and J. K. Freericks, Phys. Rev. A 90, 053630 (2014). Copyright 2020 by the American Physical Society.
Once the field is turned on, it is expected that the onset of the electric current will lead to Joule heating that will increase the temperature until the system has reached an infinite-temperature state where all points in momentum space, or equivalently in [band energy:E(k) ≡ ϵk; band velocity:]-space, are equally likely to be occupied. In this state, the current vanishes and the Wigner distribution is now homogeneous for all k. This is translated into the false color plot being entirely white for the plotted region. It was previously reported that the evolution between the initial configuration of Figure 11 to this uniform configuration goes through the development of different patterns that depend on the field and interaction strength. For instance, for a strong electric field and weak interaction (E = 2.0, U = 0.25), we observe in the false-color plots of the Wigner distribution as a function of time, the formation of ring-shaped disturbances on a timescale of 2π/U (Figures 12a,c,d). These rings spiral around the center of the graph on a timescale of 2π/E (Figure 12b) and we see the formation of additional rings after every 2π/U time step (Figures 12c,d). 2π/E is the period of Bloch oscillations while 2π/U is the timescale for the collapse and revival of Bloch oscillations [1, 42–45]. As the interaction is increased (E = 2.0, U = 1.0), these two timescales merge and we no longer observe well-separated individual rings but rather the growth of a single spiral that gradually scrambles the occupation of the states. We also observe at larger interaction strengths (E = 2.0, U = 3.0) that long-lived features with both a stable region of high occupation and a region of low occupation rotate around the origin at the Bloch period.
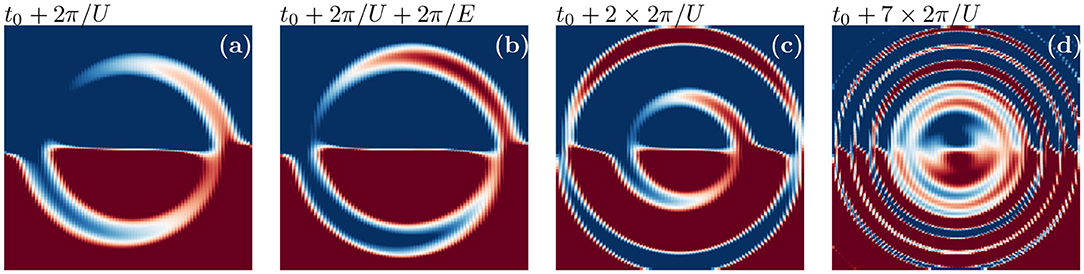
Figure 12. False color snapshots of the evolution of the gauge-invariant Wigner distribution in momentum space at different times for E = 2.0, and U = 0.25 [40]. Each panel shows nk(t) at an instant in time after the field is switched on (at t0). New rings are formed on a timescale of 2π/U (a,c,d) and spiral around the origin on a 2π/E timescale (b). When the distribution function is larger than 0.55, it is plotted with the color at 0.55 and similarly when it is smaller than 0.45. This is done to zoom in on the interesting patterns, which are a few percent effect. Reprinted figure with permission from H. F. Fotso, J. C. Vicente and J. K. Freericks, Phys. Rev. A 90, 053630 (2014). Copyright 2020 by the American Physical Society.
5. Discussion
In general, the fluctuation-dissipation theorem is not satisfied once a system is driven away from equilibrium. This review describes non-equilibrium DMFT studies for both the transient and the steady-state of the Falicov–Kimball model, describing a Fermi-Fermi mixture of heavy-light particles, when it is driven away from equilibrium by a constant electric field. We showed the complex range of relaxation scenarios exhibited by this non-equilibrium system. In particular, the density of states is fundamentally altered by the electric fields with the formation of Wannier-Stark ladders and a dielectric breakdown that arises with the presence of mid-gap states that are absent in equilibrium. This density of states however switches to its steady-state value rapidly after the field is turned on. For an isolated system, the relaxation to a steady state satisfying the fluctuation-dissipation theorem can then occur in several identified scenarios. We have particularly examined the monotonic thermalization scenario where the system monotonically goes to an infinite-temperature thermal state (satisfying the fluctuation-dissipation theorem) and evolves through consecutive quasi-thermal states (approximately satisfying the fluctuation-dissipation theorem) en-route. Ongoing work will take advantage of this property to develop an extrapolation scheme that bridges the gap between the transient and the steady state at minimal computational cost. We have also described how the key timescales that appear in the current in the form of Bloch oscillations and their collapse and revival, or beats, are manifested in the Wigner distribution function and its evolution toward infinite temperature where all states are equally occupied [nk = 0.5]. These results illustrate the rich physics of field-driven correlated quantum systems and the role the fluctuation-dissipation theorem plays in understanding this behavior. The non-equilibrium DMFT technique and the relaxation analysis discussed in this review for field-driven correlated systems may also be applicable to other non-equilibrium problems including quantum annealing [46] and quantum quenches [47, 48], as well as extensions of lattice models that include phonons [49] and inhomogeneities [50, 51].
Author Contributions
HF generated the data for the equilibrium and steady state calculations. Both authors contributed equally to the writing of the review.
Funding
This work was supported by the Department of Energy, Office of Basic Energy Sciences, Division of Materials Sciences and Engineering under Contract No. DE-FG02-08ER46542 (Georgetown). JF was also supported by the McDevitt bequest at Georgetown.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
1. Greiner M, Mandel O, Hänsch TW, Bloch I. Collapse and revival of the matter wave field of a Bose-Einstein condensate. Nature. (2002) 419:51–4. doi: 10.1038/nature00968
2. Bloch I, Dalibard J, Zwerger W. Many-body physics with ultracold gases. Rev Mod Phys. (2008) 80:885–964. doi: 10.1103/RevModPhys.80.885
3. Meir Y, Wingreen NS. Landauer formula for the current through an interacting electron region. Phys Rev Lett. (1992) 68:2512–5. doi: 10.1103/PhysRevLett.68.2512
4. Caroli C, Combescot R, Nozieres P, Saint-James D. Direct calculation of the tunneling current. J Phys C Sol State Phys. (1971) 4:916. doi: 10.1088/0022-3719/4/8/018
5. Perfetti L, Loukakos PA, Lisowski M, Bovensiepen U, Berger H, Biermann S, et al. Time evolution of the electronic structure of 1T − TaS2 through the insulator-metal transition. Phys Rev Lett. (2006) 97:067402. doi: 10.1103/PhysRevLett.97.067402
6. Deutsch JM. Quantum statistical mechanics in a closed system. Phys Rev A. (1991) 43:2046–9. doi: 10.1103/PhysRevA.43.2046
7. Rigol M, Dunjko V, Olshanii M. Thermalization and its mechanism for generic isolated quantum systems. Nature. (2008) 452:854–8. doi: 10.1038/nature06838
8. Srednicki M. Chaos and quantum thermalization. Phys Rev E. (1994) 50:888–901. doi: 10.1103/PhysRevE.50.888
9. Fotso HF, Mikelsons K, Freericks JK. Thermalization of field driven quantum systems. Sci Rep. (2014) 4:4699. doi: 10.1038/srep04699
10. Dean M, Cao Y, Liu X, Wall S, Zhu D, Mankowsky R, et al. Ultrafast energy- and momentum-resolved dynamics of magnetic correlations in the photo-doped Mott insulator Sr2IrO4. Nat Mater. (2016) 15:601–5. doi: 10.1038/nmat4641
11. Ogasawara T, Ashida M, Motoyama N, Eisaki H, Uchida S, Tokura Y, et al. Ultrafast optical nonlinearity in the quasi-one-dimensional Mott insulator Sr2CuO3. Phys Rev Lett. (2000) 85:2204–7. doi: 10.1103/PhysRevLett.85.2204
12. Freericks JK, Turkowski VM, Zlatić V. Nonequilibrium dynamical mean-field theory. Phys Rev Lett. (2006) 97:266408. doi: 10.1103/PhysRevLett.97.266408
13. Metzner W, Vollhardt D. Correlated lattice fermions in d = ∞ dimensions. Phys Rev Lett. (1989) 62:324–7. doi: 10.1103/PhysRevLett.62.324
14. Kuramoto Y. Self-consistent perturbation theory for valence-fluctuating lattice systems. In: Kasuya T, Saso T, editors. Theory of Heavy Fermions and Valence Fluctuations. Berlin; Heidelberg: Springer (1985) p. 152–62. doi: 10.1007/978-3-642-82618-4_11
15. Müller-Hartmann E. Correlated fermions on a lattice in high dimensions. Z Phys B. (1989) 74:507. doi: 10.1007/BF01311397
16. Freericks JK, Zlatić V. Exact dynamical mean-field theory of the Falicov-Kimball model. Rev Mod Phys. (2003) 75:1333–82. doi: 10.1103/RevModPhys.75.1333
17. Freericks JK. Quenching Bloch oscillations in a strongly correlated material: nonequilibrium dynamical mean-field theory. Phys Rev B. (2008) 77:075109. doi: 10.1103/PhysRevB.77.075109
18. Aoki H, Tsuji N, Eckstein M, Kollar M, Oka T, Werner P. Nonequilibrium dynamical mean-field theory and its applications. Rev Mod Phys. (2014) 86:779–837. doi: 10.1103/RevModPhys.86.779
19. Freericks JK, Joura AV. Nonequilibrium density of states and distribution functions for strongly correlated materials across the Mott transition. In: Bonca J, Kruchinin S, editors. Electron Transport in Nanosystems. Berlin: Springer (2008) p. 219–36. doi: 10.1007/978-1-4020-9146-9_17
20. Joura V, Freericks JK, Pruschke T. Steady-state nonequilibrium density of states of driven strongly correlated lattice models in infinite dimensions. Phys Rev Lett. (2008) 101:196401. doi: 10.1103/PhysRevLett.101.196401
21. Tsuji N, Oka T, Aoki H. Correlated electron systems periodically driven out of equilibrium: Floquet + DMFT formalism. Phys Rev B. (2008) 78:235124. doi: 10.1103/PhysRevB.78.235124
22. Aron C, Kotliar G, Weber C. Dimensional crossover driven by an electric field. Phys Rev Lett. (2012) 108:086401. doi: 10.1103/PhysRevLett.108.086401
23. Falicov LM, Kimball JC. Simple model for semiconductor-metal transitions: SmB6 and transition-metal oxides. Phys Rev Lett. (1969) 22:997–9. doi: 10.1103/PhysRevLett.22.997
24. Ates C, Ziegler K. Quantum phases in mixtures of Fermionic atoms. Phys Rev A. (2005) 71:063610. doi: 10.1103/PhysRevA.71.063610
27. Lieb EH, Wu FY. Absence of Mott transition in an exact solution of the short-range, one-band model in one dimension. Phys Rev Lett. (1968) 20:1445–8. doi: 10.1103/PhysRevLett.20.1445
28. Eckstein M, Werner P. Nonequilibrium dynamical mean-field calculations based on the noncrossing approximation and its generalizations. Phys Rev B. (2010) 82:115115. doi: 10.1103/PhysRevB.82.115115
29. Schmidt P, Monien H. Nonequilibrium dynamical mean-field theory of a strongly correlated system. arXiv:cond-mat/0202046 (2002).
30. Eckstein M, Kollar M, Werner P. Thermalization after an interaction quench in the Hubbard model. Phys Rev Lett. (2009) 103:056403. doi: 10.1103/PhysRevLett.103.056403
31. Balzer M, Gdaniec N, Potthoff M. Krylov-space approach to the equilibrium and nonequilibrium single-particle Green's function. J Phys Condens Matter. (2012) 24:3. doi: 10.1088/0953-8984/24/3/035603
32. Arrigoni E, Knap M, von der Linden W. Nonequilibrium dynamical mean-field theory: an auxiliary quantum master equation approach. Phys Rev Lett. (2013) 110:086403. doi: 10.1103/PhysRevLett.110.086403
34. Turkowski VM, Freericks JK. Nonlinear response of Bloch electrons in infinite dimensions. Phys Rev B. (2005) 71:085104. doi: 10.1103/PhysRevB.71.085104
35. Shirley JH. Solution of the Schrödinger equation with a Hamiltonian periodic in time. Phys Rev. (1965) 138:B979–87. doi: 10.1103/PhysRev.138.B979
36. Sambe H. Steady states and quasienergies of a quantum-mechanical system in an oscillating field. Phys Rev A. (1973) 7:2203–13. doi: 10.1103/PhysRevA.7.2203
37. Wannier GH. Possibility of a Zener effect. Phys Rev. (1956) 101:1835. doi: 10.1103/PhysRev.100.1227
38. Wannier GH. Wave functions and effective Hamiltonian for Bloch electrons in an electric field. Phys Rev. (1960) 117:432. doi: 10.1103/PhysRev.117.432
39. Wannier GH. Dynamics of band electrons in electric and magnetic fields. Rev Mod Phys. (1962) 34:645–55. doi: 10.1103/RevModPhys.34.645
40. Fotso HF, Vicente JC, Freericks JK. Frustrated phase separation in the momentum distribution of field-driven light-heavy Fermi-Fermi mixtures of ultracold atoms. Phys Rev A. (2014) 90:053630. doi: 10.1103/PhysRevA.90.053630
41. Bertoncini R, Jauho AP. Gauge-invariant formulation of the intracollisional field effect including collisional broadening. Phys Rev B. (1991) 44:3655–64. doi: 10.1103/PhysRevB.44.3655
42. Mierzejewski M, Bonča J, Prelovšek P. Integrable Mott insulators driven by a finite electric field. Phys Rev Lett. (2011) 107:126601. doi: 10.1103/PhysRevLett.107.126601
43. Buchleitner A, Kolovsky AR. Interaction-induced decoherence of atomic Bloch oscillations. Phys Rev Lett. (2003) 91:253002. doi: 10.1103/PhysRevLett.91.253002
44. Kolovsky AR. New Bloch period for interacting cold atoms in 1D optical lattices. Phys Rev Lett. (2003) 90:213002. doi: 10.1103/PhysRevLett.90.213002
45. Meinert F, Mark MJ, Kirilov E, Lauber K, Weinmann P, Gröbner M, et al. Interaction-induced quantum phase revivals and evidence for the transition to the quantum chaotic regime in 1D atomic Bloch oscillations. Phys Rev Lett. (2014) 112:193003. doi: 10.1103/PhysRevLett.112.193003
46. Das A, Chakrabarti BK. Colloquium: quantum annealing and analog quantum computation. Rev Mod Phys. (2008) 80:1061–81. doi: 10.1103/RevModPhys.80.1061
47. Eckstein M, Kollar M. Nonthermal steady states after an interaction quench in the Falicov-Kimball model. Phys Rev Lett. (2008) 100:120404. doi: 10.1103/PhysRevLett.100.120404
48. Eckstein M, Kollar M, Werner P. Interaction quench in the Hubbard model: relaxation of the spectral function and the optical conductivity. Phys Rev B. (2010) 81:115131. doi: 10.1103/PhysRevB.81.115131
49. Sayyad S, Žitko R, Hugo Strand UR, Werner P, Golež D. Comparative study of nonequilibrium insulator-to-metal transitions in electron-phonon systems. Phys Rev B. (2019) 99:045118. doi: 10.1103/PhysRevB.99.045118
50. Freericks JK. Dynamical mean-field theory for strongly correlated inhomogeneous multilayered nanostructures. Phys Rev B. (2004) 70:195342. doi: 10.1103/PhysRevB.70.195342
Keywords: non-equilibrium, dynamics, correlated systems, field-driven, Keldysh, thermalization
Citation: Fotso HF and Freericks JK (2020) Characterizing the Non-equilibrium Dynamics of Field-Driven Correlated Quantum Systems. Front. Phys. 8:324. doi: 10.3389/fphy.2020.00324
Received: 22 May 2020; Accepted: 14 July 2020;
Published: 26 August 2020.
Edited by:
Horacio Sergio Wio, Institute of Interdisciplinary Physics and Complex Systems (IFISC), SpainReviewed by:
Bikas K. Chakrabarti, Saha Institute of Nuclear Physics (SINP), IndiaIgnazio Licata, Institute for Scientific Methodology (ISEM), Italy
Copyright © 2020 Fotso and Freericks. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Herbert F. Fotso, aGZvdHNvQGFsYmFueS5lZHU=; James K. Freericks, amFtZXMuZnJlZXJpY2tzQGdlb3JnZXRvd24uZWR1
 Herbert F. Fotso
Herbert F. Fotso James K. Freericks
James K. Freericks